Low-Loss Coupling of Quantum Cascade Lasers into Hollow-Core Waveguides with Single-Mode Output in the 3.7–7.6 μm Spectral Range
Abstract
:1. Introduction
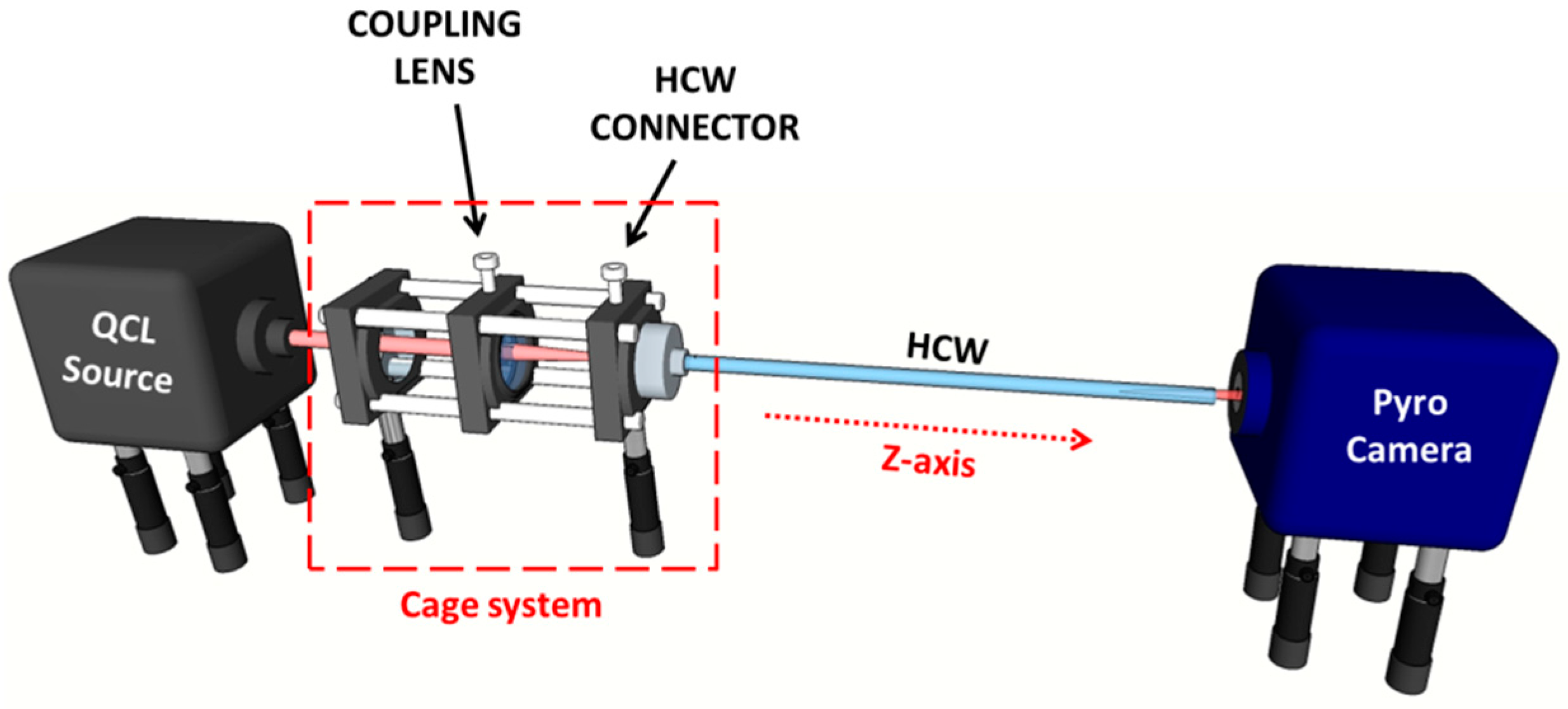
2. Experimental Setup
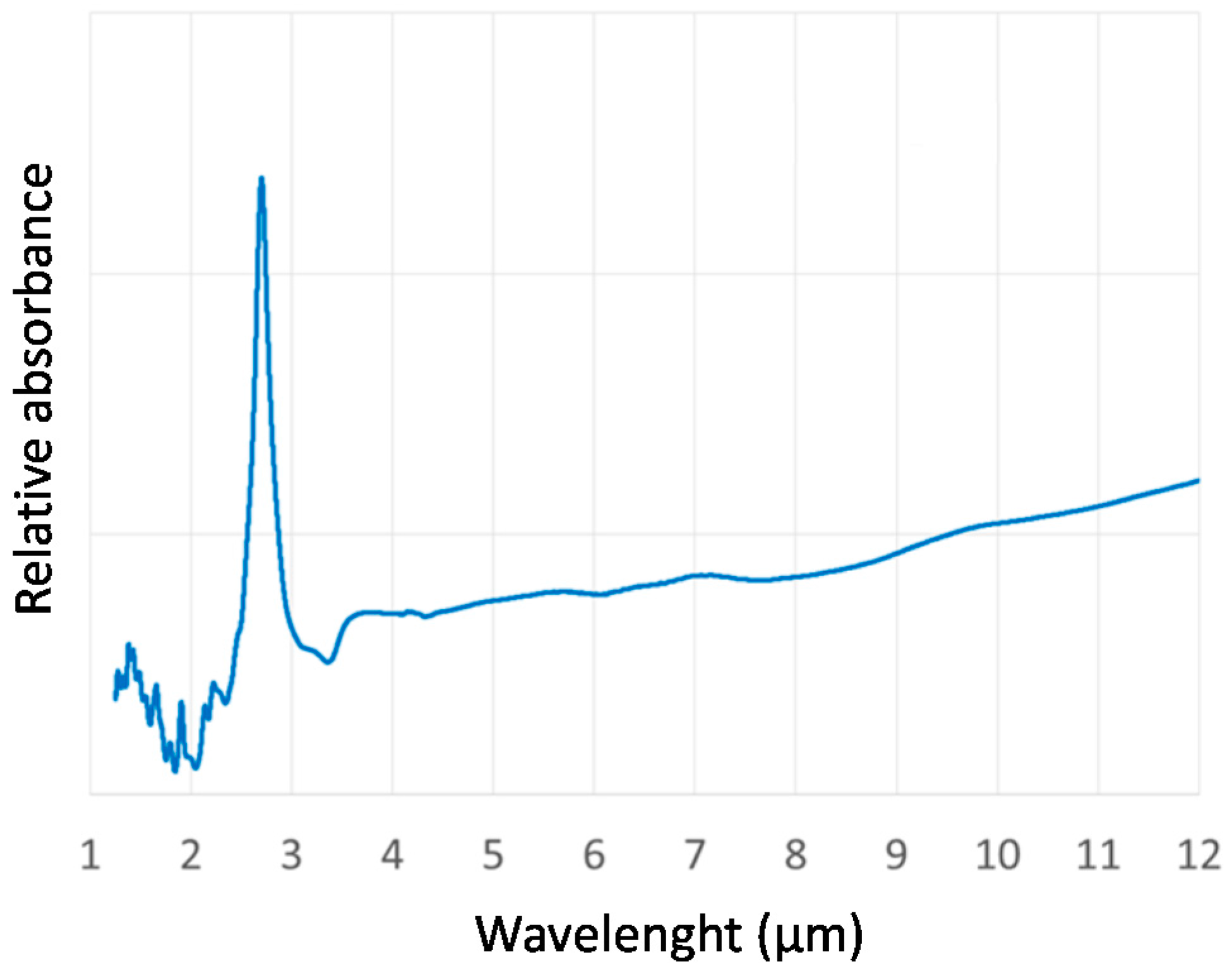
3. Optical Coupling Conditions
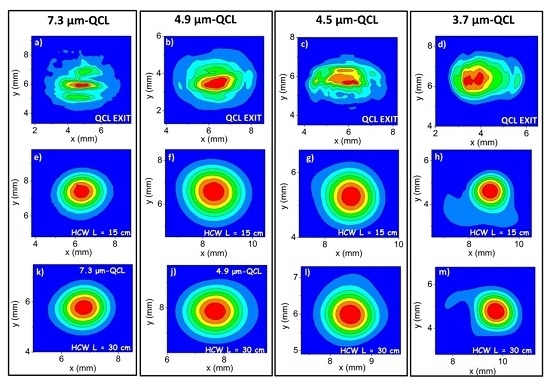
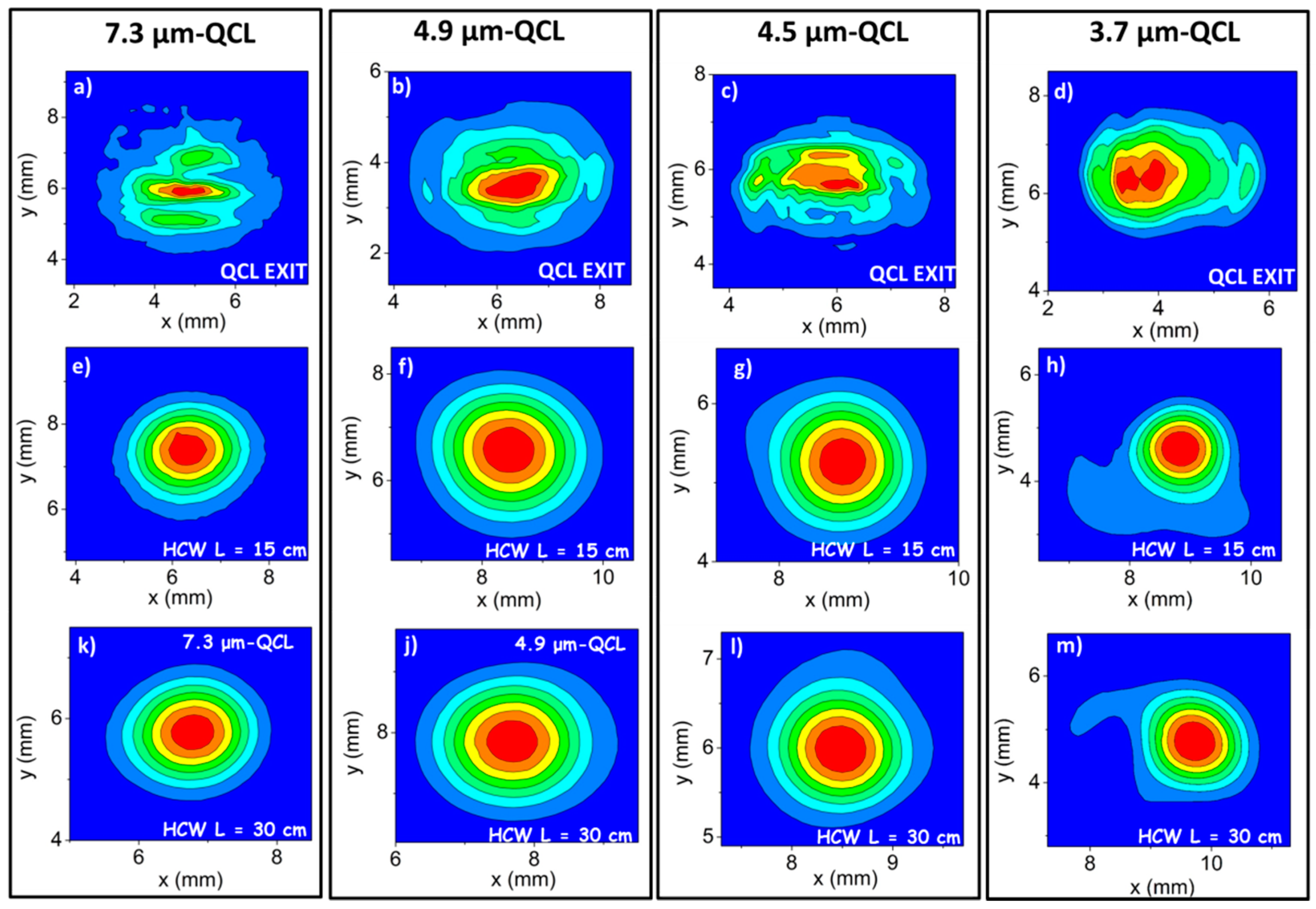
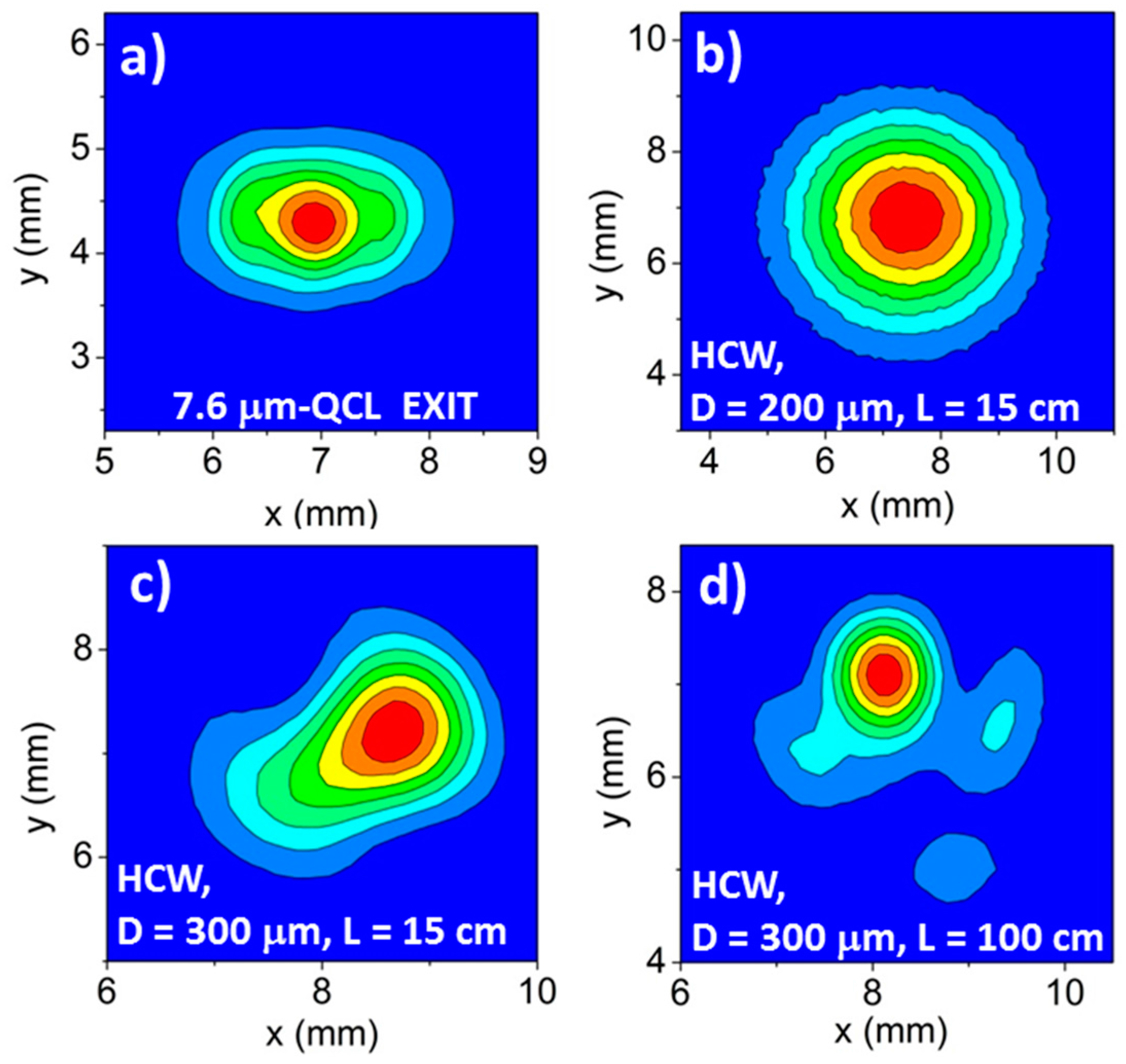
4. Beam Profiles and Related Spatial Quality
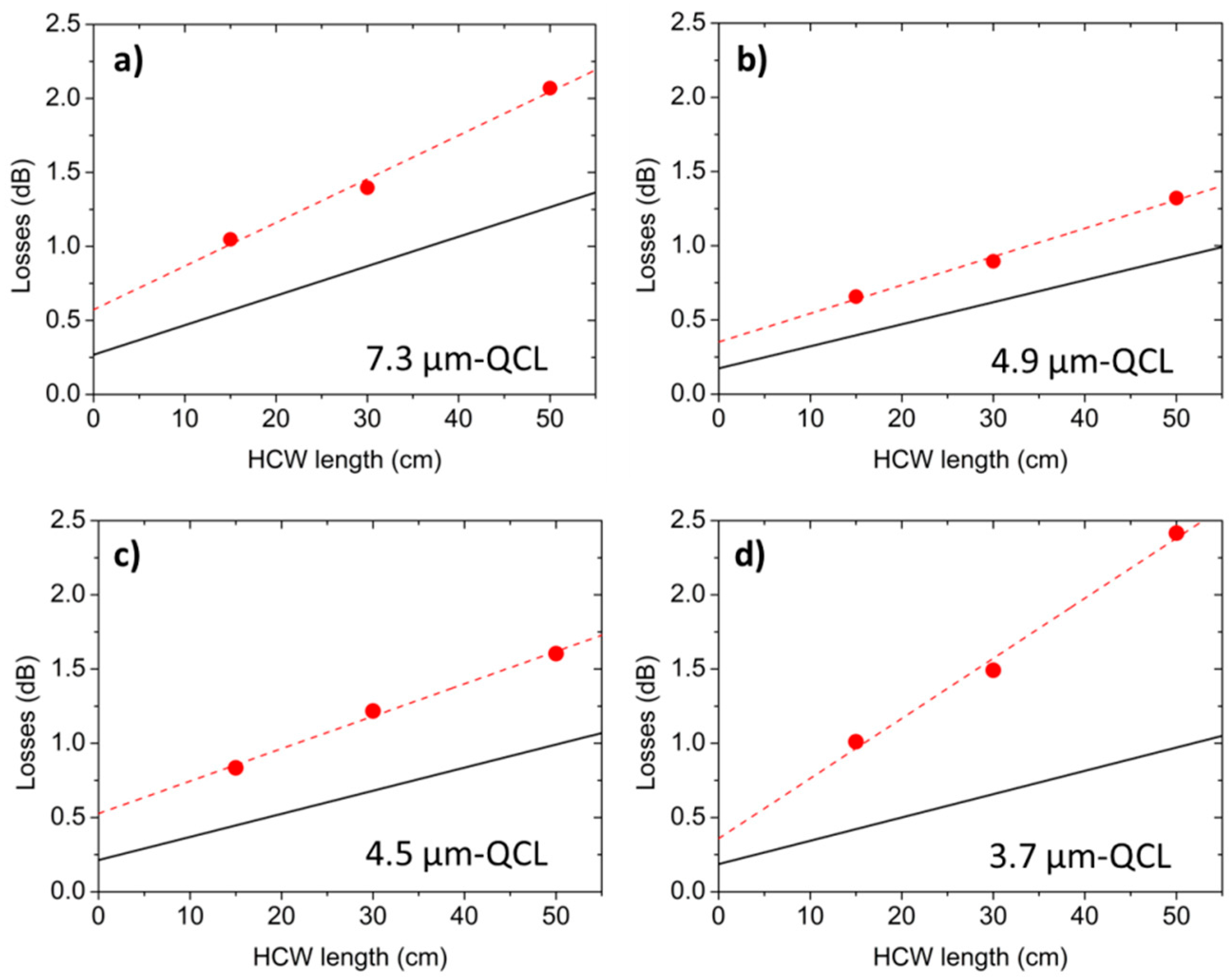
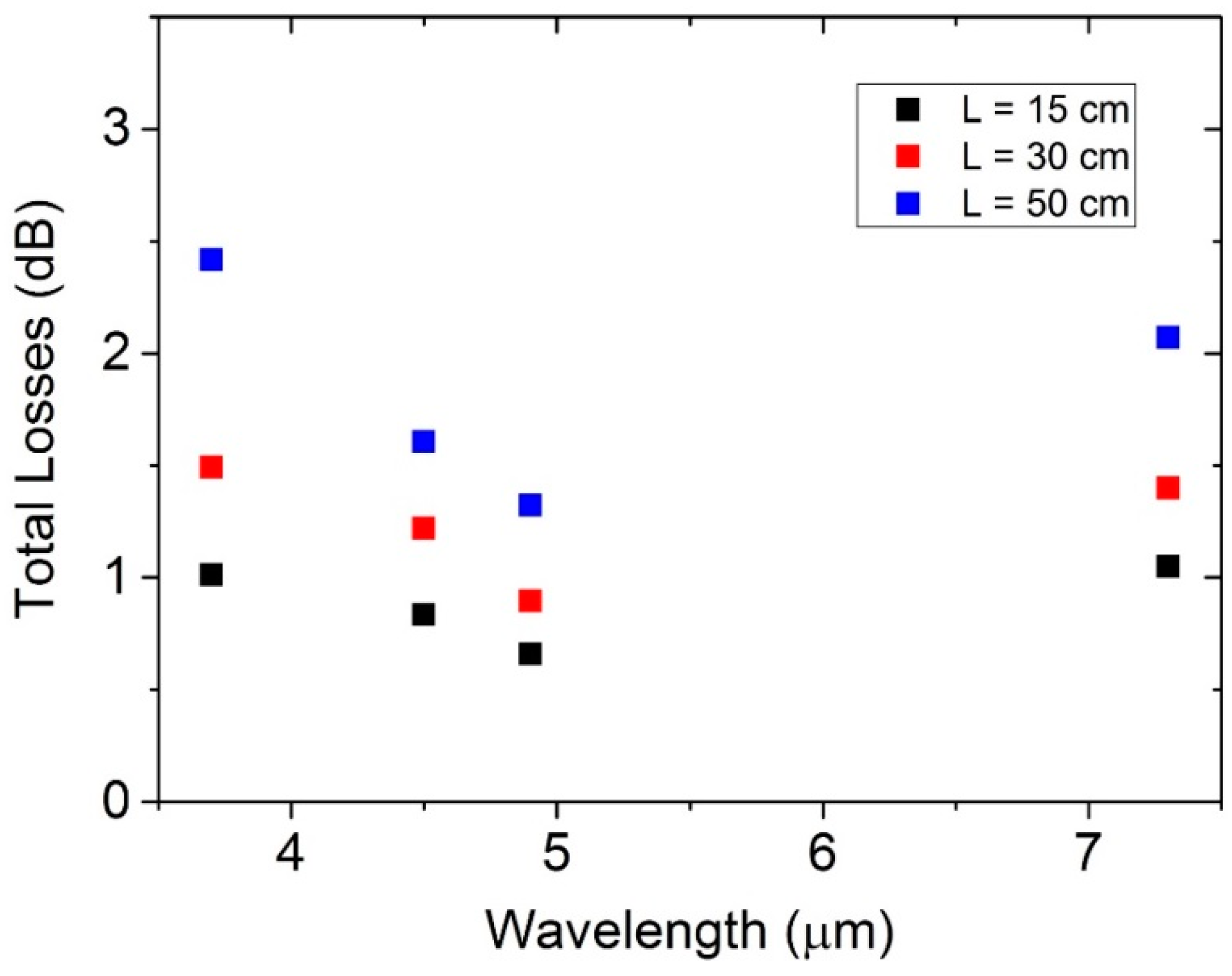
5. Total Losses and Coupling Efficiency
6. Influence of Bore Diameter and HCW Length on the Output Beam Quality
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Patimisco, P.; Scamarcio, G.; Tittel, F.K.; Spagnolo, V. Quartz-Enhanced Photoacoustic Spectroscopy: A Review. Sensors 2014, 14, 6165–6206. [Google Scholar] [CrossRef] [PubMed]
- Gagliardi, G.; Loock, H.P. Cavity-Enhanced Spectroscopy and Sensing; Springer: London, UK, 2014. [Google Scholar]
- Willer, U.; Saraji, M.; Khorsandi, A.; Geiser, P.; Schade, W. Near- and mid-infrared laser monitoring of industrial processes, environment and security applications. Opt. Laser. Eng. 2006, 44, 699–710. [Google Scholar] [CrossRef]
- Hariharan, P. Optical Holography; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kermene, V.; Saviot, A.; Vampouille, M.; Colombeau, B.; Froehly, C.; Dohnalik, T. Flattening of the spatial laser beam profile with low losses and minimal beam divergence. Opt. Lett. 1992, 17, 859–861. [Google Scholar] [CrossRef] [PubMed]
- Ksendzov, A.; Lay, O.; Martin, S.; Sanghera, J.S.; Busse, L.E.; Kim, W.H.; Pureza, P.C.; Nguyen, V.Q.; Aggarwal, I.D. Characterization of mid-infrared single mode fibers as modal filters. Appl. Opt. 2007, 46, 7957–7962. [Google Scholar] [CrossRef] [PubMed]
- Houizot, P.; Boussard-Plédel, C.; Faber, A.J.; Cheng, L.K.; Bureau, B.; Van Nijnatten, P.A.; Gielesen, W.L.M.; Pereira do Carmo, J.; Lucas, J. Infrared single mode chalcogenide glass fiber for Space. Opt. Express 2007, 15, 12529–12538. [Google Scholar] [CrossRef] [PubMed]
- Caillaud, C.; Renversez, G.; Brilland, L.; Mechin, D.; Calvez, L.; Adam, J.-L.; Troles, J. Photonic bandgap propagation in all-solid chalcogenide microstructured optical fibers. Materials 2014, 7, 6120–6129. [Google Scholar] [CrossRef]
- Butvina, L.N.; Sereda, O.V.; Dianov, E.M.; Lichkova, N.V.; Zagorodnev, V.N. Single-mode microstructured optical fiber for the middle infrared. Opt. Lett. 2007, 32, 334–336. [Google Scholar] [CrossRef] [PubMed]
- Kriesel, J.M.; Hagglund, G.M.; Gat, N.; Spagnolo, V.; Patimisco, P. Spatial mode filtering of mid-infrared (mid-IR) laser beams with hollow core fiber optics. Proc. SPIE 2013, 8993. [Google Scholar] [CrossRef]
- Patimisco, P.; Sampaolo, A.; Giglio, M.; Kriesel, J.M.; Tittel, F.K.; Spagnolo, V. Hollow core waveguide as mid-infrared laser modal beam filter. J. Appl. Phys. 2015, 118, 113102–113106. [Google Scholar] [CrossRef]
- Harrington, J.A. Infrared Fibers and Their Applications; SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Kriesel, J.M.; Gat, N.; Bernacki, B.E.; Erikson, R.L.; Cannon, B.D.; Myers, T.L.; Bledt, C.M.; Harrington, J.A. Hollow Core Fiber Optics for Mid-Wave and Long-Wave Infrared Spectroscopy. Proc. SPIE 2011, 8018. [Google Scholar] [CrossRef]
- Bledt, C.M.; Harrington, J.A.; Kriesel, J.M. Loss and modal properties of Ag/AgI hollow glass waveguides. Appl. Opt. 2012, 51, 3114–3119. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, V.; Patimisco, P.; Borri, S.; Scamarcio, G.; Bernacki, B.E.; Kriesel, J. Part-per-trillion level SF6 detection using a quartz enhanced photoacoustic spectroscopy-based sensor with single-mode fiber-coupled quantum cascade laser excitation. Opt. Lett. 2012, 37, 4461–4463. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, V.; Patimisco, P.; Borri, S.; Scamarcio, G.; Bernacki, B.E.; Kriesel, J. Mid-infrared fiber-coupled QCL-QEPAS sensor. Appl. Phys. B 2013, 112, 25–33. [Google Scholar] [CrossRef]
- Siciliani de Cumis, M.; Viciani, S.; Borri, S.; Patimisco, P.; Sampaolo, A.; Scamarcio, G.; De Natale, P.; D’Amato, F.; Spagnolo, V. A widely-tunable mid-infrared fiber-coupled quartz-enhanced photoacoustic sensor for environmental monitoring. Opt. Express 2014, 22, 28222–28231. [Google Scholar] [CrossRef] [PubMed]
- Sampaolo, A.; Patimisco, P.; Kriesel, J.M.; Tittel, F.K.; Scamarcio, G.; Spagnolo, V. Single mode mid-IR hollow fibers operating in the range 5.1–10.5 μm. Opt. Express 2015, 23, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Patimisco, P.; Sampaolo, A.; Kriesel, J.M.; Tittel, F.K.; Scamarcio, G.; Spagnolo, V. Mid-IR quantum cascade laser mode coupling in hollow-core, fiber-optic waveguides with single-mode beam delivery. Proc. SPIE 2015, 9370. [Google Scholar] [CrossRef]
- Nubling, R.; Harrington, J.A. Launch conditions and mode coupling in hollow glass waveguides. Opt. Eng. 1998, 37, 2454–2458. [Google Scholar] [CrossRef]
- Patimisco, P.; Spagnolo, V.; Vitiello, M.S.; Tredicucci, A.; Scamarcio, G.; Bledt, C.M.; Harrington, J.A. Coupling external cavity mid-IR quantum cascade lasers with low loss hollow metallic/dielectric waveguides. Appl. Phys. B 2012, 108, 255–260. [Google Scholar] [CrossRef]
- Patimisco, P.; Spagnolo, V.; Vitiello, M.S.; Tredicucci, A.; Scamarcio, G.; Bledt, C.M.; Harrington, J.A. Low-Loss Hollow Waveguide Fibers for Mid-Infrared Quantum Cascade Laser Sensing Applications. Sensors 2013, 13, 1329–1340. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, M.; Kawakami, S. Design theory of dielectric-coated circular metallic waveguides for infrared transmission. J. Lightw. Technol. 1984, 2, 116–126. [Google Scholar] [CrossRef]
- George, R.; Harrington, J.A. Infrared transmissive, hollow plastic waveguides with inner Ag–AgI coatings. Appl. Opt. 2005, 44, 6449–6455. [Google Scholar] [CrossRef] [PubMed]
- Mid-Infrared Optical Fiber, Fiber Patch Cables, and Bundles. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=7062#SingleMode (accessed on 12 April 2016).
| 7.3-μm QCL | 4.9-μm QCL | 4.5-μm QCL | 3.7-μm QCL | |
|---|---|---|---|---|
| wx (mm) | 5.26 | 4.24 | 4.19 | 4.27 |
| wy (mm) | 4.79 | 3.97 | 3.48 | 3.67 |
| f (mm) | 50 | 75 | 75 | 75 |
| w0,x (μm) | 132 | 114 | 96 | 100 |
| w0,y (μm) | 144 | 122 | 120 | 116 |
| 7.3-μm QCL | 4.9-μm QCL | 4.5-μm QCL | 3.7-μm QCL | |
|---|---|---|---|---|
| θx,QCL (mrad) | 2.1 | 1.9 | 1.5 | 1.3 |
| θy,QCL (mrad) | 2.0 | 1.7 | 2.2 | 1.1 |
| M2x, QCL | 4.75 | 5.16 | 4.39 | 4.71 |
| M2y, QCL | 4.12 | 4.32 | 4.85 | 3.42 |
| θx,HCW (mrad) | 30.72 | 22.48 | 21.97 | 20.48 |
| θy,HCW (mrad) | 31.53 | 22.22 | 22.30 | 19.92 |
| M2x, HCW | 1.12 | 1.18 | 1.26 | 1.44 |
| M2y, HCW | 1.15 | 1.17 | 1.28 | 1.40 |
| 7.3-μm QCL | 4.9-μm QCL | 4.5-μm QCL | 3.7-μm QCL | |
|---|---|---|---|---|
| η1 | 0.94 | 0.96 | 0.95 | 0.96 |
| ηexp | 0.88 | 0.92 | 0.89 | 0.92 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patimisco, P.; Sampaolo, A.; Mihai, L.; Giglio, M.; Kriesel, J.; Sporea, D.; Scamarcio, G.; Tittel, F.K.; Spagnolo, V. Low-Loss Coupling of Quantum Cascade Lasers into Hollow-Core Waveguides with Single-Mode Output in the 3.7–7.6 μm Spectral Range. Sensors 2016, 16, 533. https://doi.org/10.3390/s16040533
Patimisco P, Sampaolo A, Mihai L, Giglio M, Kriesel J, Sporea D, Scamarcio G, Tittel FK, Spagnolo V. Low-Loss Coupling of Quantum Cascade Lasers into Hollow-Core Waveguides with Single-Mode Output in the 3.7–7.6 μm Spectral Range. Sensors. 2016; 16(4):533. https://doi.org/10.3390/s16040533
Chicago/Turabian StylePatimisco, Pietro, Angelo Sampaolo, Laura Mihai, Marilena Giglio, Jason Kriesel, Dan Sporea, Gaetano Scamarcio, Frank K. Tittel, and Vincenzo Spagnolo. 2016. "Low-Loss Coupling of Quantum Cascade Lasers into Hollow-Core Waveguides with Single-Mode Output in the 3.7–7.6 μm Spectral Range" Sensors 16, no. 4: 533. https://doi.org/10.3390/s16040533
APA StylePatimisco, P., Sampaolo, A., Mihai, L., Giglio, M., Kriesel, J., Sporea, D., Scamarcio, G., Tittel, F. K., & Spagnolo, V. (2016). Low-Loss Coupling of Quantum Cascade Lasers into Hollow-Core Waveguides with Single-Mode Output in the 3.7–7.6 μm Spectral Range. Sensors, 16(4), 533. https://doi.org/10.3390/s16040533