Three-Factor User Authentication and Key Agreement Using Elliptic Curve Cryptosystem in Wireless Sensor Networks
Abstract
:1. Introduction
2. Preliminaries
2.1. Notations
2.2. Elliptic Curves Cryptosystem
2.3. Fuzzy Extraction
- This probabilistic algorithm takes a biometric template as an input and then outputs a biometric key , which is a uniform and random string, and a helper string . can be the same under the assistance of even if the biometric information changes slightly.
- This deterministic algorithm takes noisy biometric information and a helper string as inputs, then reproduces the biometric key . To reproduce the same , the metric space distances between and have to meet the given verification threshold.
2.4. Network Model
- : A user who receives a smart card from and uses it to access multiple servers. After a successful authentication process with , the user is given access to mobile services. Furthermore, the user’s smart card is not tamper-resistant and can be lost or stolen by an adversary.
- : A sensor node that collects information and provides services to users who successfully complete the authentication process. Sensors are not equipped with tamper-resistant hardware due to cost constraints, thus an adversary will know all of the keying materials stored in that sensor’s memory.
- : A trusted third-party that generates system parameters. It provides smart cards to users and pre-shared keys to sensors. is assumed to be trustworthy and never compromised by an adversary.
2.5. Security Requirements
3. Review of Chang et al.’s Authentication and Key Agreement Scheme
3.1. Registration Phase
- Step 1:
- chooses and a random number , then computes and sends to via a secure channel.
- Step 2:
- computes , , , , . Then, sends the smart card to via a secure channel. stores in its storage, where , is a nonce, and , where means contains nothing.
- Step 3:
- computes and inserts it into .
3.2. Login Phase
- Step 1:
- inputs and into .
- Step 2:
- computes , , , . Then, verifies . If it is valid, computes , , , where is the timestamp.
- Step 3:
- sends to .
3.3. Authentication and Key Agreement Phase
- Step 1:
- checks the validity of and retrieves from . Then, computes , , , , then checks . If it is correct, computes , , then sends to , where is the timestamp.
- Step 2:
- checks the validity of and computes , then checks . If it is successful, computes , , , , then sends to , where is the timestamp.
- Step 3:
- checks the validity of and computes , , , then checks . If it is correct, computes , , , then sends , where is the timestamp. Additionally, updates as .
- Step 4:
- checks the validity of and computes , , then checks If it is correct, computes and updates as .
3.4. Password Change Phase
- Step 1:
- inputs into , where is a new password.
- Step 2:
- The smart card computes , , , , then checks . If it is correct, computes updated values , , , . Then, replaces with .
4. Security Weaknesses of Chang et al.’s Scheme
- An adversary can be either a user or a sensor node, but not a gateway node [26].
- An adversary has total control over the public communication channel. Thus, the adversary can intercept, insert, delete or modify any message transmitted via a public channel.
- An adversary may steal a user’s smart card and extract the information stored in it by means of analyzing the power consumption [27].
- An adversary can easily guess low-entropy passwords in an off-line manner, but the guessing of two secret parameters is computationally infeasible in polynomial time [28].
4.1. Off-Line Password Guessing Attack
4.2. Lack of Perfect Forward Secrecy
- Step 1:
- intercepts and stores all messages exchanged in previous sessions, such as and .
- Step 2:
- computes , then finally retrieves a previous session key .
4.3. Incorrectness of Password Change
- Step 1:
- Once the user performs the password change phase, the previous password is changed into , and information in the smart card, , is replaced with .
- Step 2:
- Then, the user performs the login phase using the new password ; however, is not allowed to access for not computing the proper from . is not updated in the password change phase; therefore, and, finally, .
5. The Proposed Three-Factor Authentication and Key Agreement Scheme
5.1. Registration Phase
- Step 1:
- :chooses and and imprints , then computes and and sends to through a secure channel.
- Step 2:
- :computes , , , , .
- Step 3:
- stores parameters , where ( is a nonce); . is empty at first time because has not been updated; however, this parameter is required to check the correctness of the received and retrieve safely when does not find a proper updated in the case of an unsuccessful update process.Then, issues the smart card and sends it to through a secure channel.
5.2. Login Phase
- Step 1:
- inserts , inputs , and imprints .
- Step 2:
- computes , , , . Then, verifies . If it is correct, generates a random number and computes , , , , where is the current timestamp.
- Step 3:
- sends the login request message to .
5.3. Authentication and Key Agreement Phase
- Step 1:
- :After receiving , checks the validity of and retrieves from . If no is found, checks . If it still is not found, rejects the login request; otherwise, computes and . Then, verifies . If it is valid, authenticates and computes , then sends to , where is the current timestamp.
- Step 2:
- :After receiving , checks the validity of and verifies using its stored secret value . If it is valid, authenticates and computes , , where is the current timestamp. Then, generates a random number and computes and a session key . Finally, computes and sends to .
- Step 3:
- :After receiving , checks the validity of , computes , and verifies . If it is valid, authenticates and computes , , , where is the current timestamp. Then, sends to and updates as in its storage.
- Step 4:
- After receiving , checks the validity of , computes and verifies . If it is valid, computes the session key . Finally, updates as .
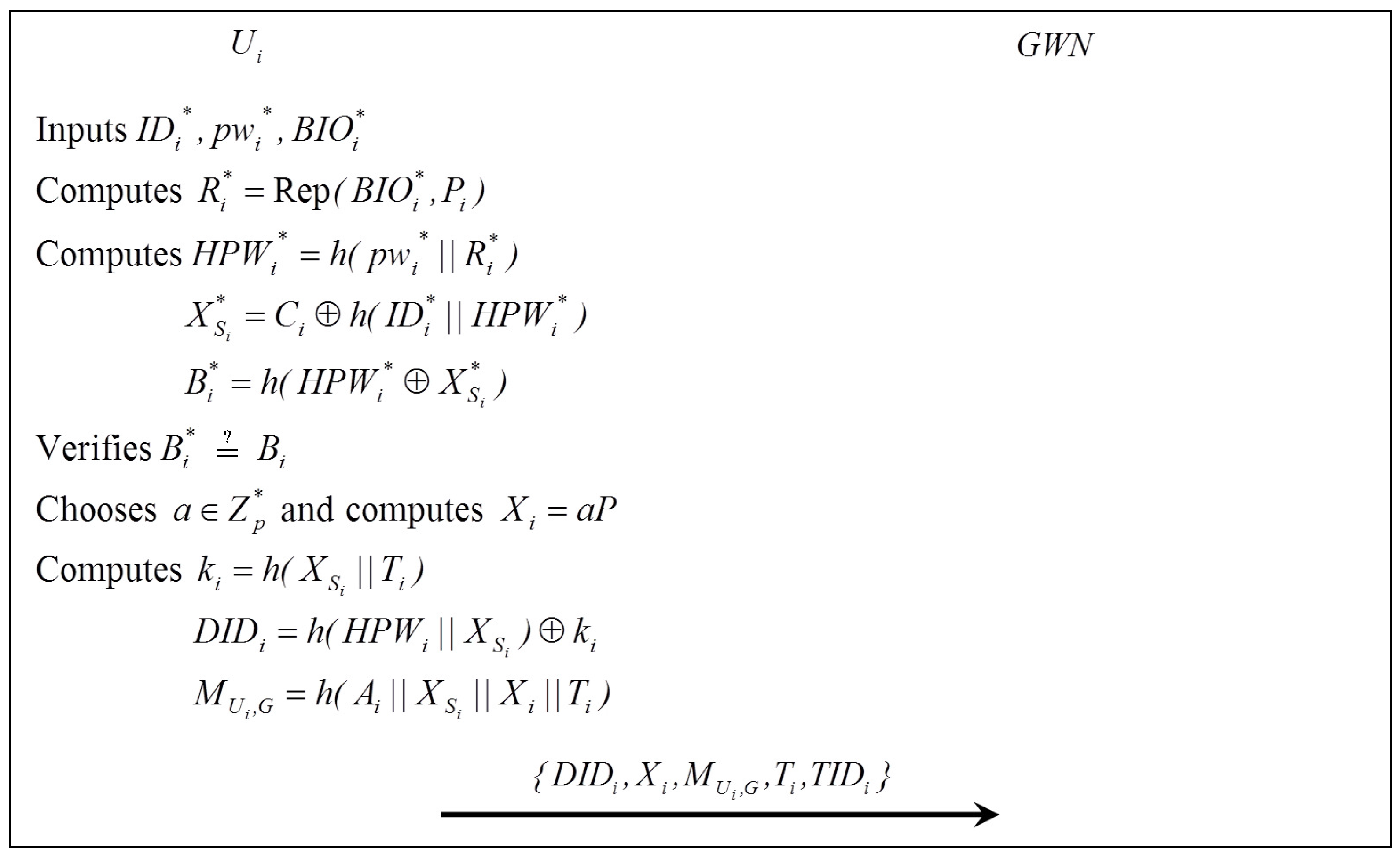
5.4. Password Change Phase
- Step 1:
- imprints and computes , then inputs into .
- Step 2:
- computes , , . Then, verifies to check the validity of . If it is correct, computes updated values , , , . Then, replaces with .
6. Analysis
6.1. Proof of Authentication and Key Agreement Based on BAN Logic
- The BAN logic postulates:
- (a)
- Message meaning rule:
- (b)
- Nonce-verification rule:
- (c)
- Jurisdiction rule:
- (d)
- Freshness-conjuncatenation rule:
- Security goals:The proposed scheme should satisfy the following goals:
- g1.
- g2.
- g3.
- g4.
- Idealized scheme:We transform our scheme into the idealized form as follows:
- Msg1.
- Msg2.
- Msg3.
- Msg4.
- Initiative premises:
- Security analysis of the idealized form of the proposed scheme:
- a1.
- According to , we could get:
- a2.
- According to , we apply the message-meaning rule to obtain:
- a3.
- According to , we apply the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a4.
- According to , we could get:
- a5.
- According to , we apply the message-meaning rule to obtain:
- a6.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a7.
- According to , we could get:
- a8.
- According to , we apply the message-meaning rule to obtain:
- a9.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a10.
- According to , we could get:
- a11.
- According to , we apply the message-meaning rule to obtain:
- a12.
- According to , we apply the the freshness-conjuncatenation rule to obtain:Then, from and , we apply the nonce-verification rule to obtain:
- a13.
- Because , according to and , we could produce:Likewise, , according to and , we could produce:
- a14.
- According to and , we apply the jurisdiction rule to produce:Likewise, according to and , we apply the jurisdiction rule to produce:
According to Goal 1, Goal 2, Goal 3 and Goal 4, we conclude that both and believe they share the session key.
6.2. Security Analysis against Various Attacks
- •
- User anonymity and untraceability: Our scheme provides anonymity of users. The user does not reveal a real identity in open channels; instead, generates and sends a pseudonym identity to in the registration phase and updates it as before finalizing the session. The identity is dynamic for every session; thus, an adversary cannot obtain the user’s true identity. The proposed scheme also provides untraceability by having all messages used in the session satisfy a freshness requirement. Therefore, cannot trace the user.
- •
- Perfect forward secrecy: A session key is computed as . Even though the long-term private keys and are disclosed to , he/she cannot compute previous session keys, because it is hard to compute using and due to the difficulty of ECDH. Thus, cannot compute previous session keys using long-term private keys. Therefore, our scheme provides forward secrecy.
- •
- Mutual authentication: In our scheme, and authenticate each other, and and authenticate each other, respectively. authenticates by checking . needs to compute and to reconstruct ; however, only a legal user can compute those values. authenticates by checking . needs to compute and to reconstruct ; however, only a legal can compute those values. Therefore, and mutually authenticate. Similarly, authenticates by checking , and authenticates by checking . Additionally, only legal and can reconstruct them, then authenticate mutually. Therefore, our scheme provides proper mutual authentication.
- •
- Off-line password guessing attack: may attempt to guess the password by extracting the values stored in the smart card . could guess correctly if he/she generates a series of equations and computes the valid using guessing passwords. However, is required to know the biometric information of the user, which cannot be forged, for generating equations. Therefore, it is infeasible to correctly guess the user’s password in our scheme.
- •
- Smart card loss attack: can extract values in the smart card by means of power analysis and other techniques. Suppose obtains the user’s smart card and extracts stored parameters . From these values, cannot obtain any useful information because the parameters are safeguarded with a one-way hash function, and is just a nonce. Furthermore, may attempt to log in by generating a login request message. However, cannot even pass the login phase and generate a valid login request message without proper , and . Therefore, the proposed scheme withstands smart card loss attacks.
- •
- User impersonation attack: who somehow possesses a valid smart card of and wants to access is required to generate and send a valid login request message to . must know and to compute these values. However, in our scheme, and are not revealed. Thus, cannot compute the temporal key and generate a valid login request message. Therefore, our scheme is secure against the user impersonation attack.
- •
- Man-in-the-middle attack and replay attack: who knows public channel information and has the smart card of may attempt to establish a secure channel with . However, cannot authenticate with because cannot generate a valid login request message, as mentioned above. In addition, those messages captured in a public channel are refreshed in every session, so that cannot use them repeatedly. Therefore, our scheme withstands man-in-the-middle and replay attacks.
- •
- Stolen verifier attack: who obtains the verifier table of may attempt to attack users to gain some advantages. However, still cannot compute , and and will fail to pass the login phase. Of course, will fail to compute a login request message without and . Therefore, even if has the verifier table, our protocol withstands stolen verifier attacks.
- •
- Known-key attack: A session key is computed as , and , and are independent in each session. Though , who somehow possesses each value, attempts to generate other session keys, he/she will find that they cannot successfully derive valid session keys. Therefore, our proposed scheme withstands known-key attacks.
6.3. Performance Comparisons
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 102–114. [Google Scholar] [CrossRef]
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Futur. Gene Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Pathan, A.S.K.; Lee, H.W.; Hong, C.S. Security in wireless sensor networks: Issues and challenges. In Proceedings of the 8th International Conference Advanced Communication Technology (ICACT), Phoenix Park, Korea, 20–22 February 2006; pp. 1043–1048.
- Perrig, A.; Stankovic, J.; Wagner, D. Security in wireless sensor networks. ACM Commun. 2004, 47, 53–57. [Google Scholar] [CrossRef]
- Al Ameen, M.; Liu, J.; Kwak, K. Security and privacy issues in wireless sensor networks for healthcare applications. J. Med. Syst. 2012, 36, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.H.; Zheng, Y.; Cao, J.; Wang, S. A dynamic user authentication scheme for wireless sensor networks. In Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Taichung, Taiwan, 5–7 June 2006; pp. 1–8.
- Das, M.L. Two-factor user authentication scheme in wireless sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1086–1090. [Google Scholar] [CrossRef]
- He, D.; Gao, Y.; Chan, S.; Chen, C.; Bu, J. An enhanced two-factor user authentication scheme in wireless sensor networks. Ad Hoc Sens. Wirel. Netw. 2010, 10, 361–371. [Google Scholar]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and security improvements of two-factor user authentication in wireless sensor networks. Sensors 2010, 10, 2450–2459. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.H.; Shih, W.K. A robust mutual authentication protocol for wireless sensor networks. ETRI J. 2010, 32, 704–712. [Google Scholar] [CrossRef]
- Vaidya, B.; Makrakis, D.; Mouftah, H. Two-factor mutual authentication with key agreement in wireless sensor networks. Secur. Commun. Netw. 2016, 9, 171–183. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Jeon, W.; Lee, Y.; Won, D. Security analysis and improvements of two-factor mutual authentication with key agreement in wireless sensor networks. Sensors 2014, 14, 6443–6462. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.P.; Lee, T.F.; Lin, T.H.; Liu, C.M. Enhanced two-factor authentication and key agreement using dynamic identities in wireless sensor networks. Sensors 2015, 15, 29841–29854. [Google Scholar] [CrossRef] [PubMed]
- Yoon, E.J.; Yoo, K.Y. A biometric-based authenticated key agreement scheme using ECC for wireless sensor networks. In Proceedings of the 29th Annual ACM Symposium on Applied Computing, Gyeongju, Korea, 24–28 March 2014; pp. 699–705.
- Das, A.K. A secure and efficient user anonymity-preserving three-factor authentication protocol for large-scale distributed wireless sensor networks. Wirel. Pers. Commun. 2015, 82, 1377–1404. [Google Scholar] [CrossRef]
- Das, A.K. A secure and effective biometric-based user authentication scheme for wireless sensor networks using smart card and fuzzy extractor. Int. J. Commun. Syst. 2015, 2015, 1–25. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, Y.; Won, D. Security improvement on biometric based authentication scheme for wireless sensor networks using fuzzy extraction. Int. J. Dist. Sens. Netw. 2016, 8572410, 1–16. [Google Scholar] [CrossRef]
- Park, Y.; Lee, S.; Kim, C.; Park, Y. Secure biometric-based authentication scheme with smart card revocation/reissue for wireless sensor networks. Int. J. Dist. Sens. Netw. 2016, 12, 1–11. [Google Scholar] [CrossRef]
- Li, C.T.; Hwang, M.S. An efficient biometric-based remote authentication scheme using smart cards. J. Netw. Comp. Appl. 2010, 33, 1–5. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R.M. A logic of authentication. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1989, 426, 233–271. [Google Scholar] [CrossRef]
- Lu, R.; Cao, Z.; Chai, Z.; Liang, X. A Simple User Authentication Scheme for Grid Computing. IJ Netw. Sec. 2008, 7, 202–206. [Google Scholar]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; pp. 523–540.
- Tan, Z. A user anonymity preserving three-factor authentication scheme for telecare medicine information systems. J. Med. Syst. 2014, 38, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Kim, J.; Choi, Y.; Won, D. An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors 2016, 16, 1299. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H.L.; Chen, T.H.; Liu, P.C.; Kim, T.H.; Wei, H.W. A secured authentication protocol for wireless sensor networks using elliptic curves cryptography. Sensors 2011, 11, 4767–4779. [Google Scholar] [CrossRef] [PubMed]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Proceedings of the Advances in Cryptology-CRYPTO’99, Santa Barbara, CA, USA, 15–19 August 1999; Volume 1666, pp. 388–397.
- Amin, R.; Biswas, G.P. A secure light weight scheme for user authentication and key agreement in multi-gateway based wireless sensor networks. Ad Hoc Netw. 2016, 36, 58–80. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Chilamkurti, N. A secure temporal-credential-based mutual authentication and key agreement scheme with pseudo identity for wireless sensor networks. Inf. Sci. 2015, 321, 263–277. [Google Scholar] [CrossRef]
- Jiang, Q.; Kumar, N.; Ma, J.; Shen, J.; He, D.; Chilamkurti, N. A privacy-aware two-factor authentication protocol based on elliptic curve cryptography for wireless sensor networks. Int. J. Netw. Manag. 2016. [Google Scholar] [CrossRef]
- Lu, Y.; Li, L.; Yang, X.; Yang, Y. Robust biometrics based authentication and key agreement scheme for multi-server environments using smart cards. PLoS ONE 2015, 10, e0126323. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, Q.; Yan, R.; Sun, R. Efficient authenticated key exchange protocols for wireless body area networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 1–11. [Google Scholar] [CrossRef]



| Notation | Meaning |
|---|---|
| two large primes | |
| user i | |
| sensor node j | |
| gateway node | |
| smart card of the user | |
| identity/password of | |
| biometric template of | |
| temporal identity of | |
| identity of | |
| identity of | |
| adversary | |
| K | a master secret of |
| cyclic group of order q | |
| P | generator of |
| timestamps | |
| ⨁ | XOR operation |
| concatenate operation | |
| a secure one-way hash function |
| Notations | Meaning |
|---|---|
| P believes X | |
| P sees X | |
| P once said X | |
| P has jurisdiction over X | |
| X is fresh | |
| P and Q may use the shared key K | |
| The session key shared between two principals | |
| X combined with the formula Y | |
| X hashed under the key K | |
| X encrypted under the key K |
| Kim et al.’ Scheme [13] | Chang et al.’ Scheme [14] | Yoon and Yoo’s Scheme [15] | Choi et al.’ Scheme [18] | Proposed Scheme | |
|---|---|---|---|---|---|
| Provides user anonymity | × | ∘ | × | × | ∘ |
| Provides user untraceability | × | Δ | × | × | ∘ |
| Provides forward secrecy | × | × | ∘ | ∘ | ∘ |
| Provides secure password update | ∘ | × | − | − | ∘ |
| Provides mutual authentication | ∘ | ∘ | ∘ | ∘ | ∘ |
| Resists off-line password guessing attack | × | × | − | − | ∘ |
| Resists user impersonation attack | × | Δ | ∘ | × | ∘ |
| Resists lost smart card attack | × | Δ | ∘ | ∘ | ∘ |
| Resists stolen verifier attack | × | Δ | − | − | ∘ |
| Resists man-in-the-middle attack | × | Δ | ∘ | ∘ | ∘ |
| Resists replay attack | ∘ | ∘ | ∘ | ∘ | ∘ |
| Resist biometric recognition error | − | − | × | ∘ | ∘ |
| Usage of biometrics | × | × | ∘ | ∘ | ∘ |
| Usage of ECC | × | × | ∘ | ∘ | ∘ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.; Park, Y. Three-Factor User Authentication and Key Agreement Using Elliptic Curve Cryptosystem in Wireless Sensor Networks. Sensors 2016, 16, 2123. https://doi.org/10.3390/s16122123
Park Y, Park Y. Three-Factor User Authentication and Key Agreement Using Elliptic Curve Cryptosystem in Wireless Sensor Networks. Sensors. 2016; 16(12):2123. https://doi.org/10.3390/s16122123
Chicago/Turabian StylePark, YoHan, and YoungHo Park. 2016. "Three-Factor User Authentication and Key Agreement Using Elliptic Curve Cryptosystem in Wireless Sensor Networks" Sensors 16, no. 12: 2123. https://doi.org/10.3390/s16122123
APA StylePark, Y., & Park, Y. (2016). Three-Factor User Authentication and Key Agreement Using Elliptic Curve Cryptosystem in Wireless Sensor Networks. Sensors, 16(12), 2123. https://doi.org/10.3390/s16122123






