Trend-Residual Dual Modeling for Detection of Outliers in Low-Cost GPS Trajectories
Abstract
:1. Introduction
2. Methods
2.1. Trend Modeling
2.2. Outlier Detection from Residuals
2.3. Selection of the Smoothness Parameter
2.4. Solution Procedure
- Consider a trajectory data sequence , where is the number of GPS points.
- Use the cubic smooth spline to extract the trend within data and obtain residuals.
- (a)
- Set the smoothness parameter by (15).
- (b)
- Estimate i.e., the value of data trend at by (3).
- (c)
- Calculate the residuals between the observations and the trend for .
- If , where is a predetermined critical value (3, 3.5 or 4), remove the point , where .
- Let the cleaned data be the new data sequence. Note that the number of the current data sequence is one point fewer than the previous data sequence. Go to step 2 until .
3. Experiments and Evaluation
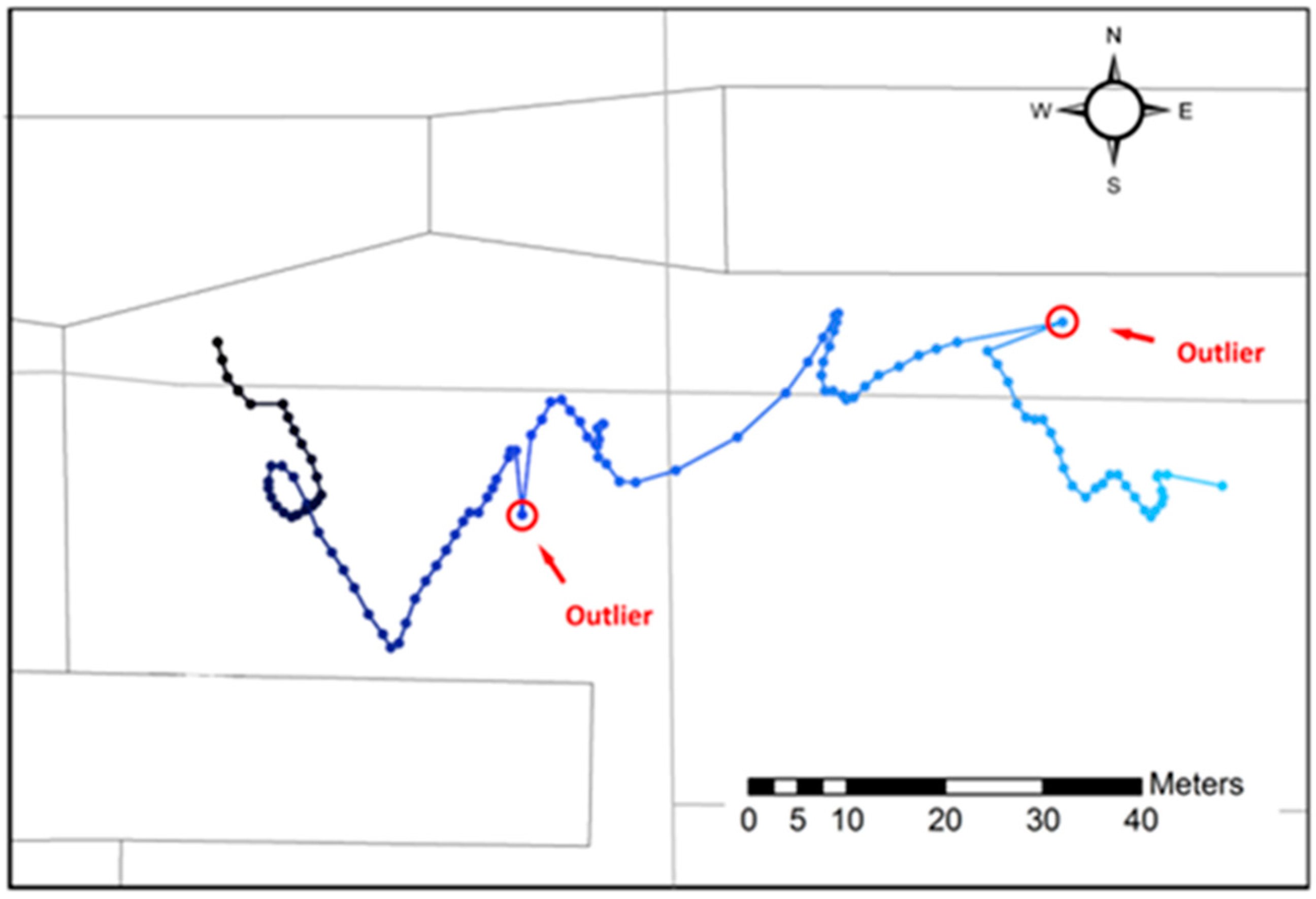
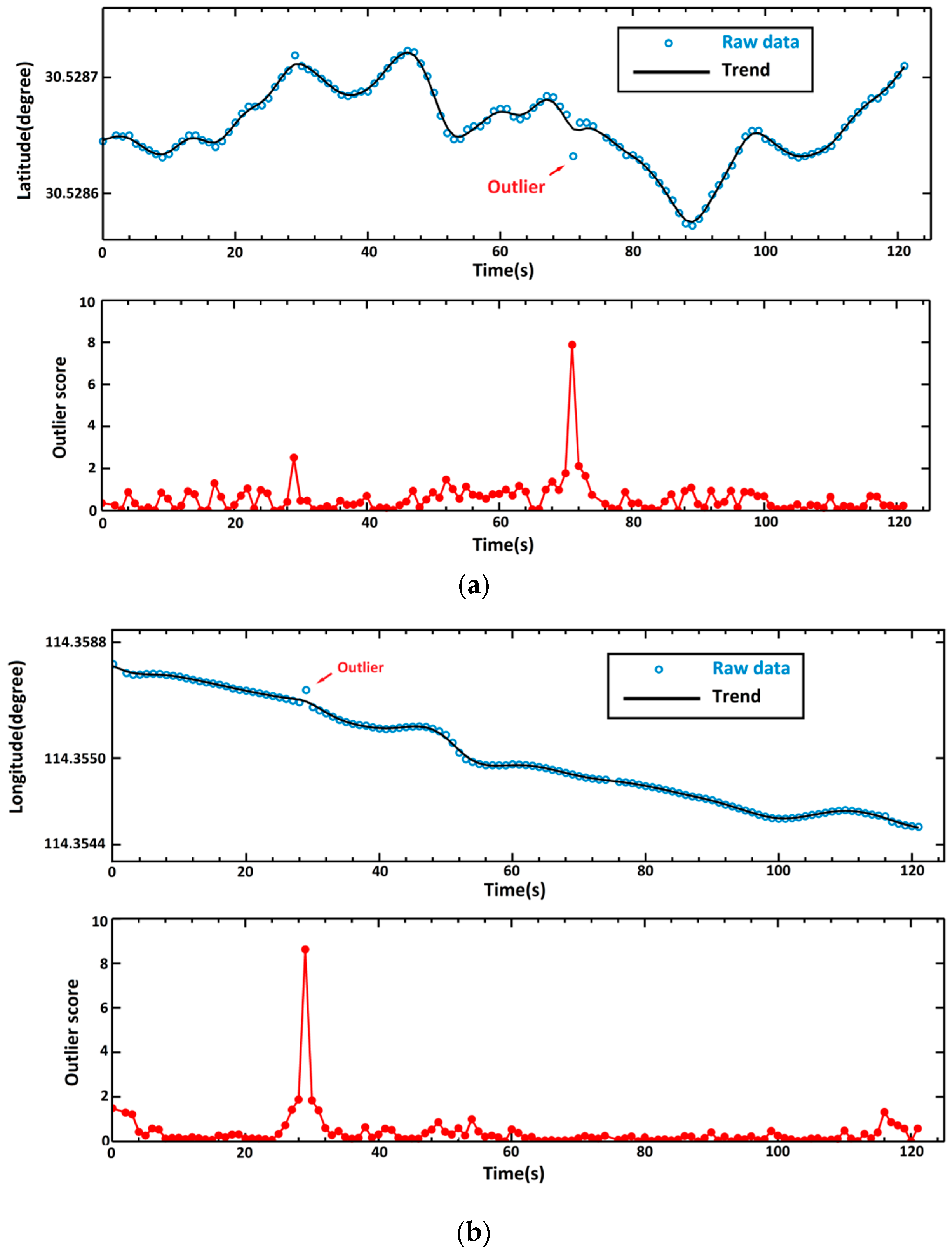
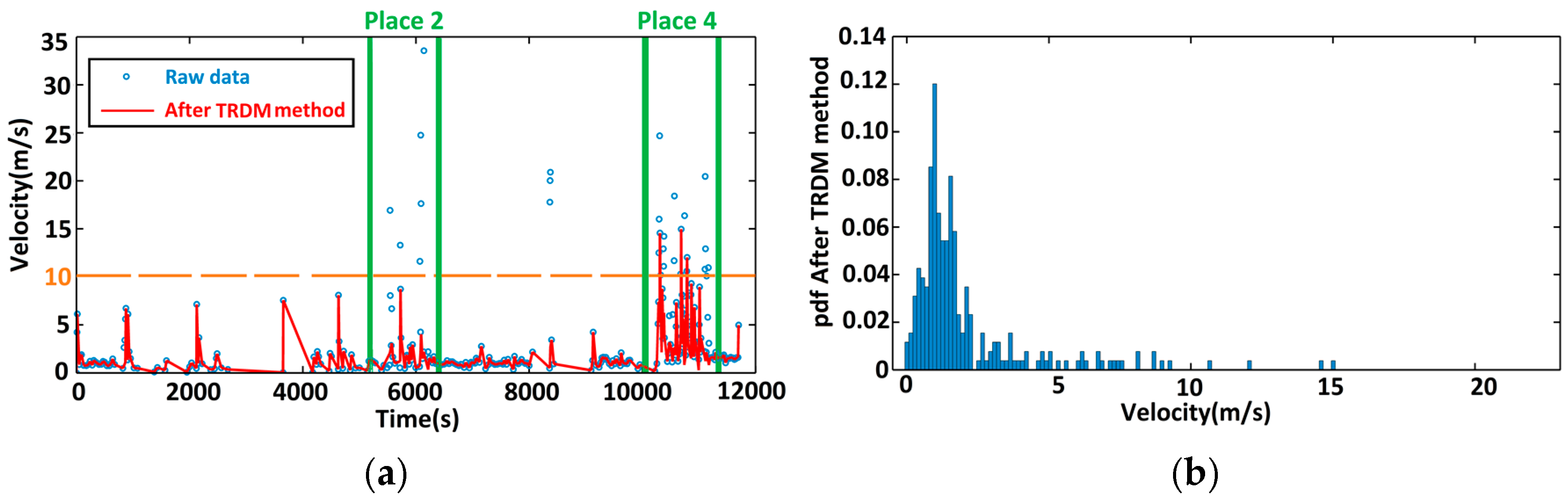
3.1. Vehicle Trajectory
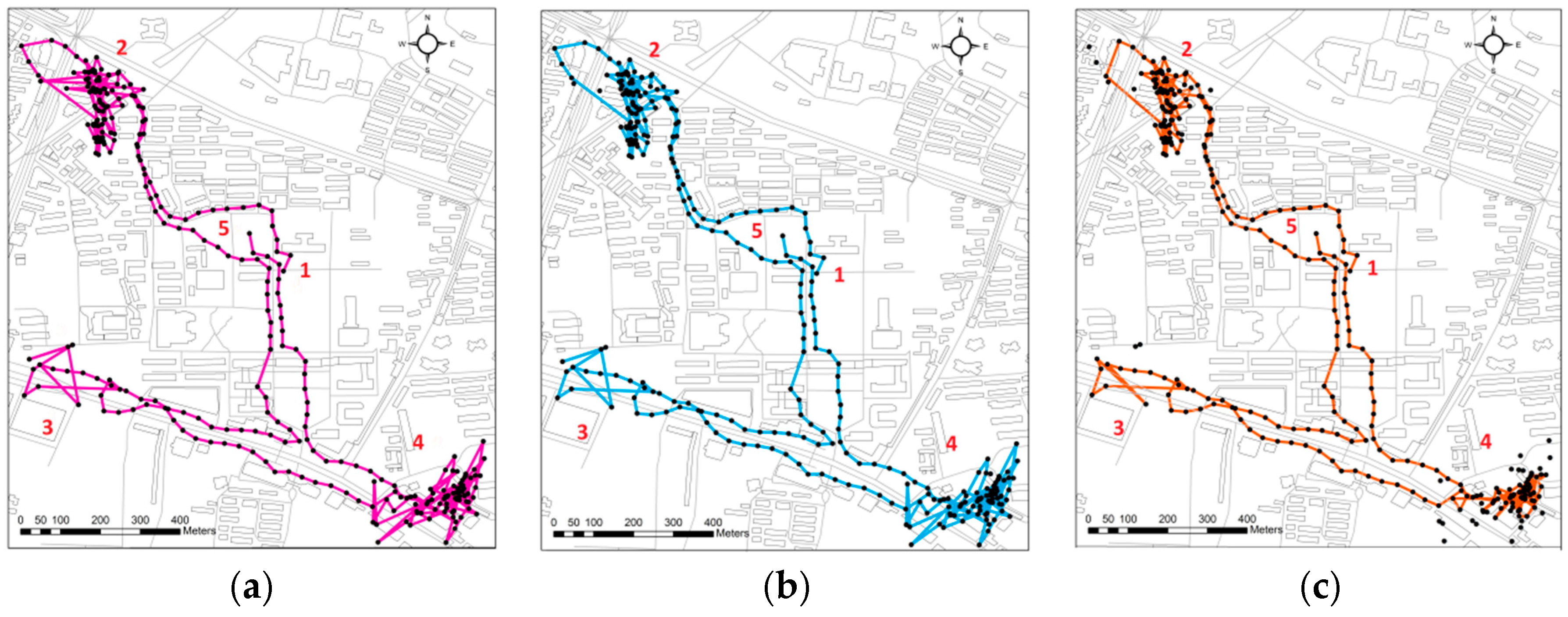
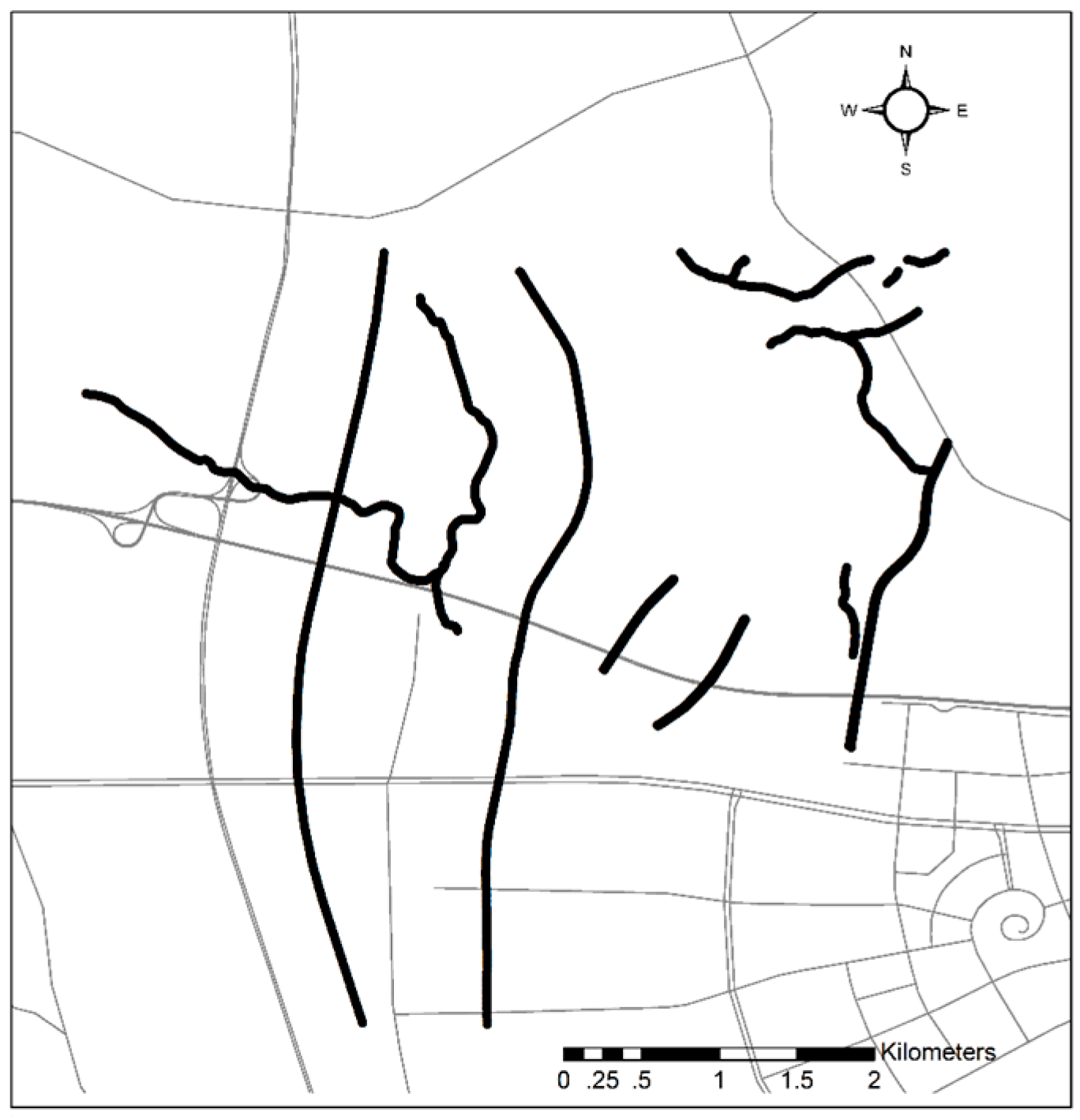
3.2. Walker Trajectories
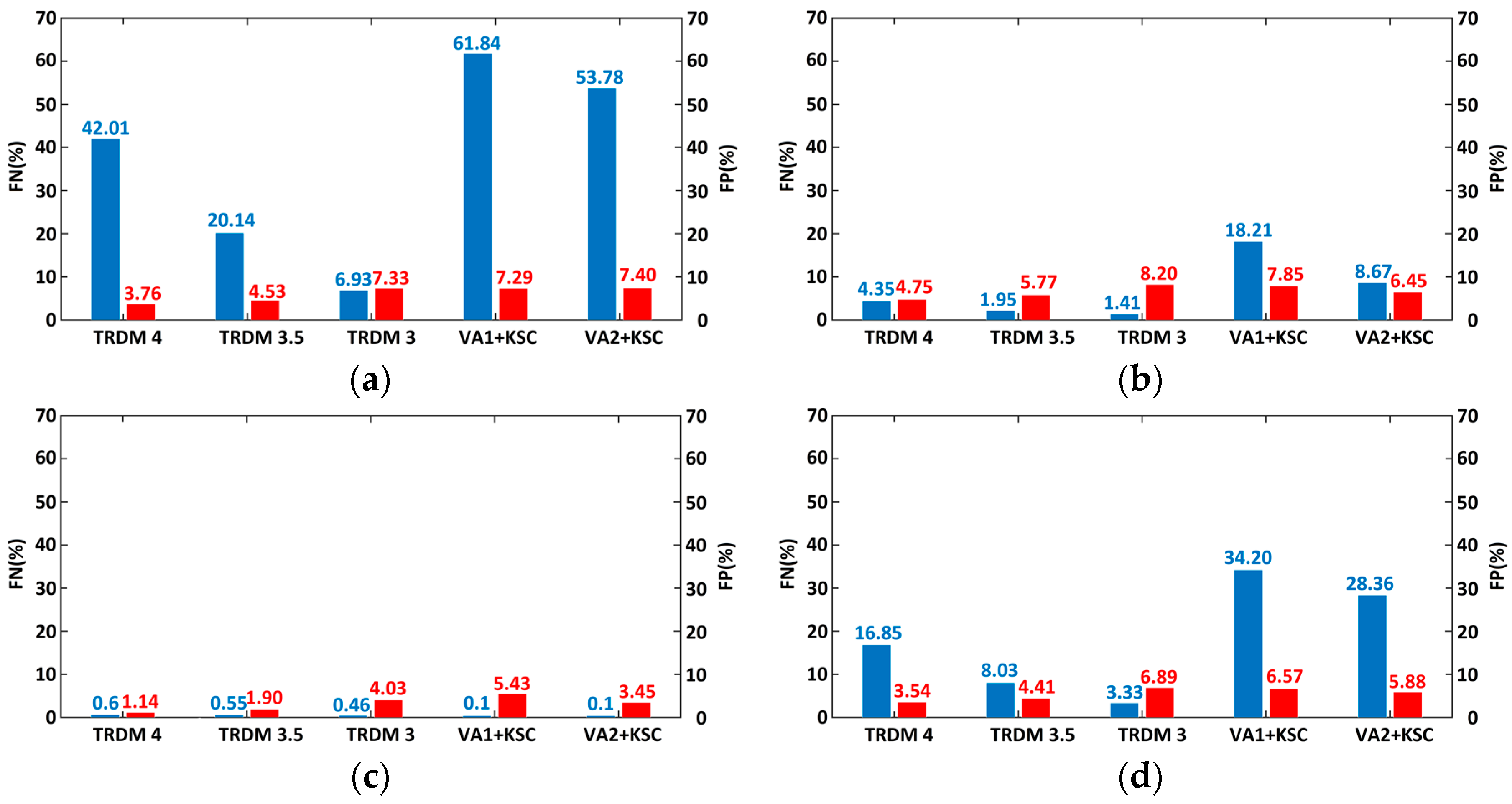
3.3. Performance Evaluation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahmed, M.; Karagiorgou, S.; Pfoser, D.; Wenk, C. A comparison and evaluation of map construction algorithms using vehicle tracking data. GeoInformatica 2015, 19, 601–632. [Google Scholar] [CrossRef]
- Djahel, S.; Doolan, R.; Muntean, G.M.; Murphy, J. A communications-oriented perspective on traffic management systems for smart cities: Challenges and innovative approaches. IEEE Commun. Surv. Tutor. 2015, 17, 125–151. [Google Scholar] [CrossRef]
- Liu, Y.; Seah, H.S. Points of interest recommendation from GPS trajectories. Int. J. Geogr. Inf. Sci. 2015, 29, 953–979. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Wang, J.; Tan, X. Performance analysis on carrier phase-based tightly-coupled GPS/BDS/INS integration in GNSS degraded and denied environments. Sensors 2015, 15, 8685–8711. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Lv, C.; Dong, Q. A novel robust H∞ filter based on Krein space theory in the SINS/CNS attitude reference system. Sensors 2016, 16, 396. [Google Scholar] [CrossRef] [PubMed]
- Tamazin, M.; Noureldin, A.; Korenberg, M.J.; Massoud, A. Robust fine acquisition algorithm for GPS receiver with limited resources. GPS Solut. 2016, 20, 77–88. [Google Scholar] [CrossRef]
- Ye, N.; Wang, Z.Q.; Malekian, R.; Lin, Q.; Wang, R.C. A method for driving route predictions based on hidden Markov model. Math. Probl. Eng. 2015, 2015, 824532. [Google Scholar] [CrossRef]
- Hung, C.C.; Peng, W.C.; Lee, W.C. Clustering and aggregating clues of trajectories for mining trajectory patterns and routes. VLDB J. 2015, 24, 169–192. [Google Scholar] [CrossRef]
- Lv, C.; Chen, F.; Xu, Y.; Song, J.; Lv, P. A trajectory compression algorithm based on non-uniform quantization. In Proceedings of the 2015 IEEE 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 2469–2474.
- Terroso-Saenz, F.; Valdes-Vela, M.; den Breejen, E.; Hanckmann, P.; Dekker, R.; Skarmeta-Gomez, A.F. CEP-traj: An event-based solution to process trajectory data. Inf. Syst. 2015, 52, 34–54. [Google Scholar] [CrossRef]
- Liu, H.; Shah, S.; Jiang, W. On-line outlier detection and data cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar] [CrossRef]
- Lee, W.C.; Krumm, J. Trajectory preprocessing. In Computing with Spatial Trajectories; Zheng, Y., Zhou, X., Eds.; Springer: New York, NY, USA, 2011; pp. 3–33. [Google Scholar]
- Van Winden, K.; Biljecki, F.; van der Spek, S. Automatic update of road attributes by mining GPS tracks. Trans. GIS 2016, 20, 664–683. [Google Scholar] [CrossRef]
- Qiu, W.; Bandara, A. GPS trace mining for discovering behaviour patterns. In Proceedings of the 2015 IEEE International Conference on Intelligent Environments (IE), Prague, Czech, 15–17 July 2015; pp. 65–72.
- Li, X. Using complexity measures of movement for automatically detecting movement types of unknown GPS trajectories. Am. J. Geogr. Inf. Syst. 2014, 3, 63–74. [Google Scholar]
- Sigakova, K.; Mbiydzenyuy, G.; Holmgren, J. Impacts of traffic conditions on the performance of road freight transport. In Proceedings of the 2015 18th IEEE International Conference on Intelligent Transportation Systems (ITSC), Las Palmas, Spain, 15–18 September 2015; pp. 2947–2952.
- Chen, L.; Lv, M.; Ye, Q.; Chen, G.; Woodward, J. A personal route prediction system based on trajectory data mining. Inf. Sci. 2011, 181, 1264–1284. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Y.; He, Z.; Yue, Y.; Li, Q. Challenges and Opportunities in Exploiting Large-Scale GPS Probe Data; Technical Report, HPL-2011-109; HP Laboratories: Palo Alto, CA, USA, 2011. [Google Scholar]
- Pearson, R.K. Outliers in process modeling and identification. IEEE Trans. Control Syst. Technol. 2002, 10, 55–63. [Google Scholar] [CrossRef]
- Yin, S.; Wang, G.; Yang, X. Robust PLS approach for KPI-related prediction and diagnosis against outliers and missing data. Int. J. Syst. Sci. 2014, 45, 1375–1382. [Google Scholar] [CrossRef]
- Gogoi, P.; Bhattacharyya, D.K.; Borah, B.; Kalita, J.K. A survey of outlier detection methods in network anomaly identification. Comput. J. 2011, 54, 570–588. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Real time traffic flow outlier detection using short-term traffic conditional variance prediction. Transp. Res. C Emerg. Technol. 2015, 50, 160–172. [Google Scholar] [CrossRef]
- Markou, M.; Singh, S. Novelty detection: A review—Part 1: Statistical approaches. Signal Process. 2003, 83, 2481–2497. [Google Scholar] [CrossRef]
- Chazal, F.; Chen, D.; Guibas, L.; Jiang, X.; Sommer, C. Data-driven trajectory smoothing. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 1–4 November 2011; pp. 251–260.
- Green, P.J.; Silverman, B.W. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Fox, A.J. Outliers in time series. J. R. Stat. Soc. B 1972, 34, 350–363. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tsay, R.S.; Tiao, G.C. Consistent estimates of autoregressive parameters and extended sample autocorrelation function for stationary and nonstationary ARMA models. J. Am. Stat. Assoc. 1984, 79, 84–96. [Google Scholar] [CrossRef]
- Durbin, J. Efficient estimation of parameters in moving-average models. Biometrika 1959, 46, 306–316. [Google Scholar] [CrossRef]
- Chang, I.; Tiao, G.C.; Chen, C. Estimation of time series parameters in the presence of outliers. Technometrics 1988, 30, 193–204. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Simonoff, J.S.; Tsai, C.L. Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. J. R. Stat. Soc. B 1998, 60, 271–293. [Google Scholar] [CrossRef]
- Chan, W.S. A comparison of some of pattern identification methods for order determination of mixed ARMA models. Stat. Probab. Lett. 1999, 42, 69–79. [Google Scholar] [CrossRef]
- Stadnytska, T.; Braun, S.; Werner, J. Comparison of automated procedures for ARMA model identification. Behav. Res. Methods 2008, 40, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xie, J.; Guo, J. A new maneuvering target tracking method using adaptive cubature Kalman filter. In Proceedings of the 2014 IEEE International Conference on Control Science and Systems Engineering (CCSSE), Yantai, China, 29–30 December 2014; pp. 40–44.
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Zheng, Y. Trajectory data mining: An overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 29. [Google Scholar] [CrossRef]
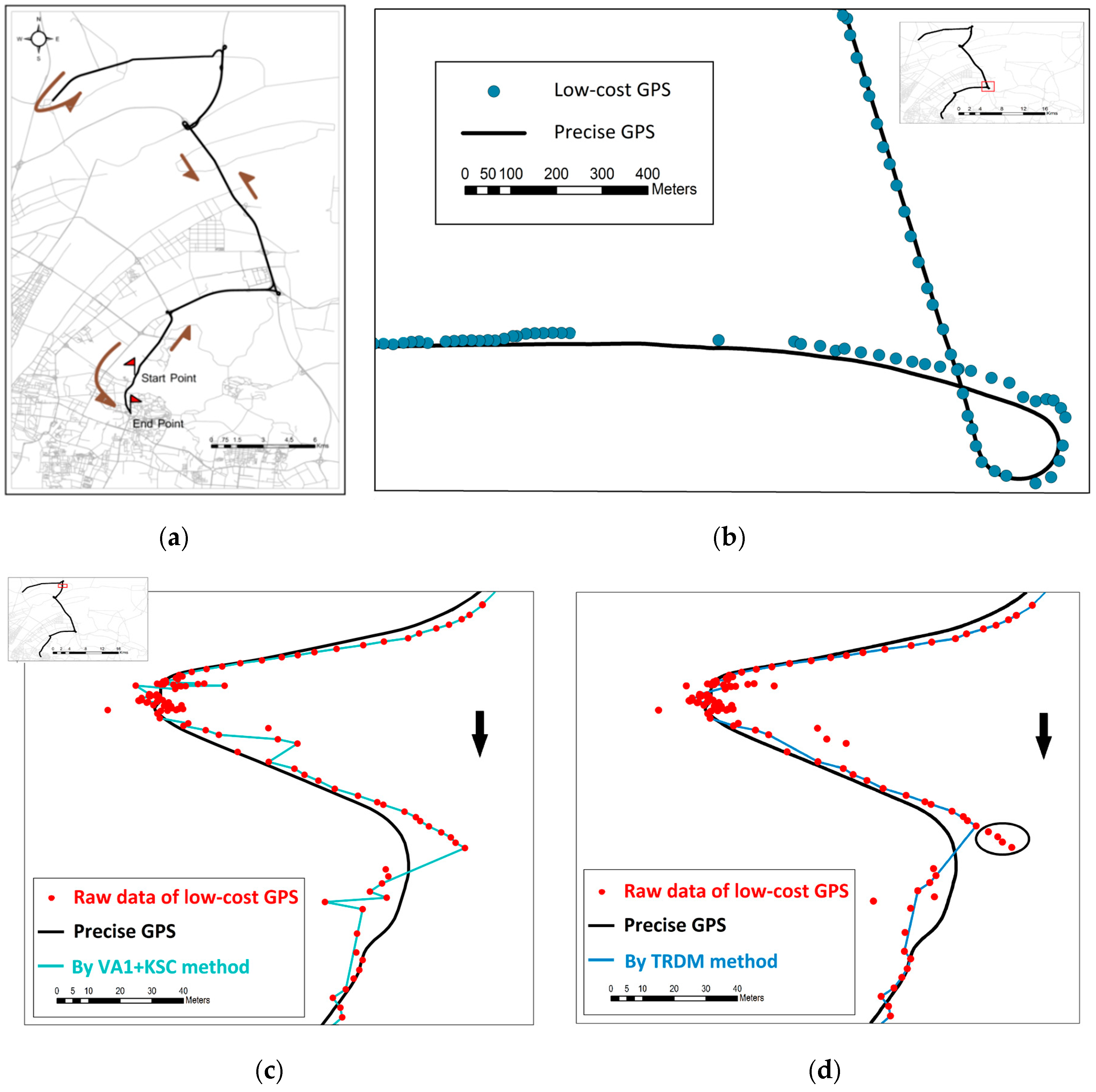


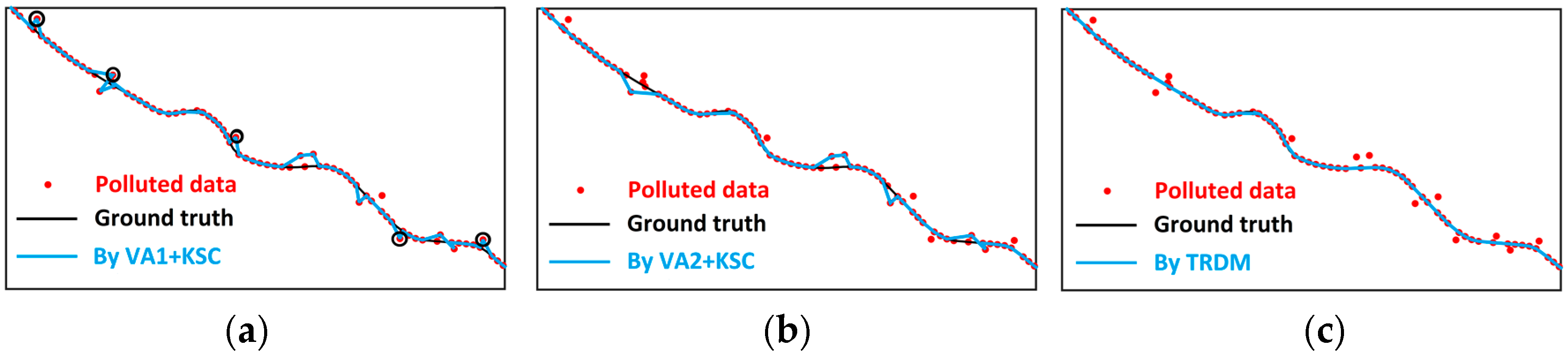
| Standard Deviation | 95th-Pecentile | |
|---|---|---|
| VA1 + KSC | 4.01 | 12.03 |
| TRDM | 2.29 | 7.14 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Cui, T.; Fu, J.; Peng, J.; Shan, J. Trend-Residual Dual Modeling for Detection of Outliers in Low-Cost GPS Trajectories. Sensors 2016, 16, 2036. https://doi.org/10.3390/s16122036
Chen X, Cui T, Fu J, Peng J, Shan J. Trend-Residual Dual Modeling for Detection of Outliers in Low-Cost GPS Trajectories. Sensors. 2016; 16(12):2036. https://doi.org/10.3390/s16122036
Chicago/Turabian StyleChen, Xiaojian, Tingting Cui, Jianhong Fu, Jianwei Peng, and Jie Shan. 2016. "Trend-Residual Dual Modeling for Detection of Outliers in Low-Cost GPS Trajectories" Sensors 16, no. 12: 2036. https://doi.org/10.3390/s16122036
APA StyleChen, X., Cui, T., Fu, J., Peng, J., & Shan, J. (2016). Trend-Residual Dual Modeling for Detection of Outliers in Low-Cost GPS Trajectories. Sensors, 16(12), 2036. https://doi.org/10.3390/s16122036






