Abstract
A quanta image sensor (QIS) is a class of single-photon imaging devices that measure light intensity using oversampled binary observations. Because of the stochastic nature of the photon arrivals, data acquired by QIS is a massive stream of random binary bits. The goal of image reconstruction is to recover the underlying image from these bits. In this paper, we present a non-iterative image reconstruction algorithm for QIS. Unlike existing reconstruction methods that formulate the problem from an optimization perspective, the new algorithm directly recovers the images through a pair of nonlinear transformations and an off-the-shelf image denoising algorithm. By skipping the usual optimization procedure, we achieve orders of magnitude improvement in speed and even better image reconstruction quality. We validate the new algorithm on synthetic datasets, as well as real videos collected by one-bit single-photon avalanche diode (SPAD) cameras.
1. Introduction
1.1. Quanta Image Sensor
Since the birth of charge coupled devices (CCD) in the late 1960s [1] and the complementary metal-oxide-semiconductor (CMOS) active pixel sensors in the early 1990s [2], the pixel pitch of digital image sensors has been continuously shrinking [3]. Shrinking the pixel pitch is intimately linked to the need of increasing image resolution, reducing power consumption and reducing the size and weight of cameras. However, as pixel pitch shrinks, the amount of photon flux detectable by each pixel drops, leading to reduced signal strength. In addition, the maximum number of photoelectrons that can be held in each pixel, known as the full-well capacity, also drops. Small full-well capacity causes reduced maximum signal-to-noise ratio and lowers the dynamic range of an image [4]. Therefore, pushing for smaller pixels, although feasible in the near future, will become a major technological hurdle to new image sensors.
A quanta image sensor (QIS) is a class of solid-state image sensors originally proposed by Eric Fossum as a candidate solution for sub-diffraction-limit pixels. The sensor was first named the digital film sensor [5] and later the quanta image sensor [6,7,8,9] (see [10] for a more comprehensive discussion of the history). A similar idea to QIS was developed a few years later by EPFL (École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland), known as the Gigavision camera [11,12,13]. In the past few years, research groups at the University of Edinburgh (Edinburgh, UK) [14,15,16], as well as EPFL [17,18] have made new progresses in QIS using binary single-photon avalanche diode (SPAD) cameras. In the industry, Rambus Inc. (Sunnyvale, CA, USA) is developing binary image sensors for high dynamic range imaging [19,20,21]. For the purpose of this paper, we shall not differentiate these sensors, but refer to them generally as the QIS, because their underlying mathematical principles are similar.
The working principle of QIS is as follows: In CCD and CMOS, one considers each pixel as a “bucket” that collects and integrates photoelectrons. The bucket is partitioned in QIS into thousands of nanoscale cells referred to as “jots”. Each jot is capable of detecting a single photon to generate a binary response indicating whether the photon count is above or below a certain threshold q. If the photon count is above q, the sensor outputs a “1”; If the photon count is below q, the sensor outputs a “0”. QIS has a very small full-well capacity because it is not designed to accumulate photons. Since the binary response is generated as soon as the number of photons exceeds the threshold, QIS can be operated at very high speed. For example, using single-photon avalanche diodes (SPAD), one can achieve 10k frames per second with a spatial resolution of pixels [14] or even 156k frames per second with a spatial resolution of pixels [17]. For a higher spatial resolution, Massondian et al. [9] reports a QIS operating at 1000 frames per second for a spatial resolution of pixels.
From a signal processing perspective, the challenge of QIS is the extremely lossy process using binary measurements to acquire the light intensity. In order to compensate for the loss, QIS over-samples the space by using a large number of jots and takes multiple exposures in time. This technique is similar to the classic approach in oversampled analog-to-digital conversions.
1.2. Scope and Contribution
The theme of this paper is about how to reconstruct images from the one-bit quantized measurements. Image reconstruction is a critical component of QIS, for without such an algorithm, we will not be able to form images. However, unlike classical Poisson image recovery problems where solutions are abundant [22,23,24,25,26,27], the one-bit quantization of QIS makes the problem uniquely challenging, and there is a limited number of existing methods [28,29,30,31]. Another challenge we have to overcome is the complexity of the algorithm, which has to be low enough that we can put them on cameras to minimize power consumption, memory consumption and runtime. Numerical optimization algorithms are generally not recommended if they are iterative and require intensive computation for every step.
The main contribution of this paper is a non-iterative image reconstruction algorithm for QIS data. We emphasize the non-iterative nature of the algorithm as it makes the algorithm different from existing methods. The new algorithm is based on a transform-denoise framework. The idea is to apply a variance stabilizing transform known as the Anscombe transform [32] to convert a sum of one-bit quantized Poisson random variables to binomial random variables with equal variances. When variance is stabilized, standard image denoising algorithms can be applied to smooth out the noise in the image. Transform-denoise is a single-pass algorithm with no iteration. Empirically, we find that the new algorithm achieves two orders of magnitude improvement in speed and provides an even better reconstruction result than existing iterative algorithms.
The rest of the paper is organized as follows. First, in Section 2, we present the imaging model of QIS. We discuss how the light intensity of the scene is over-sampled and what statistics do the one-bit quantized measurements have. Unlike existing works, which typically assume a quantization level , we make no assumption about q, except that it is a positive integer. This requires some discussion about the incomplete Gamma function. We also discuss why a simple summation over a local spatial-temporal volume is insufficient to reconstruct images. Section 3 presents the main algorithm. We discuss the concept of variance stabilizing transform, its derivation and its limitations. We also discuss how various image denoising algorithms can be plugged into the framework. In Section 4, we present experimental results. There are two sets of data we will discuss. One is a synthetic dataset in which we can objectively measure the reconstruction quality. The other one is a set of real videos captured by SPAD cameras. We compare the proposed algorithm with existing methods. Proofs of major theorems are given in the Appendix A.
2. QIS Imaging Model
In this section, we provide a quick overview of the QIS imaging model. A similar description of the model was previously discussed in [13,29]. For notational simplicity, we consider one-dimensional signals. The extension to the two-dimensional images is straightforward. Furthermore, we follow [5] by referring to sub-pixels of a QIS as “jots”.
The mathematics of QIS is built upon two concepts: (1) a spatial oversampling process to model the acquisition by the sensor; and (2) a quantized Poisson process to model the photon arrivals. The block diagram of the model is summarized in Figure 1.
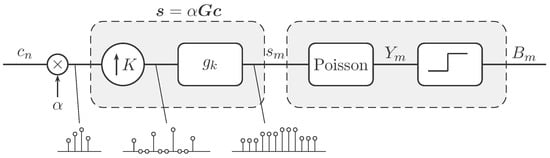
Figure 1.
Block diagram of the QIS imaging model. An input signal is scaled by a constant . The first part of the block diagram is the upsampling followed by a linear filter . The overall process can be written as . The second part of the block diagram is to generate a binary random variable from Poisson random variable . The example at the bottom shows the case where .
2.1. Oversampling Mechanism
We represent the light intensity of a scene using a digital signal . To avoid the ambiguity of the scaling, we assume that is normalized so that for . A fixed and known constant is multiplied to scale to the proper range.
QIS is a spatial oversampling device. For an N-element signal , QIS uses number of jots to acquire . Thus, every in the signal is sampled by jots. The ratio is called the spatial oversampling factor. To model the oversampling process, we follow [13] by considering an upsampling operator and a low-pass filter with filtering coefficients , as shown in Figure 1. Since upsampling and low-pass filtering are linear operations, the overall process can be compactly expressed using a matrix-vector multiplication
where is the light intensity arriving at those M jots, and the matrix encapsulates the upsampling process and the linear filtering.
There are a variety of choices for the low-pass filter depending on which filter provides a better model of the light intensity. In this paper, we make the following assumption about the low-pass filter.
Assumption 1.
We assume that is a boxcar function, such that for . Consequently, the matrix is
where is a K-by-one all one vector, is an N-by-N identity matrix and ⊗ denotes the Kronecker product.
Intuitively, what Assumption 1 does is to assume that the light intensity is piecewise constant. As will be discussed in Section 3, this is important for us to derive simple algorithms.
2.2. Quantized Poisson Observation
At the surface of the m-th jot, the light intensity generates photons according to the Poisson distribution
where denotes the Poisson random variable at the m-th jot and denotes the realization of .
The one-bit quantization of QIS is a truncation of with respect to a threshold . Precisely, the observed one-bit measurement at the m-th jot is
Denoting the random variable of the one-bit measurement at the m-th jot, it follows that the probability of observing is
and the probability of observing is .
For general q, keeping track of the sum of exponentials in Equation (5) could be cumbersome. To make our notations simple, we adopt a useful function called the incomplete Gamma function [33], defined as follows.
Definition 1.
The incomplete Gamma function for a fixed threshold is defined as
where is the standard Gamma function evaluated at q.
The incomplete Gamma function is continuous in s, but discrete in q. For every fixed s, is the cumulative distribution of a Poisson random variable evaluated at . When q is fixed, is the likelihood function of the random variable . In this paper, we will focus on the latter case where q is fixed so that is a function of s. Since is continuous, the derivative of is available:
Property 1.
Example 1.
When , the incomplete Gamma function becomes . In this case,
2.3. Image Reconstruction for QIS
We consider a multiple exposure setting. Assuming that the scene is stationary, the measurement we obtain is a sequence of binary bit maps , where the first index m runs through the M jots spatially, and the second index t runs through the T frames in time. The image reconstruction task is to find the signal that best explains . Translating into a probabilistic framework, this can be formulated as maximizing the likelihood:
where the constraint follows from Equation (1). Taking the logarithm on the right-hand side of Equation (9), the maximization becomes
The optimization in Equation (10) is known as the maximum likelihood estimation (MLE). As shown in [13], the objective function of Equation (10) is concave (for any q), and therefore, the global maximum exists and is unique. When satisfies Assumption 1, the closed form solution is available, and we will show it in Section 3. However, for general or if we include additional constraints to enforce the smoothness of the solution, e.g., using total variation [34] or sparsity [35], then numerical algorithms are required. Some existing methods include the gradient descent method [13], Newton method [28] and the alternating direction method of multipliers [29]. These algorithms are iterative, and the computation for each iteration is costly.
3. Non-Iterative Image Reconstruction
In this section, we present a non-iterative image reconstruction algorithm for QIS. There are three components behind the algorithm. The first is the closed-form solution of Equation (10), which is coherent to [13]. The second component is a variance stabilizing transform that transforms the sum of one-bit quantized Poisson random variables to a binomial random variable with equal variances. The transformation is known as the Anscombe transform, named after the English statistician Frank Anscombe (1918–2001). The third idea is the application of an off-the-shelf image denoiser.
3.1. Component 1: Approximate MLE
Because of the piecewise constant property of Assumption 1, the sequence can be partitioned into N blocks where each block contains binary bits. This leads to a decomposition of Equation (10) as
where the subsequence denotes the n-th block of the t-th frame. Define
be the sum of the bits (i.e., the number of one’s) in . Then, Equation (11) becomes
where . The maximum of Equation (13) is attained when each individual term in the sum attains its maximum. In this case, the closed form solution of Equation (13), for every n, can be derived as in Proposition Equation 1.
Proposition 1.
The solution of Equation (13) is
where , K is the spatial oversampling factor and T is the number of exposures.
Proof.
See Appendix A. ☐
It would be instructive to illustrate Proposition 1 using a figure. Figure 2 shows the case when , i.e., a single exposure, and . The one-bit measurements are first averaged to compute the number of ones within a block of size K. Then, applying the inverse incomplete Gamma function and a scaling constant , we obtain the solution .
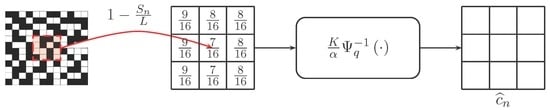
Figure 2.
Pictorial interpretation of Proposition 1: Given an array of one-bit measurements (black = 0, white = 1), we compute the number of ones within a block of size K. Then, the solution of the MLE problem in Equation (13) is found by applying an inverse incomplete Gamma function and a scaling factor .
Proposition 1 shows why a simple summation is inadequate to achieve the desired result, although such summation has been used in [18,36]. By only summing the number of ones, the resulting value is the empirical average of these one-bit measurements. Since the probability of drawing a one in QIS follows a quantized Poisson distribution and not a Bernoulli distribution, the nonlinearity due to the quantized Poisson distribution must be taken into account. A comparison of the ground truth image, the summation result and the MLE solution is shown in Figure 3.

Figure 3.
Image reconstruction using synthetic data. In this experiment, we generate one-bit measurements using a ground truth image (a) with , , , (so ). The result shown in (b) is obtained using the simple summation, whereas the result shown in (c) is obtained using the MLE solution. It can be seen that the simple summation has a mismatch in the tone compared to the ground truth.
As an immediate corollary of Proposition 1, we can simplify the inverse incomplete Gamma function when . This result is sometimes known as the exponential correction function [37].
Corollary 1.
When , the MLE solution of the n-th pixel is
where is the number of ones in the n-th block (See Equation. (12)) and is the total number of pixels in the block.
Proof.
The result follows from the fact that for . Thus, . ☐
3.2. Component 2: Anscombe Transform
The MLE solution computed through Proposition 1 is noisy, as illustrated in Figure 3. The reason is that for a relatively small K and T, the randomness in the one-bit measurement has not yet been eliminated by the summation in . Therefore, in order to improve the image quality, additional steps must be taken to improve the smoothness of the image.
At first glance, this question seems easy because if one wants to mitigate the noise in , then directly applying an image denoising algorithm to would be sufficient, e.g., Figure 4a. However, a short afterthought will suggest that such an approach is invalid for the following reason. For the majority of image denoising algorithms in the literature, the noise is assumed to be independently and identically distributed (i.i.d.) Gaussian. In other words, the variance of the noise should be spatially invariant. However, the resulting random variable in Figure 2 does not have this property.
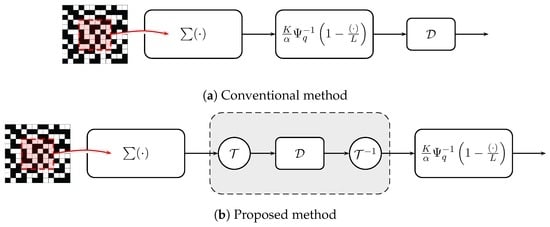
Figure 4.
Two possible ways of improving image smoothness for QIS. (a) The conventional approach denoises the image after is computed; (b) the proposed approach: apply the denoiser before the inverse incomplete Gamma function, together with a pair of Anscombe transforms . The symbol in this figure denotes a generic Gaussian noise image denoiser.
Our proposed solution is to apply an image denoiser before the inverse incomplete Gamma function as shown in Figure 4b. Besides the order of denoising and the Gamma function, we also add a pair of nonlinear transforms and before and after the denoiser . The reasons for these two changes are based on the following observations.
Observation 1.
Under Assumption 1, the random variables are i.i.d. Bernoulli of equal probability for and .
The proof of Observation 1 follows immediately from Assumption 1 that if , we can divide the M jots into N groups each having entries. Within the group, the one-bit measurements are all generated from the same pixel .
The consequence of Observation 1 is that for a sequence of i.i.d. Bernoulli random variables, the sum is a Binomial random variable. This is described in Observation 2.
Observation 2.
If are i.i.d. Bernoulli random variables with probability for and , then the sum defined in Equation (12) is a Binomial random variable with mean and variance:
Observation 2 is a classic result in probability. The mean of the Bernoulli random variables is specified by the incomplete Gamma function , which approaches one as K increases. Thus, for fixed T, the probability as . When this happens, the binomial random variable can be approximated by a Poisson random variable with mean [38]. However, as T also grows, the binomial random variable can be further approximated by a Gaussian random variable due to the central limit theorem. Therefore, for a reasonably large K and T, the resulting random variable is approximately Gaussian.
The variance of this approximated Gaussian is, however, not constant. The variance changes across different locations n because is a function of . Therefore, if we want to apply a conventional image denoiser (which assumes i.i.d. Gaussian noise) to smooth , we must first make sure that the noise variance is spatially invariant. The technique used to accomplish this goal is called the variance stabilizing transform [39]. In this paper, we use a specific variance stabilizing transform known as the Anscombe transform [32]. Anscombe transform is best known in the image processing literature for Poisson denoising, where one transforms observed Poisson data to approximately Gaussian with equal variance [24]. For binomial random variables , the Anscombe transform and its property are given in Theorem 1.
Theorem 1
(Anscombe transform for binomial random variables). Let be a binomial random variable with parameters , where and . Define the Anscombe transform of as a function , such that
Then, the variance of is for all n.
Proof.
The proof of Theorem 1 is given in the Appendix A. It is a simplified version of a technical report by Brown et al. [40]. The original paper by Anscombe [32] also contains a sketch of the proof. However, the sketch is rather brief, and we believe that a complete derivation would make this paper self-contained. ☐
The implication of Theorem 1 is that regardless of the location n, the transformed random variable has a constant variance when L is large. Therefore, the noise variance is now location independent, and hence, a standard i.i.d. Gaussian denoiser can be used.
Example 2.

To provide readers a demonstration of the effectiveness of Theorem 1, we consider a checkerboard image of pixels with intensity levels . The n-th pixel generates binary quantized Poisson measurements using , , (so ). From each of these K measurements, we sum to obtain a binomial random variable . We then compute the variance of and using independent Monte Carlo trials. The results are shown in Figure 5, where we observe that varies with the location n, and is nearly constant for all n.

Figure 5.
Illustration of Anscombe transform. Both sub-figures contain () pixels . For each pixel, we generate 100 binary Poisson measurements and sum to obtain binomial random variables . We then calculate the variance of each . Note the constant variance after the Anscombe transform.
Remark 1.
The inverse Anscombe transform is
which we call the algebraic inverse. Another possible inverse of the Anscombe transform is the asymptotic unbiased inverse [32], defined as
The performance of the unbiased inverse is typically better for low noise (large L), whereas the algebraic inverse is better for high noise (small L). This is consistent with the Poisson denoising literature. (e.g., [24]).
Example 3.

Table 1 shows the peak signal to noise ratio (PSNR) values of the reconstructed images using the algebraic inverse and the asymptotic unbiased inverse. In this experiment, we consider 10 standard images commonly used in the image processing literature: Baboon, Barbara, Boat, Bridge, Couple, Hill, House, Lena, Man and Peppers. The sizes of the images are either or . For each image, we set , and and vary . The results in Table 1 indicate that is consistently better than for , although the difference diminishes as K grows.

Table 1.
PSNR values using algebraic inverse and asymptotic unbiased inverse . The results are averaged over 10 standard images. In this experiment, we set , and .
3.3. Component 3: Image Denoiser
An important feature of the proposed algorithm is that it can take any off-the-shelf image denoiser for the operator . Here, by image denoiser, we meant an image denoising algorithm designed to remove i.i.d. Gaussian noise from an observed image.
Image denoising is an important research topic by its own. In the following, we provide a few popular image denoising algorithms.
- Total variation denoising [34]: Total variation denoising was originally proposed by Rudin, Osher and Fatemi [34], although other researchers had proposed similar methods around the same time [41]. Total variation denoising formulates the denoising problem as an optimization problem with a total variation regularization. Total variation denoising can be performed very efficiently using the alternating direction method of multipliers (ADMM), e.g., [42,43,44].
- Bilateral filter [45]: The bilateral filter is a nonlinear filter that denoises the image using a weighted average operator. The weights in a bilateral filter are the Euclidean distance between the intensity values of two pixels, plus the spatial distance between the two pixels. A Gaussian kernel is typically employed for these distances to ensure proper decaying of the weights. Bilateral filters are extremely popular in computer graphics for applications, such as detail enhancement. Various fast implementations of bilateral filters are available, e.g., [46,47].
- Non-local Means [48]: non-local means (NLM) was proposed by Buades et al. [48] and, also, an independent work of Awante and Whitaker [49]. Non-local means (NLM) is an extension of the bilateral filter where the Euclidean distance is computed from a small patch instead of a pixel. Experimentally, it has been widely agreed that such patch-based approaches are very effective for image denoising. Fast NLM implementations are now available [50,51,52].
- BM3D [53]: 3D block matching (BM3D) follows the same idea of non-local means by considering patches. However, instead of computing the weighted average, BM3D groups similar patches to form a 3D stack. By applying a 3D Fourier transform (or any other frequency domain transforms, e.g., discrete cosine transform), the commonality of the patches will demonstrate a group sparse behavior in the transformed domain. Thus, by applying a threshold in the transformed domain, one can remove the noise very effectively. BM3D is broadly regarded as a benchmark of today’s image denoising algorithm.
The factors to consider in choosing an image denoiser are typically the complexity and quality. Low complexity algorithms, such as bilateral filter, are fast, but the denoising ability is limited. High end algorithms, such as BM3D and non-local means, produce very good images, but require much computation. The trade-off between complexity and performance is a choice of the user.
Readers at this point may perhaps ask a question: What will happen if we apply a denoiser after the MLE solution, like the one shown in the block diagram in Figure 4a? As we have explained in the Anscombe transform section, this will lead to a suboptimal result because the noise is not i.i.d. Gaussian. To illustrate the difference in terms of performance, we show in Figure 6 a comparison between applying image denoising using the two block diagrams shown in Figure 4. The denoiser we use in this experiment is BM3D. The metric we use to evaluate the performance is the peak signal to noise ratio (PSNR), which will be defined formally in Section 4. In short, a large PSNR value is equivalent to a low mean squared error comparing the estimated image and the ground truth image. The results are shown in Figure 6. Although denoising after the MLE (the conventional idea) generates some reasonable images, the PSNR values are indeed significantly lower than the proposed Anscombe approach. This is not surprising, because the denoiser tends to oversmooth the dark regions and undersmooth the bright regions due to the signal-dependent noise levels.

Figure 6.
Comparison between image denoising after the MLE solution and using the proposed Anscombe transform. The denoiser we use in this experiment is 3D block matching (BM3D) [53]. The binary observations are generated using the configurations , , , . The values shown are the peak signal to noise ratio (PSNR).
3.4. Related Work in the Literature
The proposed algorithm belongs to a family of methods we call the transform-denoise methods. The idea of transform-denoise is similar to what we do here: transform the random variable using a variance stabilizing transform, then denoise using an off-the-shelf image denoiser. Among the existing transform-denoise methods, perhaps the most notable work is the one by Makitalo and Foi [24], where they considered the optimal inverse of the Anscombe transform for the case of Poisson–Gaussian random variables. A more recent work by the same research group [27] showed that it is possible to boost the denoising performance by applying the transform-denoise iteratively. We should also mention the work by Foi [54], which considered the modeling and transformation for clipped noisy images. The problem setting of that work is for conventional sensors. However, the underlying principle using the transform-denoise approach is similar to that of QIS.
The approximate MLE solution in Section 3.1 is based on the piecewise constant assumption (Assumption 1). Under this assumption, summing of the Bernoulli random variables can be thought of as performing a “binning” of the pixels. Binning is a common technique in restoring images from Poisson noise, especially when the signal-to-noise ratio is low [23,25,26]. Binning can also be applied together with transform-denoise, e.g., in [27], to achieve improved results. For QIS, the result of binning is different from that of the Poisson noise, for the sum of QIS bits leads to a binomial random variables, whereas the sum of Poisson noise leads to a Poisson random variable.
4. Experimental Results
In this section, we provide further experimental results to evaluate the proposed algorithm.
4.1. Synthetic Data
In this experiment, we consider 100 natural images downloaded from the Berkeley Segmentation database [55]. The input resolution of these images is (or ), and all images are converted to a gray-scale image with values in the range . To generate the synthetic data, for each image, we consider an oversampling factor of four along the horizontal and the vertical directions (so ). The sensor gain is set as , and the threshold level is to simulate a single photon sensor that triggers at one photon. We generate one-bit observations using a quantized Poisson statistics and use the proposed algorithm to reconstruct. As a comparison, we also test the MLE solution, i.e., a summation followed by the inverse incomplete Gamma transform (see Theorem 1), and an ADMM algorithm using a total variation regularization [29,31]. For the proposed algorithm, we use BM3D as the image denoiser.
We report two results in this experiment. First, we consider the peak signal to noise ratio (PSNR) as an evaluation metric. The PSNR of an estimated image compared to the ground truth image is defined as
where N is the number of pixels in . Typically, higher PSNR values imply better image reconstruction quality. The PSNR values of these 100 images are shown in Figure 7. In this figure, we observe that the proposed algorithm is better than the MLE solution and the ADMM solution by 10.20 dB and 2.75 dB, respectively, which are very substantial amounts from a reconstruction perspective.
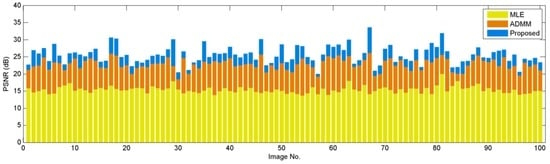
Figure 7.
PSNR comparison of various image reconstruction algorithms on the Berkeley Segmentation database [55]. In this experiment, we fix , , and . The proposed algorithm uses BM3D [53] as the image denoiser.
Apart form the PSNR values, we also report the runtimes of the algorithms. The runtimes of the algorithms are recorded by running the methods on the same machine and the same platform, which is an Intel i7-6700 3.4-GHz desktop with Windows 7/MATLAB 2014. As shown in Figure 8, the runtime of the proposed algorithm is approximately two orders of magnitude () faster than the ADMM algorithm.
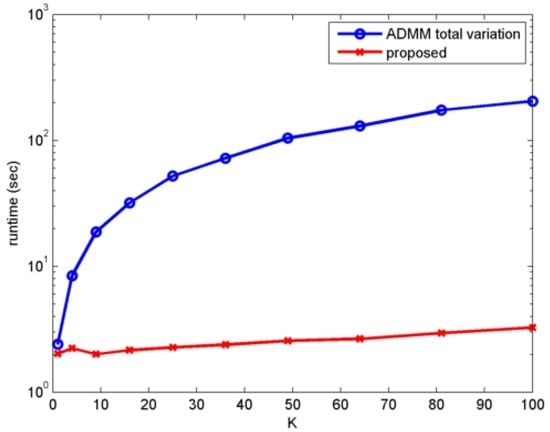
Figure 8.
Runtime comparison of the proposed algorithm and the alternating direction method of multipliers (ADMM) algorithm [31].
As for the influence of the oversampling factor K on the reconstruction quality, we show in Figure 9 the reconstructed results using and the binary one-bit measurements. While it is clear from the figure that the reconstructed image improves as K increases, we observe that most of the visual content has been recovered even at .

Figure 9.
Influence of the oversampling factor K on the image reconstruction quality. In this experiment, we set , . .
4.2. Real Data
In this experiment, we consider two single-photon avalanche diode (SPAD) cameras for capturing high speed videos. The first camera is a CMOS SPAD-based image sensor developed by Dutton et al. [14,15,16]. This camera has a resolution of , with a frame rate of 10k frames per second. The second camera is the SwissSPAD camera developed by Burri et al. [17,18]. This camera has a resolution of , with frame rate of 156k frames per second. Both cameras capture one-bit measurements from a scene containing a stationary background with a rapidly moving foreground. Our experimental goal is to test if the proposed algorithm can resolve the spatial content with minimal trade-off in the temporal resolution.
There are several points of this experiment on which we should comment. First, since the spatial resolution of these two cameras is relatively small (as compared to the synthetic case), we do not assume any spatial oversampling, i.e., . Instead, we use T temporal frames to reconstruct one output image. To ensure smooth transitions across adjacent frames, we use a temporally-sliding window as we progress to the next output image. Second, since these real videos do not have a ground truth, we can only compare the quality of the resulting images visually.
We first look at the results of the SPAD camera by Dutton et al. [14,15,16]. Figure 10 shows several snapshots of the “fan” sequence and the “milk” sequence. To generate this result, we run the proposed algorithm using frames in a sliding window mode. That is, we use Frames 1 to 16 to recover Frame 1 and Frames 2 to 17 to recover Frame 2, etc. The quantization level q is set as , and the sensor gain α is adjusted to produce the best visual quality. For the “fan” sequence, we set , and for the “milk” sequence, we set . As we can see from the figures, the proposed algorithm recovers most of the content from the scene, even revealing the textures of the milk in the scene.
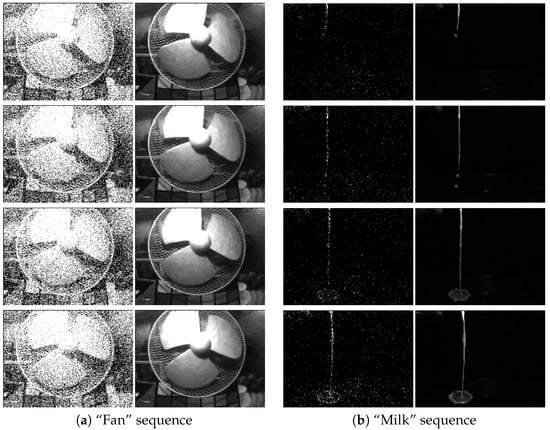
Figure 10.
Image reconstruction of two real video sequences captured using a single-photon avalanche diode (SPAD) camera running at 10k frames per second [14,15,16]. In this experiment, we use frames to construct one output frame. In both columns, the left are the raw one-bit measurements, and the right are the recovered images using the proposed algorithm.
As for the SwissSPAD camera, we consider a video sequence “oscilloscope” captured at a frame rate of 156k frames per second. The goal is to track the sinusoid shown on the oscilloscope’s screen. We consider four values of T = 4, 16, 64 and 256 for the number of frames. The results are shown in Figure 11. As one may expect, when , the image quality improves because we are effectively summing 256 frames to reconstruct one output frame. However, since we are summing the 256 frames, the temporal resolution is severely distorted. In particular, the trace of the sinusoid signal disappears because of the strong averaging effect. When we reduce the number of frames to , we observe that the trace of the signal can be observed clearly. The same image obtained by the MLE (i.e., simple summation) is still highly noisy.

Figure 11.
Image reconstruction of real video sequences captured using the SwissSPAD camera running at 156k frames per second [17,18]. (a) is a snapshot of the raw one-bit image. (b) shows the result of summing T = 4, 16, 64, 256 temporal frames with . (c) shows the corresponding results using the proposed algorithm.
5. Conclusions
We present a new image reconstruction algorithm to recover images from one-bit quantized Poisson measurements. Different from existing algorithms that are mostly iterative, the new algorithm is non-iterative. The algorithm consists of three key components: (1) an approximation to the standard maximum likelihood estimation formulation that allows us to decouple the dependency of pixels; (2) a nonlinear transform known as the Anscombe transform that converts a sum of one-bit quantized Poisson random variables to a Gaussian random variable with equal variance; (3) an off-the-shelf image denoising algorithm that performs the smoothing. Experimental results confirm the performance of the proposed algorithm. The algorithm demonstrates two orders of magnitude improvement in speed compared to existing iterative methods and shows several dBs of improvement in terms of the peak signal to noise ratio (PSNR) as a metric of image quality.
Acknowledgments
We thank Guest Editor Eric R. Fossum for inviting us to submit this work. We thank Neale Dutton and his team for sharing the “fan” and the “milk” sequences collected by their SPAD camera. We thank Edoardo Charbon and his team for sharing the “oscilloscope” sequence collected by the SwissSPAD camera. We would like to give special thanks to the anonymous reviewers, who provided us tremendously helpful feedback on this paper.
Author Contributions
S.H.C.initiated and developed the algorithm. S.H.C. and O.A.E. conducted the analysis of the Anscombe transform. S.H.C. and X.W. analyzed the image denoising algorithms. S.H.C. designed the experiments. O.A.E. and X.W. conducted the experiments. S.H.C. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CCD | Charge coupled device |
| CMOS | Complementary metal-oxide-semiconductor |
| QIS | Quanta image sensors |
| MLE | Maximum likelihood estimation |
| ADMM | Alternating direction method of multipliers |
| SPAD | Single-photon avalanche diode |
| PSNR | Peak signal to noise ratio |
| BM3D | 3D block matching |
| i.i.d. | Independently and identically distributed |
Appendix A
Appendix A.1. Proof of Proposition 1
Proof.
For notational simplicity, we drop the subscript n. Then, the optimization problem is
Taking the first order derivative with respect to c and setting to zero yields (with the help of Property 1):
Rearranging the terms leads to the desired result that
☐
Appendix A.2. Proof of Theorem 1
Proof.
For notational simplicity, we drop the subscript n. Our goal is to show that if X∼, then the transformed variable:
has a variance . To this end, we first consider the function , such that
Since for any c, by letting , we observe that showing Proposition 1 is equivalent to showing .
To show the desired result, we note that for any α and β, the arcsin function has the property that
Define , and substitute , ; it follows that
There are two terms in this equation. The first term can be expanded (using Taylor expansion) to its first second order as
The arcsin function can be expanded to its second order as
for .
We next consider the standardized binomial random variable by defining
Then, by Lemma A1, it follows that
Therefore,
where
Since the first four moments of Y are
we conclude that
☐
Lemma A1.
Let and . It holds that
Proof.
Note that is equivalent to . Thus, F can be expressed in terms of Y as
For large L, we have . Thus, by expanding , we have
where
By expanding , we arrive at
Multiplying both sides by and substituting for yields
The proof of the second equality can be done by expressing in terms of Y as
where
By expanding , we arrive at
Multiplying both sides by and substituting for yields
☐
References
- Press Release of Nobel Prize 2009. Available online: http://www.nobelprize.org/nobel_prizes/physics/laureates/2009/press.html (accessed on 18 November 2016).
- Fossum, E.R. Active Pixel Sensors: Are CCD’s Dinosaurs? Proc. SPIE 1993, 1900, 2–14. [Google Scholar]
- Clark, R.N. Digital Camera Reviews and Sensor Performance Summary. Available online: http://www.clarkvision.com/articles/digital.sensor.performance.summary (accessed on 18 November 2016).
- Fossum, E.R. Some Thoughts on Future Digital Still Cameras. In Image Sensors Signal Processing for Digital Still Cameras; Nakamura, J., Ed.; CRC Press: Boca Raton, FL, USA, 2005; Chapter 11; pp. 305–314. [Google Scholar]
- Fossum, E.R. What to do with sub-diffraction-limit (SDL) pixels?—A proposal for a gigapixel digital film sensor (DFS). In Proceedings of the IEEE Workshop Charge-Coupled Devices and Advanced Image Sensors, Nagano, Japan, 9–11 June 2005; pp. 214–217.
- Fossum, E.R. The Quanta Image Sensor (QIS): Concepts and Challenges. In OSA Technical Digest (CD), Paper JTuE1, Proceedings of the OSA Topical Mtg on Computational Optical Sensing and Imaging, Toronto, ON, Canada, 10–14 July 2011; Optical Society of America: Washington, DC, USA, 2011. [Google Scholar]
- Masoodian, S.; Song, Y.; Hondongwa, D.; Ma, J.; Odame, K.; Fossum, E.R. Early research progress on quanta image sensors. In Proceedings of the International Image Sensor Workshop (IISW), Snowbird, UT, USA, 12–16 June 2013.
- Ma, J.; Fossum, E.R. Quanta image sensor jot with sub 0.3 e− r.m.s. read noise and photon counting capability. IEEE Electron Device Lett. 2015, 36, 926–928. [Google Scholar] [CrossRef]
- Masoodian, S.; Rao, A.; Ma, J.; Odame, K.; Fossum, E.R. A 2.5 pJ/b binary image sensor as a pathfinder for quanta image sensors. IEEE Trans. Electron Devices 2016, 63, 100–105. [Google Scholar] [CrossRef]
- Fossum, E.R.; Ma, J.; Masoodian, S. Quanta image sensor: Concepts and progress. Proc. SPIE Adv. Photon Count. Tech. X 2016, 9858, 985804. [Google Scholar]
- Sbaiz, L.; Yang, F.; Charbon, E.; Susstrunk, S.; Vetterli, M. The gigavision camera. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009; pp. 1093–1096.
- Yang, F.; Sbaiz, L.; Charbon, E.; Süsstrunk, S.; Vetterli, M. On pixel detection threshold in the gigavision camera. Proc. SPIE 2010, 7537. [Google Scholar] [CrossRef]
- Yang, F.; Lu, Y.M.; Sbaiz, L.; Vetterli, M. Bits from photons: Oversampled image acquisition using binary Poisson statistics. IEEE Trans. Image Process. 2012, 21, 1421–1436. [Google Scholar] [CrossRef] [PubMed]
- Dutton, N.A.W.; Parmesan, L.; Holmes, A.J.; Grant, L.A.; Henderson, R.K. 320 × 240 oversampled digital single photon counting image sensor. In Proceedings of the IEEE Symposium VLSI Circuits Digest of Technical Papers, Honolulu, HI, USA, 9–13 June 2014; pp. 1–2.
- Dutton, N.A.W.; Gyongy, I.; Parmesan, L.; Henderson, R.K. Single photon counting performance and noise analysis of CMOS SPAD-based image sensors. Sensors 2016, 16, 1122. [Google Scholar] [CrossRef] [PubMed]
- Dutton, N.A.W.; Gyongy, I.; Parmesan, L.; Gnecchi, S.; Calder, N.; Rae, B.R.; Pellegrini, S.; Grant, L.A.; Henderson, R.K. A SPAD-based QVGA image sensor for single-photon counting and quanta imaging. IEEE Trans. Electron Devices 2016, 63, 189–196. [Google Scholar] [CrossRef]
- Burri, S.; Maruyama, Y.; Michalet, X.; Regazzoni, F.; Bruschini, C.; Charbon, E. Architecture and applications of a high resolution gated SPAD image sensor. Opt. Express 2014, 22, 17573–17589. [Google Scholar] [CrossRef] [PubMed]
- Antolovic, I.M.; Burri, S.; Hoebe, R.A.; Maruyama, Y.; Bruschini, C.; Charbon, E. Photon-counting arrays for time-resolved imaging. Sensors 2016, 16, 1005. [Google Scholar] [CrossRef] [PubMed]
- Vogelsang, T.; Stork, D.G. High-dynamic-range binary pixel processing using non-destructive reads and variable oversampling and thresholds. In Proceedings of the 2012 IEEE Sensors, Taipei, Taiwan, 28–31 October 2012; pp. 1–4.
- Vogelsang, T.; Guidash, M.; Xue, S. Overcoming the full well capacity limit: High dynamic range imaging using multi-bit temporal oversampling and conditional reset. In Proceedings of the International Image Sensor Workshop, Snowbird, UT, USA, 16 June 2013.
- Vogelsang, T.; Stork, D.G.; Guidash, M. Hardware validated unified model of multibit temporally and spatially oversampled image sensor with conditional reset. J. Electron. Imaging 2014, 23, 013021. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Bioucas-Dias, J.M. Restoration of Poissonian images using alternating direction optimization. IEEE Trans. Image Process. 2010, 19, 3133–3145. [Google Scholar] [CrossRef] [PubMed]
- Harmany, Z.T.; Marcia, R.F.; Willet, R.M. This is SPIRAL-TAP: Sparse Poisson intensity reconstruction algorithms: Theory and practice. IEEE Trans. Image Process. 2011, 21, 1084–1096. [Google Scholar] [CrossRef] [PubMed]
- Makitalo, M.; Foi, A. Optimal inversion of the generalized Anscombe transformation for Poisson–Gaussian noise. IEEE Trans. Image Process. 2013, 22, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Salmon, J.; Harmany, Z.; Deledalle, C.; Willet, R. Poisson noise reduction with non-local PCA. J. Math Imaging Vis. 2014, 48, 279–294. [Google Scholar] [CrossRef]
- Rond, A.; Giryes, R.; Elad, M. Poisson inverse problems by the Plug-and-Play scheme. J. Visual Commun. Image Represent. 2016, 41, 96–108. [Google Scholar] [CrossRef]
- Azzari, L.; Foi, A. Variance stabilization for noisy+estimate combination in iterative Poisson denoising. IEEE Signal Process. Lett. 2016, 23, 1086–1090. [Google Scholar] [CrossRef]
- Yang, F.; Lu, Y.M.; Sbaiz, L.; Vetterli, M. An optimal algorithm for reconstructing images from binary measurements. Proc. SPIE 2010, 7533, 75330K. [Google Scholar]
- Chan, S.H.; Lu, Y.M. Efficient image reconstruction for gigapixel quantum image sensors. In Proceedings of the 2014 IEEE Global Conference on Signal Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014; pp. 312–316.
- Remez, T.; Litany, O.; Bronstein, A. A picture is worth a billion bits: Real-time image reconstruction from dense binary threshold pixels. In Prroceedings of the 2016 IEEE International Conference on Computational Photography (ICCP), Evanston, IL, USA, 13–15 May 2016; pp. 1–9.
- Elgendy, O.; Chan, S.H. Image reconstruction and threshold design for quanta image sensors. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 978–982.
- Anscombe, F.J. The transformation of Poisson, binomial and negative-binomial data. Biometrika 1948, 35, 246–254. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Elad, M. Sparse and Redundant Representations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Fossum, E.R.; Ma, J.; Masoodian, S.; Anzagira, L.; Zizza, R. The quanta image sensor: Every photon counts. Sensors 2016, 16, 1260. [Google Scholar] [CrossRef] [PubMed]
- Antolovic, I.M.; Burri, S.; Bruschini, C.; Hoebe, R.; Charbon, E. Nonuniformity analysis of a 65-kpixel CMOS SPAD imager. IEEE Trans. Electron Devices 2016, 63, 57–64. [Google Scholar] [CrossRef]
- Leon-Garcia, A. Probability, Statistics, and Random Processes for Electrical Engineering; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Wasserman, L. All of Nonparametric Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Brown, L.; Cai, T.; DasGupta, A. On Selecting a Transformation: With Applications. Available online: http://www.stat.purdue.edu/~dasgupta/vst.pdf (accessed on 18 November 2016).
- Sauer, K.; Bouman, C.A. Bayesian estimation of transmission tomograms using segmentation based optimization. IEEE Trans. Nucl. Sci. 1992, 39, 1144–1152. [Google Scholar] [CrossRef]
- Afonso, M.; Bioucas-Dias, J.; Figueiredo, M. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.H.; Khoshabeh, R.; Gibson, K.B.; Gill, P.E.; Nguyen, T.Q. An augmented Lagrangian method for total variation video restoration. IEEE Trans. Image Process. 2011, 20, 3097–3111. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, Y.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846.
- Paris, S.; Durand, F. A fast approximation of the bilateral filter using a signal processing approach. Int. J. Comput. Vis. 2009, 81, 24–52. [Google Scholar] [CrossRef]
- Chaudhury, K.N.; Sage, D.; Unser, M. Fast (1) bilateral filtering using trigonometric range kernels. IEEE Trans. Image Process. 2011, 20, 3376–3382. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; Volume 2, pp. 60–65.
- Awate, S.P.; Whitaker, R.T. Higher-order image statistics for unsupervised, information-theoretic, adaptive, image filtering. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; Volume 2, pp. 44–51.
- Adams, A.; Baek, J.; Davis, M.A. Fast high-dimensional filtering using the permutohedral lattice. Comput. Graph. Forum 2010, 29, 753–762. [Google Scholar] [CrossRef]
- Chan, S.H.; Zickler, T.; Lu, Y.M. Monte Carlo non-local means: Random sampling for large-scale image filtering. IEEE Trans. Image Process. 2014, 23, 3711–3725. [Google Scholar] [CrossRef] [PubMed]
- Gastal, E.; Oliveira, M. Adaptive manifolds for real-time high-dimensional filtering. ACM Trans. Graph. 2012, 31, 33. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Foi, A. Clipped noisy images: Heteroskedastic modeling and practical denoising. Signal Process. 2009, 89, 2609–2629. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV), Vancouver, BC, Canada, 9–12 July 2001; Volume 2, pp. 416–423.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).