1. Introduction
China is rich in the reserve of CBM (coalbed methane). China’s CBM is buried under a depth of less than 2000 m with a volume of 36.81 trillion m
3, accounting for approximately 15.3% of the world’s CBM reserve and ranking the third largest in the world [
1,
2]. To best exploit CBM resources, the Chinese government has accelerated the research and development of CBM extraction technologies in recent years and explored a set of CBM extraction techniques by drilling several test wells. However, vertical wells are commonly used in CBM extraction in China due to the limited technical conditions.
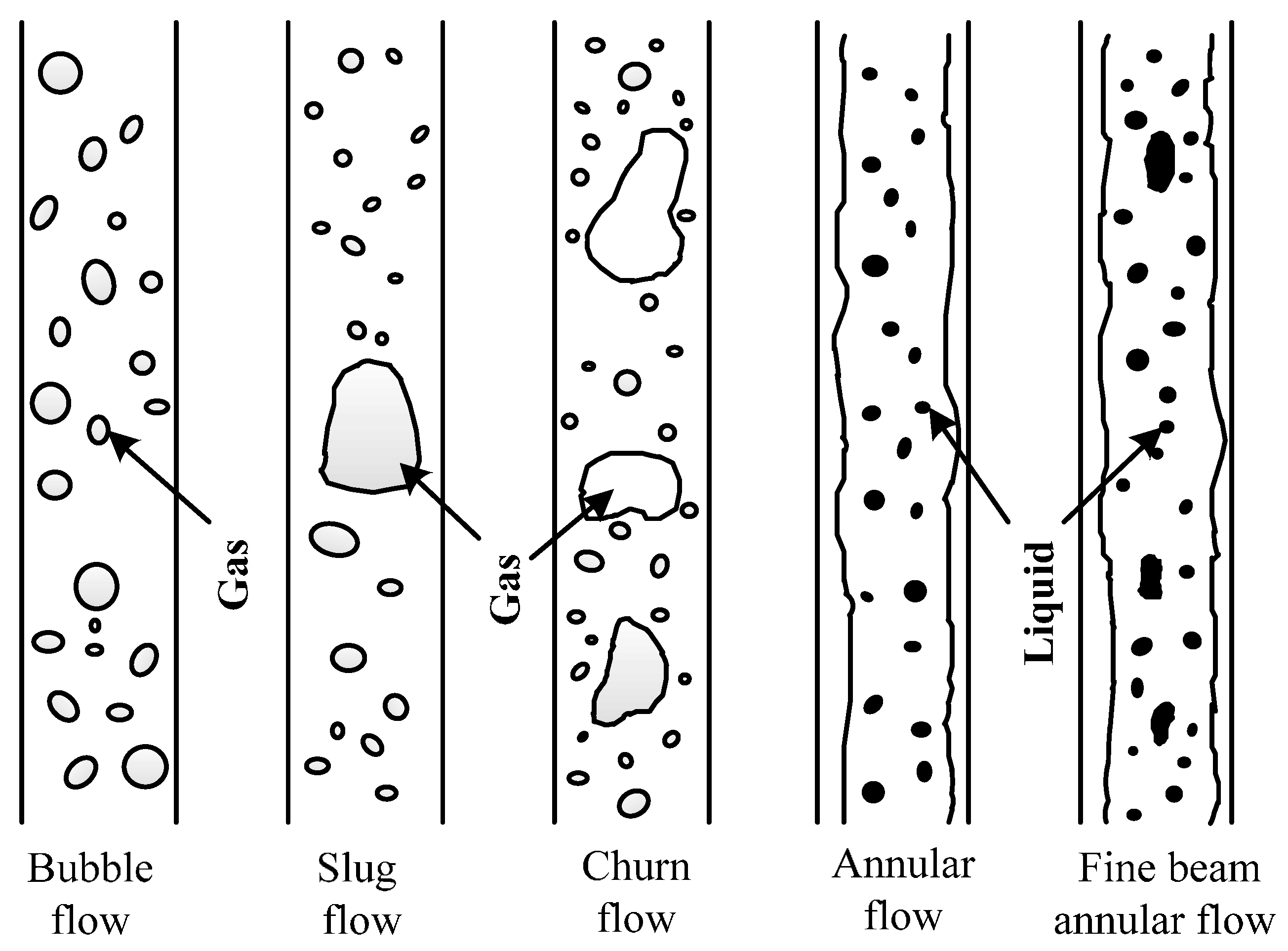
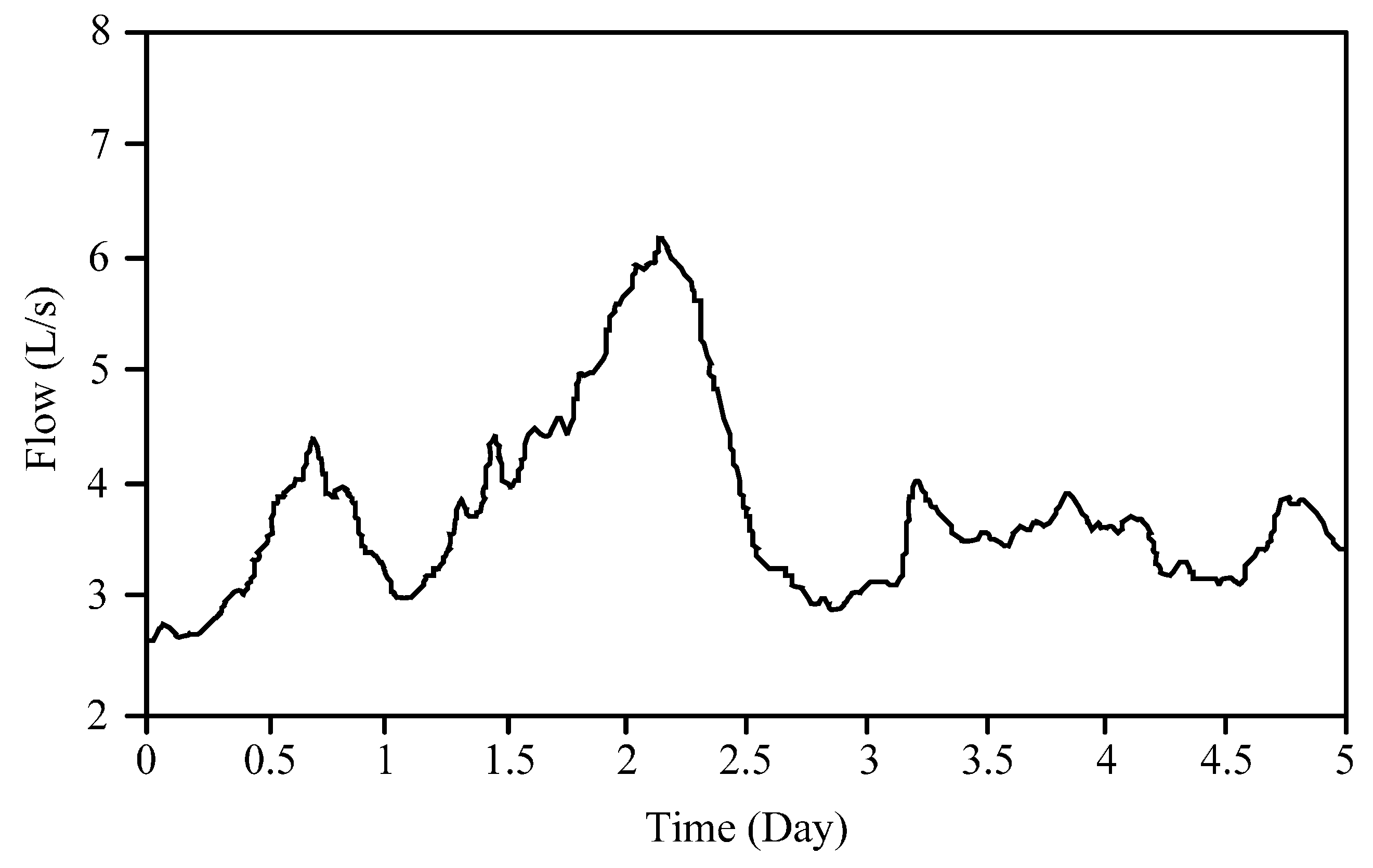
Due to the natural fracture structure of coalbeds, CBM wells need drainage and depressurization, during which groundwater and CBM are both produced from the vertical wellbore annulus, resulting in gas–liquid two-phase flow (hereinafter referred to as two-phase flow) in the wellbore annulus. For CBM wells, especially commingled CBM drainage and extraction wells, the measurement of wellbore annulus two-phase flow is of great significance for developing reasonable gas drainage and extraction processes, estimating CBM output, judging the operating conditions in CBM wells and analyzing stratum conditions [
3]. Therefore, the real-time measurement of two-phase flow in CBM wellbore annulus is imperative.
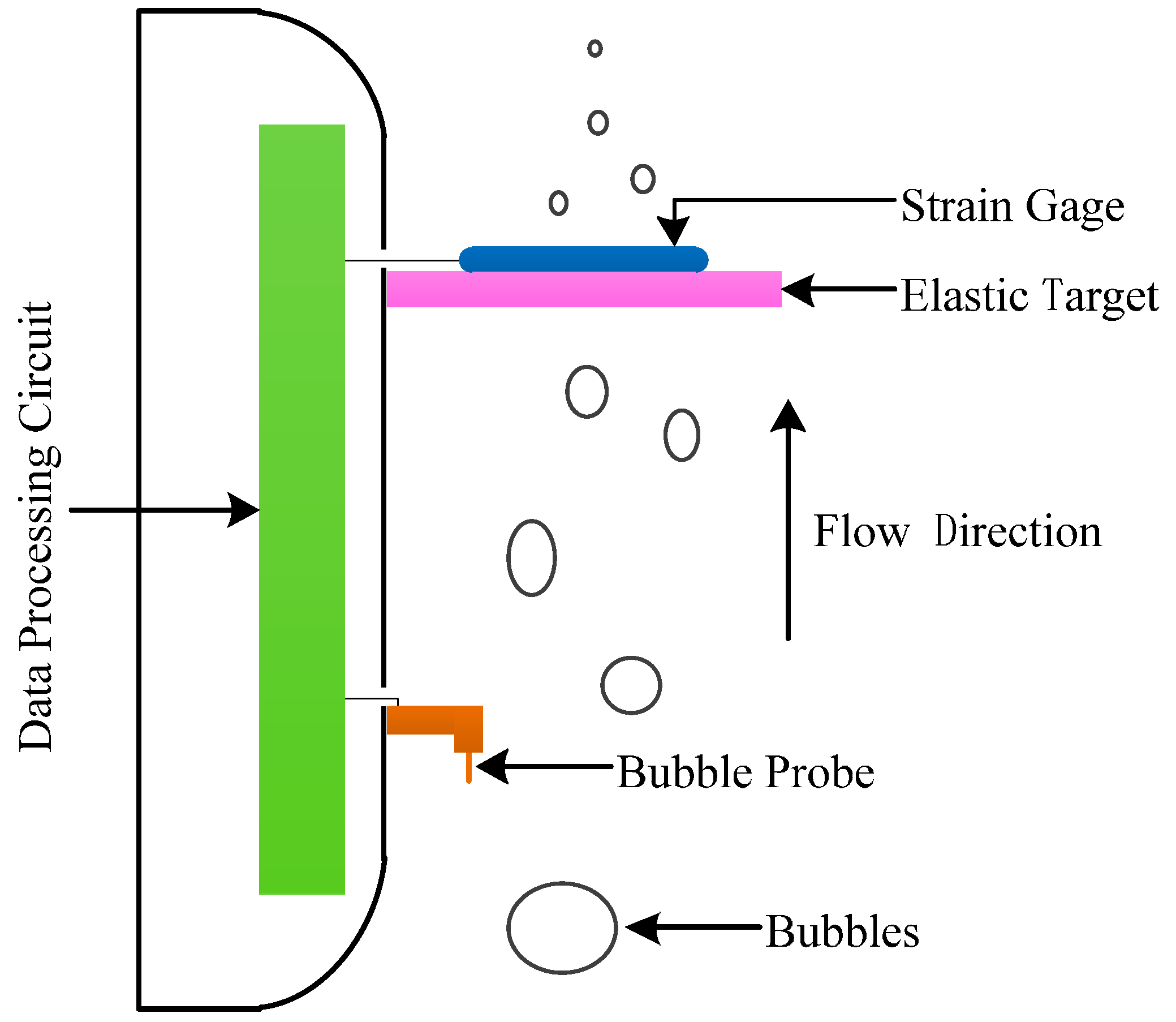
Generally, the size of the wellbore annulus of common CBM extraction wells shall not exceed 26 mm, and the pressure of the operating environment is up to 10 MPa. Meanwhile, a few pulverized coal particles inevitably exist in the wellbore. Due to the above factors, the operating environment must be considered during the selection or design of the flow sensor.
Existing flow sensors can be divided into volumetric flow sensors and inferential flow sensors [
4]. Due to their overlarge size, volumetric flow sensors cannot adapt to the narrow space of CBM wells. Inferential flow sensors include target flow sensors, differential pressure flow sensors, ultrasonic flow sensors, and so on, which are also inadequate for the operating environment of CBM wells. The detailed reasons are as follows.
(1) Target Flow Sensor [
5]
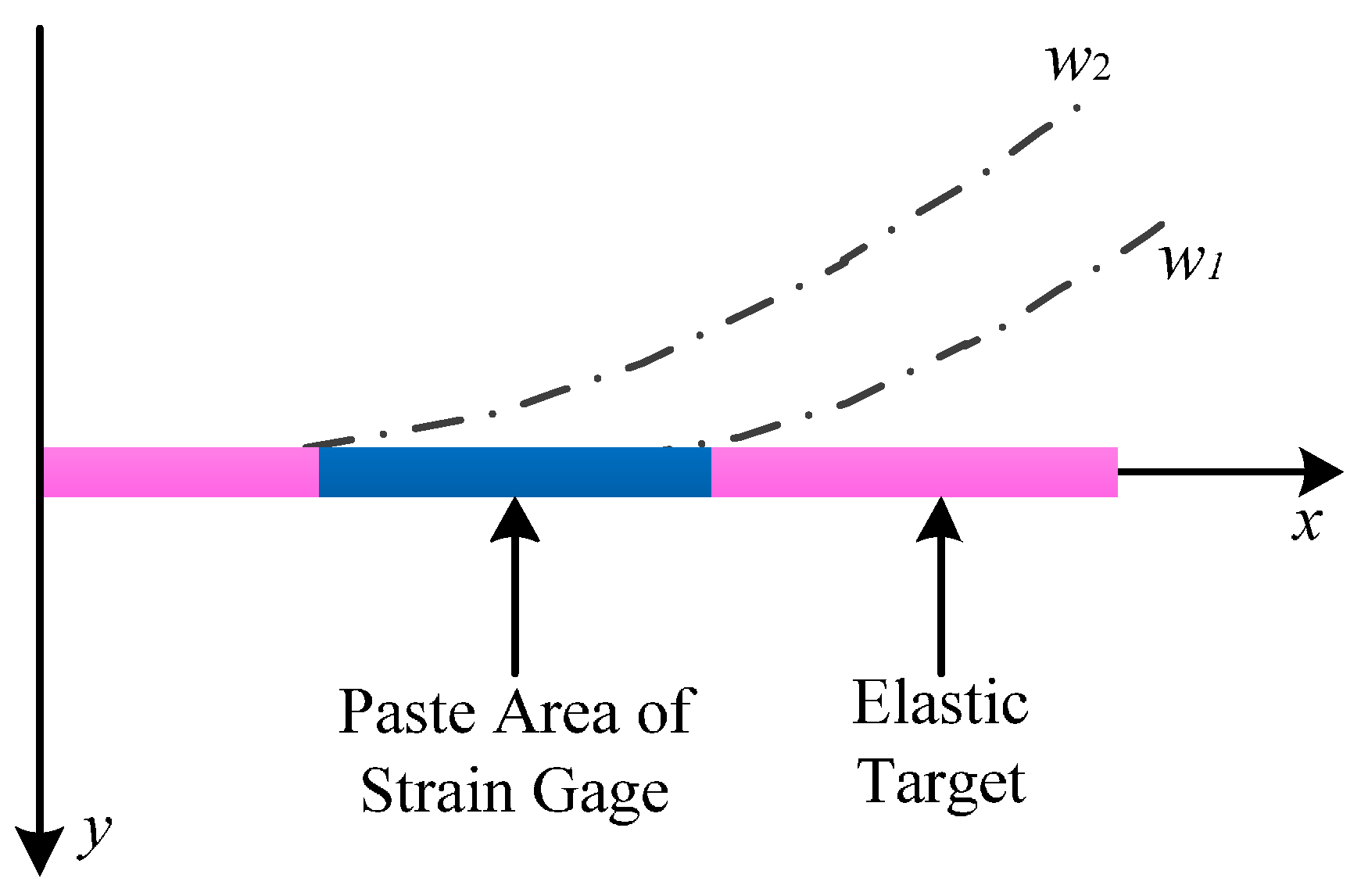
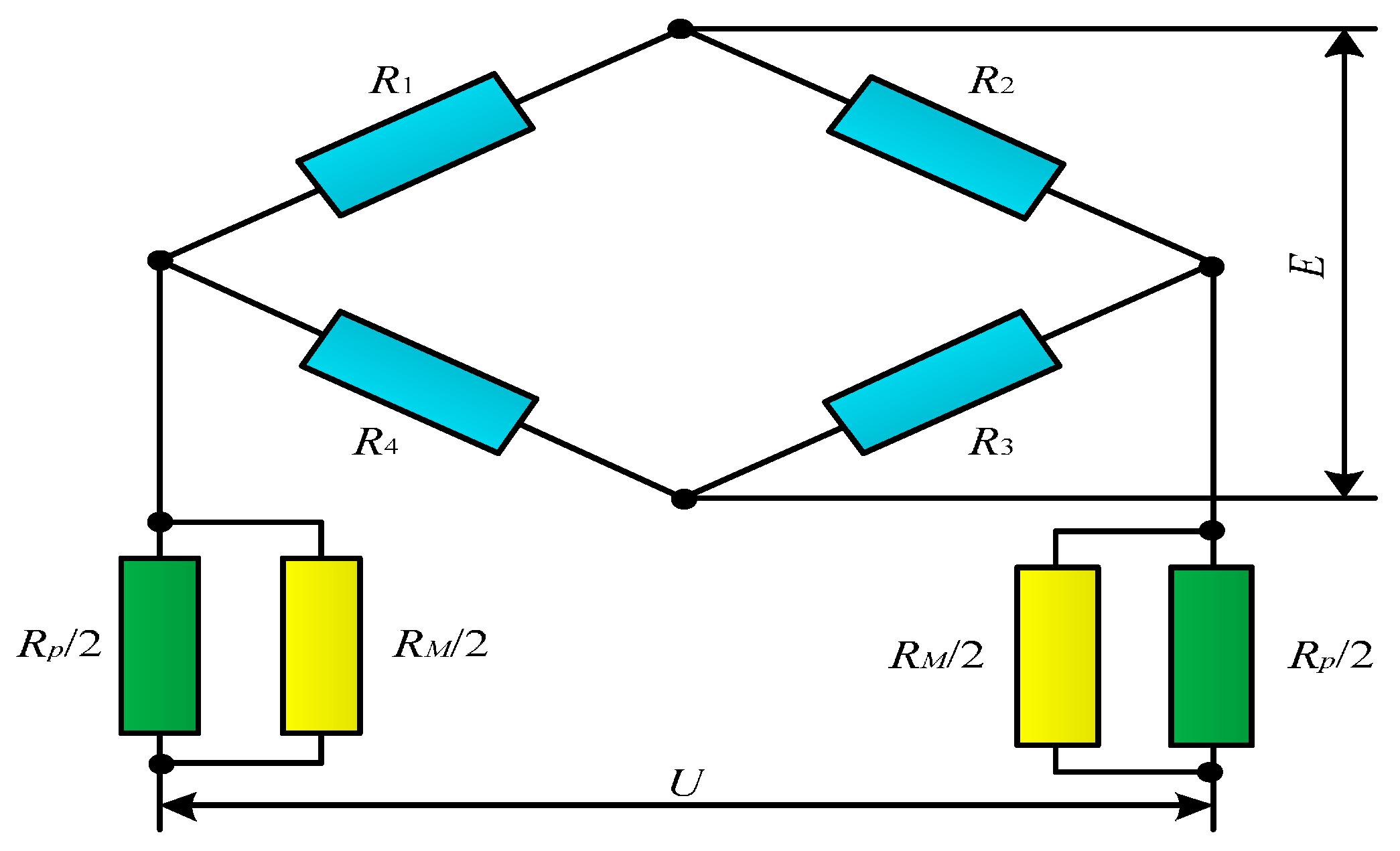
Basic principles: When flowing through the target flow sensor, the fluid impacts the target bar. The impact force is transmitted from the target bar to the elastomer, causing the deformation of the elastomer. The deformation of the elastomer can be obtained from the deformation measurement component installed on the elastomer. The deformation amount is proportional to the flow.
Advantages: The target flow sensor is relatively simple in structure, not easily jammed, and convenient to maintain. It is adaptable to the environment with high viscosity, high contamination and suspended solid particles.
Disadvantages: The sensor causes large pressure loss.
Analysis: Existing target flow sensors are large, and their sealability fails to meet the requirement, so they are inapplicable to CBM wells.
(2) Differential Pressure Flow Sensor [
6]
Basic principles: When fluids with different flow velocities flow through a pipeline with a variable cross-sectional diameter, a differential pressure will occur between the different cross-sections of the pipeline. The differential pressure is proportional to the flow velocities of the fluids. The differential pressure flow sensor is made according to this principle.
Advantages: The sensor is relatively simple in structure without moving parts, so it is highly reliable. With high linearity, it is widely applicable.
Disadvantages: The principle of the sensor determines that long, straight pipelines are needed at the front and back of the sensor, so its installation requirements are higher. In addition, it has disadvantages such as large size, narrow measurement range, large pressure loss, difficulty in measuring pipelines with small diameters, and large error.
Analysis: The differential pressure flow sensor is large due to the restriction of its measuring principle, and the CBM well environment fails to meet its installation requirements, so it cannot be used in CBM wells.
(3) Ultrasonic Flow Sensor [
7]
Basic principles: When an ultrasonic wave passes through a fluid, the fluid flow will disturb the ultrasonic wave. Hence, the flow of the fluid can be obtained by comparing and analyzing the received ultrasonic signal and the original signal.
Advantages: The measurement is unaffected by the properties (electrical conductivity, temperature, pressure, viscosity, etc.) of the fluid. There is no contact between the sensor and the measured media, so the sensor is more suitable for the measurement of corrosive fluids. Its pressure loss is negligible and measurement accuracy is higher.
Disadvantages: The use and installation of the sensor are more complicated compared with common flow sensors. In addition, the sensor can be used only when the pipeline is filled with the fluid.
Analysis: The use and installation of the sensor are relatively complex, and the environment in CBM wells cannot meet its installation requirements. Meanwhile, the sensor requires the measured fluid to be a single medium or stable when measuring the flow, but the fluids (most two-phase flow and some pulverized coal particles) in a CBM wellbore annulus are not single media. Therefore, the sensor cannot be used in CBM wells.
(4) Electromagnetic Flow Sensor [
8]
Basic principles: The electromagnetic flow sensor measures the fluid flow according to Faraday’s Electromagnetic Induction Law. When fluid flows through the sensor, the fluid will cut magnetic induction lines, which produce inductive electromotive force on both sides of the sensor electrode. The greater the flow, the greater the inductive electromotive force.
Advantages: The electromagnetic flow sensor is a noncontact flow measurement device, so its pressure loss is almost negligible when the fluid flows through the flow sensor, and its measurement accuracy is higher.
Disadvantages: With a higher requirement for the conductivity of the fluid, the sensor is inapplicable to fluids with low conductivity, such as steam and gas.
Analysis: With a higher requirement for measured fluids, the sensor is inapplicable to gas or two-phase flow, which has a higher void fraction, but the wellbore annulus two-phase flow is gas–liquid, and the void fraction is very high in annular flow and fine beam annular flow, so the sensor cannot be used in CBM wells.
(5) Floater Flow Sensor [
9]
Basic principles: When the fluid enters the sensor from the inlet, differential pressure occurs between the upstream and downstream of the floater due to the closure effect of the floater. This differential pressure forces the floater to move along in the height direction of the sensor, eventually achieving a force balance state. Hence, the height of the floater is proportional to the flow of the fluid.
Advantages: The sensor has such advantages as simple structure, easy maintenance, low installation requirements, smaller and constant pressure loss, and wide measuring range.
Disadvantages: The sensor has low measurement accuracy. The measurement results are largely influenced by the viscosity, pressure, purity, density and temperature of the measured fluid.
Analysis: The measurement results of the sensor are susceptible to the physical parameters of the fluid, including viscosity, pressure, purity, density, and temperature. The above physical parameters of two-phase flow in a CBM wellbore annulus are all variable. Therefore, it cannot be used.
(6) Jet Flow Sensor [
10,
11]
Basic principles: Due to the special structure of the sensor, the Coanda effect occurs when the fluid enters the sensor. The additional feedback channel forces the fluid to produce oscillation inside the sensor. The oscillation frequency of the fluid is proportional to its flow. Therefore, the value of the flow can be obtained by measuring the oscillation frequency.
Advantages: The flow of the fluid is proportional to the oscillation frequency of the sensor. The measurement results are unaffected by the composition, pressure, temperature, viscosity, density, etc., of the fluid. With strong anti-interference capability and high stability, it is suitable for the measurement of medium- and high-speed flows.
Disadvantages: The flow sensor has such disadvantages as complex structure, large pressure drop, and large error during the measurement of low-speed flows.
Analysis: The sensor does not meet the requirement for the following reasons:
- ①
This sensor is suitable for the measurement of medium- and high-speed flows, but the two-phase flow in the wellbore annulus is low-speed.
- ②
Because of its complex structure and difficulty in processing, the sensor is difficult or even unable to be redesigned into a miniaturized form.
(7) Vortex Flow Sensor [
12]
Basic principles: When viscous fluid at a certain velocity swirls around the vortex-generating body, the fluid micelle will form a pair of symmetric vortexes with inverse rotation directions somewhere behind the vortex-generating body, which is called the “Karman Vortex Street Phenomenon”. When the Reynolds number of the fluid is within a stable range, the vortex frequency is proportional to the flow. Therefore, the flow of the fluid can be obtained by measuring the vortex frequency by the sensor.
Advantages: The sensor has a wide scope of application (applicable to gas, liquid and steam), and the measurement results are unaffected by the composition, pressure, temperature, viscosity, density, etc., of the fluid. In addition, it has such advantages as simple structure, long service life, small pressure loss and high measurement accuracy.
Disadvantages: The pulsation and velocity distribution of the fluid exert a direct influence on the measurement accuracy. Moreover, the contamination of the vortex-generating body will also lead to large error in the measured results.
Analysis: During the use of this sensor, the pulsation of the fluid and the contamination of the vortex-generating body will exert great influence on the measurement accuracy of the sensor. Due to the obvious pulsation phenomenon of the two-phase flow in the wellbore annulus and the contamination of the vortex-generating body caused by pulverized coal particles, the sensor cannot be used.
(8) Turbine Flow Sensor [
13]
Basic principles: When fluid flows through the sensor, the turbine blade of the sensor will rotate under the impetus of the fluid. The larger the flow, the greater the rotary speed. Therefore, the flow of the fluid can be obtained by measuring the rotary speed of the turbine blade.
Advantages: Among all flow sensors, the turbine flow sensor has the highest measurement accuracy. It also has other advantages such as a simple structure, strong anti-interference capability, and wide operating temperature range (−200 to 400 °C).
Disadvantages: The sensor has a high requirement for the measured medium; that is, the measured medium should be clean without particles. It is more suitable for fluids with high viscosity.
Analysis: The sensor has high cleanliness requirements for the measured medium, but the two-phase flow in the wellbore annular has poorer cleanliness. The bearing of turbine blades is easily jammed by pulverized coal particles, damaging the flow sensor. Therefore, the sensor cannot be used.
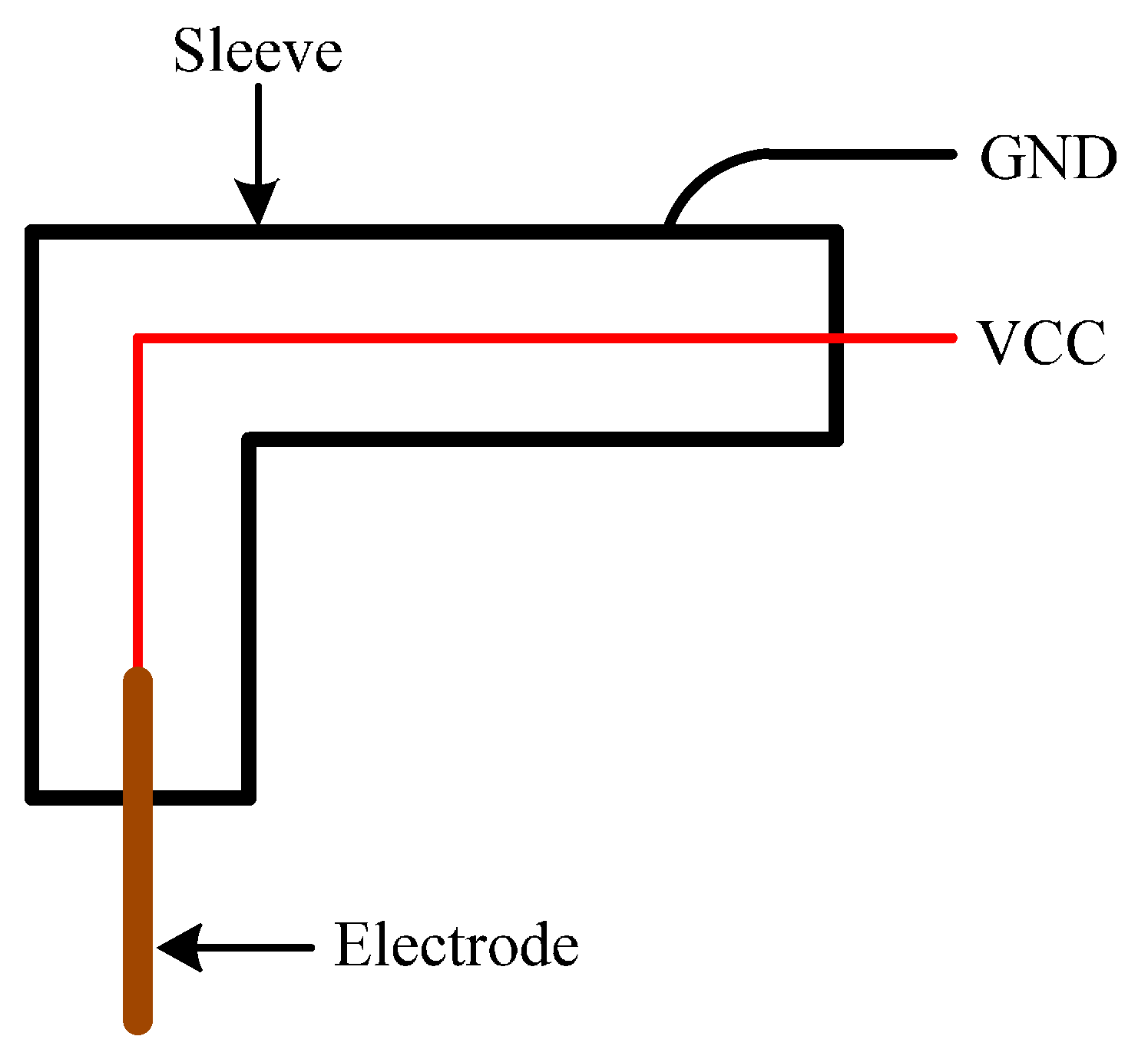
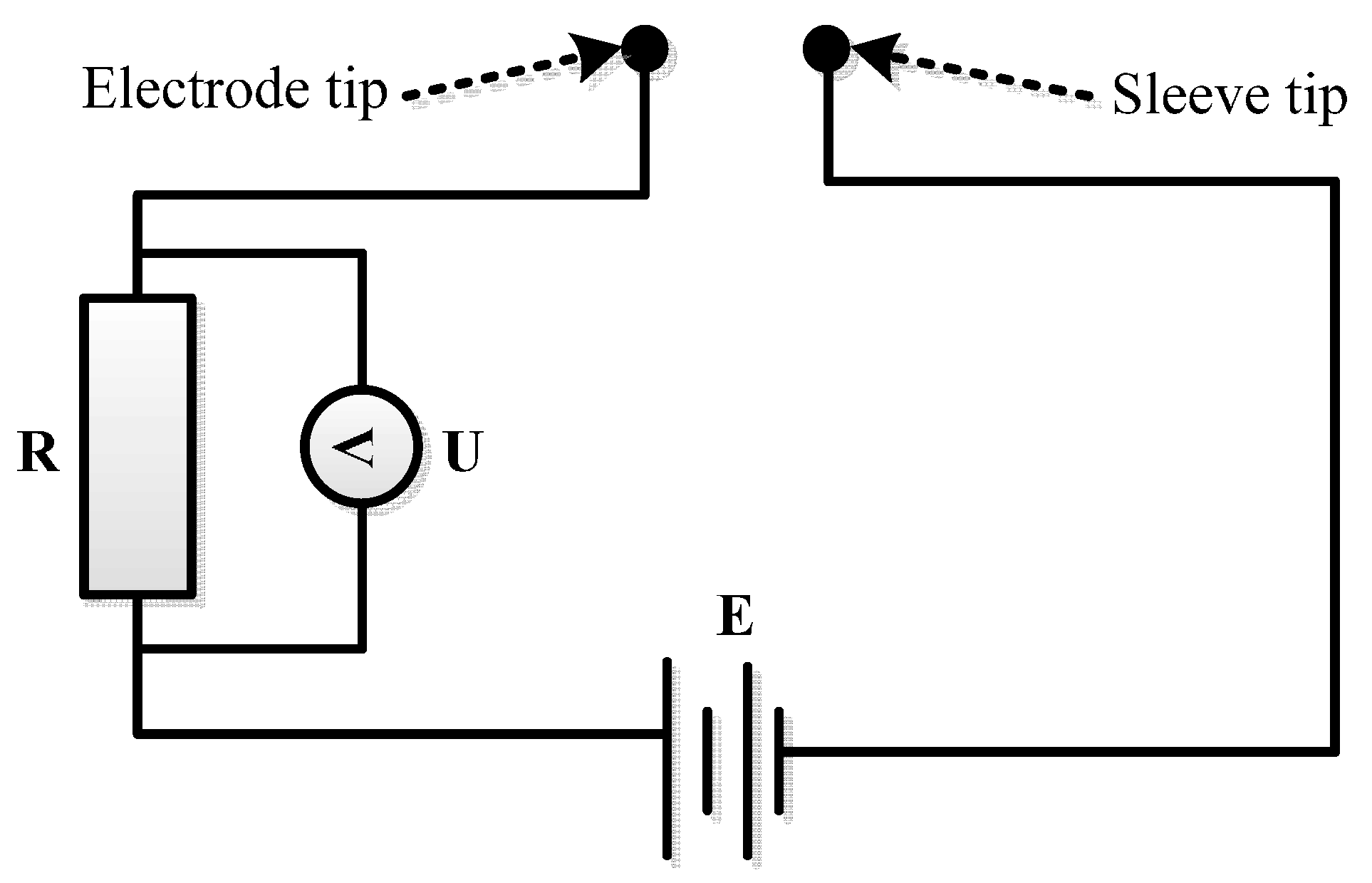
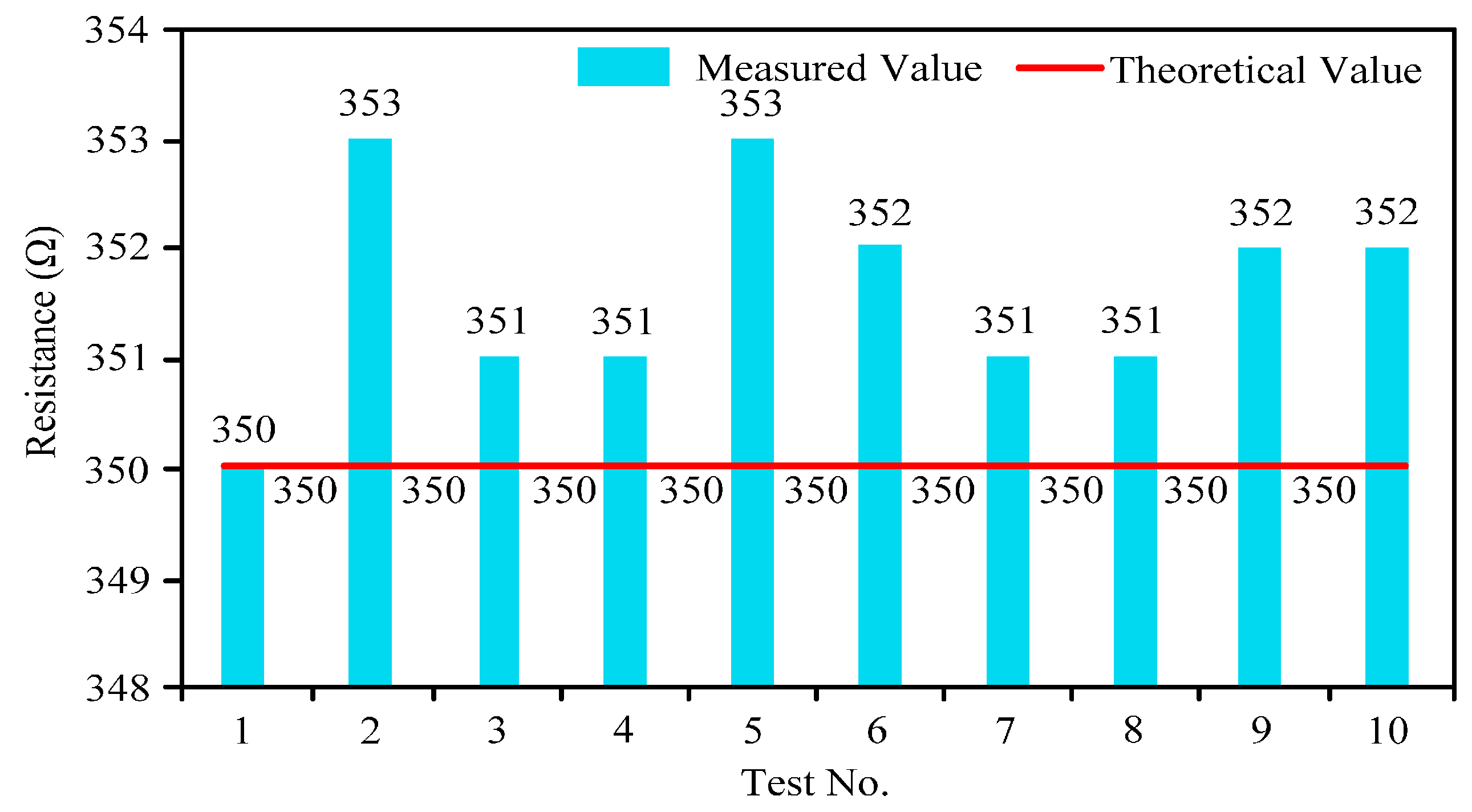
The above analysis shows that existing flow sensors cannot be used in a CBM wellbore annulus due to such factors as size, installation requirements, measuring principles, fluid media, and sealing performance. Among them, the target flow sensor can still be used under the conditions of high contamination and suspended solids and is suitable for the operating conditions of CBM wells. Meanwhile, based on its measurement principle, the sealing and size reduction of the sensor are easily realized. Therefore, it is finally determined that the new two-phase flow sensor be researched and developed based on the target flow sensor. Moreover, the two-phase flow pattern can be classified differently according to the gas content. Thus, the accuracy will increase greatly if the sensor can automatically discriminate and become calibrated to every flow pattern.
In conclusion, the basic principle of the sensor is that it can automatically discriminate and calibrate every flow pattern first and then automatically calibrate the flow value according to the deflection of the sensor’s part when impacted. The technological difficulties are as follows:
- ①
The automatic discrimination and calibration of every flow pattern of the two-phase flow of CBM.
- ②
The small size requirement, suitability of the sealing property for the conditions under the shaft, corrosion resistance, easy installation, suitability for the installation environment of the downhole tubing, etc.
- ③
The circuit to process the leak signal.