Sensor Location Problem Optimization for Traffic Network with Different Spatial Distributions of Traffic Information
Abstract
:1. Introduction
2. Typical Sensor Information Credibility Functions and Optimization Models
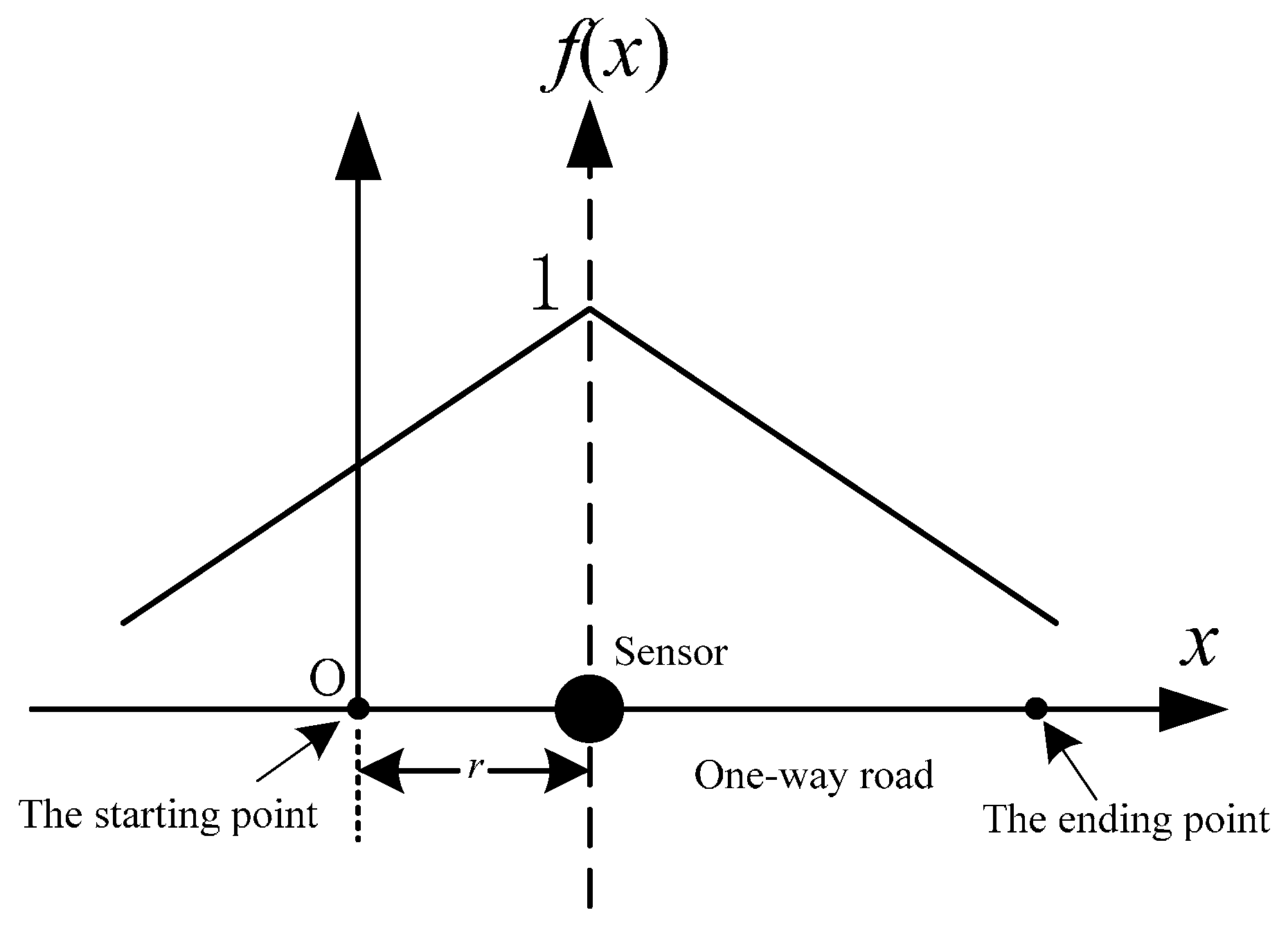
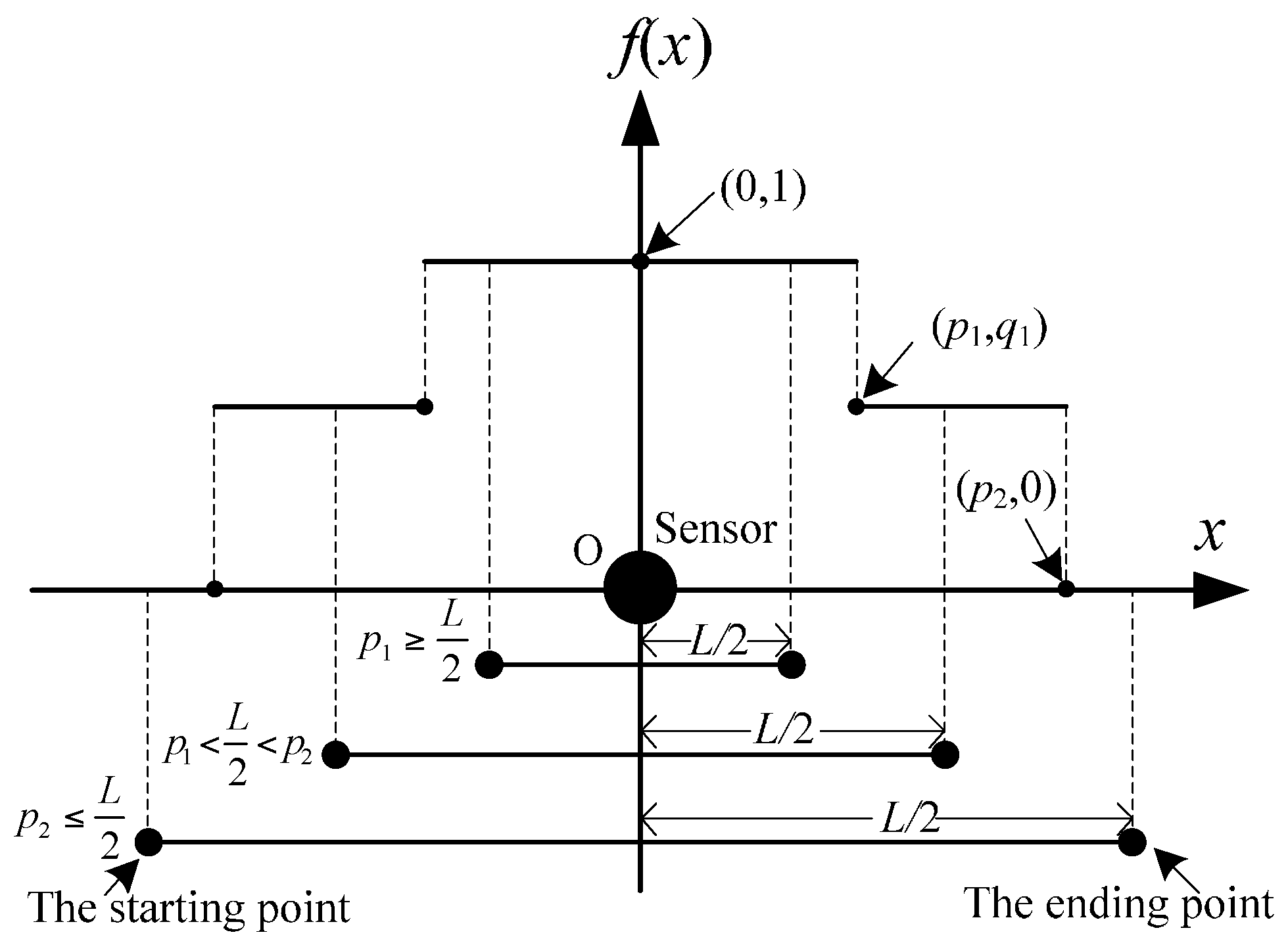
2.1. Spatial Heterogeneity of Traffic Information Credibility
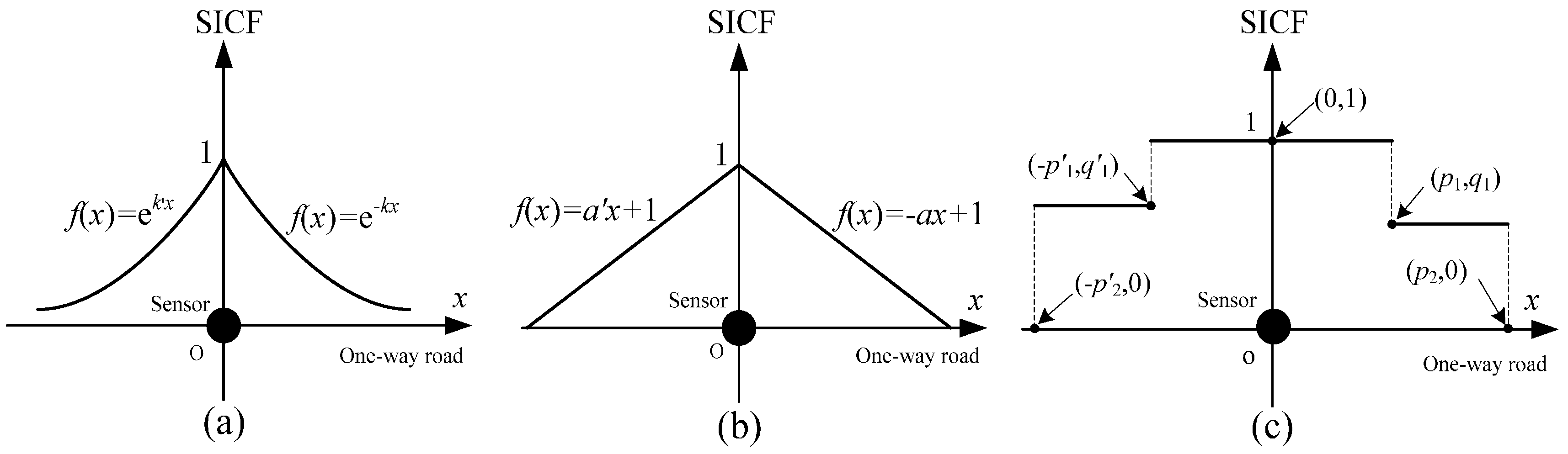
2.2. Typical Options of SICF
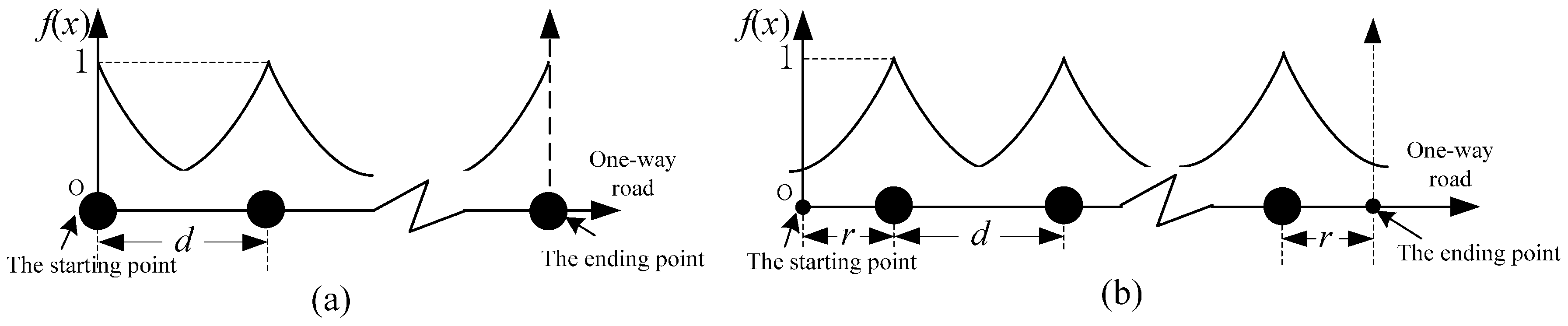
2.3. Optimization Models of One-Way Road
3. Expanding Models and Algorithms with Different SICFs
3.1. Exponential Attenuation SICF (EAF)
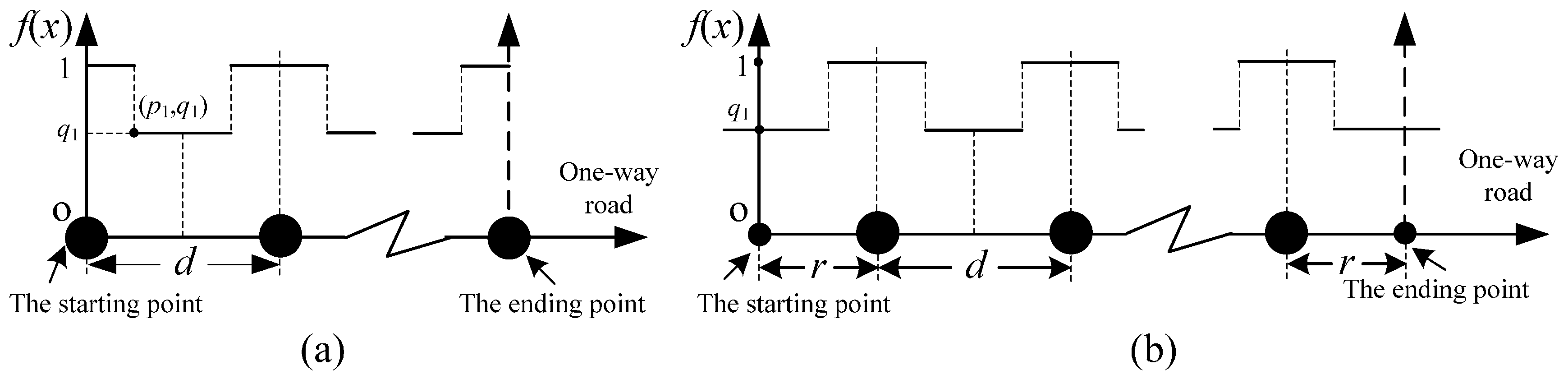
3.1.1. Case A: Fixation at Both Ends with EAF
| Algorithm 1. Solving Equation (6) | |
| Input: | Model parameters Q, V, C, L, and k |
| Output: | NA, zAm |
| 1: | Initialization: Q, V, C, L, k; z_temp = 0; zAm = 0; n = 2; |
| 2: | Done = 1; |
| 3: | while done |
| 4: | z = (n − 1) × Q × V × (1 − exp(−0.5 × k × L/(n − 1))) |
| 5: | – n × C; |
| 6: | if z > z_temp |
| 7: | n++; |
| 8: | z_temp = z; |
| 9: | else |
| 10: | done = 0; |
| 11: | end if |
| 12: | end while |
| 13: | NA = n; |
| zAm = z_temp. | |
3.1.2. Case B: Freeness at Both Ends with EAF
3.2. Linear Attenuation SICF (LAF)
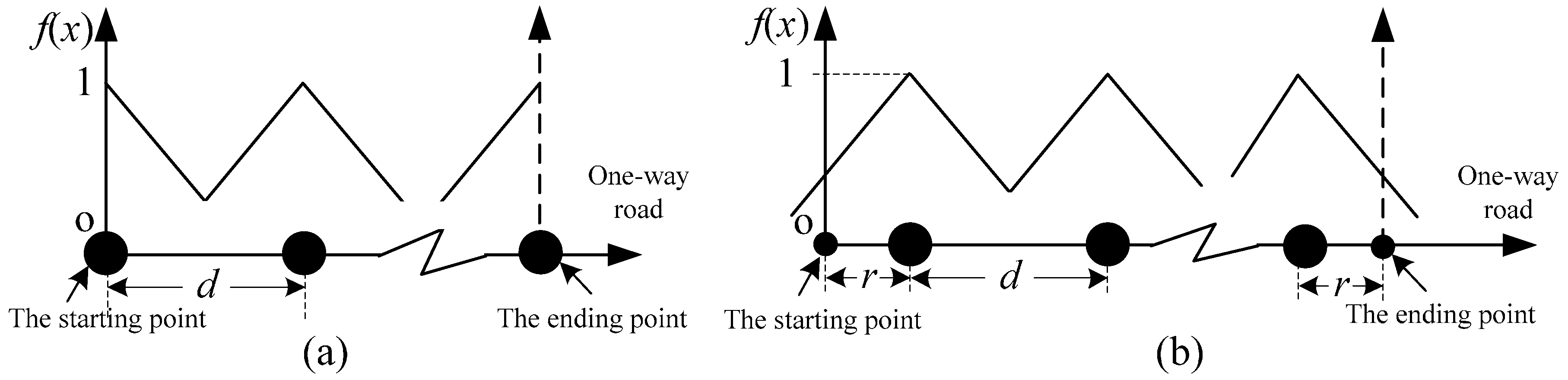
3.2.1. Case C: Fixation at Both Ends with LAF
3.2.2. Case D: Freeness at Both Ends with LAF
3.3. Two-Step Attenuation SICF (Two-SAF)
3.3.1. Case E: Fixation at Both Ends with SAF
3.3.2. Case F: Freeness at Both Ends with SAF
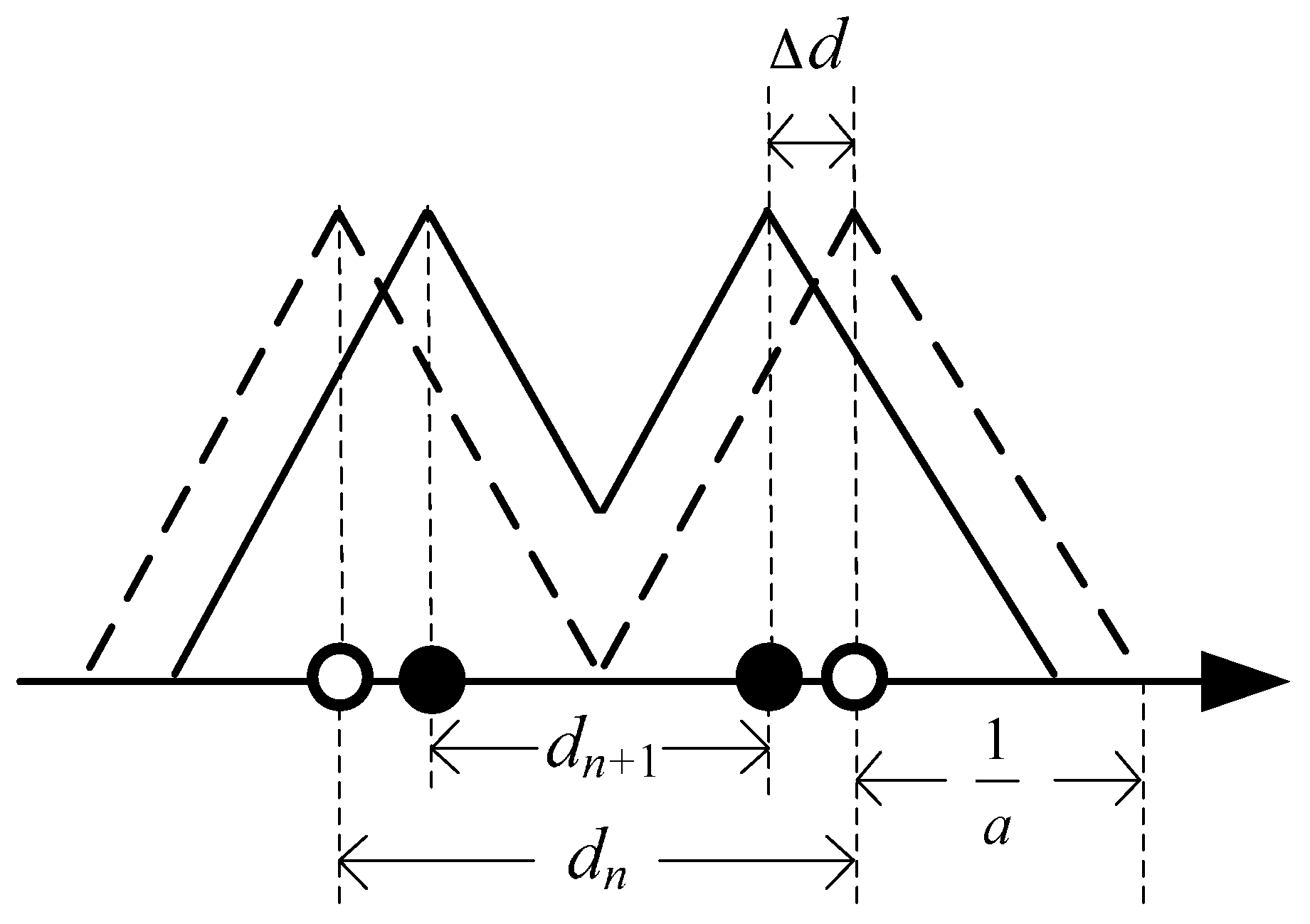
3.4. Discussion
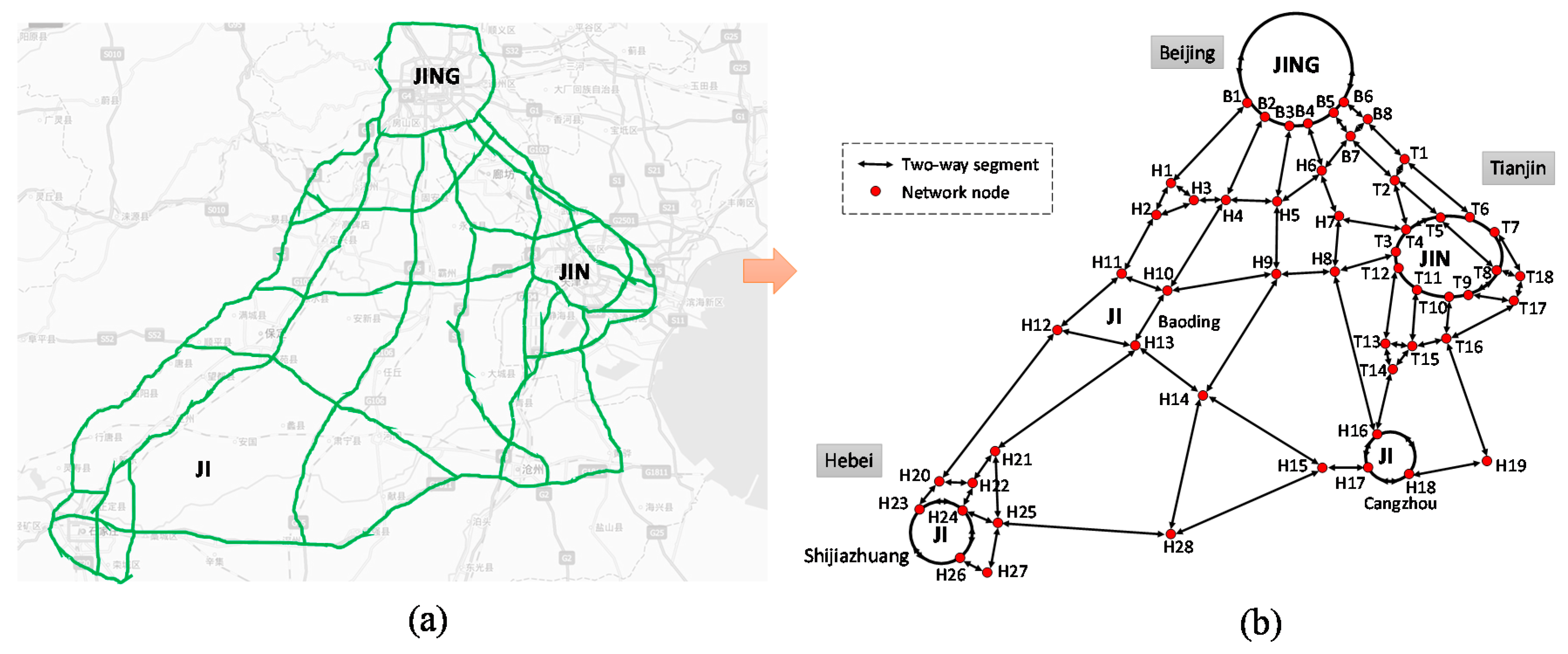
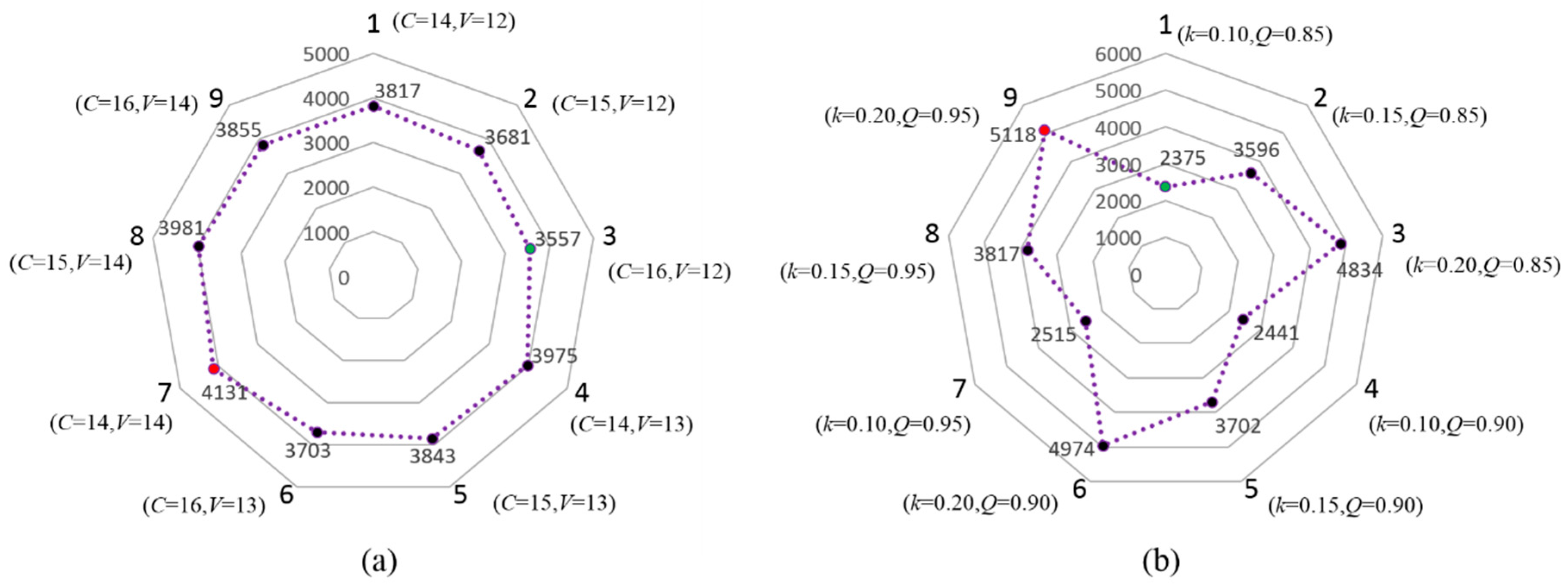
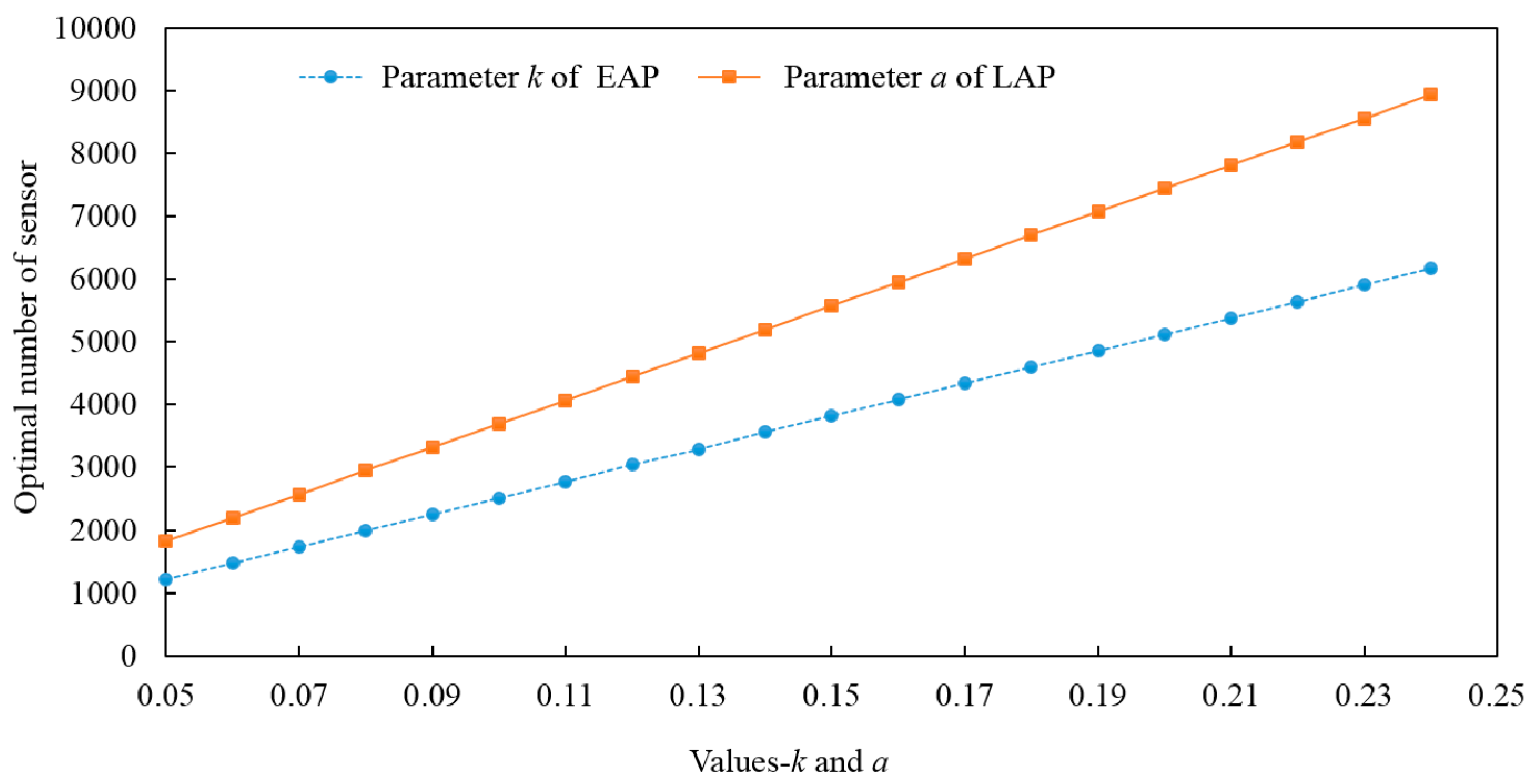
4. Numerical Example
5. Conclusions and Application Prospects
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, X.; List, G. An information-theoretic sensor location model for traffic origin-destination demand estimation applications. Transp. Sci. 2010, 44, 254–273. [Google Scholar] [CrossRef]
- Ng, M. Synergistic sensor location for link flow inference without path enumeration: A node-based approach. Transp. Res. Part B Methodol. 2012, 46, 781–788. [Google Scholar] [CrossRef]
- Ng, M.; Travis Waller, S. A static network level model for the information propagation in vehicular ad hoc networks. Transp. Res. Part C Emerg. Technol. 2010, 18, 393–407. [Google Scholar] [CrossRef]
- Ban, X.; Herring, R.; Margulici, J.D.; Bayen, A.M. Optimal Sensor Placement for Freeway Travel Time Estimation. In Transportation and Traffic Theory 2009: Golden Jubilee; Lam, W.H.K., Wong, S.C., Lo, H.K., Eds.; Springer: Hong Kong, China, 2009; pp. 697–721. [Google Scholar]
- Guo, W.; Healy, W.M.; Zhou, M. Battery discharge characteristics of wireless sensors in building applications. In Proceedings of the 9th IEEE International Conference on Networking, Sensing and Control, Beijing, China, 11–14 April 2012; pp. 133–138.
- Wang, Q.W.Q.; Hempstead, M.; Yang, W. A Realistic Power Consumption Model for Wireless Sensor Network Devices. In Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 25–29 September 2006; Volume 1, pp. 286–295.
- Li, R.; Jia, L. On the layout of fixed urban traffic detectors: An application study. IEEE Intell. Transp. Syst. Mag. 2009, 1, 6–12. [Google Scholar]
- Li, X. Reliable Facility Location Design and Traffic Sensor Deployment under Probabilistic Disruptions. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2011. [Google Scholar]
- Li, X.; Ouyang, Y. Reliable sensor deployment for network traffic surveillance. Transp. Res. Part B Methodol. 2011, 45, 218–231. [Google Scholar] [CrossRef]
- Hu, S.R.; Peeta, S.; Chu, C.H. Identification of vehicle sensor locations for link-based network traffic applications. Transp. Res. Part B Methodol. 2009, 43, 873–894. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B. Locating sensors on traffic networks: Models, challenges and research opportunities. Transp. Res. Part C Emerg. Technol. 2012, 24, 227–255. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, J. Optimal traffic counting locations for origin–destination matrix estimation. Transp. Res. Part B Methodol. 1998, 32, 109–126. [Google Scholar] [CrossRef]
- Ma, S.; Liu, Y.; Jia, N.; Zhu, N. Traffic sensor location approach for flow inference. IET Intell. Transp. Syst. 2015, 9, 184–192. [Google Scholar]
- Ehlert, A.; Bell, M.G.H.; Grosso, S. The optimisation of traffic count locations in road networks. Transp. Res. Part B Methodol. 2006, 40, 460–479. [Google Scholar] [CrossRef]
- Castillo, E.; Menéndez, J.M.; Sánchez-Cambronero, S. Traffic estimation and optimal counting location without path enumeration using bayesian networks. Comput. Civ. Infrastruct. Eng. 2008, 23, 189–207. [Google Scholar] [CrossRef]
- Morrison, D.R.; Martonosi, S.E. Characteristics of optimal solutions to the sensor location problem. Ann. Oper. Res. 2014, 226, 463–478. [Google Scholar] [CrossRef]
- He, S.X. A graphical approach to identify sensor locations for link flow inference. Transp. Res. Part B Methodol. 2013, 51, 65–76. [Google Scholar] [CrossRef]
- Mínguez, R.; Sánchez-Cambronero, S.; Castillo, E.; Jiménez, P. Optimal traffic plate scanning location for OD trip matrix and route estimation in road networks. Transp. Res. Part B Methodol. 2010, 44, 282–298. [Google Scholar] [CrossRef]
- Hu, S.R.; Peeta, S.; Liou, H.T. Integrated determination of network origin-destination trip matrix and heterogeneous sensor selection and location strategy. IEEE Trans. Intell. Transp. Syst. 2016, 17, 195–205. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, N.; Ling, S.; Ma, S.; Huang, Y. Heterogeneous sensor location model for path reconstruction. Transp. Res. Part B Methodol. 2016, 91, 77–97. [Google Scholar] [CrossRef]
- Bianco, L.; Confessore, G.; Reverberi, P. A Network Based Model for Traffic Sensor Location with Implications on O/D Matrix Estimates. Transp. Sci. 2001, 35, 50–60. [Google Scholar] [CrossRef]
- Gan, L.; Yang, H.; Wong, S.C. Traffic Counting Location and Error Bound in Origin-Destination Matrix Estimation Problems. J. Transp. Eng. 2005, 131, 524–534. [Google Scholar] [CrossRef]
- Zangui, M.; Yin, Y.; Lawphongpanich, S. Sensor location problems in path-differentiated congestion pricing. Transp. Res. Part C Emerg. Technol. 2015, 55, 217–230. [Google Scholar] [CrossRef]
- Viti, F.; Rinaldi, M.; Corman, F.; Tampere, C.M.J. Assessing partial observability in network sensor location problems. Transp. Res. Part B Methodol. 2014, 70, 65–89. [Google Scholar] [CrossRef]
- Castillo, E.; Grande, Z.; Calviño, A.; Szeto, W.; Lo, H. A State-of-the-Art Review of the Sensor Location, Flow Observability, Estimation, and Prediction Problems in Traffic Networks. J. Sens. 2015, 2015, 903563. [Google Scholar] [CrossRef]
- Castillo, E.; Nogal, M.; Rivas, A.; Sánchez-Cambronero, S. Observability of traffic networks. Optimal location of counting and scanning devices. Transp. B Transp. Dyn. 2013, 1, 68–102. [Google Scholar] [CrossRef]
- Ivanchev, J.; Aydt, H.; Knoll, A. Information Maximizing Optimal Sensor Placement Robust Against Variations of Traffic Demand Based on Importance of Nodes. IEEE Trans. Intell. Transp. Syst. 2016, 17, 714–725. [Google Scholar] [CrossRef]
- Xu, X.; Lo, H.K.; Chen, A.; Castillo, E. Robust network sensor location for complete link flow observability under uncertainty. Transp. Res. Part B Methodol. 2016, 88, 1–20. [Google Scholar] [CrossRef]
- Shao, M.; Sun, L.; Shao, X. Sensor Location Problem for Network Traffic Flow Derivation Based on Turning Ratios at Intersection. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Li, H.; Dong, H.; Jia, L.; Ren, M.; Li, S. Analysis of Factors that Influence the Sensor Location Problem for Freeway Corridors. J. Adv. Transp. 2015, 49, 10–28. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B. Locating active sensors on traffic networks. Ann. Oper. Res. 2005, 136, 229–257. [Google Scholar] [CrossRef]
- Fei, X.; Mahmassani, H.S.; Eisenman, S.M. Sensor Coverage and Location for Real-Time Traffic Prediction in Large-Scale Networks. Transp. Res. Rec. 2008, 2039, 1–15. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C.; Gan, L. Models and algorithms for the screen line-based traffic-counting location problems. Comput. Oper. Res. 2006, 33, 836–858. [Google Scholar] [CrossRef]
- Kima, J.; Park, B.; Leeb, J.; Won, J. Determining optimal sensor locations in freeway using genetic algorithm-based optimization. Eng. Appl. Artif. Intell. 2011, 24, 318–324. [Google Scholar] [CrossRef]
- Kianfar, J.; Edara, P. Optimizing freeway traffic sensor locations by clustering global-positioning-system-derived speed patterns. IEEE Trans. Intell. Transp. Syst. 2010, 11, 738–747. [Google Scholar] [CrossRef]
- Mirchandani, P.B.; Gentili, M.; He, Y. Location of vehicle identification sensors to monitor travel-time performance. IET Intell. Transp. Syst. 2009, 3, 289–303. [Google Scholar] [CrossRef]
- Chan, K.S.; Lam, W.H.K. Optimal speed detector density for the network with travel time information. Transp. Res. Part A Policy Pract. 2002, 36, 203–223. [Google Scholar] [CrossRef]
- Fujito, I.; Margiotta, R.; Huang, W.; Perez, W. Effect of sensor spacing on performance measure calculations. Transp. Res. Rec. J. Transp. Res. Board 2006, 1945, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Ouyang, Y. Reliable traffic sensor deployment under probabilistic disruptions and generalized surveillance effectiveness measures. Oper. Res. 2012, 60, 1183–1198. [Google Scholar] [CrossRef]
- Drezner, Z.; Wesolowsky, G.O. On the best location of signal detectors. IIE Trans. 1997, 29, 1007–1015. [Google Scholar] [CrossRef]
- Li, H.J.; Dong, H.H.; Jia, L.M.; Ren, M.Y.; Qin, Y. A new measure for evaluating spatially related properties of traffic information credibility. J. Cent. South Univ. 2014, 21, 2511–2519. [Google Scholar] [CrossRef]
- Li, H.; Jia, L.; Dong, H.; Qin, Y.; Xu, D.; Sun, X. Study on spacing optimization for traffic flow detector. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems (ITSC), Madeira, Portugal, 19–22 September 2010; pp. 593–598.
- Li, H. Multi-Parameter Sensing and Sensor Network Optimization for Road Traffic Information Acquisition; Beijing Jiaotong University: Beijing, China, 2014. [Google Scholar]
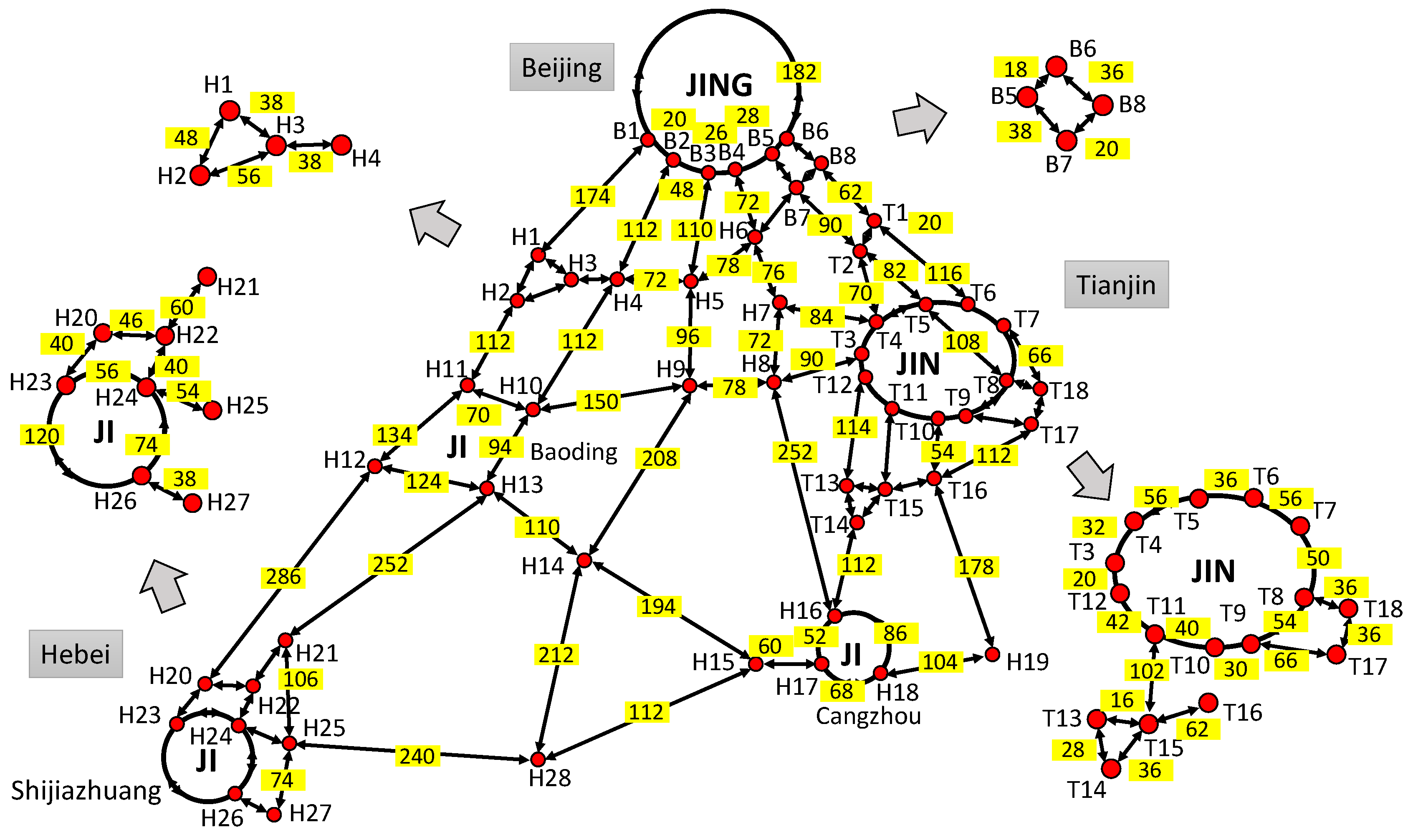
| Cases | EAF | LAF | Two-SAF |
|---|---|---|---|
| A, C, E | Xi = (i − 1)dopt = (i − 1)L/(N − 1) i = 1, 2, ..., N. | ||
| B, D, F | Xi = r + (i − 1)dopt = L/(2n) + (i − 1)L/N = (2i − 1)L/(2N), i = 1, 2, ..., N. Specifically, when n = 1, X1 = L/2. | ||
| Index | Name | Segment | L | SICF | V | C | Index | Name | Segment | L | SICF | V | C |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B-R6 | B1 ↔ B2 | 8.1 | SAF | 18 | 18 | 46 | G18 | T16 ↔ H19 | 62.1 | LAF | 14 | 16 |
| 2 | B-R6 | B1 ↔ B6 | 73.5 | SAF | 18 | 18 | 47 | G25 | T17 ↔ T18 | 12.5 | EAF | 14 | 16 |
| 3 | G5 | B1 ↔ H1 | 56.9 | LAF | 18 | 18 | 48 | G5 | H1 ↔ H2 | 16.7 | EAF | 12 | 14 |
| 4 | B-R6 | B2 ↔ B3 | 19.5 | SAF | 18 | 18 | 49 | G95 | H1 ↔ H3 | 13.1 | EAF | 12 | 14 |
| 5 | G5 | B2 ↔ H4 | 36.8 | LAF | 18 | 18 | 50 | G9511 | H2 ↔ H3 | 20.1 | EAF | 12 | 14 |
| 6 | B-R6 | B3 ↔ B4 | 10.5 | SAF | 18 | 18 | 51 | G5 | H2 ↔ H11 | 35.2 | EAF | 12 | 14 |
| 7 | G45 | B3 ↔ H5 | 36.3 | LAF | 18 | 18 | 52 | S24 | H3 ↔ H4 | 13.7 | EAF | 12 | 14 |
| 8 | B-R6 | B4 ↔ B5 | 11.3 | SAF | 18 | 18 | 53 | S24 | H4 ↔ H5 | 25.1 | EAF | 12 | 14 |
| 9 | G3 | B4 ↔ H6 | 23.5 | LAF | 18 | 18 | 54 | G4 | H4 ↔ H10 | 48.7 | EAF | 12 | 14 |
| 10 | B-R6 | B5 ↔ B6 | 7.8 | SAF | 18 | 18 | 55 | S24 | H5 ↔ H6 | 26.7 | EAF | 12 | 14 |
| 11 | G2 | B5 ↔ B7 | 12.6 | EAF | 18 | 18 | 56 | G45 | H5 ↔ H9 | 32.8 | EAF | 12 | 14 |
| 12 | S15 | B6 ↔ B8 | 12 | EAF | 18 | 18 | 57 | G3 | H6 ↔ H7 | 26.3 | EAF | 12 | 14 |
| 13 | G95 | B7 ↔ B8 | 6.7 | EAF | 18 | 18 | 58 | S3 | H7 ↔ H8 | 25.1 | EAF | 12 | 14 |
| 14 | AH3 | B7 ↔ T2 | 29.2 | LAF | 18 | 18 | 59 | G18 | H8 ↔ H9 | 26.6 | EAF | 12 | 14 |
| 15 | G95 | B7 ↔ H6 | 13.7 | LAF | 18 | 18 | 60 | S3 | H8 ↔ H16 | 85.5 | EAF | 12 | 14 |
| 16 | S15 | B8 ↔ T1 | 24.4 | LAF | 18 | 18 | 61 | G18 | H9 ↔ H10 | 50.8 | EAF | 12 | 14 |
| 17 | G3 | T1 ↔ T2 | 7.3 | EAF | 14 | 16 | 62 | G45 | H9 ↔ H14 | 70.4 | EAF | 12 | 14 |
| 18 | S30 | T1 ↔ T6 | 39.2 | EAF | 14 | 16 | 63 | S52 | H10 ↔ H11 | 24.3 | EAF | 12 | 14 |
| 19 | G2 | T2 ↔ T4 | 23.8 | EAF | 14 | 16 | 64 | G18 | H10 ↔ H13 | 32 | EAF | 12 | 14 |
| 20 | AH3 | T2 ↔ T5 | 27.9 | EAF | 14 | 16 | 65 | G5 | H11 ↔ H12 | 45.8 | EAF | 12 | 14 |
| 21 | G2 | T3 ↔ T4 | 11.2 | EAF | 14 | 16 | 66 | G107 | H12 ↔ H13 | 42.6 | EAF | 12 | 14 |
| 22 | G18 | T3 ↔ T12 | 7.2 | EAF | 14 | 16 | 67 | G5 | H12 ↔ H20 | 96.5 | EAF | 12 | 14 |
| 23 | G18 | T3 ↔ H8 | 31.8 | LAF | 14 | 16 | 68 | G107 | H13 ↔ H14 | 37.5 | EAF | 12 | 14 |
| 24 | G2501 | T4 ↔ T5 | 19 | EAF | 14 | 16 | 69 | G4 | H13 ↔ H21 | 85.2 | EAF | 12 | 14 |
| 25 | G3 | T4 ↔ H7 | 29.5 | LAF | 14 | 16 | 70 | G107 | H14 ↔ H15 | 65.8 | EAF | 12 | 14 |
| 26 | G2501 | T5 ↔ T6 | 12.6 | EAF | 14 | 16 | 71 | G45 | H14 ↔ H28 | 71.9 | EAF | 12 | 14 |
| 27 | AH3 | T5 ↔ T8 | 36.7 | EAF | 14 | 16 | 72 | G307 | H15 ↔ H17 | 21.1 | EAF | 12 | 14 |
| 28 | S30 | T6 ↔ T7 | 19.4 | EAF | 14 | 16 | 73 | G1811 | H15 ↔ H28 | 82 | EAF | 12 | 14 |
| 29 | S51 | T7 ↔ T8 | 17.6 | EAF | 14 | 16 | 74 | G3 | H16 ↔ H17 | 17.9 | EAF | 12 | 14 |
| 30 | S30 | T7 ↔ T18 | 22.6 | EAF | 14 | 16 | 75 | S3 | H16 ↔ H18 | 29.8 | EAF | 12 | 14 |
| 31 | S51 | T8 ↔ T9 | 18.8 | EAF | 14 | 16 | 76 | G1811 | H17 ↔ H18 | 23.6 | EAF | 12 | 14 |
| 32 | AH3 | T8 ↔ T18 | 12.9 | EAF | 14 | 16 | 77 | G1811 | H18 ↔ H19 | 35.5 | EAF | 12 | 14 |
| 33 | S50 | T9 ↔ T10 | 10.6 | EAF | 14 | 16 | 78 | S-Ring | H20 ↔ H22 | 15.8 | EAF | 12 | 14 |
| 34 | S50 | T9 ↔ T17 | 22.5 | EAF | 14 | 16 | 79 | G5 | H20 ↔ H23 | 14 | EAF | 12 | 14 |
| 35 | S50 | T10 ↔ T11 | 13.9 | EAF | 14 | 16 | 80 | S9902 | H21 ↔ H22 | 20.9 | EAF | 12 | 14 |
| 36 | G18 | T10 ↔ T16 | 18.9 | EAF | 14 | 16 | 81 | G4 | H21 ↔ H25 | 36.1 | EAF | 12 | 14 |
| 37 | S50 | T11 ↔ T12 | 14.8 | EAF | 14 | 16 | 82 | S9902 | H22 ↔ H24 | 14 | EAF | 12 | 14 |
| 38 | S6 | T11 ↔ T15 | 34.6 | EAF | 14 | 16 | 83 | G1811 | H23 ↔ H24 | 19.4 | EAF | 12 | 14 |
| 39 | G3 | T12 ↔ T13 | 38.6 | EAF | 14 | 16 | 84 | G20 | H23 ↔ H26 | 40.8 | EAF | 12 | 14 |
| 40 | G104 | T13 ↔ T14 | 9.8 | EAF | 14 | 16 | 85 | G1811 | H24 ↔ H25 | 18.7 | EAF | 12 | 14 |
| 41 | S60 | T13 ↔ T15 | 6 | EAF | 14 | 16 | 86 | S9902 | H24 ↔ H26 | 25.2 | EAF | 12 | 14 |
| 42 | S6 | T14 ↔ T15 | 12.6 | EAF | 14 | 16 | 87 | G4 | H25 ↔ H27 | 25.7 | EAF | 12 | 14 |
| 43 | G3 | T14 ↔ H16 | 33.1 | LAF | 14 | 16 | 88 | G1811 | H25 ↔ H28 | 81.4 | EAF | 12 | 14 |
| 44 | S60 | T15 ↔ T16 | 21.3 | EAF | 14 | 16 | 89 | G20 | H26 ↔ H27 | 13.4 | EAF | 12 | 14 |
| 45 | G25 | T16 ↔ T17 | 37.6 | EAF | 14 | 16 |
| Index | Segment | L | Nopt 1 | Index | Segment | L | Nopt 1 | Index | Segment | L | Nopt 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B1 ↔ B2 | 8.1 | 10 | 31 | T8 ↔ T9 | 18.8 | 27 | 61 | H9 ↔ H10 | 50.8 | 75 |
| 2 | B1 ↔ B6 | 73.5 | 91 | 32 | T8 ↔ T18 | 12.9 | 18 | 62 | H9 ↔ H14 | 70.4 | 104 |
| 3 | B1 ↔ H1 | 56.9 | 87 | 33 | T9 ↔ T10 | 10.6 | 15 | 63 | H10 ↔ H11 | 24.3 | 35 |
| 4 | B2 ↔ B3 | 19.5 | 24 | 34 | T9 ↔ T17 | 22.5 | 33 | 64 | H10 ↔ H13 | 32 | 47 |
| 5 | B2 ↔ H4 | 36.8 | 56 | 35 | T10 ↔ T11 | 13.9 | 20 | 65 | H11 ↔ H12 | 45.8 | 67 |
| 6 | B3 ↔ B4 | 10.5 | 13 | 36 | T10 ↔ T16 | 18.9 | 27 | 66 | H12 ↔ H13 | 42.6 | 62 |
| 7 | B3 ↔ H5 | 36.3 | 55 | 37 | T11 ↔ T12 | 14.8 | 21 | 67 | H12 ↔ H20 | 96.5 | 143 |
| 8 | B4 ↔ B5 | 11.3 | 14 | 38 | T11 ↔ T15 | 34.6 | 51 | 68 | H13 ↔ H14 | 37.5 | 55 |
| 9 | B4 ↔ H6 | 23.5 | 36 | 39 | T12 ↔ T13 | 38.6 | 57 | 69 | H13 ↔ H21 | 85.2 | 126 |
| 10 | B5 ↔ B6 | 7.8 | 9 | 40 | T13 ↔ T14 | 9.8 | 14 | 70 | H14 ↔ H15 | 65.8 | 97 |
| 11 | B5 ↔ B7 | 12.6 | 19 | 41 | T13 ↔ T15 | 6 | 8 | 71 | H14 ↔ H28 | 71.9 | 106 |
| 12 | B6 ↔ B8 | 12 | 18 | 42 | T14 ↔ T15 | 12.6 | 18 | 72 | H15 ↔ H17 | 21.1 | 30 |
| 13 | B7 ↔ B8 | 6.7 | 10 | 43 | T14 ↔ H16 | 33.1 | 47 | 73 | H15 ↔ H28 | 82 | 121 |
| 14 | B7 ↔ T2 | 29.2 | 45 | 44 | T15 ↔ T16 | 21.3 | 31 | 74 | H16 ↔ H17 | 17.9 | 26 |
| 15 | B7 ↔ H6 | 13.7 | 21 | 45 | T16 ↔ T17 | 37.6 | 56 | 75 | H16 ↔ H18 | 29.8 | 43 |
| 16 | B8 ↔ T1 | 24.4 | 37 | 46 | T16 ↔ H19 | 62.1 | 89 | 76 | H17 ↔ H18 | 23.6 | 34 |
| 17 | T1 ↔ T2 | 7.3 | 10 | 47 | T17 ↔ T18 | 12.5 | 18 | 77 | H18 ↔ H19 | 35.5 | 52 |
| 18 | T1 ↔ T6 | 39.2 | 58 | 48 | H1 ↔ H2 | 16.7 | 24 | 78 | H20 ↔ H22 | 15.8 | 23 |
| 19 | T2 ↔ T4 | 23.8 | 35 | 49 | H1 ↔ H3 | 13.1 | 19 | 79 | H20 ↔ H23 | 14 | 20 |
| 20 | T2 ↔ T5 | 27.9 | 41 | 50 | H2 ↔ H3 | 20.1 | 29 | 80 | H21 ↔ H22 | 20.9 | 30 |
| 21 | T3 ↔ T4 | 11.2 | 16 | 51 | H2 ↔ H11 | 35.2 | 51 | 81 | H21 ↔ H25 | 36.1 | 53 |
| 22 | T3 ↔ T12 | 7.2 | 10 | 52 | H3 ↔ H4 | 13.7 | 19 | 82 | H22 ↔ H24 | 14 | 20 |
| 23 | T3 ↔ H8 | 31.8 | 45 | 53 | H4 ↔ H5 | 25.1 | 36 | 83 | H23 ↔ H24 | 19.4 | 28 |
| 24 | T4 ↔ T5 | 19 | 28 | 54 | H4 ↔ H10 | 48.7 | 71 | 84 | H23 ↔ H26 | 40.8 | 60 |
| 25 | T4 ↔ H7 | 29.5 | 42 | 55 | H5 ↔ H6 | 26.7 | 39 | 85 | H24 ↔ H25 | 18.7 | 27 |
| 26 | T5 ↔ T6 | 12.6 | 18 | 56 | H5 ↔ H9 | 32.8 | 48 | 86 | H24 ↔ H26 | 25.2 | 37 |
| 27 | T5 ↔ T8 | 36.7 | 54 | 57 | H6 ↔ H7 | 26.3 | 38 | 87 | H25 ↔ H27 | 25.7 | 37 |
| 28 | T6 ↔ T7 | 19.4 | 28 | 58 | H7 ↔ H8 | 25.1 | 36 | 88 | H25 ↔ H28 | 81.4 | 120 |
| 29 | T7 ↔ T8 | 17.6 | 25 | 59 | H8 ↔ H9 | 26.6 | 39 | 89 | H26 ↔ H27 | 13.4 | 19 |
| 30 | T7 ↔ T18 | 22.6 | 33 | 60 | H8 ↔ H16 | 85.5 | 126 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, X.; Li, H.; Qin, L.; Xu, D.; Ran, B.; Rong, J. Sensor Location Problem Optimization for Traffic Network with Different Spatial Distributions of Traffic Information. Sensors 2016, 16, 1790. https://doi.org/10.3390/s16111790
Bao X, Li H, Qin L, Xu D, Ran B, Rong J. Sensor Location Problem Optimization for Traffic Network with Different Spatial Distributions of Traffic Information. Sensors. 2016; 16(11):1790. https://doi.org/10.3390/s16111790
Chicago/Turabian StyleBao, Xu, Haijian Li, Lingqiao Qin, Dongwei Xu, Bin Ran, and Jian Rong. 2016. "Sensor Location Problem Optimization for Traffic Network with Different Spatial Distributions of Traffic Information" Sensors 16, no. 11: 1790. https://doi.org/10.3390/s16111790
APA StyleBao, X., Li, H., Qin, L., Xu, D., Ran, B., & Rong, J. (2016). Sensor Location Problem Optimization for Traffic Network with Different Spatial Distributions of Traffic Information. Sensors, 16(11), 1790. https://doi.org/10.3390/s16111790






