Robust Depth Image Acquisition Using Modulated Pattern Projection and Probabilistic Graphical Models
Abstract
:1. Introduction
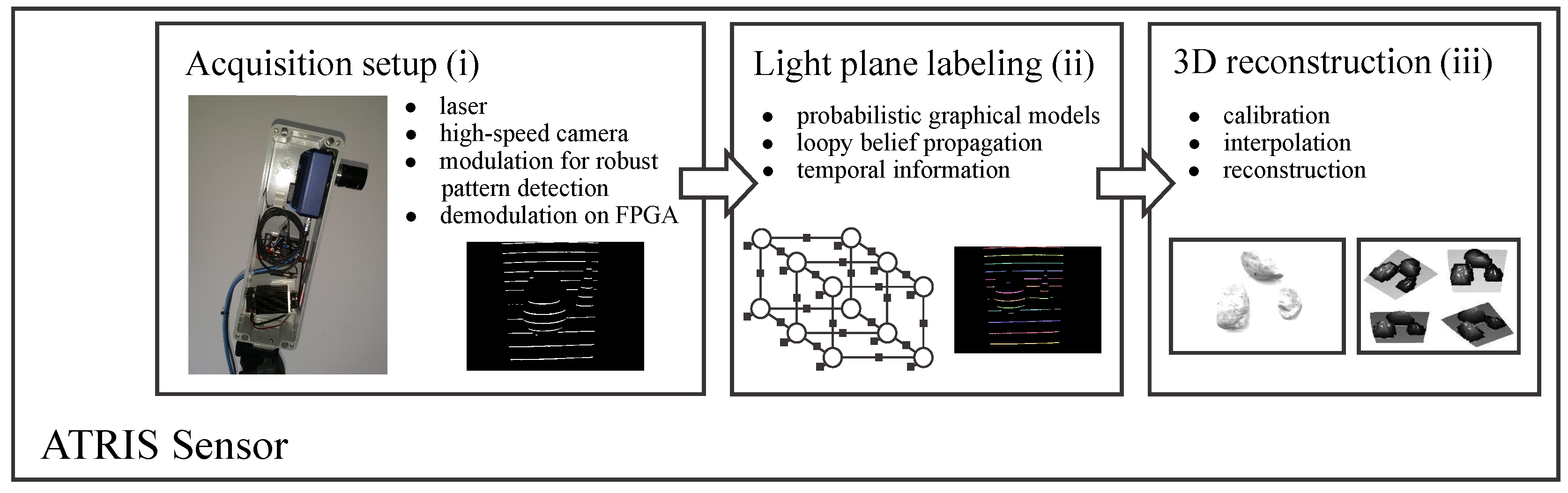
2. Sensor Overview
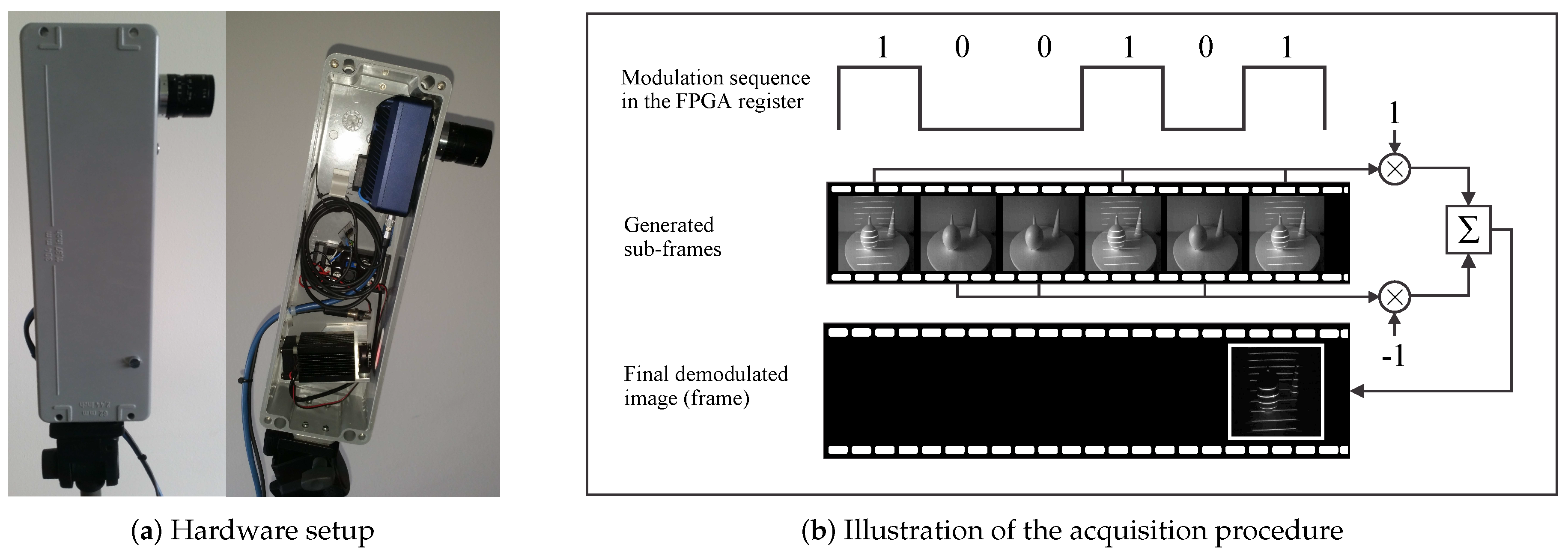
- The image acquisition procedure uses specialized hardware (comprised of a laser projector and a high-speed camera) to project a structured light pattern onto the target scene with the goal of capturing an image of the distorted pattern (i.e., a spatial distortion map). The procedure is based on the recently-introduced concept of modulated pattern projection [31,34], which ensures that spatial distortion maps of good quality can be captured in challenging conditions; for example, in the presence of strong incident sunlight or under mutual interference caused by other similar sensors directed at the same scene.
- The light plane-labeling procedure establishes the correspondence between all parts of the projected light pattern and the detected pattern that has been distorted due to the interaction with the target scene. The procedure uses loopy-belief-propagation inference over probabilistic graphical models (PGMs) as proposed in [33] to solve the correspondence problem and, differently from other existing techniques in the literature, exploits spatial relationships between parts of the projected pattern, as well as temporal information from several consecutive frames to establish correspondence.
- The 3D reconstruction procedure reconstructs the depth image of the target scene based on (i) the reference frames of the light pattern projected onto a planar surface at different distances from the camera and (ii) the established correspondence between parts of the projected pattern and the detected distortion map.
3. The Acquisition Procedure
- Noise suppression: The modulated acquisition procedure is robust for various types of noise. If information related to the visual appearance of the target scene is treated as “background noise,” then the procedure presented obviously removes the background noise as long as the control/modulation sequence employed in the FPGA register is balanced (a balanced modulation sequence is defined as a sequence with an equal number of zero- and one-valued bits). Because demodulation is a pixel-wise operation, the acquisition procedure presented also suppresses sensor noise (typically assumed to be Gaussian) caused, for instance, by poor illumination or high temperatures, where a simple pair-wise sub-frame subtraction would not suffice.
- Operation under exposure to incident sunlight: Even if the illumination of the target scene by incident sunlight is relatively strong, the modulation sequence is capable of raising the level of “signal” pixels sufficiently to recover a good-quality image of the projected pattern. This characteristic is related to the noise suppression property discussed above, because incident sunlight behaves very much like background noise under the assumption that the intensity level of the sunlight is reasonably stable.
- Mutual interference compensation: With the modulated acquisition procedure, it is possible to compensate for the mutual interference typically encountered when two or more similar sensors operate on the same target scene. This can be done by constructing the control/modulation sequences based on cyclic orthogonal (Walsh–Hadamard) codes, in which the cross-correlation properties of the modulation codes are exploited to compensate the mutual interference (see [31] for more information). Similar concepts are used in other areas, as well; for example, for synchronized CDMA (code division multiple access) systems [36] or sensor networks [37], for which mutual interference also represents a major problem.
4. Light-Plane Labeling
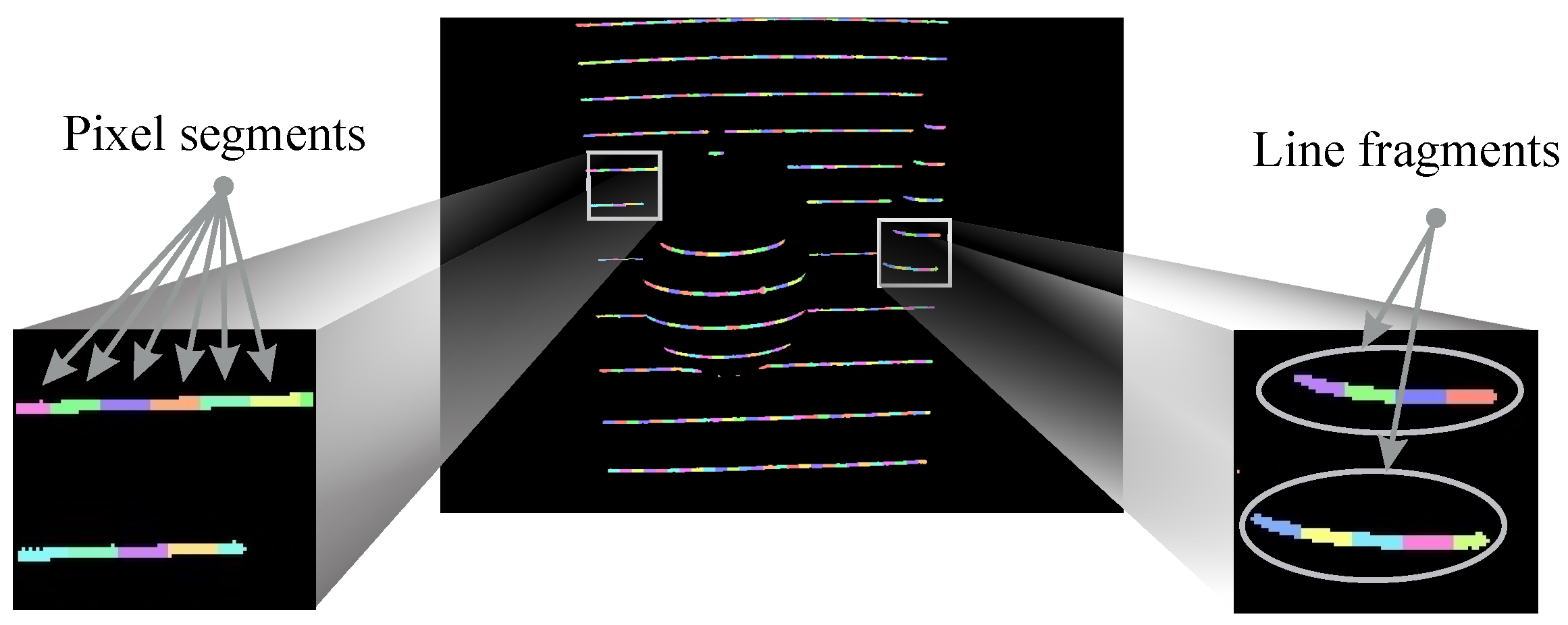
4.1. Problem Statement
4.2. Labeling with Graphical Models
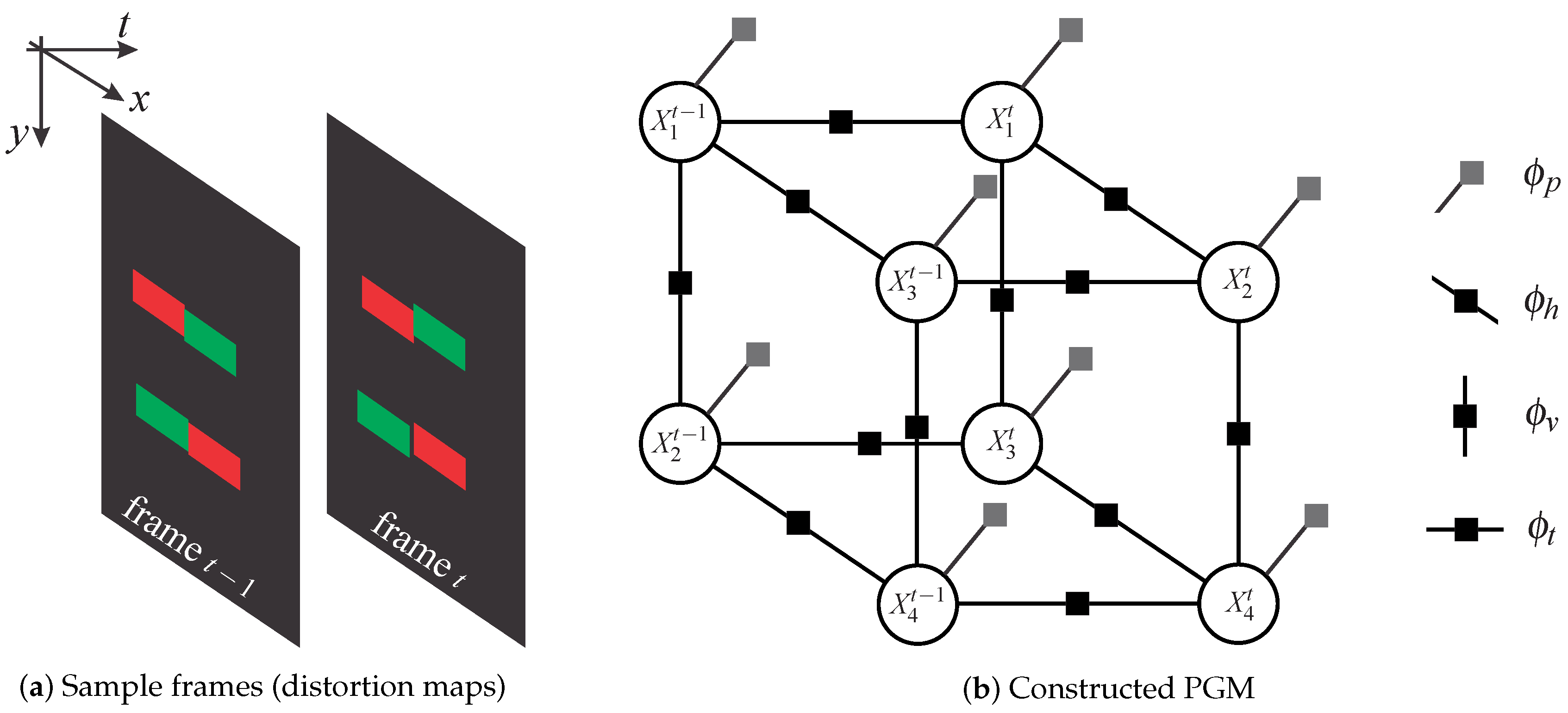
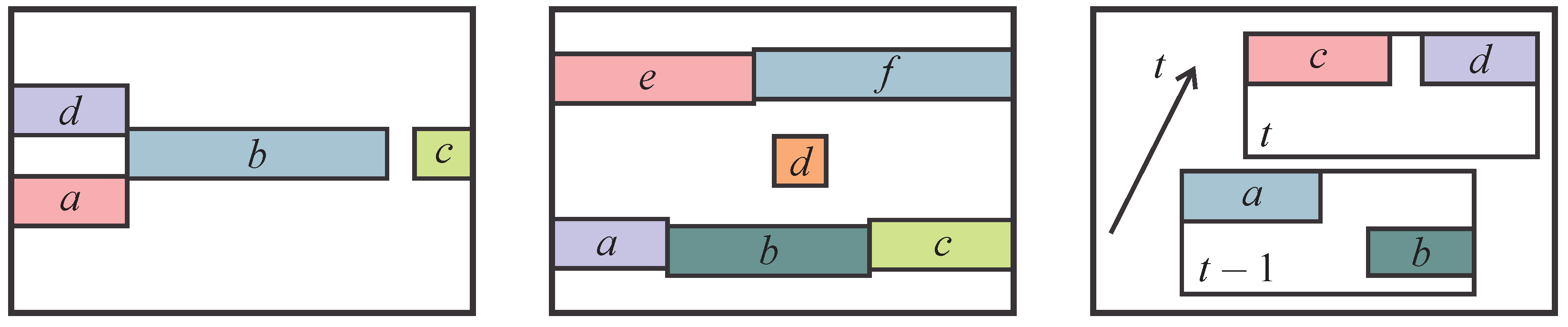
4.2.1. Graph Construction
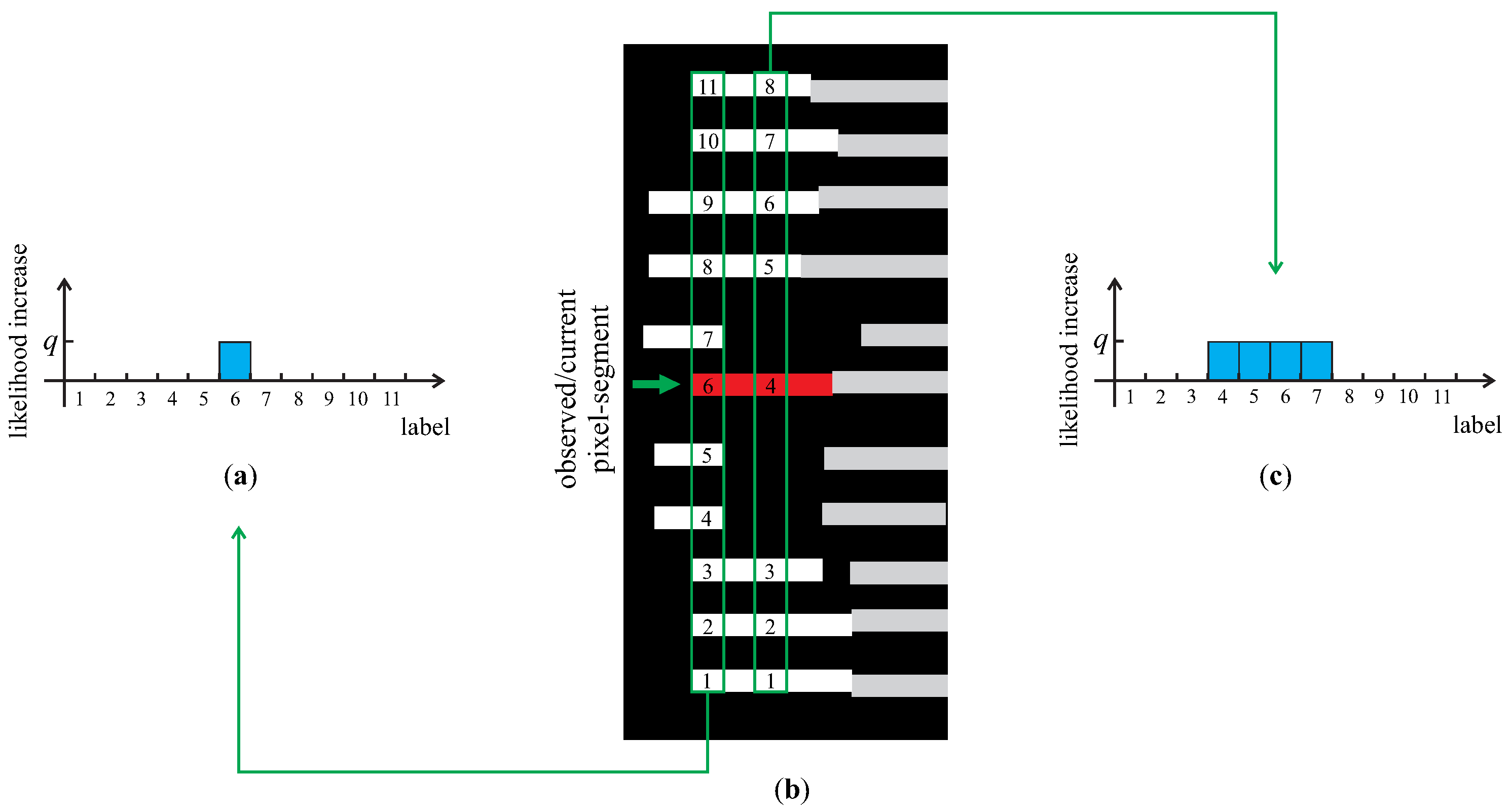
4.2.2. Factor Definition
| Algorithm 1 Calculating prior factors | |
| 1: | for all pixel-segments (i.e., random variables ) in the image I do |
| 2: | Init: Initialize as an M-dimensional vector of all zeros |
| 3: | Result: Normalized distribution (prior factor) |
| 4: | for all x-coordinates of the pixel-segment corresponding to do |
| 5: | ▹ find (at most) M biggest line fragments in I having a pixel segment at the current x-coordinate |
| 6: | ▹ record the position, k, of the pixel-segment (corresponding to ) among the found m line fragments counting from the bottom of image I up |
| 7: | if the number of found line fragments m equals M then |
| 8: | ▹ increase the k-th element of by some positive constant q |
| 9: | else |
| 10: | ▹ increase all elements of from position k to by some positive constant q |
| 11: | end if |
| 12: | end for |
| 13: | ▹ normalize the vector to unit norm; |
| 14: | end for |
4.2.3. Inference
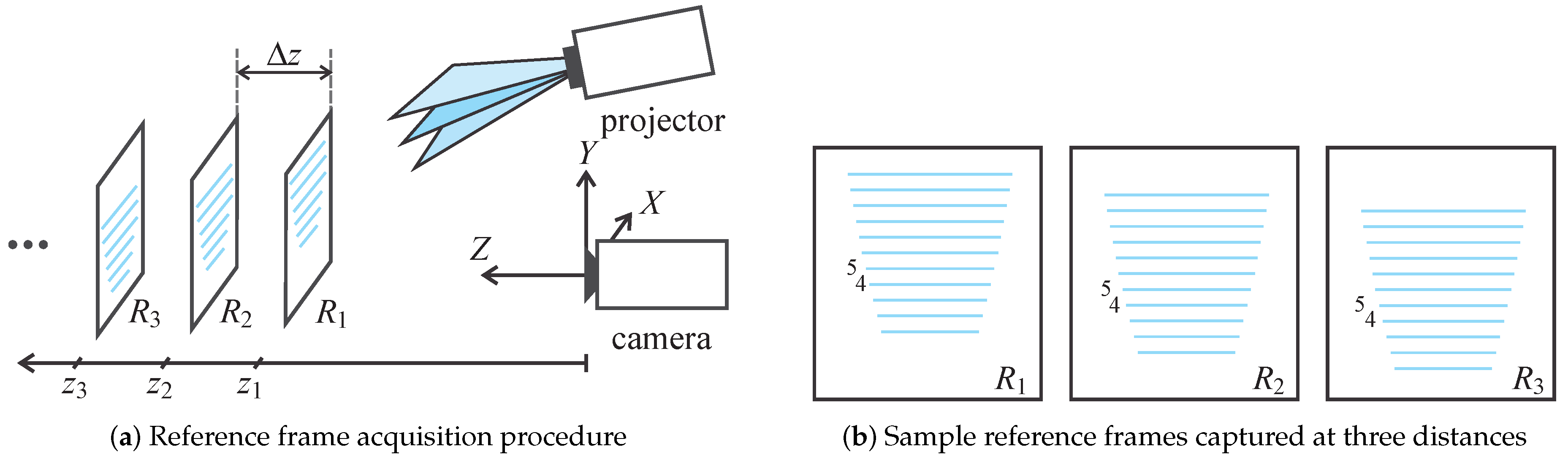
5. Depth Image Reconstruction
6. Experiments
6.1. Characteristics of the Acquisition Procedure
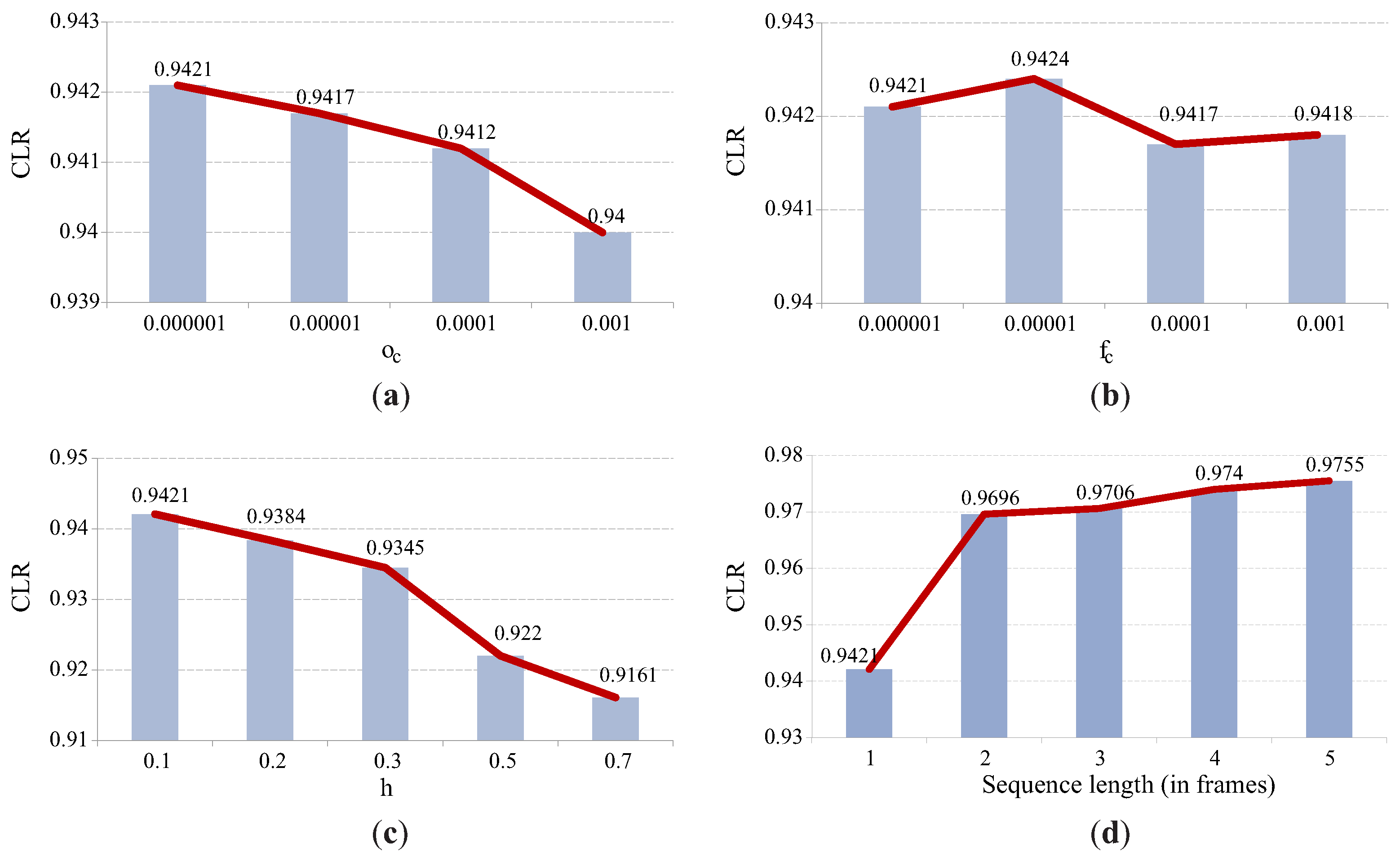
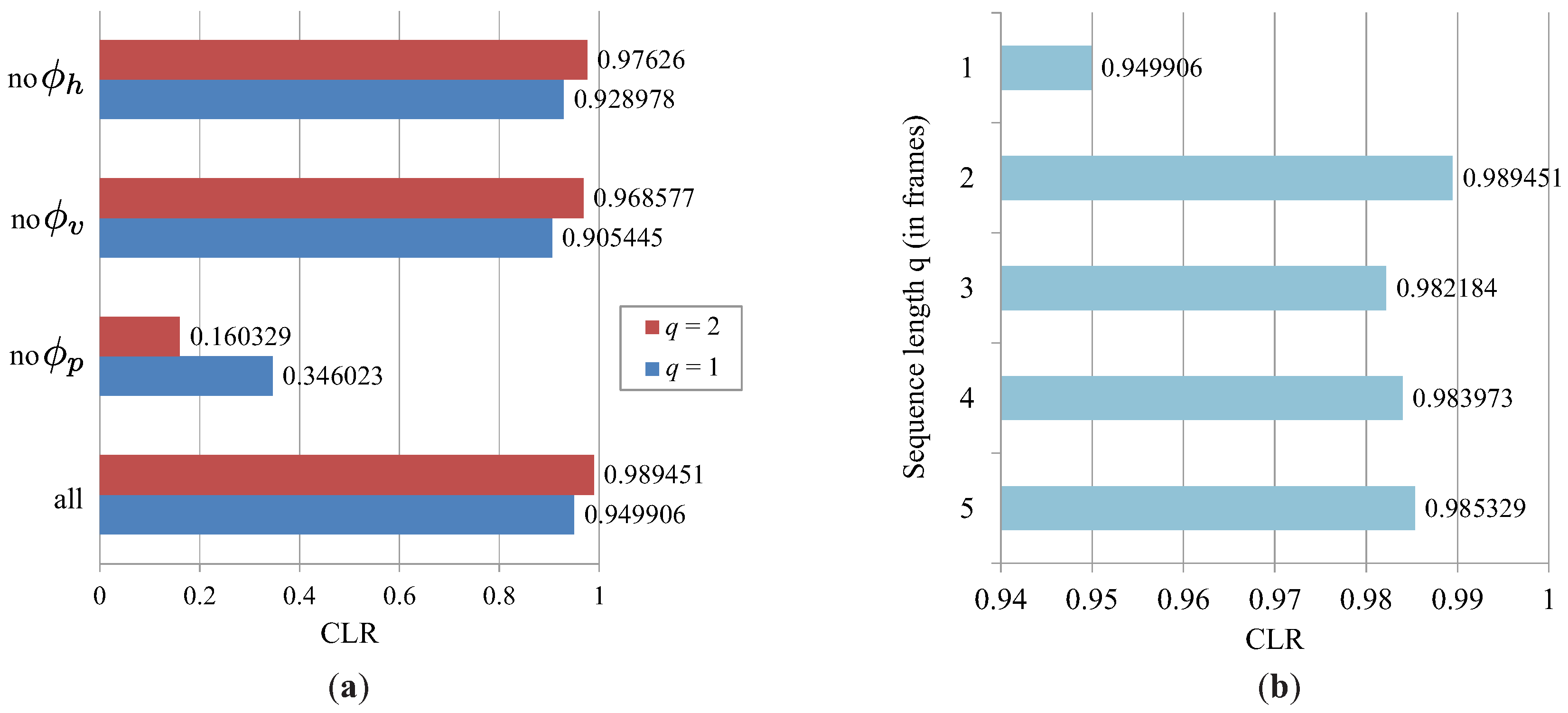
6.2. Characteristics of the Light-Plane Labeling Technique
- The naive labeling approach (NLA), which assigns light plane labels to the detected non-zero pixels in a consecutive manner. The first non-zero pixel at the given x-coordinate (looking from the bottom of the image up) is assigned the label 1; the second detected non-zero pixel at the given x-coordinate is assigned the label 2, and so on; until all 11 labels have been assigned.
- The labeling approach based on prior information (PR), which assigns light plane labels to the detected non-zero pixels by constructing a PGM based on prior factors only. This approach represents a refined version of the naive labeling technique introduced above.
- The reference approach from Ulusoy et al. (RUL) [32], which also exploits probabilistic graphical models, but relies only on spatial information to assign light plane labels to the detected non-zero pixels in the distortion map.
6.3. Constructing Depth Maps: 3D Reconstruction
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weingarten, J.W.; Gruener, G.; Siegwart, R. A state-of-the-art 3D sensor for robot navigation. In Proceedings of the 2004 IEEE/RSJ International Conference on International Conference on Intelligent Robots and Systems (IROS), Sendai, Janpan, 28 September–2 October 2004; pp. 2155–2160.
- Gutmann, J.S.; Fukuchi, M.; Fujita, M. 3D perception and environment map generation for humanoid robot navigation. Int. J. Robot. Res. 2008, 27, 1117–1134. [Google Scholar] [CrossRef]
- Ranft, B.; Dugelay, J.L.; Apvrille, L. 3D perception for autonomous navigation of a low-cost MAV using minimal landmarks. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV2013), Toulouse, France, 17–20 September 2013.
- Hohne, K.H.; Fuchs, H.; Pizer, S. 3D Imaging in Medicine: Algorithms, Systems, Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Udupa, J.K.; Herman, G.T. 3D Imaging in Medicine; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- The Kinect Sensor. Available online: http://msdn.microsoft.com/en-us/library/hh438998.aspx (accessed on 8 August 2016).
- Wallhoff, F.; Rub, M.; Rigoll, G.; Gobel, J.; Diehl, H. Surveillance and activity recognition with depth information. In Proceedings of the International Conference on Multimedia and Expo (ICME), Beijing, China, 2–5 July 2007; pp. 1103–1106.
- Lim, S.N.; Mittal, A.; Davis, L.S.; Paragios, N. Uncalibrated stereo rectification for automatic 3D surveillance. In Proceedings of the 2004 International Conference on Image Processing (ICIP), Singapore, 24–27 October 2004; pp. 1357–1360.
- Nguyen, T.T.; Slaughter, D.C.; Max, N.; Maloof, J.N.; Sinha, N. Structured light-based 3D reconstruction system for plants. Sensors 2015, 15, 18587–18612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Teng, P.; Shimizu, Y.; Hosoi, F.; Omasa, K. Estimating 3D leaf and stem shape of nursery paprika plants by a novel multi-camera photogrphy system. Sensors 2016, 16, 874. [Google Scholar] [CrossRef] [PubMed]
- Krizaj, J.; Struc, V.; Dobrisek, S. Towards robust 3D face verification using Gaussian mixture models. Int. J. Adv. Robot. Syst. 2012, 9, 1–11. [Google Scholar] [CrossRef]
- Savran, A.; Alyuz, N.; Dibeklioglu, H.; Celiktutan, O.; Gokberk, B.; Sankur, B.; Akarun, L. Bosphorus database for 3D face analysis. In European Workshop on Biometrics and Identity Management; Springer: Berlin, Germany, 2008. [Google Scholar]
- Krizaj, J.; Struc, V.; Dobrisek, S. Combining 3D face representations using region covariance descriptors and statistical models. In Proceedings of the 2013 IEEE International Conference and Workshops on Automatic Face and Gesture Recognition Workshops, Shanghai, China, 22–26 April 2013.
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-the-art and applications of 3D imaging sensors in industry, cultural heritage, medicine, and criminal investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef] [PubMed]
- Soutschek, S.; Penne, J.; Hornegger, J.; Kornhuber, J. 3D gesture-based scene navigation in medical imaging applications using time-of-flight cameras. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Anchorage, AK, USA, 23–28 June 2008; pp. 1–6.
- Natour, G.E.; Ait-Aider, O.; Rouveure, R.; Berry, F.; Faure, P. Toward 3D reconstruction of Outdoor Scenes using an MMW radar and a monocular vision sensor. Sensors 2015, 15, 25937–25967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scharstein, D.; Szeliski, R. High-accuracy stereo depth maps using structured light. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Madison, WI, USA, 18–20 June 2003.
- Salvi, J.; Pages, J.; Batlle, J. Pattern codification strategies in structured light systems. Pattern Recognit. 2004, 37, 827–849. [Google Scholar] [CrossRef]
- Batlle, J.; Mouaddib, E.; Salvi, J. Recent progress in coded structured light as a technique to solve the correspondence problem: A survey. Pattern Recognit. 1998, 31, 963–982. [Google Scholar] [CrossRef]
- Kawahito, S.; Halin, I.A.; Ushinaga, T.; Sawada, T.; Homma, M.; Maeda, Y. A CMOS time-of-flight range image sensor with gates-on-field-oxide structure. IEEE Sens. J. 2007, 12, 1578–1586. [Google Scholar] [CrossRef]
- Lange, R.; Seitz, P. Solid-state time-of-flight range camera. IEEE J. Quantum Electron. 2001, 37, 390–397. [Google Scholar] [CrossRef]
- Thiebaut, E.; Giovannelli, J.F. Image reconstruction in optical interferometry. IEEE Signal Process Mag. 2010, 1, 97–109. [Google Scholar] [CrossRef]
- Besl, P.J. Active optical range imaging sensors. In Advances in Machine Vision; Springer: New York, NY, USA, 1989; pp. 1–63. [Google Scholar]
- Blais, F. Review of 20 years of range sensor development. J. Electron. Imaging 2004, 13, 231–240. [Google Scholar] [CrossRef]
- Faugeras, O. Three-Dimensional Computer Vision: A Geometric Viewpoint; The MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Nayar, S.K.; Nakagawa, Y. Shape from focus. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 824–831. [Google Scholar] [CrossRef]
- Prados, E.; Faugeras, O. Shape from shading. In Handbook of Mathematical Models in Computer Vision; Springer: New York, NY, USA, 2006; pp. 375–388. [Google Scholar]
- Aggarwal, J.K.; Chien, C.H. 3D Structures from 2D Images. In Advances in Machine Vision; Sanz, J.L.C., Ed.; Springer: New York, NY, USA, 1989. [Google Scholar]
- Forsyth, D.A.; Ponce, J. Computer Vision: A modern Approach, 2nd ed.; Pearson: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Kravanja, J. Analiza Projiciranih Slikovnih Vzorcev Za Pridobivanje Globinskih Slik. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2016. [Google Scholar]
- Volkov, A.; Zganec-Gros, J.; Zganec, M.; Javornik, T.; Svigelj, A. Modulated acquisition of spatial distortion maps. Sensors 2013, 13, 11069–11084. [Google Scholar] [CrossRef] [PubMed]
- Ulusoy, A.O.; Calakli, F.; Taubin, G. Robust one-shot 3D scanning using loopy belief propagation. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), San Francisco, CA, USA, 13–18 June 2010; pp. 15–22.
- Kravanja, J.; Zganec, M.; Zganec-Gros, J.; Dobrisek, S.; Struc, V. Exploiting Spatio-Temporal Information for Light-Plane Labeling in Depth-Image Sensors Using Probabilistic Graphical Models. Informatica 2016, 27, 67–84. [Google Scholar] [CrossRef]
- Zganec, M.; Zganec-Gros, J. Active 3D Triangulation-Based Method and Device. US Patent 7,483,151 B2, 27 January 2009. [Google Scholar]
- Optomotive Velociraptor Camera Datasheet. Available online: http://www.optomotive.com/products/velociraptor-hs (accessed on 8 August 2016).
- Amadei, M.; Manzoli, U.; Merani, M.L. On the assignment of Walsh and quasi-orthogonal codes in a multicarrier DS-CDMA system with multiple classes of users. In Proceedings of the IEEE Global Telecommunications Conference, Taipei, Taiwan, 17–21 November 2002; pp. 841–845.
- Tawfiq, A.; Abouei, J.; Plataniotis, K.N. Cyclic orthogonal codes in CDMA-based asynchronous wireless body area networks. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 1593–1596.
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor Graphs and the Sum-Product Algorithm. IEEE Trans. Inf. Theory 2001, 14, 498–519. [Google Scholar] [CrossRef]
- Wiegerinck, W.; Heskes, T. Fractional belief propagation. In Neural Information Processing Systems (NIPS); The MIT Press: Cambridge, MA, USA, 2003; pp. 438–445. [Google Scholar]
- Gonzales, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Weiss, Y.; Freeman, W.T. On the optimality of solutions of the max-product belief-propagation algorithm in arbitrary graphs. IEEE Trans. Inf. Theory 2001, 47, 736–744. [Google Scholar] [CrossRef]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Posdamer, J.; Altschuler, M. Surface measurement by space-encoded projected beam system. Comput. Graph. Image Proc. 1982, 18, 1–17. [Google Scholar] [CrossRef]
- Ishii, I.; Yamamoto, K.; Doi, K.; Tsuji, T. High-speed 3D Image Acquisition Using Coded Structured Light Projection. In Proceedings of the 2007 IEEE/RSJ International Conference on Itenlligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 925–930.
- Li, Z.; Curless, B.; Seitz, S.M. Rapid shape acquisition using color structured light and multi-pass dynamic programming. In Proceedings of the 2002 First International Symposium on 3D Data Processing Visualization and Transmission, Padova, Italy, 19–21 June 2002.
- Horn, E.; Kiryati, N. Toward optimal structured light patterns. Image Vision Comput. 1999, 17, 87–97. [Google Scholar] [CrossRef]
- Chen, C.; Liu, M.; Zhang, B.; Han, J.; Jiang, J.; Liu, H. 3D Action Recognition Using Multi-Temporal Depth Motion Maps and Fisher Vector. Available online: https://www.researchgate.net/profile/Chen_Chen82/publication/300700290_3D_Action_Recognition_Using_Multi-temporal_Depth_Motion_Maps_and_Fisher_Vector/links/570ac58308ae8883a1fc05da.pdf (accessed on 6 October 2016).
- Chen, C.; Zhang, B.; Hou, Z.; Jiang, J.; Liu, M.; Yang, Y. Action recognition from depth sequences using weighted fusion of 2D and 3D auto-correlation of gradients features. In Multimedia Tools and Applications; Springer: New York, NY, USA, 2016; pp. 1–19. [Google Scholar]
- Ly, D.L.; Saxena, A.; Lipson, H. Pose estimation from a single depth image for arbitrary kinematic skeletons. 2011; arXiv:1106.5341. [Google Scholar]
- Qiao, M.; Cheng, J.; Zhao, W. Model-based human pose estimation with hierarchical ICP from single depth images. Adv. Autom. Robot. 2011, 2, 27–35. [Google Scholar]
- Gajšek, R.; Štruc, V.; Dobrišek, S.; Mihelič, F. Emotion recognition using linear transformations in combination with video. In Proceedings of the 10th Annual Conference of the International Speech Communication Association, Brighton, UK, 6–10 September 2009.
- Gajšek, R.; Žibert, J.; Justin, T.; Štruc, V.; Vesnicer, B.; Mihelič, F. Gender and affect recognition based on GMM and GMM-UBM modeling with relevance MAP estimation. In Proceedings of the 11th Annual Conference of the International Speech Communication Association, Chiba, Japan, 26–30 September 2010.
- Ye, M.; Zhang, Q.; Wang, L.; Zhu, J.; Yang, R.; Gall, J. A survey on human motion analysis from depth data. In Time-of-Flight and Depth Imaging. Sensors, Algorithms, and Applications; Springer: New York, NY, USA, 2013; pp. 149–187. [Google Scholar]









| Method | Outdoor Dataset (Noisy) | |||
|---|---|---|---|---|
| NLA | PR | RUL | Ours | |
| CLR | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kravanja, J.; Žganec, M.; Žganec-Gros, J.; Dobrišek, S.; Štruc, V. Robust Depth Image Acquisition Using Modulated Pattern Projection and Probabilistic Graphical Models. Sensors 2016, 16, 1740. https://doi.org/10.3390/s16101740
Kravanja J, Žganec M, Žganec-Gros J, Dobrišek S, Štruc V. Robust Depth Image Acquisition Using Modulated Pattern Projection and Probabilistic Graphical Models. Sensors. 2016; 16(10):1740. https://doi.org/10.3390/s16101740
Chicago/Turabian StyleKravanja, Jaka, Mario Žganec, Jerneja Žganec-Gros, Simon Dobrišek, and Vitomir Štruc. 2016. "Robust Depth Image Acquisition Using Modulated Pattern Projection and Probabilistic Graphical Models" Sensors 16, no. 10: 1740. https://doi.org/10.3390/s16101740
APA StyleKravanja, J., Žganec, M., Žganec-Gros, J., Dobrišek, S., & Štruc, V. (2016). Robust Depth Image Acquisition Using Modulated Pattern Projection and Probabilistic Graphical Models. Sensors, 16(10), 1740. https://doi.org/10.3390/s16101740








