Application of CCG Sensors to a High-Temperature Structure Subjected to Thermo-Mechanical Load
Abstract
:1. Introduction
2. Experimental Design
3. Experimental Results and Analysis
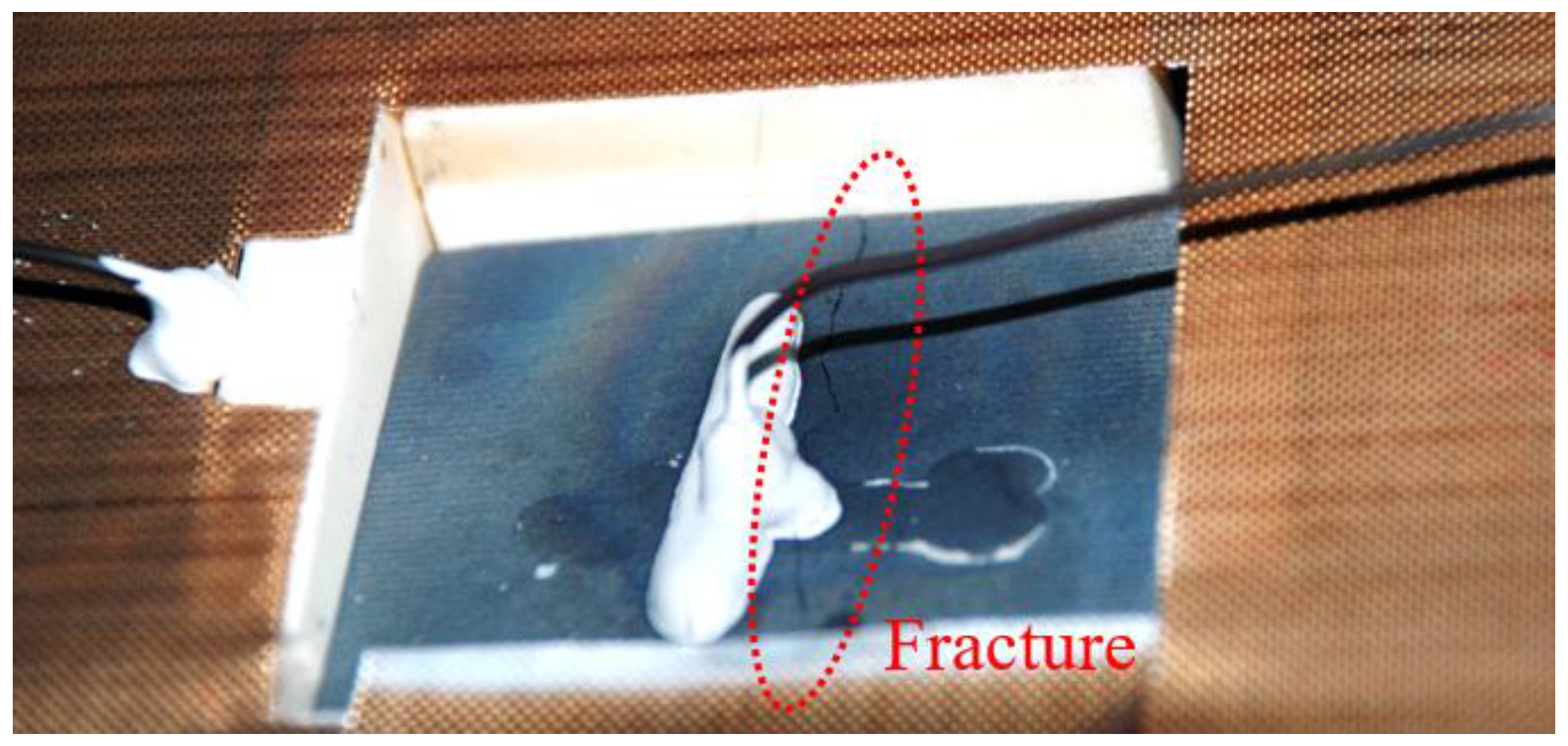
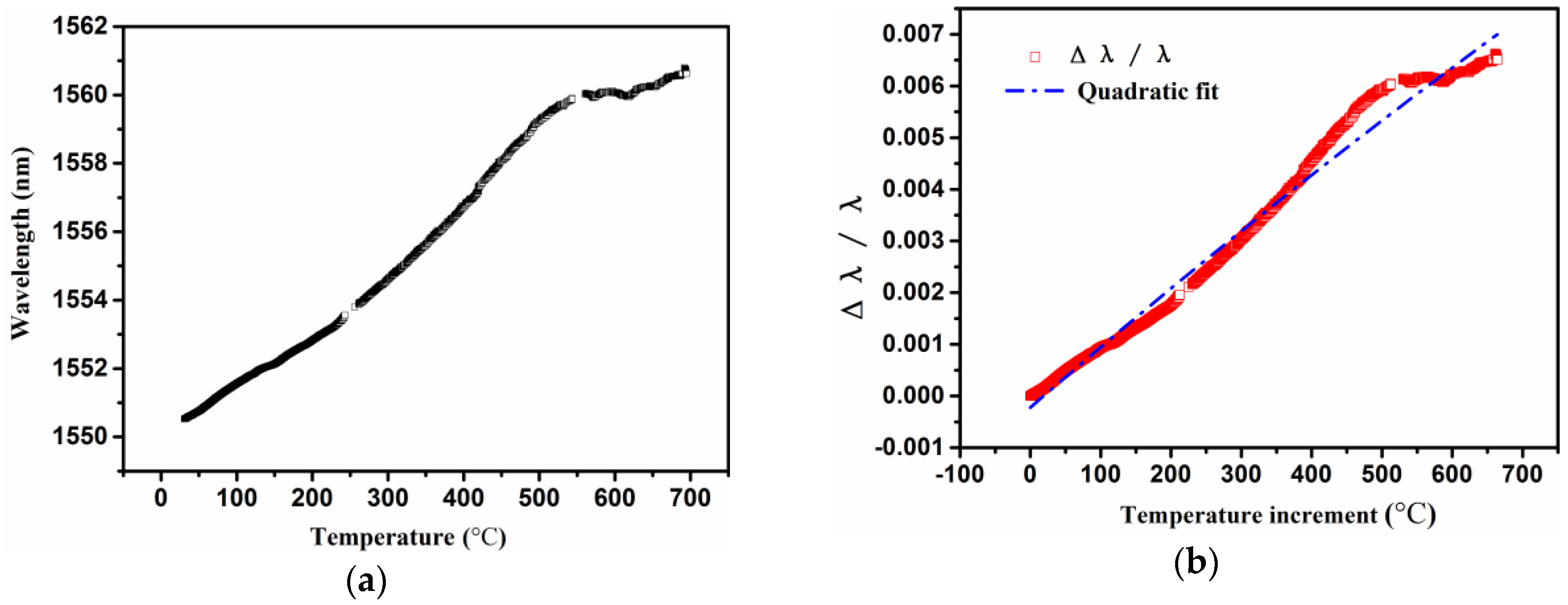
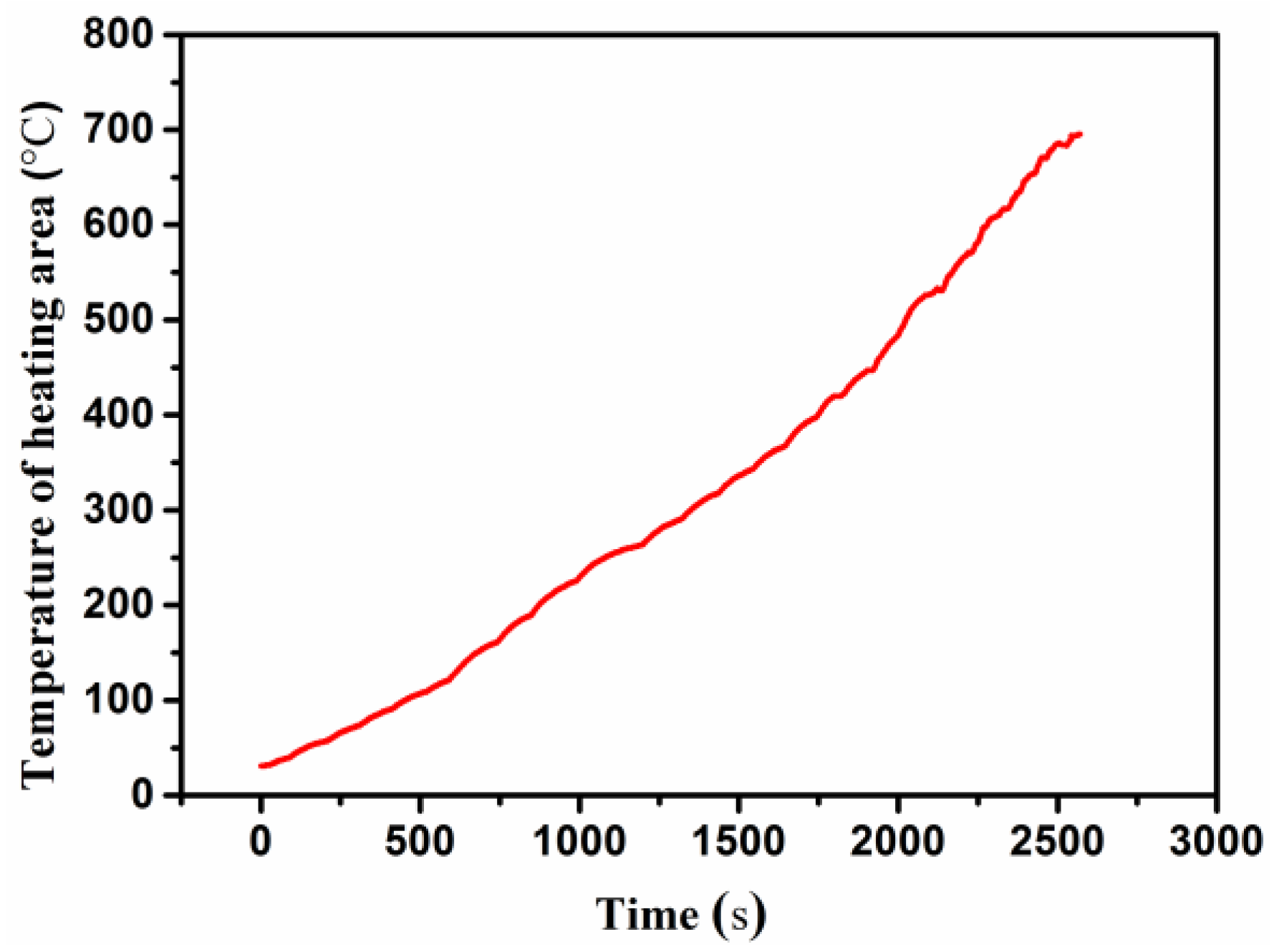
3.1. Experimental Results
3.2. Analysis of the Results
4. Finite Element Analysis and Discussions
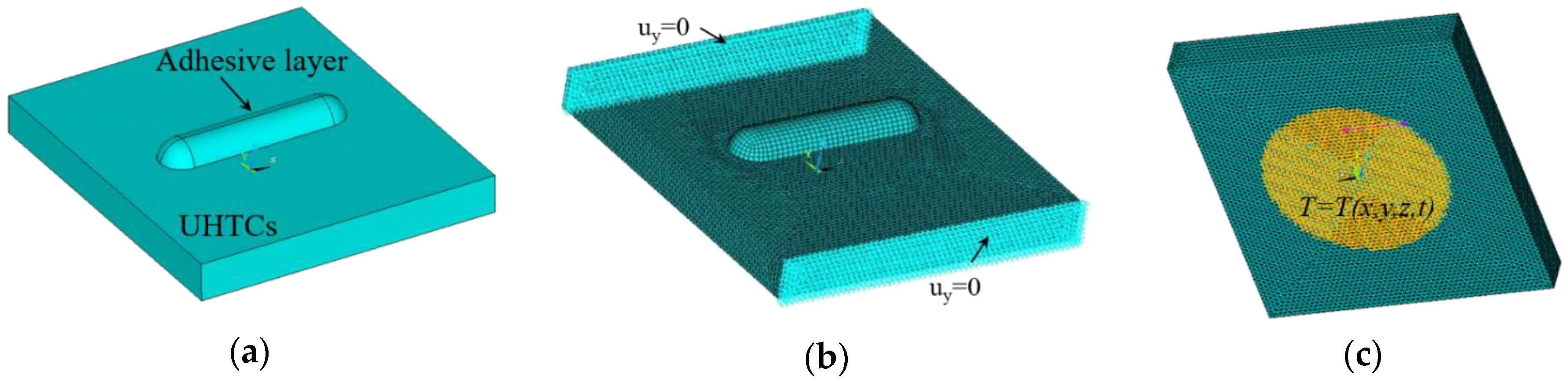
4.1. Finite Element Model
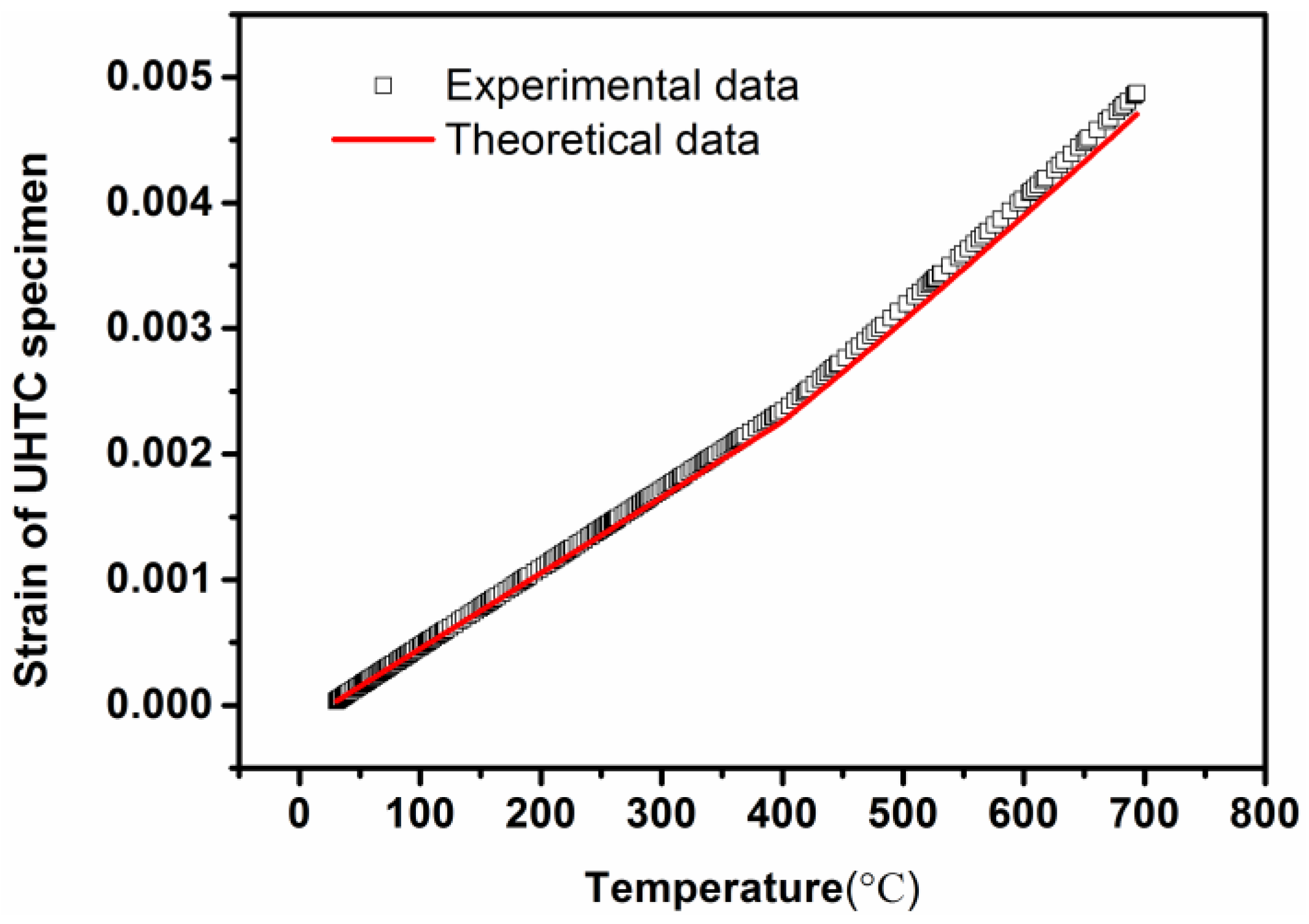
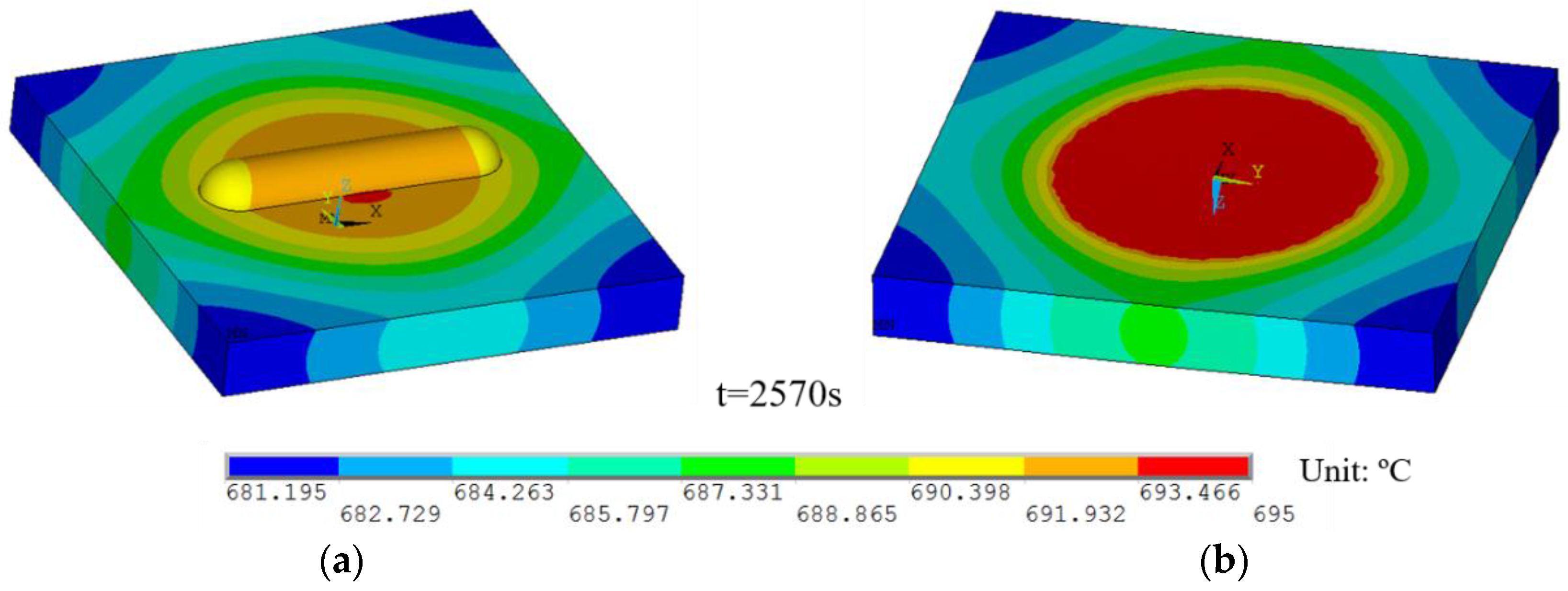
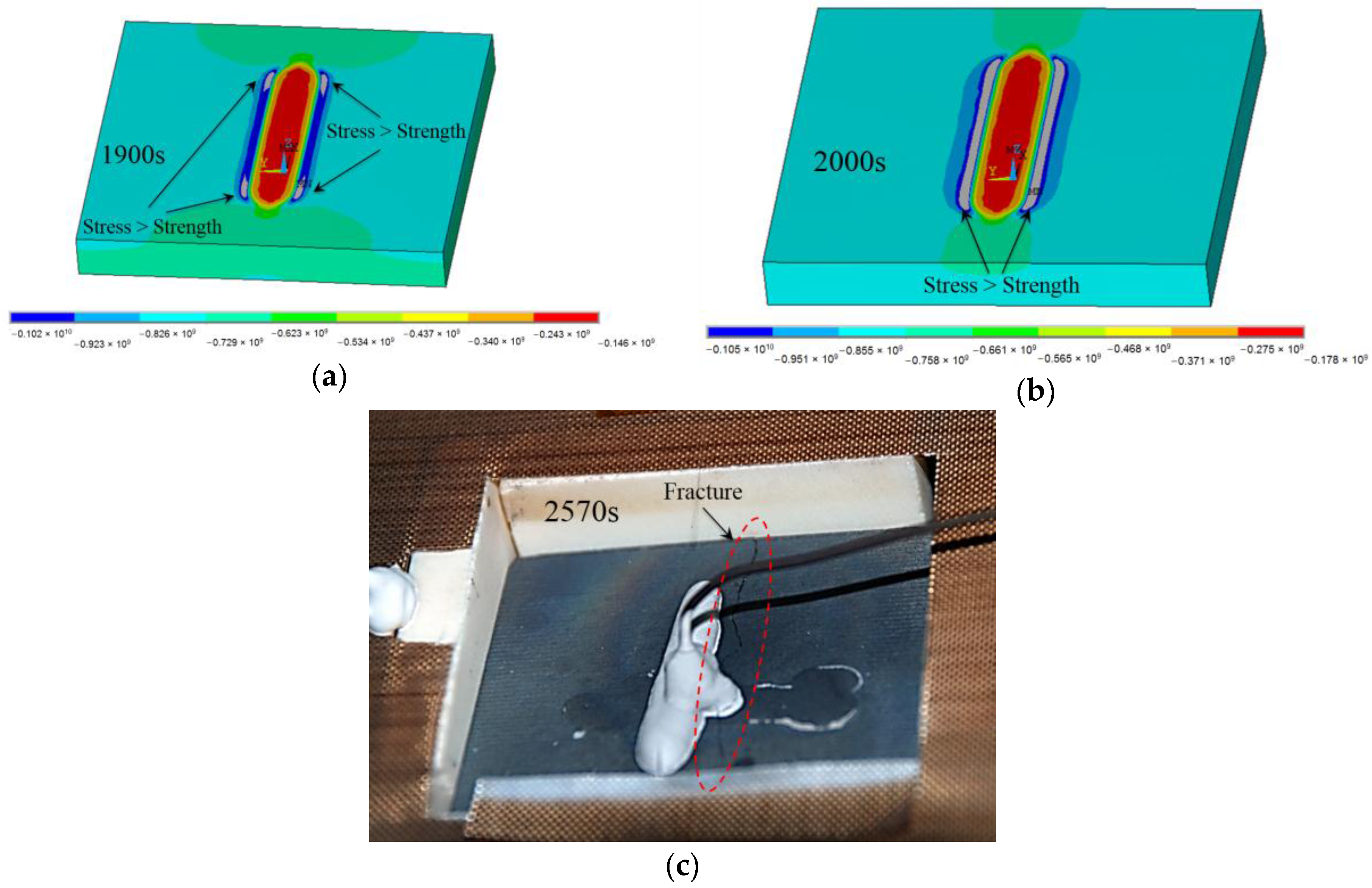
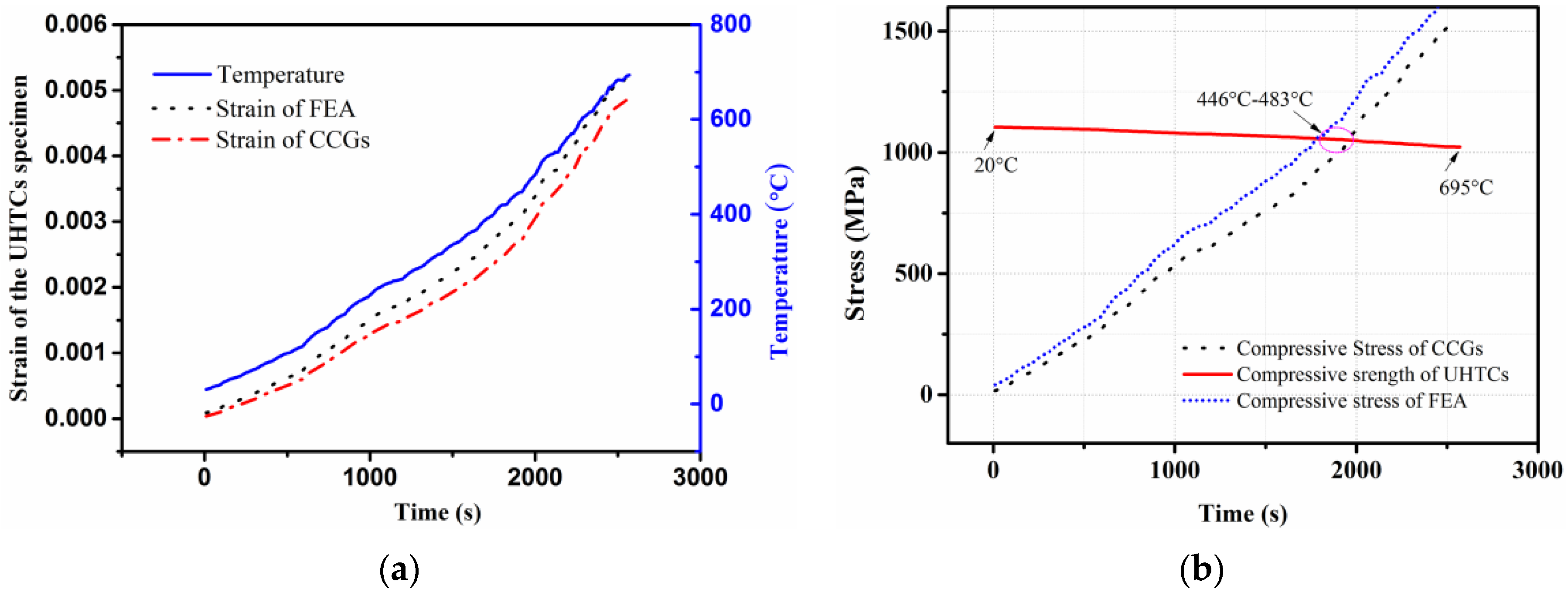
4.2. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mihailov, S.J. Fiber bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Panopoulou, A.; Roulias, D.; Loutas, T.; Kostopoulos, V. Health monitoring of aerospace structures using fibre bragg gratings combined with advanced signal processing and pattern recognition techniques. Strain 2012, 48, 267–277. [Google Scholar] [CrossRef]
- Su, D.; Qiao, X.; Yang, H.; Rong, Q.; Bai, Z.; Wang, Y.; Feng, Z. Temperature-independent fiber inclinometer based on orthogonally polarized modes coupling using a polarization-maintaining fiber bragg grating. Sensors 2014, 14, 20930–20939. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-N.; Tang, J.-L. Feasibility of fiber bragg grating and long-period fiber grating sensors under different environmental conditions. Sensors 2010, 10, 10105–10127. [Google Scholar] [CrossRef] [PubMed]
- Culshaw, B. Measuring strain using optical fibres. Strain 2000, 36, 105–113. [Google Scholar] [CrossRef]
- Bennion, I.; Zhang, L.; Everall, L. In-fibre grating techniques for strain sensing. Strain 2000, 36, 115–121. [Google Scholar] [CrossRef]
- Canning, J.; Stevenson, M.; Bandyopadhyay, S.; Cook, K. Extreme silica optical fibre gratings. Sensors 2008, 8, 6448–6452. [Google Scholar] [CrossRef]
- Bueno, A.; Kinet, D.; Mégret, P.; Caucheteur, C. Fast thermal regeneration of fiber bragg gratings. Opt. Lett. 2013, 38, 4178–4181. [Google Scholar] [CrossRef] [PubMed]
- Fokine, M. Thermal Stability of Chemical Composition Gratings in Fluorine-Germanium-Doped Silica Fibers. Opt. Lett. 2002, 27, 1016–1018. [Google Scholar] [CrossRef] [PubMed]
- Fokine, M. Photosensitivity, Chemical Composition Gratings and Optical Fiber Based Components. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, December 2002. [Google Scholar]
- Fokine, M. Formation of thermally stable chemical composition gratings in optical fibers. J. Opt. Soc. Am. B 2002, 19, 1759–1765. [Google Scholar] [CrossRef]
- Pal, S.; Mandal, J.; Sun, T.; Grattan, K.; Fokine, M.; Carlsson, F.; Fonjallaz, P.Y.; Wade, S.; Collins, S. Characteristics of potential fibre bragg grating sensor-based devices at elevated temperatures. Meas. Sci. Technol. 2003, 14, 1131. [Google Scholar] [CrossRef]
- Fokine, M. Thermal stability of oxygen-modulated chemical-composition gratings in standard telecommunication fiber. Opt. Lett. 2004, 29, 1185–1187. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, P.; Laurell, F.; Fokine, M. Influence of pre-annealing on the thermal regeneration of fiber bragg gratings in standard optical fibers. Opt. Express 2015, 23, 27520–27535. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B. Optical High Temperature Sensor Based on Fiber Bragg Grating. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, October 2007. [Google Scholar]
- Zhang, B.; Kahrizi, M. High-temperature resistance fiber bragg grating temperature sensor fabrication. IEEE Sens. J. 2007, 7, 586–591. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Canning, J.; Stevenson, M.; Cook, K. Ultrahigh-temperature regenerated gratings in boron-codoped germanosilicate optical fiber using 193 nm. Opt. Lett. 2008, 33, 1917–1919. [Google Scholar] [CrossRef] [PubMed]
- Canning, J.; Stevenson, M.; Fenton, J.; Aslund, M.; Bandyopadhyay, S. Strong regenerated gratings. In Proceedings of the 20th International Conference on Optical Fibre Sensors, Edinburgh, UK, 5–9 October 2009.
- Canning, J.; Cook, K.; Aslund, M.; Stevenson, M.; Biswas, P.; Bandyopadhyay, S. Regenerated Fibre Bragg Gratings; InTech: Rijeka, Croatia, 2010. [Google Scholar]
- Barrera, D.; Finazzi, V.; Coviello, G.; Bueno, A.; Sales, S.; Pruneri, V. Chemical composition gratings in germanium doped and boron-germanium co-doped fibers. In Proceedings of the Optical Sensing and Detection, Brussels, Belgium, 12–15 April 2010.
- David, B.; Vittoria, F.; Joel, V.; Antonio, B.; Salvador, S.; Valerio, P. On the Use of Optical Fiber Sensors (CCGs and PCFI) for Harsh Environments. Waves 2010, 126–133. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.722.5293&rep=rep1&type=pdf (accessed on 13 September 2016). [Google Scholar]
- Barrera, D. Fiber-optic sensors for high-temperature applications. SPIE Newsroom 2010, 6. [Google Scholar] [CrossRef]
- Li, G.; Guan, B.O. Research on reflectivity of chemical composition grating sensors at high temperatures. In Proceedings of the Passive Components and Fiber-Based Devices VII, Shanghai, China, 8–12 December 2010.
- Li, G.; Guan, B.O. Improvement on reflectivity of chemical composition gratings at high temperatures. Microw. Opt. Technol. Lett. 2011, 53, 963–966. [Google Scholar] [CrossRef]
- Li, G.; Liu, M.; Li, Y.; Guan, B.O. Fabrication and sensing characteristics of the chemical composition grating sensor at high temperatures. Microw. Opt. Technol. Lett. 2012, 54, 71–75. [Google Scholar] [CrossRef]
- Grobnic, D.; Smelser, C.W.; Mihailov, S.J.; Walker, R.B. Long-term thermal stability tests at 1000 °C of silica fibre bragg gratings made with ultrafast laser radiation. Meas. Sci. Technol. 2006, 17, 1009. [Google Scholar] [CrossRef]
- Coviello, G.; Finazzi, V.; Villatoro, J.; Pruneri, V. Thermally stabilized pcf-based sensor for temperature measurements up to 1000 °C. Opt. Express 2009, 17, 21551–21559. [Google Scholar] [CrossRef] [PubMed]
- Cheong, Y.; Chong, W.; Chong, S.; Lim, K.; Ahmad, H. Regenerated type-iia fibre bragg grating from a Ge-B codoped fibre via thermal activation. Opt. Laser Technol. 2014, 62, 69–72. [Google Scholar] [CrossRef]
- Laffont, G.; Cotillard, R.; Ferdinand, P. Multiplexed regenerated fiber bragg gratings for high-temperature measurement. Meas. Sci. Technol. 2013, 24, 094010. [Google Scholar] [CrossRef]
- Lindner, E.; Canning, J.; Chojetzki, C.; Brückner, S.; Becker, M.; Rothhardt, M.; Bartelt, H. Thermal regenerated type iia fiber bragg gratings for ultra-high temperature operation. Opt. Commun. 2011, 284, 183–185. [Google Scholar] [CrossRef]
- Méndez, A.; Wnuk, V.P.; Fokine, M.; Claesson, Å.; Nilsson, L.-E.; Ferguson, S.; Graver, T. Packaging process of fiber bragg grating strain sensors for use in high-temperature applications. In Proceedings of the Fiber Optic Sensor Technology and Applications IV, Boston, MA, USA, 24–26 October 2005.
- Wnuk, V.P.; Méndez, A.; Ferguson, S.; Graver, T. Process for mounting and packaging of fiber bragg grating strain sensors for use in harsh environment applications. In Proceedings of the Smart Structures and Materials 2005: Smart Sensor Technology and Measurement System, San Diego, CA, USA, 5–6 March 2005.
- Selfridge, R.H.; Schultz, S.M.; Lowder, T.L.; Wnuk, V.P.; Méndez, A.; Ferguson, S.; Graver, T. Packaging of surface relief fiber bragg gratings for use as strain sensors at high temperature. In Proceedings of the Smart Structures and Materials 2006: Smart Sensor Monitoring Systems and Applications, San Diego, CA, USA, 27 February–1 March 2006.
- Reddy, P.S.; Sai Prasad, R.L.; Srimannarayana, K.; Shankar, M.S.; Gupta, D.S. A novel method for high temperature measurements using fiber bragg grating sensor. Opt. Appl. 2010, 40, 685–692. [Google Scholar]
- Mamidi, V.R.; Kamineni, S.; Ravinuthala, L.S.P.; Thumu, V.; Pachava, V.R. Characterization of encapsulating materials for fiber bragg grating-based temperature sensors. Fiber Integr. Opt. 2014, 33, 325–335. [Google Scholar] [CrossRef]
- Reddy, P.S.; Prasad, R.L.N.S.; Gupta, D.S.; Shankar, M.S.; Narayana, K.S.; Kishore, P. Encapsulated fiber bragg grating sensor for high temperature measurements. Opt. Eng. 2011, 50, 114401–114406. [Google Scholar] [CrossRef]
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Performance of a high-temperature sensor based on regenerated fiber bragg gratings. In Proceedings of the 21st International Conference on Optical Fibre Sensors (OFS21), Ottawa, ON, Canada, 15–19 May 2011; pp. 775381–775384.
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Packaged optical sensors based on regenerated fiber bragg gratings for high temperature applications. IEEE Sens. J. 2012, 12, 107–112. [Google Scholar] [CrossRef]
- Azhari, A.; Liang, R.; Toyserkani, E. A novel fibre bragg grating sensor packaging design for ultra-high temperature sensing in harsh environments. Meas. Sci. Technol. 2014, 25, 075104. [Google Scholar] [CrossRef]
- Xie, W.; Meng, S.; Jin, H.; Du, C.; Wang, L.; Peng, T.; Scarpa, F.; Huo, S. Measurement of the high-temperature strain of uhtc materials using chemical composition gratings. Meas. Sci. Technol. 2016, 27, 055101. [Google Scholar] [CrossRef]
- Glass, D.E. Ceramic matrix composite (CMC) thermal protection systems (TPS) and hot structures for hypersonic vehicles. In Proceedings of the 15th AIAA Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; pp. 1–36.
- Latini, V.; Striano, V.; Coppola, G.; Rendina, I. Fiber optic sensors system for high-temperature monitoring of aerospace structures. In Proceedings of the Photonic Materials, Devices, and Applications II, Maspalomas, Spain, 2–4 May 2007.
- Manor, D.; Lau, K.Y.; Johnson, D.B. Aerothermodynamic environments and thermal protection for a wave-rider second stage. J. Spacecr. Rockets 2005, 42, 208–212. [Google Scholar] [CrossRef]
- Zhang, X.-H.; Hu, P.; Han, J.-C. Structure evolution of ZrB2-SiC during the oxidation in air. J. Mater. Res. 2008, 23, 1961–1972. [Google Scholar] [CrossRef]
- Ge, Y.; Elshafie, M.Z.; Dirar, S.; Middleton, C.R. The response of embedded strain sensors in concrete beams subjected to thermal loading. Constr. Build. Mater. 2014, 70, 279–290. [Google Scholar] [CrossRef]
- Li, G.-Y.; Guan, B.O. The strain response of chemical composition gratings at high temperatures. Meas. Sci. Technol. 2009, 20, 025204. [Google Scholar] [CrossRef]
- Maier, R.R.; MacPherson, W.N.; Barton, J.S.; Jones, J.D.; McCulloch, S.; Burnell, G. Temperature dependence of the stress response of fibre bragg gratings. Meas. Sci. Technol. 2004, 15, 1601. [Google Scholar] [CrossRef]
- Meng, S.; Du, C.; Xie, W.; Huo, S.; Jiao, L.; Jin, H.; Song, L. Application of high-temperature optical fiber sensor in temperature and strain testing of hot structure. J. Sol. Rocket Technol. 2013, 36, 701–705. [Google Scholar]
- Du, C.; Xie, W.; Meng, S.; Yin, Y.; Jiao, L.; Song, L. The connection technology based on high temperature silica fiber optic sensor. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2012, San Diego, CA, USA, 11–15 March 2012.
- Du, C.; Xie, W.; Huo, S.; Meng, S.; Xu, K.; Jiao, L. The response of high-temperature optical fiber sensor applied to different materials. In Proceedings of the Fourth International Conference on Smart Materials and Nanotechnology in Engineering, Gold Coast, Australia, 10–12 July 2013.
- Wang, L.; Fang, G.; Liang, J.; Wang, C. Formation mechanism and high temperature mechanical property characterization of SiC depletion layer in ZrB2/SiC ceramics. Mater. Charact. 2014, 95, 245–251. [Google Scholar] [CrossRef]
- Wang, L.-L.; Liang, J.; Fang, G.-D.; Wan, X.-Y.; Xie, J.-B. Effects of strain rate and temperature on compressive strength and fragment size of ZrB2-SiC-Graphite composites. Ceram. Int. 2014, 40, 5255–5261. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, C.; Zhang, X.; Sun, X.; Han, J. Microstructure and thermal shock behavior of ZrB2-SiC-Graphite composite. Mater. Chem. Phys. 2009, 113, 338–341. [Google Scholar] [CrossRef]
- 3000 °F ResbondTM 989FS High Purity Alumina Adhesive Rapid Curing Formulation. Available online: http://www.cotronics.com/WEB%20SHEETS/989FS%20NP.pdf (accessed on 13 September 2016).


| Parameter | Value | Standard Error |
|---|---|---|
| Coefficient of the first-order term KT1 | 1.18 × 10−5 | 9.98 × 10−8 |
| Coefficient of the second-order term KT2 | −1.39 × 10−9 | 1.52 × 10−10 |
| Universal constant C | −2.20 × 10−4 | 1.28 × 10−5 |
| Parameter | Adhesive Layer | UHTC Specimen | ||||
|---|---|---|---|---|---|---|
| Length | Width | Height (Sagitta) | Length | Width | Thickness | |
| Value (mm) | 20 | 6 | 2.5 | 45 | 40 | 5 |
| Density (kg/m3) | Poisson’s Ratio | Elastic Modulus (GPa) | Compressive Strength (MPa) | ||
|---|---|---|---|---|---|
| 20 °C | 1400 °C | 20 °C | 800 °C | ||
| 4960 | 0.165 | 463.0 | 158.7 | 1106.4 | 1009.2 |
| T (°C) | 20 | 303 | 594 | 891 | 1196 | 1499 | 1806 |
|---|---|---|---|---|---|---|---|
| Thermal conductivity (W/m·°C) | 112.00 | 110.63 | 88.86 | 67.70 | 61.67 | 64.04 | 50.77 |
| Specific heat (J/kg·°C) | 700.00 | 777.61 | 828.19 | 869.36 | 1013.46 | 1016.08 | 1083.27 |
| CTE (10−6 °C−1) | 3.31 | 5.45 | 6.67 | 7.20 | 7.62 | 8.03 | 8.43 |
| Density (kg/m3) | CTE (10−6 °C−1) | Thermal Conductivity (W/m·°C) | Specific Heat (J/kg·°C) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| 3700 | 8.1E-6 | 85.18 | 1004.16 | 370 | 0.2 |
| Temperature (°C) | 100 | 200 | 300 | 400 | 500 | 600 | 695 |
|---|---|---|---|---|---|---|---|
| Relative Errors | 18.96% | 14.92% | 13.79% | 13.19% | 9.91% | 8.10% | 6.71% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Meng, S.; Jin, H.; Du, C.; Wang, L.; Peng, T.; Scarpa, F.; Xu, C. Application of CCG Sensors to a High-Temperature Structure Subjected to Thermo-Mechanical Load. Sensors 2016, 16, 1686. https://doi.org/10.3390/s16101686
Xie W, Meng S, Jin H, Du C, Wang L, Peng T, Scarpa F, Xu C. Application of CCG Sensors to a High-Temperature Structure Subjected to Thermo-Mechanical Load. Sensors. 2016; 16(10):1686. https://doi.org/10.3390/s16101686
Chicago/Turabian StyleXie, Weihua, Songhe Meng, Hua Jin, Chong Du, Libin Wang, Tao Peng, Fabrizio Scarpa, and Chenghai Xu. 2016. "Application of CCG Sensors to a High-Temperature Structure Subjected to Thermo-Mechanical Load" Sensors 16, no. 10: 1686. https://doi.org/10.3390/s16101686
APA StyleXie, W., Meng, S., Jin, H., Du, C., Wang, L., Peng, T., Scarpa, F., & Xu, C. (2016). Application of CCG Sensors to a High-Temperature Structure Subjected to Thermo-Mechanical Load. Sensors, 16(10), 1686. https://doi.org/10.3390/s16101686






