Data Analytics for Smart Parking Applications
Abstract
:1. Introduction
2. Related Work
3. System Model
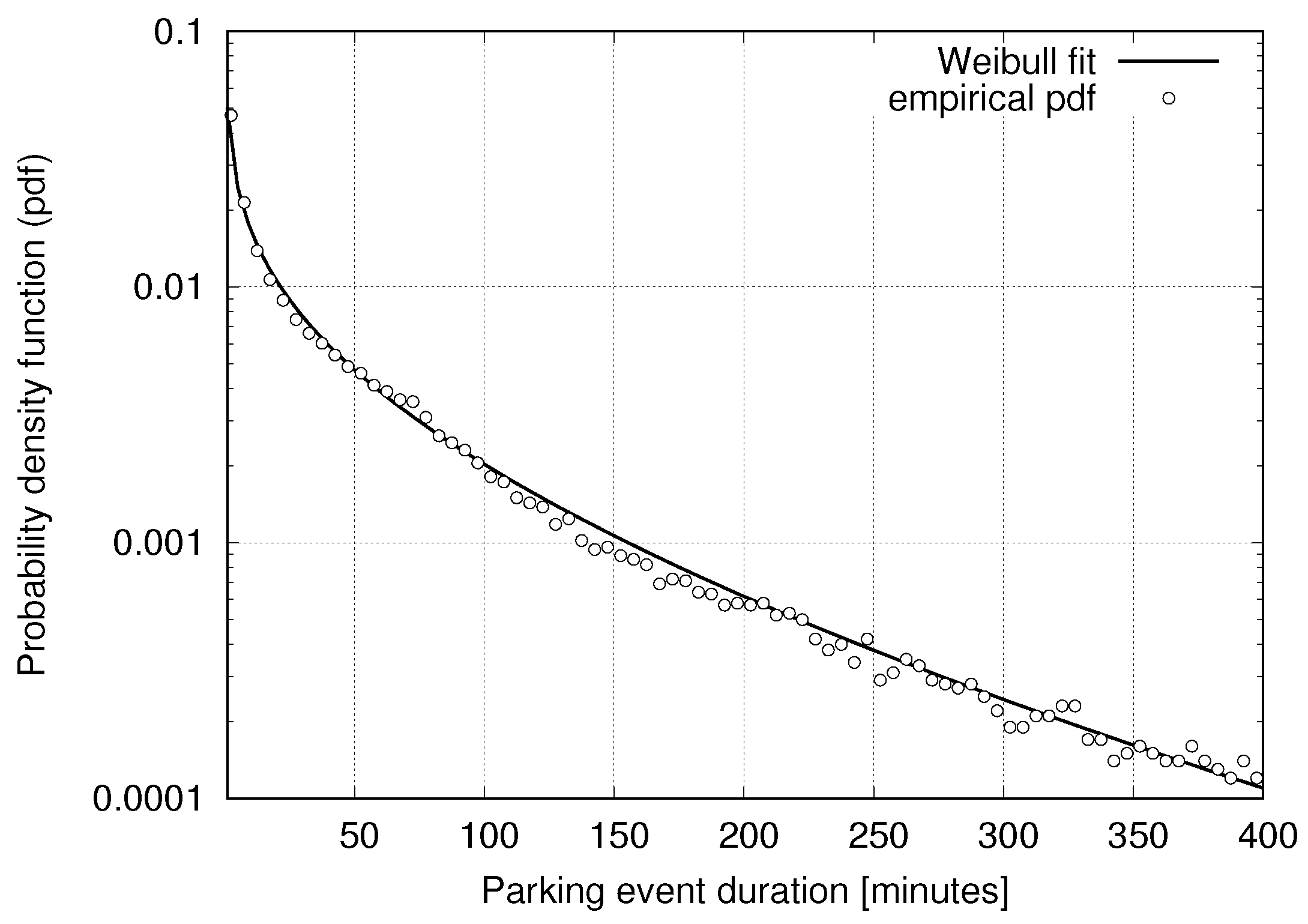
3.1. Statistical Models for Parking Data
3.2. Event-Based Simulator
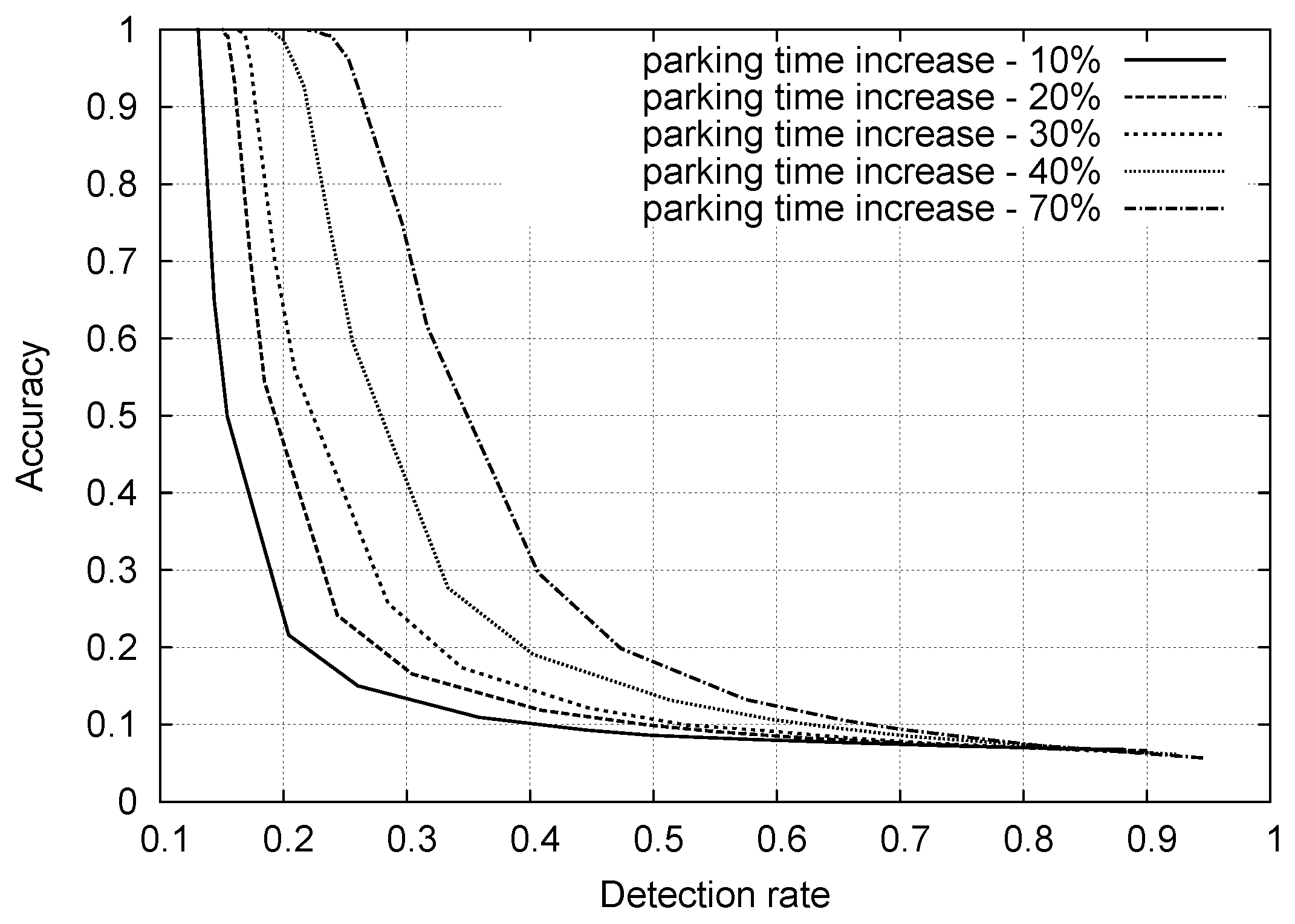
4. A Simple Anomaly Detection Approach
- (1)
- a threshold is set and,
- (2)
- a parking event with duration τ is flagged as anomalous if .
5. Advanced Classification Techniques
5.1. Discussion on Outliers
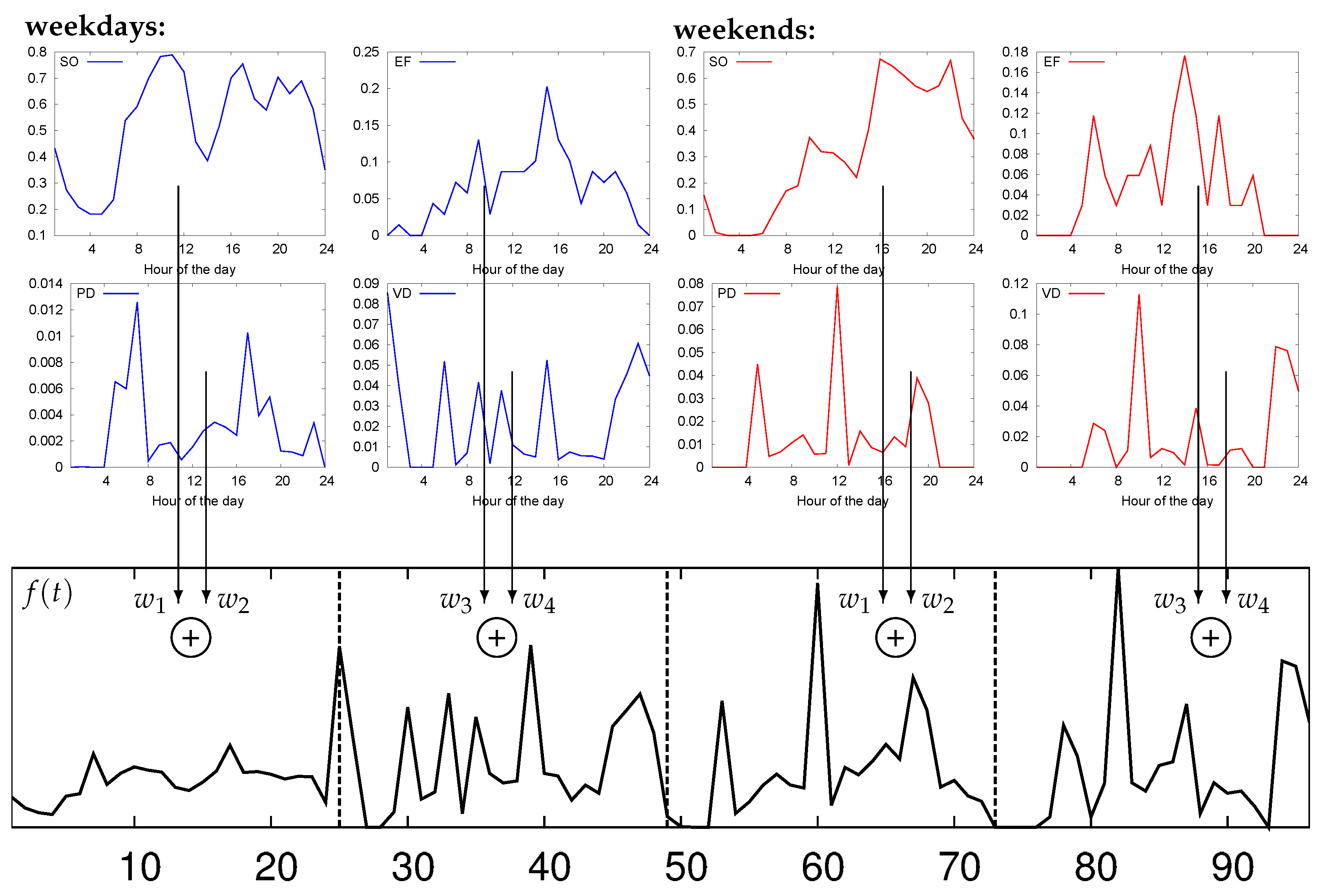
5.2. Features for Parking Analysis
- (1)
- Sensor occupation (SO): accounts for the amount of time during which , i.e., the corresponding parking space is occupied.
- (2)
- Event frequency (EF): accounts for the number of parking events per unit time.
- (3)
- Parking event duration (PD): measures the duration of parking events.
- (4)
- Vacancy duration (VD): measures the duration of vacancies.
5.3. Selected Clustering Techniques from the Literature
- (1)
- Compute the distances between each input data vector and each cluster centroid.
- (2)
- Assign each input vector to the cluster associated with the closest centroid.
- (3)
- Compute the new average of the points (data vectors) in each cluster to obtain the new cluster centroids.
- (1)
- Initial values of the normal distribution model (mean and standard deviation) are arbitrarily assigned.
- (2)
- Mean and standard deviations are iteratively refined through the expectation and maximization steps of the EM algorithm. The algorithm terminates when the distribution parameters converge or a maximum number of iterations is reached.
- (3)
- Data vectors are assigned to the cluster with the maximum membership probability.
- (1)
- ε: used to define the ε-neighborhood of any input vector , which corresponds to the region of space whose distance from is smaller than or equal to ε.
- (2)
- MinPts: representing the minimum number of points needed to form a so-called dense region.
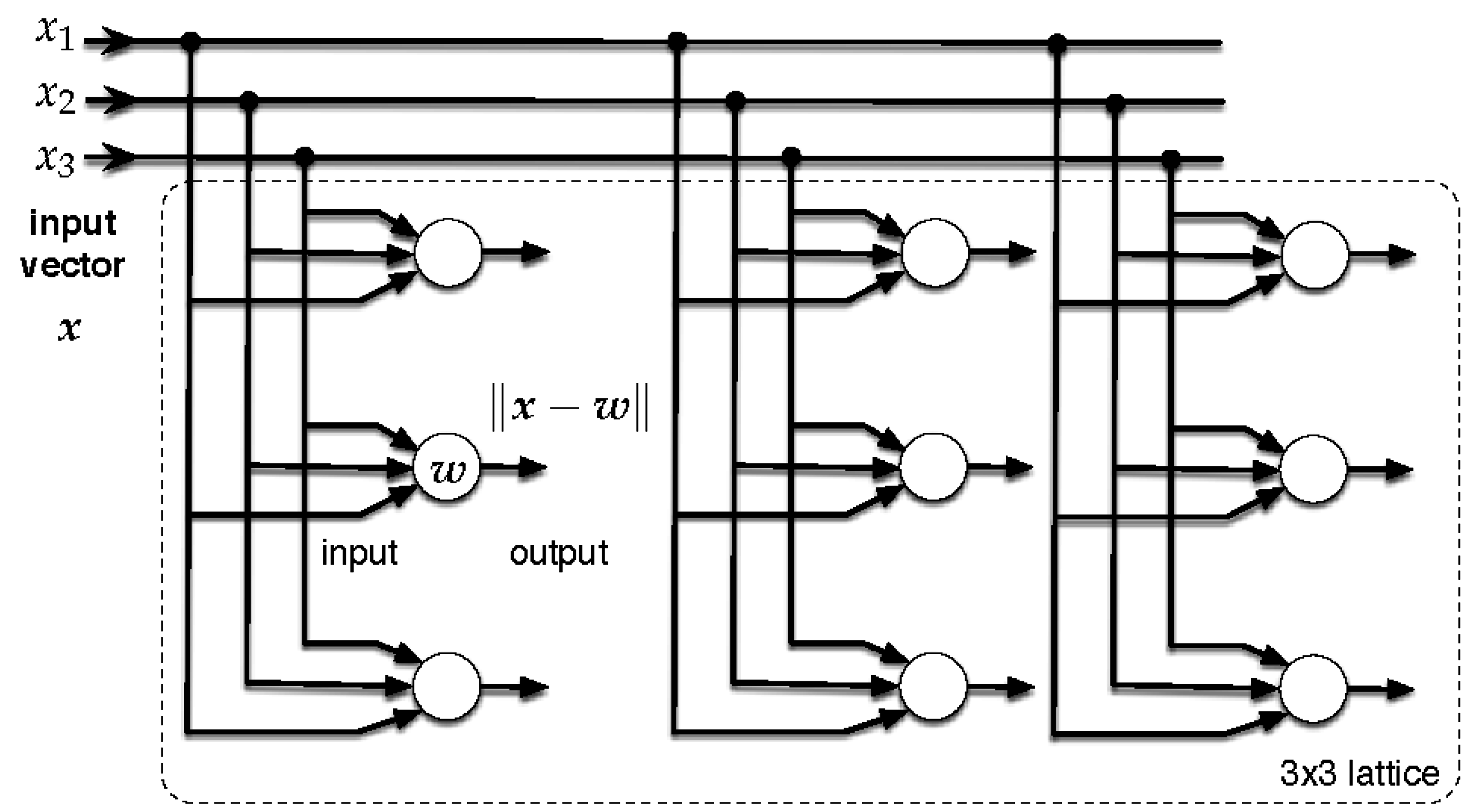
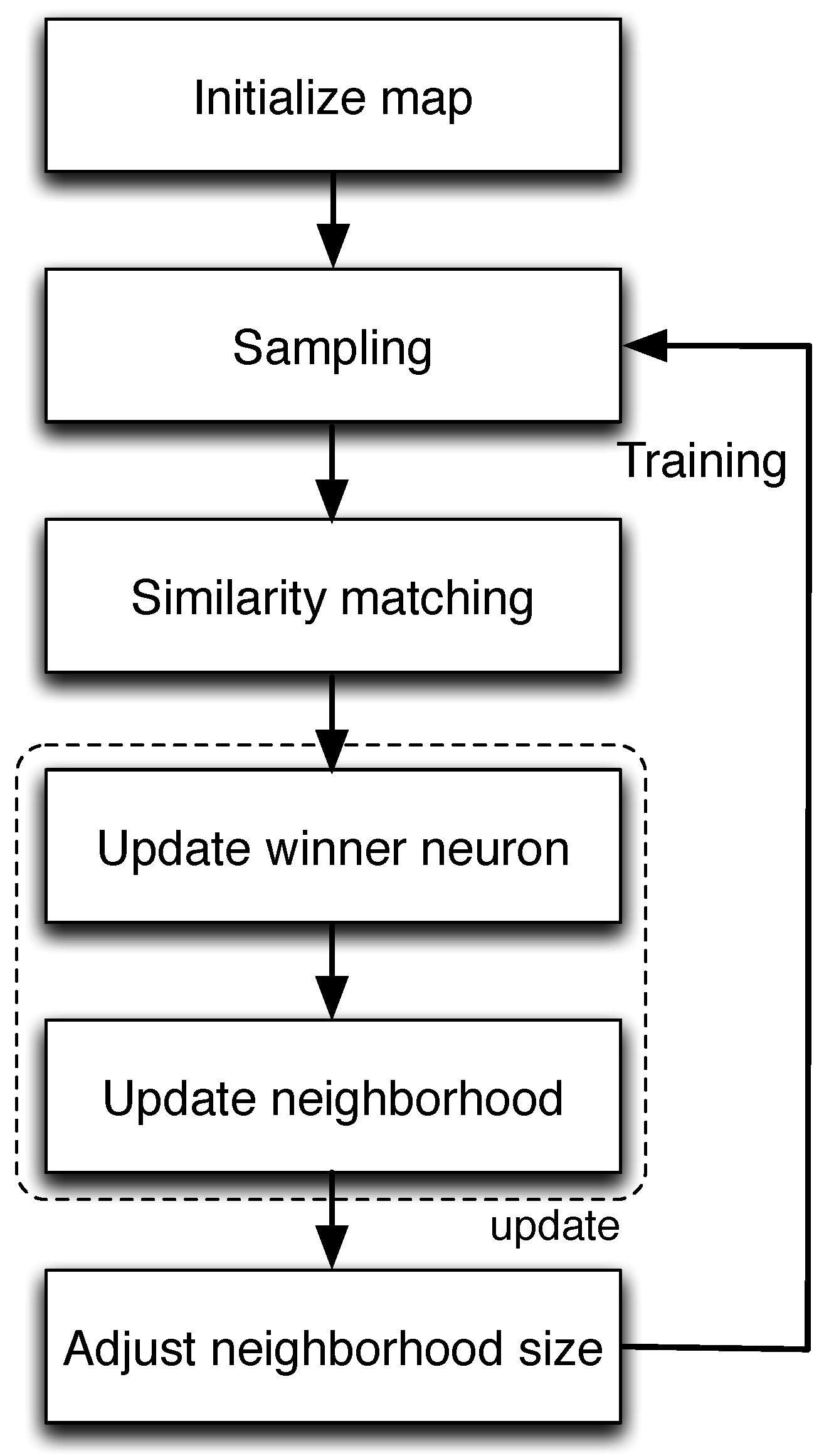
5.4. Classification Based on Self-Organizing Maps
| Algorithm 1 (SOM): |
|
- Data point: The input dataset is composed of N data points, where “data point” i is the feature column vector associated with the parking sensor . These vectors are conveniently represented through the full feature matrix . With , we mean a submatrix of obtained by collecting p columns (feature vectors), not necessarily the first p. A generic cluster containing p elements is then uniquely identified by a collection of p sensors and by the corresponding feature matrix .
- Cluster cohesiveness: Consider a cluster with p elements, and let be the corresponding feature matrix. We use a scatter function as a measure of its cohesiveness, i.e., to gauge the distance among the cluster elements and its mean (centroid). The centroid of is computed as: . The dispersion of the cluster members around is assessed through the sample standard deviation:where is the Euclidean norm of vector . Likewise, the dispersion of the full feature matrix is denoted by , and we define a further threshold for a suitable .
- Global vs. local clustering metrics: In our tests, we experimented with different metrics, and the best results were obtained by tracking the correlation among features, as we now detail. We proceed by computing two statistical measures: (1) a first metric, referred to as global, is obtained for the entire feature matrix ; (2) a local metric is computed for the smaller clusters (matrix ).
- (1)
- Global metric: Let be the full feature matrix. From , we obtain the correlation matrix , where . Thus, we average by row, obtaining the N-sized vector , with . We respectively define and as the sample standard deviation and the mean of . We finally compute two global measures for matrix as:
- (2)
- Local metric: The local metric is computed on a subsection of the entire dataset, namely on the clusters that are obtained at runtime. Now, let us focus on one such cluster, say cluster with . Hence, we build the corresponding feature matrix by selecting the p columns of associated with the elements in . Thus, we compute the correlation matrix of , which we call , and the p-sized vector , obtained averaging by row as above. The local measures associated with matrix are:where returns the smallest element in .
- Global vs. local dominance: We now elaborate on the comparison of global and local metrics. Let and respectively be the full feature matrix and that of a cluster obtained at runtime by our algorithm. Global and local metrics are respectively computed using Equations (6) and (7) and are compared in a Pareto [37] sense as follows. We say that the global metric (matrix ) dominates the local one (matrix ) if the following inequalities are jointly verified:For the first measure (meas1), global dominance occurs when the global standard deviation is strictly larger than the local one. For the second measure (meas2), global dominance occurs when the global mean is smaller than the local minimum. Full dominance occurs when the two conditions are jointly verified. Note that when the local metrics are non-dominated by the global ones, this means that the vectors in the associated cluster either have a larger variance or that the minimum correlation in the cluster is larger than the average correlation in the entire dataset. In both cases, the local measures are not desirable, as the cluster still has worse correlation properties than the full data. Hence, we infer that the cluster has to be split, as it either contains uncorrelated data points or at least one outlier.
| Algorithm 2 Unsupervised SOM clustering: |
|
6. Numerical Results
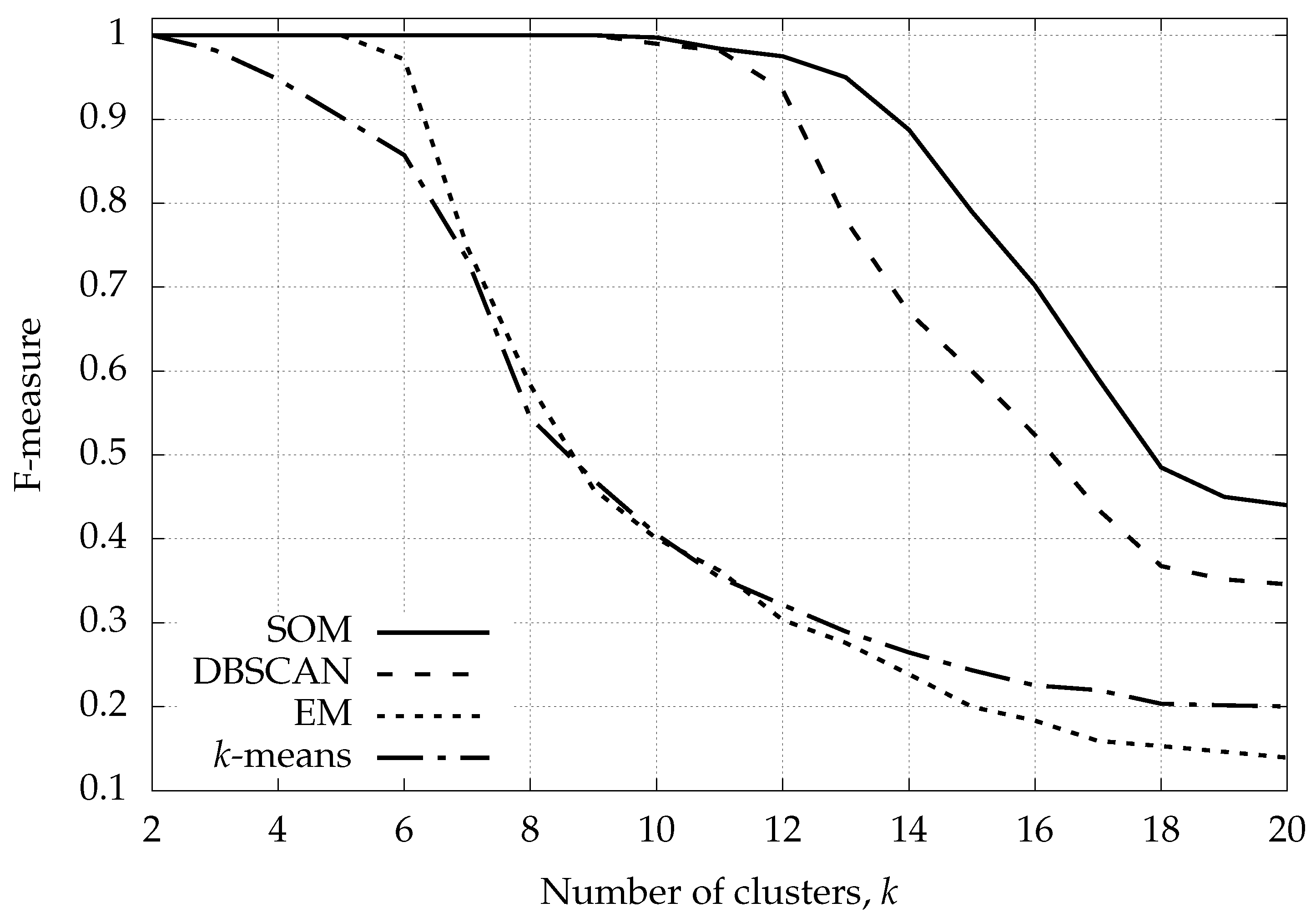
6.1. Synthetic Data: Classification Performance with Varying Number of Clusters
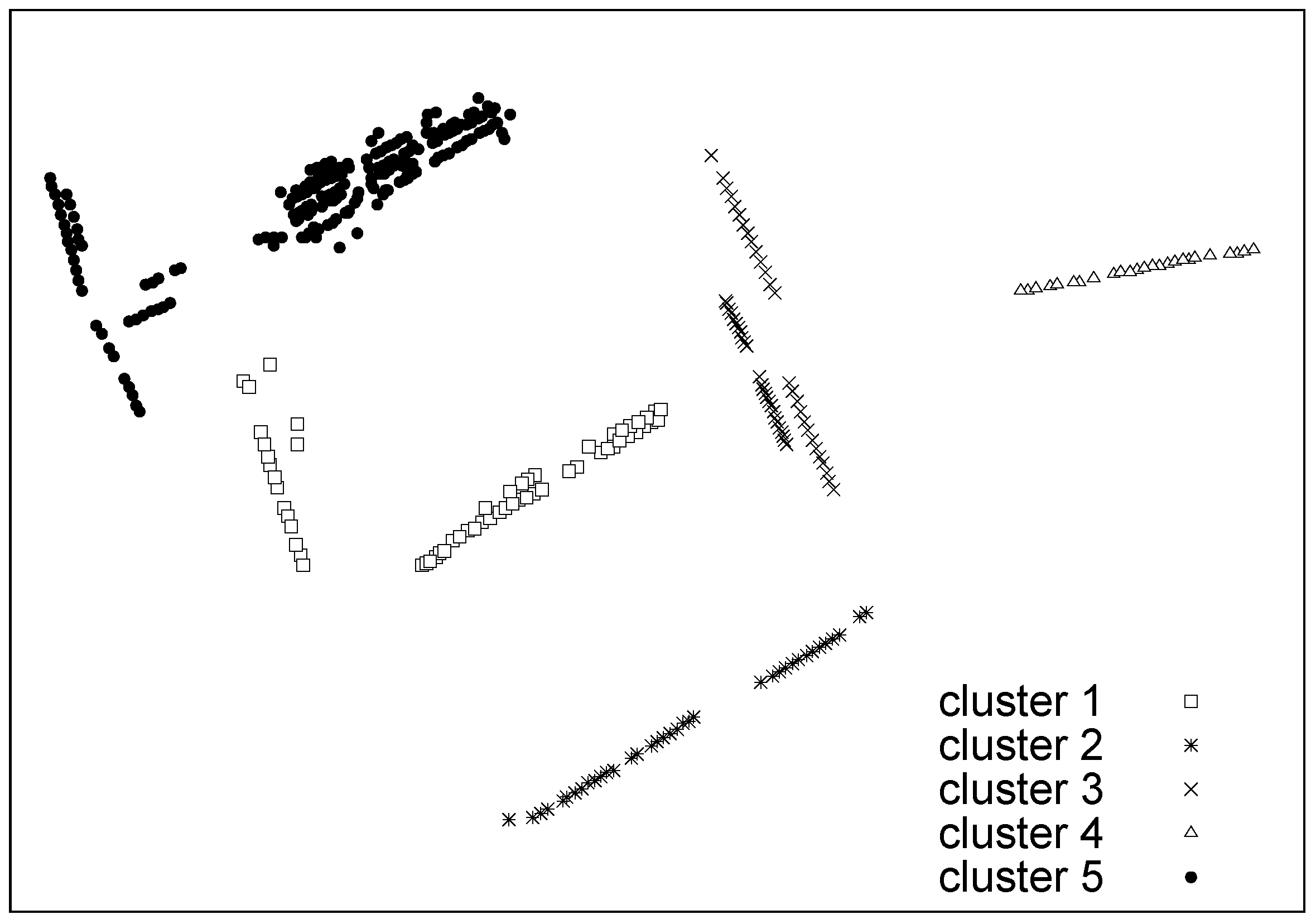
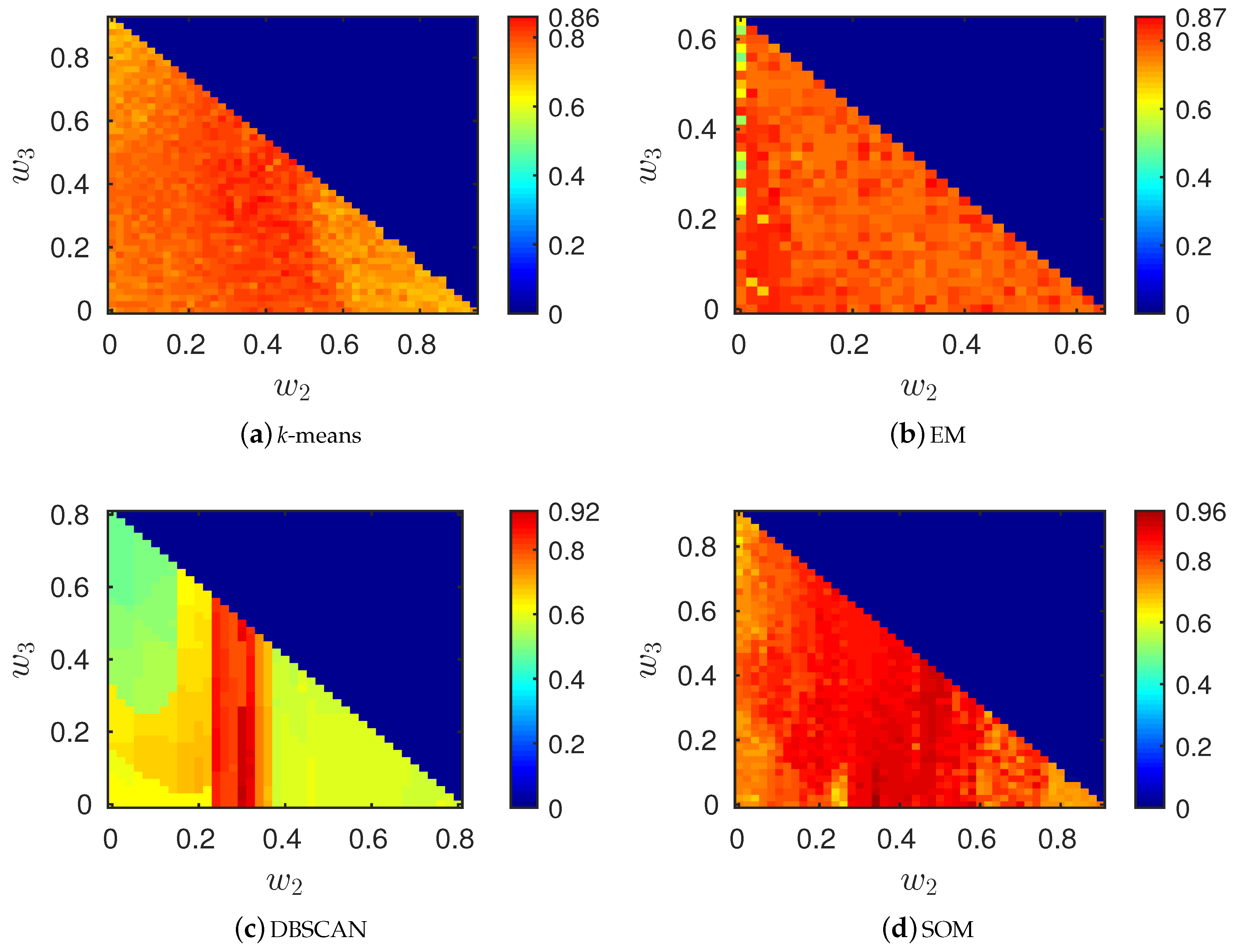
6.2. Synthetic Data: Classification Performance with Outliers and Complex Statistics
- k-means: and .
- EM: , and .
- DBSCAN: , , , and MinPts .
- SOM: , , and ().
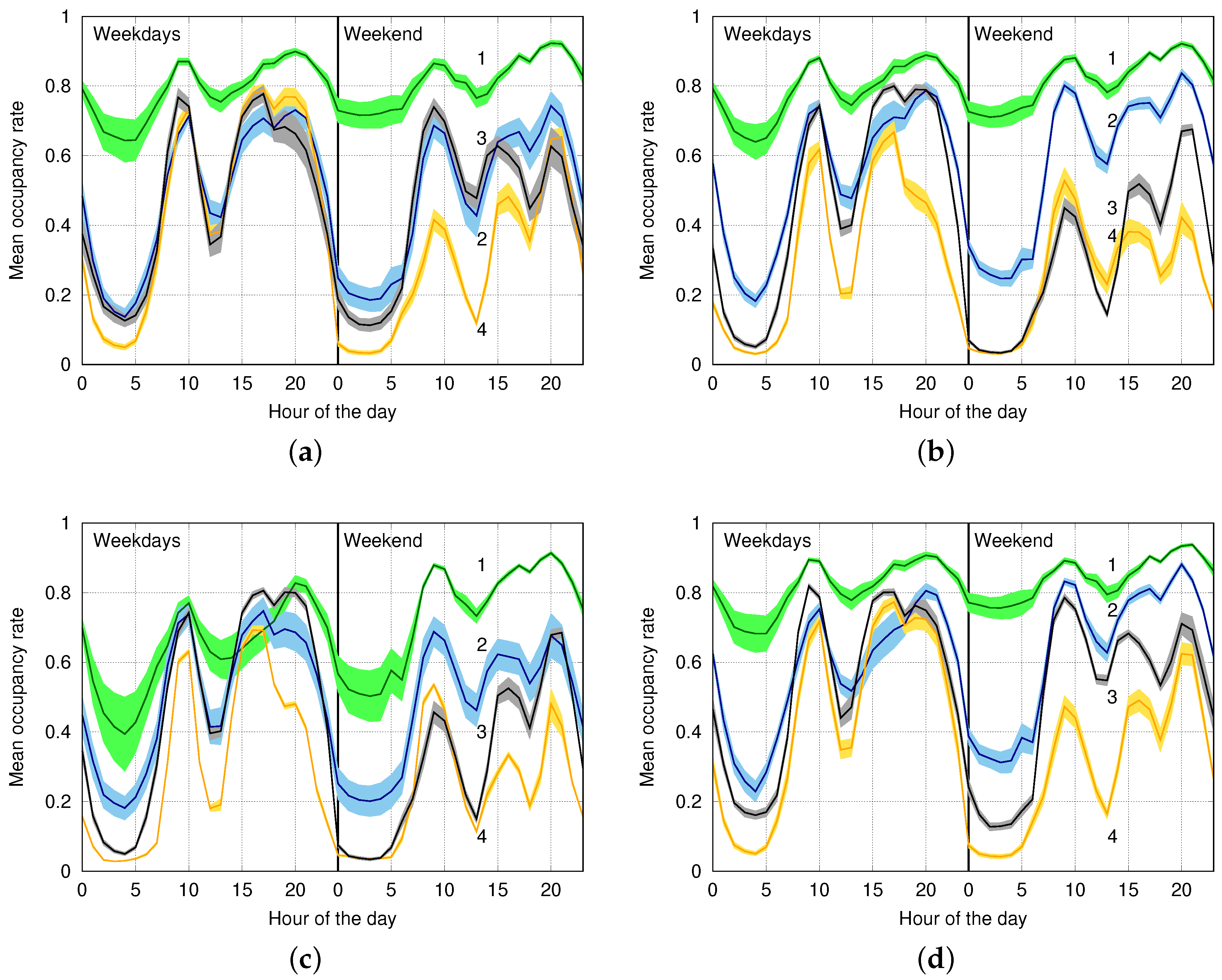
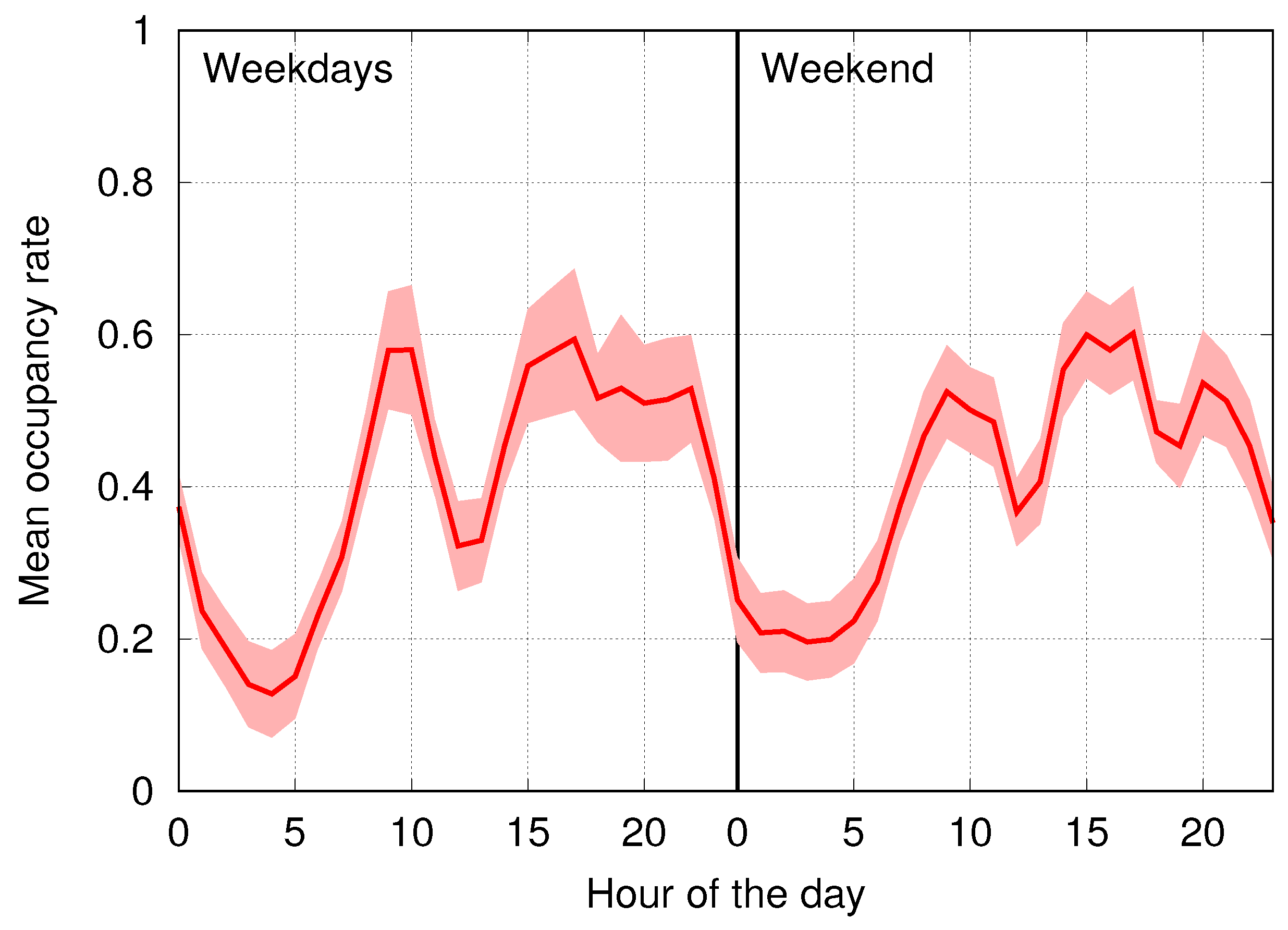
6.3. Classification Performance on Real Data
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| EF | Event Frequency |
| EM | Expectation Maximization |
| GMM | Gaussian Mixture Model |
| IoT | Internet of Things |
| PD | Parking Duration |
| PGI | Parking Guidance and Information |
| SO | Sensor Occupation |
| SOM | Self-Organizing Maps |
| SVDD | Support Vector Data Description |
| VD | Vacancy duration |
| WSN | Wireless Sensor Networks |
References
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of things for smart cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Jog, Y.; Sajeev, A.; Vidwans, S.; Mallick, C. Understanding smart and automated parking technology. Int. J. u- e-Serv. Sci. Technol. 2015, 8, 251–262. [Google Scholar] [CrossRef]
- Rathorea, M.M.; Ahmada, A.; Paul, A.; Rho, S. Urban planning and building smart cities based on the internet of things using big data analytics. Comput. Netw. 2016, 101, 63–80. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. Density-based clustering in spatial databases: The algorithm GDBSCAN and its applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- McLachlan, G.; Krishnan, T. The EM Algorithm and Extensions, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Yanxu, Z.; Rajasegarar, S.; Leckie, C.; Palaniswami, M. Smart car parking: Temporal clustering and anomaly detection in urban car parking. In Proceedings of the IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014.
- Kohonen, T. Self-Organization and Associative Memory; Springer: Berlin, Germany, 1984. [Google Scholar]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin, Germany, 2001. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Polycarpou, E.; Lambrinos, L.; Protopapadakis, E. Smart parking solutions for urban areas. In Proceedings of the IEEE International Symposium and Workshops on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Madrid, Spain, 4–7 June 2013.
- Dance, C. Lean smart parking. Park. Prof. 2014, 30, 26–29. [Google Scholar]
- Pierce, G.; Shoup, D. Getting the prices right. J. Am. Plan. Assoc. 2013, 79, 67–81. [Google Scholar] [CrossRef]
- Worldsensing. Smartprk—Making Smart Cities Happen. Available online: http://www.fastprk.com/ (accessed on 21 September 2016).
- Yang, J.; Portilla, J.; Riesgo, T. Smart parking service based on wireless sensor networks. In Proceedings of the Annual Conference on IEEE Industrial Electronics Society (IECON), Montreal, QC, Canada, 25–28 October 2012.
- Shoup, D.C. Cruising for parking. Transp. Policy 2006, 13, 479–486. [Google Scholar] [CrossRef]
- Wang, H.; He, W. A Reservation-based smart parking system. In Proceedings of the IEEE Conference on Computer Communications Workshops, Shanghai, China, 10–15 April 2011; pp. 690–695.
- Geng, Y.; Cassandras, C. New “Smart Parking” system based on resource allocation and reservations. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1129–1139. [Google Scholar] [CrossRef]
- Khan, Z.; Anjum, A.; Kiani, S.L. Cloud based big data analytics for smart future cities. In Proceedings of the IEEE/ACM International Conference on Utility and Cloud Computing, Dresden, Germany, 9–12 December 2013.
- Anastasi, G.; Antonelli, M.; Bechini, A.; Brienza, S.; de Andrea, E.; de Guglielmo, D.; Ducange, P.; Lazzerini, B.; Marcelloni, F.; Segatori, A. Urban and social sensing for sustainable mobility in smart cities. In Proceedings of the 2013 Sustainable Internet and ICT for Sustainability (SustainIT), Palermo, Italy, 30–31 October 2013.
- Barone, R.E.; Giuffrè, T.; Siniscalchi, S.M.; Morgano, M.A.; Tesoriere, G. Architecture for parking management in smart cities. IET Intell. Transp. Syst. 2014, 8, 445–452. [Google Scholar] [CrossRef]
- Gupta, A.; Sharma, V.; Ruparam, N.K.; Jain, S.; Alhammad, A.; Ripon, M.A.K. Integrating pervasive computing, InfoStations and swarm intelligence to design intelligent context-aware parking-space location mechanism. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014.
- He, W.; Yan, G.; Xu, L.D. Developing vehicular data cloud services in the IoT environment. IEEE Trans. Ind. Inform. 2014, 10, 1587–1595. [Google Scholar] [CrossRef]
- Vlahogiannia, E.I.; Kepaptsogloua, K.; Tsetsosa, V.; Karlaftisa, M.G. A real-time parking prediction system for smart cities. J. Intell. Transp. Syst. Technol. Plan. Oper. 2016, 20, 192–204. [Google Scholar] [CrossRef]
- Martinez, B.; Vilajosana, X.; Vilajosana, I.; Dohler, M. Lean sensing: Exploiting contextual information for most energy-efficient sensing. IEEE Trans. Ind. Inform. 2016, 11, 1156–1165. [Google Scholar] [CrossRef]
- Lin, T.; Rivano, H.; Le Mouël, F. How to choose the relevant MAC protocol for wireless smart parking urban networks? In Proceedings of the ACM International Symposium on Performance Evaluation of Wireless Ad Hoc, Sensor, and Ubiquitous Networks (PE-WASUN), Montreal, QC, Canada, 21–26 September 2014.
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2007. [Google Scholar]
- Jain, A.K. Data clustering: 50 Years beyond k-means. Pattern Recognit. Lett. 2010, 38, 651–666. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms (SODA), New Orleans, LA, USA, 7–9 January 2007.
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Boley, D.L. Principal direction divisive partitioning. Data Min. Knowl. Discov. 1998, 2, 325–344. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Boley, D.L.; Bittanti, S.; Gazzaniga, G. Cluster selection in divisive clustering algorithms. In Proceedings of the International Conference on Data Mining (SIAM), Arlington, VA, USA, 11–13 April 2002.
- Hofmey, D.P.; Pavlidis, N.G.; Eckley, I.A. Divisive clustering of high dimensional data streams. Stat. Comput. 2016, 26, 1101–1120. [Google Scholar] [CrossRef]
- Qu, B.; Zhang, Y.; Yang, T. Local-global joint decision based clustering for airport recognition. In Intelligence Science and Big Data Engineering; Sun, C., Fang, F., Zhou, Z.H., Yang, W., Liu, Z.Y., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Pareto, V. Cours d’Economie Politique; Librairie Droz: Lausanne, Switzerland, 1896; Volume 1. [Google Scholar]
- Karypis, G.; Han, E.H.; Kumar, V. Chameleon: Hierarchical clustering using dynamic modeling. IEEE Comput. 1999, 32, 68–75. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Musicant, D.R.; Kumar, V.; Ozgur, A. Optimizing F-measure with support vector machines. In Proceedings of the International FLAIRS Conference, St. Augustine, FL, USA, 20–23 October 2003; pp. 356–360.
- Tsai, C.F.; Lin, W.C.; Ke, S.W. Big data mining with parallel computing: A comparison of distributed and MapReduce methodologies. J. Syst. Softw. 2016, 122, 83–92. [Google Scholar] [CrossRef]

| Parking | Weekday (wd) | Weekend (we) | Mean (in Minutes) |
|---|---|---|---|
| Average | (wd) (we) | ||
| Max | (wd) (we) | ||
| Min | (wd) (we) | ||
| Vacancies | Weekday (wd) | Weekend (we) | Mean (in Minutes) |
| Average | (wd) (we) | ||
| Max | (wd) (we) | ||
| Min | (wd) (we) |
| Weibull | Weekday (wd) | Weekend (we) | Mean (in Minutes) |
|---|---|---|---|
| Cluster 1 (Min) | (wd) (we) | ||
| Cluster 2 | (wd) (we) | ||
| Cluster 3 (Average) | (wd) (we) | ||
| Cluster 4 | (wd) (we) | ||
| Cluster 5 (Max) | (wd) (we) |
| Occupancy Stat. | December 2014 | January 2015 | February 2015 |
|---|---|---|---|
| Avg/Hour | % | % | % |
| Max/Hour | % 24 December 2014 at time 23:00 | % 23 January 2015 at time 20:00 | % 7 February 2015 at time 19:00 |
| March 2015 | April 2015 | May 2015 | |
| Avg/Hour | % | % | % |
| Max/Hour | % 21 March 2015 at time 19:00 | % 4 April 2015 at time 19:00 | % 9 May 2015 at time 19:00 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piovesan, N.; Turi, L.; Toigo, E.; Martinez, B.; Rossi, M. Data Analytics for Smart Parking Applications. Sensors 2016, 16, 1575. https://doi.org/10.3390/s16101575
Piovesan N, Turi L, Toigo E, Martinez B, Rossi M. Data Analytics for Smart Parking Applications. Sensors. 2016; 16(10):1575. https://doi.org/10.3390/s16101575
Chicago/Turabian StylePiovesan, Nicola, Leo Turi, Enrico Toigo, Borja Martinez, and Michele Rossi. 2016. "Data Analytics for Smart Parking Applications" Sensors 16, no. 10: 1575. https://doi.org/10.3390/s16101575
APA StylePiovesan, N., Turi, L., Toigo, E., Martinez, B., & Rossi, M. (2016). Data Analytics for Smart Parking Applications. Sensors, 16(10), 1575. https://doi.org/10.3390/s16101575






