Micro-Doppler Signal Time-Frequency Algorithm Based on STFRFT
Abstract
:1. Introduction
2. STFRFT-Based Time-Frequency Analysis Technique
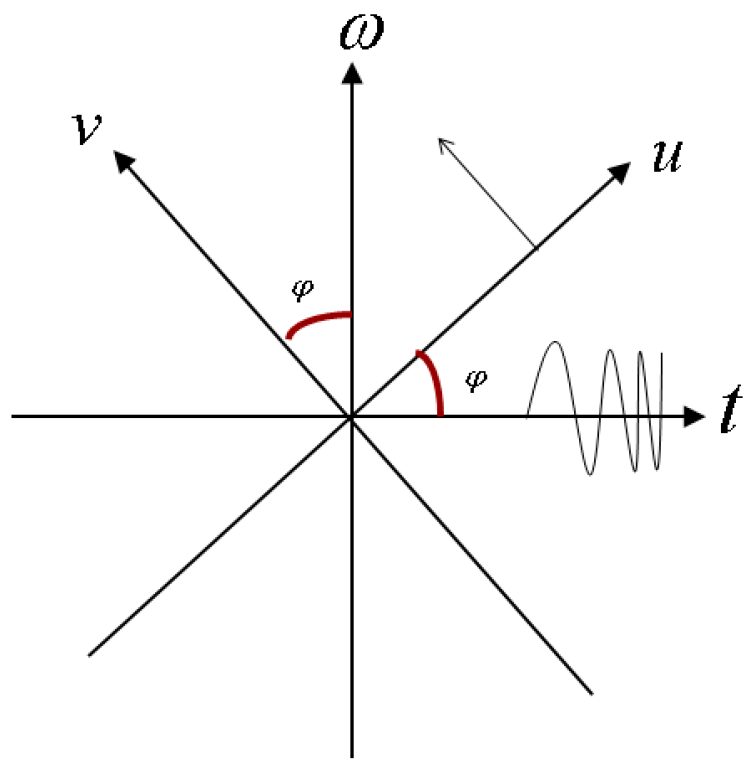
2.1. Basic Principle of STFRFT
2.2. Quick Order Selection for STFRFT Domain Transformation
2.2.1. Order Selection
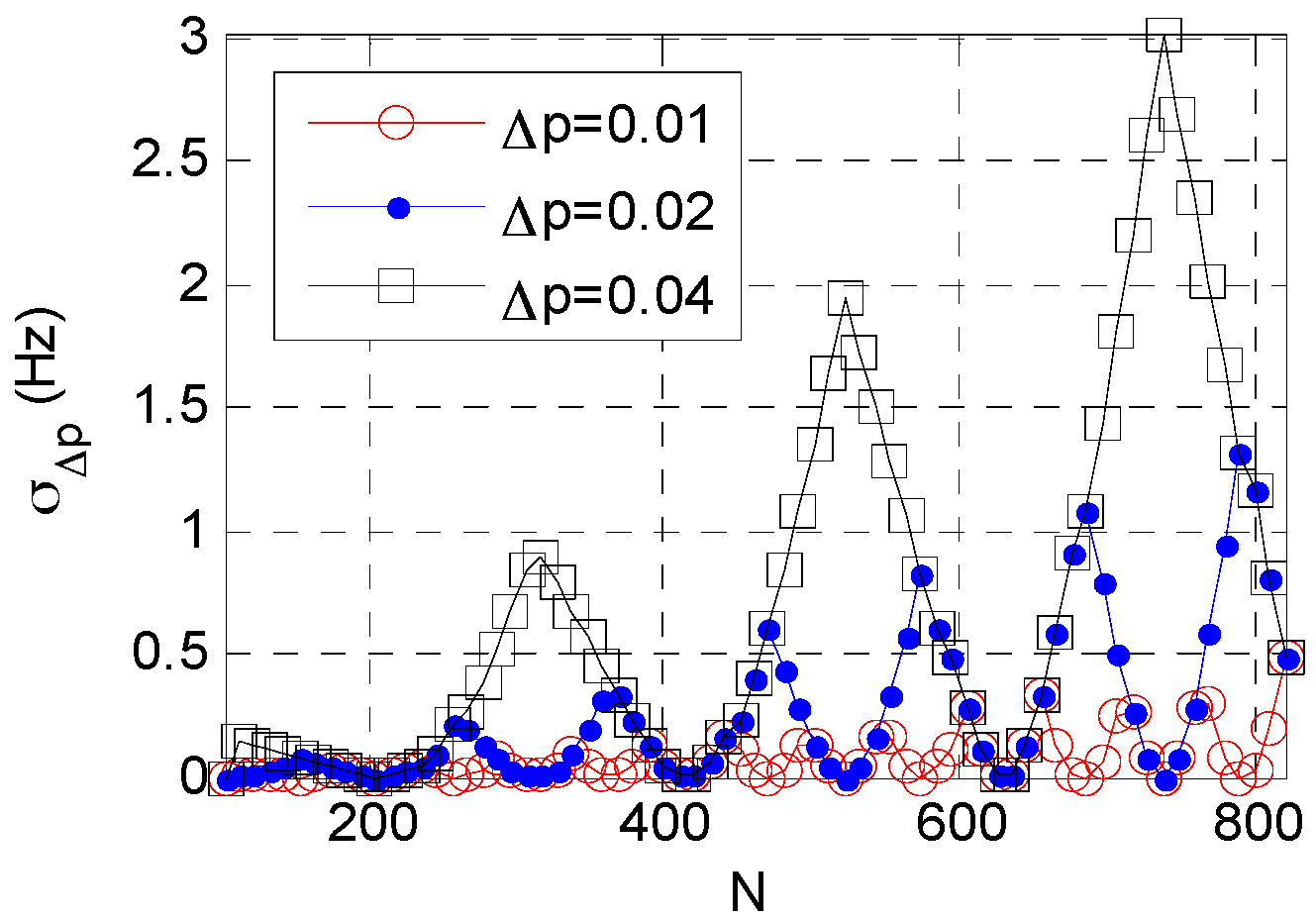
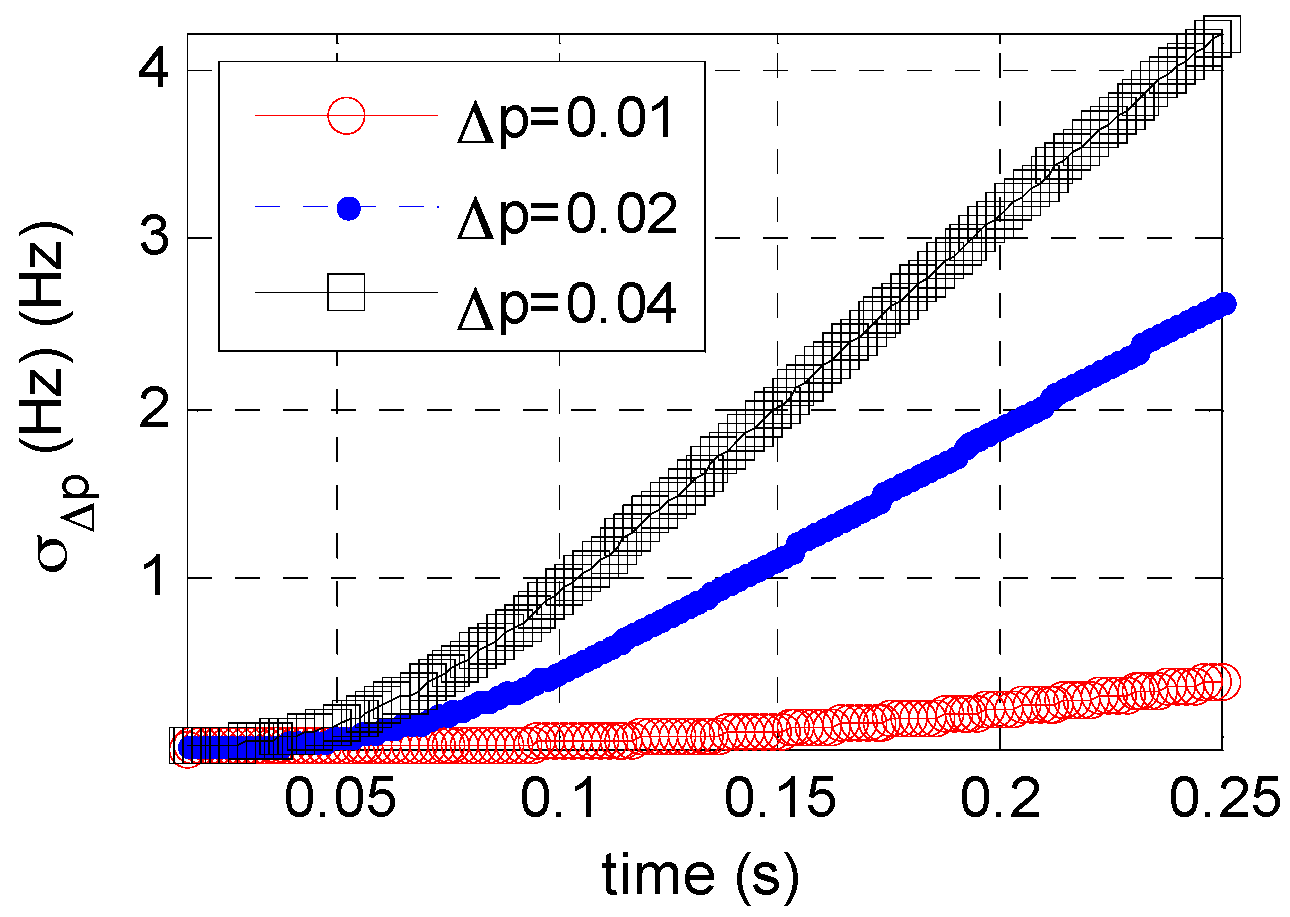
2.2.2. Analysis of Frequency Resolution Error
2.3. STFRFT’s Time-Frequency Analysis Capability of Time-Varying Signal
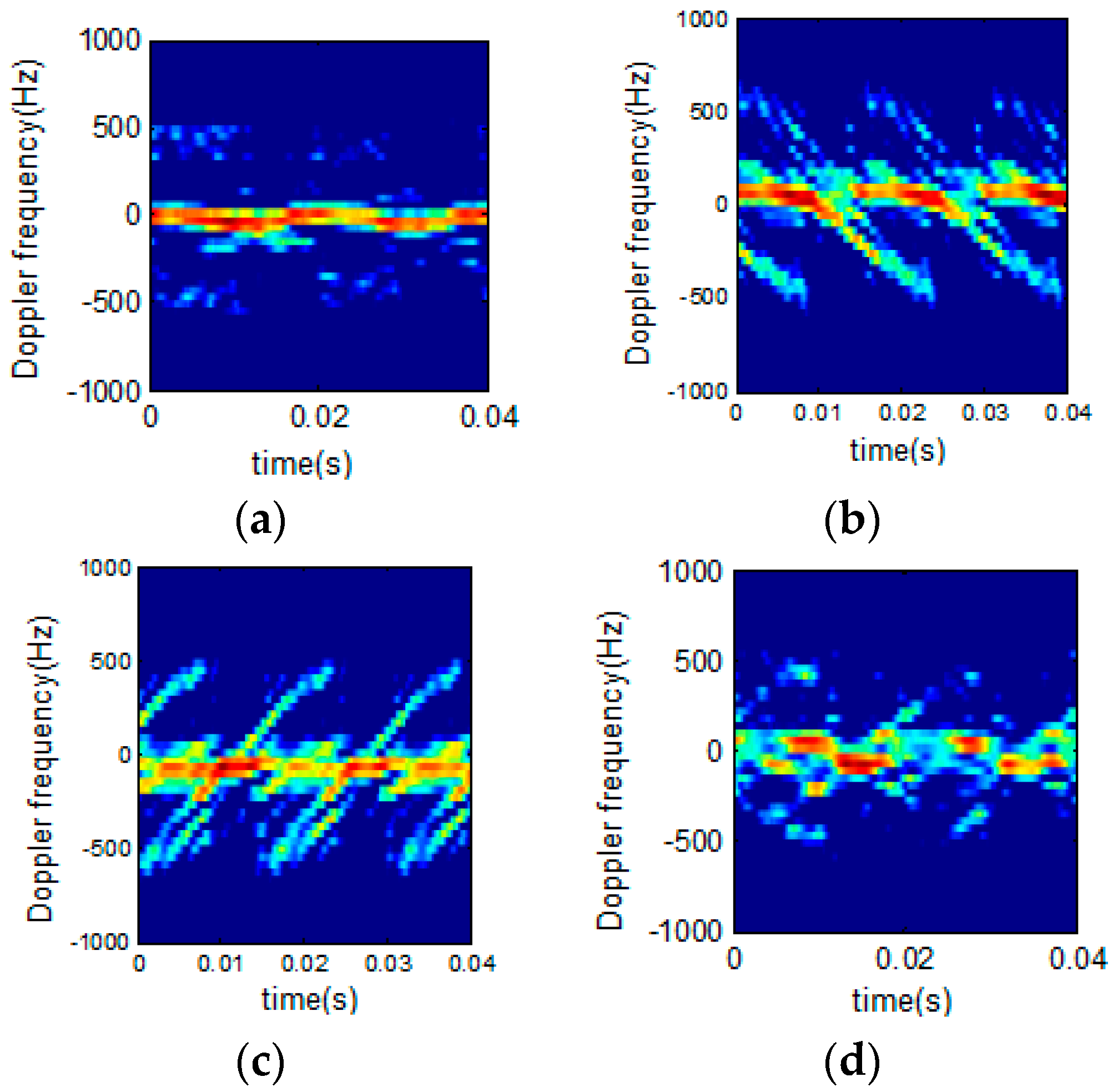
2.3.1. One-Component Signal Analysis
2.3.2. Computation Load Analysis
2.3.3. Analysis of a Sinusoidal Signal
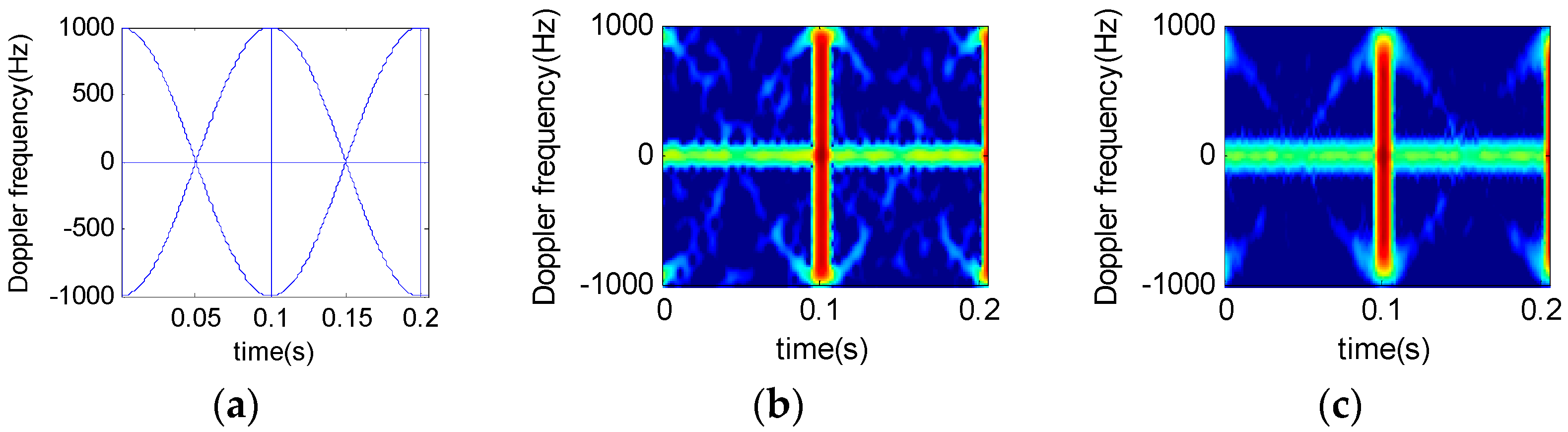
2.3.4. Multi-Component Signal Analysis
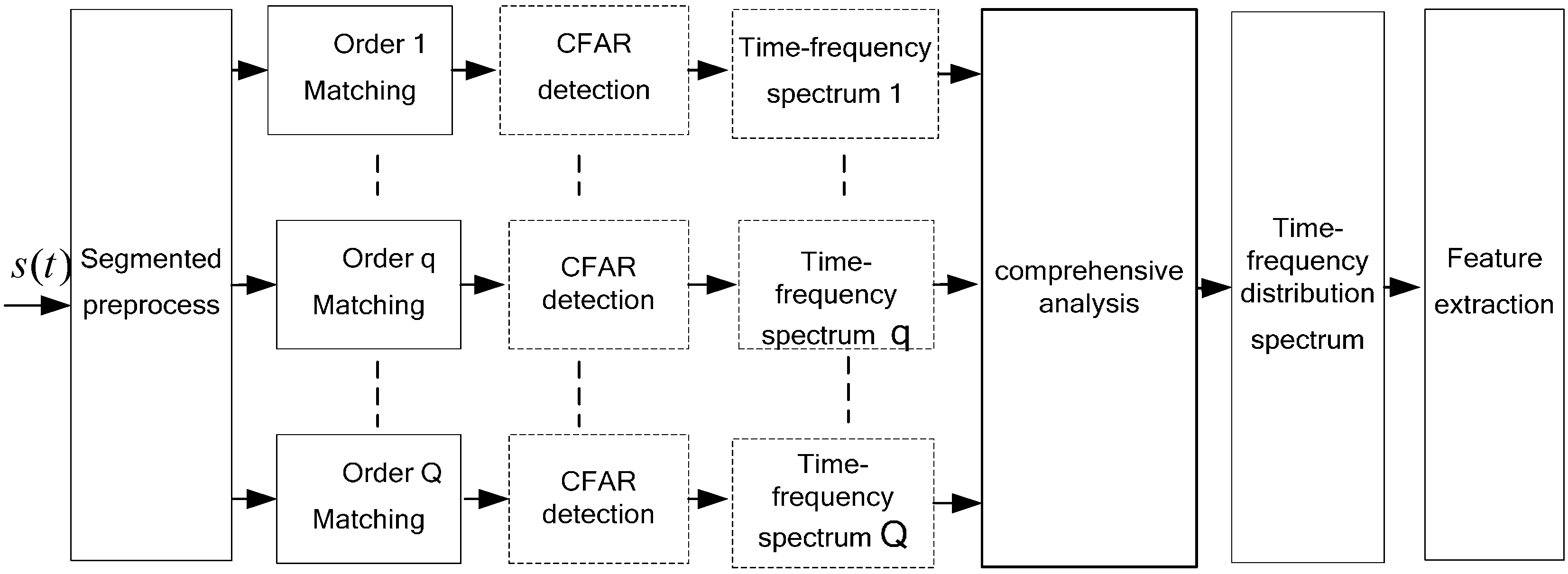
3. Multi-Order STFRFT Time-Frequency Analysis Technique
4. Experiment Analysis
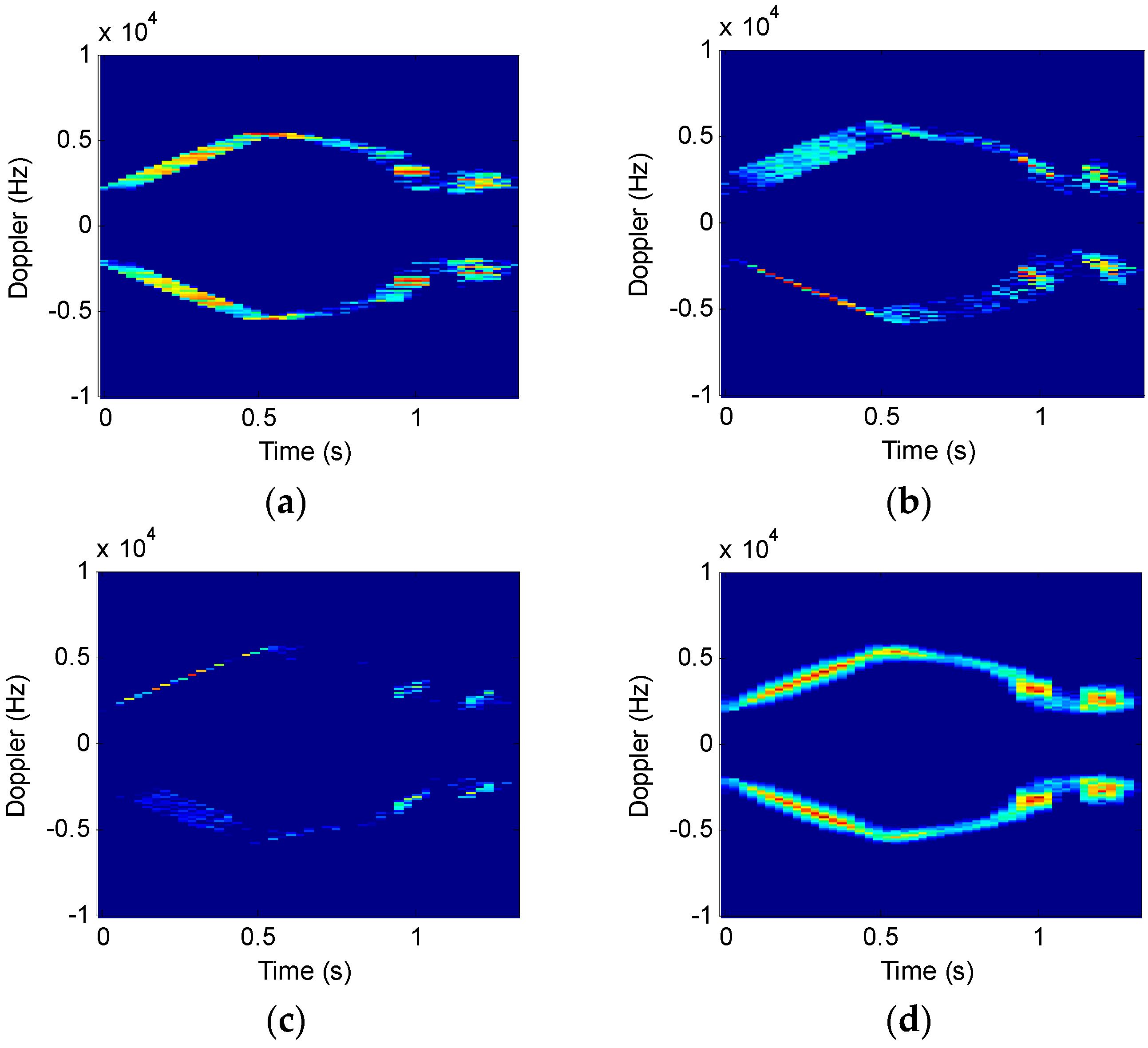
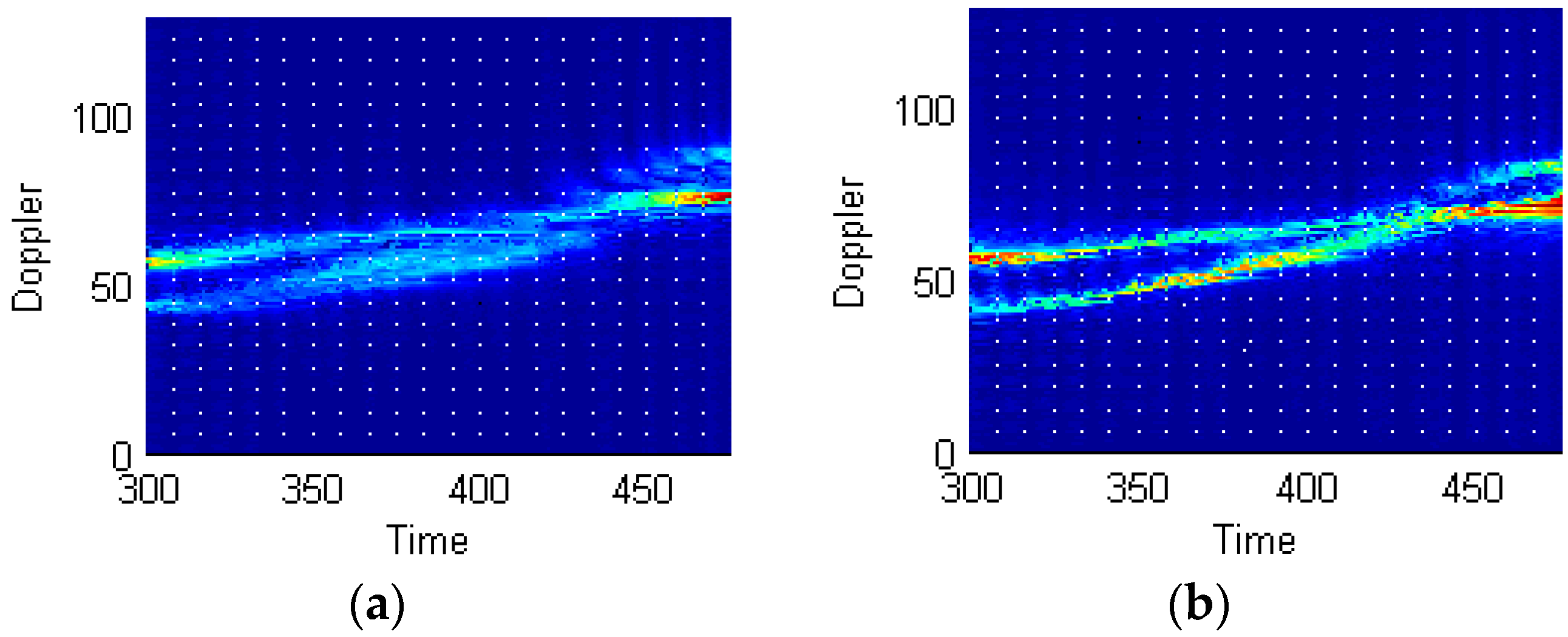
4.1. Actual Signals from a Rocket Projectile Target
4.2. Signals from a Real Model Helicopter Target
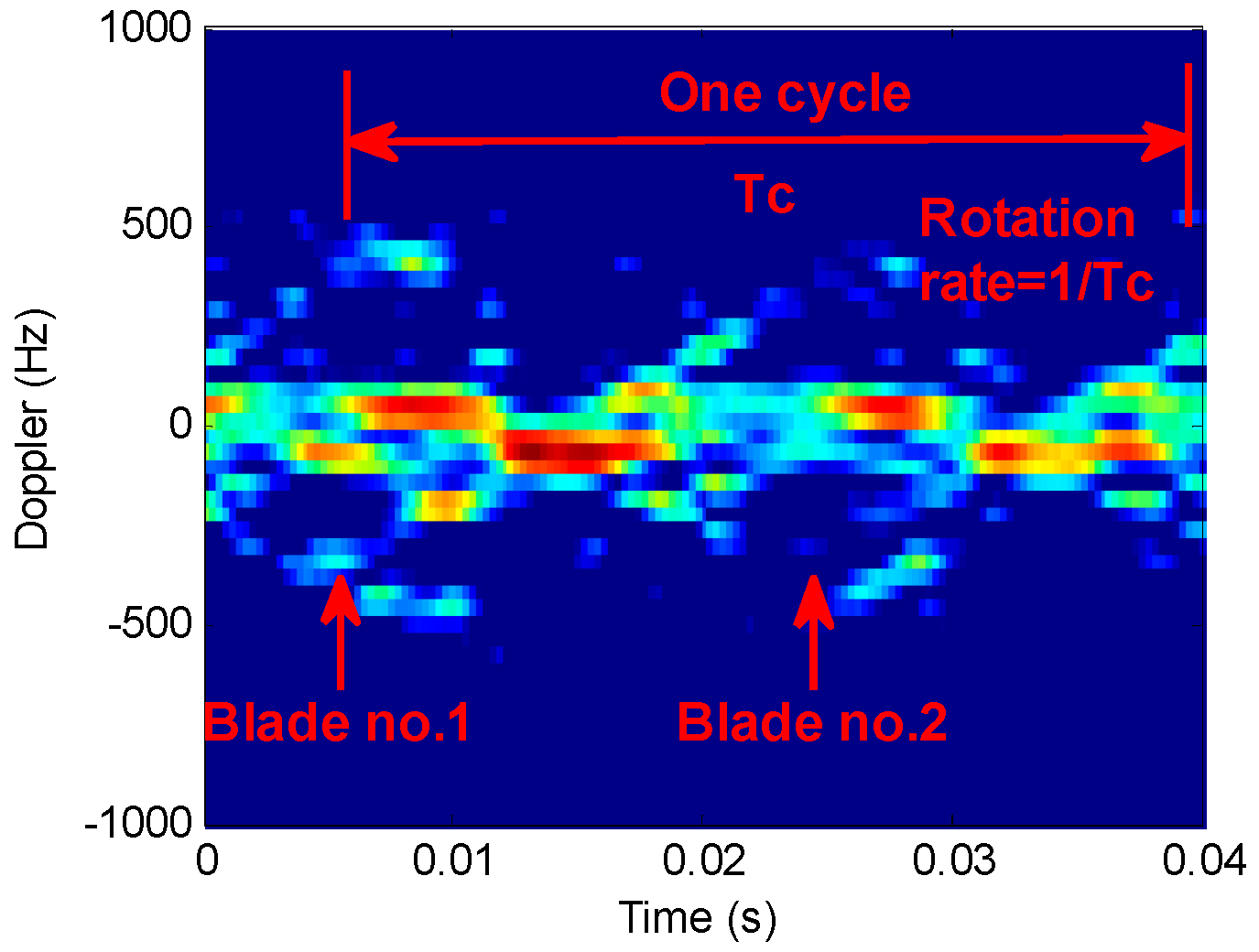
4.3. Signals from the Bird Target
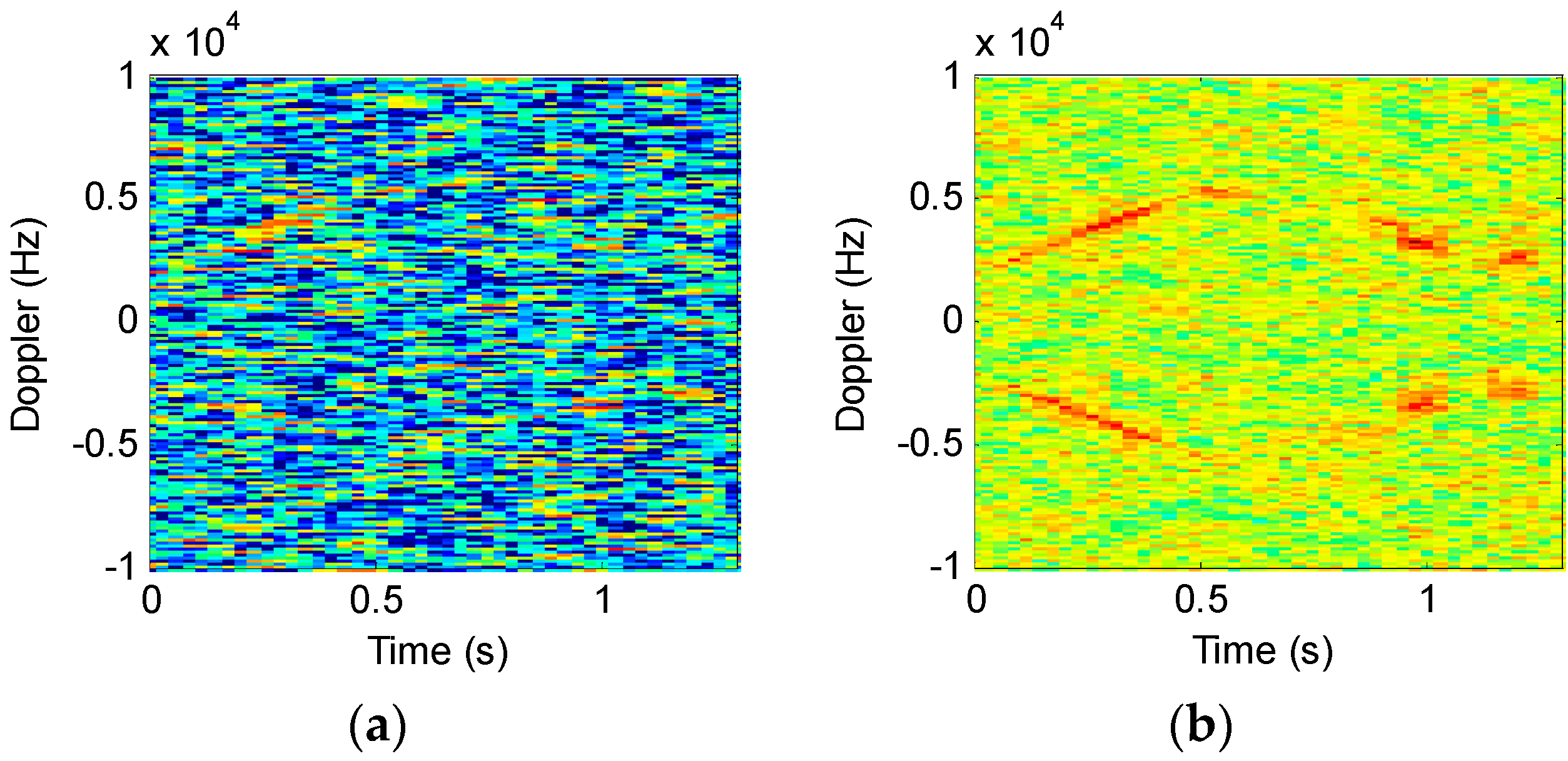
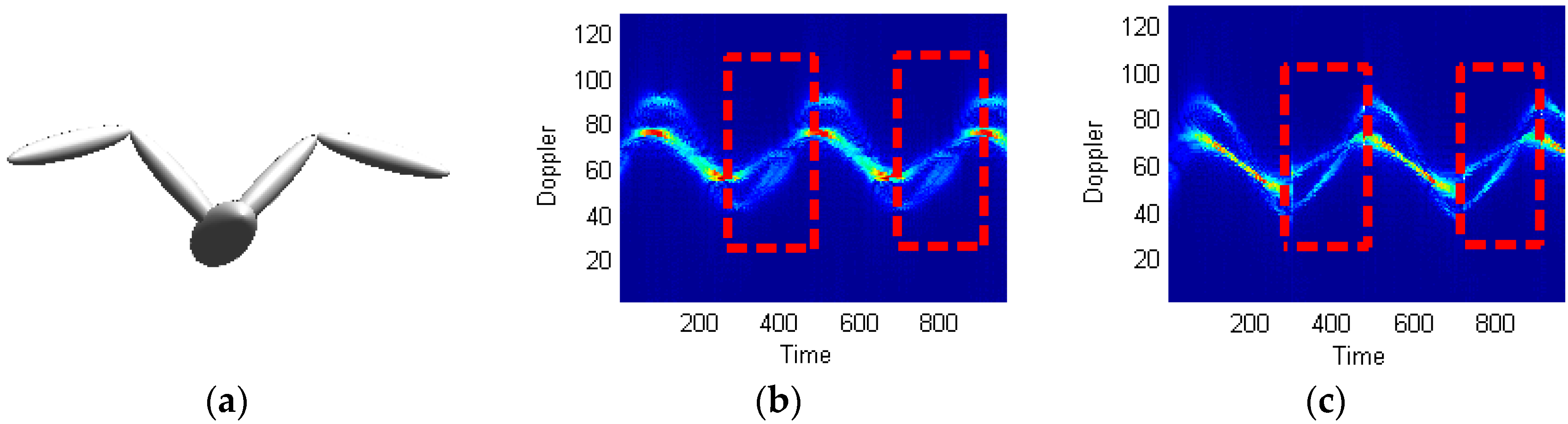
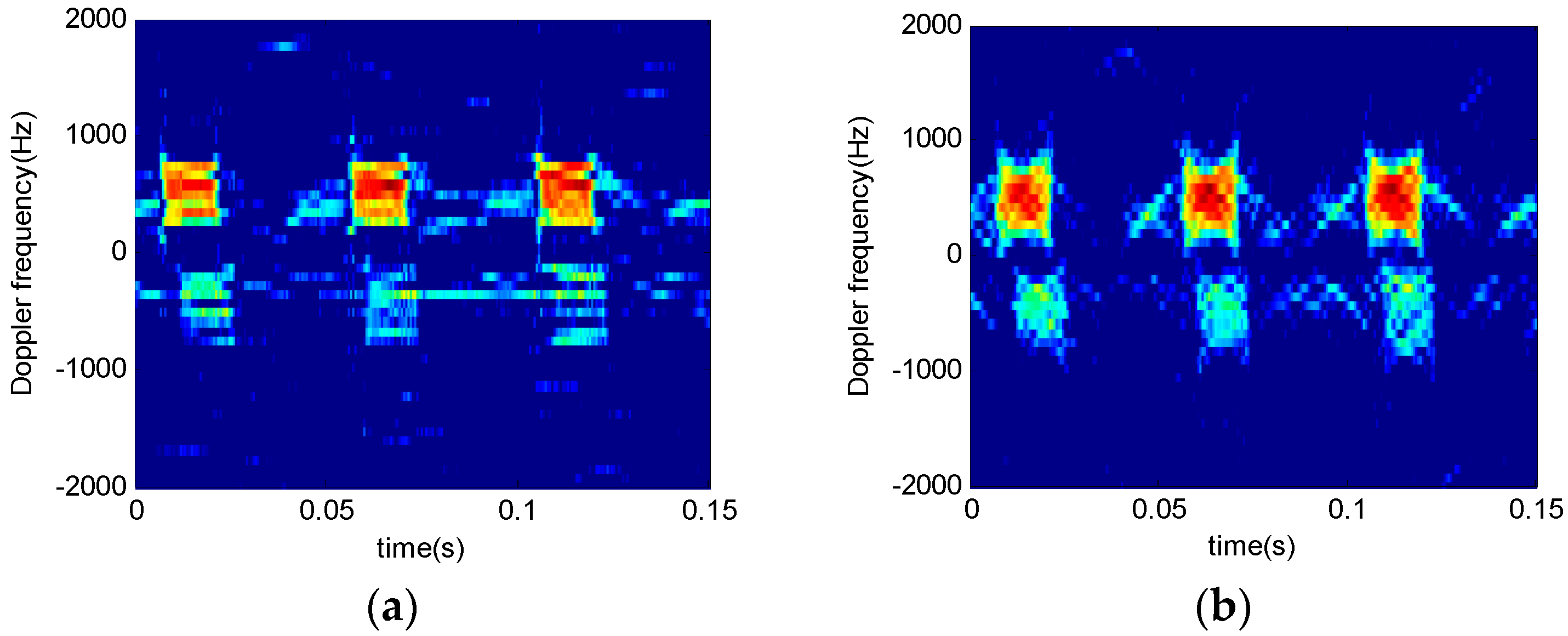
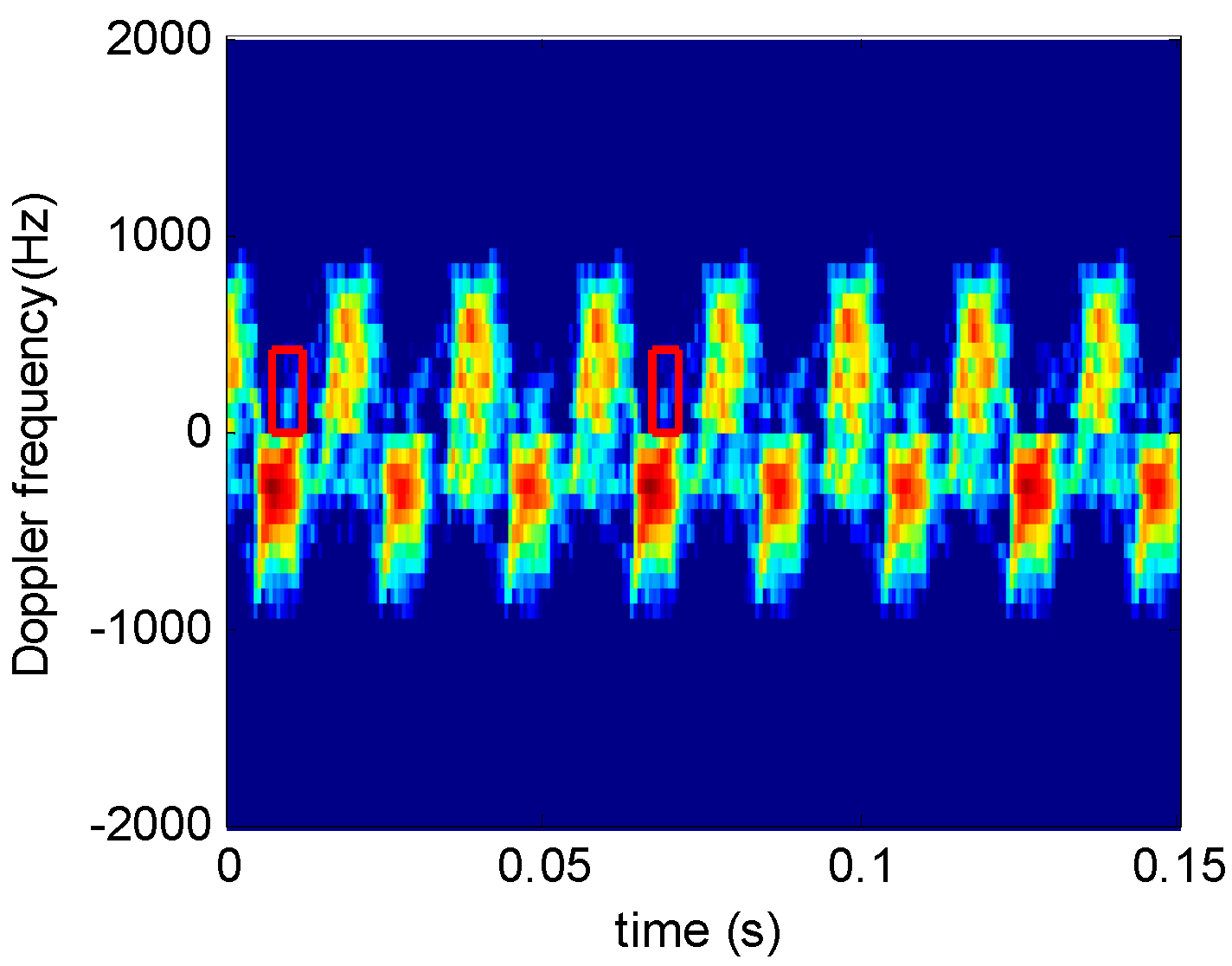
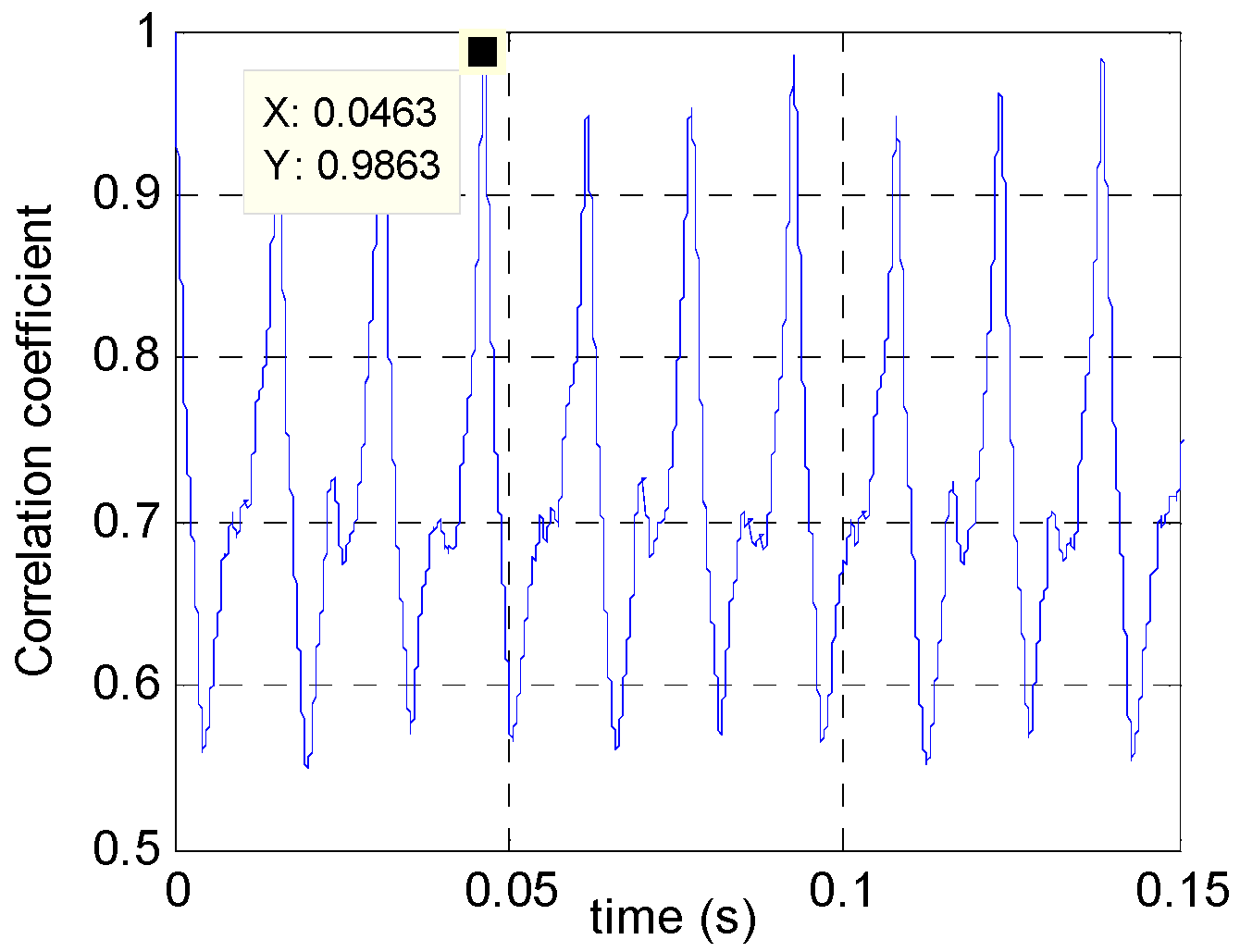
4.4. Actual Fan Target Signals
4.4.1. Dual-Blade Fan
4.4.2. Three-Blade Fan
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, V.C.; Li, F.; Ho, S.S. Analysis of micro-Doppler signatures. IEEE Proc. Radar Sonar Navig. 2003, 150, 271–276. [Google Scholar] [CrossRef]
- Thayaparan, T.; Abrol, S.; Riseborough, E.; Stankovic, L.J.; Lamothe, D.; Duff, G. Analysis of radar micro-Doppler signatures from experimental helicopter and human data. IEEE Proc. Radar Sonar Navig. 2007, 1, 289–299. [Google Scholar] [CrossRef]
- Ding, Y.; Tang, J. Micro-Doppler trajectory estimation of pedestrians using continuous-wave radar. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5807–5819. [Google Scholar] [CrossRef]
- Zhang, W.; Li, K.; Jiang, W. Parameter estimation of radar targets with macro-motion and micro-motion based on circular correlation coefficients. IEEE Signal Process. Lett. 2015, 22, 633–637. [Google Scholar] [CrossRef]
- Lie-Svendsen, O.; Olsen, K.E.; Johnsen, T. Measurements and signal processing of helicopter micro-Doppler signatures. In Proceedings of the 11th European Radar Conference (EuRAD), Rome, Italy, 8–10 October 2014; pp. 121–124.
- Bączyk, M.K.; Samczyński, P.; Kulpa, K. Micro-Doppler signatures of helicopters in multistatic passive radars. IEEE Proc. Radar Sonar Navig. 2015, 9, 1276–1283. [Google Scholar] [CrossRef]
- Yang, B.; He, F.; Jin, J.; Xiong, H.; Xu, G. DOA estimation for attitude determination on communication satellites. Chin. J. Aeronaut. 2014, 27, 670–677. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Xu, M. Cubature Information SMC-PHD for Multi-Target Tracking. Sensors 2016, 16, 653. [Google Scholar] [CrossRef] [PubMed]
- Tahmoush, D. Review of micro-Doppler signatures. IEEE Proc. Radar Sonar Navig. 2015, 9, 1140–1146. [Google Scholar] [CrossRef]
- Fairchild, D.P.; Narayanan, R.M. Multistatic micro-doppler radar for determining target orientation and activity classification. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 512–521. [Google Scholar] [CrossRef]
- Stanković, L.; Stanković, S.; Thayaparan, T. Separation and reconstruction of the rigid body and micro-doppler signal in ISAR Part I-Theory. IEEE Proc. Radar Sonar Navig. 2015, 9, 1147–1154. [Google Scholar] [CrossRef]
- Satzoda, R.K.; Suchitra, S.; Srikanthan, T. Parallelizing the Hough transform computation. IEEE Signal Process. Lett. 2008, 15, 297–300. [Google Scholar] [CrossRef]
- Thayaparan, T.; Stankovic, L.; Dakovic, M.; Popovic, V. Micro-Doppler parameter estimation from a fraction of the period. IEEE Signal Process. Lett. 2010, 4, 201–212. [Google Scholar] [CrossRef]
- Suresh, P.; Thayaparan, T.; Obulesu, T.; Venkataramaniah, K. Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3204–3210. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Clemente, C.; Varshney, P.K. Helicopter classification via period estimation and time-frequency masks. In Proceedings of the IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Saint Martin, France, 13–16 December 2015; pp. 61–64.
- Du, L.; Li, L.; Wang, B.; Xiao, J. Micro-Doppler Feature Extraction Based on Time-Frequency Spectrogram for Ground Moving Targets Classification With Low-Resolution Radar. IEEE Sens. J. 2016, 16, 3756–3763. [Google Scholar] [CrossRef]
- Jokanović, B.; Amin, M.; Dogaru, T. Time-frequency signal representations using interpolations in joint-variable domains. IEEE Trans. Geosci. Remote Sens. 2015, 12, 204–208. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-linear canonical ambiguity function-based detection and estimation method for marine target with micro motion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Tao, R.; Deng, B.; Zhang, W.Q.; Wang, Y. Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain. IEEE Trans Signal Process. 2008, 56, 158–171. [Google Scholar] [CrossRef]
- Suo, P.C.; Tao, S.; Tao, R.; Nan, Z. Detection of high-speed and accelerated target based on the linear frequency modulation radar. IEEE Radar Sonar Navig. 2014, 8, 37–47. [Google Scholar] [CrossRef]
- Pang, C.S.; Hou, H.L.; Han, Y. Acceleration target detection based on LFM radar. Optik-Int. J. Light Electron Opt. 2014, 125, 5708–5714. [Google Scholar] [CrossRef]
- Hou, H.; Pang, C.; Guo, H.; Qu, X.; Han, Y. Study on high-speed and multi-target detection algorithm based on STFT and FRFT combination. Optik-Int. J. Light Electron Opt. 2016, 127, 713–717. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, H.W.; Gu, F.F.; Zhang, Q. Ground moving targets imaging via compressed sensing based on discrete FrFT. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 19–22 September 2015; pp. 1–5.
- Qian, W.; Fei, Y.; Yi, Z.; En, C. Gabor Wigner Transform based on fractional Fourier transform for low signal to noise ratio signal detection. In Proceedings of the OCEANS, Shanghai, China, 10–13 April 2016; pp. 1–4.
- Tao, R.; Li, Y.L.; Wang, Y. Short-time fractional Fourier transform and its applications. IEEE Trans. Signal Process. 2010, 58, 2568–2580. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Bao, Z.; He, Y. Detection and extraction of target with micro motion in spiky sea clutter via short-time fractional Fourier transform. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1002–1018. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Sidorenko, P.; Mixon, D.G.; Barel, S.; Cohen, O. Sparse phase retrieval from short-time Fourier measurements. IEEE Signal Process. Lett. 2015, 22, 638–642. [Google Scholar] [CrossRef]
- Catherall, A.T.; Williams, D.P. High resolution spectrograms using a component optimized short-term fractional Fourier transform. Signal Process. 2010, 90, 1591–1596. [Google Scholar] [CrossRef]
- Bai, X.; Tao, R.; Wang, Z.; Wang, Y. ISAR imaging of a ship target based on parameter estimation of multicomponent quadratic frequency-modulated signals. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1418–1429. [Google Scholar] [CrossRef]
- Griffin, D.; Lim, J. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Giv, H.H. Directional short-time Fourier transform. J. Math. Anal. Appl. 2013, 399, 100–107. [Google Scholar] [CrossRef]
- Pang, C.S. An accelerating target detection algorithm based on DPT and fractional Fourier transform. Acta Electron. Sin. 2012, 40, 184–188. [Google Scholar]
- Kim, B.; Kong, S.H.; Kim, S. Low computational enhancement of STFT-based parameter estimation. IEEE J. Sel. Top. Signal Process. 2015, 9, 1610–1619. [Google Scholar] [CrossRef]
- Chen, V.C. The micro-Doppler Effect in Radar; Artech House: Boston, MA, USA, 2011. [Google Scholar]






| Time Point (s) | A(0) | B(0.2) | C(0.4) | D(0.6) | E(0.8) |
|---|---|---|---|---|---|
| Order of matching | 0.99 | 1.0 | 1.02 | 1.03 | 1.05 |
| STFT | 1.0094 | 0.9520 | 1.1650 | 1.3858 | 1.9287 |
| STFRFT | 0.9520 | ||||
| Time-frequency resolution ratio | 1.1 | 1.1 | 1.4 | 1.7 | 2.3 |
| SNR | Technique 1 | Technique 2 | Technique 3 | T2/T1 | T3/T1 |
|---|---|---|---|---|---|
| −4 dB | 18,0096 | 11,340 | 11,310 | 15.90 | 15.88 |
| −6 dB | 18,0096 | 12,430 | 12,400 | 14.52 | 14.48 |
| −8 dB | 18,0096 | 13,570 | 13,540 | 13.33 | 13.27 |
| Parameter | Value |
|---|---|
| Carrier frequency | 3 GHz (continuous wave) |
| Baseband sampling rate | 78 kHz |
| Frame signal accumulation time | 72.1 ms |
| Target | Rocket projectile |
| Parameter | Time-Frequency Resolution Ratio |
|---|---|
| A | 1.27 |
| B | 1.25 |
| C | 1.23 |
| Parameter | Value |
|---|---|
| Frequency | 674 MHz |
| Baseband sampling rate | 5 kHz |
| Signal accumulation time | 1 s |
| Target | Align 750e |
| Parameter | Value |
|---|---|
| Frequency | 3 GHz (continuous wave) |
| Baseband sampling rate | 20 kHz |
| Accumulation time | 0.15 s |
| Target | Fan |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, C.; Han, Y.; Hou, H.; Liu, S.; Zhang, N. Micro-Doppler Signal Time-Frequency Algorithm Based on STFRFT. Sensors 2016, 16, 1559. https://doi.org/10.3390/s16101559
Pang C, Han Y, Hou H, Liu S, Zhang N. Micro-Doppler Signal Time-Frequency Algorithm Based on STFRFT. Sensors. 2016; 16(10):1559. https://doi.org/10.3390/s16101559
Chicago/Turabian StylePang, Cunsuo, Yan Han, Huiling Hou, Shengheng Liu, and Nan Zhang. 2016. "Micro-Doppler Signal Time-Frequency Algorithm Based on STFRFT" Sensors 16, no. 10: 1559. https://doi.org/10.3390/s16101559
APA StylePang, C., Han, Y., Hou, H., Liu, S., & Zhang, N. (2016). Micro-Doppler Signal Time-Frequency Algorithm Based on STFRFT. Sensors, 16(10), 1559. https://doi.org/10.3390/s16101559






