Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing
Abstract
:1. Introduction
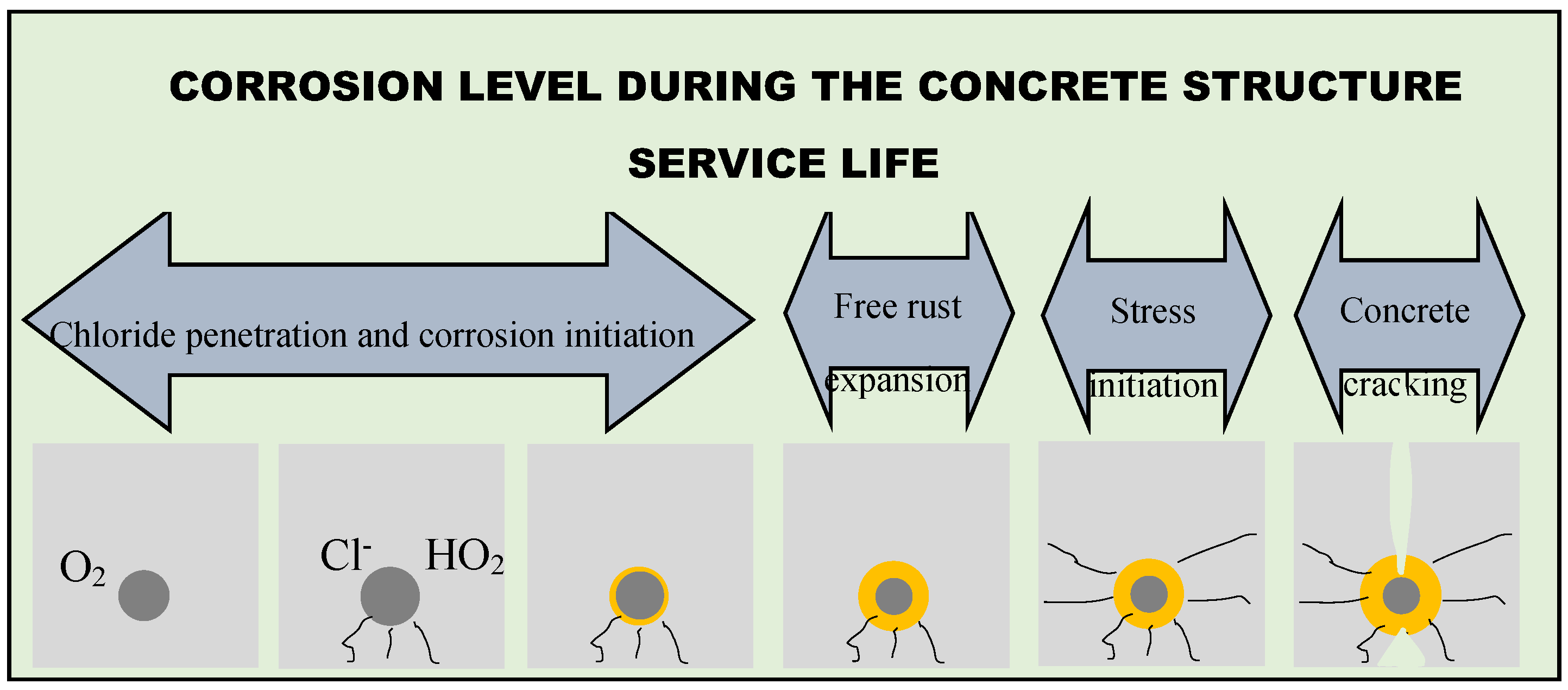
2. A very Brief Survey of the Corrosion Assessment of Reinforced Concrete Structures
2.1. Electrochemical Techniques
- (1)
- A metal body in contact with the surrounding media develops an electric potential. In reinforced concrete structures, the concrete acts as an electrolyte, generating an electrostatic potential, which can vary from place to place, depending on the state of the concrete. The principle involved in the open circuit potential measurements is essentially the measurement of the corrosion potential of the rebar to a standard reference electrode. This is the most typical procedure for the routine inspection of reinforced concrete structures (Erdogdu et al. [5]).
- (2)
- During the corrosion process, an electrical current flows through the concrete between the anodic and cathodic regions. Measurements of the difference of potential at the concrete surface detect this current flow. Surface potential measurements are a non-destructive test to identify anodic and cathodic regions in concrete structures and, indirectly, to detect corrosion processes of the reinforcement. Two reference electrodes are used for the measurements, and no electrical connection to the rebar is required. An electrode is held fixed on the structure in a symmetrical point. The other electrode, called moving electrode, is moved to the nodal points of a grid, along the structure. The measurements are done using a high-impedance voltmeter. A positive reading of the voltage represents an anodic area where corrosion is possible. The higher the potential difference between the anodic and cathodic areas, the higher is the probability of corrosion (Song and Saraswathy [6]).
- (3)
- The unique electrochemical technique with quantitative ability regarding the corrosion rate is the so-called polarization resistance, Rp. This technique is based on the application of a small electrical perturbation to the rebar by using a counter electrode and a reference electrode. If the electrical signal is uniformly distributed throughout the reinforcement, the ∆E/∆I ratio defines Rp. The corrosion current, Icorr, is inversely proportional to Rp, or, Icorr = B/Rp, where B is a constant. Rp can be measured employing direct current or alternating current techniques (Andrade and Alonso [7]).
- (4)
- The galvanostatic pulse method is a transient polarization technique working in the time domain. A short time anodic current pulse is impressed galvanostatically on the reinforcement from a counterelectrode placed on the concrete surface. The reinforcement is polarized in the anodic direction compared to its free corrosion potential. A reference electrode records the resulting change of the electrochemical potential of the reinforcement. Applying a constant current to the system, an intermediate ohmic potential jumps, and a slight polarization of the rebars occur. Under the assumption that a simple Randles circuit describes the transient behavior of the rebars, the potential of the reinforcement, V(t), at a given time t, can be expressed by an exponential expression, plus a constant resistance (Sathiyanarayanan et al. [8]).
- (5)
- Measurement of the electrochemical impedance is done by imposing a sinusoidal voltage (or current) signal of small amplitude, and by measuring the response signal of voltage and current. The amplitudes and the phase difference between the two signals are then analyzed. The frequencies vary between 10−5 and 105 Hz, and the amplitudes between 10 mV and 10 V (MacDonald et al. [9]).
- (6)
- The harmonic analysis method is an extension of the impedance method. Its execution is faster and leads to results that are more straightforward than those of the electrochemical impedance method. This technique is carried out by imposing an A.C. voltage perturbation at a single frequency and measuring the A.C. current density, i1. Two higher harmonics i2 and i3 are also measured. The harmonic analysis uses the fact that the corroding interface acts as a rectifier, in that the second harmonic current response is not linear about the free corrosion potential (Vedalakshmi et al. [10]).
- (7)
- In the electrochemical noise method, measurements of the spontaneous fluctuations of the corrosion potentials and currents, which are observed as electrically coupled pairs, are taken. This method is random in nature. The range of frequency is typically from 10−3 to 1.0 Hz. Typical amplitudes are of the order of µV to mV, for voltage, and from nA to µA, for current. Electrochemical noise is a low-cost nondestructive technique reasonably straightforward, although attention must be paid to avoid problems, such as instrument noise, extraneous noise, aliasing, and quantization (Sheng et al. [11]).
2.2. Electromagnetic Techniques
3. Description and Basics of the Developed ECT Sensors for Steel Bar Inspections
3.1. Mathematical Basics

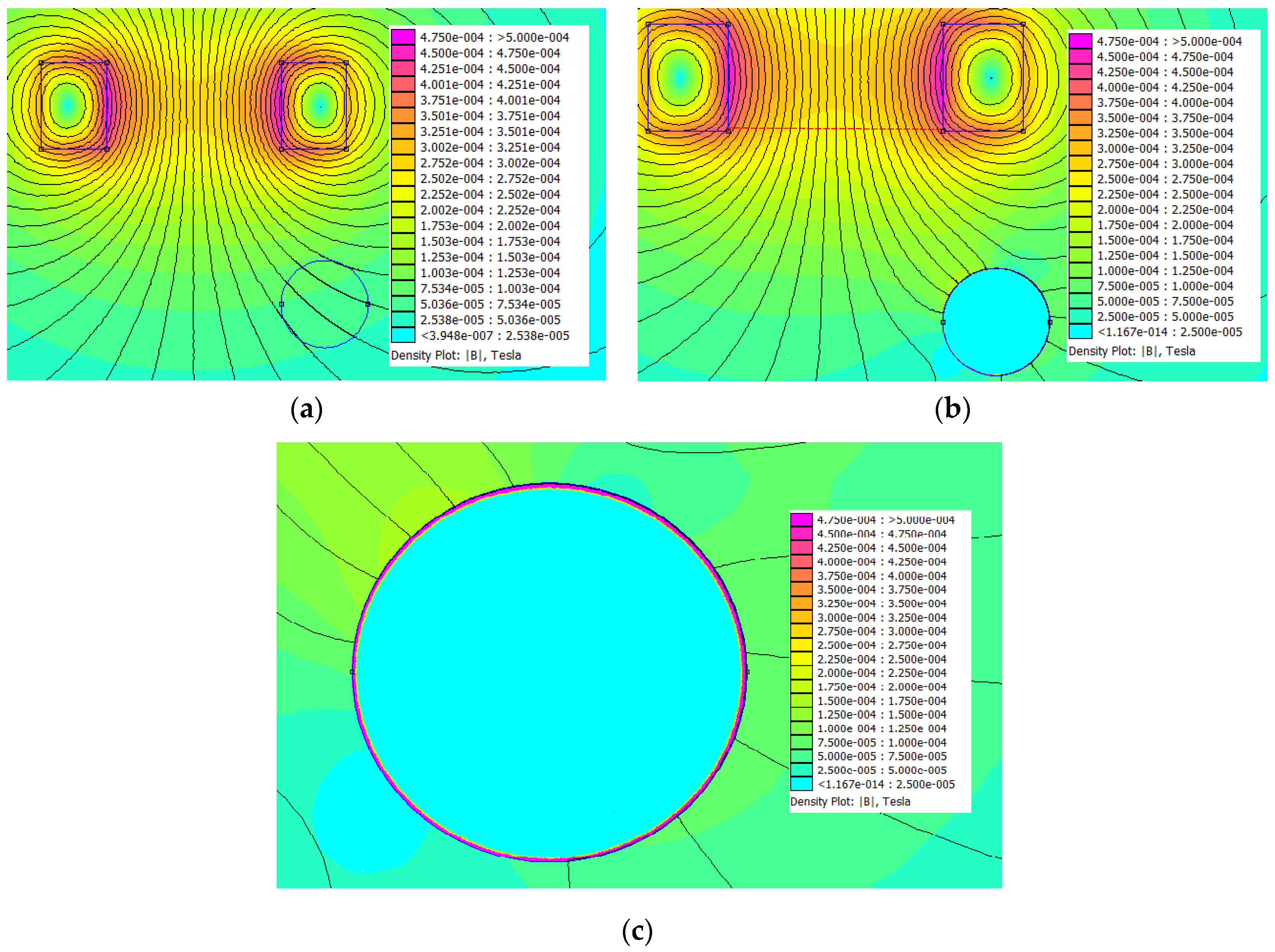
| Bx (Wb/m2) | By (Wb/m2) | |
|---|---|---|
| Without the bar | −3.665 × 10−6 − j6.346 × 10−7 | 2.526 × 10−4 − j1.224 × 10−6 |
| With the bar | −4.240 × 10−8 − j5.172 × 10−11 | 2.522 × 10−4 + j1.815 × 10−7 |
3.2. The Frequency-Adjustment Method to Calculate the Effective Resistance and Inductance
3.3. Finite Element Simulations and Experimental Comparisons for an ECT Sensor


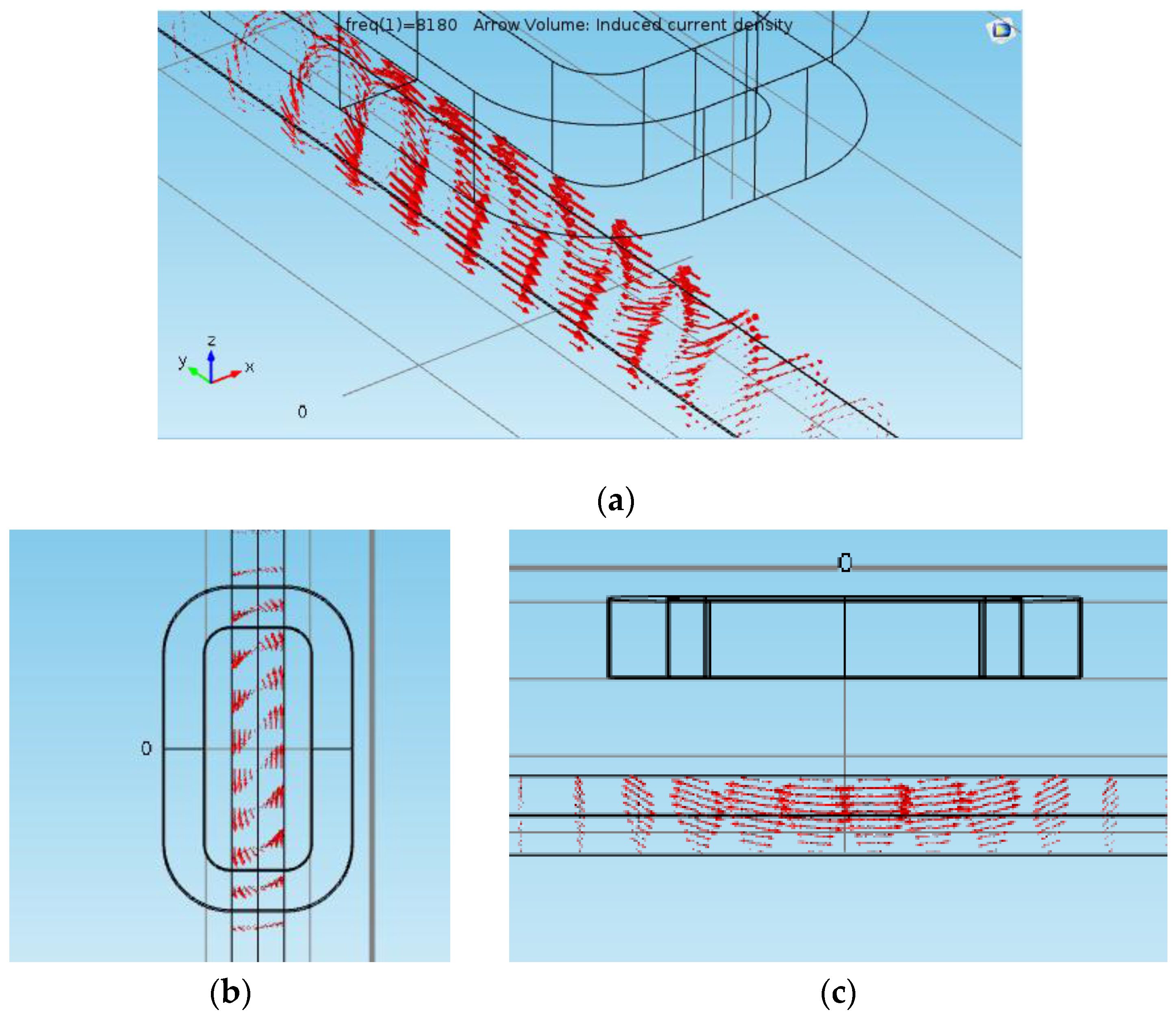

4. The Production of Corroded Samples of Steel Bars



5. Results
5.1. Experimental Setup

5.2. The Movement of the Sensor
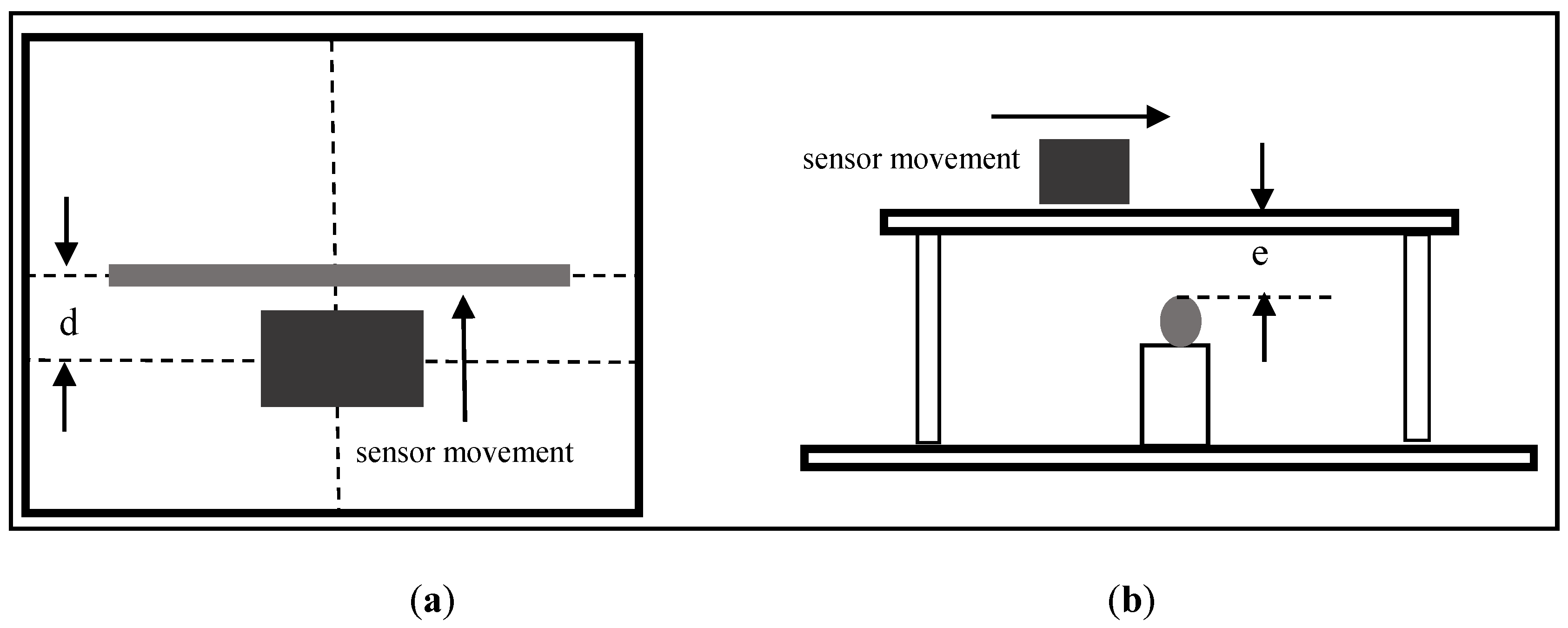
5.3. The Procedure for the Measurements
- -
- At no-load condition (no steel bar under the sensor):
- (1)
- The equipment is turned on, the resonant frequency is set in the signal generator and slightly changed until to reach the real resonant frequency for the sensor, 8043 Hz in this case. This frequency was used as starting frequency for all measurements with corroded or non-corroded steel bars, from this point on.
- (2)
- The coil inductance is calculated, using Equation (13).
- (3)
- The coil resistance is calculated, using Equation (14).
- -
- At load condition:
- (4)
- A steel bar is placed under the sensor aligned with its main axis. The voltage at the capacitive array is measured and recorded. After this, the frequency slightly changed, up to the new resonance condition, and steps (2) and (3) are repeated, to calculate the effective resistance and effective inductance.
- (5)
- The phase angle of the current in the sensor is calculated using the extracted values of resistance and inductance.

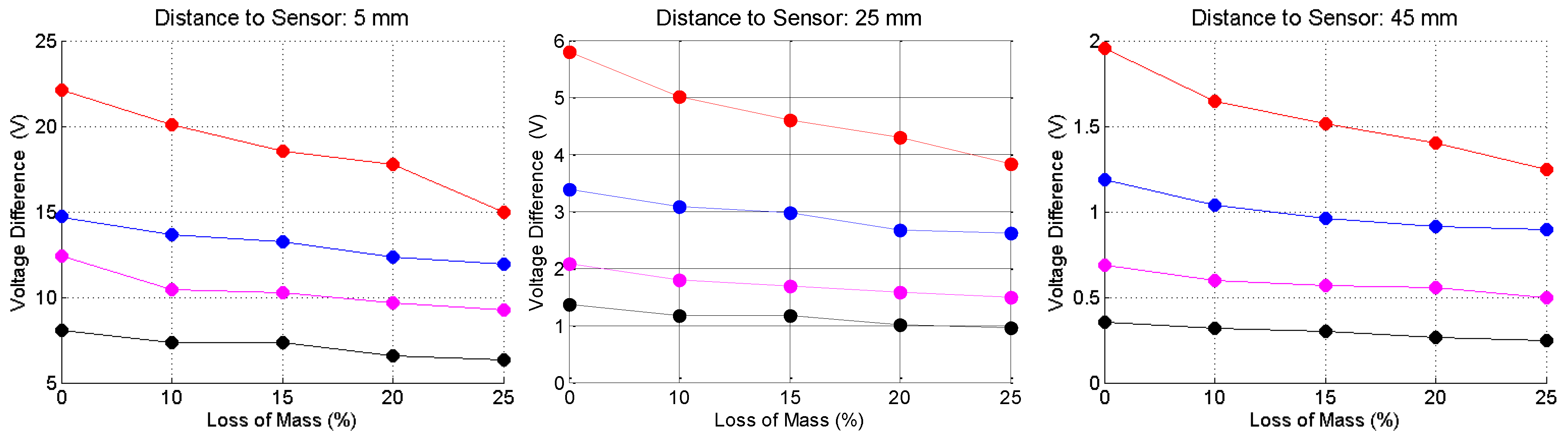
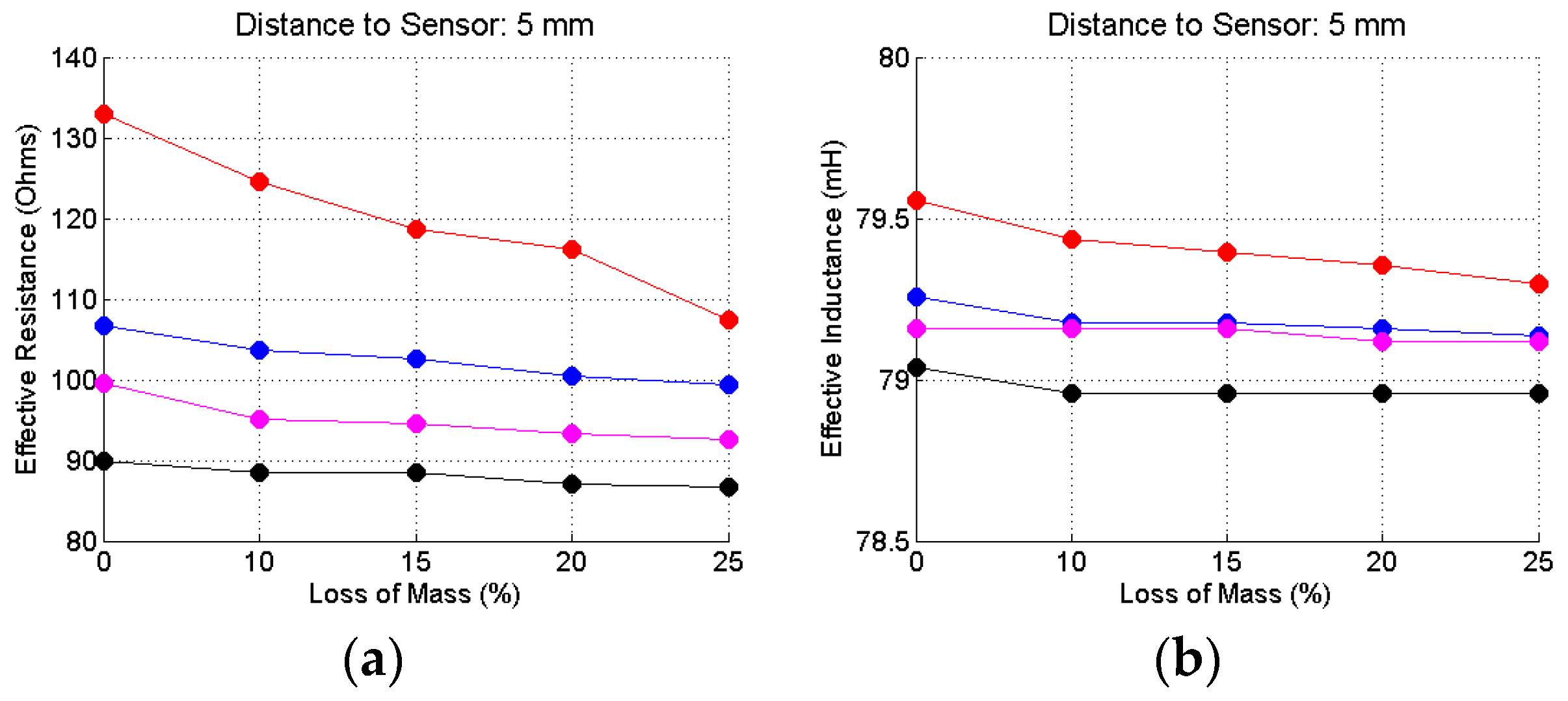
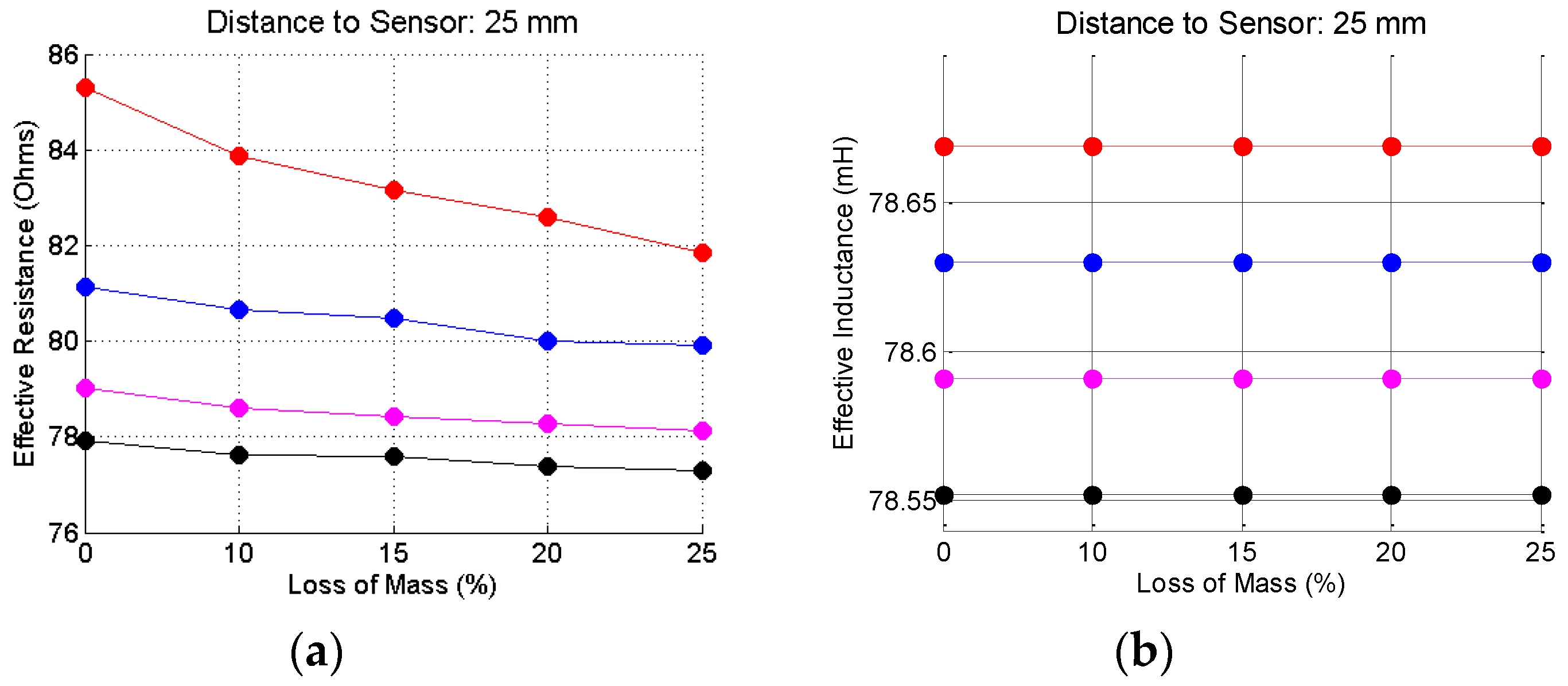
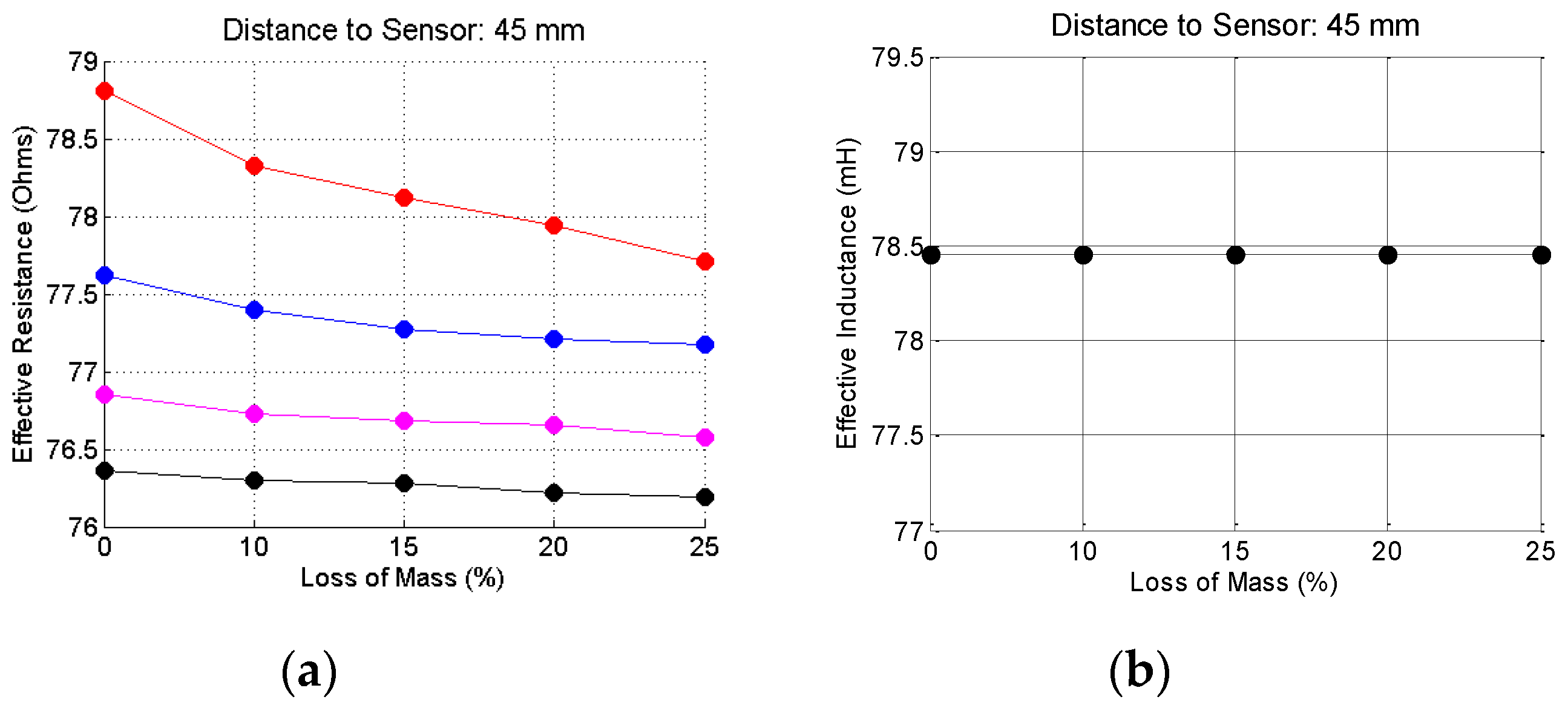
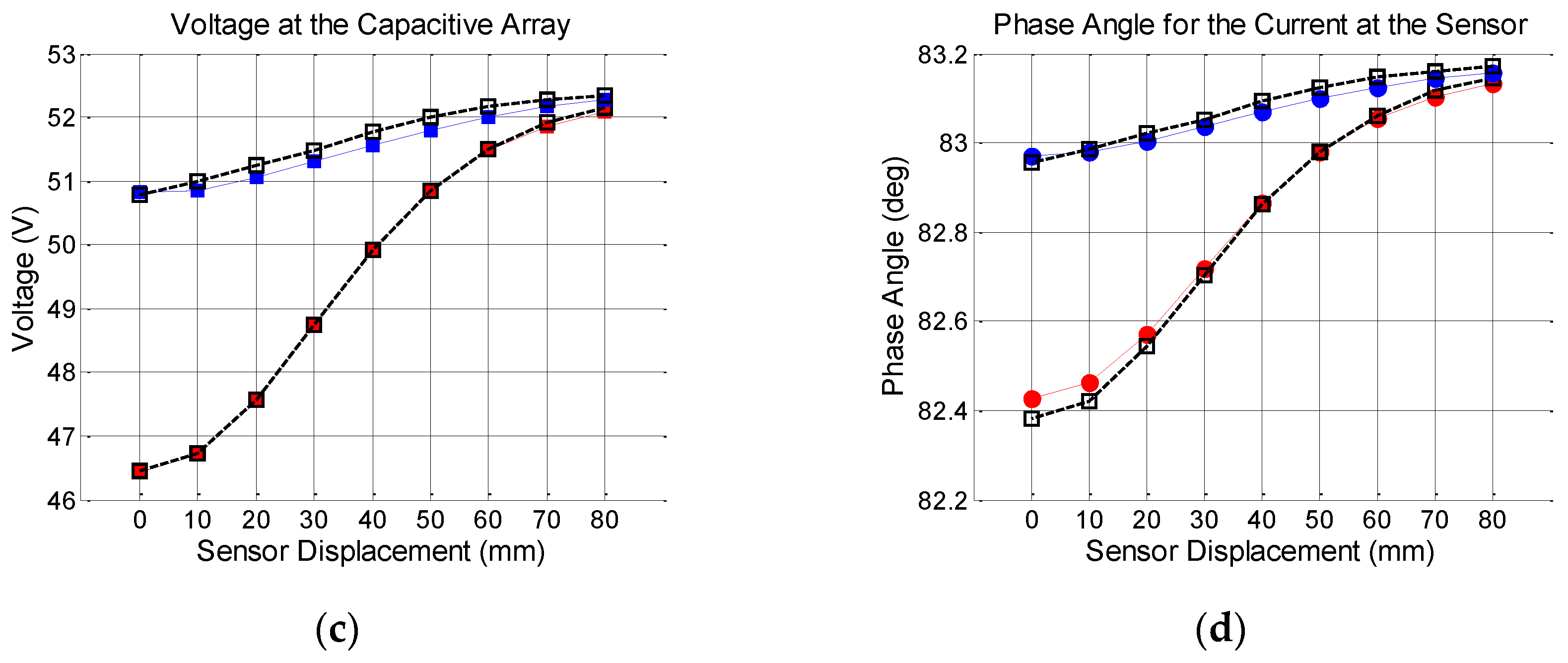
5.4. The Lift-Off Effect


5.5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- El Maaddawy, T.A.; Soudky, K.A. Effectiveness of impressed current techniques to simulate corrosion of steel reinforcement in concrete. J. Mater. Civil Eng. 2003, 15, 41–47. [Google Scholar] [CrossRef]
- Maruya, T.; Takeda, H.; Horiguchi, K.; Koyama, S.; Hsu, K.L. Simulation of Steel Corrosion in Concrete Based on the Model of Macro-Cell Corrosion Circuit. J. Adv. Concrete Technol. 2007, 6, 343–362. [Google Scholar] [CrossRef]
- Roqueta, G.; Jofre, L.; Feng, M.Q. Analysis of the Electromagnetic Signature of Reinforced Concrete Structures for Nondestructive Evaluation of Corrosion Damage. IEEE Trans. Instrum. Meas. 2012, 61, 1090–1098. [Google Scholar] [CrossRef]
- Arndt, R.; Jalinoos, F. NDE for corrosion dectection in reinforced concrete structures—A benchmark approach. In Proceedings of Non-Destructive Testing in Civil Engineering (NDTCE’09), Nantes, France, 30 June–3 July 2009; pp. 1–6.
- Erdogdu, S.; Kondratova, I.L.; Bremner, T.W. Determination of Chloride Diffusion Coefficient of Concrete Using Open-Circuit Potential Measurements. Cem. Concr. Res. 2004, 34, 603–609. [Google Scholar] [CrossRef]
- Song, H.W.; Saraswathy, V. Corrosion Monitoring of Reinforced Concrete Structures—A Review. Int. J. Electrochem. Sci. 2007, 2, 1–28. [Google Scholar]
- Andrade, C.; Alonso, C. Test Methods for on Site Corrosion Rate Measurement of Steel Reinforcement in Concrete by Means of the Polarization Resistance Method. Mater. Struct. 2004, 37, 623–643. [Google Scholar] [CrossRef]
- Sathiyanarayanan, S.; Natarajan, P.; Saravanan, K.; Srinivasan, S.; Venkatachari, G. Corrosion Monitoring of Steel in Concrete by Galvanostatic Pulse Technique. Cem. Conc. Compos. 2006, 28, 630–637. [Google Scholar] [CrossRef]
- MacDonald, D.D.; El-Tantawy, Y.A.; Rocha-Filho, R.C. Evaluation of Electrochemical Impedance Techniques for Detecting Corrosion on Rebar in Reinforced Concrete. Available online: http://onlinepubs.trb.org/onlinepubs/shrp/SHRP-91-524.pdf (accessed on 20 Setember 2015).
- Vedalakshmi, R.; Manoharan, S.P.; Song, H.W.; Palaniswamy, N. Application of harmonic analysis in measuring the corrosion rate of rebar in concrete. Corros. Sci. 2009, 51, 2777–2789. [Google Scholar] [CrossRef]
- Sheng, Y.F.; Luo, J.J.; Wilmott, M. Spectral analysis of electrochemical noise with different transient shapes. Electrochimica Acta 2000, 45, 1763–1771. [Google Scholar]
- Makar, K.; Desnoyers, R. Magnetic Field Techniques for the Inspection of Steel Under the Concrete Cover. NDT&E Int. 2001, 34, 445–456. [Google Scholar]
- Wolf, T.; Vogel, T. Detection of Reinforcement Breaks: Laboratory Experiments and an Application of the Magnetic Flux Leakage Method. In Proceedings of the 14th International Conference and Exhibition on Structural Faults and Repair, Edinburgh, UK, 3–5 July 2012; pp. 1–9.
- Shull, P.J. Nondestructive Evaluation: Theory, Techniques and Applications; CRC Press: New York, NY, USA, 2002. [Google Scholar]
- García-Martin, J.; Gomez-Gil, J.; Vazquez-Sanchez, E. Non-Destructive Techniques Based on Eddy Current Testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef] [PubMed]
- Rubinacci, G.; Tamburrino, A.; Ventre, S. Concrete Rebar Inspection by Eddy Current Testing. Int. J. Appl. Electromagn. Mech. 2007, 25, 333–339. [Google Scholar]
- Alcantara, N.P., Jr. Identification of Steel Bars Immersed in Reinforced Concrete Based on Experimental Results of Eddy Current Testing and Artificial Neural Network Analysis. Nondest. Test. Eval. 2013, 28, 58–71. [Google Scholar] [CrossRef]
- Annan, A.P. Electromagnetic Principles of Ground Penetrating Radar. In Ground Penetrating Radar: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2009; pp. 3–40. [Google Scholar]
- Blindow, N.; Eisenburger, D.; Illich, B.; Petzold, H.; Richter, T. Ground Penetrating Radar. In Environmental Geology; Springer: Berlin, Germany, 2007; pp. 283–335. [Google Scholar]
- Farnoosh, N.; Shoory, A.; Moini, R.; Sadeghi, S.H.H. Analysis of Thin-Wire Ground Penetrating Radar Systems for Buried Target Detection, Using a Hybrid MoM-FDTD, Technique. NDT&E Int. 2008, 41, 266–272. [Google Scholar]
- Shaw, M.R.; Millard, S.G.; Molyneaux, T.C.K.; Taylor, M.J.; Bungey, J.H. Location of Steel Reinforcement in Concrete Using Ground Penetrating Radar and Neural Networks. NDT&E Int. 2005, 38, 203–212. [Google Scholar]
- Hugenschmidt, J.; Loser, R. Detection of chlorides and moisture in concrete structures with ground penetrating radar. Mater. Struct. 2007, 41, 785–792. [Google Scholar] [CrossRef]
- Buyukozturk, O. Imaging of Concrete Structures. NDT&E Int. 1998, 31, 233–243. [Google Scholar]
- Baek, S.; Xue, W.; Feng, M.Q.; Kwon, S. Nondestructive corrosion detection in RC through integrated heat Induction and IR thermography. J. Nondest. Eval. 2012, 31, 181–190. [Google Scholar] [CrossRef]
- FEMM—Finite Element Method Magnetics. Available online: http://www.femm.info/ (accessed on 20 November 2015).
- COMSOL Multiphysics. Available online: http://comsol.com (accessed on 20 September 2015).
- Ahmad, S. Techniques for Inducing Accelerated Corrosion of Steel in Concrete. Arab. J. Sci. Eng. 2009, 34, 95–104. [Google Scholar]
- Shetty, A.; Venkataramana, K.; Gogoi, I. Performance Evaluation of Rebar in Accelerated Corrosion by Gravimetric Loss Method. Int. J. Earth Sci. Eng. 2012, 5, 154–159. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Alcantara, N.P., Jr.; Da Silva, F.M.; Guimarães, M.T.; Pereira, M.D. Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing. Sensors 2016, 16, 15. https://doi.org/10.3390/s16010015
De Alcantara NP Jr., Da Silva FM, Guimarães MT, Pereira MD. Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing. Sensors. 2016; 16(1):15. https://doi.org/10.3390/s16010015
Chicago/Turabian StyleDe Alcantara, Naasson P., Jr., Felipe M. Da Silva, Mateus T. Guimarães, and Matheus D. Pereira. 2016. "Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing" Sensors 16, no. 1: 15. https://doi.org/10.3390/s16010015
APA StyleDe Alcantara, N. P., Jr., Da Silva, F. M., Guimarães, M. T., & Pereira, M. D. (2016). Corrosion Assessment of Steel Bars Used in Reinforced Concrete Structures by Means of Eddy Current Testing. Sensors, 16(1), 15. https://doi.org/10.3390/s16010015





