Configuration Analysis of the ERS Points in Large-Volume Metrology System
Abstract
:1. Introduction
2. Measurement Uncertainty Estimation Model
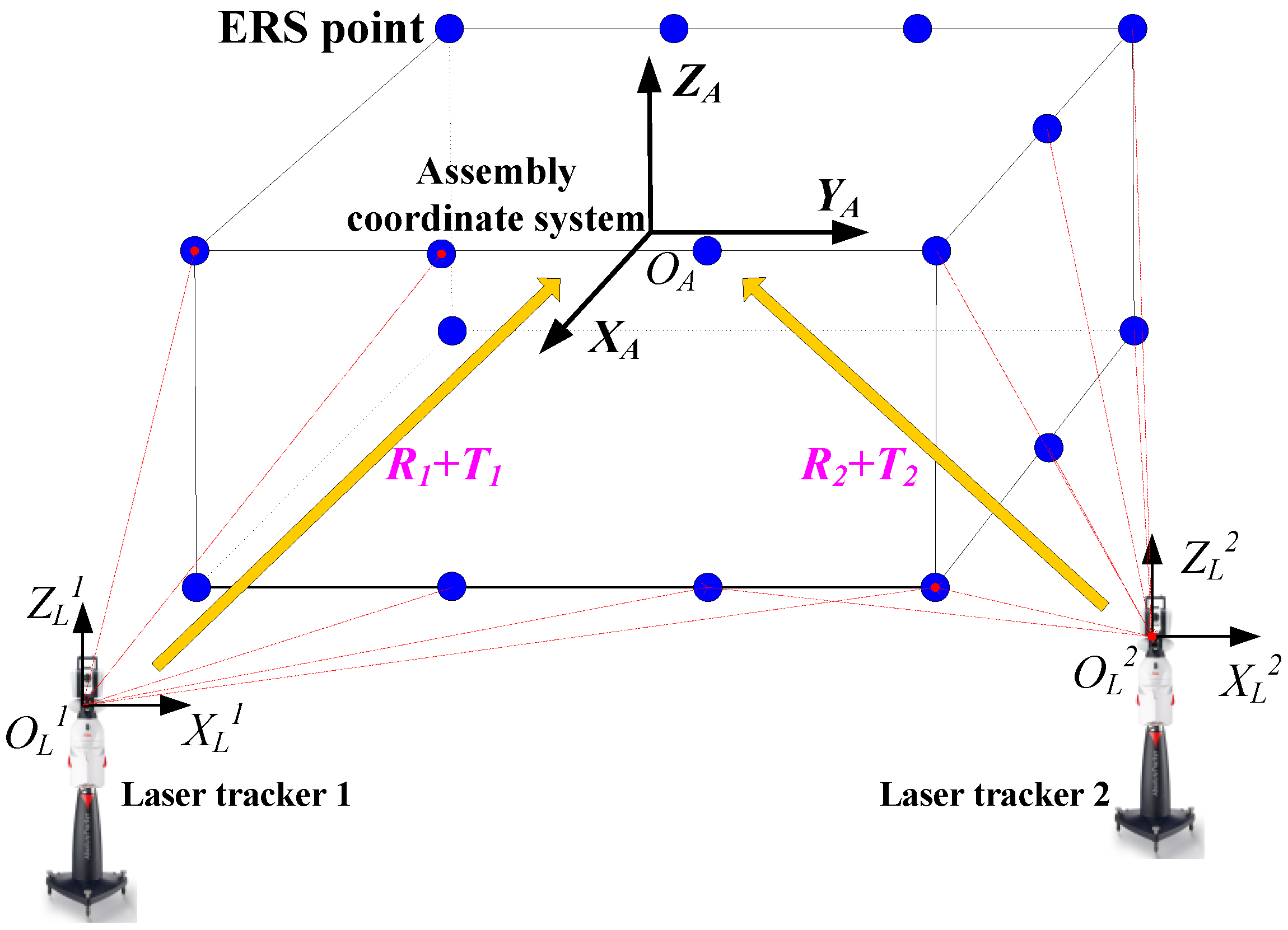
2.1. Error Propagation Model in Registration
2.2. Uncertainty Estimation of the Transformation Parameter Errors
2.3. Experimental Verification
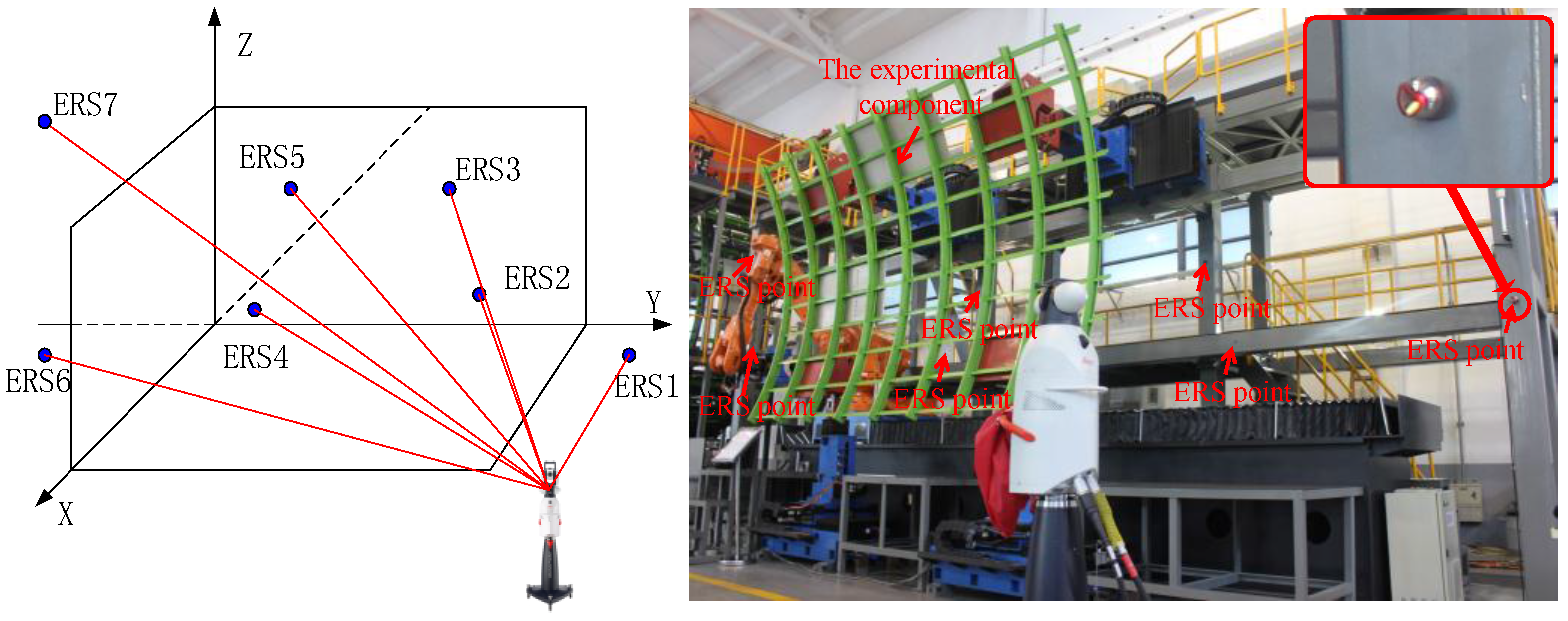
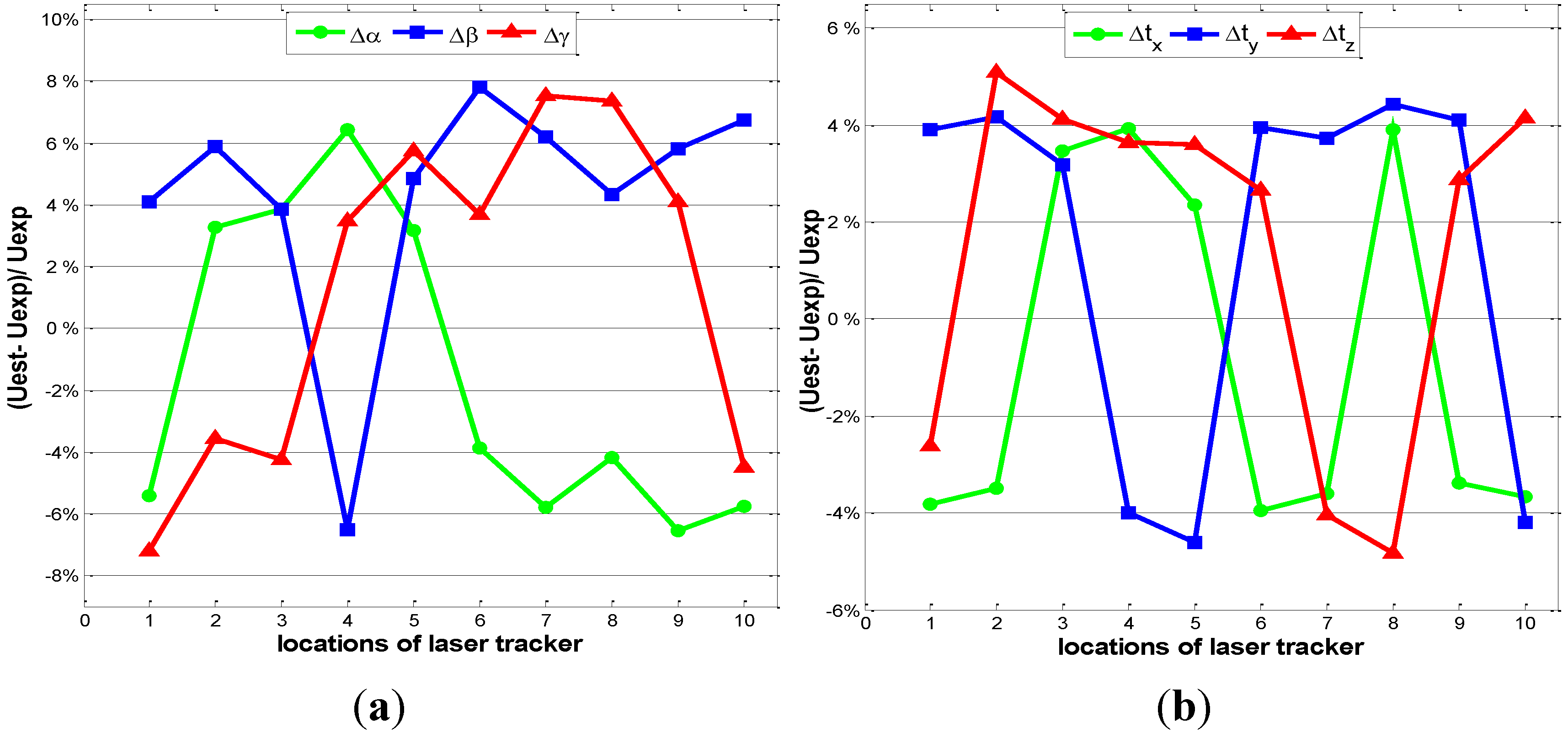
3. Configuration analysis of the ERS points
3.1. The Evaluation Criteria
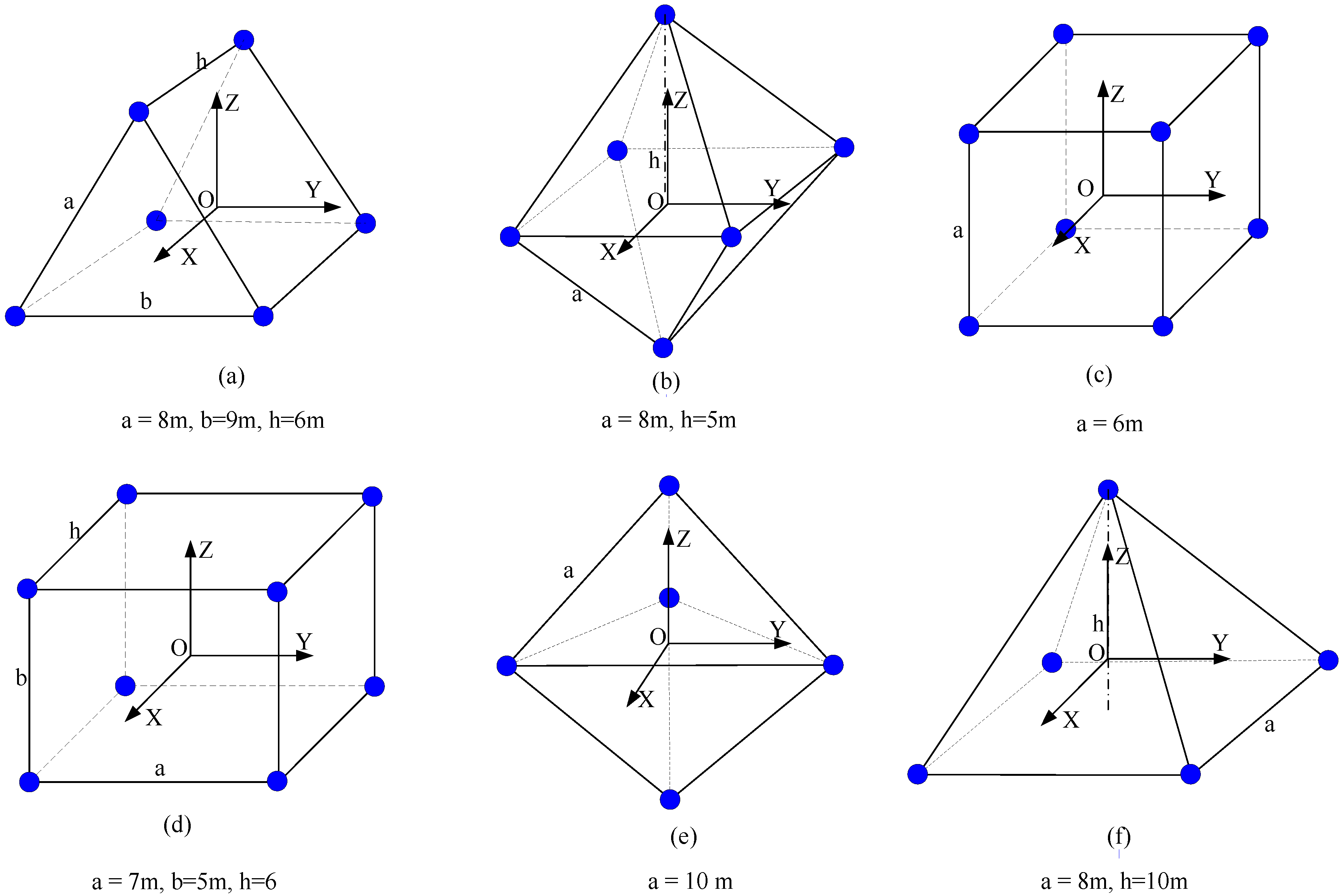
3.2. The Impact of the Layout of the ERS Points
| Layout | Kα | Kβ | Kγ | Kα + Kβ + Kγ | Kx | Ky | Kz | Kx + Ky + Kz |
|---|---|---|---|---|---|---|---|---|
| a | 0.0080 | 0.0069 | 0.0052 | 0.0200 | 0.1667 | 0.1667 | 0.1667 | 0.5000 |
| b | 0.0088 | 0.0088 | 0.0078 | 0.0254 | 0.1667 | 0.1667 | 0.1667 | 0.5000 |
| c | 0.0069 | 0.0069 | 0.0069 | 0.0208 | 0.1250 | 0.1250 | 0.1250 | 0.3750 |
| d | 0.0082 | 0.0059 | 0.0068 | 0.0208 | 0.1250 | 0.1250 | 0.1250 | 0.3750 |
| e | 0.0055 | 0.0055 | 0.0100 | 0.0209 | 0.2000 | 0.2000 | 0.2000 | 0.6000 |
| f | 0.0069 | 0.0069 | 0.0078 | 0.0217 | 0.2000 | 0.2000 | 0.2000 | 0.6000 |
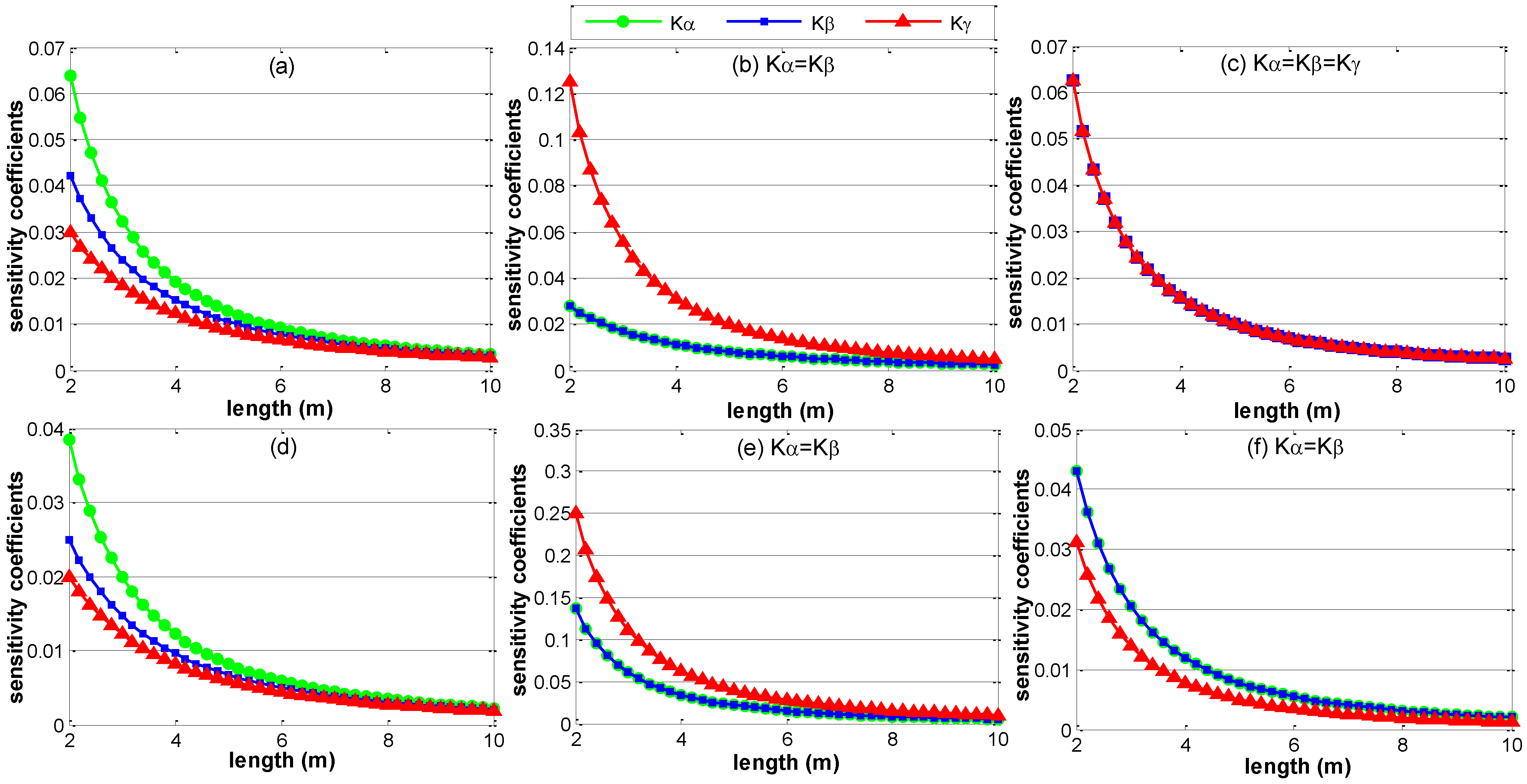
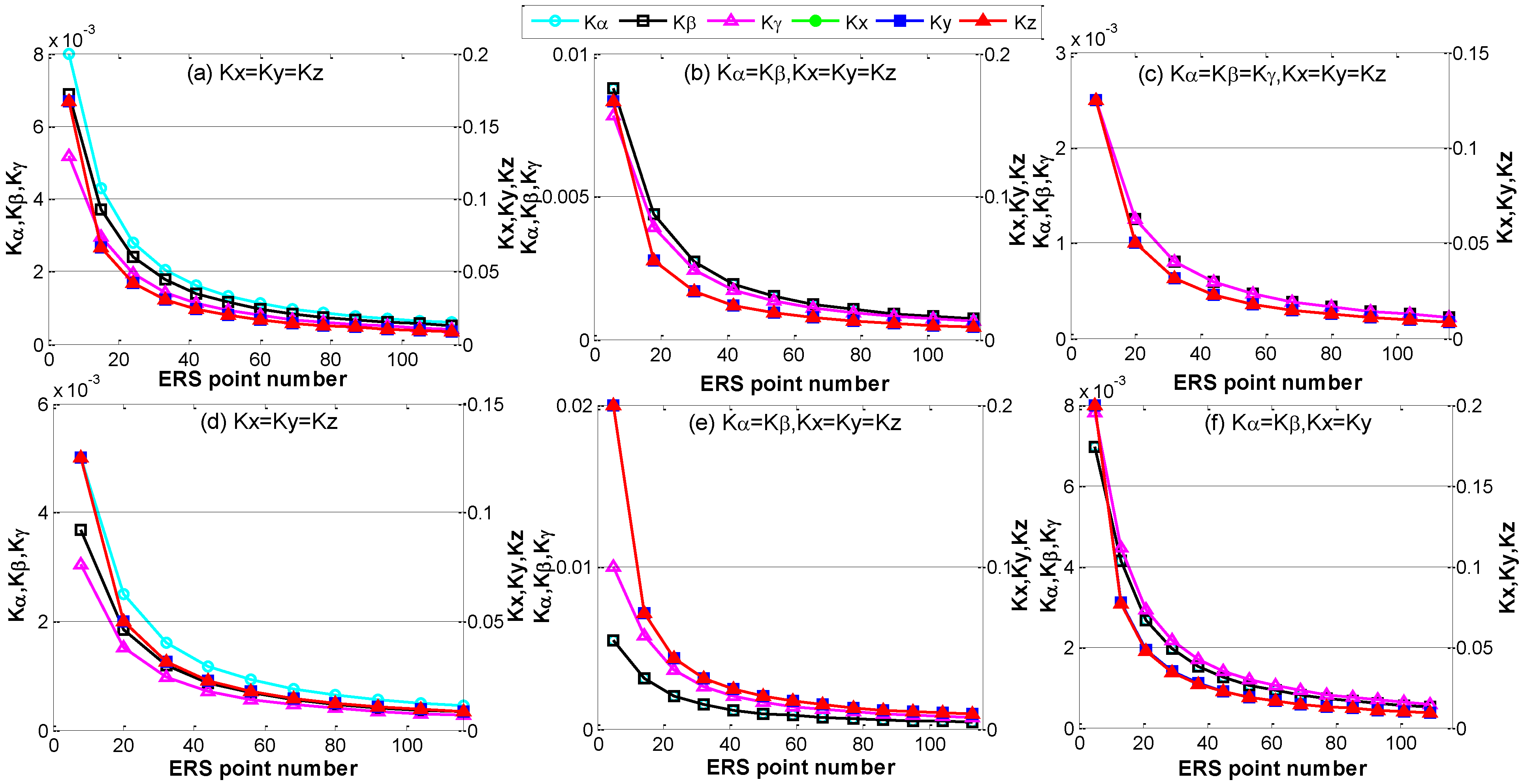
3.3. The Impact of the Assembly Coordinate System
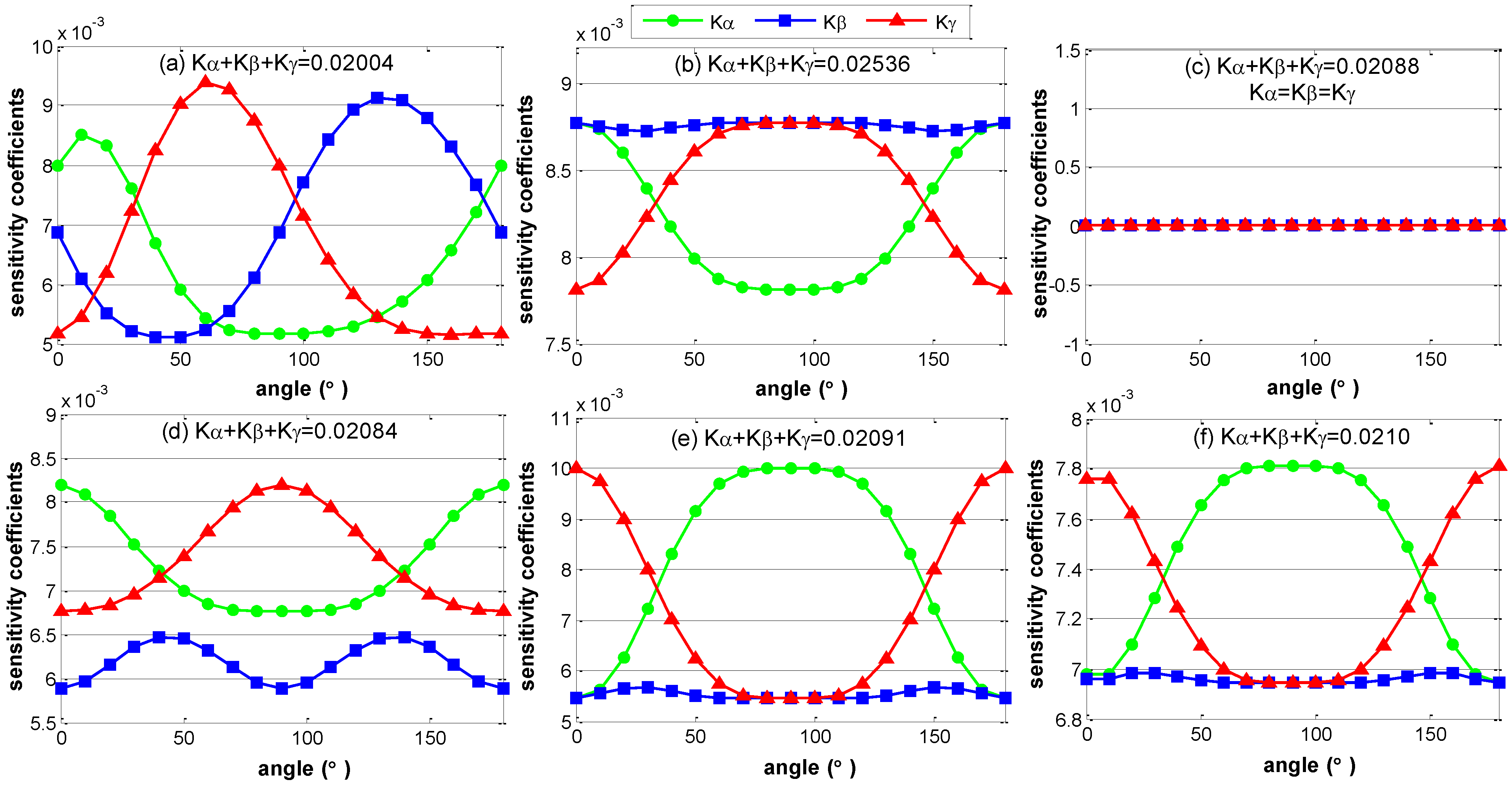
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Muelaner, J.; Maropoulos, P.G. Large scale metrology in aerospace assembly. In Proceedings of the 5th International Conference on Digital Enterprise Technology, Bath, UK, 22–24 October 2008.
- Li, Y.; Qiu, Y.; Chen, Y.; Guan, K. A novel orientation and position measuring system for large & medium scale precision assembly. Opt. Lasers Eng. 2014, 62, 31–37. [Google Scholar]
- Eggert, D.W.; Lorusso, A.; Fisher, R.B. Estimating 3-D rigid body transformations: A comparison of four major algorithms. Mach. Vis. Appl. 1997, 9, 272–290. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 5, 698–700. [Google Scholar] [CrossRef]
- Umeyama, S. Least-Square estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 4, 376–380. [Google Scholar] [CrossRef]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A 1988, 4, 629–642. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Hilden, H.M.; Negahdaripour, S. Closed-form solution of absolute orientation using orthonormal matrices. J. Opt. Soc. Am. A 1988, 5, 1127–1137. [Google Scholar] [CrossRef]
- Chetverikov, D.; Stepanov, D.; Krsek, P. Robust Euclidean alignment of 3D point sets: the trimmed iterative closet point algorithm. Image Vis. Comput. 2005, 23, 299–309. [Google Scholar] [CrossRef]
- Alfons, M.; Scott, S. Dynamic weighting of laser tracker measurement for bundle adjustment. Available online: http://www.leica-geosystems.com/ (accessed on 17 September 2015).
- Calkins, J.M.; Salerno, R.J. A practical method for evaluating measurement system uncertainty. In Proceedings of the 2000 Boeing Large Metrology Conference, Long Beach, CA, USA, 23–24 February 2000.
- Calkins, J.M. Quantifying Coordinate Uncertainty Fields in Coupled Spatial Measurement Systems. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2002. [Google Scholar]
- Predmore, C.R. Bundle adjustment of multi position measurements using the mahalanobis distance. Precis. Eng. 2010, 34, 113–123. [Google Scholar] [CrossRef]
- Mitchell, J.P.; Spence, A.D.; Hoang, M.; Free, A. Sensor fusion of laser trackers for use in large volume precision metrology. Intell. Manuf. 2004, 5263, 57–65. [Google Scholar]
- Fitzpatrick, M.; West, J.B. The distribution of Target Registration Error in Rigid-Body Point-Based Registration. IEEE Trans. Med. Imaging 2001, 20, 917–927. [Google Scholar] [CrossRef] [PubMed]
- Uncertainty of Measurement. Part 3. Guide to the Expression of Uncertainty in Measurement (GUM:1995); ISO/IEC Guide 98-3; International Organization for Standardization: Geneva, Switzerland, 2008.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Yu, C.; Li, J.; Ke, Y. Configuration Analysis of the ERS Points in Large-Volume Metrology System. Sensors 2015, 15, 24397-24408. https://doi.org/10.3390/s150924397
Jin Z, Yu C, Li J, Ke Y. Configuration Analysis of the ERS Points in Large-Volume Metrology System. Sensors. 2015; 15(9):24397-24408. https://doi.org/10.3390/s150924397
Chicago/Turabian StyleJin, Zhangjun, Cijun Yu, Jiangxiong Li, and Yinglin Ke. 2015. "Configuration Analysis of the ERS Points in Large-Volume Metrology System" Sensors 15, no. 9: 24397-24408. https://doi.org/10.3390/s150924397
APA StyleJin, Z., Yu, C., Li, J., & Ke, Y. (2015). Configuration Analysis of the ERS Points in Large-Volume Metrology System. Sensors, 15(9), 24397-24408. https://doi.org/10.3390/s150924397





