Generalized Parameter-Adjusted Stochastic Resonance of Duffing Oscillator and Its Application to Weak-Signal Detection
Abstract
:1. Introduction
2. Principle of SR in a Duffing Oscillator
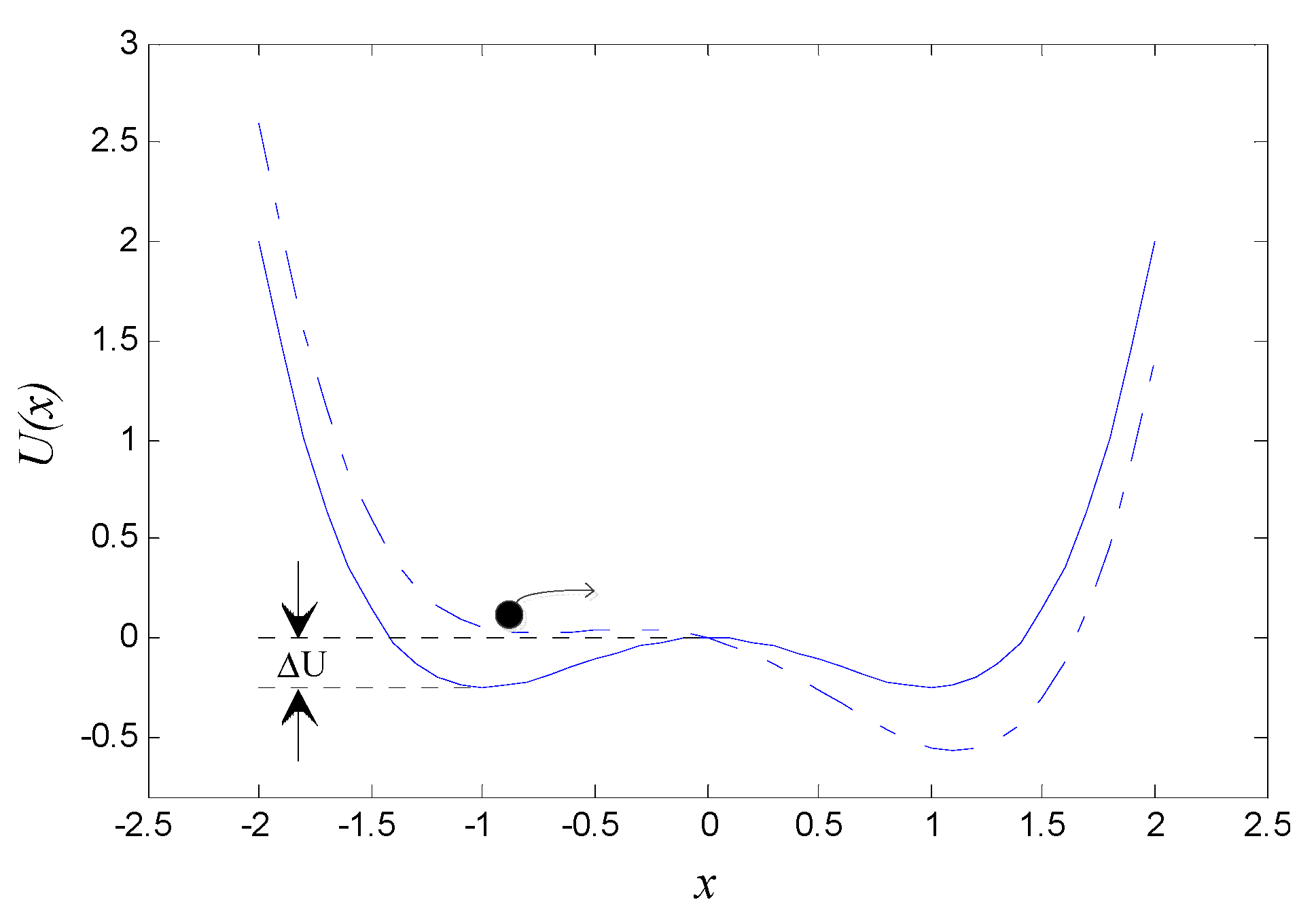
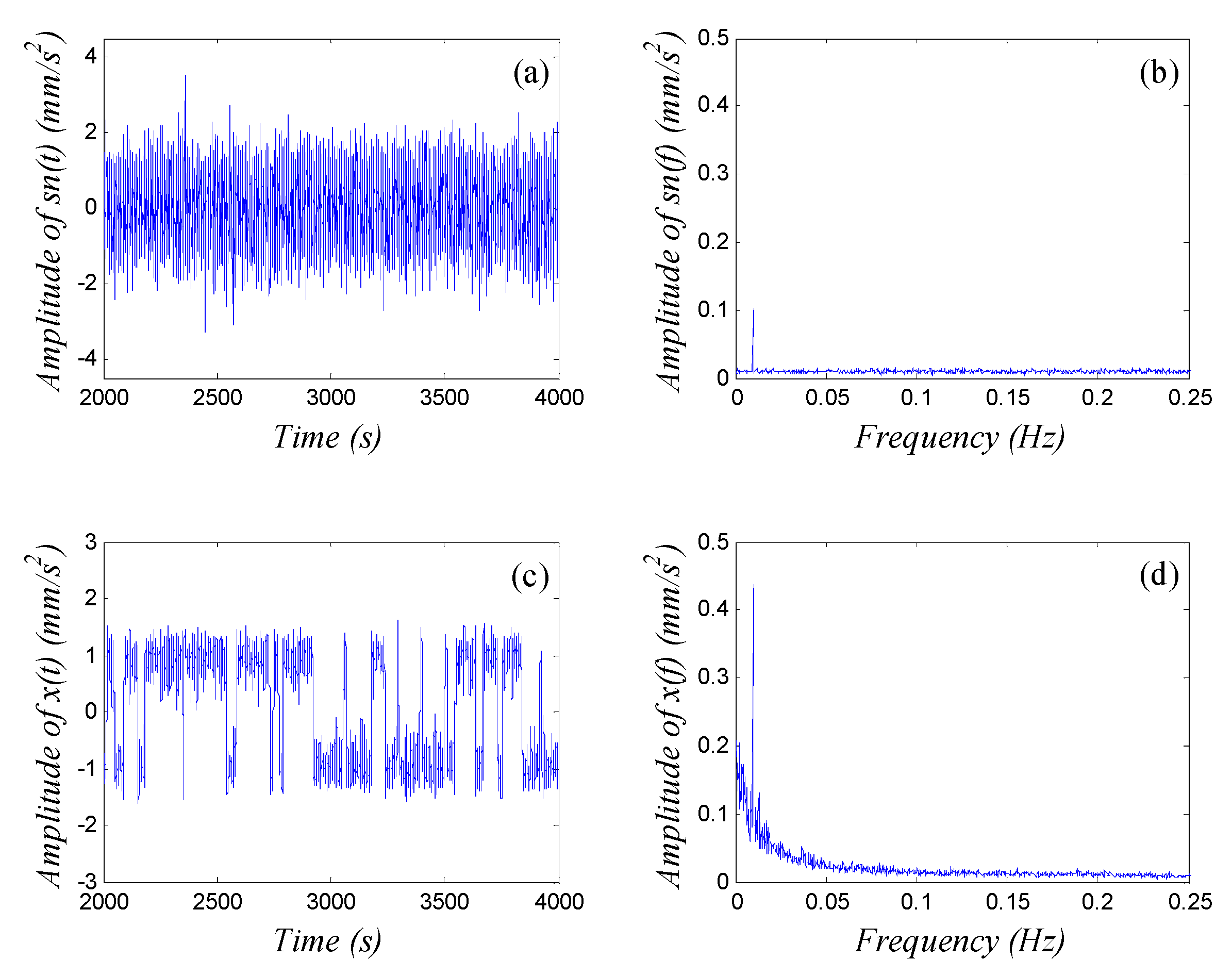
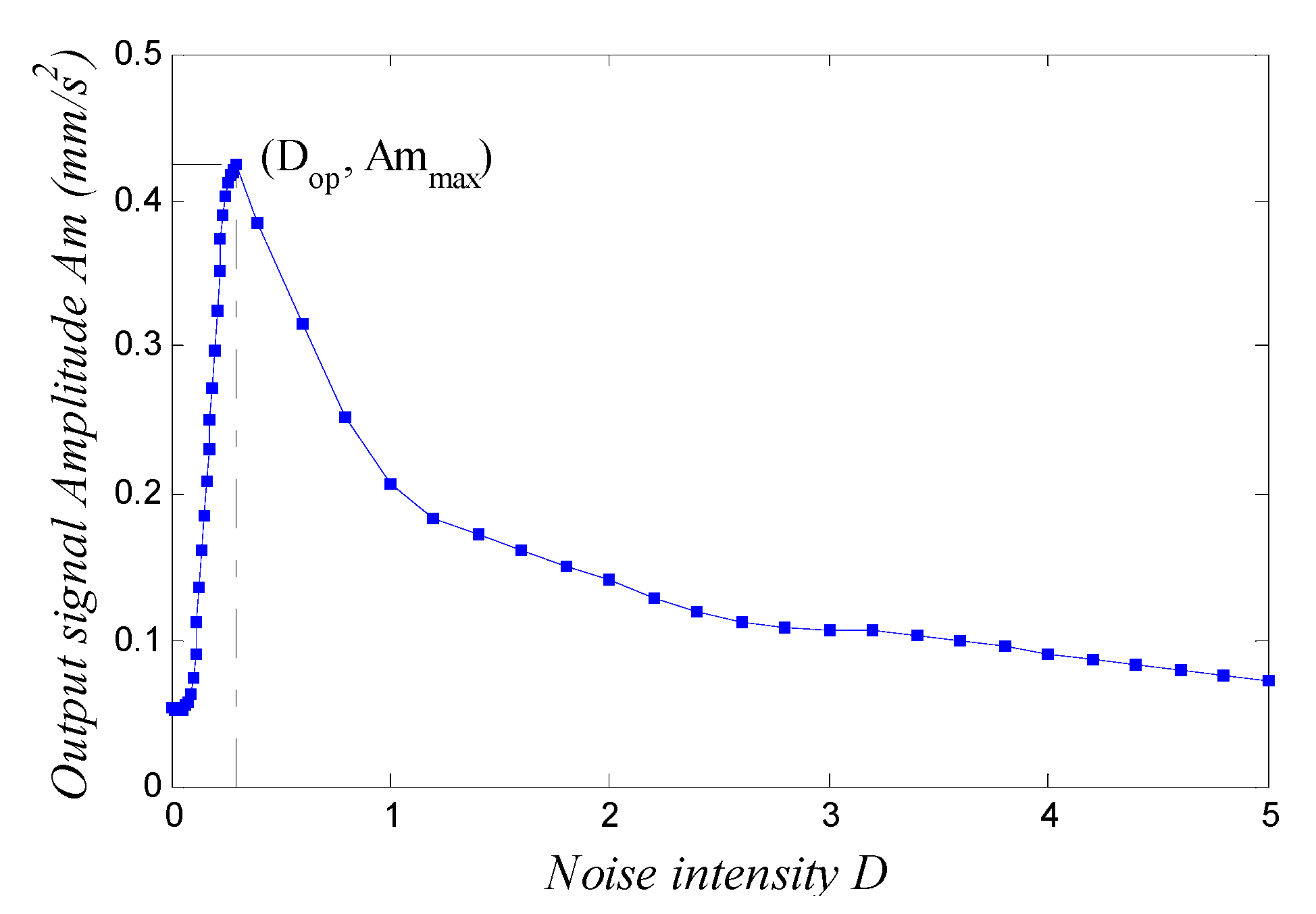
3. GPASR in a Duffing Oscillator Based on Kramers Rate
3.1. GPASR of a Duffing Oscillator
3.2. Parameters Analysis of a Duffing System Based on Kramers Rate
- (i)
- the value of is independent of ;
- (ii)
- is a monotone increasing Function of , , , and ;
- (iii)
- is a monotone decreasing Function of , and ;
- (iv)
- is a monotone increasing Function of when , and is a monotone decreasing Function of when .
3.3. GPASR in a Duffing Oscillator under Unmatched Signal Amplitude

3.4. GPASR in a Duffing Oscillator under Unmatched Signal Frequency
3.5. GPASR in a Diffing Oscillator under Unmatched Noise-Intensity
3.5.1. Adjustment of Damping Ratio k
3.5.2. Adjustment of System Parameter a
3.5.3. Adjustment of System Parameter b
3.5.4. Adjustment of Amplitude-Transformation Coefficient ε
3.5.5. Adjustment of Scale-Transformation Coefficient R
3.6. Conclusion of the GPASR Rules of a Duffing Oscillator
| k | a | b | ε | R | ||
|---|---|---|---|---|---|---|
| Large | Invalid | Invalid | Invalid | Decrease ε | Invalid | |
| Small | Invalid | Invalid | Invalid | Increase ε | Invalid | |
| f0 is a large-parameter | Invalid | Invalid | Invalid | Invalid | Adjust R to make satisfy the small-parameter limits | |
| Large | Increase k | Adjust a far from when | Decrease b | Decrease ε appropriately | Decrease R appropriately | |
| Small | Decrease k | Adjust a near when | Increase b | Increase ε appropriately | Increase R appropriately | |
4. Engineering Applications
4.1. Weak-signal Detection Method Based on GPASR of a Duffing Oscillator

4.2. Practical Examples
4.2.1. Diagnosis of a Rotor Shaft-Bending Fault
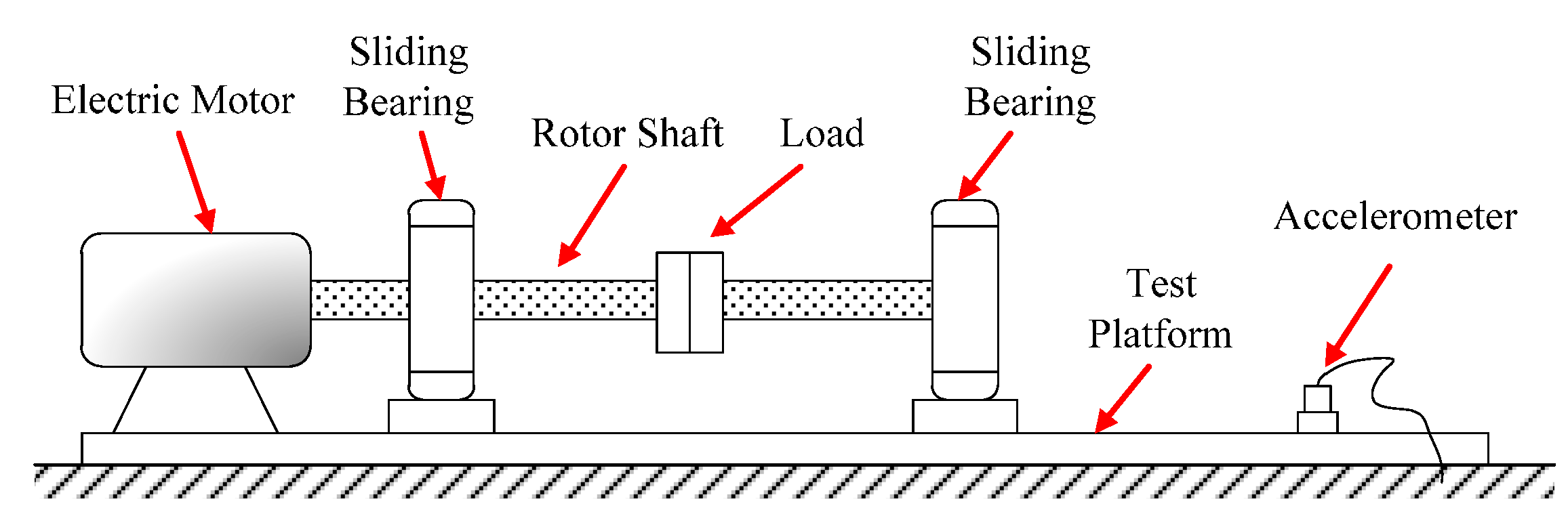

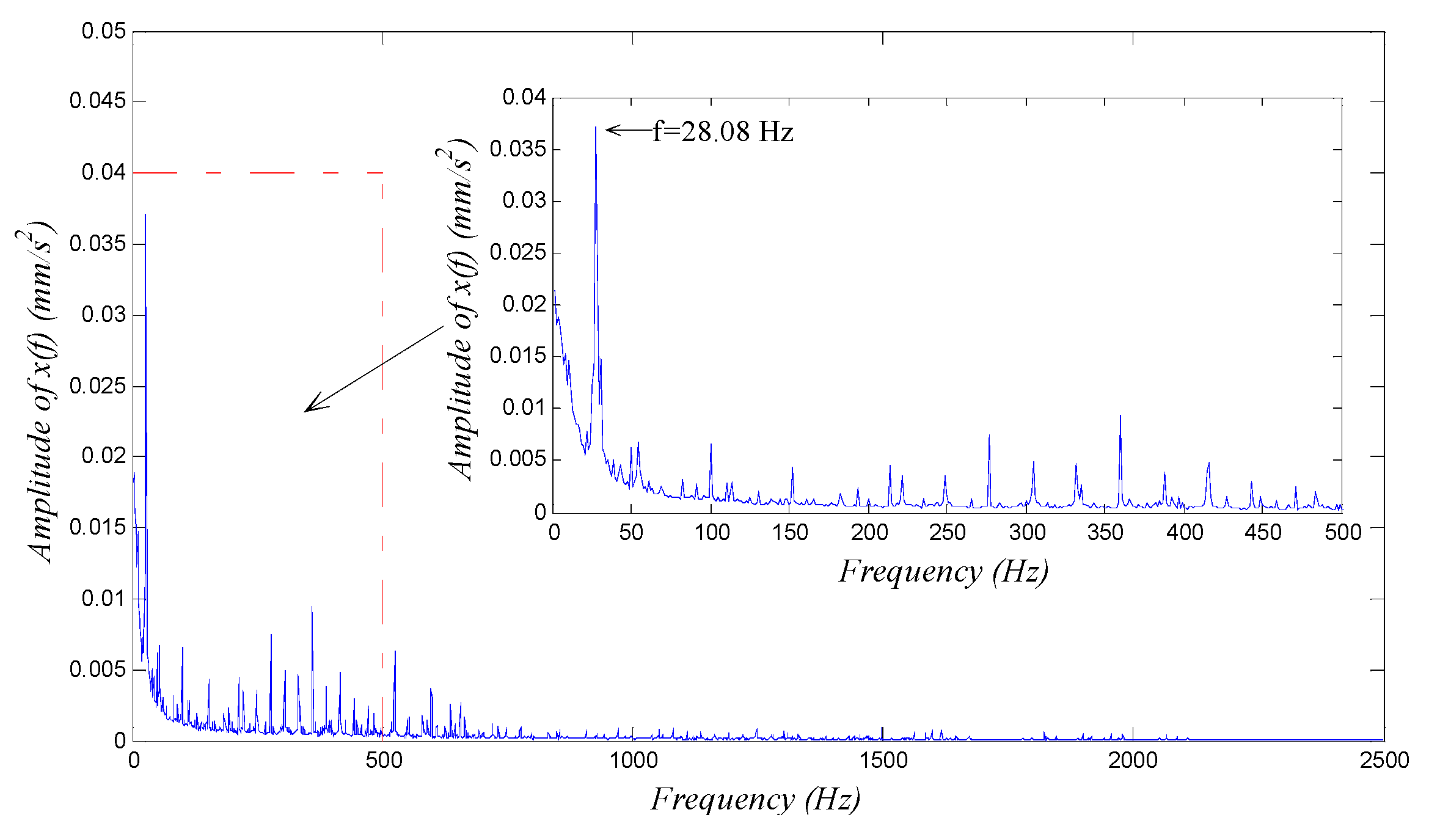
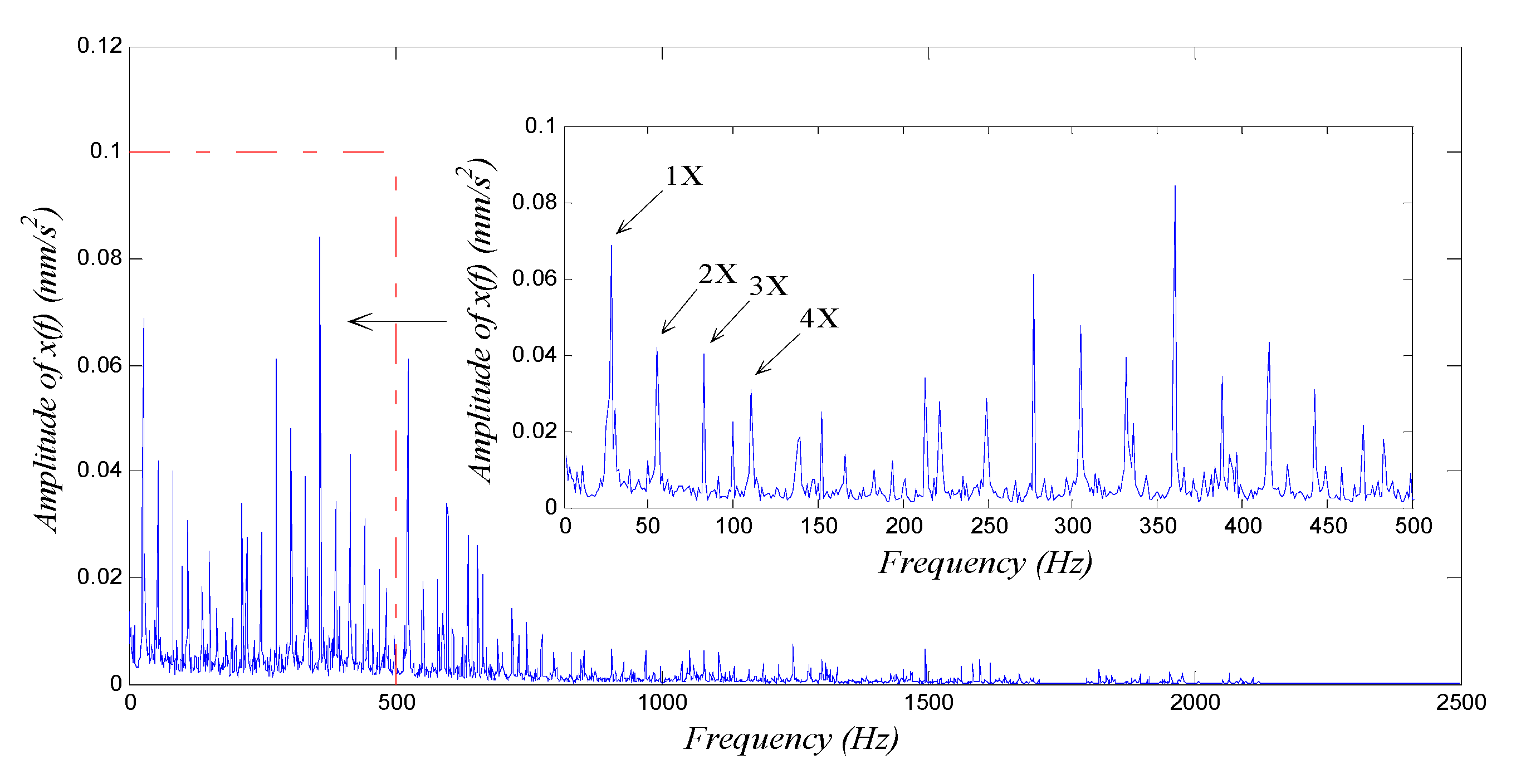
4.2.2. Diagnosis of a Rolling Bearing Outer Ring Fault

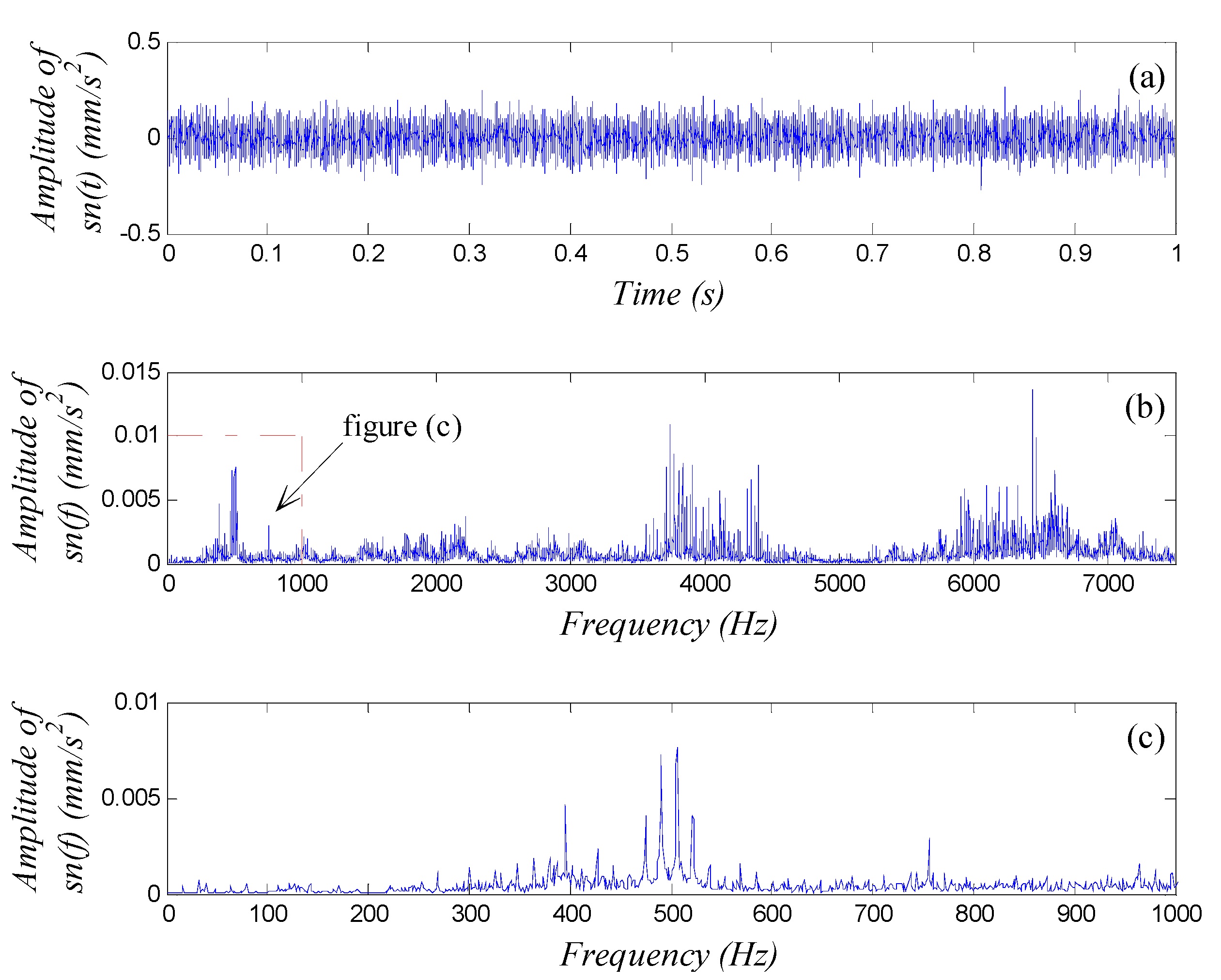
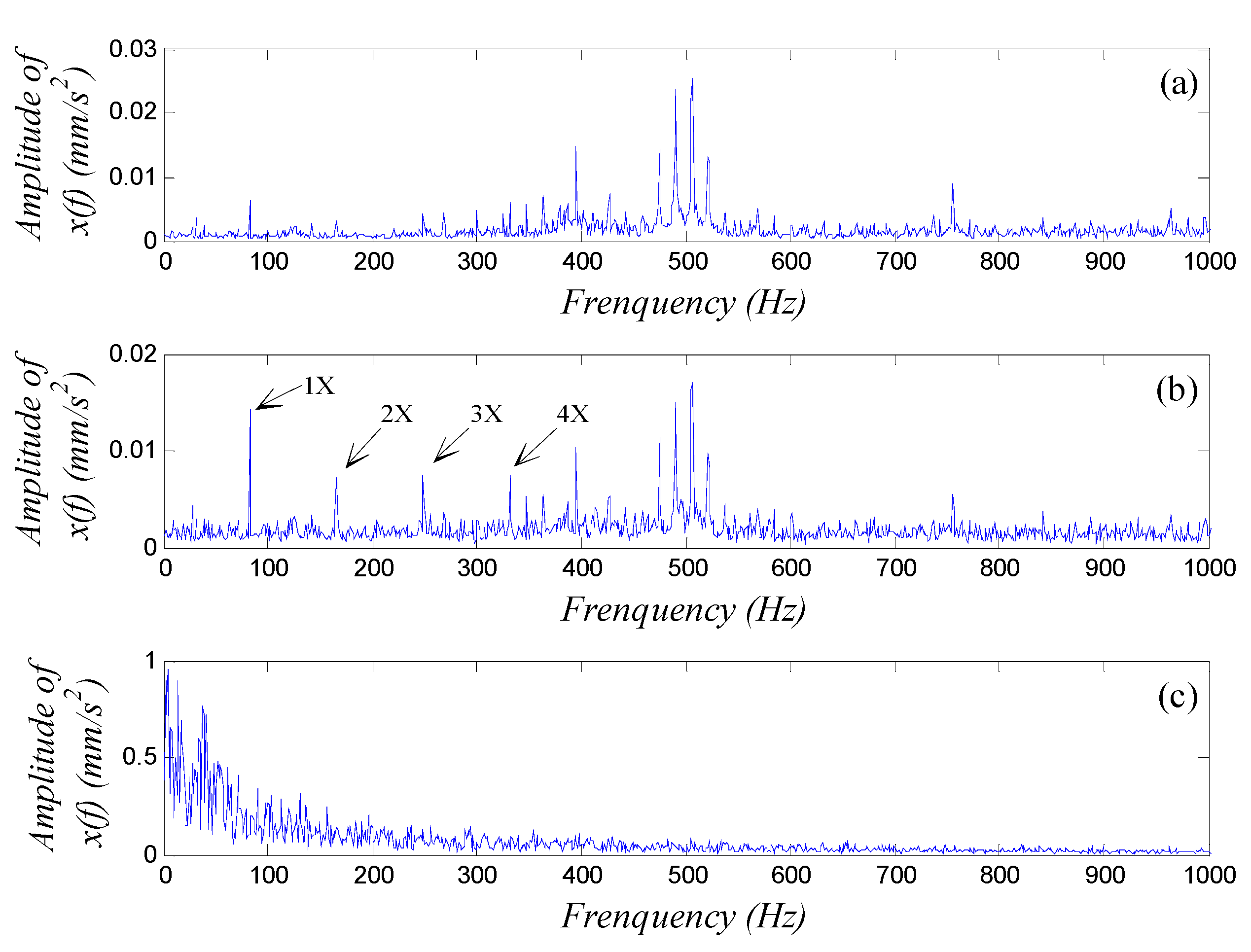
4.3. Discussion
5. Conclusions and Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benzi, R.; Sutera, A.; Vulpiana, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, 453–457. [Google Scholar] [CrossRef]
- Bensi, R.; Parisi, G.; Srutera, A. Stochastic resonance in climatic change. Tellus 1982, 34, 11–16. [Google Scholar]
- Nicolis, C. Stochastic aspects of climatic transitions—Response to a periodic forcing. Tellus 1982, 1, 1–9. [Google Scholar] [CrossRef]
- Fauve, S.; Heslot, F. Stochastic resonance in a bistable system. Phys. Lett. A 1983, 97, 5–7. [Google Scholar] [CrossRef]
- McNamara, B.; Wiesenfeld, K.; Roy, R. Observation of stochastic resonance in a ring laser. Phys. Rev. Lett. 1988, 60, 2626–2629. [Google Scholar] [CrossRef] [PubMed]
- Zheng, R.C.; Nakano, K.; Hu, H.G.; Su, D.X. An application of stochastic resonance for energy harvesting in a bistable vibrating system. J. Sound Vib. 2014, 333, 2568–2587. [Google Scholar] [CrossRef]
- Su, D.X.; Zheng, R.C.; Nakano, K; Cartmell, M.P. On square-wave-driven stochastic resonance for energy harvesting in a bistable system. AIP Adv. 2014, 4, 117140. [Google Scholar] [CrossRef]
- Gao, Y.J.; Leng, Y.G.; Fan, S.B.; Lai, Z.H. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet. Smart Mater. Struct. 2014, 23, 095003. [Google Scholar] [CrossRef]
- Leng, Y.G.; Gao, Y.J.; Tan, D.; Fan, S.B.; Lai, Z.H. An elastic-support model for enhanced bistable piezoelectric energy harvesting from random vibrations. J. Appl. Phys. 2015, 117, 064901. [Google Scholar] [CrossRef]
- Jung, P. Periodically driven stochastic systems. Phys. Rep. 1993, 234, 175–295. [Google Scholar] [CrossRef]
- Stokes, N.G.; Stein, N.D.; McClintock, P.V.E. Stochastic resonance in monostable systems. J. Phys. A Math. Gen. 1993, 26, 385–390. [Google Scholar] [CrossRef]
- Gomes, L.; Mirasso, C.R.; Toral, R.; Calvo, O. Stochastic resonance in monostable systems. Phys. A Stat. Mech. Appl. 2003, 327, 115–119. [Google Scholar] [CrossRef]
- Masoller, C. Noise-induced resonance in delayed feedback systems. Phys. Rev. Lett. 2002, 88, 034102. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.S.; Xu, G.H.; Liang, L.; Tao, T.F.; Gu, F.S. The recovery of weak impulsive signals based on stochastic resonance and moving least squares fitting. Sensors 2014, 14, 13692–13707. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.G.; Leng, Y.S.; Wang, T.Y.; Guo, Y. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Hakamata, Y.; Ohno, Y.; Maehashi, K. Enhancement of weak-signal response based on stochastic resonance in carbon nanotube field-effect transistors. J. Appl. Phys. 2010, 108, 104313. [Google Scholar] [CrossRef]
- Duan, F.B.; Chapeau-Blondeau, F.; Abbott, D. Fish-information condition for enhanced signal detection via stochastic resonance. Phys. Rev. E 2011, 84, 051107. [Google Scholar] [CrossRef]
- Klamecki, B.E. Use of stochastic resonance for enhancement of low-level vibration signal components. Mech. Syst. Signal Process. 2005, 19, 223–237. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Marchesoni, F.; Menichella-Saetta, E.; Santucci, S. Stochastic resonance in bistable systems. Phys. Rev. Lett. 1989, 62, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Gammaitoni, L.; Menichella-Saetta, E.; Santucci, S.; Marchesoni, F.; Presilla, C. Periodically time-modulated bistable systems: Stochastic resonance. Phys. Rev. A 1989, 40, 2114–2119. [Google Scholar] [CrossRef] [PubMed]
- Jung, P.; Hänggi, P. Resonantly driven Brownian motion: Basic concepts and exact results. Phys. Rev. A 1990, 41, 2977–2988. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.M.; Xu, J.X.; Xie, Y. Observing stochastic resonance in an underdamped bistable Duffing oscillator by the method of moments. Phys. Rev. E 2003, 68, 036123. [Google Scholar] [CrossRef]
- Wang, F.Z.; Chen, W.S.; Qin, G.R.; Guo, D.Y.; Liu, J.L. Experimental analysis of stochastic resonance in a Duffing system. Chin. Phys. Lett. 2003, 20, 27–30. [Google Scholar]
- Leng, Y.G.; Lai, Z.H.; Fan, S.B.; Gao, Y.J. Large parameter stochastic resonance of two-dimensional Duffing oscillator and its application on weak signal detection. Acta Phys. Sin. 2012, 61, 230502. [Google Scholar]
- Lai, Z.H.; Leng, Y.G.; Fan, S.B. Stochastic resonance of cascaded bistable Duffing oscillator. Acta Phys. Sin. 2013, 62, 070503. [Google Scholar]
- Xu, B.H.; Duan, F.B.; Bao, R.H.; Li, J.L. Stochastic resonance with tuning system parameters: the application of bistable systems in signal processing. Chaos Soliton Fract. 2002, 13, 633–644. [Google Scholar] [CrossRef]
- Leng, Y.G. Mechanism of parameter-adjusted stochastic resonance based on Kramers rate. Acta Phys. Sin. 2009, 58, 5196–5200. [Google Scholar]
- Duan, F.B.; Chapeau-Blondeau, F.; Abbott, D. Weak signal detection: condition for noise induced enhancement. Digit. Signal Process. 2013, 23, 1585–1591. [Google Scholar] [CrossRef]
- Alfonsi, L.; Gammaitoni, L.; Santucci, S.; Bulsara, A.R. Intrawell stochastic resonance versus interwell stochastic resonance in underdamped bistable systems. Phys. Rev. E 2000, 62, 299–302. [Google Scholar] [CrossRef]
- Wu, X.J.; Guo, W.M.; Cai, W.S.; Shao, X.G.; Pan, Z.X. A method based on stochastic resonance for the detection of weak analytical signal. Talanta 2003, 61, 863–869. [Google Scholar] [CrossRef]
- Leng, Y.G.; Lai, Z.H. Generalized parameter-adjusted stochastic resonance of Duffing oscillator based on Kramers rate. Acta Phys. Sin. 2014, 63, 020502. [Google Scholar]
- Holmes, P. A nonlinear oscillator with a strange attractor. Philos. Trans. R. Soc. Lond. Seri. A 1979, 292, 419–448. [Google Scholar] [CrossRef]
- Leng, Y.G. Mechanism of high frequency resonance of parameter-adjusted bistable system. Acta Phys. Sin. 2011, 61, 020503. [Google Scholar]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Hu, G. Stochastic Forces and Nonlinear System; Shanghai Science & Technology Education Press: Shanghai, China, 1994. [Google Scholar]
- Jason, R.; Ronald, G.; Thomas, G. An amplitude modulation detector for fault diagnosis in rolling element bearings. IEEE Trans. Ind. Electron. 2004, 51, 1097–1102. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Z.-H.; Leng, Y.-G. Generalized Parameter-Adjusted Stochastic Resonance of Duffing Oscillator and Its Application to Weak-Signal Detection. Sensors 2015, 15, 21327-21349. https://doi.org/10.3390/s150921327
Lai Z-H, Leng Y-G. Generalized Parameter-Adjusted Stochastic Resonance of Duffing Oscillator and Its Application to Weak-Signal Detection. Sensors. 2015; 15(9):21327-21349. https://doi.org/10.3390/s150921327
Chicago/Turabian StyleLai, Zhi-Hui, and Yong-Gang Leng. 2015. "Generalized Parameter-Adjusted Stochastic Resonance of Duffing Oscillator and Its Application to Weak-Signal Detection" Sensors 15, no. 9: 21327-21349. https://doi.org/10.3390/s150921327
APA StyleLai, Z.-H., & Leng, Y.-G. (2015). Generalized Parameter-Adjusted Stochastic Resonance of Duffing Oscillator and Its Application to Weak-Signal Detection. Sensors, 15(9), 21327-21349. https://doi.org/10.3390/s150921327





