A Novel Permanent Magnetic Angular Acceleration Sensor
Abstract
:1. Introduction
2. Mechanical Structure of the Sensor

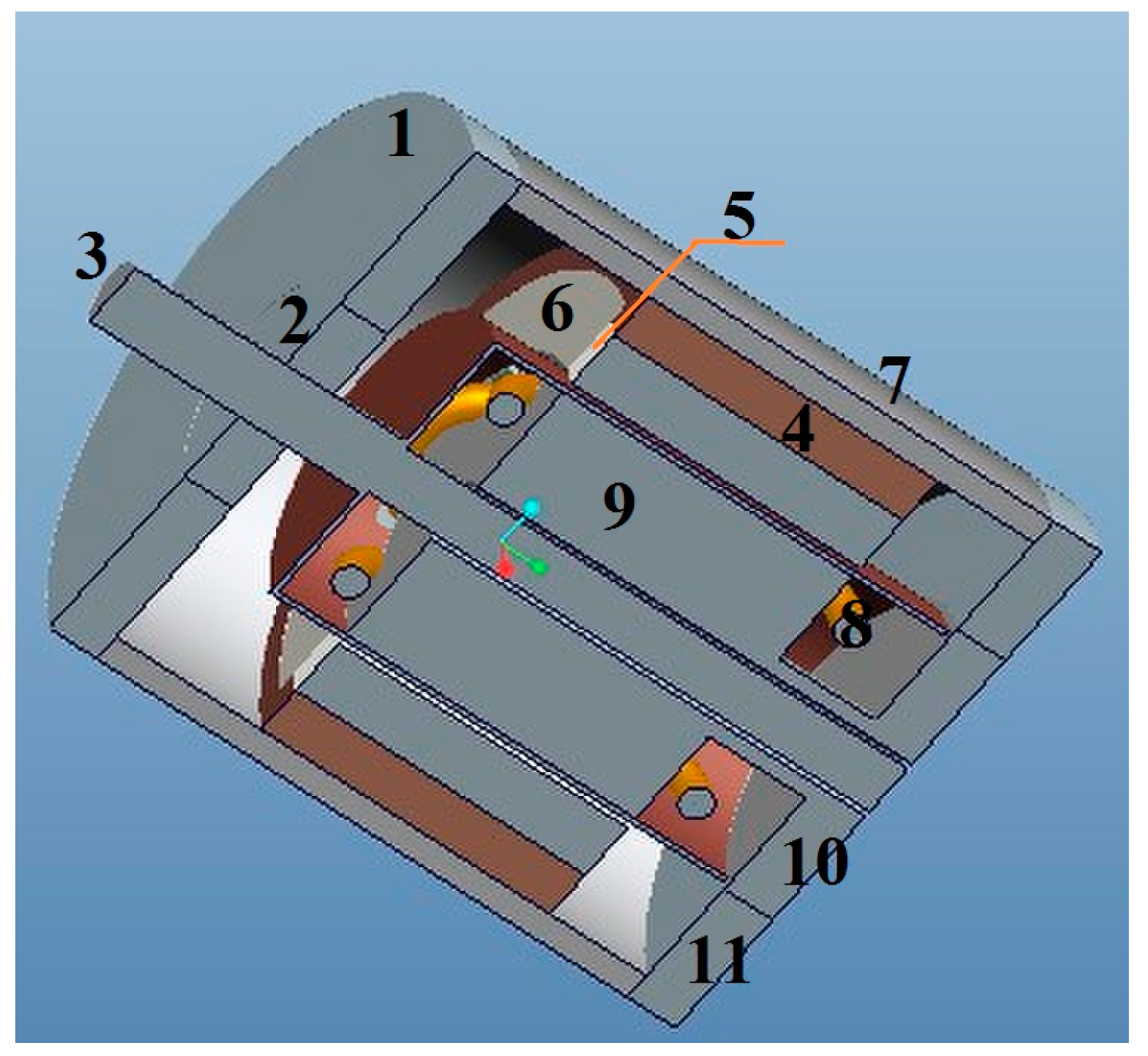
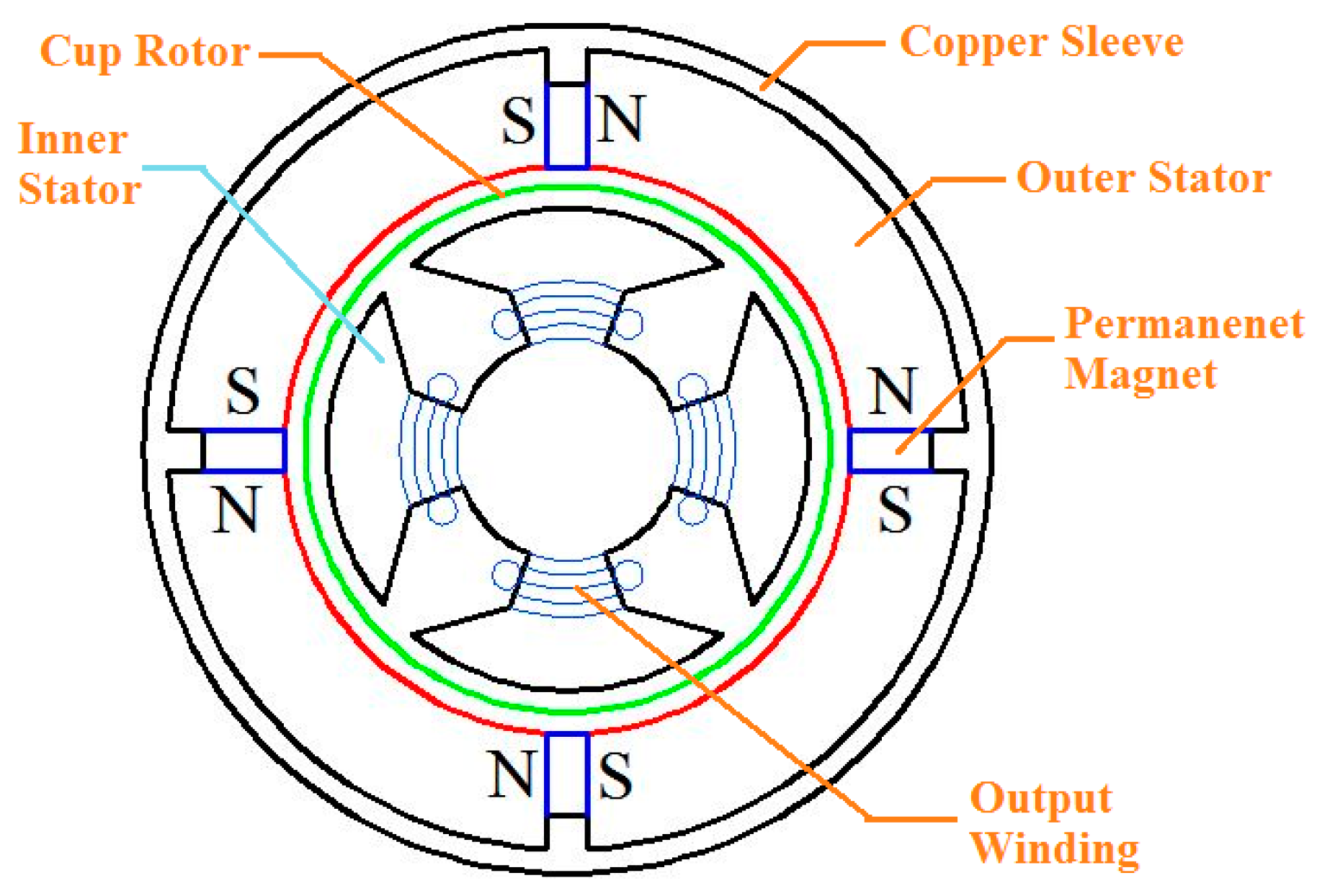

3. Operating Principle of the Sensor
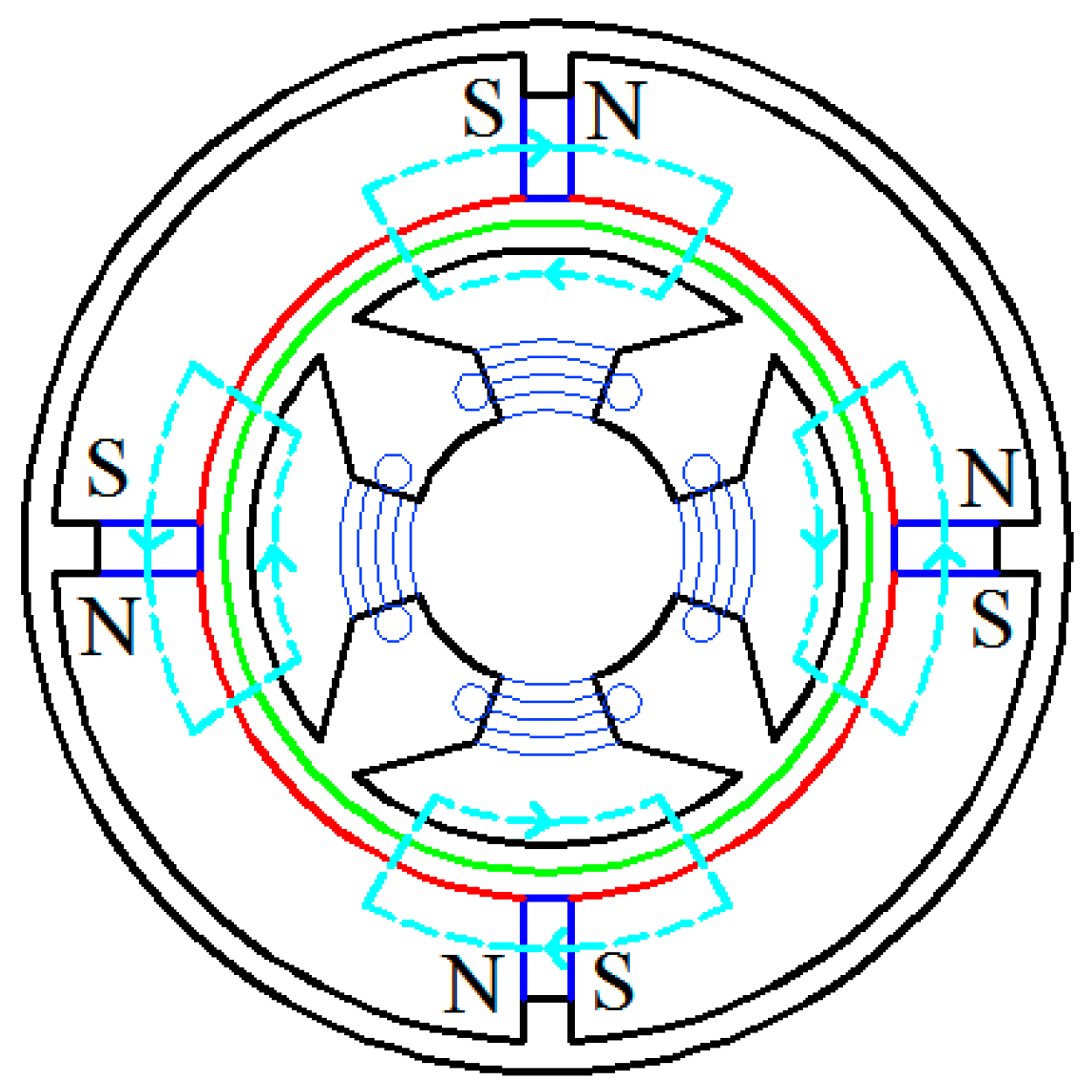
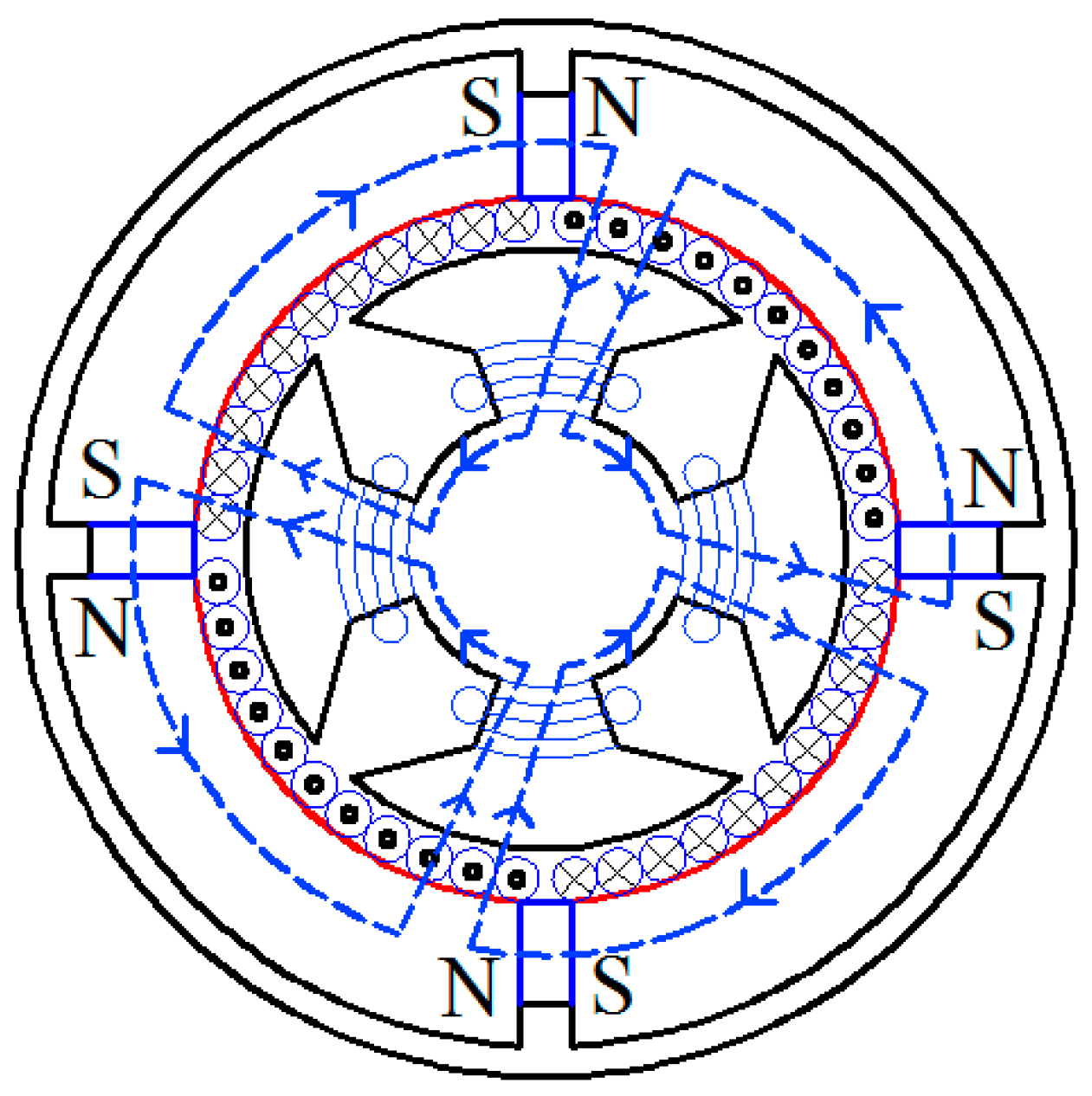
4. FEM Modeling and Simulation of the Sensor
| Component | Material | Inner Diameter | Outer Diameter | Thickness |
|---|---|---|---|---|
| copper sleeve | Brasses | 30 mm | 35 mm | 5 mm |
| permanent magnet | XG240/46 | 22 mm | 28 mm | 4 mm |
| Outer stator | DW540_50 | 22 mm | 30 mm | |
| Cup-shaped rotor | silicon manganese bronze | 21 mm | 21.5 mm | 0.5 mm |
| Inner stator | DW540_50 | 10 mm | 20.5 mm | |
| Output winding | Copper-75C | 5 mm |
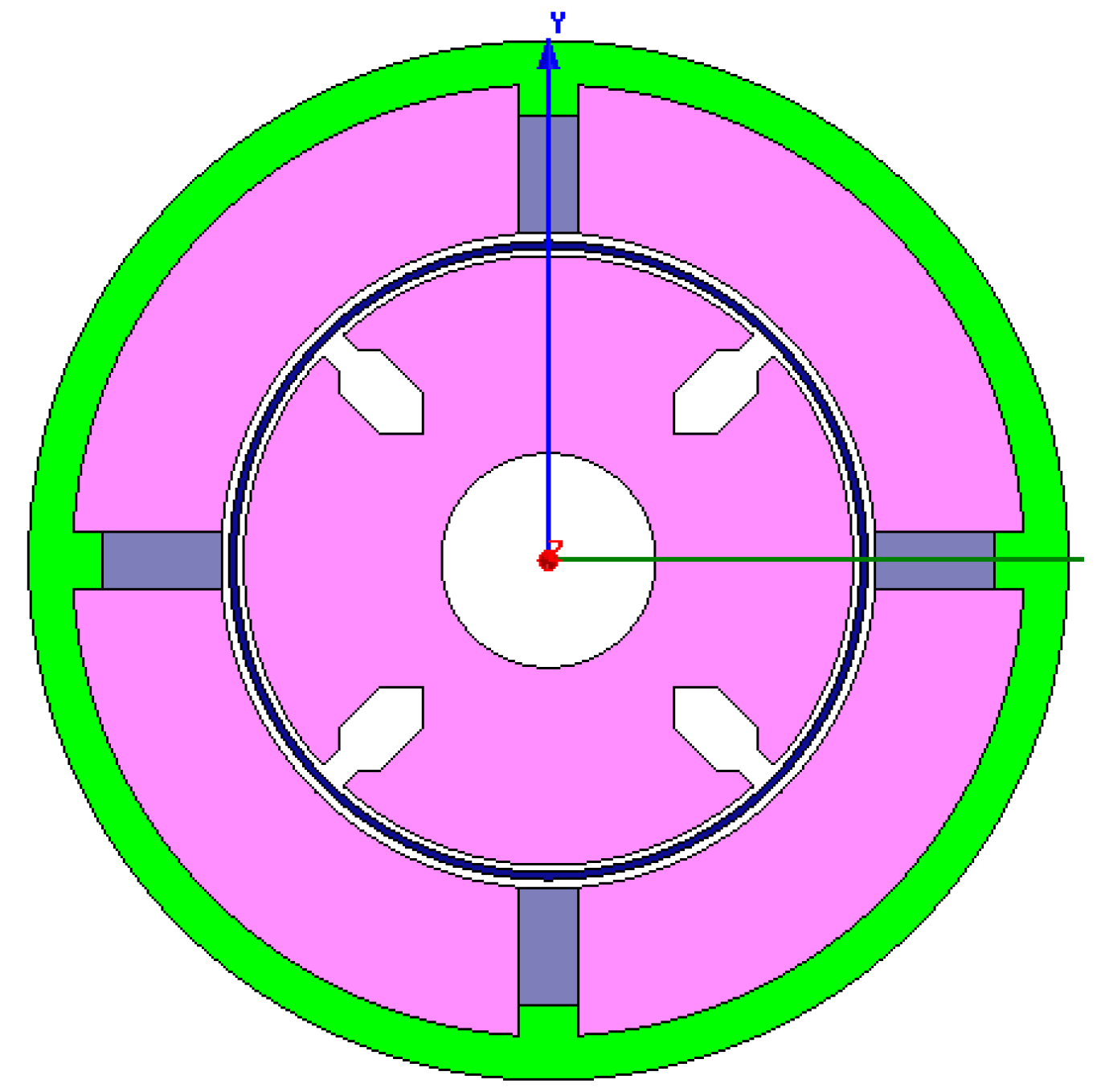
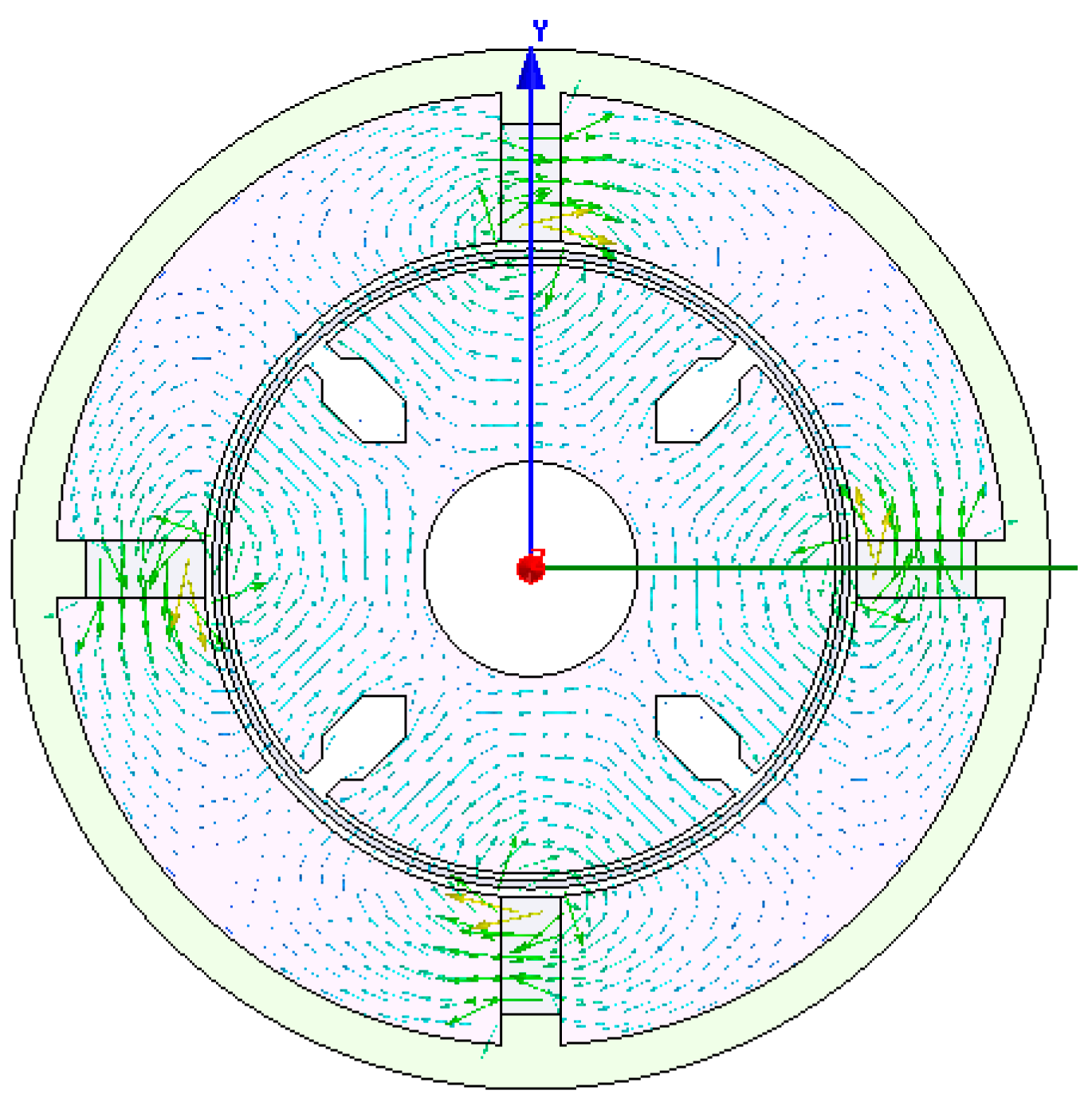
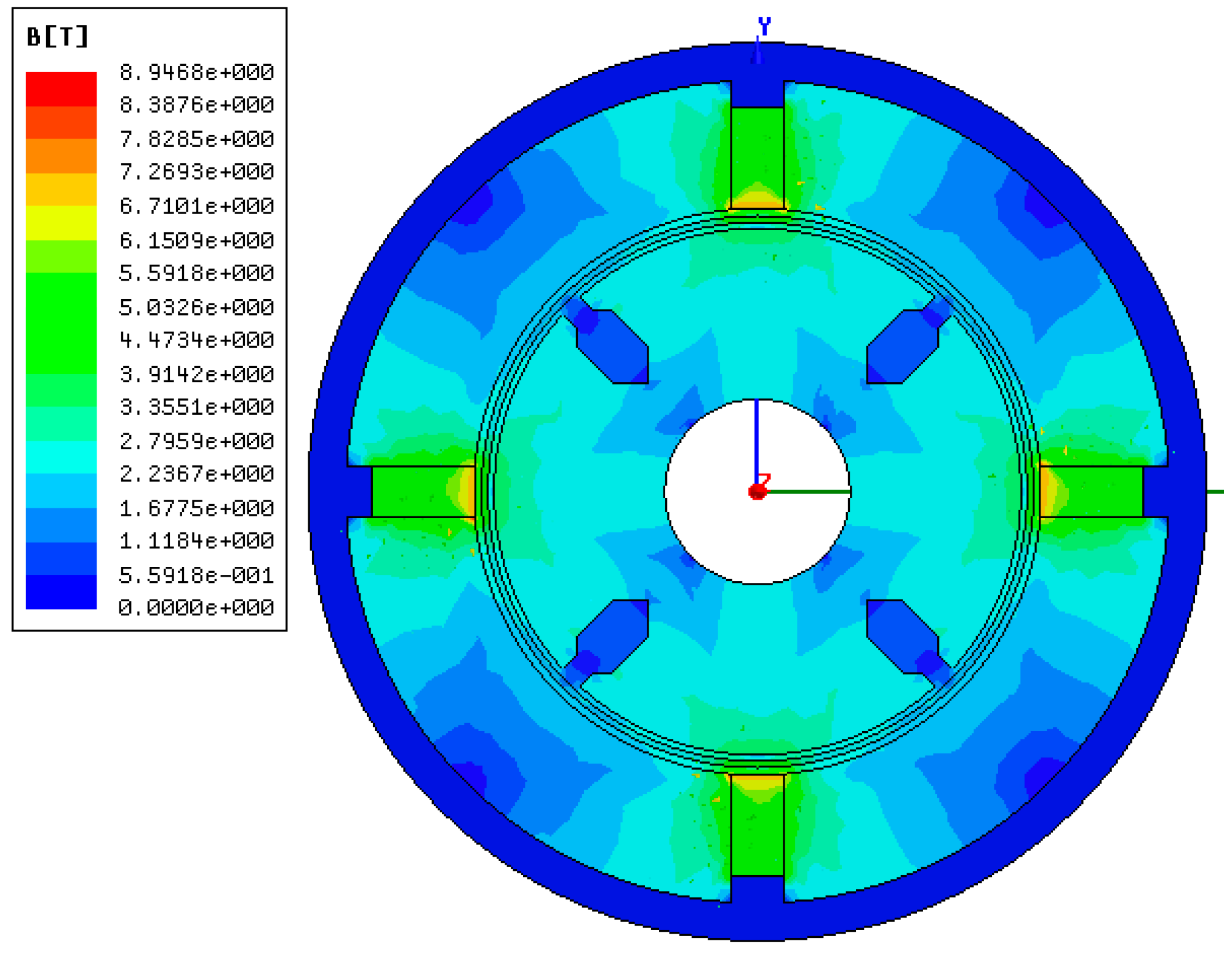
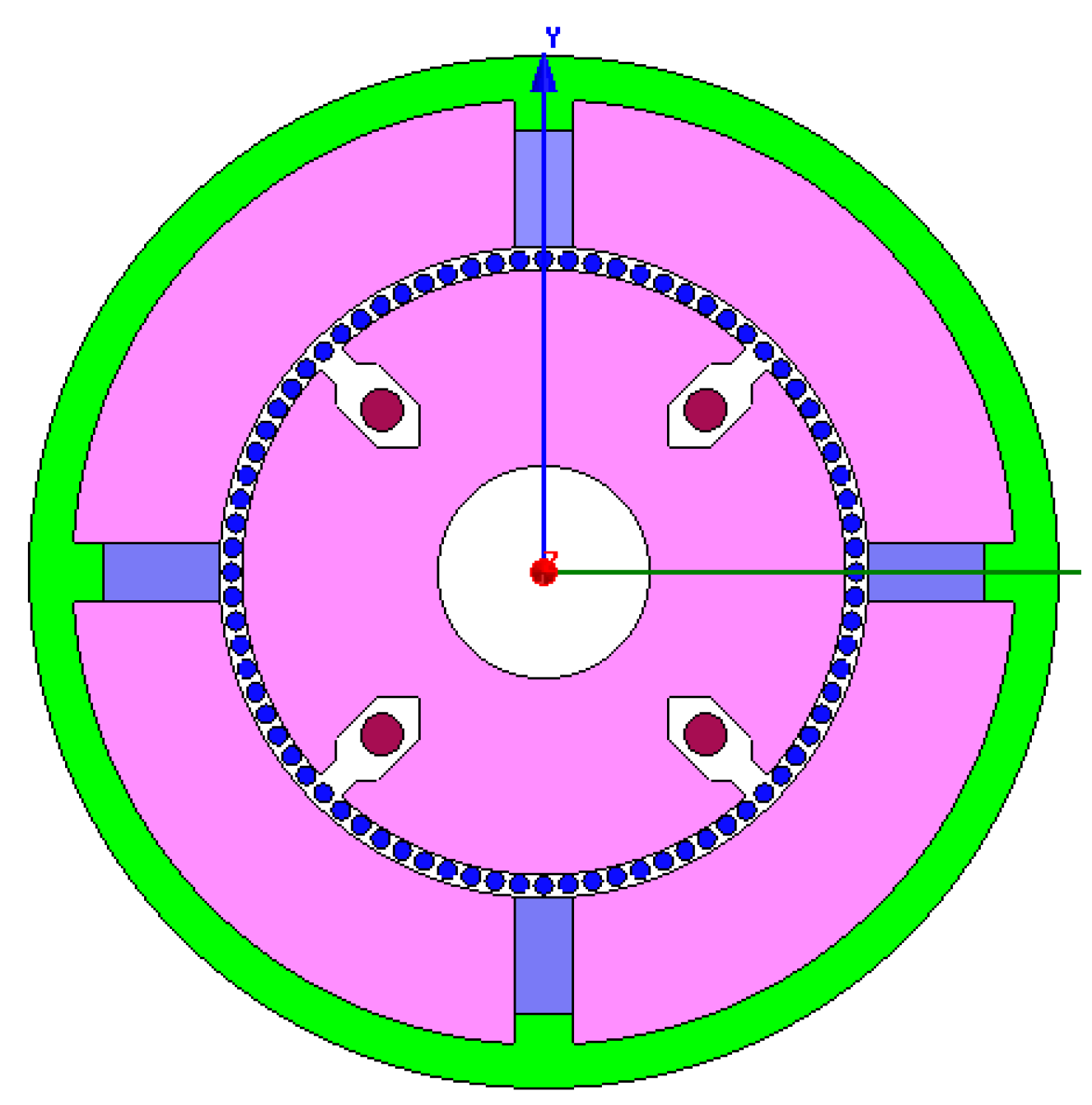
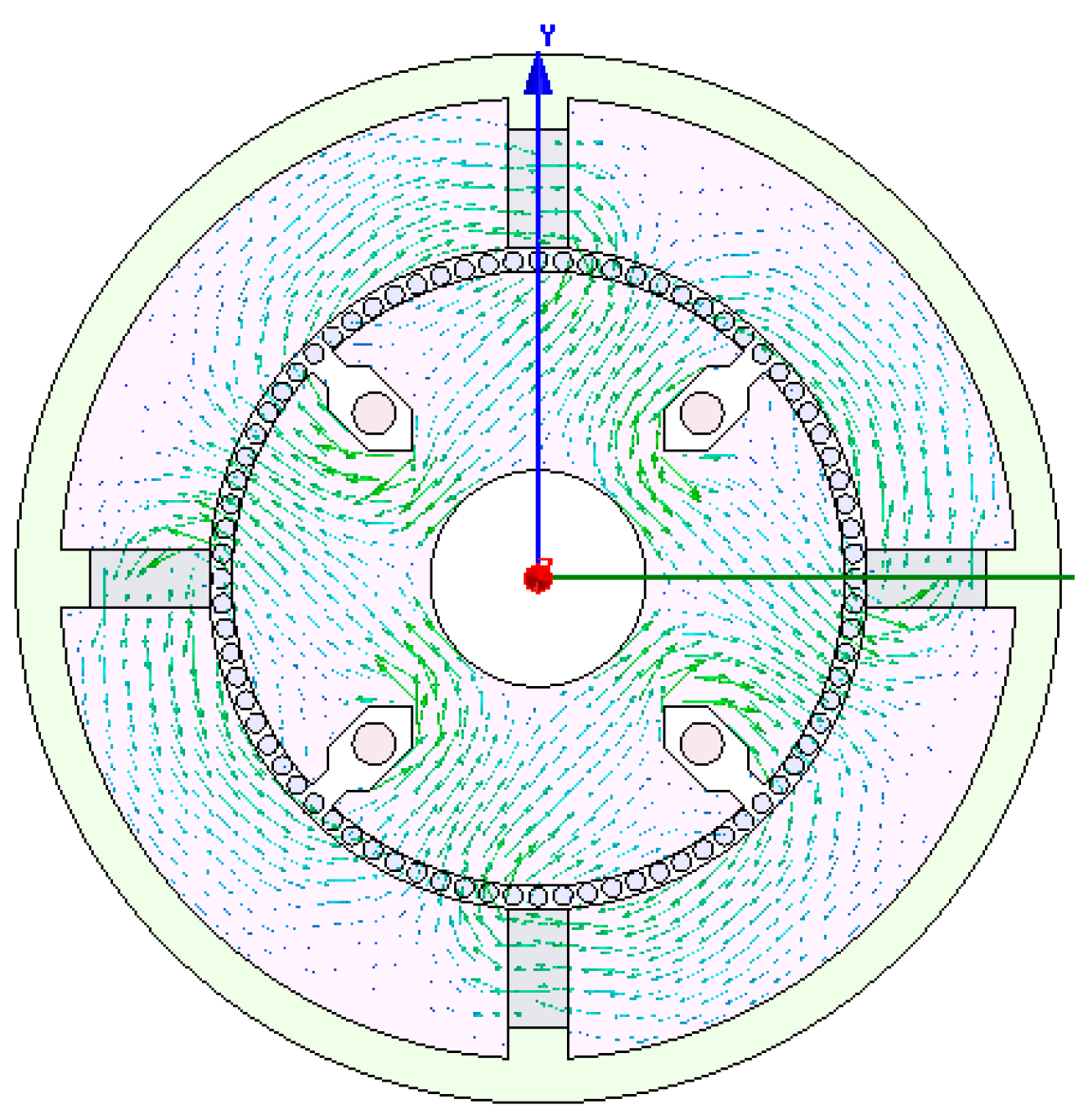

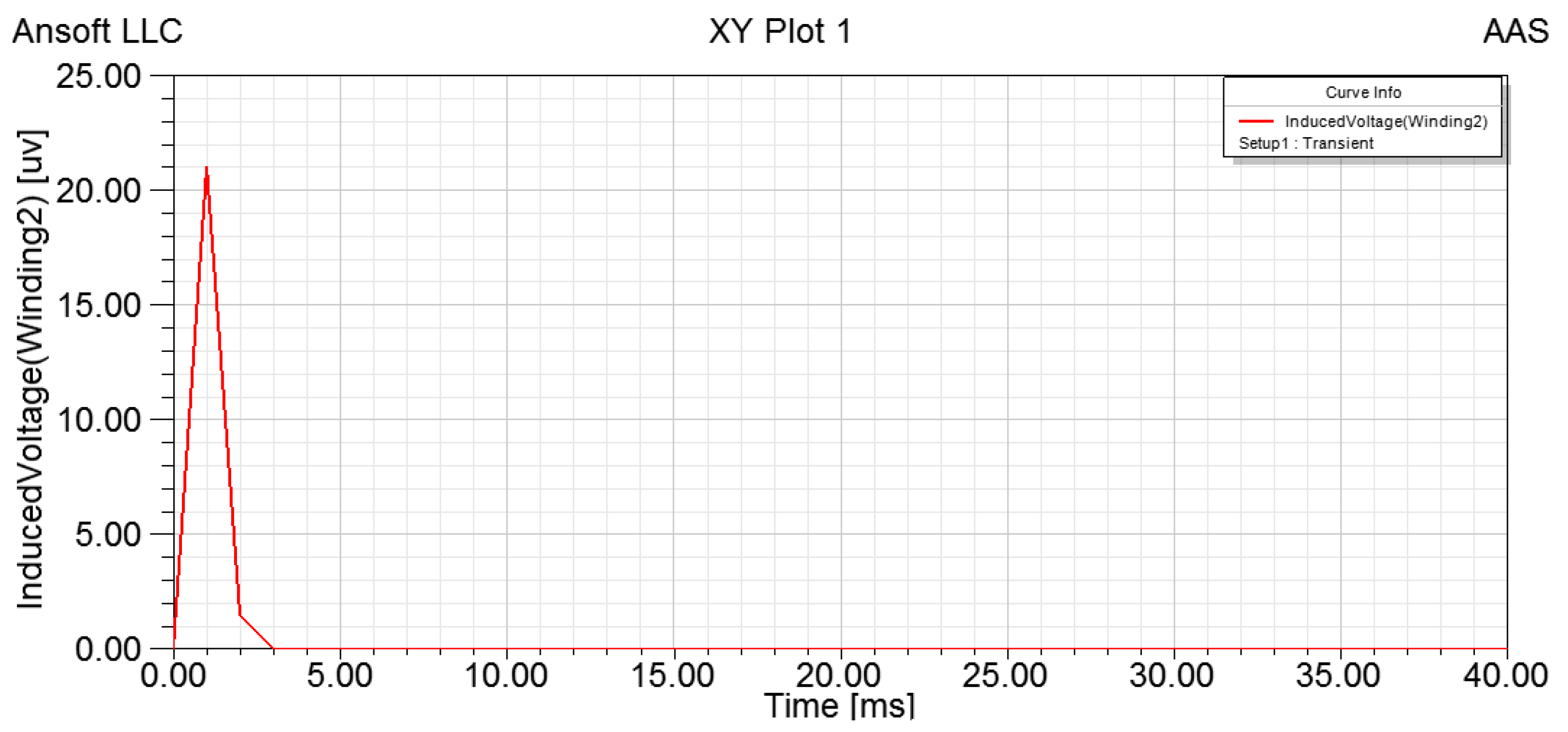
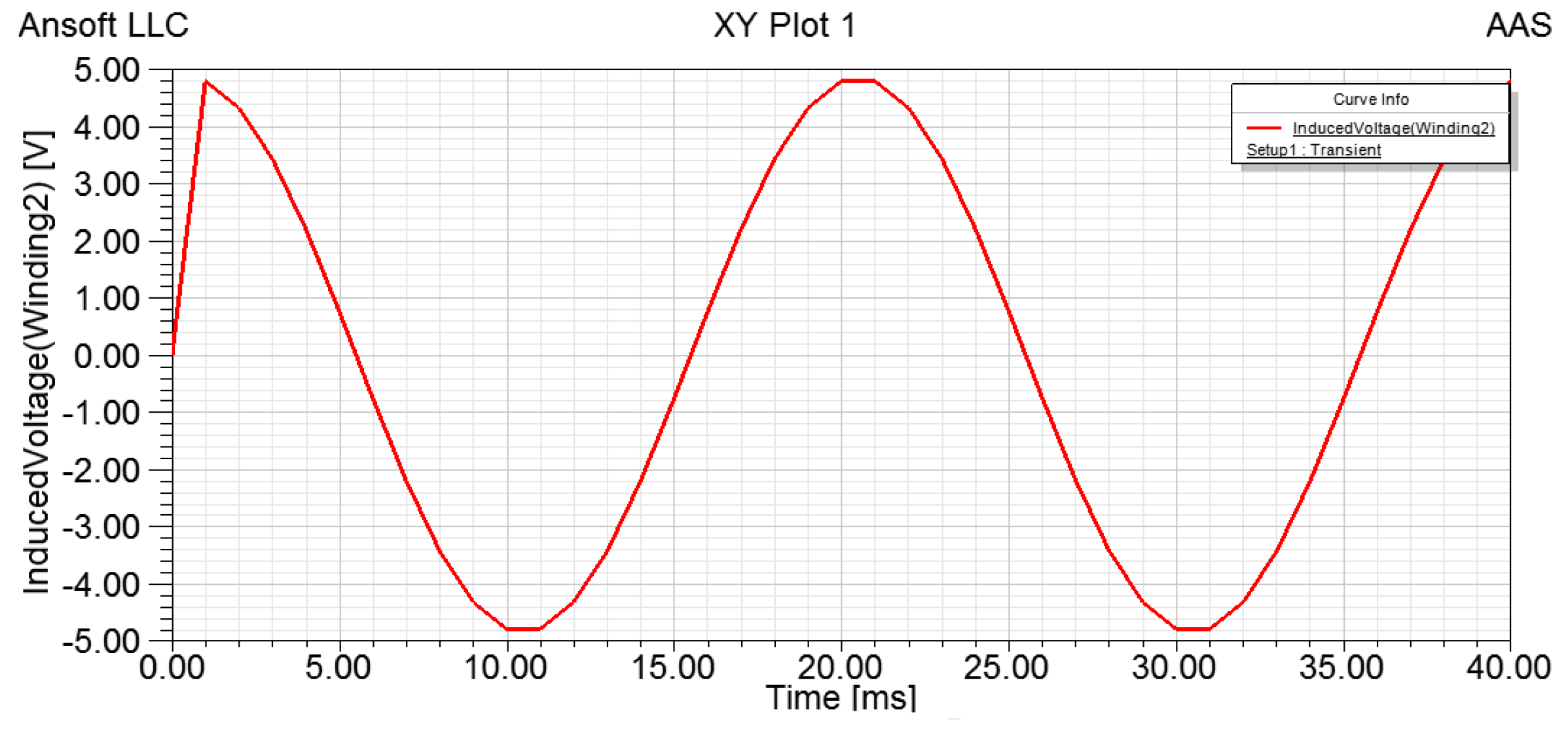
5. Calibration and Angular Acceleration Testing Experiments
5.1. The Composition and Principle of the Calibration Equipment

5.2. The Calibration Experiment Results
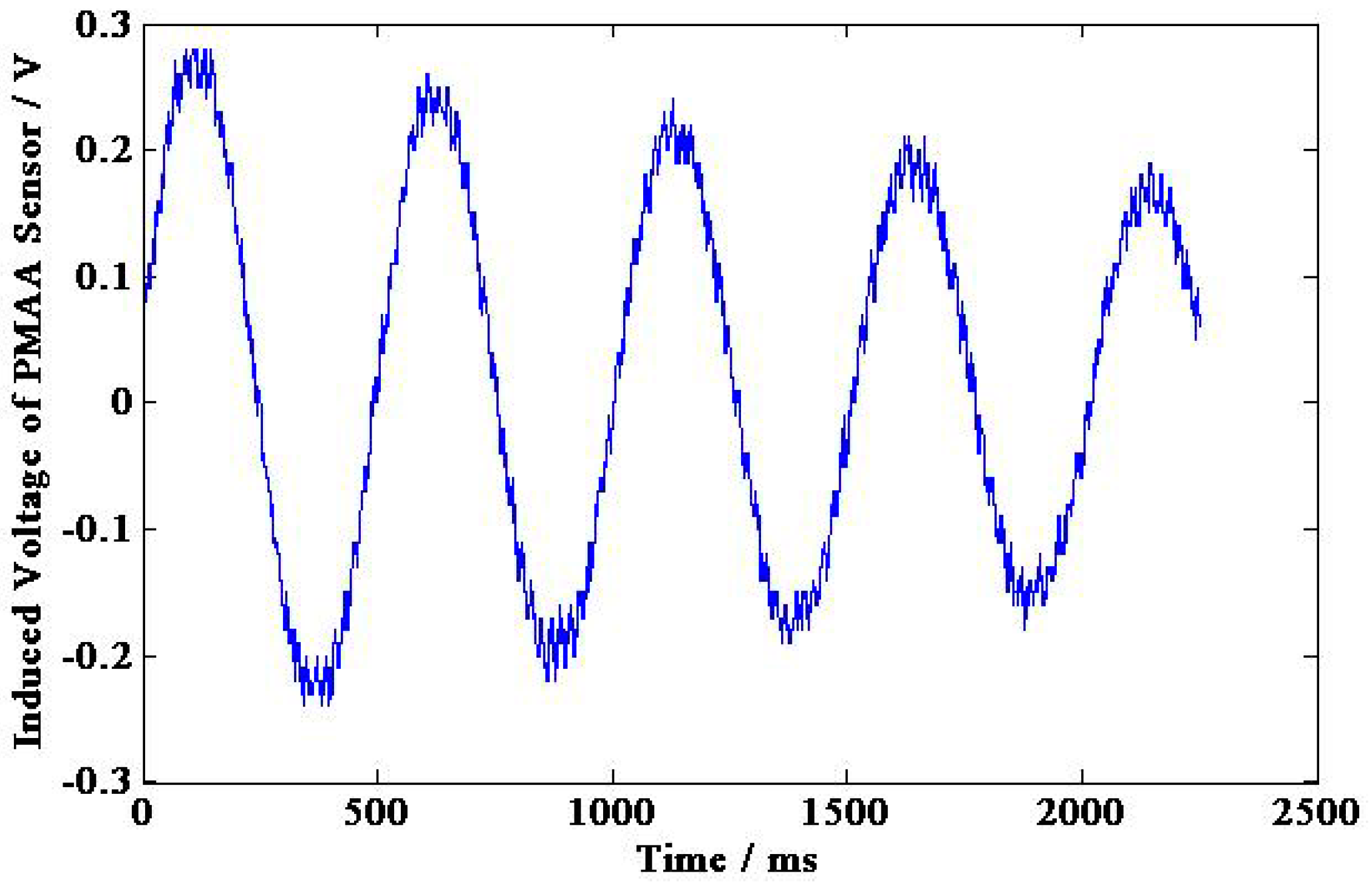
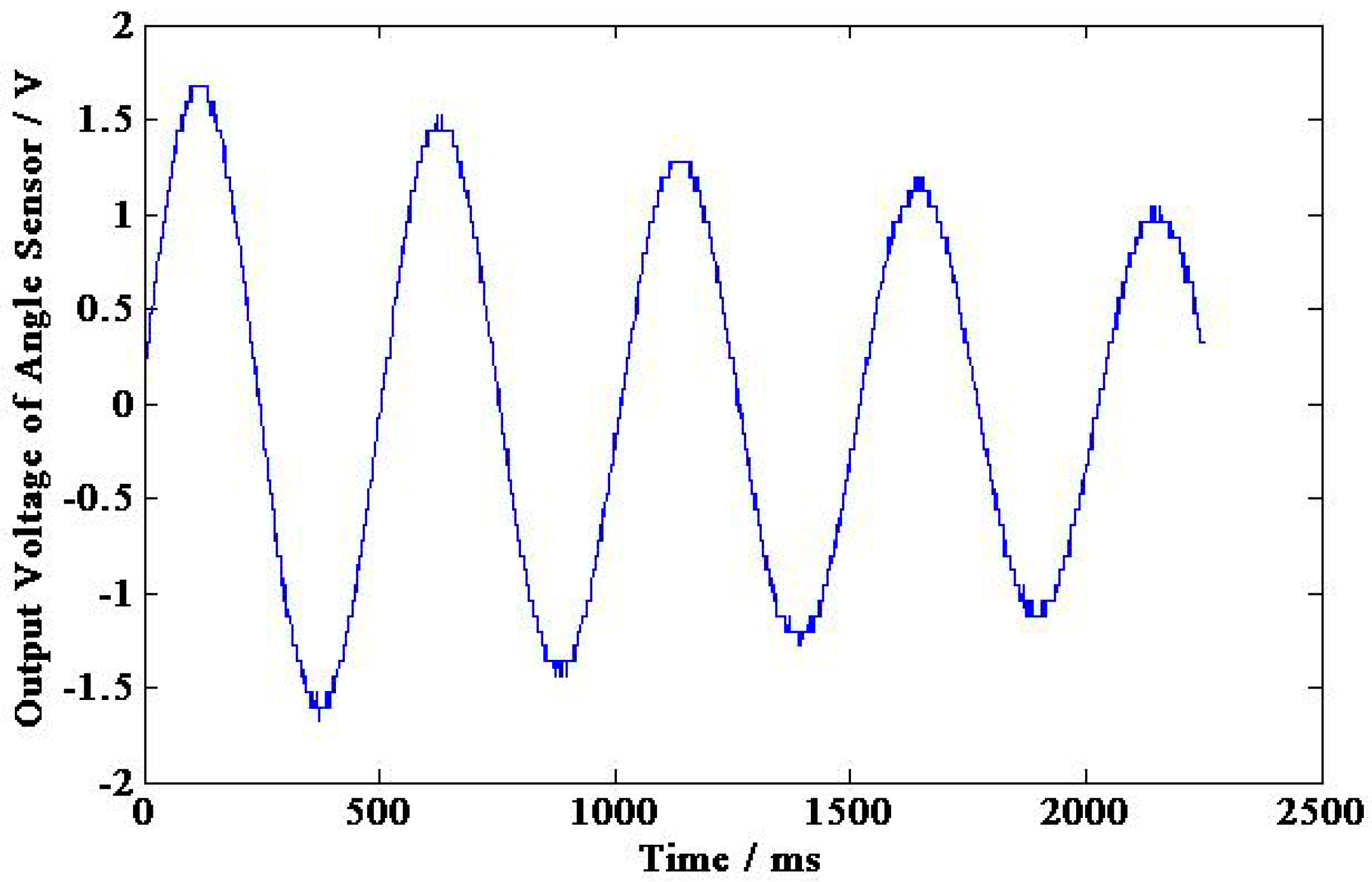
| The peak voltage of the PMAA sensor (V) | 0.28 | 0.25 | 0.22 | 0.20 | 0.17 |
| The peak voltage of angle sensor (V) | 1.68 | 1.44 | 1.28 | 1.12 | 1.04 |
| The time corresponding peak (s) | 0.11 | 0.60 | 1.13 | 1.65 | 2.14 |
| Oscillation period t/(s) | (0.49 + 0.53 + 0.52 + 0.49)/4 = 0.5075 | ||||
| Angle values (rad) | 2.11 | 1.809 | 1.608 | 1.407 | 1.307 |
| System damping ratio coefficient β | (ln(2.11 ÷ 1.307)) ÷ 4 ÷ 0.5075 = 0.2359 | ||||
| Angular acceleration value (rad/s2) | 322.4 | 276.4 | 245.7 | 215 | 199.7 |
| Sensitivity coefficient (mV/(rad/s2)) | 0.87 | 0.90 | 0.89 | 0.93 | 0.85 |
5.3. Single-Phase Asynchronous Motor Angular Acceleration Testing

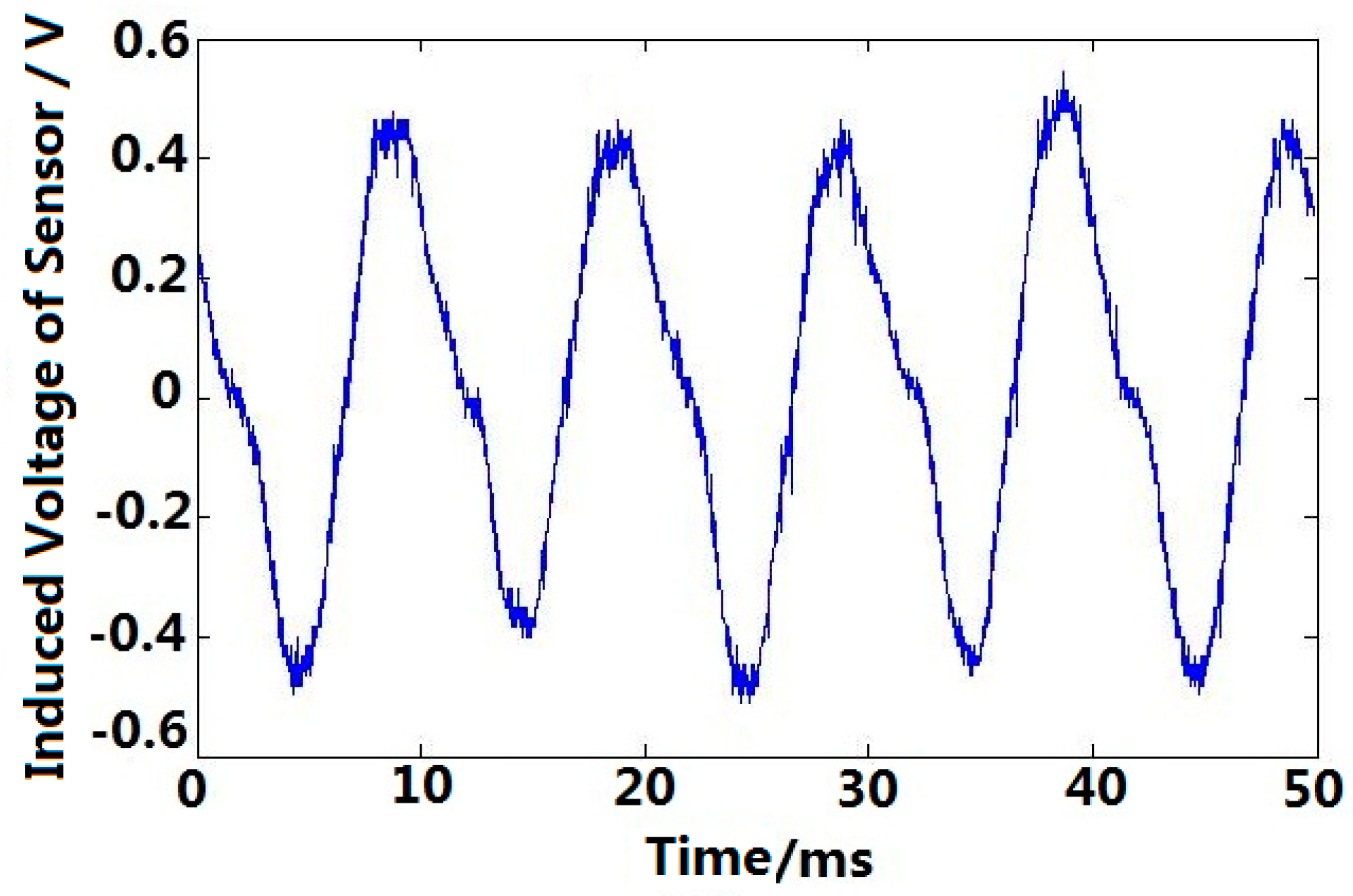
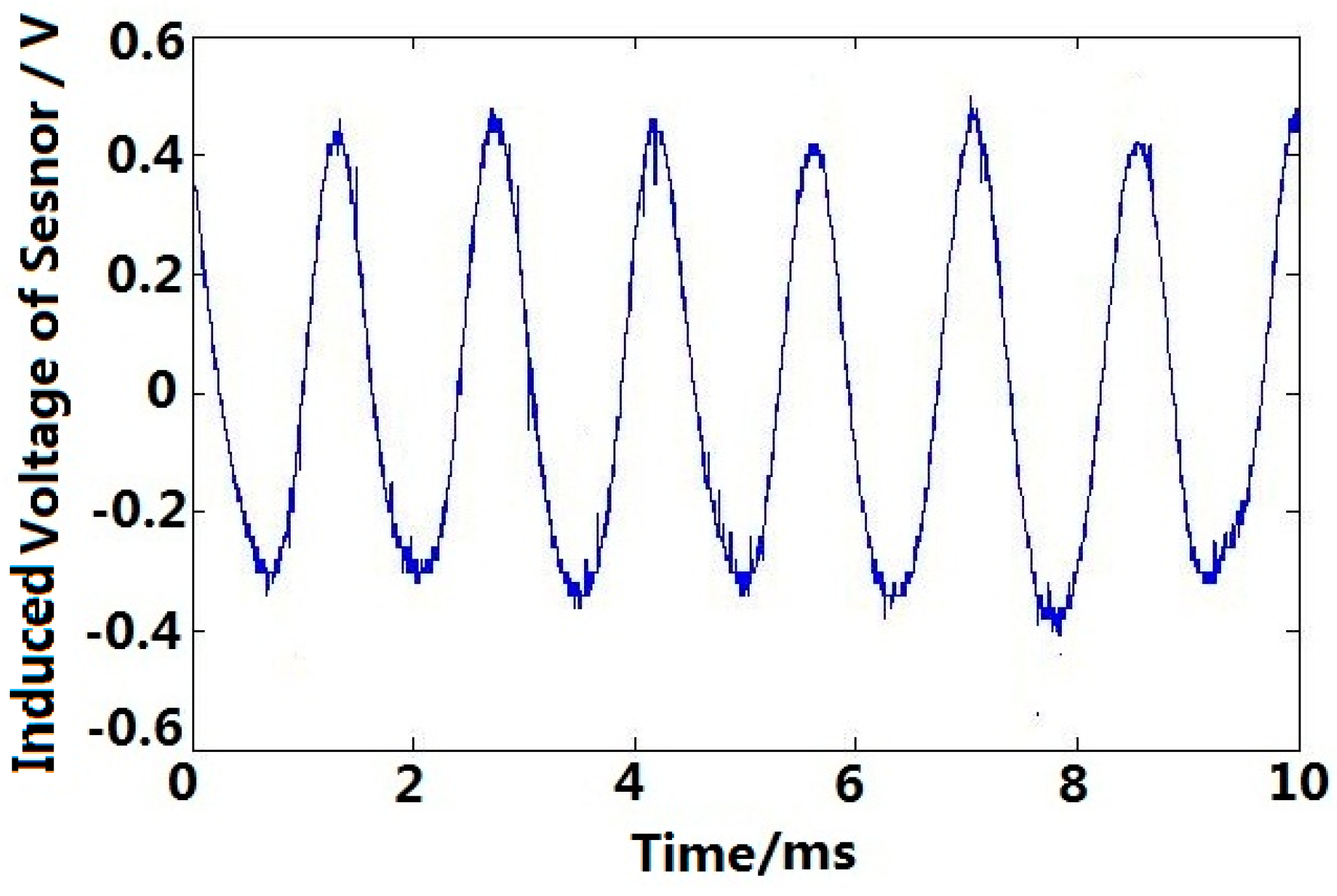
5.4. Step Motor Angular Acceleration Testing

5.5. Practicability Improvements of Angular Acceleration Sensor
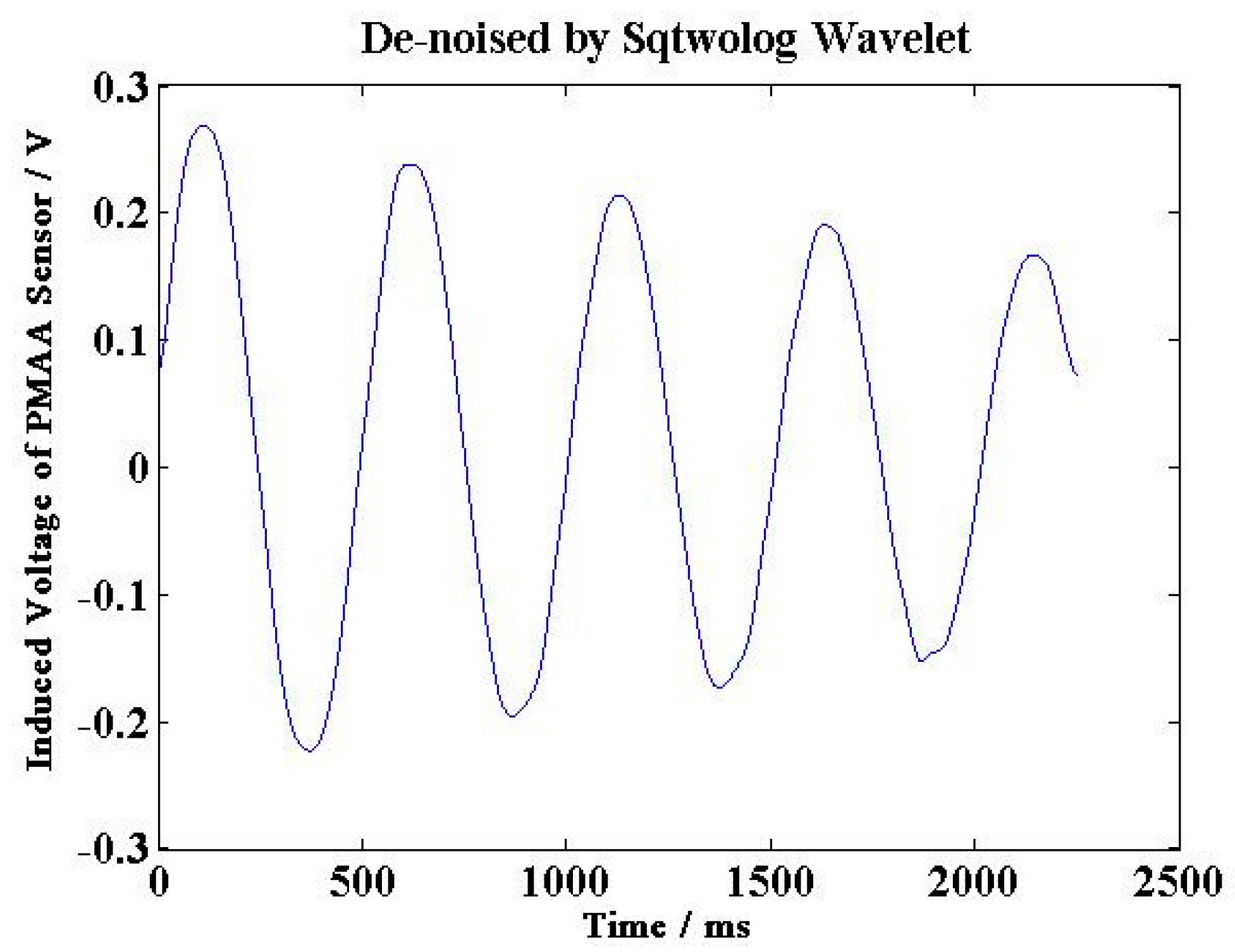
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tran, V.H.; Lee, S.G. A Stable Formation Control Using Approximation of Translational and Angular Accelerations. Int. J. Adv. Robot. Syst. 2011, 1, 65–75. [Google Scholar] [CrossRef]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction. J. Guid. Control Dyn. 2010, 6, 1732–1742. [Google Scholar] [CrossRef]
- Weenk, D.; van Beijnum, B.J.F.; Baten, C.T.M.; Hermens, H.J.; Veltink, P.H. Automatic identification of inertial sensor placement on human body segments during walking. J. Neuroeng. Rehabil. 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Rueterbories, J.; Spaich, E.G.; Andersen, O.K. Characterization of gait pattern by 3D angular accelerations in hemiparetic and healthy gait. Gait Posture 2013, 2, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Gola, A.; Chiesa, E. Interface for MEMS-based rotational accelerometer for HDD applications with 2.5 rad/s2 resolution and digital output. IEEE Sens. J. 2003, 3, 383–392. [Google Scholar] [CrossRef]
- Ovaska, S.J.; Valiviita, S. Angular Acceleration Measurement: A Review. IEEE Trans. Instrum. Meas. 1998, 47, 1211–1217. [Google Scholar] [CrossRef]
- Dunworth, A. Digital instrumentation for angular velocity and acceler-ation. IEEE Trans. Instrum. Meas. 1969, 18, 132–138. [Google Scholar] [CrossRef]
- Hancke, G.P.; Viljoen, C.F.T. The microprocessor measurement of low values of rotational speed and acceleration. IEEE Trans. Instrum. Meas. 1990, 39, 1014–1017. [Google Scholar] [CrossRef]
- Pasanen, J.; Vainio, O.; Ovaska, S.J. Predictive synchronization and restoration of corrupted velocity samples. Measurement 1994, 13, 315–324. [Google Scholar] [CrossRef]
- Brown, R.H.; Schneider, S.; CMulligan, M.G. Analysis of algorithms for velocity estimation from discrete position vs. timedata. IEEE Trans. Ind. Electron. 1992, 39, 11–19. [Google Scholar] [CrossRef]
- Laopoulos, T.; Papageorgiou, C. Microcontroller-based measure-ment of angular position, velocity and acceleration. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Brussels, Belgium, 4–6 June 1996; pp. 73–77.
- Jaritz, A.; Spong, M.W. An experimental comparison of robust control algorithms on a direct drive manipulator. IEEE Trans. Control Syst. 1996, 4, 627–640. [Google Scholar] [CrossRef]
- Furukawa, N.; Ohnishi, K. A structure of angular acceleration sensor using silicon cantilevered beam with piezoresistors. In Proceedings of the 1992 International Conference on Industrial Electronics, Control, Instrumentation, and Automation, San Diego, CA, USA, 9–13 November 1992; pp. 1524–1529.
- Godler, I.; Akahane, A.; Ohnishi, K.; Yamashita, T. A novel rotary acceleration sensor. IEEE Control Syst. Mag. 1995, 15, 56–60. [Google Scholar] [CrossRef]
- Mizuno, J.; Nottmeyer, K.; Amemori, M.; Kanai, Y.; Kobayashi, T. The study of silicon bulk micro-machined angular acceleration sensor. JSAE Rev. 2000, 21, 79–84. [Google Scholar] [CrossRef]
- O’Brien, G.J.; Monk, D.J.; Najafi, K. Angular accelerometer with dual anchor support. In Proceedings of the 12th International Conference on Solid-State Sensors, Actuators and Micro-systems, Boston, MA, USA, 8–12 June 2003; pp. 1371–1374.
- Amarasinghe, R.; Dao, D.V.; Toriyama, T.; Sugiyama, S. Design and fabrication of a miniaturized six-degree-of-freedom piezo-resistive accelerometer. J. Micromech. Microeng. 2005, 15, 1745–1753. [Google Scholar] [CrossRef]
- Wolfaardt, H.J.; Heyns, P.S. Dynamic modeling of a novel micro-fluidic channel angular accelerometer. J. Vib. Control 2008, 14, 451–467. [Google Scholar] [CrossRef]
- Yu, S.D.; Zhang, X. A data processing method for determining instantaneous angular speed and acceleration of crankshaft in an aircraft engine-propeller system using a magnetic encoder. Mech. Syst. Signal Process. 2010, 24, 1032–1048. [Google Scholar] [CrossRef]
- Li, J.L.; Fang, J.C.; Du, M.; Dong, H.F. Analysis and fabrication of a novel MEMS pendulum angular accelerometer with electrostatic actuator feedback. Microsyst. Technol. 2013, 19, 9–16. [Google Scholar] [CrossRef]
- Carvalho, M.M.; Cazo, R.M.; Almeida, V.R.; Barbosa, C.L. Fiber Bragg grating based angular accelerometer: A first approach. Proc. SPIE 2013, 8794. [Google Scholar] [CrossRef]
- Lin, J.M.; Luo, W.C.; Lin, C.H. A More Reliable and Easy Manufacturing Wireless Thermal Convection Angular Accelerometer without any Movable Parts and Grooved Cavity. Appl. Math. Inf. Sci. 2013, 7, 369–373. [Google Scholar] [CrossRef]
- Restivo, M.T.; Almeida, F.G.; Freitas, D. Measuring relative acceleration: A relative angular acceleration prototype transducer. Meas. Sci. Technol. 2013, 24. [Google Scholar] [CrossRef]
- Schloeffel, G.; Seiler, F. Unidirectional fiber optic sensor for angular acceleration measurement. Opt. Lett. 2013, 38, 1500–1502. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Feng, H. A Novel Permanent Magnetic Angular Acceleration Sensor. Sensors 2015, 15, 16136-16152. https://doi.org/10.3390/s150716136
Zhao H, Feng H. A Novel Permanent Magnetic Angular Acceleration Sensor. Sensors. 2015; 15(7):16136-16152. https://doi.org/10.3390/s150716136
Chicago/Turabian StyleZhao, Hao, and Hao Feng. 2015. "A Novel Permanent Magnetic Angular Acceleration Sensor" Sensors 15, no. 7: 16136-16152. https://doi.org/10.3390/s150716136
APA StyleZhao, H., & Feng, H. (2015). A Novel Permanent Magnetic Angular Acceleration Sensor. Sensors, 15(7), 16136-16152. https://doi.org/10.3390/s150716136





