An Electromagnetic Sensor with a Metamaterial Lens for Nondestructive Evaluation of Composite Materials
Abstract
:1. Introduction
2. Electromagnetic Sensor with Metamaterial Lens
2.1. Theoretical Principles
2.1.1. Constitutive Parameters of Conical Swiss Rolls
2.1.2. Functioning Principle of a MM Lens Sensor
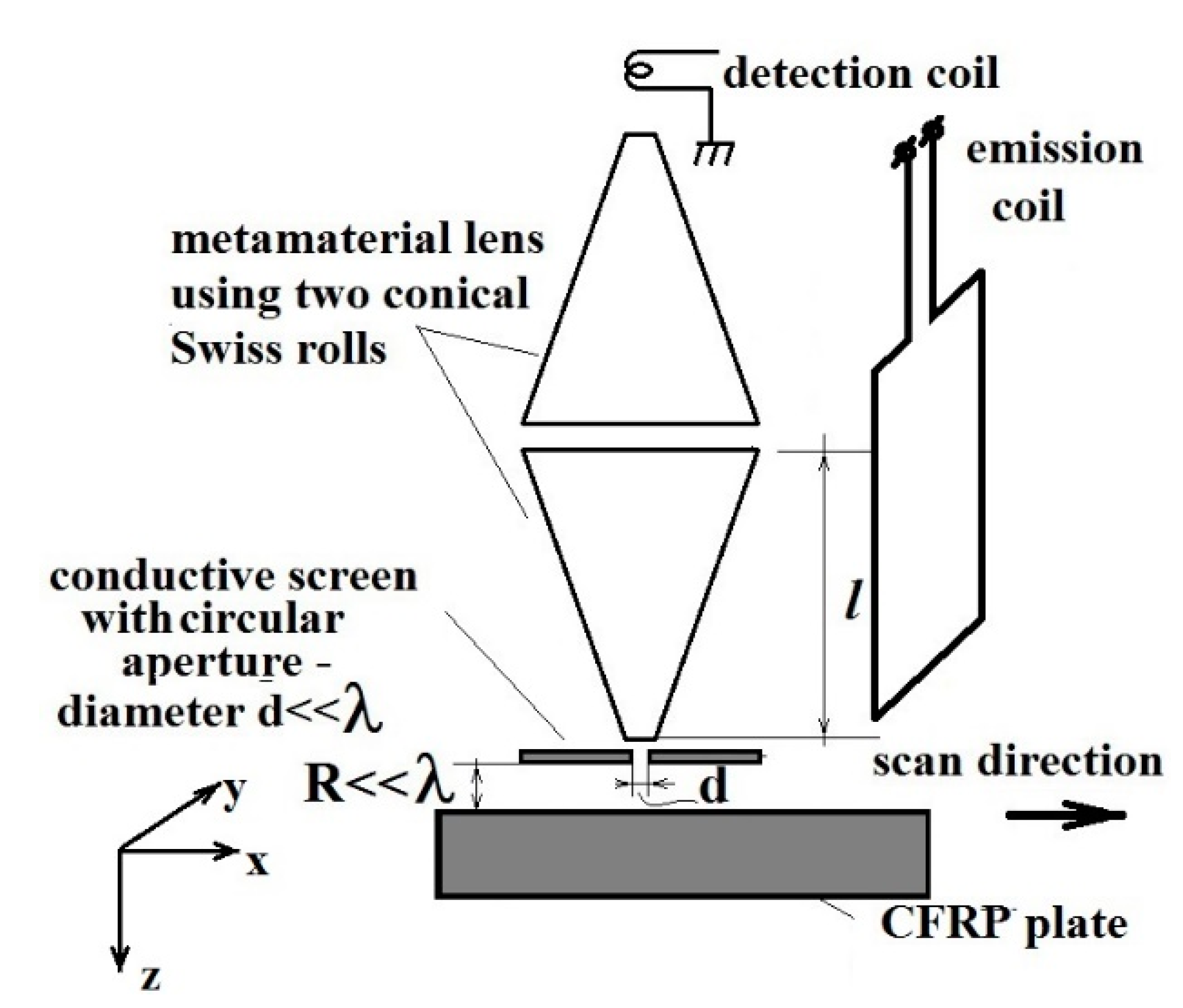
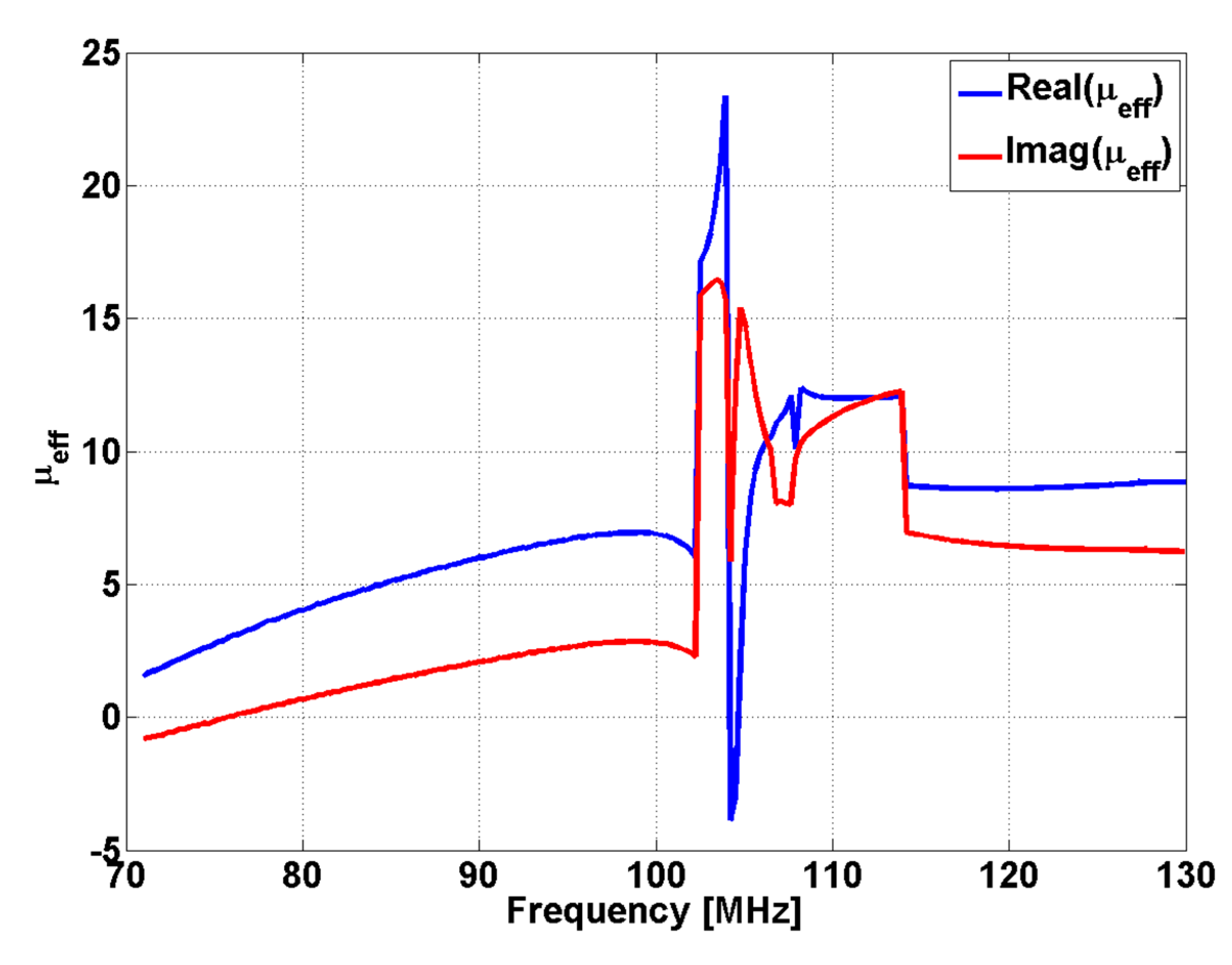
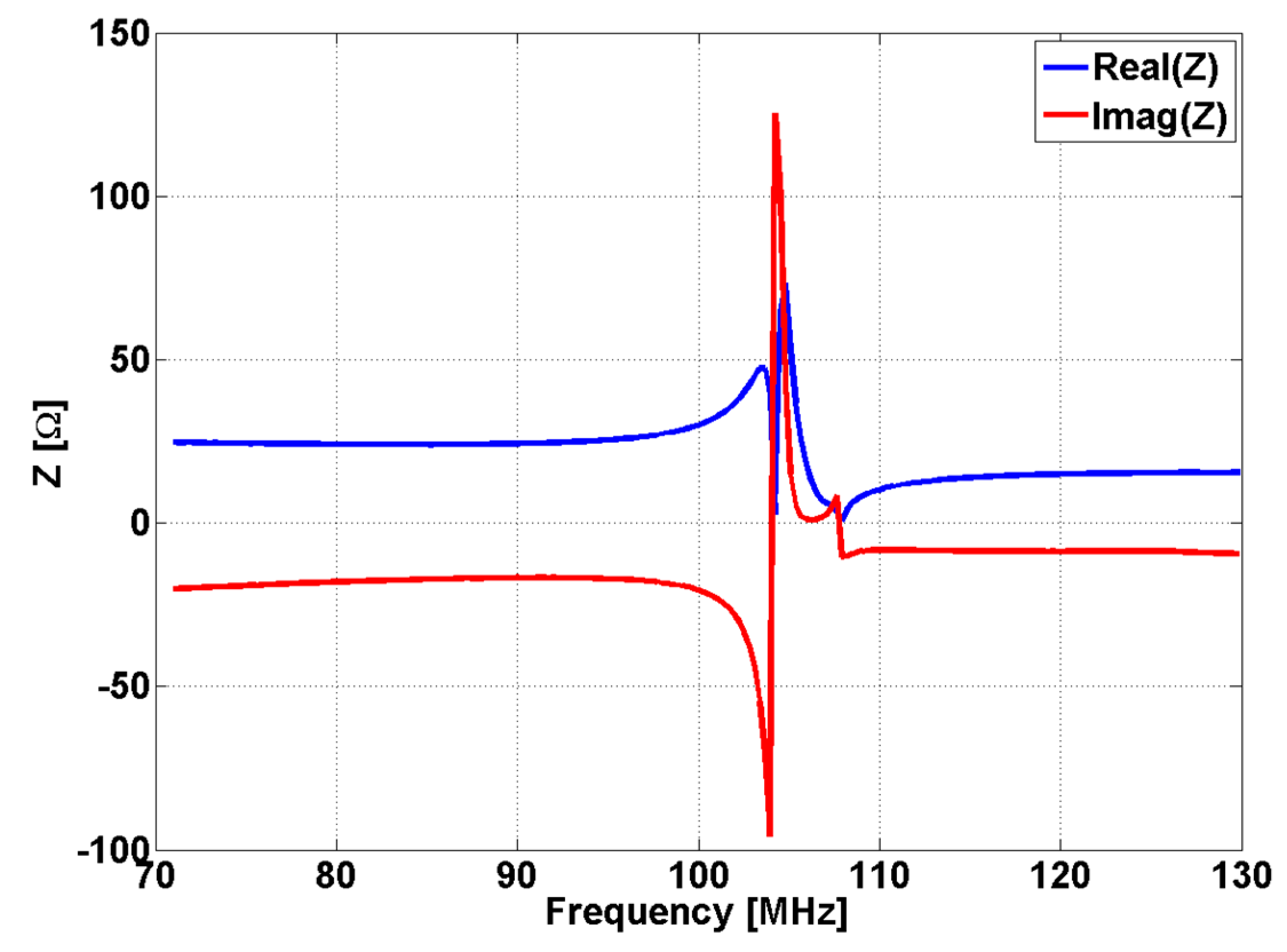
2.2. Physical Realization of MM Lens Sensor

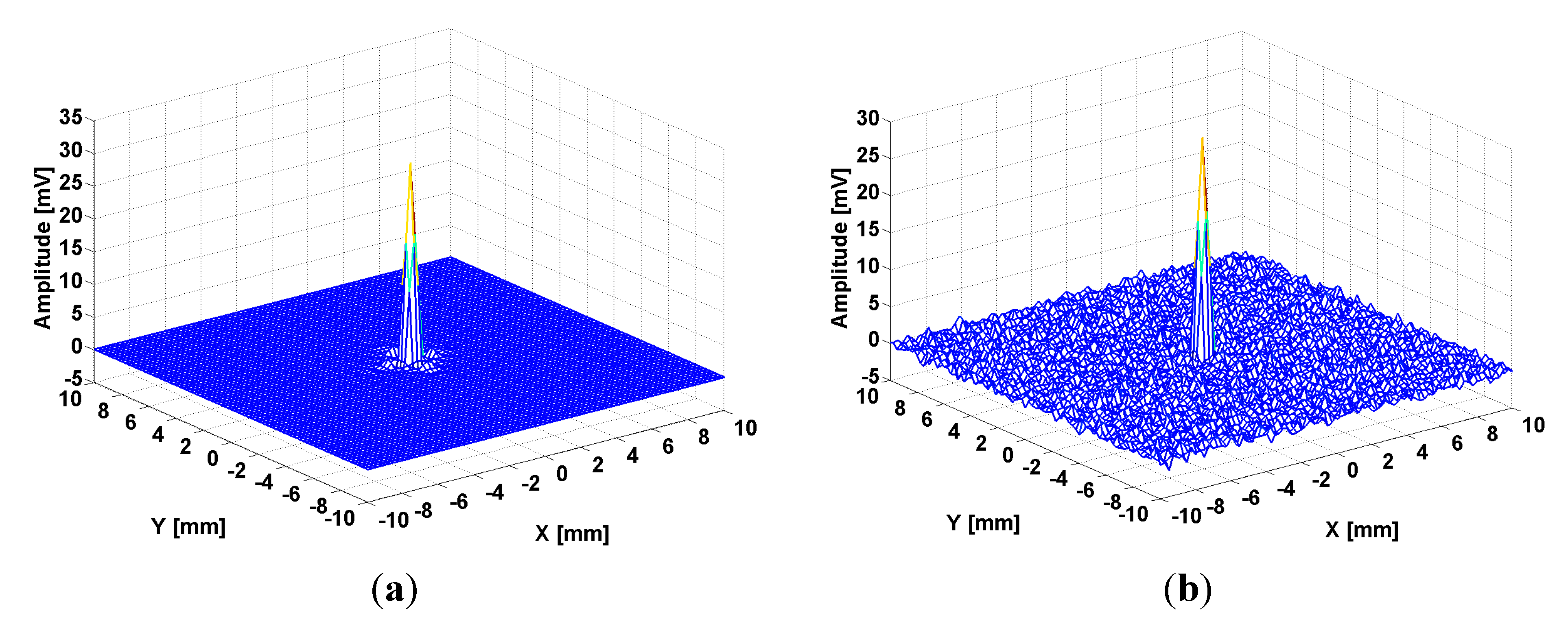
3. Studied Samples and Experimental Set-Up


4. Experimental Results
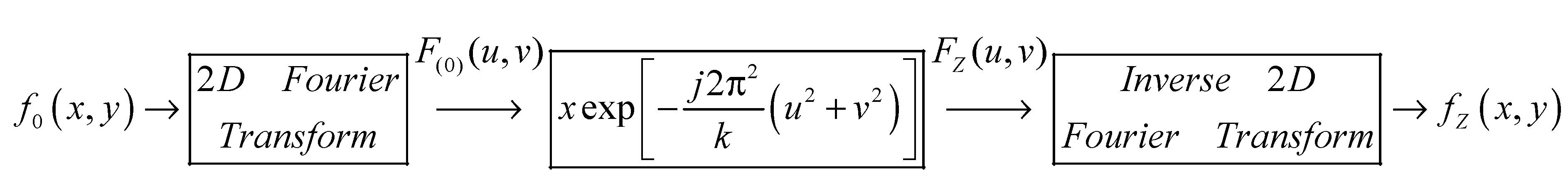
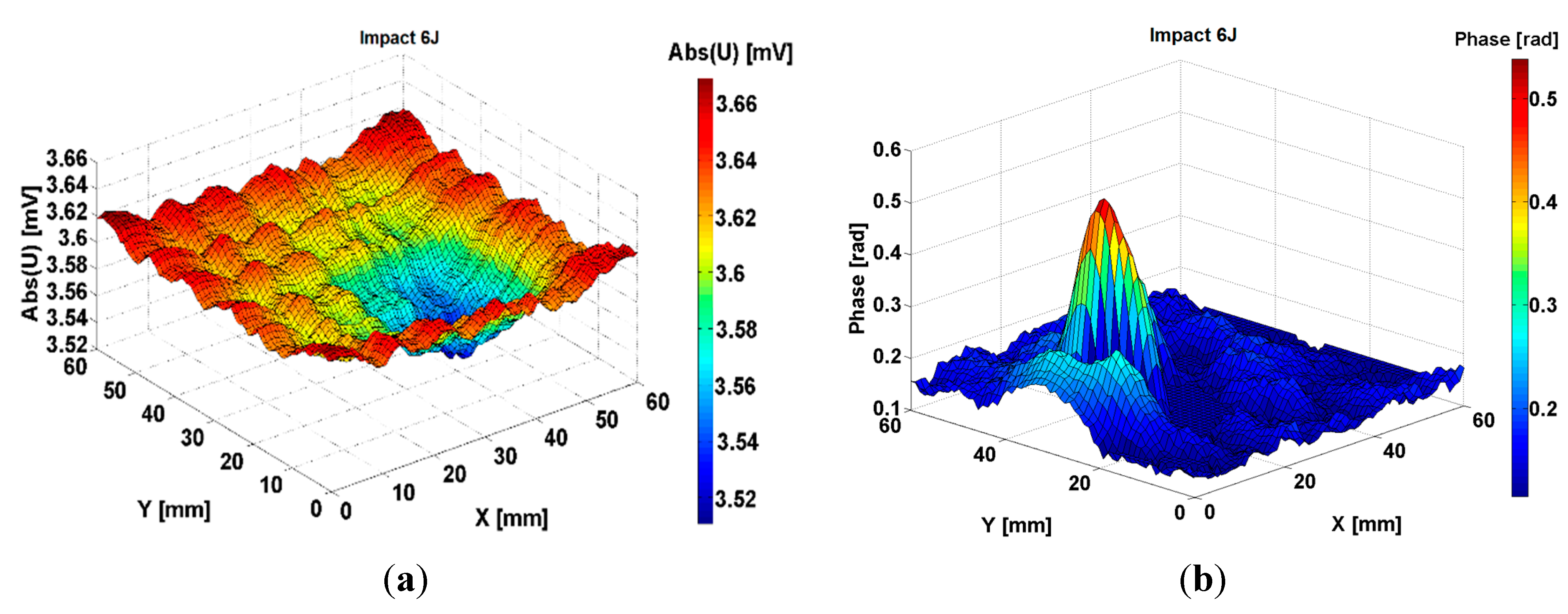
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schwartz, M.M. Composite Materials: Properties, Non-Destructive Testing, and Repair; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1997; Volume I. [Google Scholar]
- Morgan, P. Carbon Fibers and Their Composites; Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Pilato, L.A.; Michno, M.J. Advanced Composite; Springer Verlag: Berlin, Germany, 1994. [Google Scholar]
- Landel, R.F.; Nielsen, L.E. Mechanical Properties of Polymers and Composites; CRC Press: New York, NY, USA, 1993. [Google Scholar]
- TenCate Advanced Composites. Available online: http://www.tencate.com/ (accessed on 15 September 2014).
- Greisel, M.; Jäger, J.; Moosburger-Will, J.; Sause, M.G.R.; Mueller, W.M.; Horn, S. Influence of residual thermal stress in carbon fiber-reinforced thermoplastic composites on interfacial fracture toughness evaluated by cyclic single-fiber push-out tests. Compos. Part A 2014, 66, 17–127. [Google Scholar] [CrossRef]
- Elmarakbi, A.; Mollón, V.; Bonhomme, J.; Viña, J.; Argüelles, A. Advanced Composite Materials for Automotive Applications: Structural Integrity and Crashworthiness; John Wiley & Sons Ltd.: West Sussex, UK, 2013. [Google Scholar]
- Gros, X.E.; Ogi, K.; Takahashi, K. Eddy Current, Ultrasonic C-Scan and Scanning Acoustic Microscopy Testing of Delaminated Quasi-Isotropic CFRP Materials: A Case Study. J. Reinf. Plast. Compos. 1998, 17, 389–405. [Google Scholar]
- Lemistre, M.; Gallaud, C.; Gouyon, R.; Balageas, D. Une methode magnetique radiofrequence de localisation des defauts dans les structures en composite carbone. In Proceedings of the Congress Cofrend 97 sur les Essais non Destructifs, Nantes, France, 22–26 September 1997. (In French)
- Grimberg, R.; Savin, A.; Radu, E.; Mihalache, O. Nondestructive evaluation of the severity of discontinuities in flat conductive materials by an eddy-current transducer with orthogonal coils. IEEE Trans. Magn. 2000, 36, 299–307. [Google Scholar] [CrossRef]
- Mook, G.; Michel, F.; Simonin, J. Electromagnetic imaging using probe arrays. Strojniški Vestnik J. Mech. Eng. 2011, 57, 227–236. [Google Scholar] [CrossRef]
- Schulze, M.H.; Meyendorf, N.; Heuer, H. Analysis Techniques for Eddy Current Imaging of Carbon Fiber Materials. Mater. Test. 2010, 52, 603–609. [Google Scholar] [CrossRef]
- Grimberg, R.; Premel, D.; Savin, A.; le Bihan, Y.; Placko, D. Eddy current holography evaluation of delamination in carbon-epoxy composites. INSIGHT 2001, 43, 260–264. [Google Scholar]
- Gros, X.E. Some Aspects of Electromagnetic Testing of Composites. INSIGHT 1996, 38, 492–495. [Google Scholar]
- Heuer, H.; Schulze, M.; Pooch, M.; Gäbler, S.; Nocke, A.; Bardl, G.; Petrenz, S. Review on quality assurance along the CFRP value chain—Non-destructive testing of fabrics, preforms and CFRP by HF radio wave techniques. Compos. Part B Eng. 2015, 77, 494–501. [Google Scholar] [CrossRef]
- Mizukami, K.; Mizutani, Y.; Todoroki, A.; Suzuki, Y. Detection of delamination in thermoplastic CFRP weld parts using eddy current testing and induction heating. In Proceedings of the 11th European Conference on Non-Destructive Testing (ECNDT 2014), Prague, Czech Republic, 6–10 October 2014.
- Davis, C.W.; Nath, S.; Fulton, J.P.; Namkung, M. Combined investigation of eddy current and ultrasonic techniques for composite materials NDE. Rev. Prog. Quant. Nondestruct. Eval. 1995, 1295–1301. [Google Scholar] [CrossRef]
- Hung, Y.Y.; Chen, Y.S.; Ng, S.P.; Liu, L.; Huang, Y.H.; Luk, B.L.; Ip, R.W.L.; Wu, C.M.L.; Chung, P.S. Review and comparison of shearography and active thermography for nondestructive evaluation. Mater. Sci. Eng. R 2009, 64, 73–112. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared thermography for temperature measurement and non-destructive testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef] [PubMed]
- Staszewski, W.J.; Mahzan, S.; Traynor, R. Health monitoring of aerospace composite structures—Active and passive approach. Compos. Sci. Technol. 2009, 69, 1678–1685. [Google Scholar] [CrossRef]
- Bladel, J. Electromagnetic Fields, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Cacciola, M.; Calcagno, S.; Megali, G.; Pellicano, D.; Versaci, M.; Morabito, F.C. Eddy current modeling in composite materials. PIERS Online 2009, 5, 591–595. [Google Scholar]
- Xu, X.; Liu, M.; Zhang, Z.; Jia, Y. A Novel High Sensitivity Sensor for Remote Field Eddy Current Non-Destructive Testing Based on Orthogonal Magnetic Field. Sensors 2014, 14, 24098–24115. [Google Scholar] [CrossRef] [PubMed]
- Grimberg, R.; Savin, A.; Radu, E.; Chifan, S. Eddy current sensor for holographic visualization of material discontinuities. Sens. Actuators A Phys. 2000, 81, 251–253. [Google Scholar] [CrossRef]
- Savin, A.; Faktorová, D.; Pápežová, M.; Steigmann, R. Electromagnetic nondestructive evaluation using metamaterials sensor. In Proceedings of 10th International Conference ELEKTRO 2014, Rajecke Teplice, Slovak, 19–20 May 2014; pp. 535–538.
- Miorelli, R.; Reboud, C.; Lesselier, D.; Theodoulidis, T. Fast simulation method of multiple narrow cracks in planar stratified media. In Electromagnetic Non-Destructive Evaluation (XV); Studies in Applied Electromagnetics and Mechanics 36; IOS Press: Amsterdam, The Netherlands, 2012; pp. 11–18. [Google Scholar]
- Mandache, C.; Lefebvre, J.H.V. Transient and harmonic eddy currents: Lift-Off point of intersection. NDT & E Int. 2006, 39, 57–60. [Google Scholar]
- Sophian, A.; Tian, G.Y.; Taylor, D.; Rudlin, J. Electromagnetic and eddy current NDT: A review. INSIGHT 2001, 43, 302–306. [Google Scholar]
- Bonavolontà, C.; Valentino, M.; Marrocco, N.; Pepe, G.P. Eddy Current Technique Based on SQUID and GMR Sensors for Non-Destructive Evaluation of Fiber/Metal Laminates. IEEE Trans. Appl. Supercond. 2009, 19, 808–811. [Google Scholar] [CrossRef]
- Sommerfeld, A. Mathematical Theory of Diffraction; Birkhauser: Boston, MA, USA, 2004. [Google Scholar]
- Grimberg, R.; Tian, G.Y. High Frequency Electromagnetic Non-destructive Evaluation for High Spatial Resolution using Metamaterial. Proc. R. Soc. A 2012, 468, 3080–3099. [Google Scholar] [CrossRef]
- Grbic, A.; Eleftheriades, G.V. Growing evanescent waves in negative-refractive-index transmission-line media. Appl. Phys. Lett. 2003, 82, 1815–1817. [Google Scholar] [CrossRef]
- Grbic, A.; Eleftheriades, G.V. Overcoming the Diffraction Limit with a Planar Left-Handed Transmission-Line Lens. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Blaikie, R.J.; Melville, D.O. Imaging through planar silver lenses in the optical near field. J. Opt. A Pure Appl. Opt. 2005, 7, S176–S183. [Google Scholar] [CrossRef]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub-Diffraction-Limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Wiltshire, M.C.K.; Pendry, J.B.; Hajnal, J.V. Sub-Wavelength imaging at radio frequency. J. Phys. Condens. Matter 2006, 18. [Google Scholar] [CrossRef]
- Grimberg, R.; Savin, A.; Rotundu, C.R. Eddy current microscopy applied to graphite-epoxy composite. Sens. Actuators A Phys. 2001, 91, 73–75. [Google Scholar] [CrossRef]
- Ozbey, B.; Unal, E.; Ertugrul, H.; Kurc, O.; Puttlitz, C.M.; Erturk, V.B.; Altintas, A.; Demir, H.V. Wireless Displacement Sensing Enabled by Metamaterial Probes for Remote Structural Health Monitoring. Sensors 2014, 14, 1691–1704. [Google Scholar] [CrossRef] [PubMed]
- Savin, A.; Steigmann, R.; Dobrescu, G.S. Metamaterial Sensors for Structural Health Monitoring. In Proceedings of the ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis, Copenhagen, Denmark, 25–27 July 2014.
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Wiltshire, M.C.K. Radio frequency (RF) metamaterials. Phys. Status Solidi B 2007, 244, 1227–1236. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Nemat-Nasser, S.C.; Schultz, S. Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial. Appl. Phys. Lett. 2001, 78, 489–491. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef]
- Engheta, N.; Ziolkowski, R.W. Electromagnetic Metamaterials: Physics and Engineering Explorations; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Physics-Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative Refraction Makes on Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Grimberg, R.; Savin, A.; Steigmann, R.; Serghiac, B.; Bruma, A. Electromagnetic non-destructive evaluation using metamaterials. INSIGHT 2011, 53, 132–137. [Google Scholar] [CrossRef]
- Grimberg, R.; Savin, A.; Steigmann, R. Electromagnetic imaging using evanescent waves. NDT&E Int. 2012, 46, 70–76. [Google Scholar]
- Grimberg, R.; Savin, A. Electromagnetic Transducer for Evaluation of Structure and Integrity of the Composite Materials with Polymer Matrix Reinforced with Carbon Fibers. Romanian Patent No. RO126245-A0.
- Savin, A.; Steigmann, R.; Bruma, A. Metallic Strip Gratings in the Sub-subwavelength Regime. Sensors 2014, 14, 11786–11804. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principle of Optics, 5th ed.; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts and Company: Englewood, CO, USA, 2005. [Google Scholar]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Kong, J.A. Electromagnetic Wave Theory; EMW Publishing: Cambridge, MA, USA, 2000. [Google Scholar]
- Grimberg, R. Electromagnetic metamaterials. Mater. Sci. Eng. B 2013, 178, 1285–1295. [Google Scholar] [CrossRef]
- Akkerman, R. Laminate mechanics for balanced woven fabrics. Compos. Part B Eng. 2006, 37, 108–116. [Google Scholar] [CrossRef]
- Steigmann, R.; Savin, A. Advanced Sensor for Enhancement of Electromagnetic Imaging of Impacted Carbon Fibers-PPS Composites; Chapter 52 in DAAAM International Scientific Book; Katalinic, B., Ed.; DAAAM International: Vienna, Austria, 2014; pp. 633–644. [Google Scholar]
- Menana, H.; Féliachi, M. Electromagnetic characterization of the CFRPs anisotropic conductivity: Modeling and measurements. Eur. Phys. J. Appl. Phys. 2011, 53. [Google Scholar] [CrossRef]
- Ullah, H.; Abdel-Wahab, A.A.; Harland, A.R.; Silberschmidt, V.V. Damage in woven CFRP laminates subjected to low velocity impacts. J. Phys.: Conf. Ser. 2012, 382, 012015. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savin, A.; Steigmann, R.; Bruma, A.; Šturm, R. An Electromagnetic Sensor with a Metamaterial Lens for Nondestructive Evaluation of Composite Materials. Sensors 2015, 15, 15903-15920. https://doi.org/10.3390/s150715903
Savin A, Steigmann R, Bruma A, Šturm R. An Electromagnetic Sensor with a Metamaterial Lens for Nondestructive Evaluation of Composite Materials. Sensors. 2015; 15(7):15903-15920. https://doi.org/10.3390/s150715903
Chicago/Turabian StyleSavin, Adriana, Rozina Steigmann, Alina Bruma, and Roman Šturm. 2015. "An Electromagnetic Sensor with a Metamaterial Lens for Nondestructive Evaluation of Composite Materials" Sensors 15, no. 7: 15903-15920. https://doi.org/10.3390/s150715903
APA StyleSavin, A., Steigmann, R., Bruma, A., & Šturm, R. (2015). An Electromagnetic Sensor with a Metamaterial Lens for Nondestructive Evaluation of Composite Materials. Sensors, 15(7), 15903-15920. https://doi.org/10.3390/s150715903





