Collaborative Localization and Location Verification in WSNs
Abstract
:1. Introduction
| Notations | Meaning |
|---|---|
| m | The number of anchor nodes |
| n | The number of normal nodes |
| Canchor | Coordinate of anchor |
| Cnormal | Actual coordinate of normal node |
| Ce | Estimated coordinate of normal node |
| dij | Actual pairwise distance |
| Ranging distance | |
| Calculated distance after localization | |
| ∆ | Localization error |
| Ad | Collection of unreliable anchors |
| ω1 and ω2 | Threshold in the two location refinement process |
| and | Amount of virtual force in the two location refinement process |
| Resultant | |
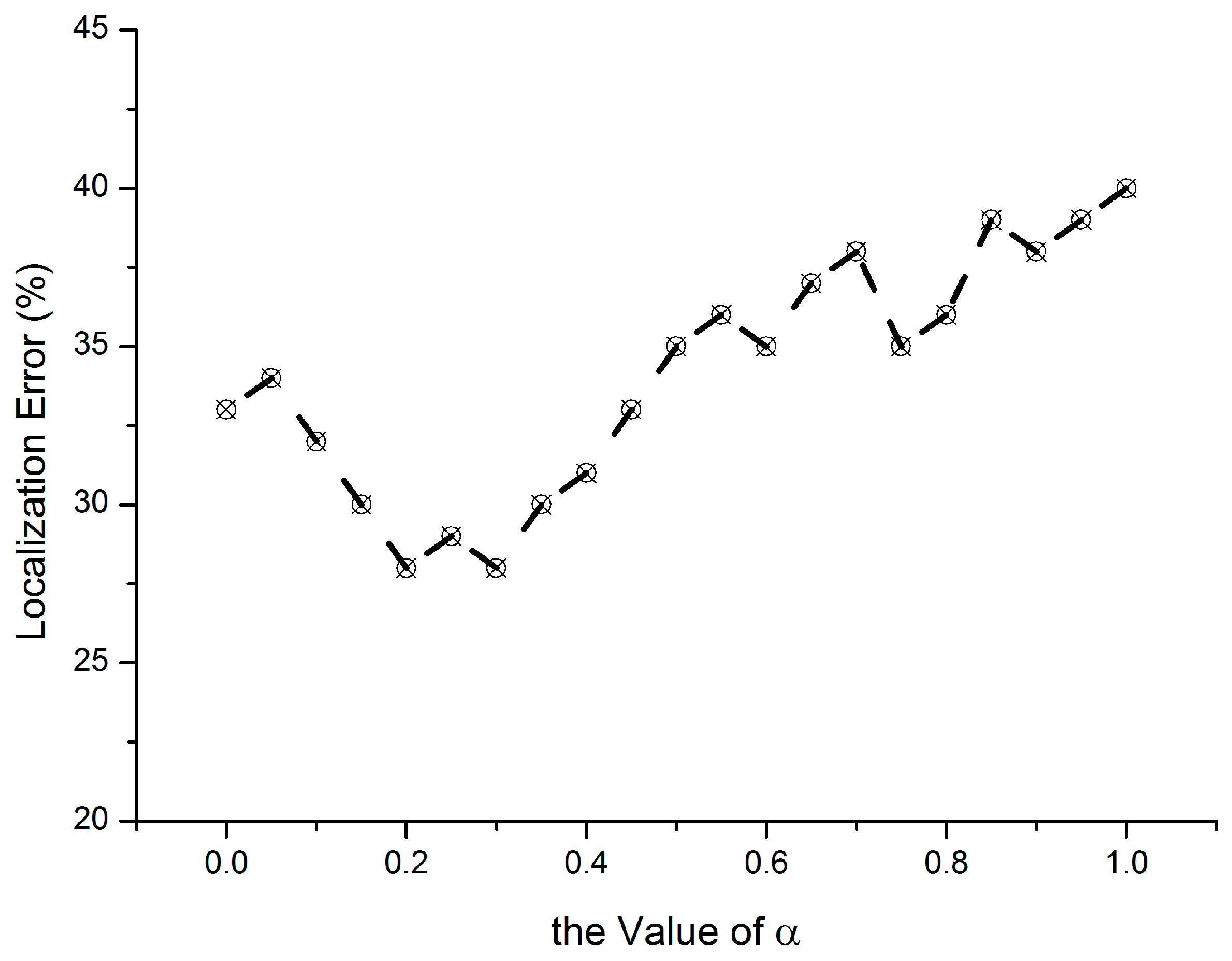
| α j | Distance weight |
| wj | Reference weight |
2. Related Work
2.1. Location Verification
2.2. Location Calibration
2.3. Virtual Force Model
3. Problem Modeling
3.1. Motivation
- (1)
- A lightweight distributed localization algorithm for WSNs.
- (2)
- A location verification algorithm which can detect drifted nodes and unreliable anchors.
- (3)
- A re-located algorithm which adapts to anchor sparse WSNs.
3.2. Problem Statement
- (1)
- With Canchor, and Ce estimated from f(·), to minimize the ∆, i.e.,
- (2)
- Construct a function g(·), to make A'd approximate to Ad, i.e.,
4. Cooperative Localization and Location Verification
4.1. Assumptions
- (1)
- All of the nodes in the network have the same communication radius, i.e., r, and the sensing model is an ideal circle.
- (2)
- (The pairwise ranging distances of (ni, nj) are unbiased, i.e., =.
- (3)
- There are not collusions between these malicious anchors.
- (4)
- All of the nodes can be drifted, but only the anchor nodes might be compromised.
- (5)
- The proportion of unreliable nodes including drifted nodes and malicious anchors is lower than 50%. Otherwise, we cannot recognize the unreliable nodes [33].
4.2. Cooperative Localization Algorithm
- (1)
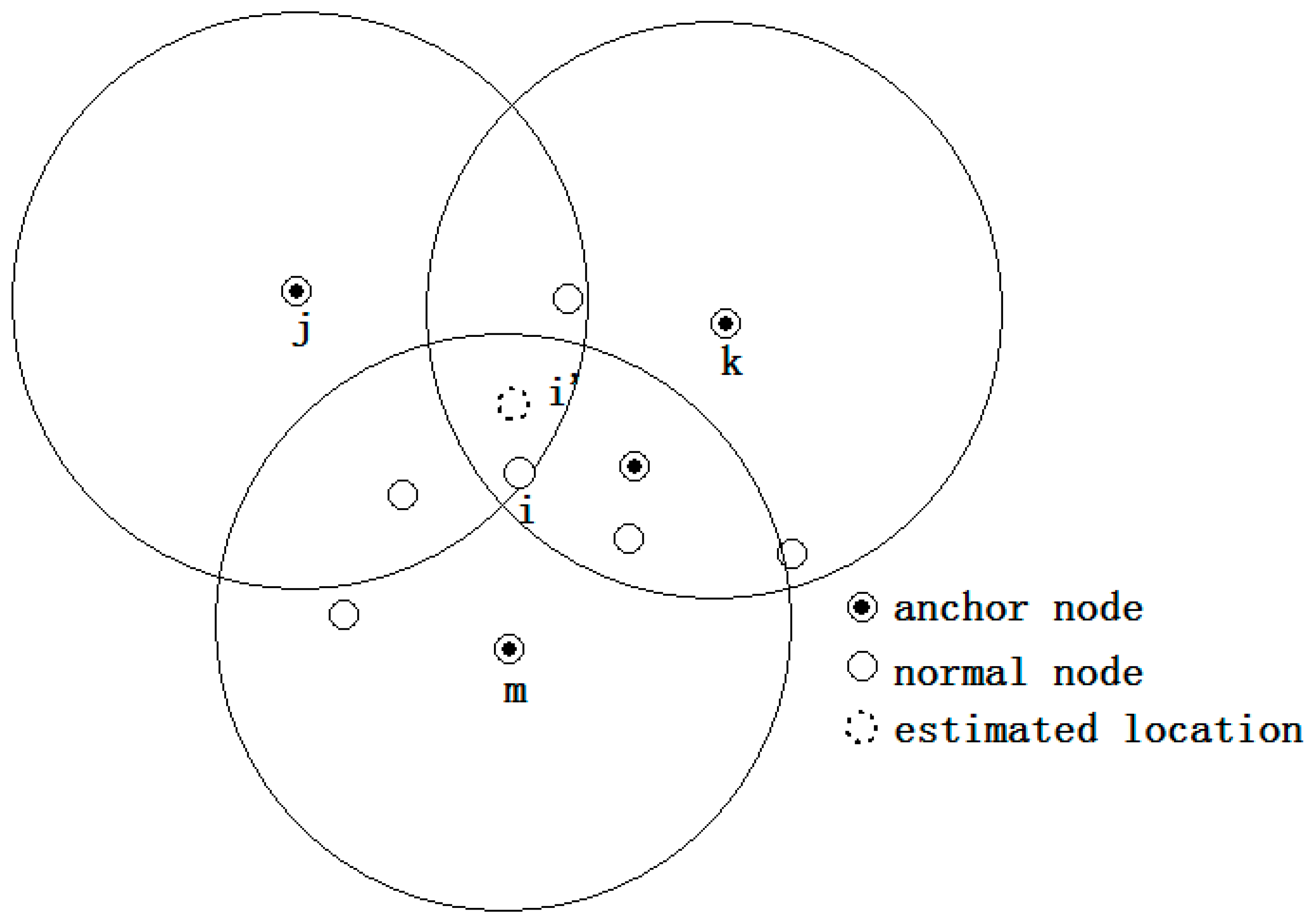
- The initial location estimation: to enlarge the location search range, the three anchors whose ranging distances are the largest are selected to derive the initial location of a certain node that needs to be located. The centroid of the intersection of these three anchors is used as the initial location. As Figure 1 shows, j, k and m are the three farthest anchors of node i, and the initial location of node i is i'.
- (2)
- Location adjustment: the initial location is adjusted to the final location using the virtual force model. As illustrated in Figure 2, the location of node i “moves” toward the correct position under the effect of virtual force that caused by other nodes. The movement ceases when the magnitude of the resultant force imposed on i is lower than the pre-set value ω1.
- (3)
- Localization refinement: the step size of node “movement” is reduced so as to improve the localization accuracy. This iteration process ceases when the magnitude of the resultant force is lower than another pre-set value ω2 or when the iteration number reaches the pre-set T.

| Algorithm 1 Location Refinement |
| Input: and |
| Output: Location of node i |
| While (T > 0 and < ω2) |
| Location initiation; //centroid algorithm |
| While ( < ω1) node i updates its location according to step size calculated by ; |
| node i updates its location according to step size calculated by ; |
| end; |
4.3. Location Verification

| Algorithm 2 Location Verification |
| Input: and |
| Output: |
| For each node |
| if () send message to its 2-hop neighbor nodes; |
| recalculate after removing the declared drifted node from its neighbor table; |
| recognize drifted nodes and unreliable anchors; |
| end |
4.4. Re-Localization Algorithm

| Algorithm 3 Re-localization |
| Input: and |
| Output: location of each node |
| For each drifted node |
| Pseudo anchor selection; |
| call Algorithm 1; |
| end |
4.5. Analysis of Effectiveness and Complexity
5. Simulations and Discussion
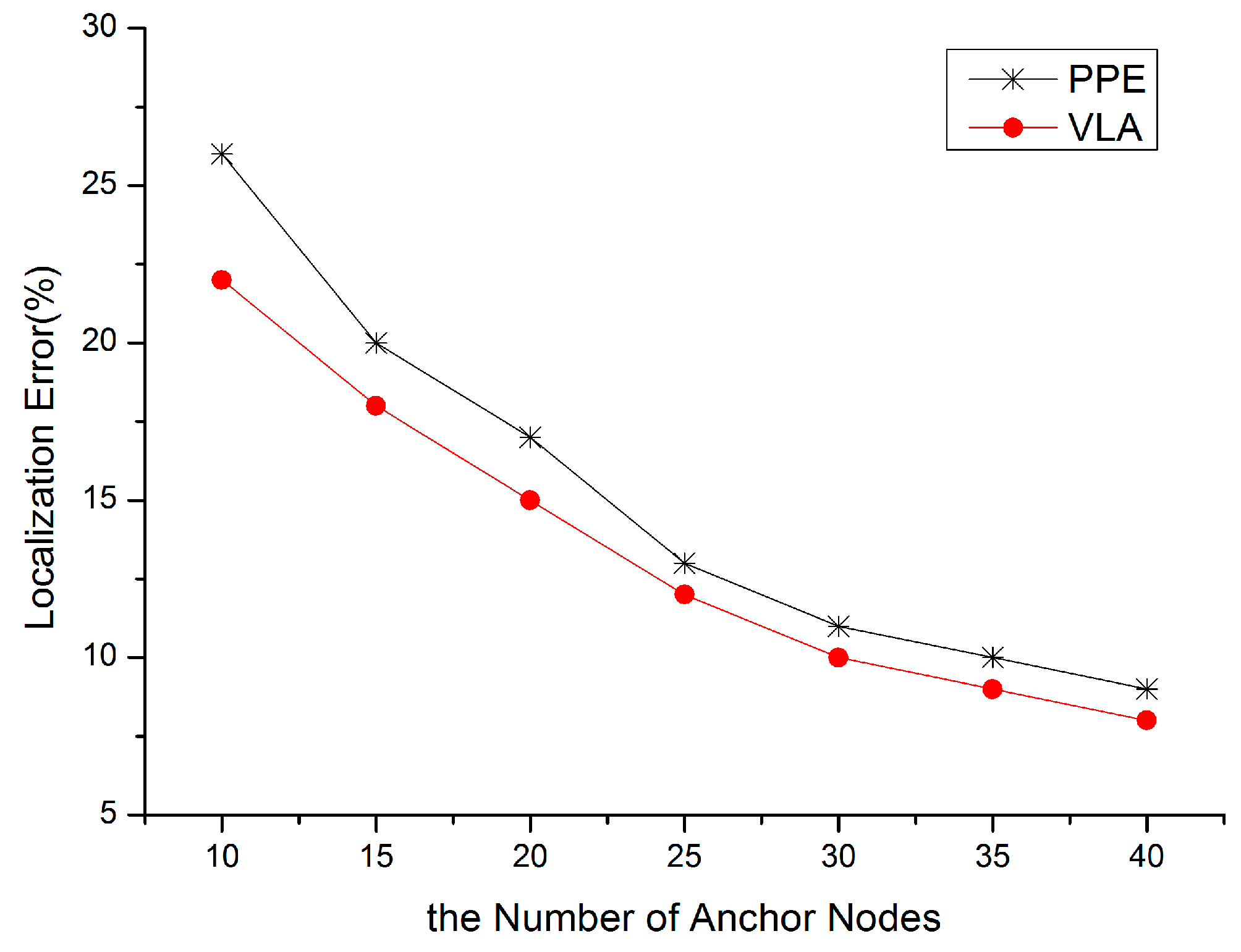
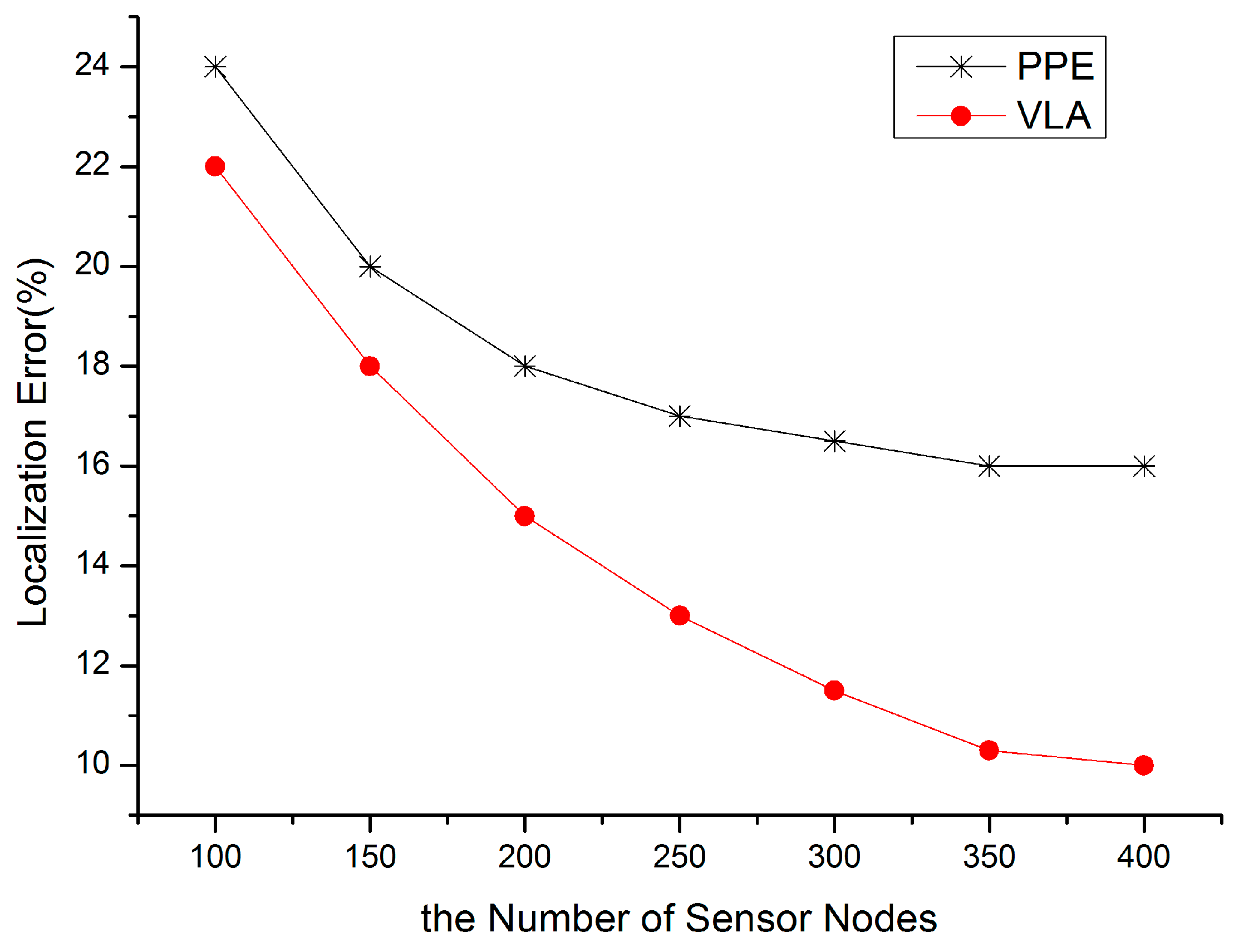
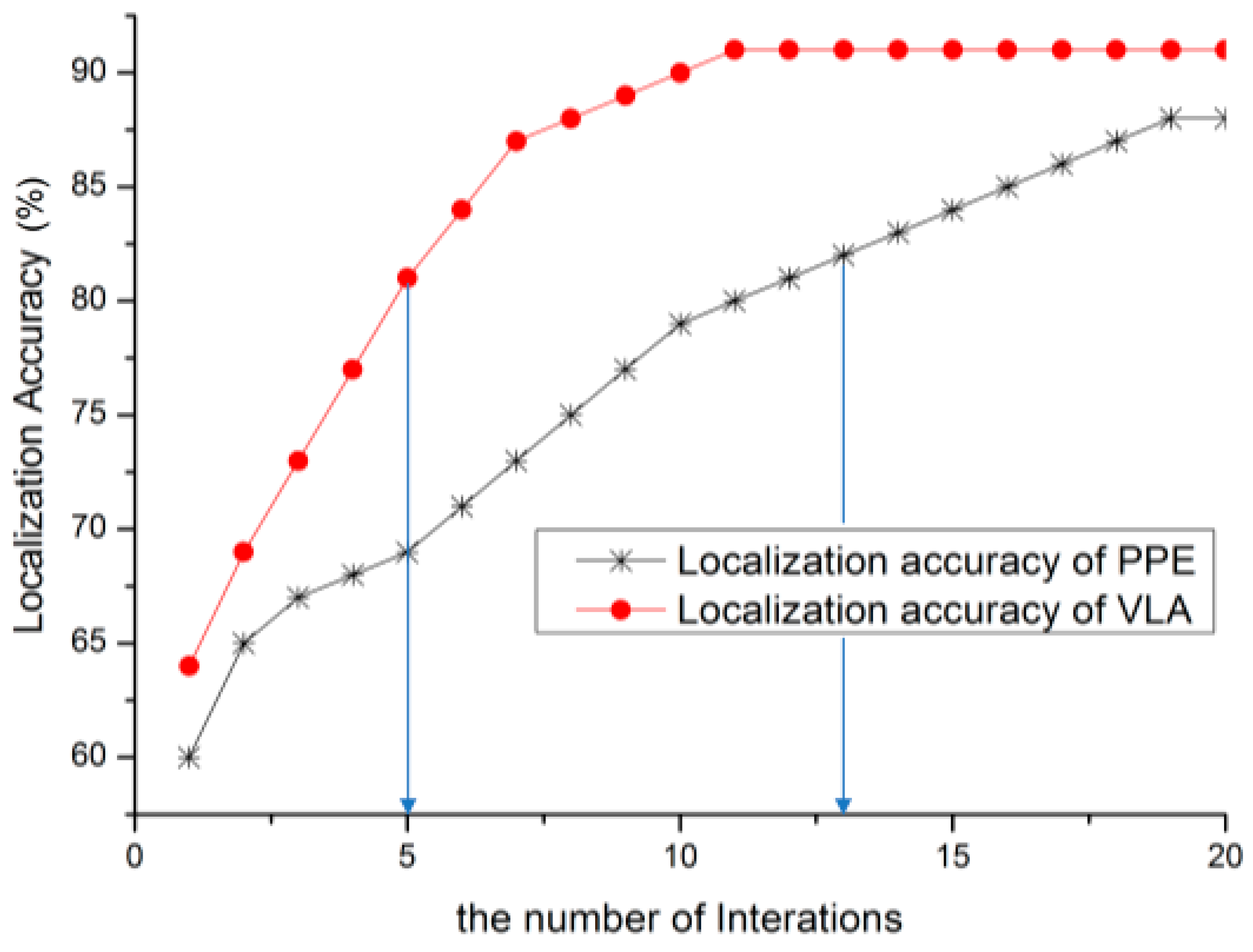
5.1. Localization Accuracy
5.2. Performance of Location Verification
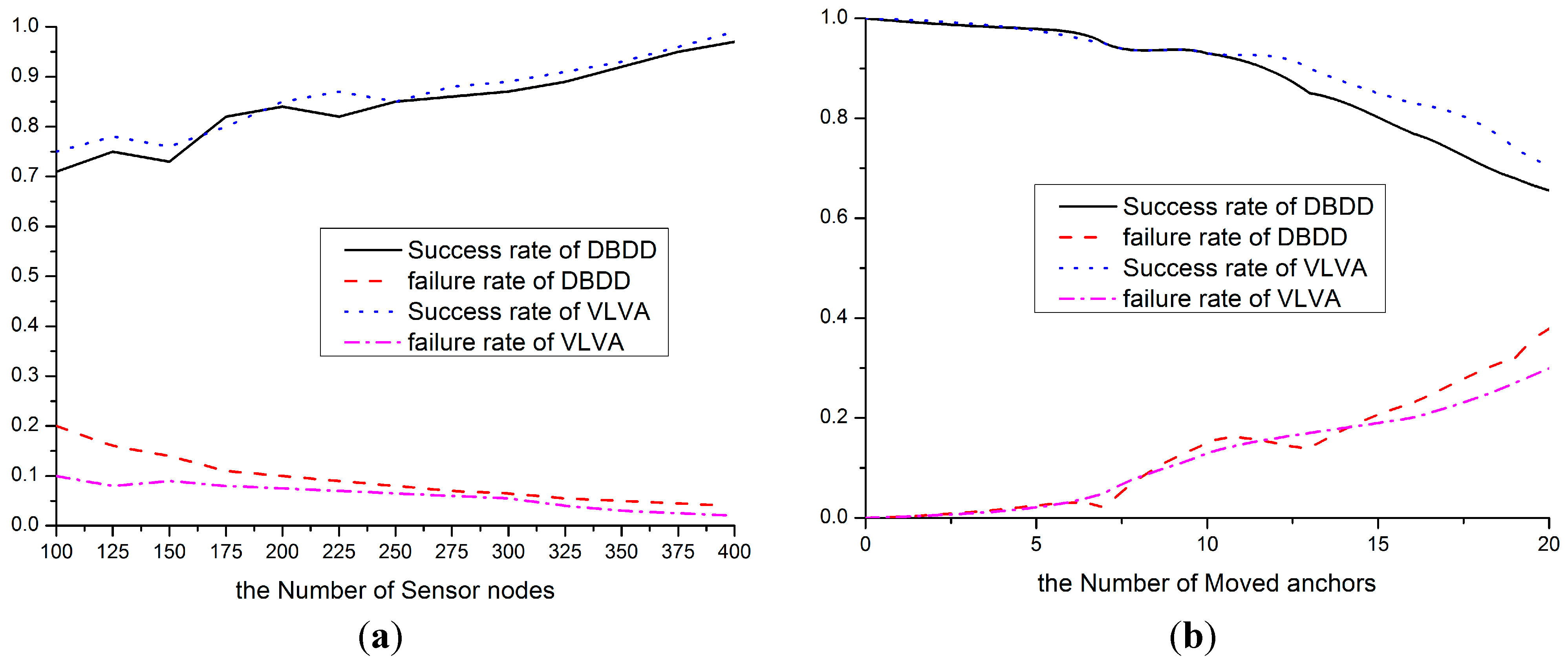
5.3. Re-Localization Performance
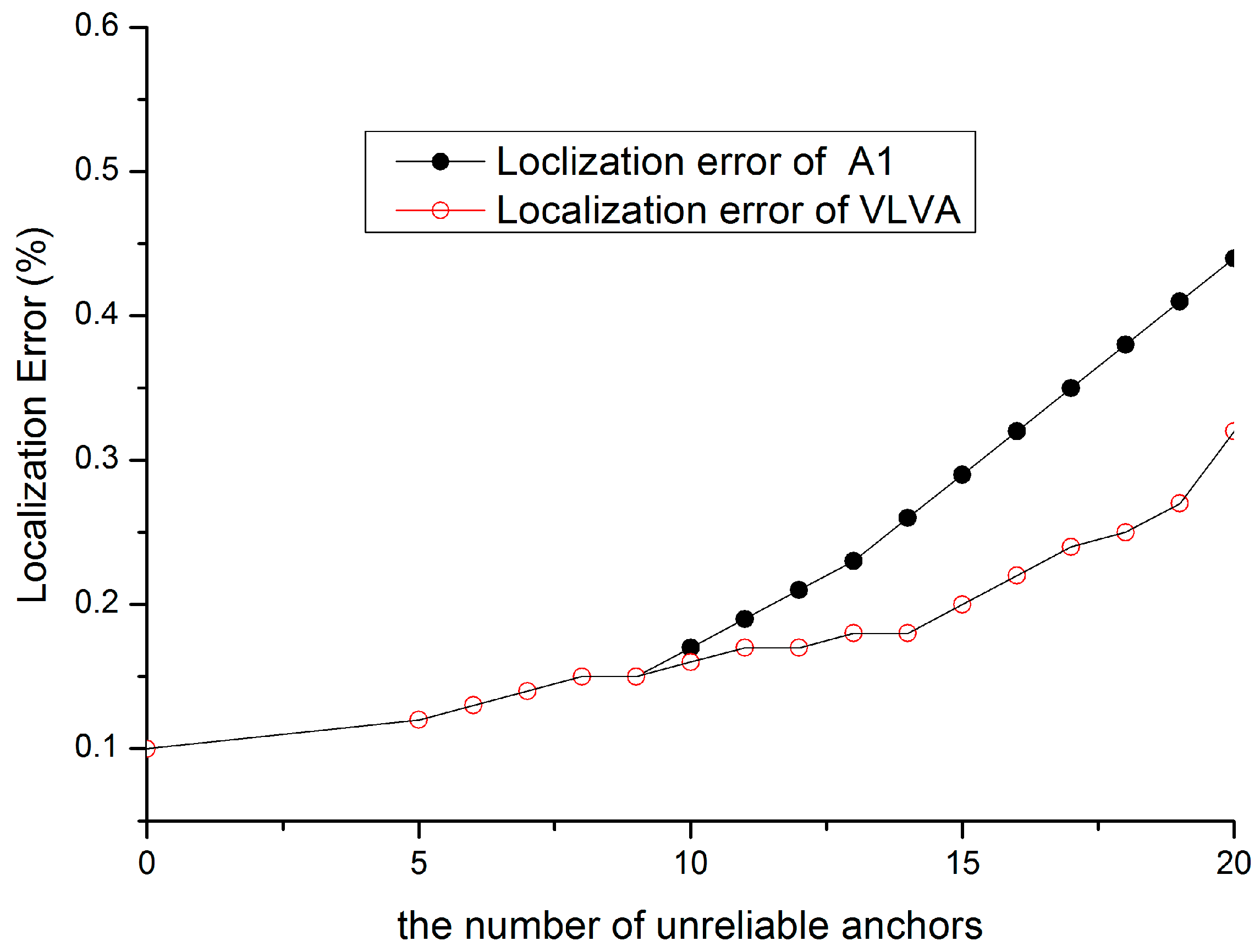
5.4. Communication Overhead
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Han, K.; Luo, J.; Liu, Y.; Vasilakos, A.V. Algorithm design for data communications in duty-cycled wireless sensor networks: A survey. IEEE Commun. Mag. 2013, 51, 107–113. [Google Scholar] [CrossRef]
- Sheng, Z.G.; Yang, S.S.; Yu, Y.F.; Vasilakos, A.V.; McCann, J.A.; Leung, K.K. A survey on the ietf protocol suite for the internet of things: Standards, challenges, and opportunities. IEEE Wirel. Commun. 2013, 20, 91–98. [Google Scholar] [CrossRef]
- Jiang, J.A.; Zheng, X.Y.; Chen, Y.F.; Wang, C.H.; Chen, P.T.; Chuang, C.L.; Chen, C.P. A distributed rss-based localization using a dynamic circle expanding mechanism. IEEE Sens. J. 2013, 13, 3754–3766. [Google Scholar] [CrossRef]
- Pescaru, D.; Curiac, D.I. Anchor node localization for wireless sensor networks using video and compass information fusion. Sensors 2014, 14, 4211–4224. [Google Scholar] [CrossRef] [PubMed]
- Safa, H. A novel localization algorithm for large scale wireless sensor networks. Comput. Commun. 2014, 45, 32–46. [Google Scholar] [CrossRef]
- Woo, H.; Lee, S.; Lee, C. Range-free localization with isotropic distance scaling in wireless sensor networks. In Proceedings of the 2013 International Conference on Information Networking (ICOIN), Bangkok, Thailand, 28–30 January 2013; pp. 632–636.
- Oliveira, L.; Li, H.B.; Almeida, L.; Abrudan, T.E. Rssi-based relative localisation for mobile robots. Ad Hoc Netw. 2014, 13, 321–335. [Google Scholar] [CrossRef]
- Mao, G.; Fidan, B.; Anderson, B.D. Wireless sensor network localization techniques. Comput. Netw. 2007, 51, 2529–2553. [Google Scholar] [CrossRef]
- Kulakowski, P.; Vales-Alonso, J.; Egea-Lopez, E.; Ludwin, W.; Garcia-Haro, J. Angle-of-arrival localization based on antenna arrays for wireless sensor networks. Comput. Electr. Eng. 2010, 36, 1181–1186. [Google Scholar] [CrossRef]
- Xu, X.H.; Gao, X.Y.; Wan, J.; Xiong, N.X. Trust index based fault tolerant multiple event localization algorithm for WSNs. Sensors 2011, 11, 6555–6574. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Chen, L.; Xiao, Q.J.; Li, M.L. Reliable anchor-based sensor localization in irregular areas. IEEE Trans. Mob. Comput. 2010, 9, 60–72. [Google Scholar] [CrossRef]
- Zhong, S.; Jadliwala, M.; Upadhyaya, S.; Qiao, C. Towards a Theory of Robust Localization Against Malicious Beacon Nodes. In Proceedings of the 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008.
- Hwang, J.; He, T.; Kim, Y. Detecting Phantom Nodes in Wireless Sensor Networks. In Proceedings of the 26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 2391–2395.
- Liu, D.W.; Lee, M.C.; Wu, D. A node-to-node location verification method. IEEE Trans. Ind. Electron. 2010, 57, 1526–1537. [Google Scholar] [CrossRef]
- He, D.J.; Cui, L.; Huang, H.J.; Ma, M.D. Design and verification of enhanced secure localization scheme in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1050–1058. [Google Scholar] [CrossRef]
- Kuo, S.P.; Kuo, H.J.; Tseng, Y.C. The beacon movement detection problem in wireless sensor networks for localization applications. IEEE Trans. Mob. Comput. 2009, 8, 1326–1338. [Google Scholar] [CrossRef]
- Kuo, S.P.; Kuo, H.J.; Tseng, Y.C.; Lee, Y.F. Detecting Movement of Beacons in Location-Tracking Wireless Sensor Networks. In Proceedings of the 2007 IEEE 66th Vehicular Technology Conference, Baltimore, MD, USA, 30 September–3 October 2007; pp. 362–366.
- Zeng, Y.P.; Cao, J.N.; Hong, J.; Zhang, S.G.; Xie, L. Secure localization and location verification in wireless sensor networks: A survey. J. Supercomput. 2013, 64, 685–701. [Google Scholar] [CrossRef]
- Yang, Z.; Jian, L.R.; Wu, C.S.; Liu, Y.H. Beyond triangle inequality: Sifting noisy and outlier distance measurements for localization. ACM Trans. Sens. Netw. 2013, 9. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, C.S.; Chen, T.; Zhao, Y.Y.; Gong, W.; Liu, Y.H. Detecting outlier measurements based on graph rigidity for wireless sensor network localization. IEEE Trans. Veh. Technol. 2013, 62, 374–383. [Google Scholar] [CrossRef]
- Garg, R.; Varna, A.L.; Wu, M. An efficient gradient descent approach to secure localization in resource constrained wireless sensor networks. IEEE Trans. Inf. Forensics Secur. 2012, 7, 717–730. [Google Scholar] [CrossRef]
- Srinivasan, A.; Teitelbaum, J.; Wu, J. Drbts: Distributed Reputation-based Beacon Trust System. In Proceedings of the 2nd IEEE International Symposium on Dependable, Autonomic and Secure Computing, Indianapolis, IN, USA, 29 September–1 October 2006; pp. 277–283.
- Wei, Y.W.; Guan, Y. Lightweight location verification algorithms for wireless sensor networks. IEEE Trans Parallel Distrib. Syst. 2013, 24, 938–950. [Google Scholar] [CrossRef]
- Xia, M.; Sun, P.L.; Wang, X.Y.; Jin, Y.; Chen, Q.Z. Distributed beacon drifting detection for localization in unstable environments. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O.; Moses, R.L.; Correal, N.S. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Moore, D.; Leonard, J.; Rus, D.; Teller, S. Robust Distributed Network Localization with Noisy Range Measurements. In Proceedings of the 2nd international conference on Embedded networked sensor systems, Baltimore, MD, USA, 3–5 November 2004; pp. 50–61.
- Kannan, A.A.; Fidan, B.; Mao, G. Robust distributed sensor network localization based on analysis of flip ambiguities. In Proceedings of the Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6.
- Yang, Z.; Liu, Y. Quality of trilateration: Confidence-based iterative localization. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 631–640. [Google Scholar] [CrossRef]
- Sheu, J.P.; Hu, W.K.; Lin, J.C. Distributed localization scheme for mobile sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 516–526. [Google Scholar] [CrossRef]
- Zou, Y.; Chakrabarty, K. Sensor Deployment and Target Localization based on Virtual Forces. In Proceedings of the Twenty-Second Annual Joint Conference of the IEEE Computer and Communications, San Francisco, CA, USA, 30 March–3 April 2003; pp. 1293–1303.
- Dang, V.H.; Le, V.D.; Lee, Y.K.; Lee, S. Distributed push–pull estimation for node localization in wireless sensor networks. J. Parallel Distrib. Comput. 2011, 71, 471–484. [Google Scholar] [CrossRef]
- Alfaro, J.; Barbeau, M.; Kranakis, E. Secure Localization of Nodes in Wireless Sensor Networks with Limited Number of Truth Tellers. In Proceedings of the Seventh Annual Communication Networks and Services Research Conference, Moncton, NB, Canada, 11–13 May 2009; pp. 86–93.
- Dixon, W.J.; Massey, F.J. Regression and Correlation. In Introduction to statistical analysis; McGraw-Hill: New York, NY, USA, 1969; Volume 344, pp. 189–201. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, C.; Dai, G.; Ying, K.; Chen, Q. Collaborative Localization and Location Verification in WSNs. Sensors 2015, 15, 10631-10649. https://doi.org/10.3390/s150510631
Miao C, Dai G, Ying K, Chen Q. Collaborative Localization and Location Verification in WSNs. Sensors. 2015; 15(5):10631-10649. https://doi.org/10.3390/s150510631
Chicago/Turabian StyleMiao, Chunyu, Guoyong Dai, Kezhen Ying, and Qingzhang Chen. 2015. "Collaborative Localization and Location Verification in WSNs" Sensors 15, no. 5: 10631-10649. https://doi.org/10.3390/s150510631
APA StyleMiao, C., Dai, G., Ying, K., & Chen, Q. (2015). Collaborative Localization and Location Verification in WSNs. Sensors, 15(5), 10631-10649. https://doi.org/10.3390/s150510631





