Research on Joint Parameter Inversion for an Integrated Underground Displacement 3D Measuring Sensor
Abstract
:1. Introduction
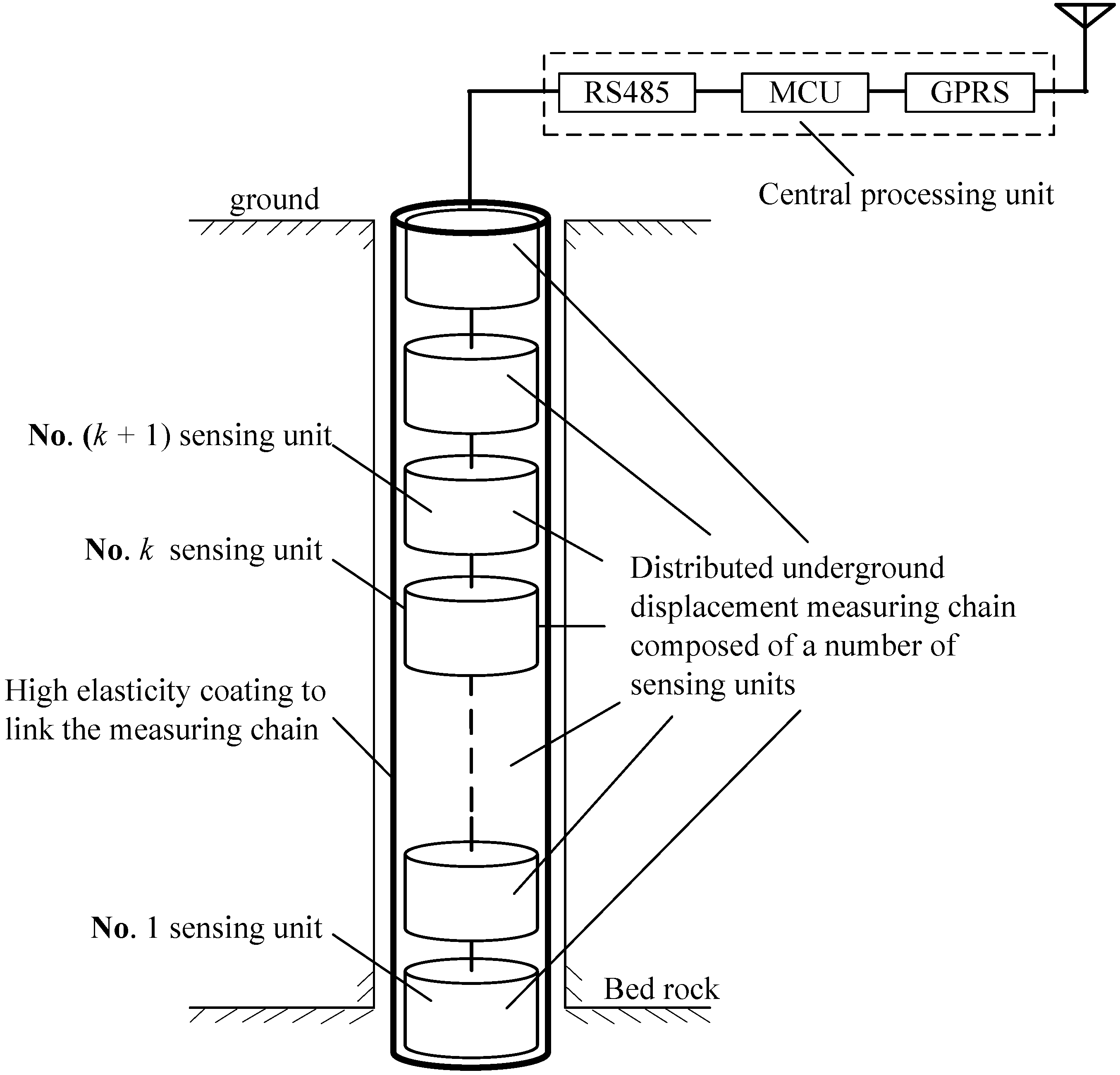
- (1)
- Simple structure, convenient manufacturing and relatively low cost.
- (2)
- Relatively convenient installation and good portability thanks to its measuring chain assembly.
- (3)
- Big measuring range, quite high measuring and positing accuracy.
- (4)
- Good consistency between the measured and the actual deformation of geotechnical mass, thanks to the flexible structure of the sensing unit measuring array, where each sensing unit can freely move and deform accompanying the movement of the surrounding geotechnical mass.
- (5)
- Three-dimensional measurement of the geotechnical underground displacement, rather than one-dimensional measurement by most of the existing instruments.
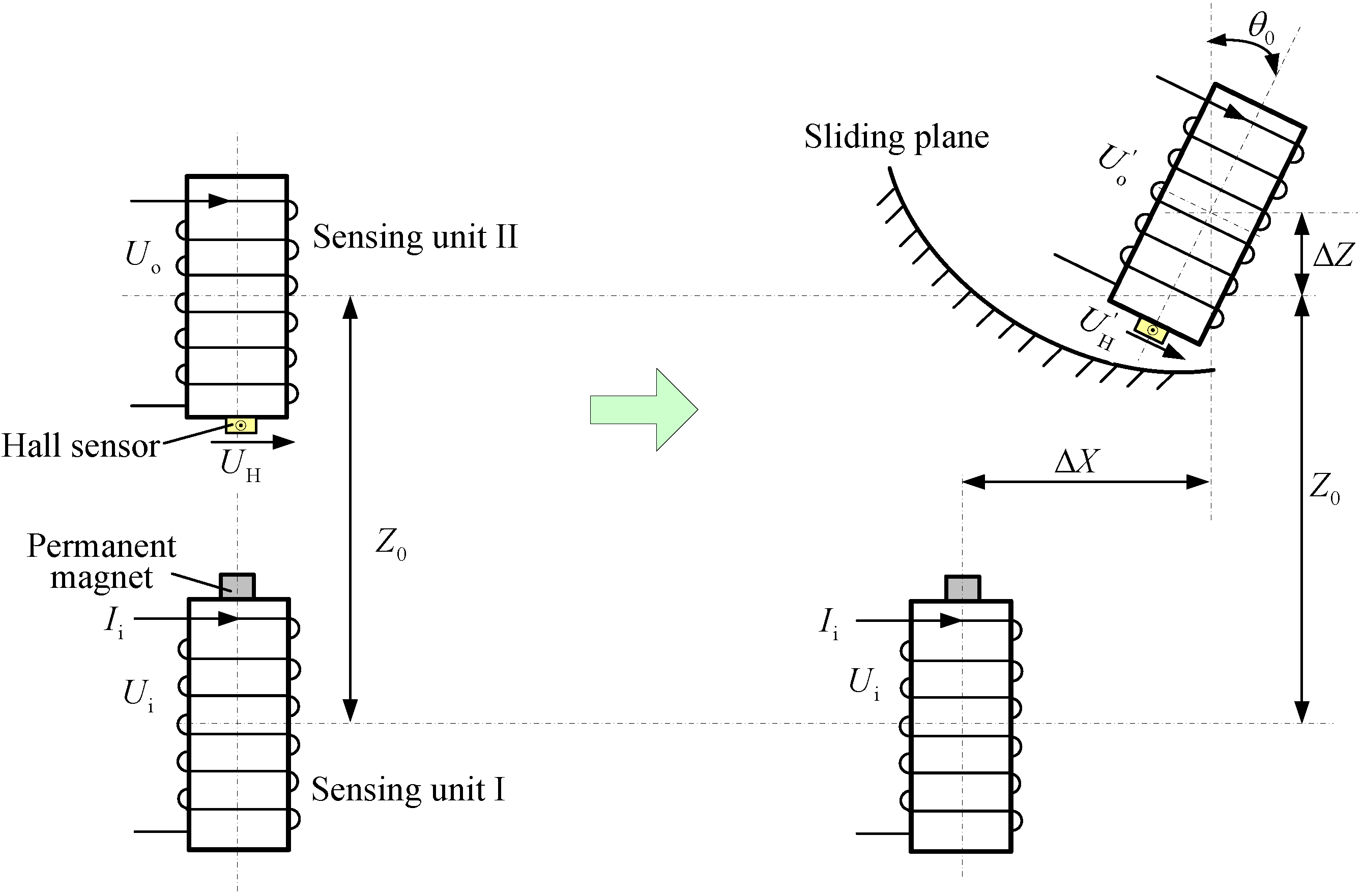
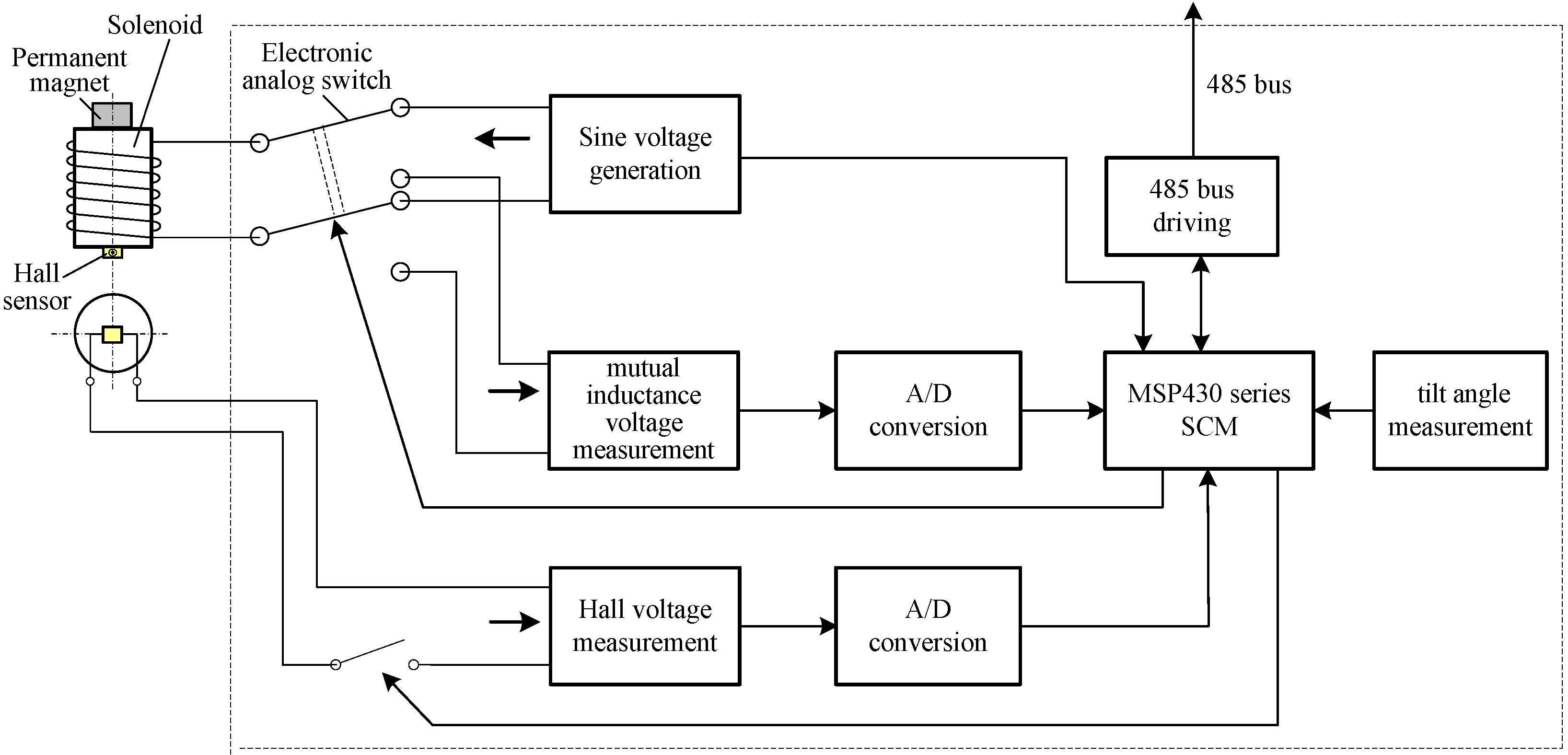
2. Sensor Working Principle and Theoretical Modeling
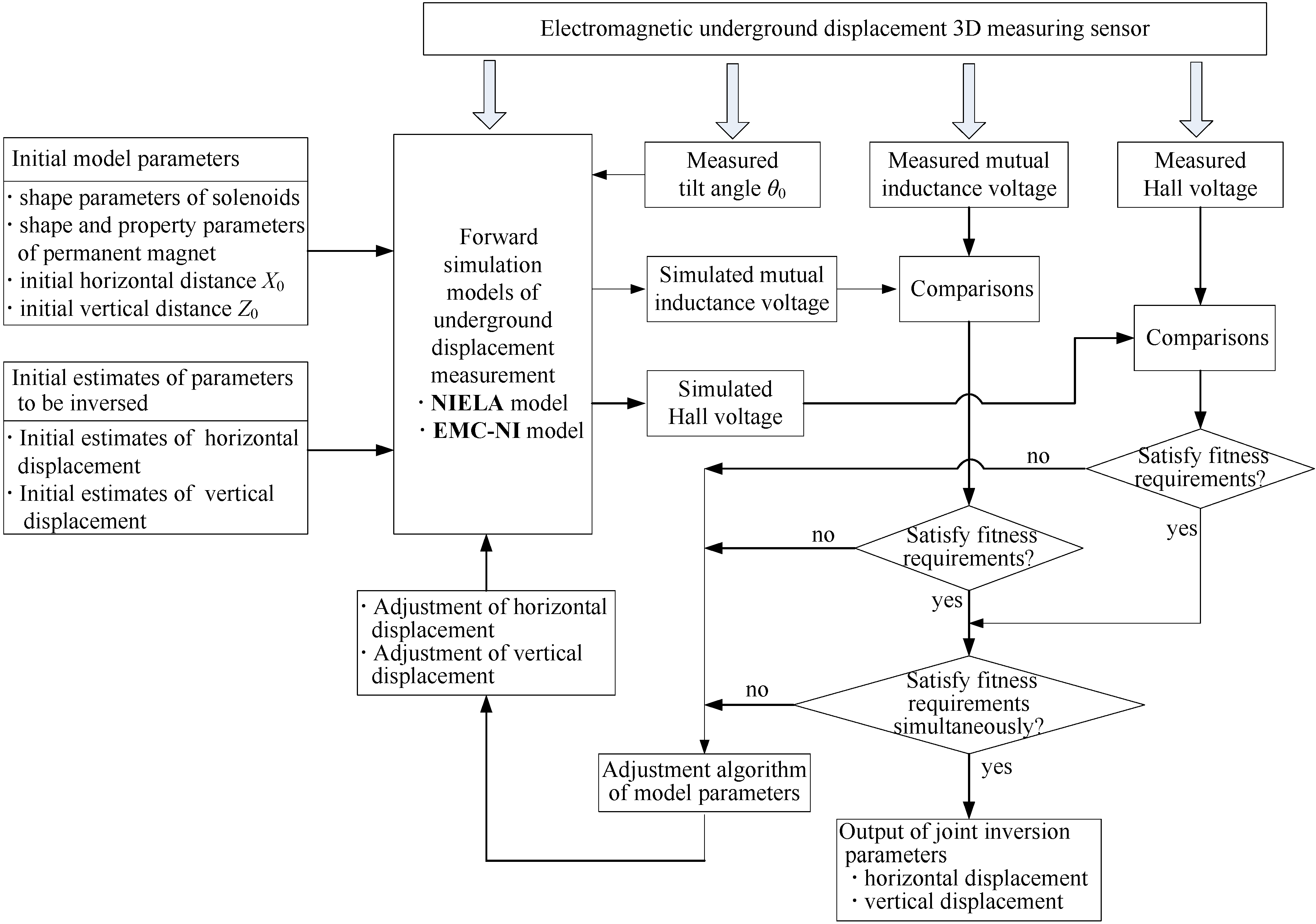
3. Underground Displacement Parameter Joint Inversion Method
- (1)
- Data collected from the unknown system should be as precise and timely as possible;
- (2)
- The calculation model to describe the unknown system should be sensible and representative;
- (3)
- The parameter adjustment algorithm must be efficient and convergent.
- (1)
- Data acquisition of mutual inductance voltage Uo, Hall voltage UH and tilt angle θ0 for the proposed sensor. The data may come from two ways: Usually, it is the on-site measuring results when the sensor has been buried into the monitored rock and soil masses for months or years. Sometimes, it can be the experimental measurement values for sensor testing and research purposes, where the values of relative displacement and tilt angle (ΔX, ΔZ, θ0) between two adjacent sensing units are artificially varied, so as to measure and record the synchronous variations of Uo and UH. In this paper, the latter way is adopted.
- (2)
- Execution of the NIELA and EMC-NI joint forward simulation process. The initial model parameters and the initial estimate values of relative horizontal displacement and vertical displacement are fed into the execution programs of the forward simulation models. Therefore, the simulated values of mutual inductance voltage and Hall voltage can be generated. The initial model parameters include the geometrical and property parameters of the solenoids and permanent magnets.
- (3)
- Execution of the joint optimization inverse process. Make a combined comparison between the simulated values of the mutual inductance voltage and Hall voltage obtained in Step (2) with the corresponding measured values in Step (1) and gradually adjust the relative horizontal displacement and vertical displacement values by the joint parameters modification algorithm. This process continues until not only the fitness between the simulated and the measured mutual inductance voltage can meet the required accuracy (or gets the minimum discrepancy under certain conditions), but also the fitness between the simulated and measured Hall voltage achieves optimality under specified constrains. The final iterative results are then output as the joint inversion results of horizontal displacement ΔX and vertical displacement ΔZ for the proposed sensor. They can be treated as the measuring values of relative horizontal displacement and vertical displacement at some underground depth where the corresponding sensing units are buried. The iterative values of ΔX and ΔZ combined with the measured value of relative tilt angle θ0 constitute the complete monitoring results at the corresponding subsurface depth within the monitored geological mass for the proposed 3D sensor.
4. Experiments and Verifications of Underground Displacement Joint Inversion
4.1. Experiment Setup and Procedure
4.1.1. Experiment Equipment
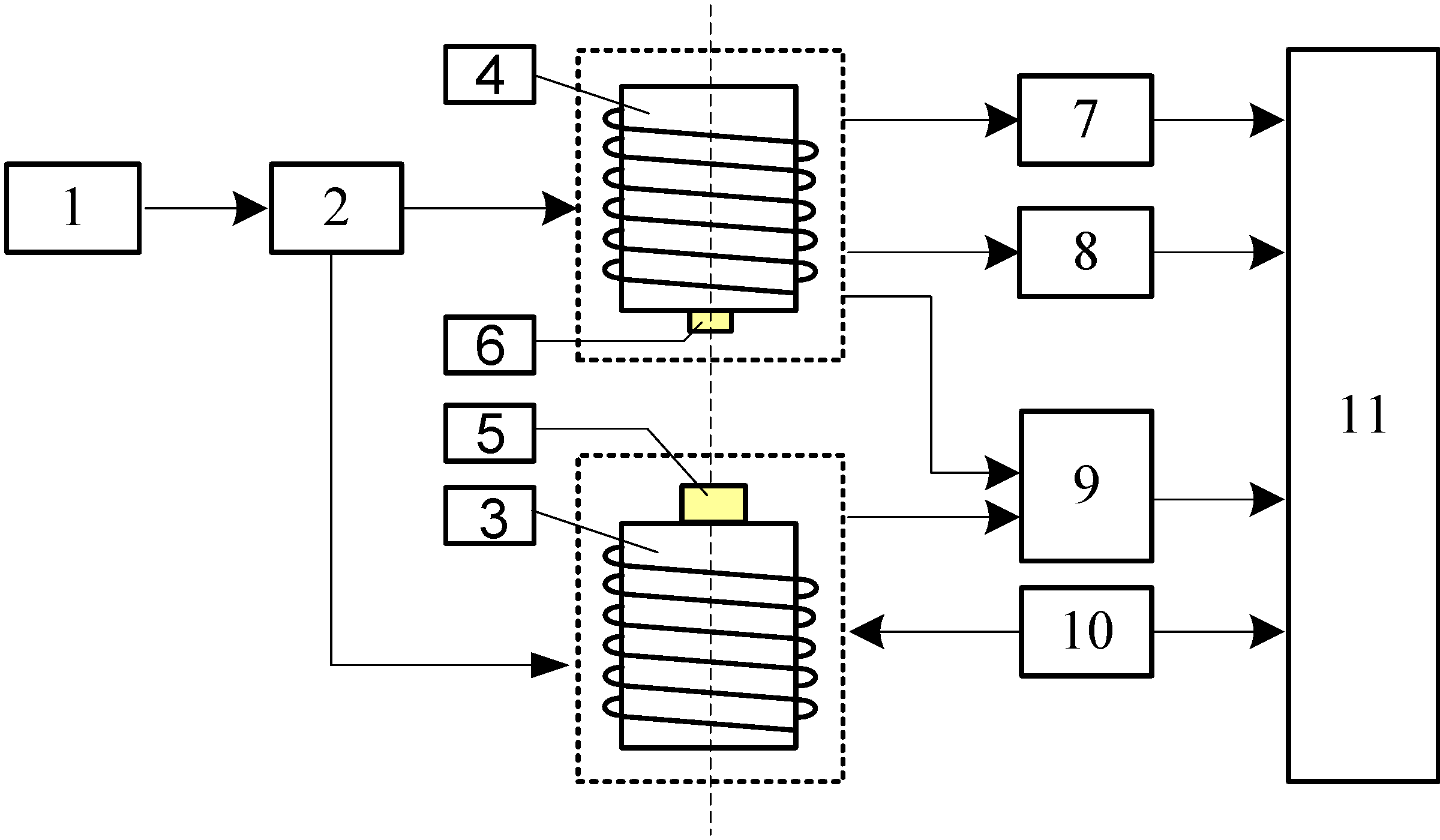
4.1.2. Experiment and Evaluation Scheme
- (1)
- Before the experiment, the initial vertical distance Z0 and axial tilt angle θ0 for the proposed sensor are set as fixed values, and the initial horizontal distance X0 is set as zero. During the experiment, we change point-by-point the sensor’s relative horizontal displacement ∆Xi (i = 1, 2, …, m) and vertical displacement ∆Zj (j = 1, 2, …, n) and record the synchronous output values of the mutual inductance voltage Uoij and Hall voltage UHij, thus forming the variation sequences of measured mutual inductance voltage Uo = {Uo11, Uo12, …, Uomn} and Hall voltage UH = {UH11, UH12, …, UHmn} required by the parameter inversion process. Meanwhile, these two sets of measured horizontal displacement and vertical displacement variable series ∆X = {∆X1, ∆X2, …, ∆Xm} and ∆Z = {∆Z1, ∆Z2, …, ∆Zm} can be treated as the true (measured) values of horizontal displacement and vertical displacement needing inversing for the proposed sensor.
- (2)
- Both the initial model parameters and the trial estimate sequences of horizontal displacement and vertical displacement (ΔX' and ΔZ') are input into the NIEAL and EMC-NI joint forward simulation models. The initial model parameters include two parts: (i) shape parameters, mainly composed of the diameter d = 75 mm, length a = 70 mm, coil turns w = 400 of Solenoid I and II, the diameter D = 7.5 mm and height H = 18 mm of the permanent magnet; (ii) initial geometric position parameters, representing by Z0, X0 and θ0 and setting as the same values as in Step (1).
- (3)
- Execution of the joint forward simulation-optimization inversion procedure on every point pair [Uoij, UHij] of the measured sequences of mutual inductance voltage Uoi and Hall voltage UHij, to figure out the inversed values of horizontal displacement ∆X'i and vertical displacement ∆Z'j; then arranging ∆X'i and ∆Z'j chronologically to form the complete inversed sequence of ∆X' = {∆X'1, ∆X'2, …, ∆X'm} and ∆Z' = {∆Z'1, ∆Z'2, …, ∆Z'n}.
- (4)
- Making the deviation calculation and fitting analysis between the inversed series of horizontal displacement and vertical displacement in Step (3) with their corresponding measured series in Step (4), so as to testify to the suitability and stability of the proposed joint parameter inversion method.
4.2. Evaluation of Parameter Inversion Experiments
4.2.1. Experiments and Parameter Inversion 1
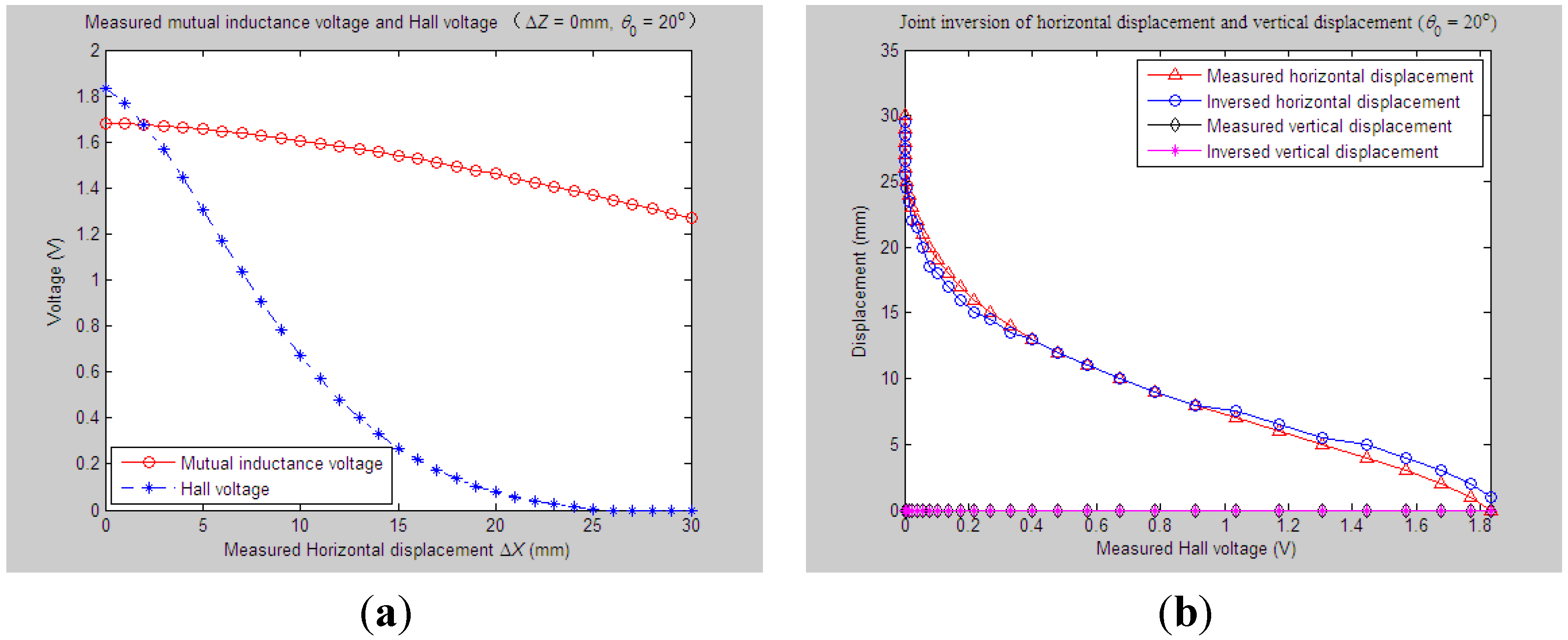
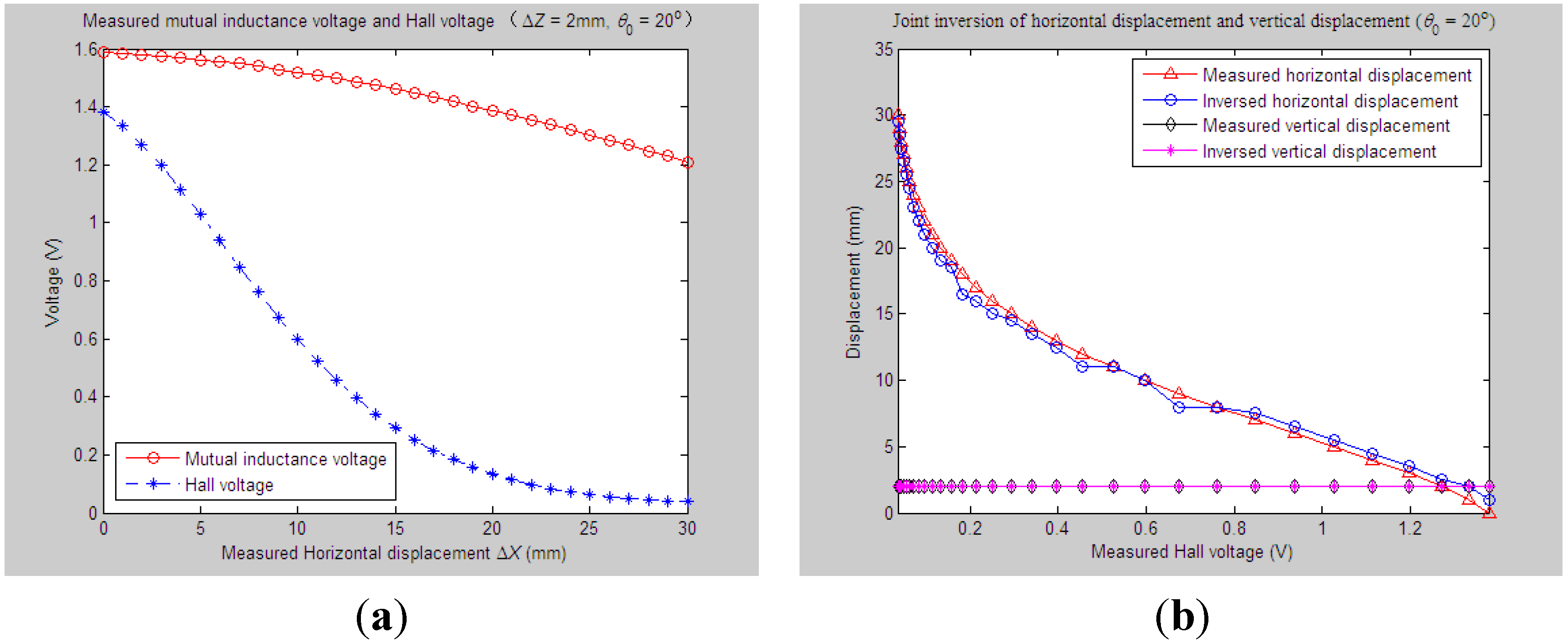
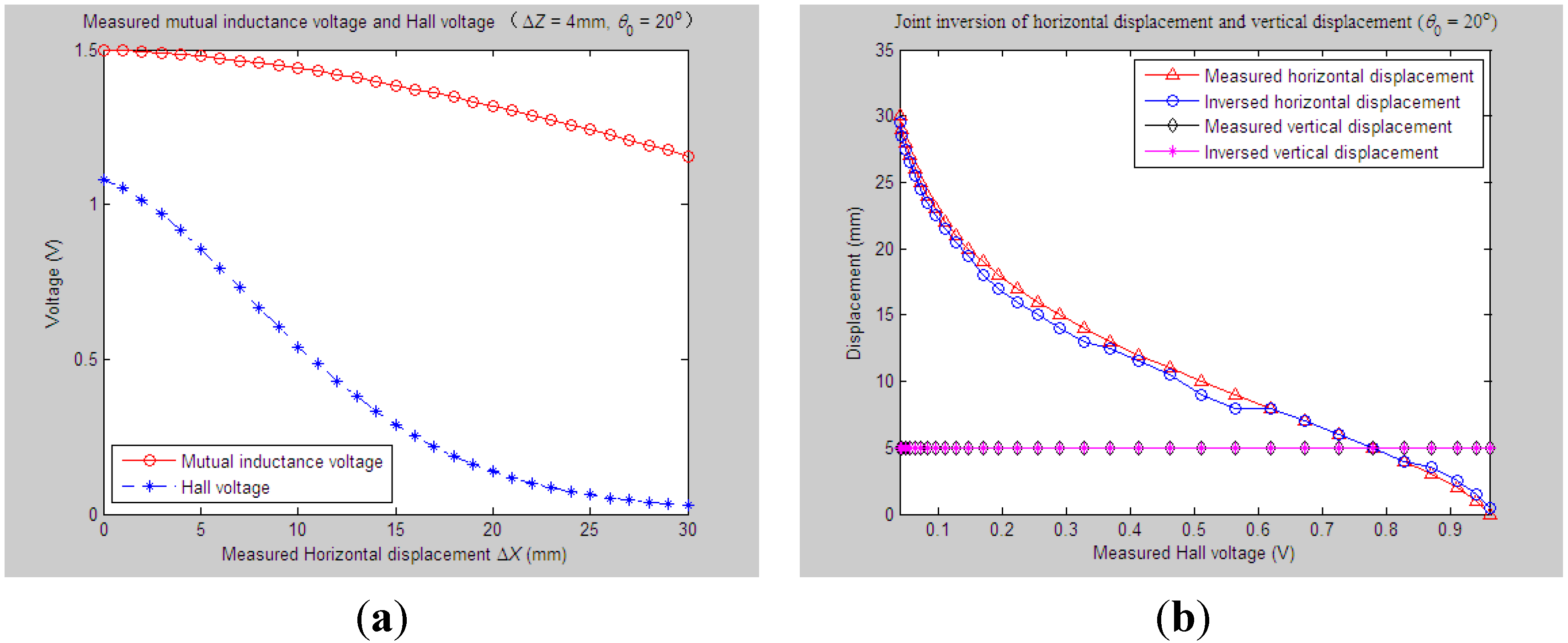
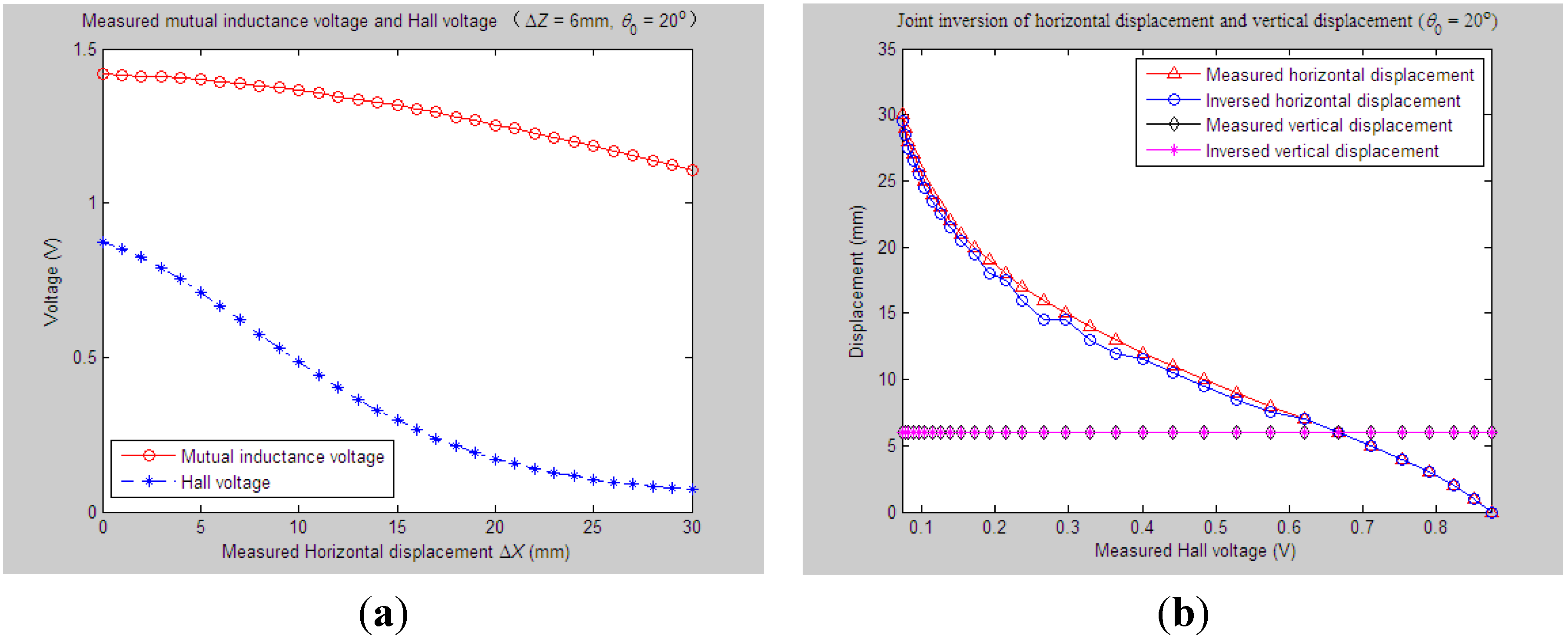
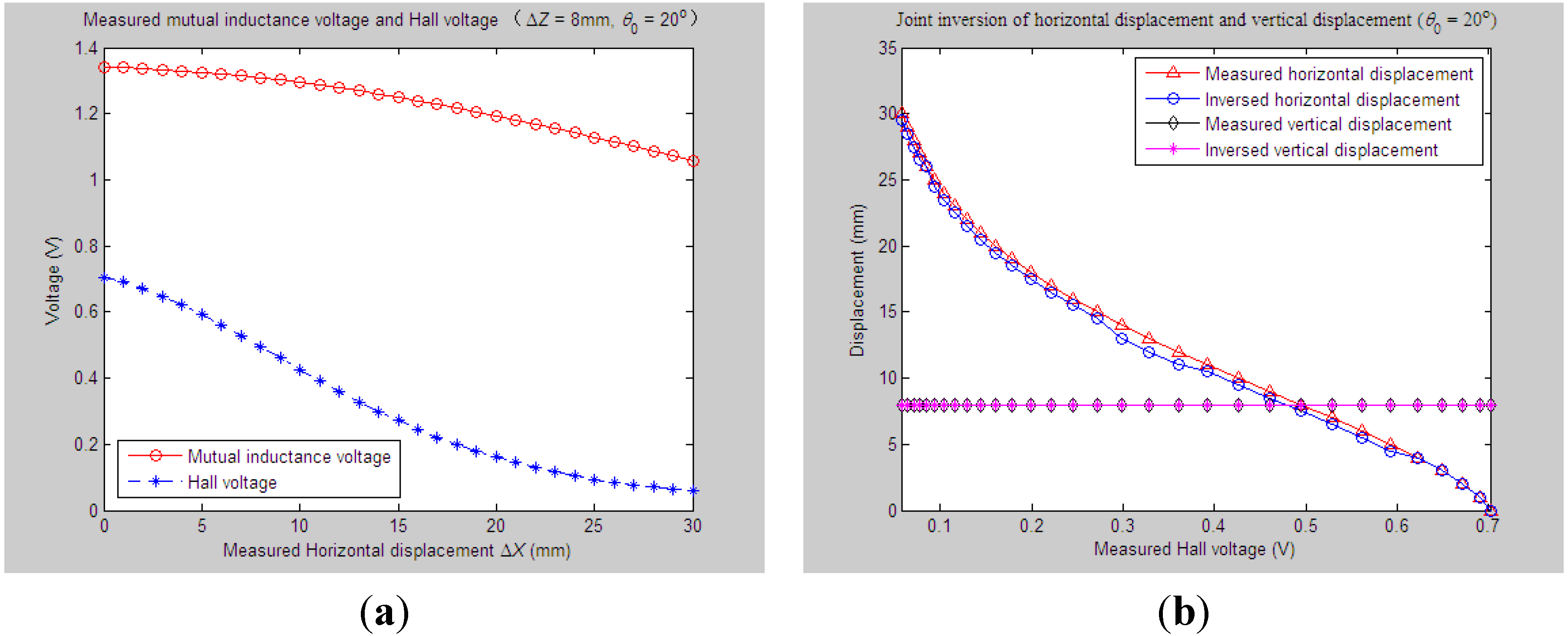
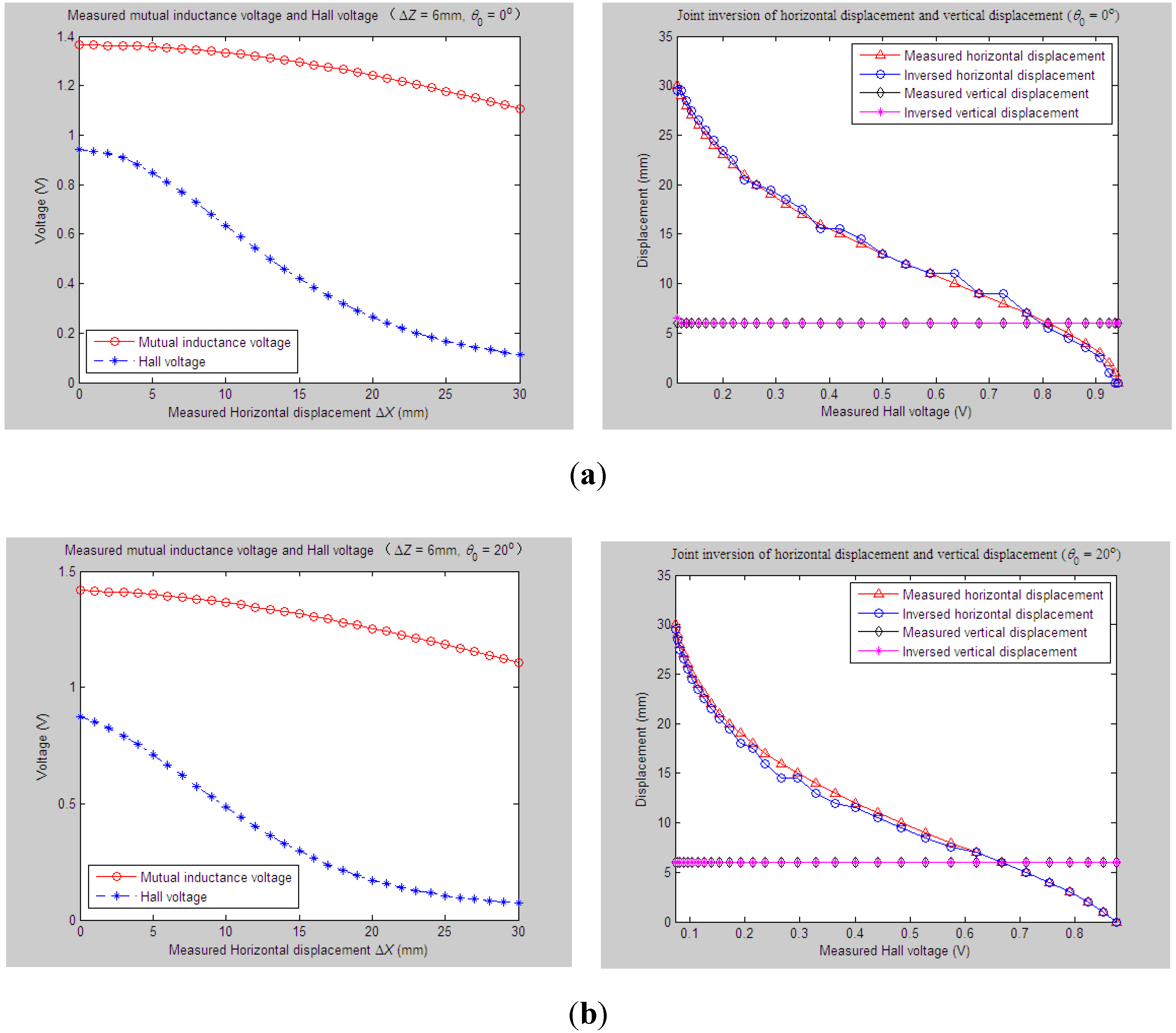
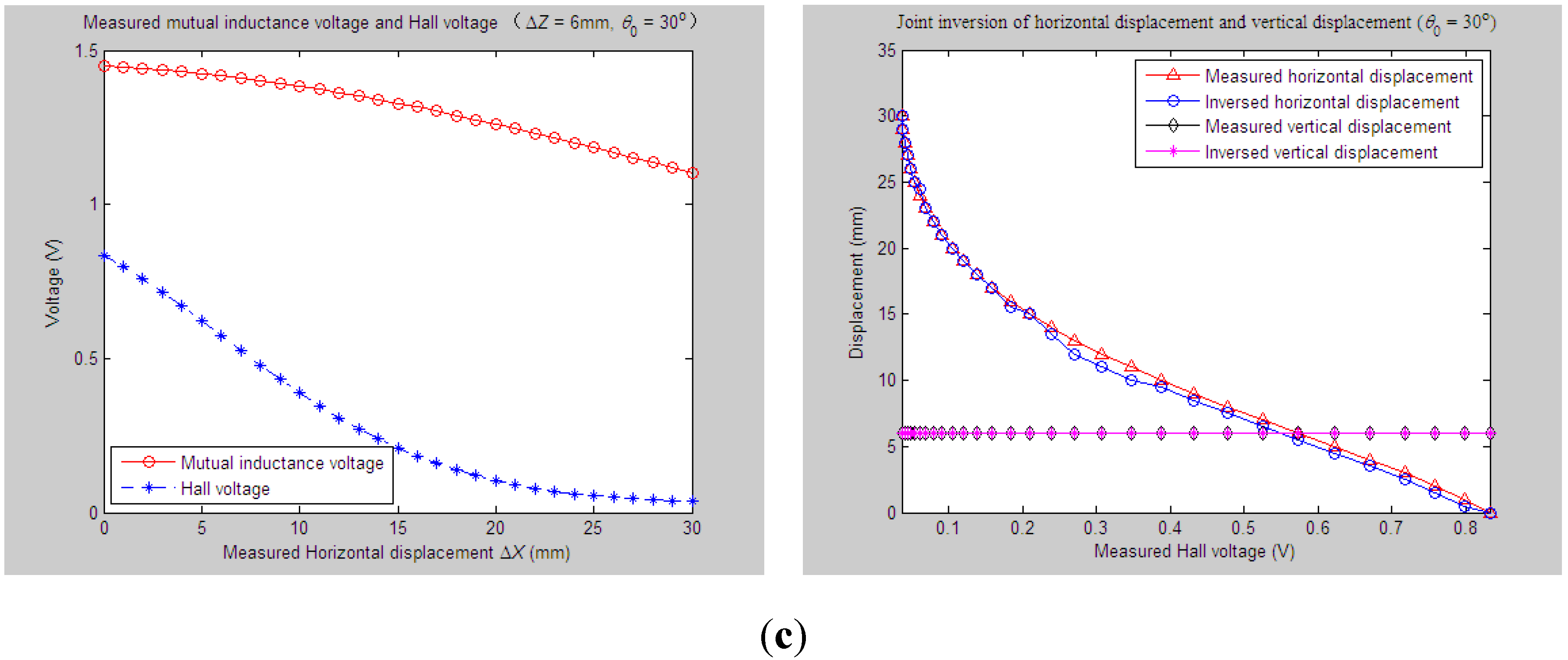
4.2.2. Experiments and Parameter Inversion 2
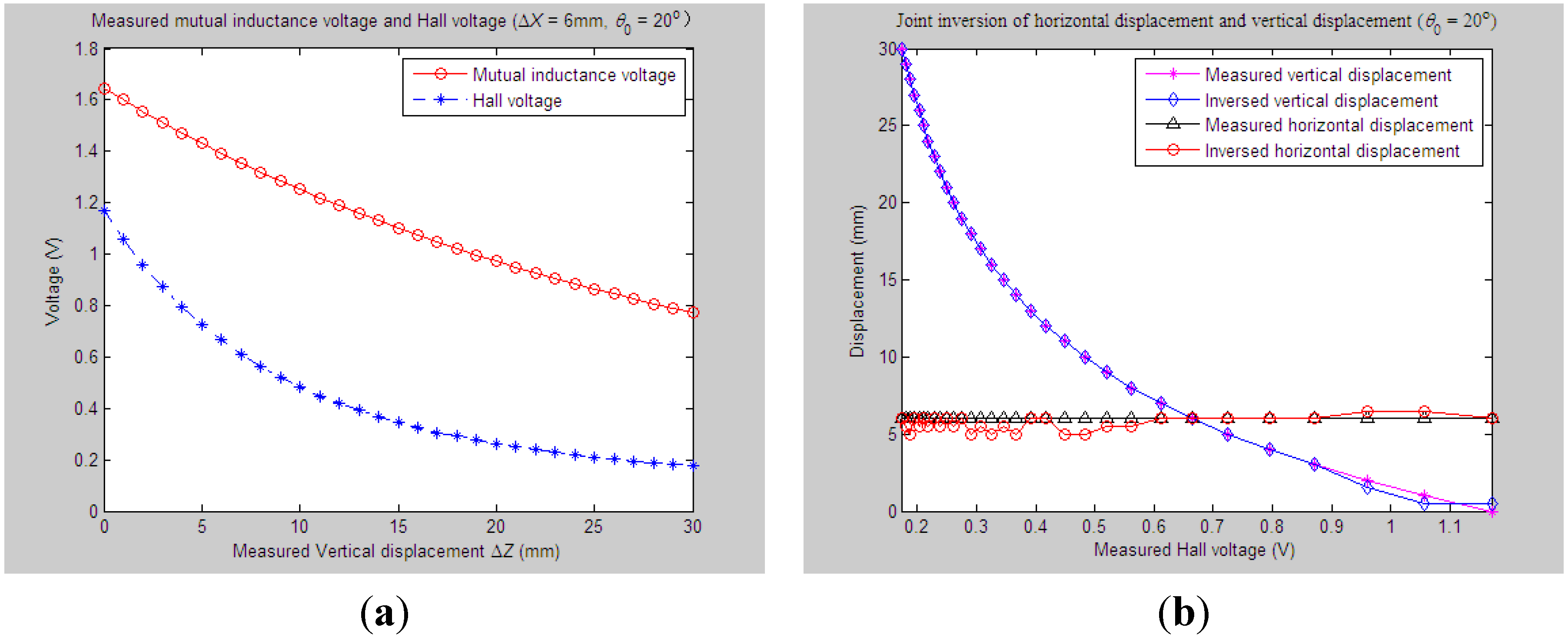
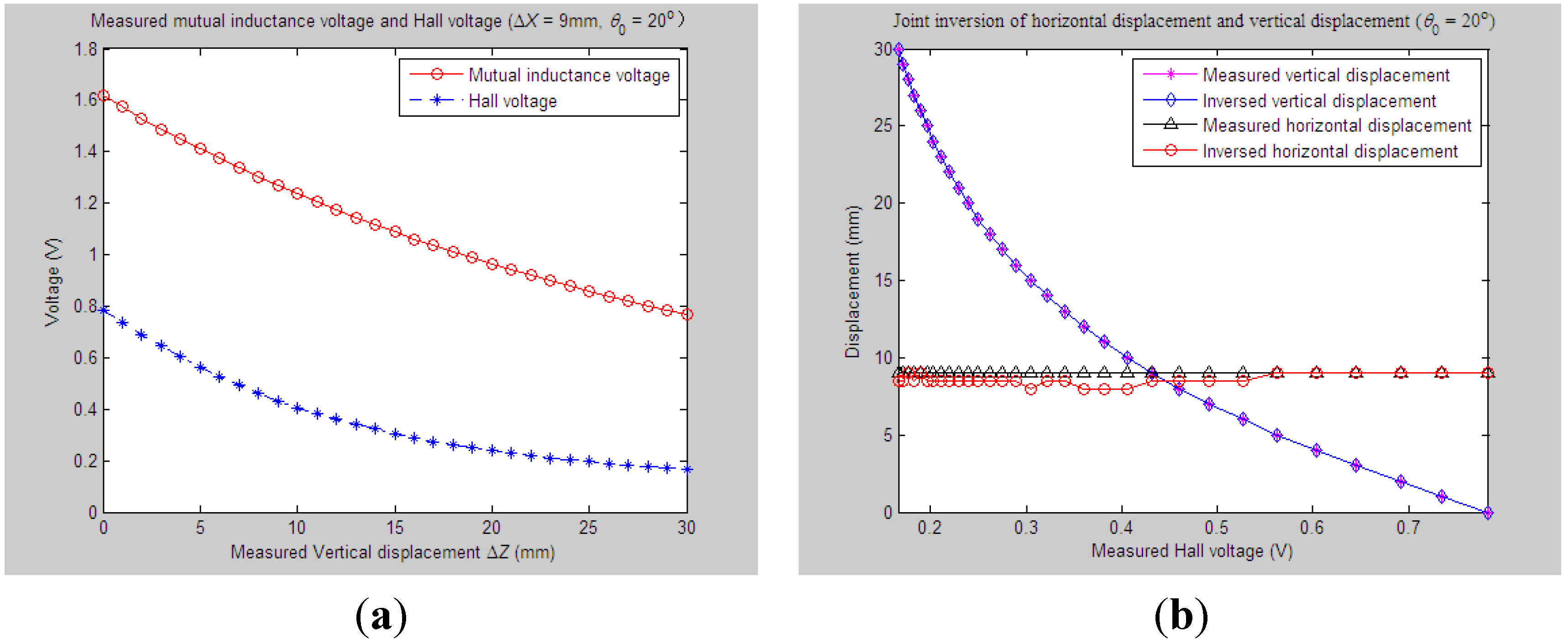
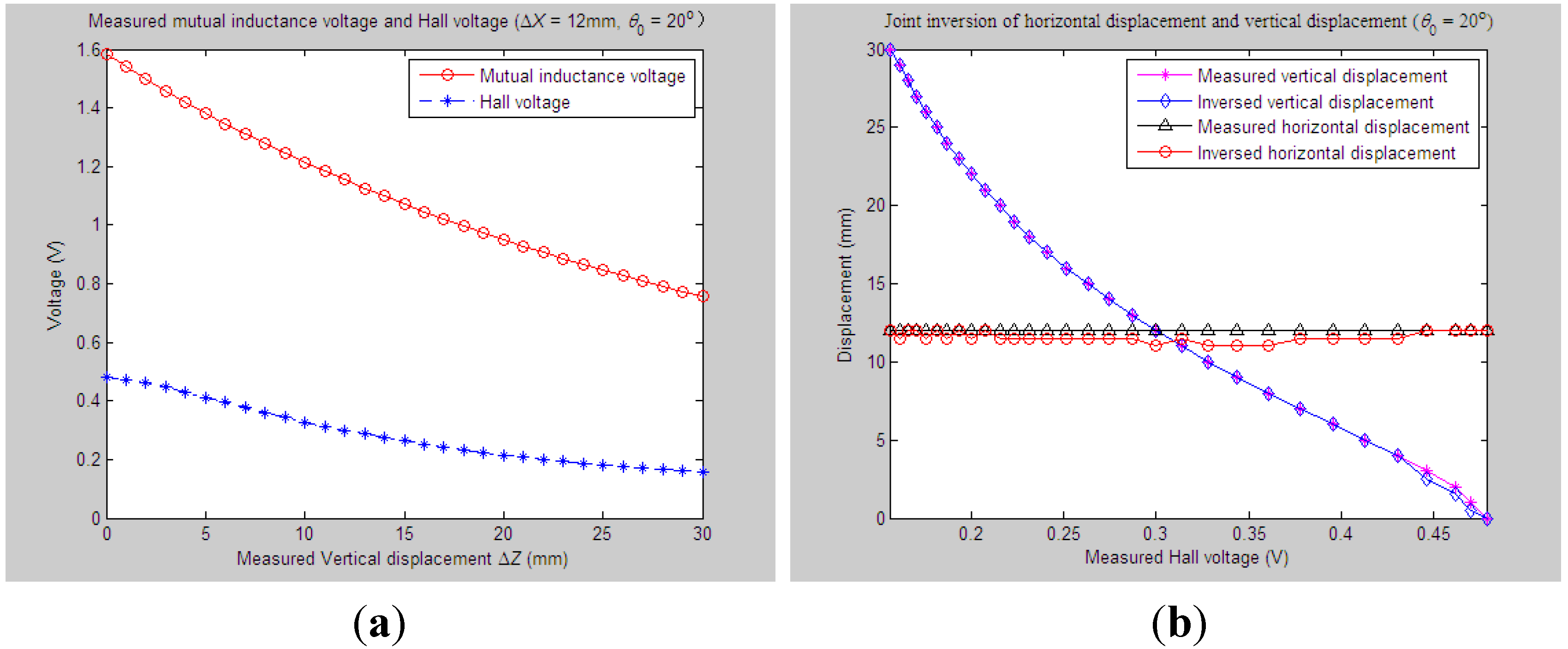
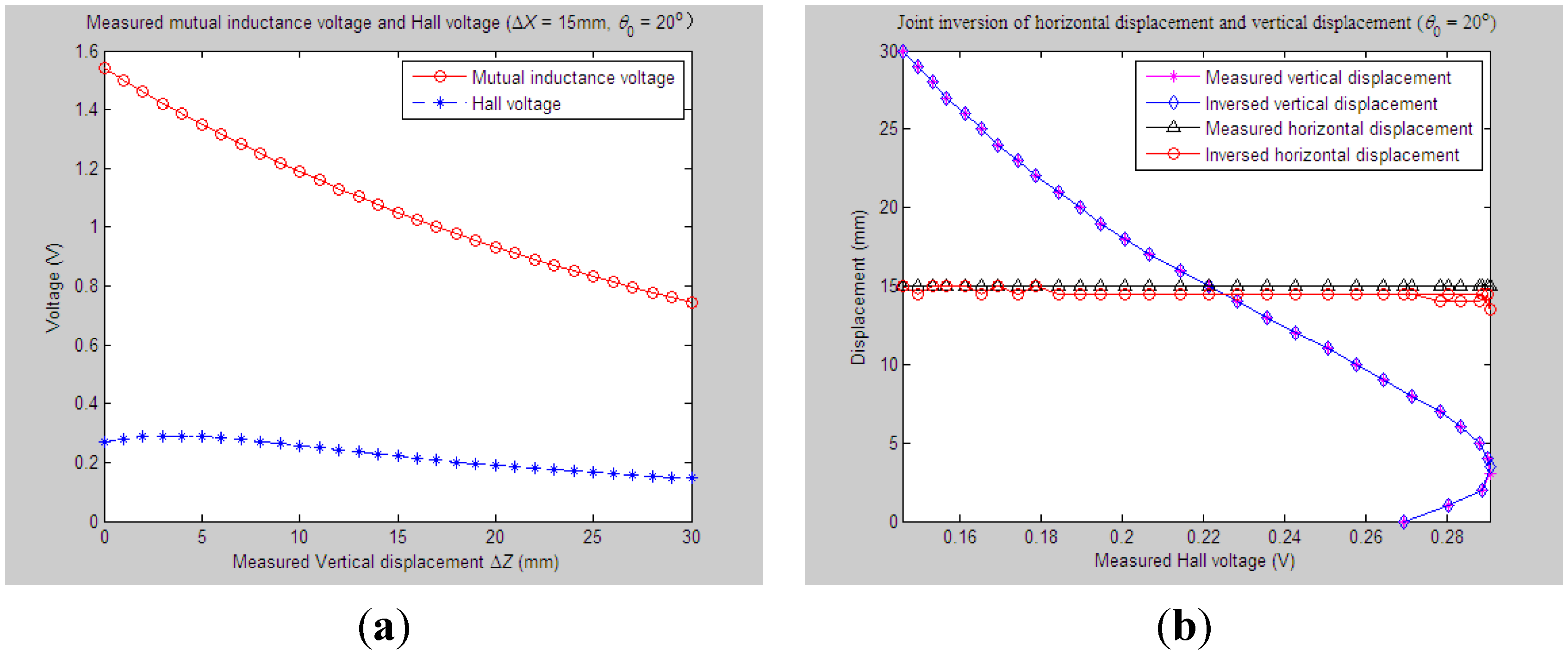
4.2.3. Experiments and Parameter Inversion 3
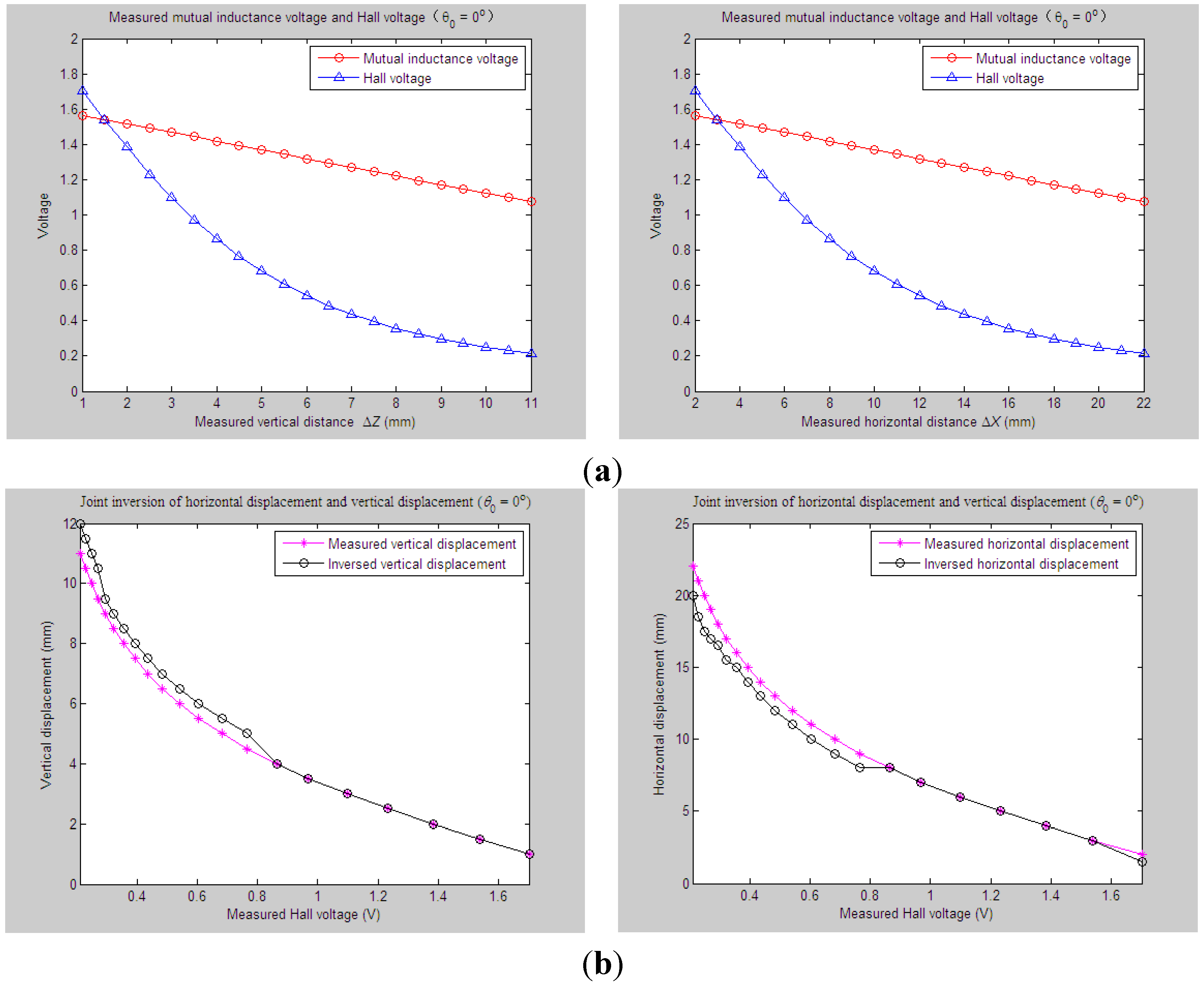
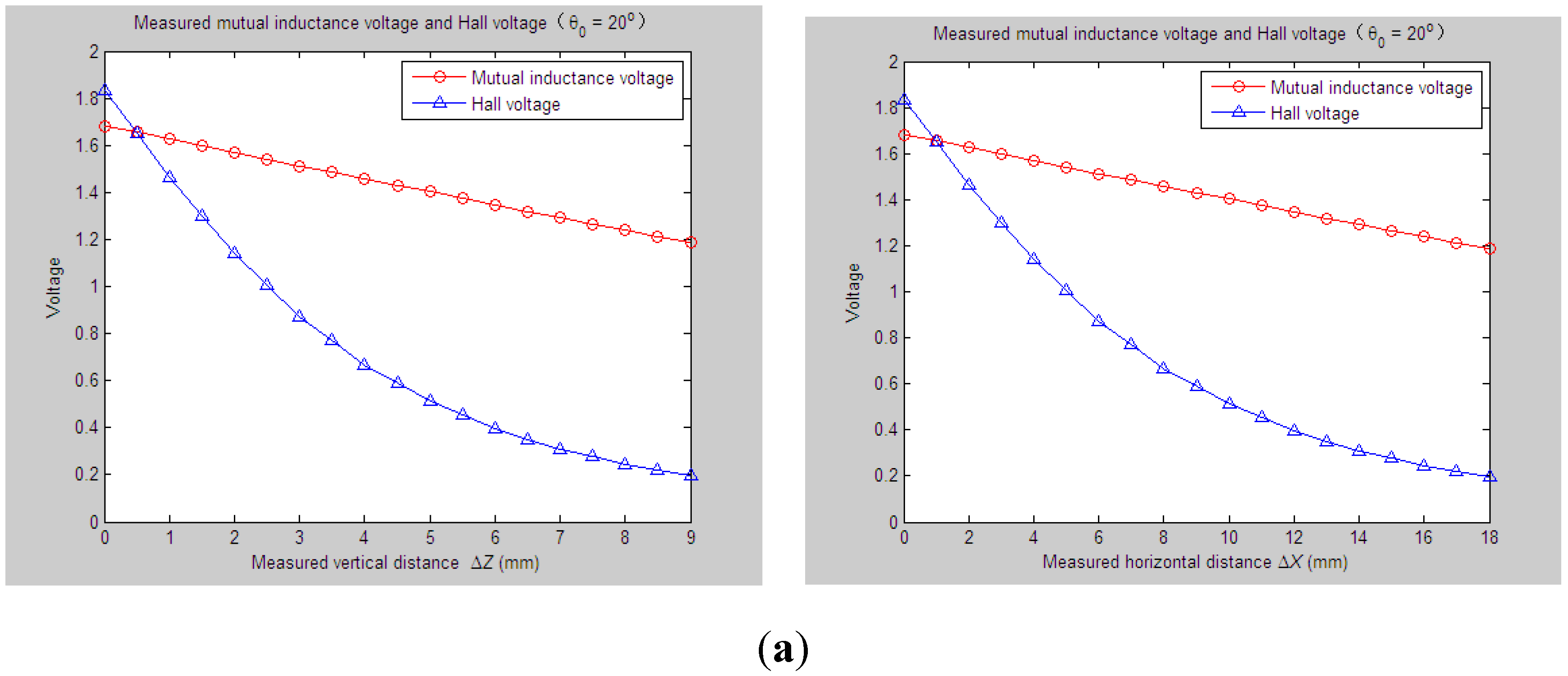
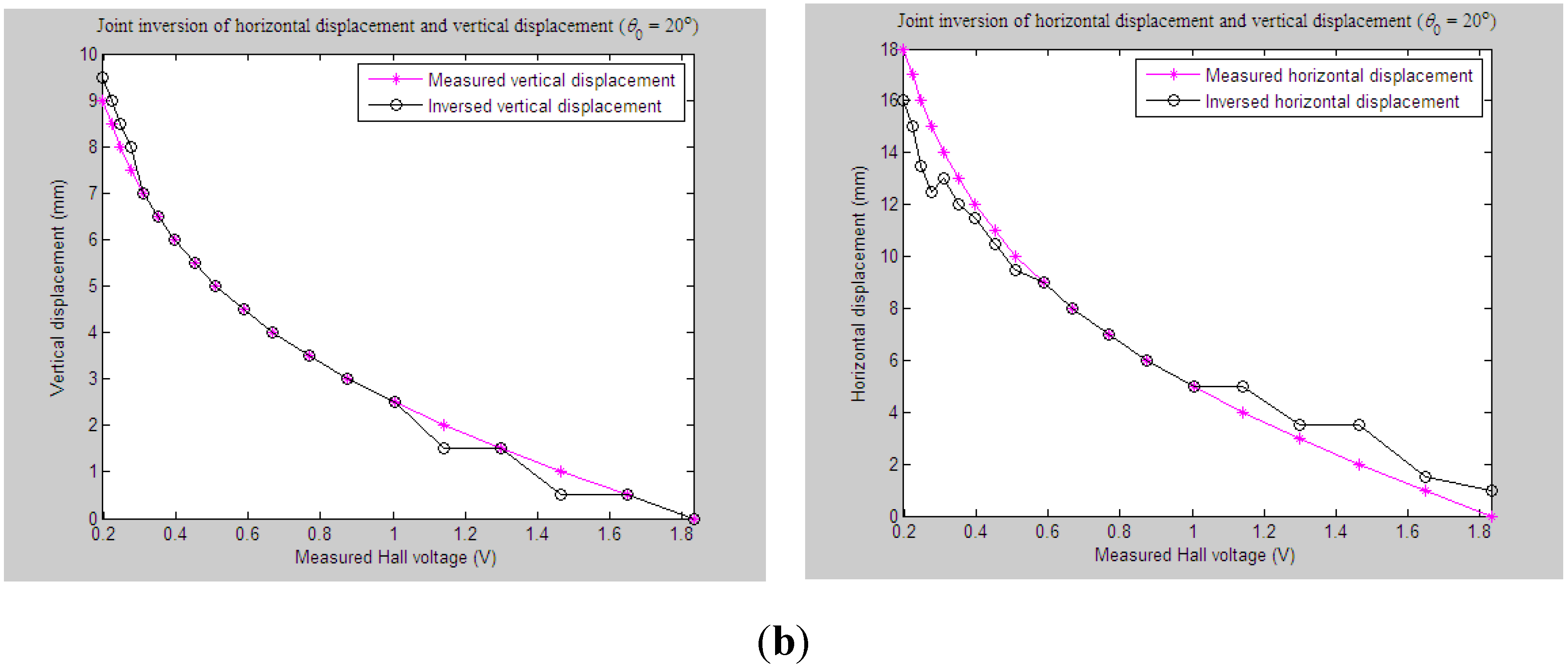
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, F.; Okuno, T.; Matsumoto, T. Deformation characteristics and influential factors for the giant Jinnosuke-dani landslide in the Haku-san Mountain area, Japan. Landslides 2006, 4, 19–31. [Google Scholar] [CrossRef]
- Bayoumi, A. On the Evaluation of Settlement Measurements Using Borehole Extensometers. Geotech. Geol. Eng. 2011, 29, 75–90. [Google Scholar] [CrossRef]
- Picarelli, L.; Urciuoli, G.; Ramondini, M.; Comegna, L. Main features of mudslides in tectonised highly fissured clay shales. Landslides 2005, 2, 15–30. [Google Scholar] [CrossRef]
- Zhu, W.S.; Li, X.J.; Zhang, Q.B.; Zheng, W.H.; Xin, X.L.; Sun, A.H.; Li, S.C. A study on sidewall displacement prediction and stability evaluations for large underground power station caverns. Int. J. Rock Mech. Min. Sci. 2010, 47, 1055–1062. [Google Scholar] [CrossRef]
- Li, X.J.; Yang, W.M.; Wang, L.G.; Butler, I.B. Displacement Forecasting Method in Brittle Crack Surrounding Rock Under Excavation Unloading Incorporating Opening Deformation. Rock Mech. Rock Eng. 2014, 47, 2211–2223. [Google Scholar] [CrossRef]
- Zhang, J.F.; Chen, J.J.; Wang, J.H.; Zhu, Y.F. Prediction of tunnel displacement induced by adjacent excavation in soft soil. Tunn. Undergr. Space Technol. 2013, 36, 24–33. [Google Scholar] [CrossRef]
- Ran, L.; Ye, X.W.; Zhu, H.H. Long-Term Monitoring and Safety Evaluation of A Metro Station During Deep Excavation. Proc. Eng. 2011, 14, 785–792. [Google Scholar] [CrossRef]
- Barla, G.; Antolini, F.; Barla, M.; Mensi, E.; Piovano, G. Monitoring of the Beauregard landslide (Aosta Valley, Italy) using advanced and conventional techniques. Eng. Geol. 2010, 116, 218–235. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, H.; Gao, Y.; Li, X. Real-time monitoring and early warning of landslides at relocated Wushan Town, the Three Gorges Reservoir, China. Landslides 2010, 7, 339–349. [Google Scholar] [CrossRef]
- Yin, H.Y.; Wei, J.C.; Guo, J.B.; Li, Z.J.; Zhu, Z.W.; Guan, Y.Z.; Liu, R.X.; Hu, D.X. Dynamic monitoring research on displacement of rock mass in coal seam floor on the 1604 workface in NanTun coalmine, Shandong Province, China. Proc. Eng. 2011, 26, 876–882. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, Y.S.; Shen, S.L.; Sun, W.J. Field performance of underground structures during shield tunnel construction. Tunn. Undergr. Space Technol. 2012, 28, 272–277. [Google Scholar] [CrossRef]
- Abdellah, W.; Raju, G.D.; Mitri, H.S.; Thibodeau, D. Stability of underground mine development intersections during the life of a mine plan. Int. J. Rock Mech. Min. Sci. 2014, 72, 173–181. [Google Scholar]
- Bhalla, S.; Yang, Y.W.; Zhao, J.; Soh, C.K. Structural health monitoring of underground facilities—Technological issues and challenges. Tunn. Undergr. Space Technol. 2005, 20, 487–500. [Google Scholar] [CrossRef]
- Stark, T.D.; Choi, H. Slope inclinometers for landslides. Landslides 2008, 5, 339–350. [Google Scholar] [CrossRef]
- Dowding, C.H.; Dussud, M.L.; Kane, W.F.; Connor, K.M.O. Monitoring Deformation in rock and soil with TDR sensor cables. Geotech. News 2003, 21, 51–59. [Google Scholar]
- Antunes, P.; Rodrigues, H.; Travanca, R.; Ferreira, L.; Varum, H.; André, P. Structural health monitoring of different geometry structures with optical fiber sensors. Photon. Sens. 2012, 2, 357–365. [Google Scholar] [CrossRef]
- Rodrigues, C.; Cavadas, F.; Félix, C.; Figueiras, J. FBG based strain monitoring in the rehabilitation of a centenary metallic bridge. Eng. Struct. 2012, 44, 281–290. [Google Scholar] [CrossRef]
- Habel, W.R.; Krebber, K. Fiber-optic sensor applications in civil and geotechnical engineering. Photon. Sens. 2011, 1, 268–280. [Google Scholar] [CrossRef]
- Zhu, H.H.; Ho, A.N.L.; Yin, J.H.; Sun, H.W.; Pei, H.F.; Hong, C.Y. An optical fibre monitoring system for evaluating the performance of a soil nailed slope. Smart Struct. Syst. 2012, 9, 393–410. [Google Scholar] [CrossRef]
- Pei, H.F.; Yin, J.H.; Zhu, H.H.; Hong, C.Y.; Jin, W.; Xu, D.S. Monitoring of lateral displacements of a slope using a series of special fibre Bragg grating-based in-place inclinometers. Measur. Sci. Technol. 2012, 23, 25007–45014. [Google Scholar] [CrossRef]
- Ho, Y.T.; Huang, A.B.; Lee, J.T. Development of a fibre Bragg grating sensored ground movement monitoring system. Measur. Sci. Technol. 2006, 17, 1733–1740. [Google Scholar] [CrossRef]
- Pei, H.; Cui, P.; Yin, J.; Zhu, H.; Chen, X.; Pei, L.; Xu, D. Monitoring and warning of landslides and debris flows using an optical fiber sensor technology. J. Mt. Sci. 2011, 8, 728–738. [Google Scholar] [CrossRef]
- Zhu, H.H.; Yin, J.H.; Zhang, L.; Jin, W.; Dong, J.H. Monitoring internal displacements of a model dam using FBG sensing bars. Adv. Struct. Eng. 2010, 13, 249–261. [Google Scholar] [CrossRef]
- Leung, C.K.; Wan, K.T.; Inaudi, D.; Bao, X.; Habel, W.; Zhou, Z.; Ou, J.; Ghandehari, M.; Chung, H.; Imai, M. Review: Optical fiber sensors for civil engineering applications. Mater. Struct. 2015, 48, 871–906. [Google Scholar] [CrossRef]
- Shentu, N.; Zhang, H.; Li, Q.; Zhou, H. Research on an electromagnetic induction-based deep displacement sensor. IEEE Sens. J. 2011, 11, 1504–1515. [Google Scholar] [CrossRef]
- Shentu, N.; Zhang, H.; Li, Q.; Zhou, H.; Tong, R.; Li, X. A theoretical model to predict both horizontal displacement and vertical displacement for electromagnetic induction-based deep displacement sensors. Sensors 2012, 12, 233–259. [Google Scholar] [CrossRef] [PubMed]
- Shentu, N.; Qiu, G.; Li, X.; Tong, R.; Li, Q. Sensing Property Modeling for the vertical Composite Underground Displacement Sensor. Sens. Transducers 2014, 176, 27–37. [Google Scholar]
- Yu, H.; Li, S.; Duan, H.; Liu, Y. A procedure of parameter inversion for a nonlinear constitutive model of soils with shield tunneling. Comput. Math. Appl. 2011, 61, 2005–2009. [Google Scholar] [CrossRef]
- Schelle, H.; Durner, W.; Iden, S.C.; Fank, J. Simultaneous estimation of soil hydraulic and root distribution parameters from lysimeter data by inverse modeling. Proc. Environ. Sci. 2013, 19, 564–573. [Google Scholar] [CrossRef]
- Zhang, K. Parameter Identification for Root Growth based on Soil Water Potential Measurements—An Inverse Modeling Approach. Proc. Environ. Sci. 2013, 19, 574–579. [Google Scholar] [CrossRef]
- Oreste, P. Back-analysis techniques for the improvement of the understanding of rock in underground constructions. Tunn. Undergr. Space Technol. 2005, 20, 7–21. [Google Scholar] [CrossRef]
- Vardakos, S.; Gutierrez, M.; Xia, C. Parameter identification in numerical modeling of tunneling using the Differential Evolution Genetic Algorithm (DEGA). Tunn. Undergr. Space Technol. 2012, 28, 109–123. [Google Scholar] [CrossRef]
- Yang, H.J.; Xu, Y.Z.; Huang, Z.B.; Chen, S.Z.; Yang, Z.L.; Wu, G.; Xiao, Z.Y. Comparison between several multi-parameter seismic inversion methods in identifying plutonic igneous rocks. Min. Sci. Technol. 2011, 21, 325–331. [Google Scholar]
- Rechea, C.; Levasseur, S.; Finno, R. Inverse analysis techniques for parameter identification in simulation of excavation support systems. Comput. Geotech. 2008, 35, 331–345. [Google Scholar] [CrossRef]
- Yun, G.J.; Ghaboussi, J.; Elnashai, A.S. Self-learning simulation method for inverse nonlinear modeling of cyclic behavior of connections. Comput. Method Appl. Mech. Eng. 2008, 197, 2836–2857. [Google Scholar] [CrossRef]
- Aquino, W.; Brigham, J.C. Self-learning finite elements for inverse estimation of thermal constitutive models. Int. J. Heat Mass Trans. 2006, 49, 2466–2478. [Google Scholar] [CrossRef]
- Miranda, T.; Dias, D.; Eclaircy-Caudron, S.; Gomes Correia, A.; Costa, L. Back analysis of geomechanical parameters by optimisation of a 3D model of an underground structure. Tunn. Undergr. Space Technol. 2011, 26, 659–673. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shentu, N.; Qiu, G.; Li, Q.; Tong, R.; Shentu, N.; Wang, Y. Research on Joint Parameter Inversion for an Integrated Underground Displacement 3D Measuring Sensor. Sensors 2015, 15, 8406-8428. https://doi.org/10.3390/s150408406
Shentu N, Qiu G, Li Q, Tong R, Shentu N, Wang Y. Research on Joint Parameter Inversion for an Integrated Underground Displacement 3D Measuring Sensor. Sensors. 2015; 15(4):8406-8428. https://doi.org/10.3390/s150408406
Chicago/Turabian StyleShentu, Nanying, Guohua Qiu, Qing Li, Renyuan Tong, Nankai Shentu, and Yanjie Wang. 2015. "Research on Joint Parameter Inversion for an Integrated Underground Displacement 3D Measuring Sensor" Sensors 15, no. 4: 8406-8428. https://doi.org/10.3390/s150408406
APA StyleShentu, N., Qiu, G., Li, Q., Tong, R., Shentu, N., & Wang, Y. (2015). Research on Joint Parameter Inversion for an Integrated Underground Displacement 3D Measuring Sensor. Sensors, 15(4), 8406-8428. https://doi.org/10.3390/s150408406




