Accurate Calibration and Uncertainty Estimation of the Normal Spring Constant of Various AFM Cantilevers
Abstract
:1. Introduction
2. Calibration Facility and Method
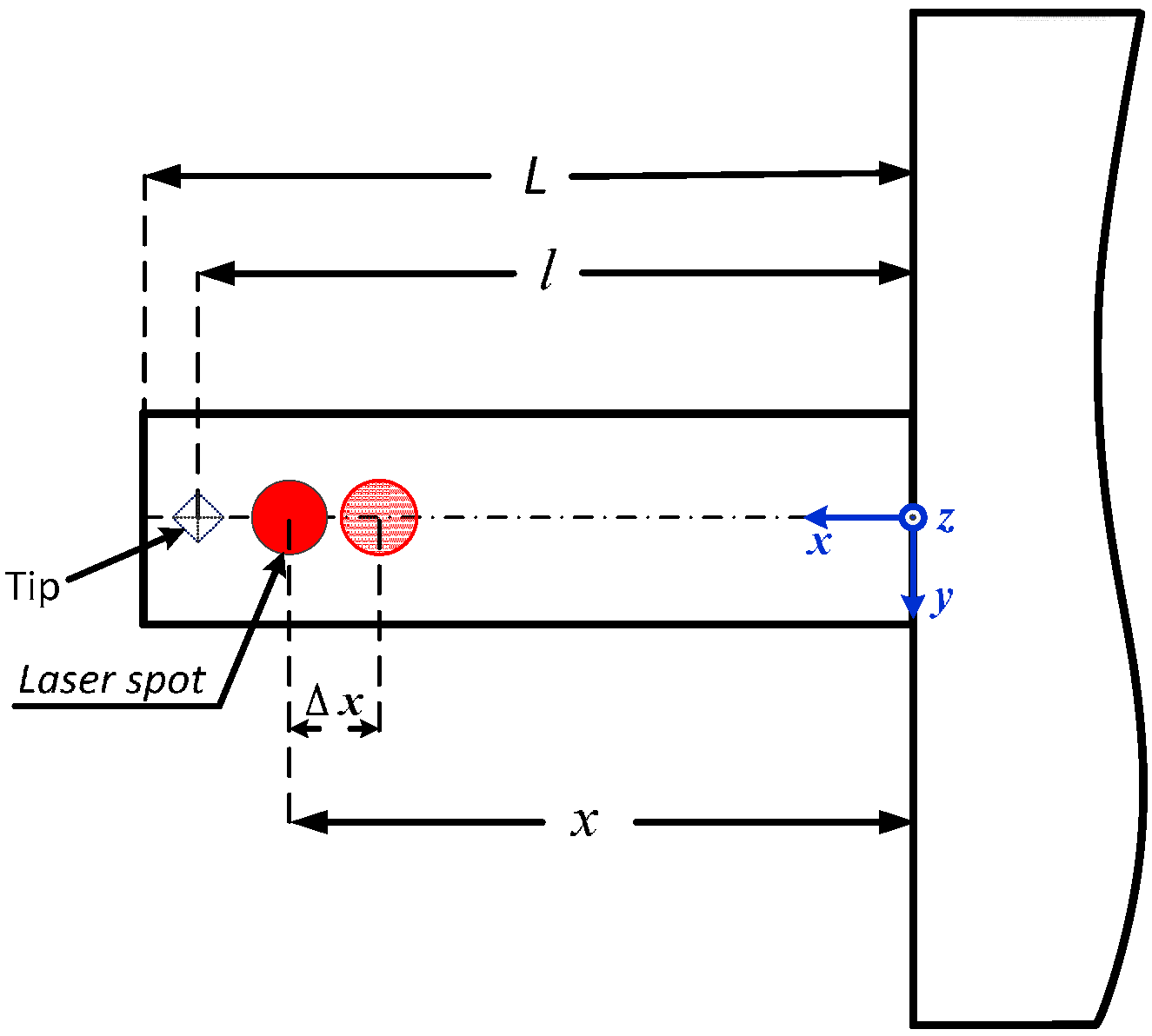
2.1. Facility Setup
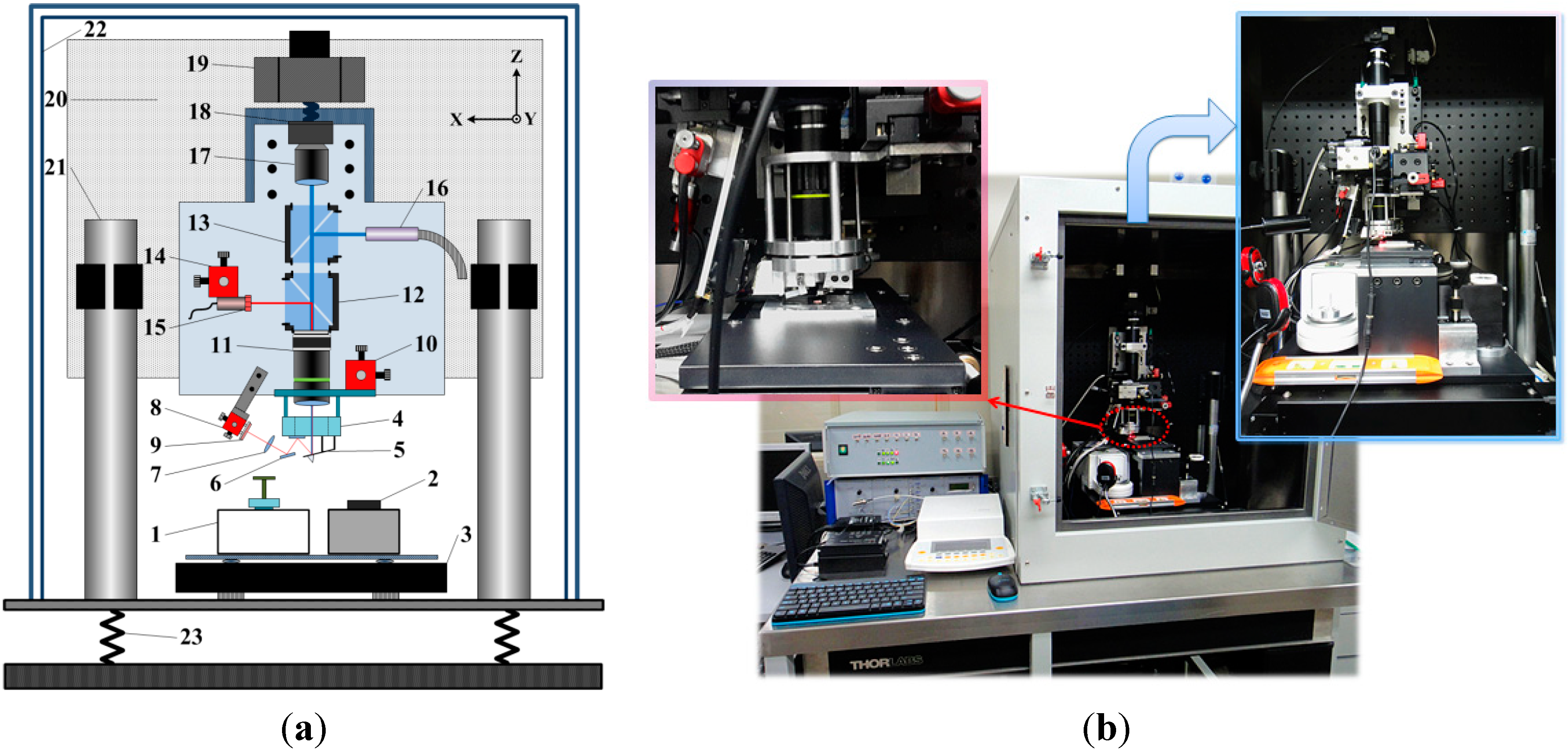
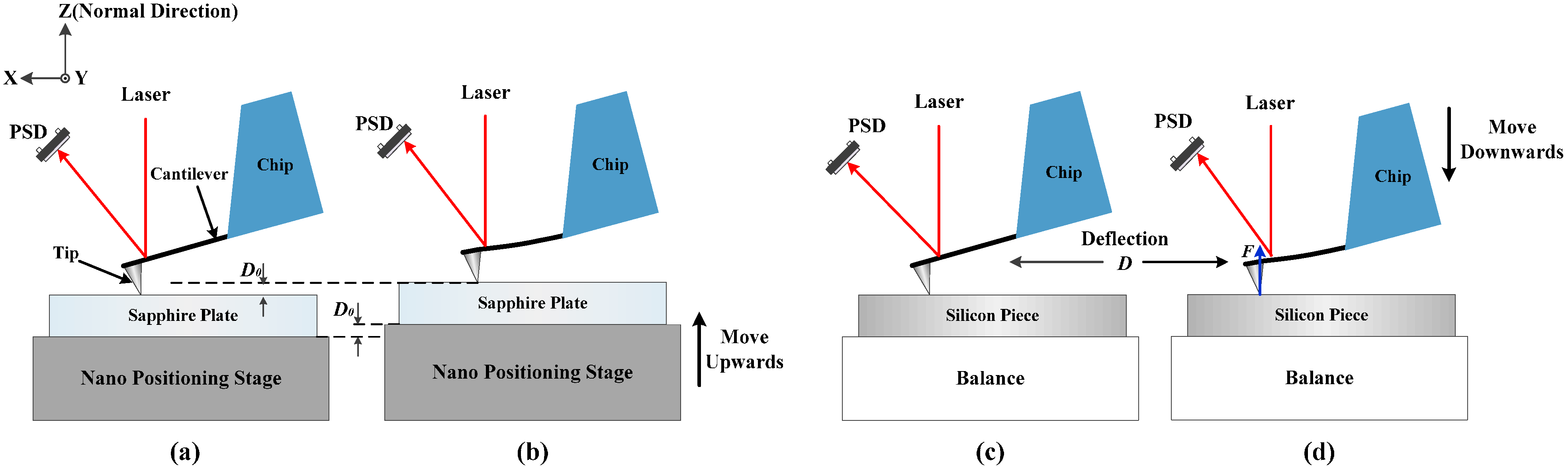
2.2. Calibration Method
3. Normal Spring Constant Calibration
3.1. Cantilevers
| Model | Application Mode | Shape | Dimension (μm) | Resonant Frequency (kHz) | Spring Constant k (N·m−1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Length | Width | Thickness | Tip Height | Nominal | Range | ||||
| CSG01 | Contact | Rectangular | 350 ± 5 | 30 ± 3 | 1.0 ± 0.5 | 14~16 | 4~17 | 0.03 | 0.003~0.130 |
| NSG01 | Tapping | Rectangular | 125 ± 5 | 30 ± 3 | 2.0 ± 0.5 | 14~16 | 87~230 | 5.10 | 1.45~15.10 |
| NSC11 | Electrostatic Force | V-shape | 200 ± 5 | 40 ± 3 | 2.0 ± 0.3 | 15~20 | 50~80 | 3.0 | 1.5~5.0 |
| MESP | Magnetic Force | Rectangular | 225 ± 25 | 28 ± 5 | 3.0 ± 0.5 | 10~15 | 50~100 | 2.8 | 1.0~5.0 |
| NSC15_F | Force Spectroscopy | Rectangular | 125 ± 5 | 35 ± 3 | 4.0 ± 0.5 | 20~25 | 265~400 | 46 | 20~75 |
3.2. Calibration Experiment
3.2.1. Calibration of the Optical Lever Sensitivity
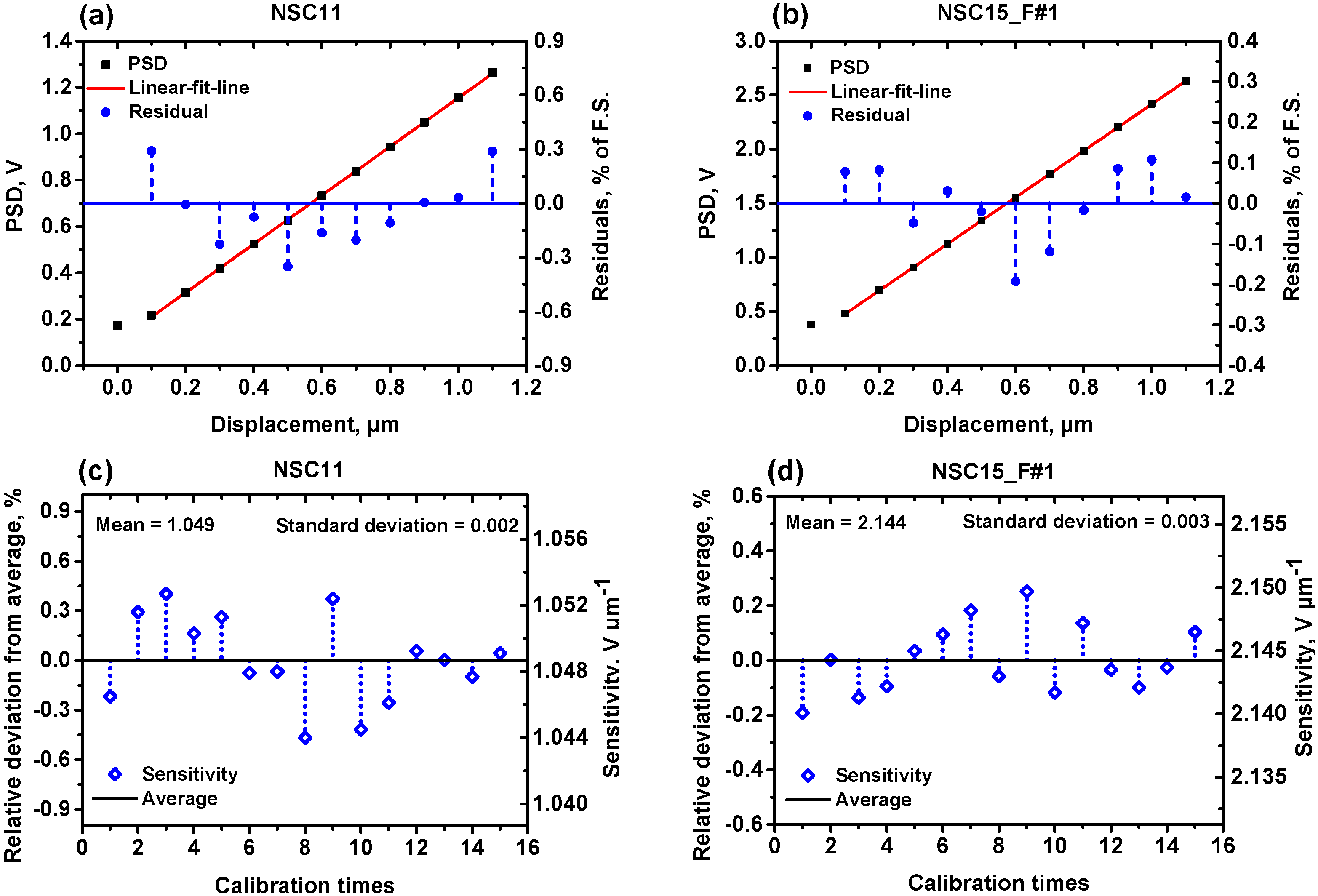
3.2.2. Force Calibration
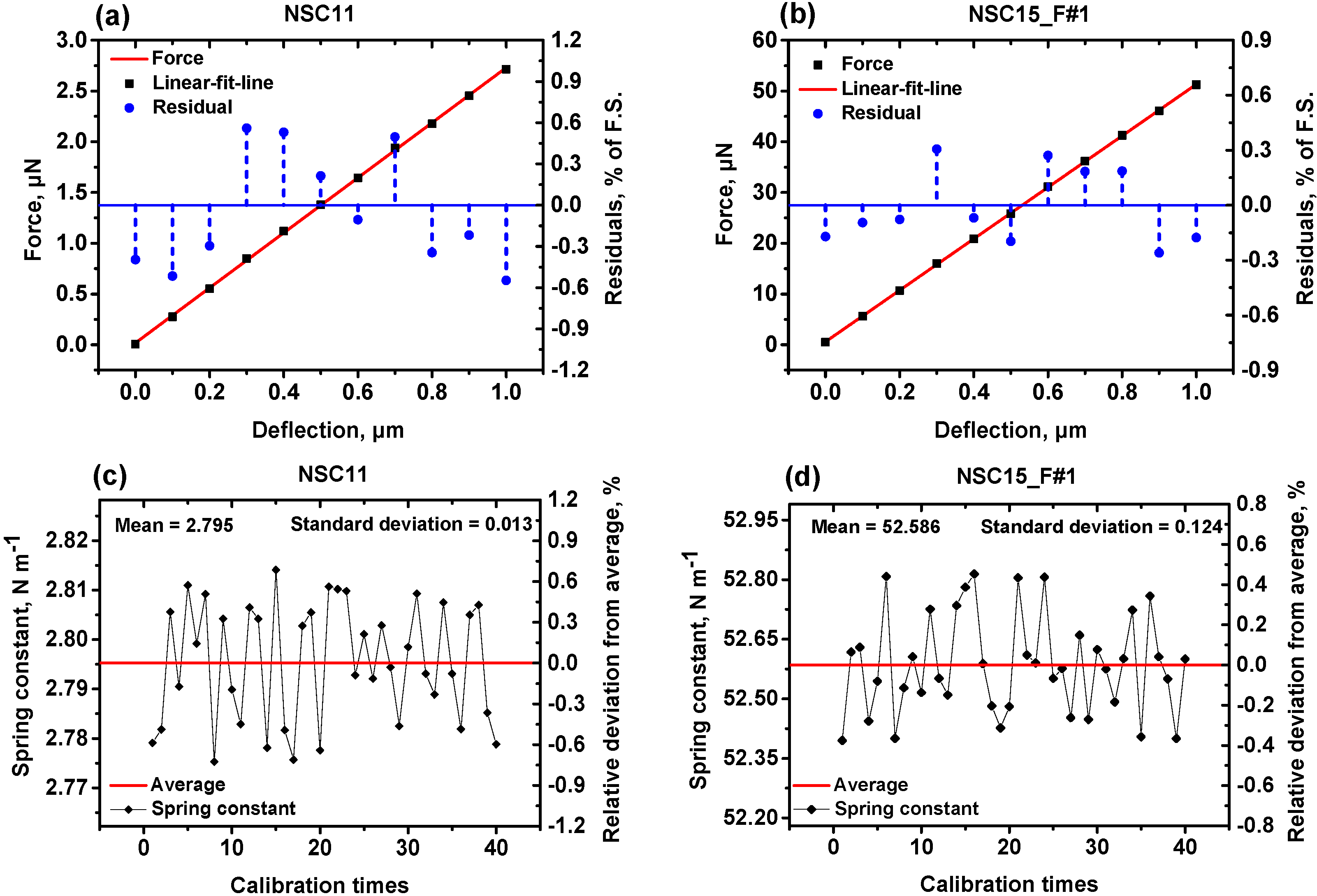
| Cantilever | Spring Constant k (N·m−1) | Relative Standard Deviation of Mean (%) | |
|---|---|---|---|
| Nominal | Calibrated (Mean) | ||
| NSC11 | 3.0 | 2.795 | 0.074 |
| CSG01 | 0.03 | 0.0273 | 0.093 |
| NSG01 | 5.10 | 8.316 | 0.067 |
| MESP | 2.8 | 4.022 | 0.079 |
| NSC15_F#1 | 46 | 52.586 | 0.036 |
| NSC15_F#2 | 46 | 51.304 | 0.059 |
| NSC15_F#3 | 46 | 44.035 | 0.075 |
4. Uncertainty Estimation
4.1. Uncertainty of the Added Mass, urel(m)
4.2. Uncertainty of the Acceleration of Gravity, urel(g)
4.3. Uncertainty of the Increase of PSD Output Signal, urel(U)
4.4. Uncertainty of the Optical Lever Sensitivity, urel(S)
4.5. Combined Uncertainty, ucrel(k)
| Inputs | Expectation | Standard Uncertainty | Distribution | Relative Standard Uncertainty | DOF |
|---|---|---|---|---|---|
| S | 2144.32 mV·μm−1 | 8.65 mV·nm−1 | Normal | 0.403% | 16.9 |
| U0 | 2144.32 mV | 0.72 mV | Normal | 0.033% | 14 |
| D0 | 1 μm | 0.00153 μm | Normal | 0.153% | 50 |
| P | 1 | ---- | Uniform | 0.373% | 12.5 |
| m | 5.0042 mg | 1.90 μg | Normal | 0.038% | 40.7 |
| Resolution | 0 | 0.03 μg | Uniform | ---- | 50 |
| Reproducibility | 0 | 0.25 μg | Uniform | ---- | 50 |
| Repeated measure | 5.004 mg | 1.88 μg | Normal | ---- | 39 |
| g | 9.8011 m·s−2 | 0.0010 m·s−2 | Uniform | 0.010% | 50 |
| U | 2000 mV | ---- | ---- | ---- | ---- |
| Output (k) | 52.586 N·m−1 | 0.213 N·m−1 | Normal | 0.405% | 17.3 |
| Uncertainty Source | Uncertainty Component | Relative Standard Uncertainty (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| NSC11 | CSG01 | NSG01 | MESP | NSC15_F | ||||
| #1 | #2 | #3 | ||||||
| Added mass | Urel(m) | 0.115 | 2.500 | 0.074 | 0.092 | 0.038 | 0.057 | 0.077 |
| Acceleration of gravity | Urel(g) | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
| Optical lever sensitivity | Urel(S) | 0.286 | 0.144 | 0.382 | 0.232 | 0.403 | 0.386 | 0.365 |
| PSD output signal | U1rel(S) | 0.066 | 0.026 | 0.069 | 0.039 | 0.033 | 0.060 | 0.031 |
| Nano stage displacement | U2rel(S) | 0.153 | 0.051 | 0.153 | 0.102 | 0.153 | 0.153 | 0.153 |
| Laser spot position shift | U3rel(S) | 0.235 | 0.133 | 0.343 | 0.205 | 0.373 | 0.349 | 0.330 |
| Combined uncertainty | Ucrel(k) | 0.308 | 2.504 | 0.389 | 0.250 | 0.405 | 0.390 | 0.373 |
5. Results and Discussion
| Model | k (N·m−1) | ucrel(k) (%) | uc(k) (N·m−1) | veff(k) | k99 | U99(k) (N·m−1) | U99rel(k) (%) | k (N·m−1) |
|---|---|---|---|---|---|---|---|---|
| NSC11 | 2.795 | 0.308 | 0.009 | 35.0 | 2.72 | 0.023 | 0.838 | 2.795 ± 0.023 |
| CSG01 | 0.0273 | 2.504 | 0.0007 | 51.6 | 2.68 | 0.0018 | 6.711 | 0.0273 ± 0.0018 |
| NSG01 | 8.316 | 0.389 | 0.032 | 24.9 | 2.79 | 0.090 | 1.085 | 8.316 ± 0.090 |
| MESP | 4.022 | 0.250 | 0.010 | 27.0 | 2.77 | 0.028 | 0.693 | 4.022 ± 0.028 |
| NSC15_F#1 | 52.586 | 0.405 | 0.213 | 17.3 | 2.90 | 0.617 | 1.173 | 52.586 ± 0.617 |
| NSC15_F#2 | 51.304 | 0.390 | 0.200 | 18.9 | 2.86 | 0.572 | 1.115 | 51.304 ± 0.572 |
| NSC15_F#3 | 44.035 | 0.373 | 0.164 | 20.0 | 2.85 | 0.468 | 1.063 | 44.035 ± 0.468 |
| Cantilevers | Effective Spring Constant Obtained from Various Methods (N·m−1) | ||
|---|---|---|---|
| Balance | Sader | Thermal Tune | |
| NSC11 | 2.795 | ---- | 2.686 (−3.9%) |
| CSG01 | 0.0273 | ---- | 0.0276 (1.1%) |
| NSG01 | 8.316 | 7.761 (−6.7%) | 7.882 (−5.2%) |
| MESP | 4.022 | 4.103 (2.0%) | 4.192 (4.2%) |
| NSC15_F#1 | 52.586 | 48.00 (−8.7%) | 43.85 (−16.6%) |
| NSC15_F#2 | 51.304 | 49.07 (−4.4%) | 40.13 (−21.8%) |
| NSC15_F#3 | 44.035 | 40.69 (−7.6%) | 40.47 (−8.1%) |

6. Conclusions
Acknowledgments
Author Contributions
Appendix
Conflict of Interest
References
- Bippes, C.A.; Muller, D.J. High-resolution atomic force microscopy and spectroscopy of native membrane proteins. Rep. Prog. Phys. 2011, 74. [Google Scholar] [CrossRef]
- Rasuli, R.; Iraji, A.; Ahadian, M.M. Mechanical properties of graphene cantilever from atomic force microscopy and density functional theory. Nanotechnology 2010, 21. [Google Scholar] [CrossRef] [PubMed]
- Butt, H.J.; Cappella, B.; Kappl, M. Force measurement with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]
- Georgakaki, D.; Mitridis, S.; Sapalidis, A.A.; Mathioulakis, E.; Polatoglou, H.M. Calibration of tapping AFM cantilevers and uncertainty estimation: Comparison between different methods. Measurement 2013, 46, 4274–4281. [Google Scholar] [CrossRef]
- Riet, J.; Katan, A.J.; Rankl, C.; Stahl, S.W.; van Buul, A.M.; Phang, I.Y.; Gomez-Casado, A.; Schön, P.; Gerritsen, J.W.; Cambi, A.; et al. Interlaboratory round robin on cantilever calibration for AFM force spectroscopy. Ultramicroscopy 2011, 111, 1659–1669. [Google Scholar] [CrossRef]
- Kim, M.S.; Choi, J.H.; Kim, J.H.; Park, Y. Accurate determination of spring constant of atomic force microscope cantilevers and comparison with other methods. Measurement 2010, 43, 520–526. [Google Scholar] [CrossRef]
- Clifford, C.A.; Seah, M.P. The determination of atomic force microscope cantilever spring constants via dimensional methods for nanomechanical analysis. Nanotechnology 2005, 16, 1666–1680. [Google Scholar] [CrossRef]
- Neumeister, J.M.; Ducker, W.A. Lateral, normal, and longitudinal spring constants of atomic-force microscopy cantilevers. Rev. Sci. Instrum. 1994, 65, 2527–2531. [Google Scholar] [CrossRef]
- Sader, J.E.; White, L. Theoretical-analysis of the static deflection of plates for atomic-force microscope applications. J. Appl. Phys. 1993, 74, 1–9. [Google Scholar] [CrossRef]
- Cleveland, J.P.; Manne, S.; Bocek, D.; Hansma, P.K. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy. Rev. Sci. Instrum. 1993, 64, 403–405. [Google Scholar] [CrossRef]
- Slattery, A.D.; Quinton, J.S.; Gibson, C.T. Atomic force microscope cantilever calibration using a focused ion beam. Nanotechnology 2012, 23. [Google Scholar] [CrossRef]
- Sader, J.E.; Larson, I.; Mulvaney, P.; White, L.R. Method for the calibration of atomic force microscope cantilevers. Rev. Sci. Instrum. 1995, 66, 3789–3798. [Google Scholar] [CrossRef]
- Sader, J.E.; Chon, J.W.M.; Mulvaney, P. Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 1999, 70, 3967–3969. [Google Scholar] [CrossRef]
- Sader, J.E.; Sanelli, J.A.; Adamson, B.D.; Monty, J.P.; Wei, X.; Crawford, S.A.; Friend, J.R.; Marusic, I.; Mulvaney, P.; Bieske, E.J. Spring constant calibration of atomic force microscope cantilevers of arbitrary shape. Rev. Sci. Instrum. 2012, 83. [Google Scholar] [CrossRef]
- Hutter, J.L.; Bechhoefer, J. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 1993, 64, 1868–1873. [Google Scholar] [CrossRef]
- Butt, H.J.; Jaschke, M. Calculation of thermal noise in atomic-force microscopy. Nanotechnology 1995, 6, 1–7. [Google Scholar] [CrossRef]
- Stark, R.W.; Drobek, T.; Heckl, W.M. Thermomechanical noise of a free V-shaped cantilever for atomic-force microscopy. Ultramicroscopy 2001, 86, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Ohler, B. Cantilever spring constant calibration using laser doppler vibrometry. Rev. Sci. Instrum. 2007, 78. [Google Scholar] [CrossRef] [PubMed]
- Gates, R.S.; Pratt, J.R. Accurate and precise calibration of AFM cantilever spring constants using laser doppler vibrometry. Nanotechnology 2012, 23. [Google Scholar] [CrossRef]
- Torii, A.; Sasaki, M.; Hane, K.; Okuma, S. A method for determining the spring constant of cantilevers for atomic force microscopy. Measur. Sci. Technol. 1996, 7, 179–184. [Google Scholar] [CrossRef]
- Slattery, A.D.; Blanch, A.J.; Quinton, J.S.; Gibson, C.T. Calibration of atomic force microscope cantilevers using standard and inverted static methods assisted by FIB-milled spatial markers. Nanotechnology 2013, 24. [Google Scholar] [CrossRef] [PubMed]
- Ying, Z.C.; Reitsma, M.G.; Gates, R.S. Direct measurement of cantilever spring constants and correction for cantilever irregularities using an instrumented indenter. Rev. Sci. Instrum. 2007, 78. [Google Scholar] [CrossRef] [PubMed]
- Diethold, C.; Kühnel, M.; Hilbrunner, F.; Fröhlich, T.; Manske, E. Determination of force to displacement curves using a nanopositioning system based on electromagnetic force compensated balances. Measurement 2014, 51, 343–348. [Google Scholar] [CrossRef]
- Kim, M.S.; Choi, J.H.; Kim, J.H.; Park, Y.K. SI-traceable determination of spring constants of various atomic force microscope cantilevers with a small uncertainty of 1%. Measur. Sci. Technol. 2007, 18, 3351–3358. [Google Scholar] [CrossRef]
- Kim, M.S.; Pratt, J.R.; Brand, U.; Jones, C.W. Report on the first international comparison of small force facilities: A pilot study at the micronewton level. Metrologia 2012, 49, 70–81. [Google Scholar] [CrossRef]
- Song, Y.P.; Wu, S.; Geng, X.Y.; Fu, X. Traceable Calibration System for the Normal Spring Constant of Atomic Force Microscope Probe. Nanotechnol. Precis. Eng. 2014, 4, 249–257. [Google Scholar]
- Wu, S.; Chen, Q.C.; Zhang, C.; Fu, X.; Hu, X.D.; Hu, X.T. Calibration of the spring constant of AFM micro-cantilever based on bending method. Chin. J. Sci. Instrum. 2012, 11, 2446–2453. [Google Scholar]
- Heim, L.O.; Kappl, M.; Butt, H.J. Tilt of atomic force microscope cantilevers: Effect on spring constant and adhesion measurements. Langmuir 2004, 20, 2760–2764. [Google Scholar] [CrossRef]
- Sader, J.E. Parallel beam approximation for V-shaped atomic force microscope cantilevers. Rev. Sci. Instrum. 1995, 66, 4583–4587. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Wu, S.; Xu, L.; Fu, X. Accurate Calibration and Uncertainty Estimation of the Normal Spring Constant of Various AFM Cantilevers. Sensors 2015, 15, 5865-5883. https://doi.org/10.3390/s150305865
Song Y, Wu S, Xu L, Fu X. Accurate Calibration and Uncertainty Estimation of the Normal Spring Constant of Various AFM Cantilevers. Sensors. 2015; 15(3):5865-5883. https://doi.org/10.3390/s150305865
Chicago/Turabian StyleSong, Yunpeng, Sen Wu, Linyan Xu, and Xing Fu. 2015. "Accurate Calibration and Uncertainty Estimation of the Normal Spring Constant of Various AFM Cantilevers" Sensors 15, no. 3: 5865-5883. https://doi.org/10.3390/s150305865
APA StyleSong, Y., Wu, S., Xu, L., & Fu, X. (2015). Accurate Calibration and Uncertainty Estimation of the Normal Spring Constant of Various AFM Cantilevers. Sensors, 15(3), 5865-5883. https://doi.org/10.3390/s150305865





