3.1. Individual Cylindrical Pipe
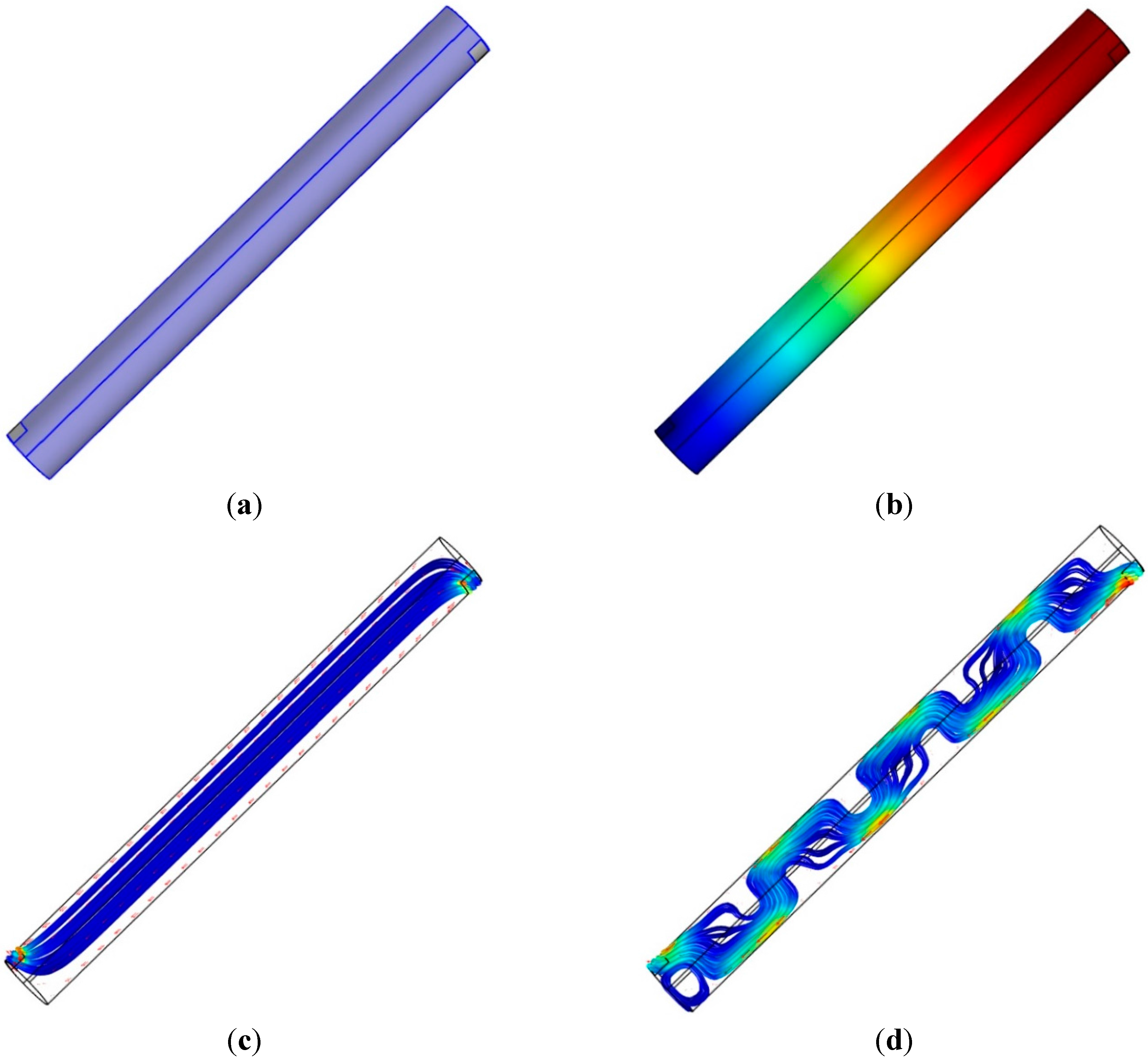
The acoustic resonance from the cylindrical pipe considers the open-end model, in which both ends of the pipe are fully open. The vertical configuration of the pipe requires the side inlet and outlet of the signal to create the resonance. For a pipe of a given length, one top side of the longitudinal face includes the rectangular signal inlet, and the other bottom side of the face has the outlet for signal reception by the NFML microphone. Both ends of the pipe are completely closed, as shown in
Figure 4a. The simulation is accomplished in the condition that the plane wave is introduced from the inlet and the propagated plane wave is freely leaving through the outlet. The processing length for the simulation and experiment is 1024 samples as data window size. The simulator produces the outcome in every spectral resolution as the sampling frequency divided by the data window size (44,100 Hz/1024) up to half of the sampling frequency.
For the 1033.6 Hz of the simulation upshot, the sound pressure distribution is represented by the color-coded plot in
Figure 4b, and the wavelength (334.8 mm) of the given frequency suitably corresponds to the distribution. The sound intensity streamline from
Figure 4c illustrates the proper propagation of the given frequency wave from and to the open windows. The longitudinal motion of the propagation and open windows of the pipe present the predictable length-wise fundamental frequency, as shown in Equation (1) in the designed structure.
Figure 4.
Simulation with single cylindrical pipe structure: (a) physical structure (pipe dimension: l = 117.7 mm and d = 10 mm; window dimension: h = 3 mm and w = 8 mm); (b) sound pressure distribution at 1033.6 Hz; (c) root mean square (RMS) sound intensity streamline at 1033.6 Hz; and (d) RMS sound intensity streamline at 22,007 Hz.
Figure 4.
Simulation with single cylindrical pipe structure: (a) physical structure (pipe dimension: l = 117.7 mm and d = 10 mm; window dimension: h = 3 mm and w = 8 mm); (b) sound pressure distribution at 1033.6 Hz; (c) root mean square (RMS) sound intensity streamline at 1033.6 Hz; and (d) RMS sound intensity streamline at 22,007 Hz.
Figure 4d demonstrates the complicated propagation pattern in the sound intensity streamline for the intended frequency at 22,007 Hz. The acoustic wave, which has a smaller wavelength (15.7 mm) than twice the pipe diameter (2 × 10 mm), provides the higher-order waves in non-longitudinal directions. For the low-frequency waves, the longitudinal motion is dominant along the principal axis, as shown in
Figure 4c; however, the transverse modes start to be excited in the high-frequency waves due to the higher-order waves along all directions.
Figure 4d presents the situation of effectively longer travel paths that cause the lower fundamental frequency. According to the multi-dimensional propagation, the acoustic response of the pipe is assumed to generate a fluctuating and complicating pattern in the high-frequency region.
Figure 5.
Simulated frequency response of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with various diameters.
Figure 5.
Simulated frequency response of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with various diameters.
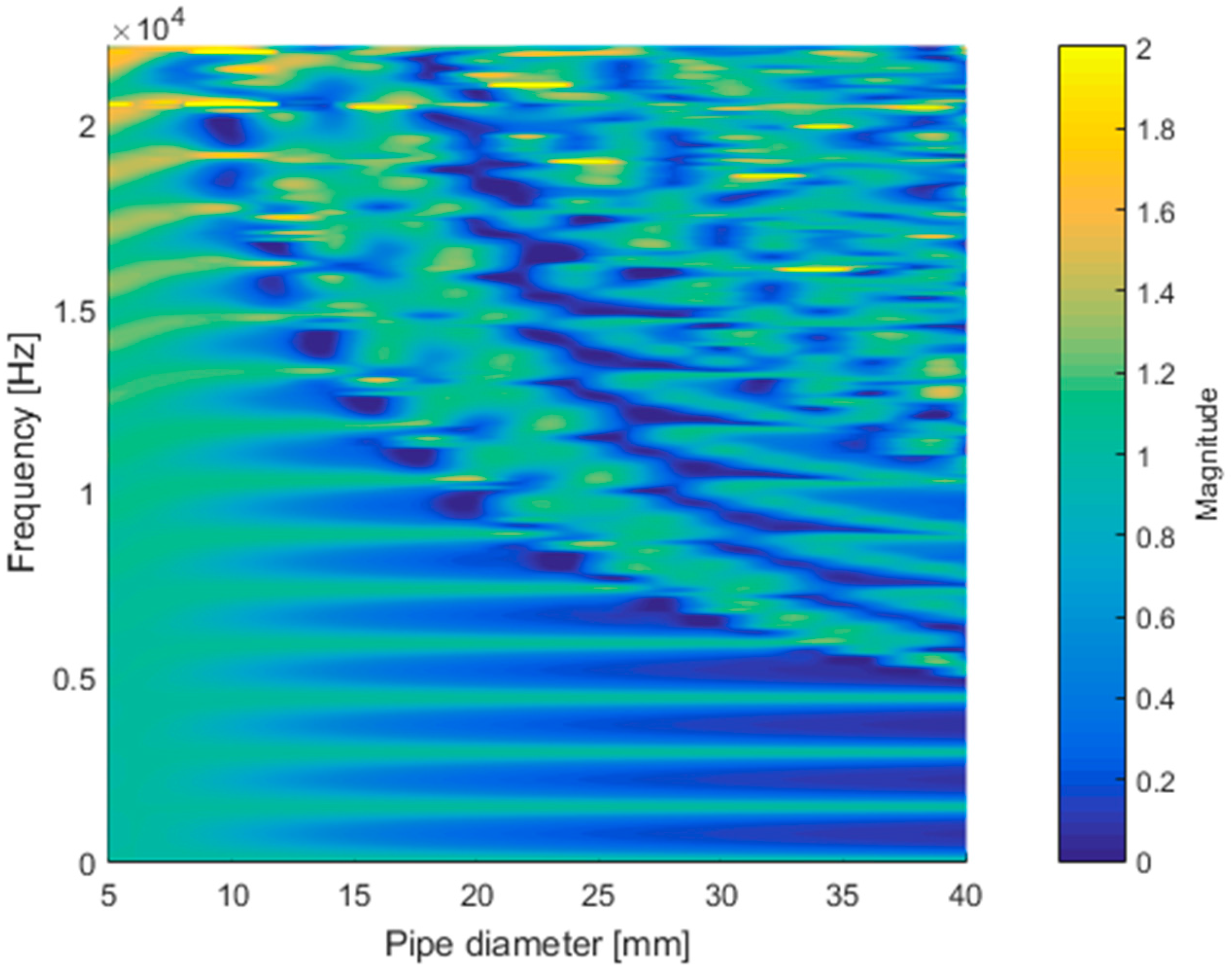
A further simulation for the pipe diameter of the given structure is performed and illustrated in
Figure 5. The simulation increased the diameter without changing any other parameters of the structure and provided the corresponding frequency response up to the half of the sampling frequency. The frequency response is defined as the ratio between the outgoing and incoming acoustic energy that denote the outgoing power at the outlet and the incoming power at the inlet, respectively. The higher value in the frequency response responds to the amplified output for the selected frequency. The parametric frequency study indicates the prevailing non-longitudinal propagation for increased diameter and high frequency as the irregular pattern in the upper-right-hand corner of
Figure 5. In the small diameter pipe, the frequency response shows a shallow but regular outline in terms of fundamental frequency over the whole range of the frequency. At around 10 mm, the regularity of the fundamental frequency starts to collapse from the high-frequency zone. However, the prominence of the regularity contrast is improved further for the larger-diameter pipes.
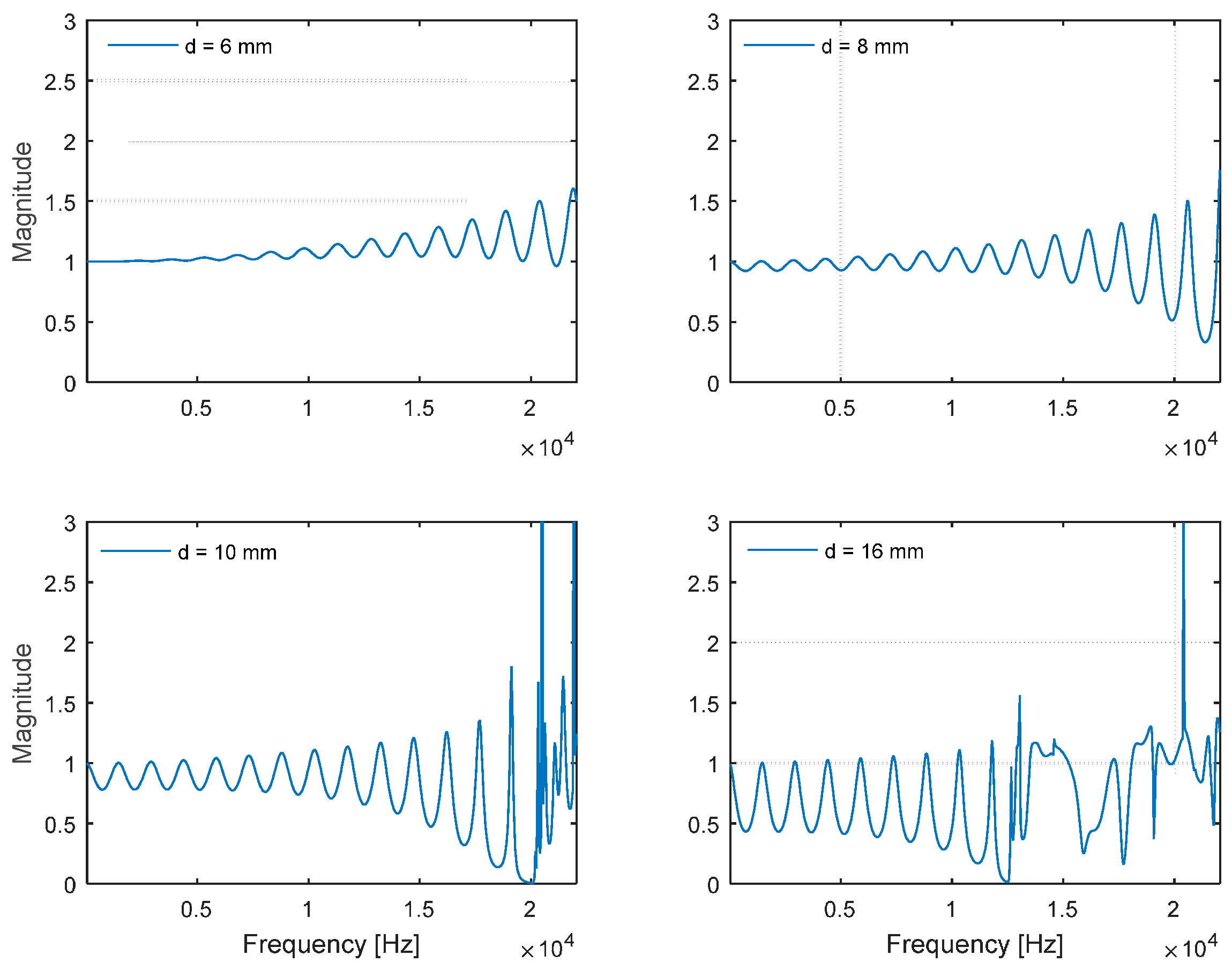
The individual plot matrix of the frequency responses for the given diameters is depicted in
Figure 6. Up to a diameter of 8 mm, the frequency response delivers the periodic sinusoidal wave over the entire frequency range. The response for a diameter of 10 mm includes rapid fluctuation above the 20 kHz area, and the phenomenon becomes worse for the larger-diameter pipe, as shown in the 16-mm plot. The second DFT in the Cepstrum is the additional Fourier transform to analyze the periodic component in the frequency information from the first DFT. The pure and noticeable sinusoidal form of the signal anticipates the generation of the prominent fundamental frequency distribution in the estimation process. The 6-mm and 8-mm frequency responses are relatively uncontaminated, but the signals indicate weak amplitudes overall. As the signal becomes stronger by increasing the diameter, the complex pattern in the response is also expected to enlarge the area, which causes the multiple side-lobes to blur the estimation result. A tradeoff is required to balance the purity and magnitude for an optimal estimation outcome.
Figure 6.
Plot matrix for simulated frequency response of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with selected diameters.
Figure 6.
Plot matrix for simulated frequency response of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with selected diameters.
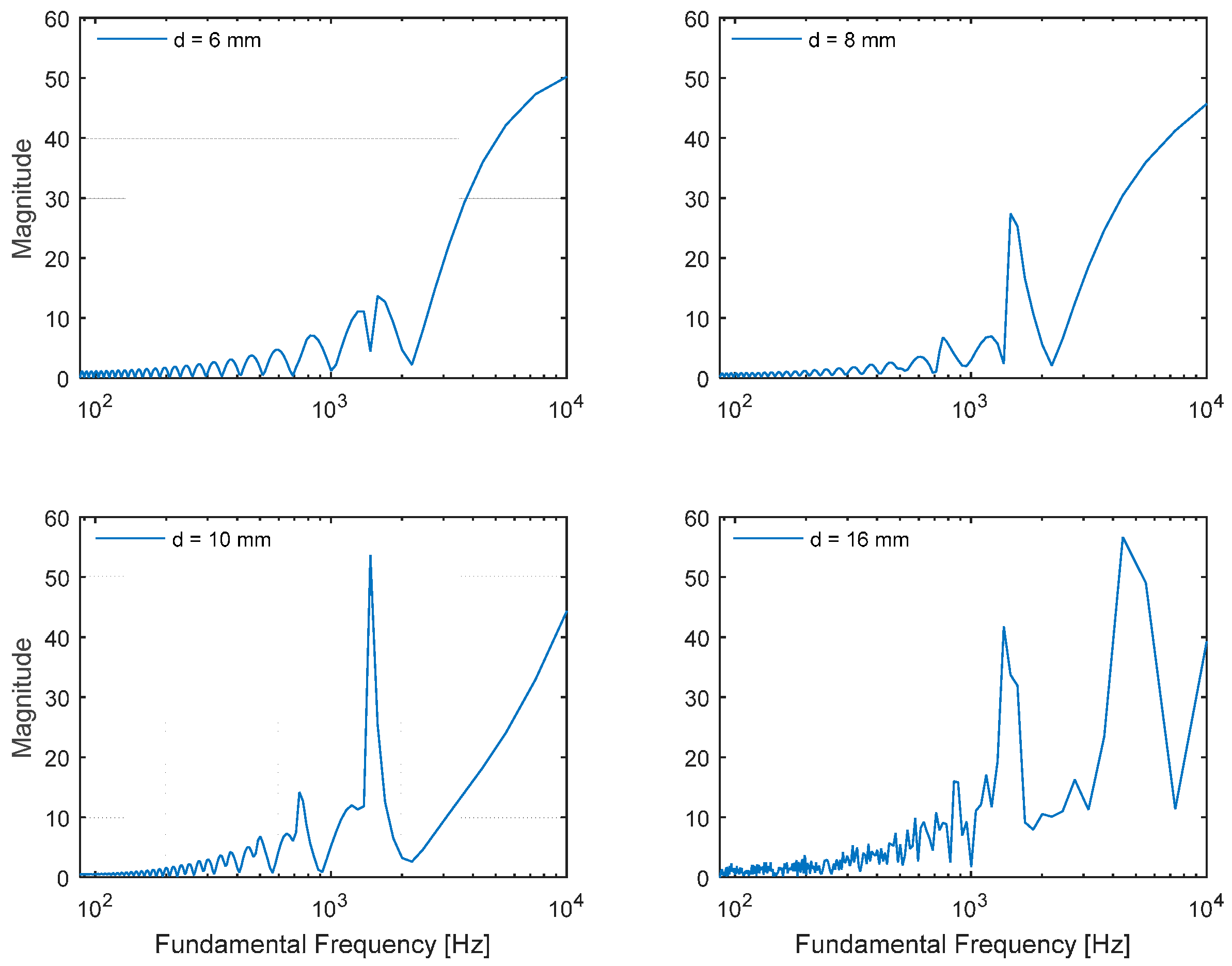
Instead of processing entire frequencies with Equation (3), the range-limited DFT is employed to compute the fundamental frequency in the Cepstral parameter. The frequency span is limited to up to 20 kHz, which is an acceptable standard range of audible frequency used for conventional audio equipment. The Cepstral parameter with a limited range is applied to the selected diameter pipes in
Figure 7. The weak magnitude of the frequency response from the narrow pipes demonstrates the low contrast on the fundamental frequency plot. On the contrary, the contaminated magnitude from the wide pipes shows the redundant strong side-lobes to mislead the fundamental frequency estimation. The 10-mm-diameter pipe delivers the optimal performance to estimate fundamental frequency according to the simulation.
Figure 7.
Plot matrix for simulated fundamental frequency of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with selected diameters.
Figure 7.
Plot matrix for simulated fundamental frequency of cylindrical pipe (l = 117.7 mm, h = 3 mm, and w = 8 mm) with selected diameters.
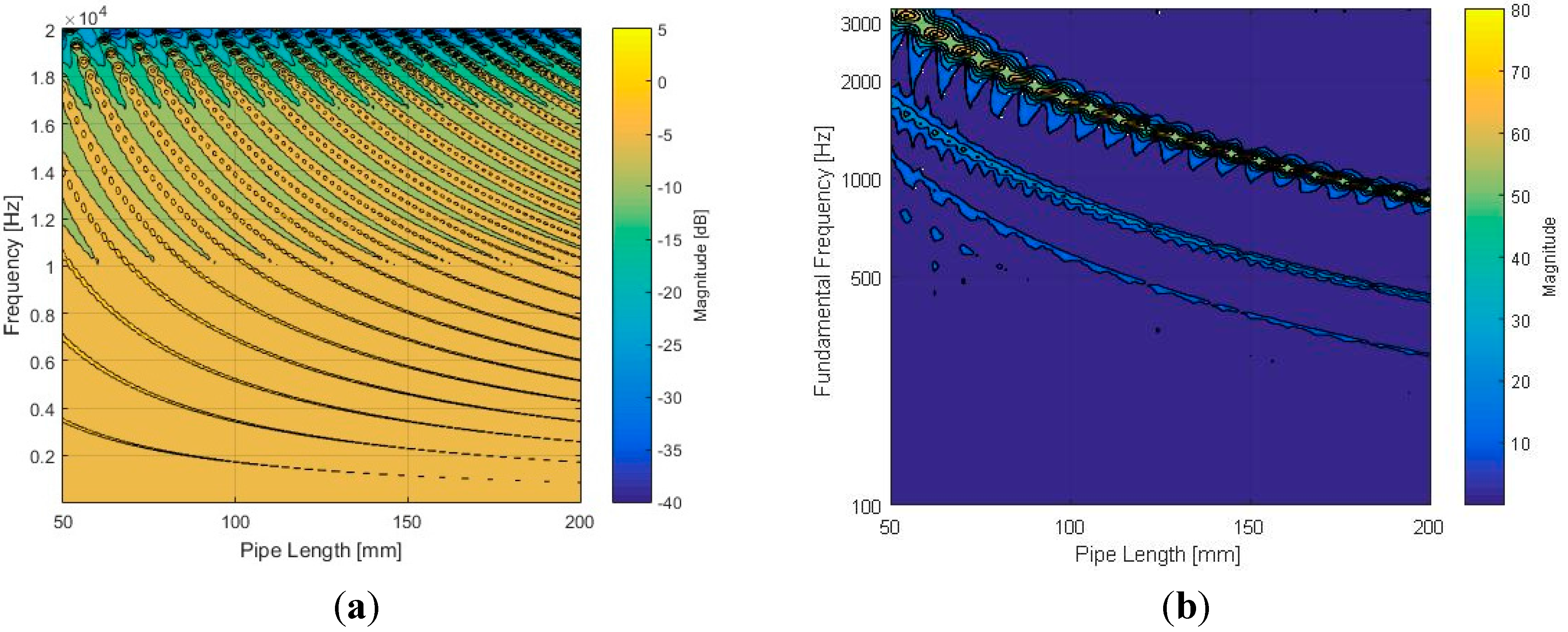
Figure 8 displays the frequency response and fundamental frequency plot for a range of pipe lengths with a 10-mm diameter. Note that both plots use the frequency up to 20 kHz. In addition, the magnitudes for the frequency response and fundamental frequency use the decibel and absolute scale, respectively.
Figure 8a demonstrates the existence of spectrum periodicity that becomes dense and cyclical populations for long-length pipes. Consequently, the Cepstral parameter for the identical structure configuration represents the decreasing fundamental frequency moving toward the right of
Figure 8b. The one-half and one-third values of the fundamental frequency are visualized with blurry lines in addition to the dominant fundamental frequency threads, because they are also the weak fundamental frequencies that respond to certain periodicities of the signal.
Figure 8.
Simulated results for cylindrical pipe (d = 10 mm, h = 3 mm, and w = 8 mm) with various lengths: (a) frequency response in decibel scale and (b) fundamental frequency distribution in absolute scale.
Figure 8.
Simulated results for cylindrical pipe (d = 10 mm, h = 3 mm, and w = 8 mm) with various lengths: (a) frequency response in decibel scale and (b) fundamental frequency distribution in absolute scale.
Figure 9.
Plot matrix for simulated fundamental frequency of cylindrical pipe (d = 10 mm, h = 3 mm, and w = 8 mm) with selected lengths.
Figure 9.
Plot matrix for simulated fundamental frequency of cylindrical pipe (d = 10 mm, h = 3 mm, and w = 8 mm) with selected lengths.
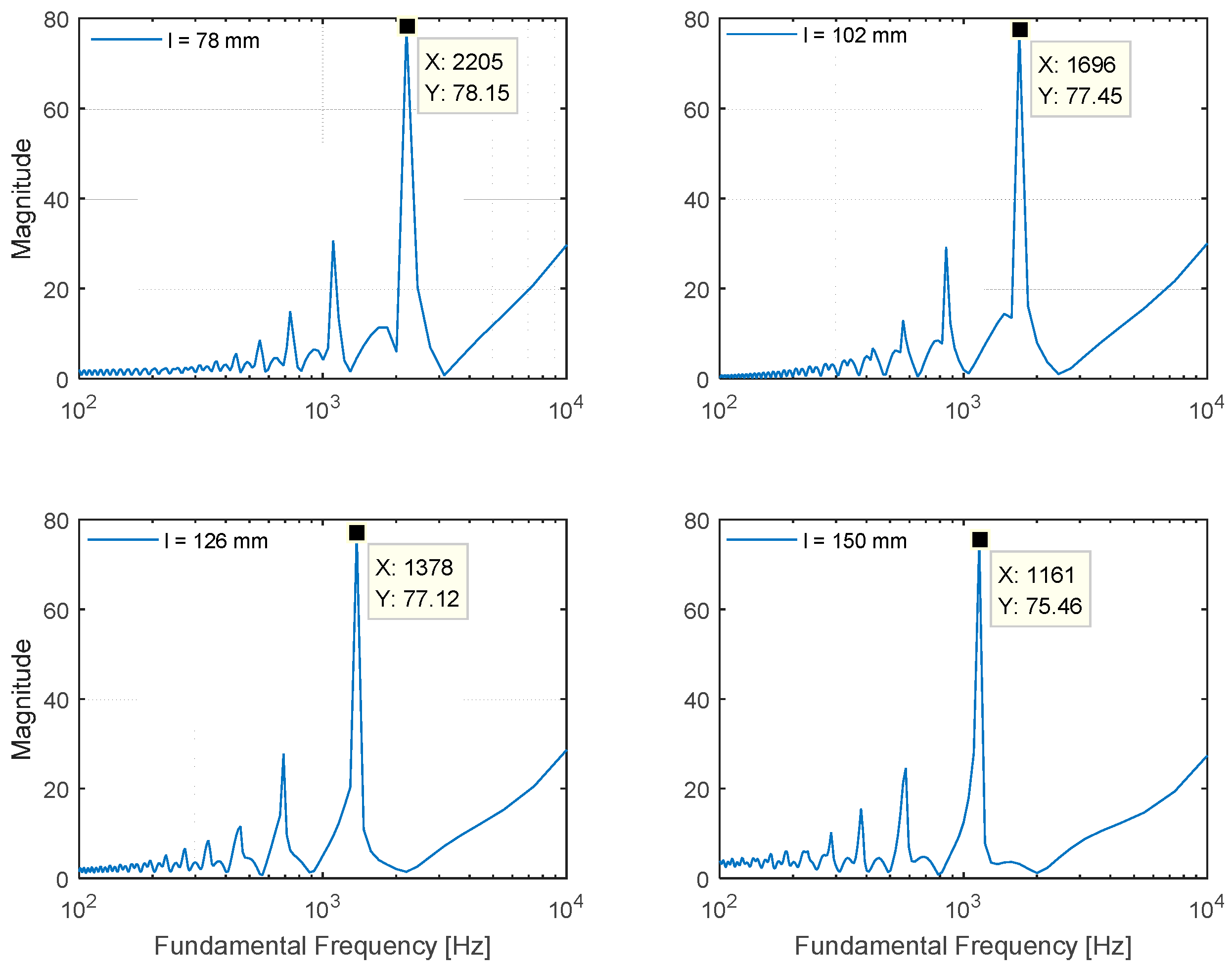
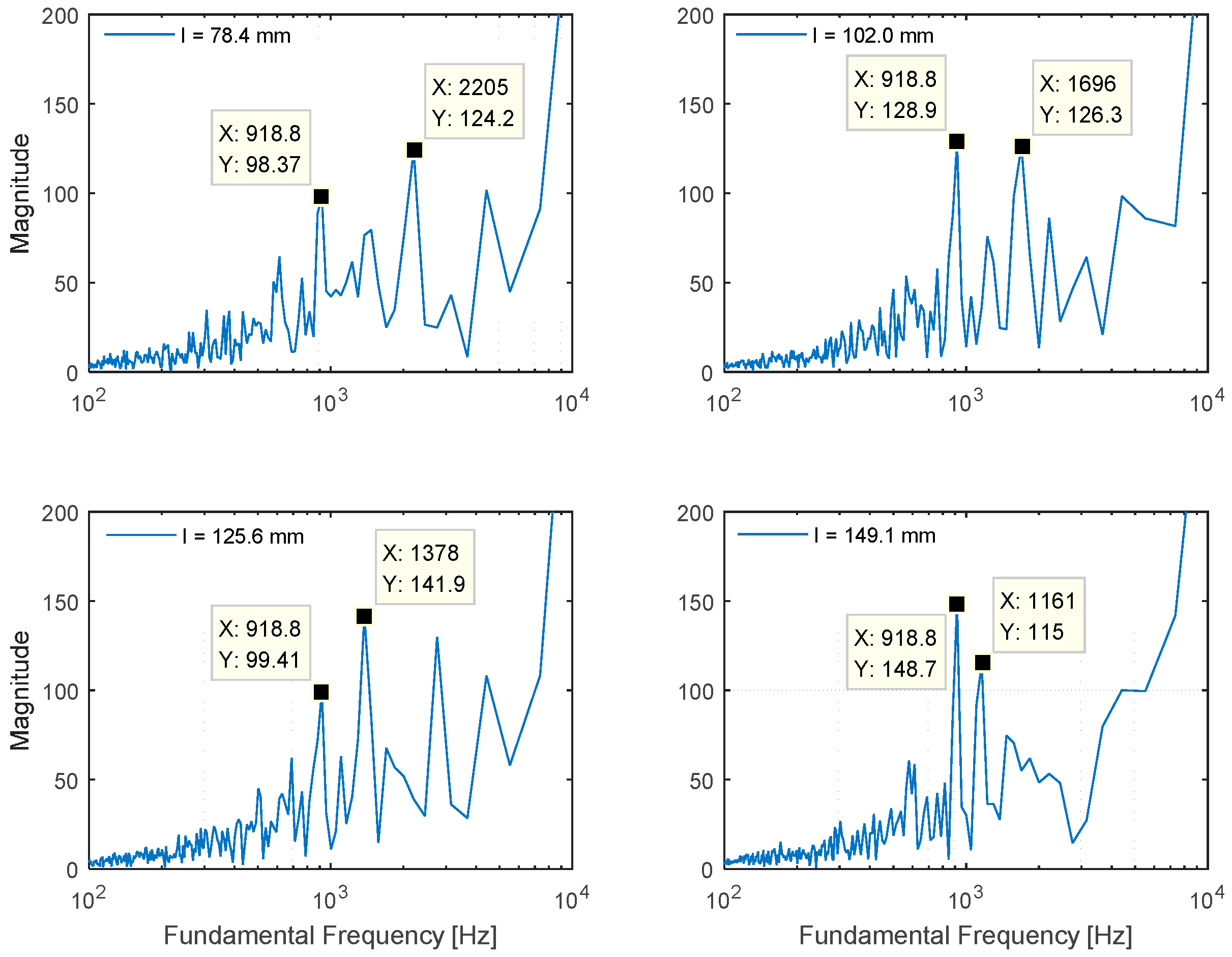
The fundamental frequency plots of the selected lengths are organized in
Figure 9. According to the figure, the estimated fundamental frequency appropriately satisfies the relation defined by Equation (1). The difference between the computed and simulated value originates from the discrete spectral resolution of the Cepstral parameter modification given by Equation (5). For example, the length of 78 mm provides the 2218 Hz (346,000/(2 × 78)) fundamental frequency according to Equation (1), and the value is sampled by the nearest frequency 2205 Hz (44,100/(2 ×
r);
r = 10) from Equation (5). Therefore, the simulation result complies well with the theoretical model that creates the distinct fundamental frequency by modifying the cylindrical pipe length. The designed cylindrical pipe with inlet and outlet windows fulfills the primitive architecture of the NFML structure, and it is modified further for azimuthal localization in the next subsection.
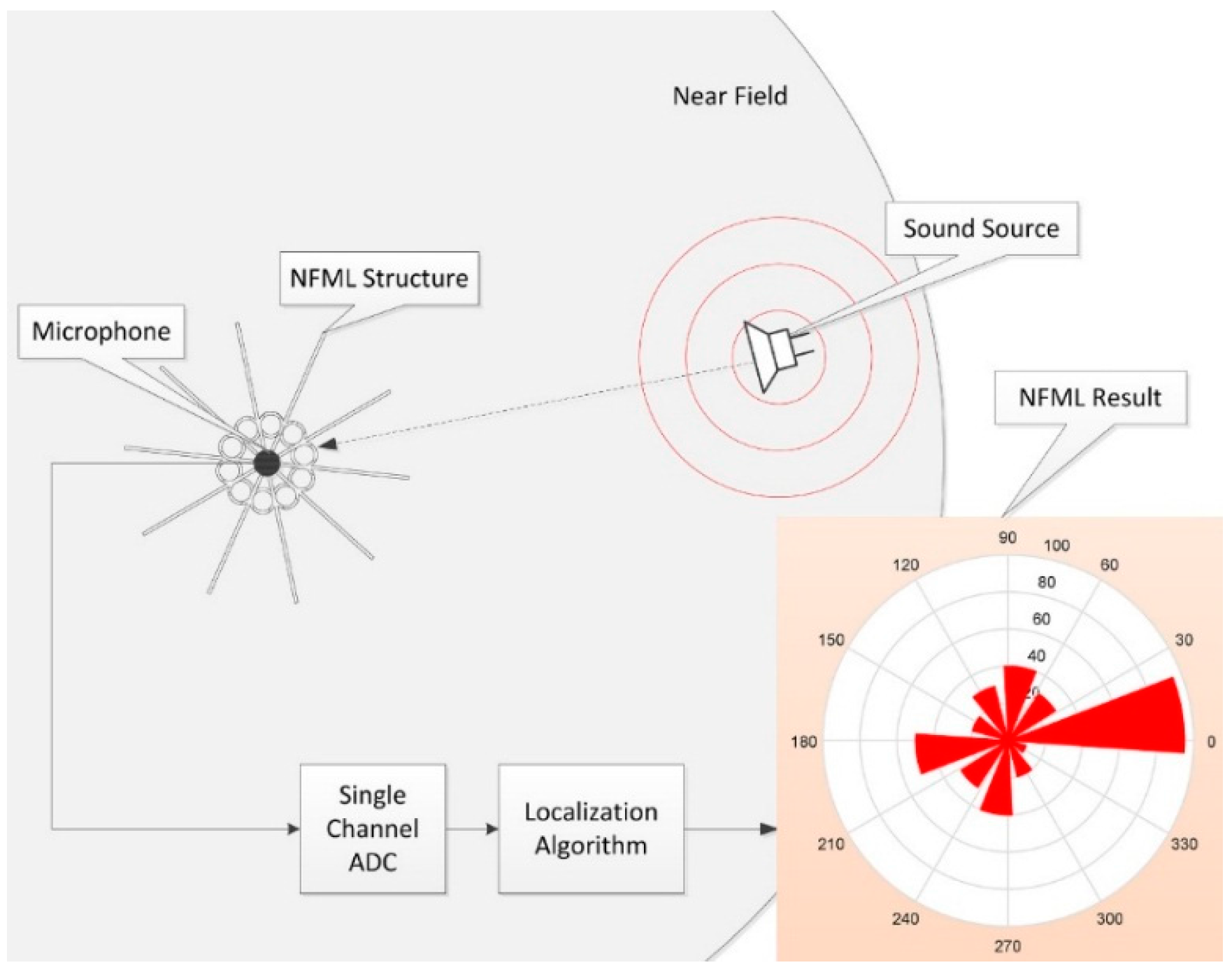
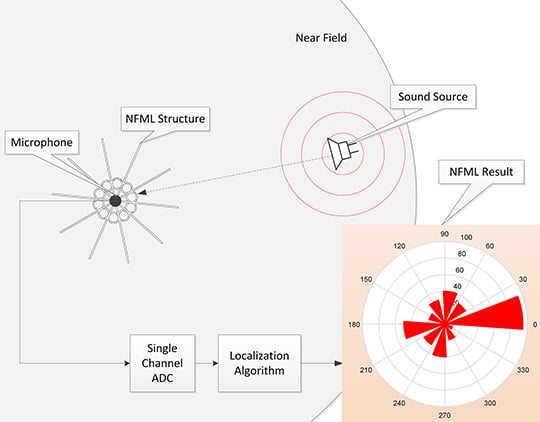
3.2. NFML Structure
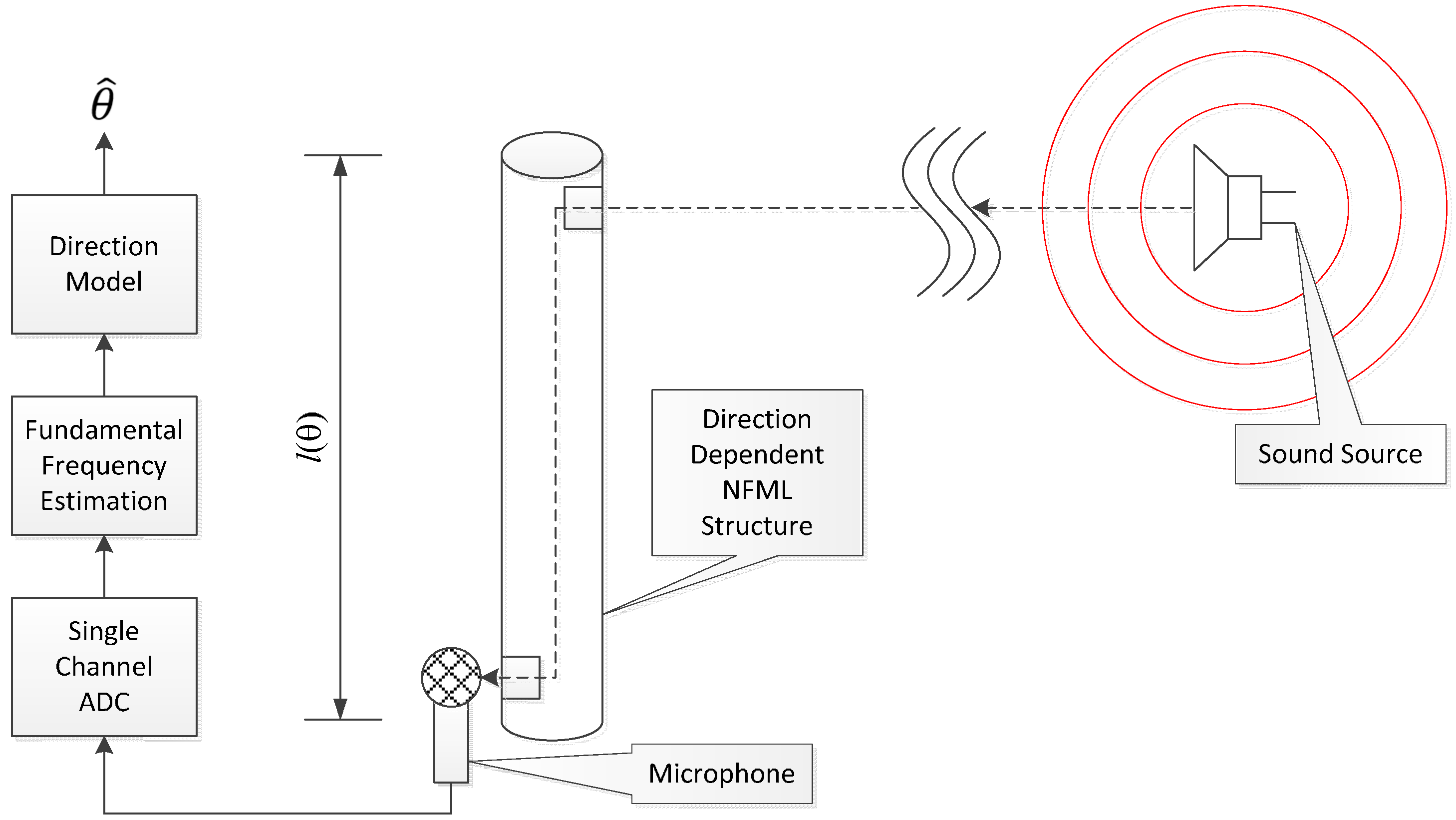
This subsection discusses and presents the entire structure of the NFML based on the cylindrical pipe from the previous subsection. The vertical arrangement of the cylindrical pipes is used to build the NFML structure for the low profile. The large-dimension cylindrical pipe in terms of length and diameter sustains the multi-directional pipes with individual lengths for fundamental frequency variation. The inlet window of the directional pipes faces outside toward the independent radial path to receive the acoustic signal from the dedicated direction. The outlet window of the directional pipe faces inside the large pipe to collect the signal for a single microphone. The center-located pipe has a sufficiently long length for a low fundamental frequency to avoid estimation collision and a diameter that provides enough horizontal space to arrange multiple pipes around the center body. With the given outline; the NFML structure is expected to provide the direction-wise fundamental frequency to localize the AoA properly.
The directional pipe with a cylindrical structure was analyzed to produce the predictable fundamental frequency in the previous subsection. The further simulation with the suggested structure in this subsection presents the numerical decision for directional pipe lengths. The dimensions of the center pipe are determined to initiate the overall NFML structure. The diameter of the center pipe is 27.8 mm for attaching the ten directional pipes around the body, and the length is 192.1 mm for responding to the 900 Hz fundamental frequency that is sufficiently far from the directional pipe producing the frequencies. The 900 Hz fundamental frequency moves to the nearest value 918.8 Hz (44,100/(2 ×
r);
r = 24) by Equation (5) in the estimation process.
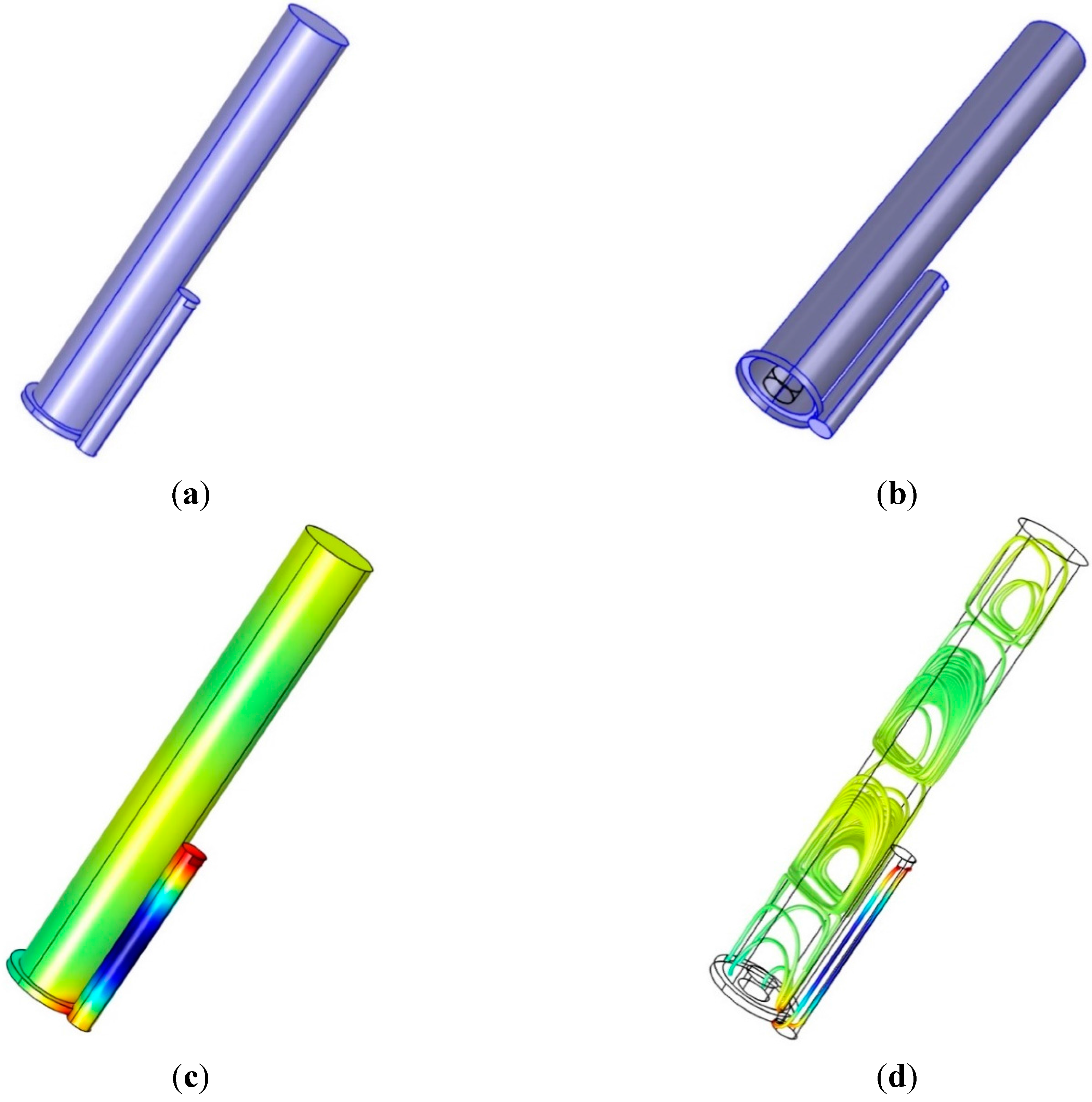
Figure 10a illustrates the center pipe with one directional pipe that contains the inlet at the upper-right-hand side of the pipe and the outlet at lower-left-hand side of the pipe. The outlet window is not explicit in the figure, since the window directly connects to the center body.
Figure 10b depicts the location of the microphone, which is the transparent cylinder at the bottom of the center pipe to collect the consistent signals from the directional pipes.
The simulation in
Figure 10 is executed with a 78.4-mm-long pipe on the side to deliver primitive insights into the NFML structure. In
Figure 10c, the sound pressure distribution is excited by a 3014.6 Hz signal. The strong and weak red colors on the windows indicate the signal inflow and outflow, respectively. According to the wavelength of the given frequency, the distribution is suitable for the 78.4-mm directional pipe; however, the acoustic movement on the center pipe is implicit with relatively flat color spreading.
Figure 10d visualizes the sound intensity streamline at the identical frequency, and the periodic motions in the center pipe are expected to create a lower fundamental frequency than the directional pipe value.
Figure 10.
Simulation with NFML structure with single directional pipe: (a) physical structure (center pipe dimension: l = 192.1 mm and d = 27.8 mm; directional pipe dimension: l = 78.4 mm and d = 10 mm); (b) at the bottom of the NFML structure, the transparent cylinder indicates the microphone; (c) sound pressure distribution at 3014.6 Hz and (d) RMS sound intensity streamline at 3014.6 Hz.
Figure 10.
Simulation with NFML structure with single directional pipe: (a) physical structure (center pipe dimension: l = 192.1 mm and d = 27.8 mm; directional pipe dimension: l = 78.4 mm and d = 10 mm); (b) at the bottom of the NFML structure, the transparent cylinder indicates the microphone; (c) sound pressure distribution at 3014.6 Hz and (d) RMS sound intensity streamline at 3014.6 Hz.
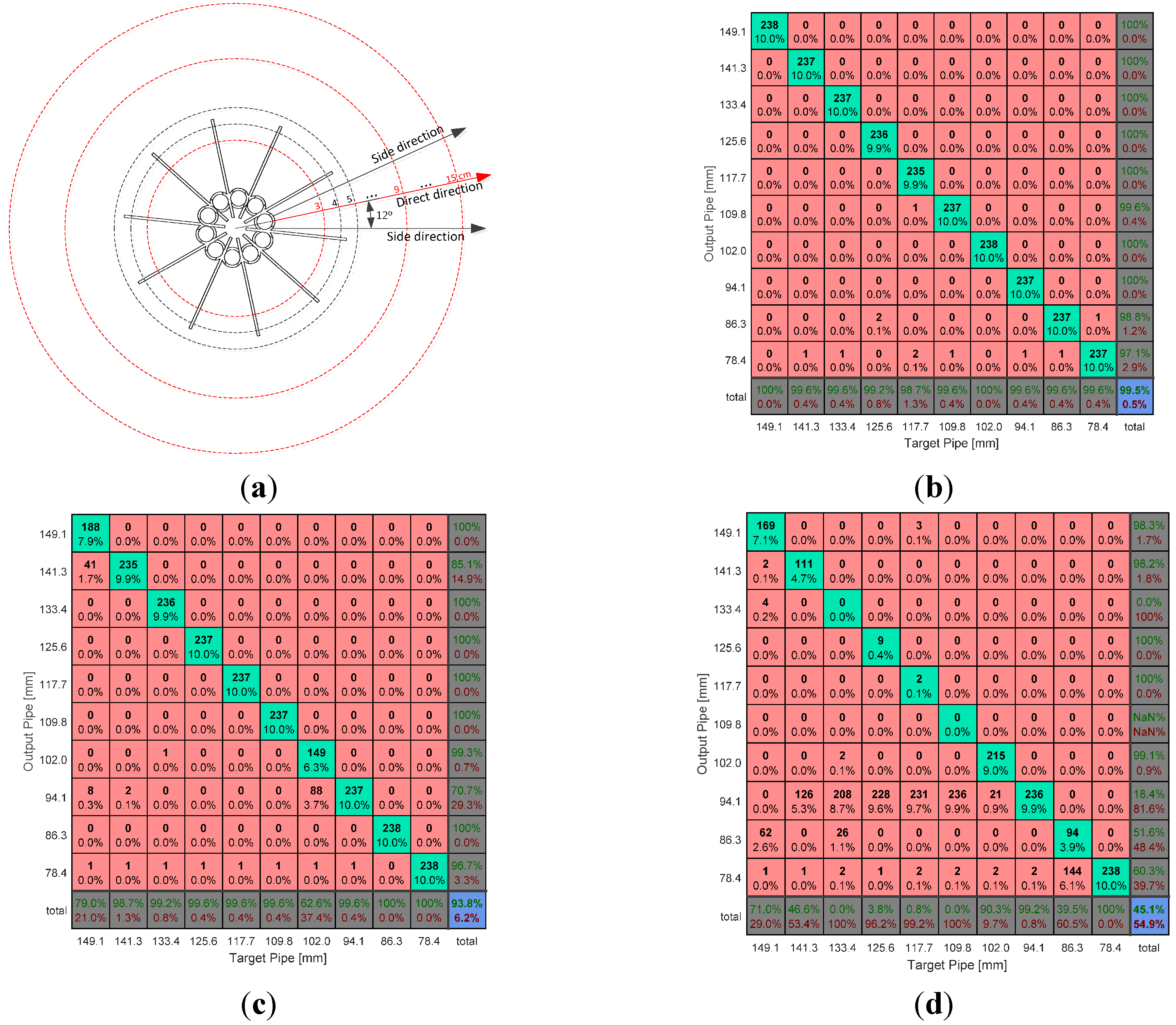
According to the limited estimation resolution in the fundamental frequency by Equation (5), the range of
r values is selected from 10 to 19, which corresponds to the fundamental frequency denoted by the second row of
Table 1. The consequent lengths of the directional pipes are computed by Equation (1) and demonstrated in the
x-axis of
Figure 11 and third row of
Table 1. Note that the adjacent pipe length difference is approximately 7.85 mm derived from the
c/
fs that is the combination of the two relationships between Equation (1) and Equation (5). The fundamental frequency resolution of Equation (5) and the length difference of 7.85 mm are consistent unless the sampling frequency
fs or sound speed
c is changed. The window size for the Cepstral parameter does not alter the resolution or difference either.
Figure 11.
Simulated fundamental frequency distribution of NFML structure for various lengths.
Figure 11.
Simulated fundamental frequency distribution of NFML structure for various lengths.
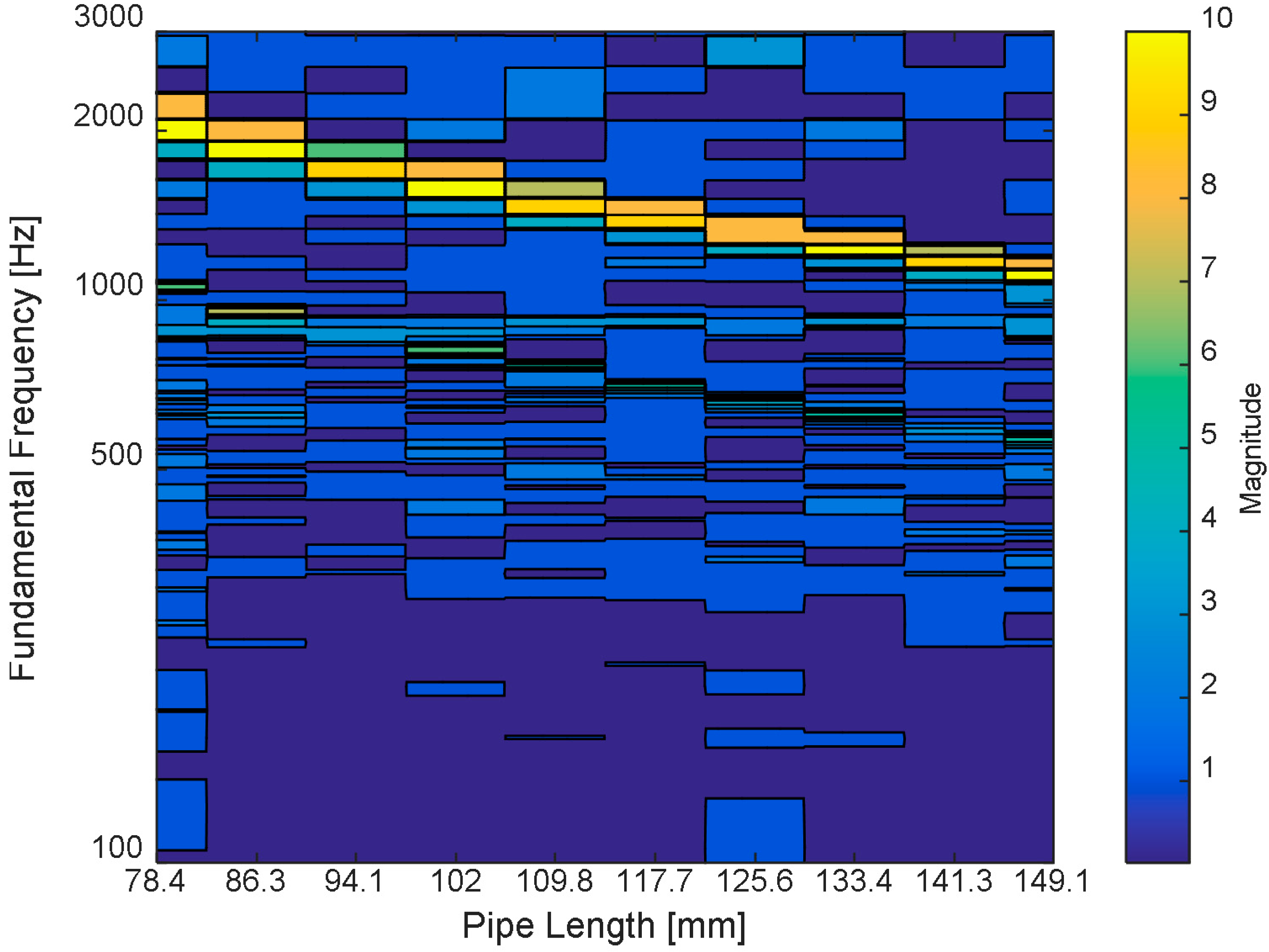
The simulation outcome for the designated directional pipes in the NFML structure is shown in
Figure 11. The results are calculated and gathered by the single model as shown in
Figure 10 that includes the center pipe with one directional pipe, whose length is changed to represent the corresponding fundamental frequency. As the pipe length is increased, the fundamental frequency gradually decreases to indicate the individual variation for the estimation process. The perceptible differences in the fundamental frequency distribution are observed in
Figure 11. Moreover, note that the one-half value of the fundamental frequency is faintly illustrated below the primary line, and the fundamental frequency of the center body 918.8 Hz is indicated by the low contrast line beneath 1000 Hz. For the given range, the fundamental frequencies from the directional pipes and from the center body do not provide any overlap that could possibly generate confusion in the estimation procedure. Therefore, the simulation result validates the NFML structure for acoustic localization by fundamental frequency.
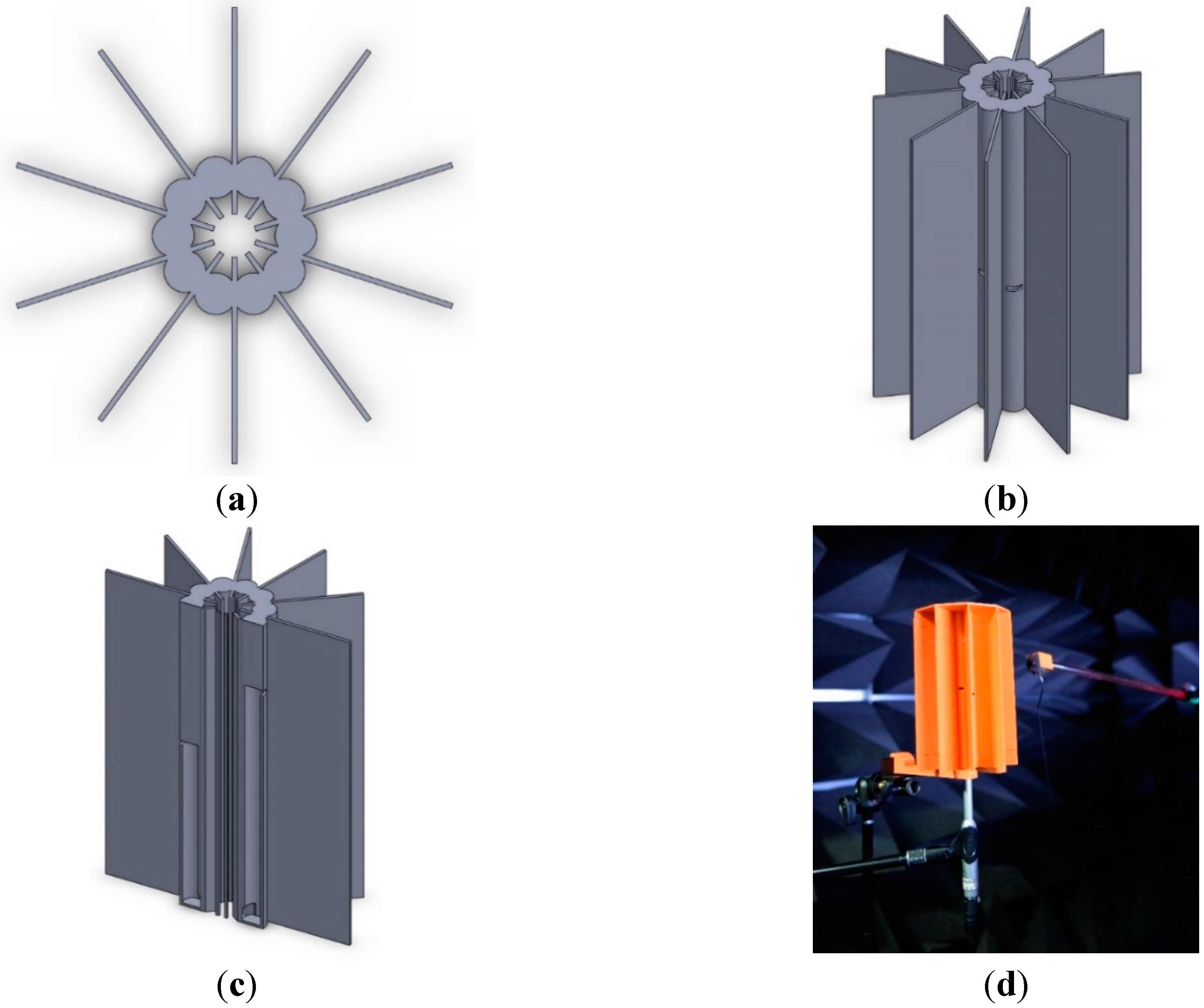
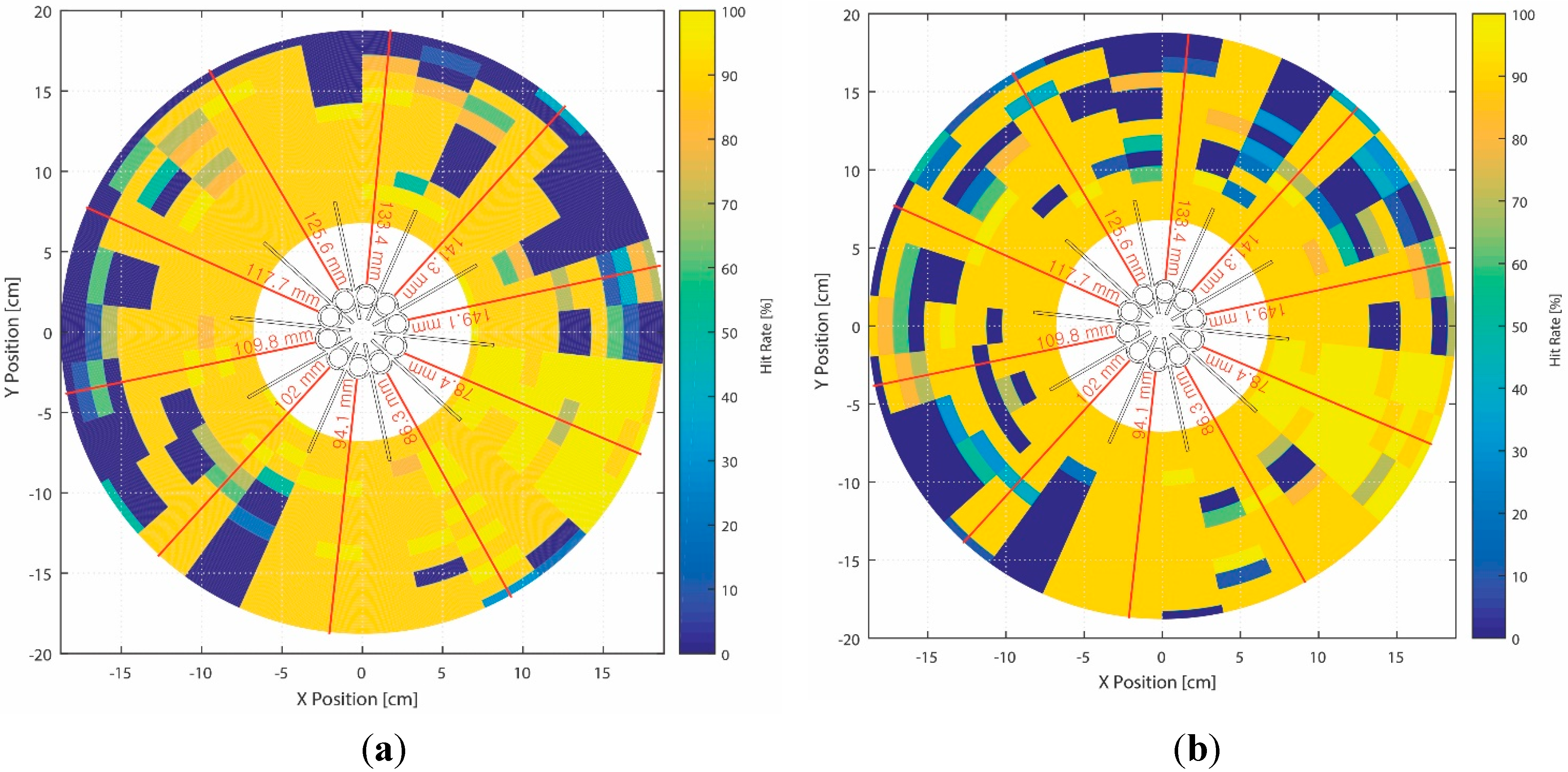
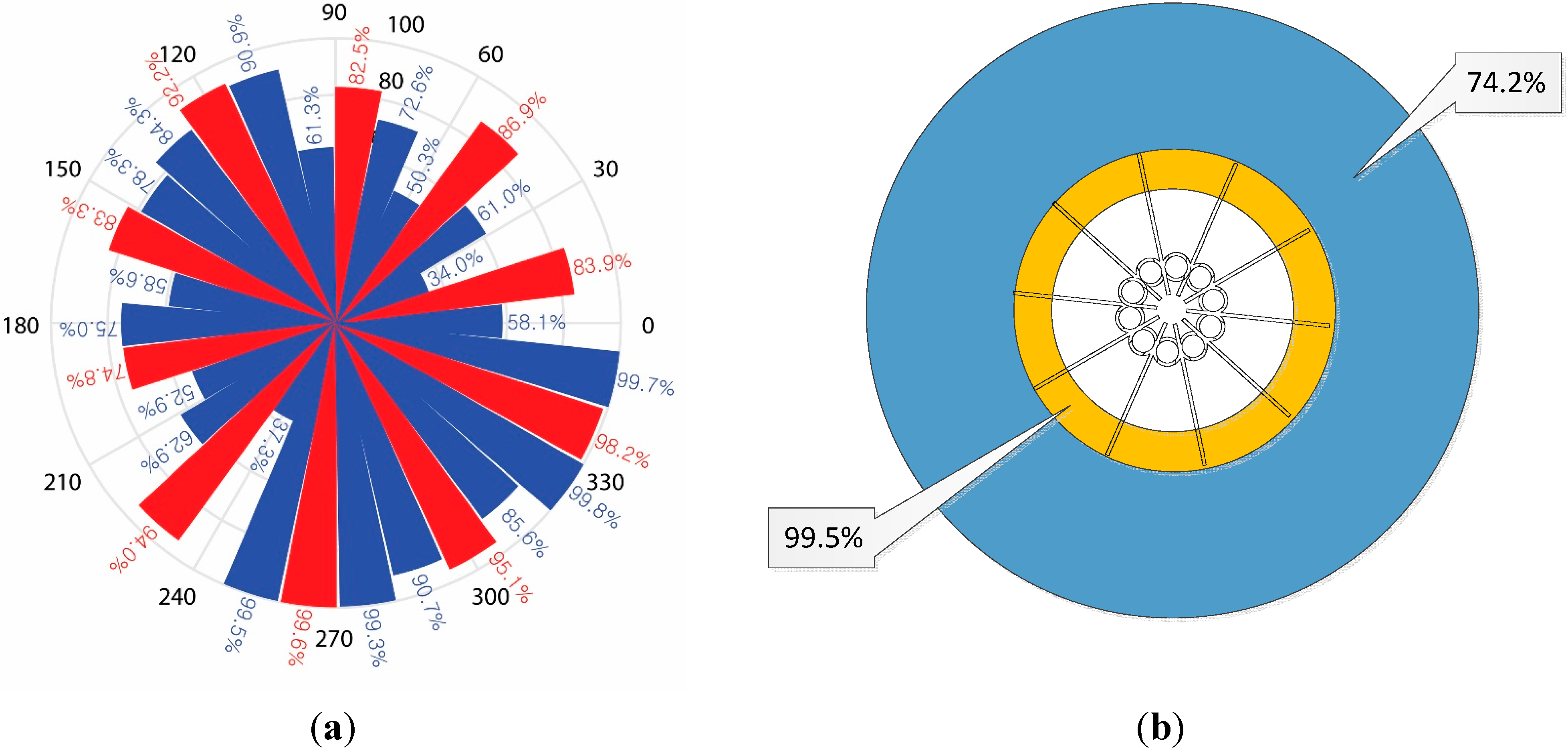
Figure 12 presents the NFML structure with devised lengths for the pipes and center body. The proposed NFML structure in the figure includes the rectangular wings between the individual pipes to avoid significant acoustic diffractions. The small profile cylindrical structure is naturally vulnerable to acoustic diffraction, and it easily propagates the broadband signal to the other side with less attenuation [
34]. The diffraction supplies a considerable amount of signals in the non-line-of-sight (NLoS) directions; hence, the estimation is substantially contaminated in the localization procedure. The radial length of the wing is 5 cm from the joint of two pipes, and the longitudinal length reaches both ends of the pipes, as shown in
Figure 12b. Around a 192.1-mm-long pipe, ten directional pipes are located vertically to receive and collect the signal to the microphone. Each directional pipe has a particular length for the fundamental frequency, as illustrated in
Figure 12c. The designated length is represented by the hollow area in the pipe, and the rest of the length is occupied by the material for symmetric structure to obtain the consistent response except fundamental frequency.
Figure 12.
Designed NFML structure: (a) top view; (b) side view; (c) cross-sectional view; and (d) acoustic experiment in anechoic chamber with 3D-printed NFML structure.
Figure 12.
Designed NFML structure: (a) top view; (b) side view; (c) cross-sectional view; and (d) acoustic experiment in anechoic chamber with 3D-printed NFML structure.
The NFML structure is realized by a 3D printer (Replicator 2, MakerBot, Brooklyn, NY, USA) based on the polylactic acid (PLA) filament, and is shown in
Figure 12d. The acoustic experiments are executed and analyzed in an anechoic chamber that has been verified to exhibit partial conformance with ISO 3745 for free field and hemi-free field conditions [
33]. The microphone (ECM8000, Behringer, Tortola, British Virgin Island), computer-connected audio device (Quad-Capture, Roland, Hamamatsu, Japan), and audio software (Sonar X2 Studio, Cakewalk, Boston, MA, USA) are identical to the experimental configuration of a previous paper [
30] except for the sound generator. To replicate the near-field point source, a high-output in-ear monitor (UE900, Logitech, Lausanne, Switzerland) is mounted on the positioning device to control the distance and height of the sound source, as shown in the right-hand side of
Figure 12d. The direction is observed by the line laser (GLL 3-80, Bosch, Stuttgart, Germany), and the distance is measured by a laser distance meter (DISTO D3a, Leica, Wetzlar, Germany). The system object by Matlab provides the real-time analysis and optimization for the structure via the direct connection to the audio devices. The results from the acoustic experiment in the environment described above are studied and organized in the next section.