Efficient Sensor Placement Optimization Using Gradient Descent and Probabilistic Coverage
Abstract
: We are proposing an adaptation of the gradient descent method to optimize the position and orientation of sensors for the sensor placement problem. The novelty of the proposed method lies in the combination of gradient descent optimization with a realistic model, which considers both the topography of the environment and a set of sensors with directional probabilistic sensing. The performance of this approach is compared with two other black box optimization methods over area coverage and processing time. Results show that our proposed method produces competitive results on smaller maps and superior results on larger maps, while requiring much less computation than the other optimization methods to which it has been compared.1. Introduction
Recent years have seen a proliferation of interest in the use of sensor networks (SN) for different application areas, such as battlefield surveillance, factory automation and environmental monitoring, among others [1]. SNs consist of a network of sensor devices, where each device can autonomously sense the target environment and communicate with other sensors to achieve the goal of delivering valuable information to the end user.
Different issues need to be addressed when deploying a SN, such as localization, data fusion and placement. In the placement problem, the goal is to find the optimal position and orientation of the sensors in the target environment. Optimal placement of sensors is an important design issue, because it directly affects the operational performance of the SN, through the overall coverage of the network [2].
Coverage represents the performance of the network, because sensors are placed inside the environment to sense a phenomena, and coverage measures the quality of the service provided by the SN. There have been several definitions for coverage depending on the application [3,4], such as the area coverage, point coverage, barrier coverage, k-coverage and least exposure coverage. In area coverage, which is the most widely used criterion, the ratio between the area covered by the sensors to the total target area is used as the objective to be maximized. Point coverage and barrier coverage could be considered as special cases of the area coverage, in which special locations in the environment have higher importance in the coverage problem. Therefore, if one finds a general solution for the area coverage problem, it can be easily extended to point coverage and barrier coverage problems. In k-coverage, each location in the environment should be covered by at least k sensors. This is the requirement for some applications with high security (e.g., military surveillance applications), so that in the case of the failure of one sensor, the security of the area is not compromised. Finally, the goal in least exposure coverage is to find a path within the environment with low observability from sensor nodes. This problem is usually formulated as the worst-case coverage for a target that is moving between two points in the environment. In this paper, we use the area coverage as the performance criterion, because it is the most widely used performance measure, and other measures could be considered as special cases of area coverage (except k-coverage and least exposure coverage, which are designed for special applications). Hereinafter, the terms area coverage and performance are used interchangeably.
Determining the coverage of a SN also depends on the coverage model used for each sensor. The common assumption [5] is that each sensor can sense a circular area around itself having a radius known as the coverage range. This assumption of omnidirectional sensing ability does not hold true for many types of sensors, such as cameras, ultrasonic sensors, etc., which have a directional sensing region. The other assumption is related to the detection ability of a sensor inside its sensing area. The conventional approach assumes a binary 0/1 coverage for each sensor [6], while a probabilistic coverage [7,8] better complies with the performance of real sensors in the environment.
The last assumption concerns the dimensionality of the target environment. The target area for the SN is a three-dimensional environment, and the simplification that sensors are placed in a two-dimensional environment [9] usually results in an overestimated performance of the network in real settings. In a realistic setting [10], the covered area of each sensor should also take into consideration the topography of the environment and obstacles occluding the sensing area of each sensor.
Optimal sensor placement has also been an active research area in civil infrastructure monitoring [11,12]. The sensors are placed in the structure to measure a wide range of properties, such as stress, displacement, acceleration, etc. The information gathered from the sensors is used within a continuous structural health monitoring system, which detects any structural damage before it becomes critical. In these applications, the coverage region of a sensor is not “local”. In other words, sensor readings from parts of the infrastructure far from each other might be highly correlated. Therefore, information theoretic criteria are usually used to evaluate the performance of a given placement. Some of the proposed criteria include the modal assurance criterion [13], information entropy [14] and the Fisher information matrix [15].
The sensor placement problem has also been addressed in the computational geometry field. Specifically, Voronoi diagrams and Delaunay triangulation have been used to estimate the coverage region of a sensor [16]. Considering the structure of Voronoi diagrams, each sensor is responsible to cover its Voronoi cell, because all of the points inside each cell are closer to the sensor generating that cell compared to other sensors. It can be easily concluded that if all Voronoi vertices of a Voronoi cell are within the coverage range of sensor, then there are no coverage holes inside that SN. Extending this idea, Wang et al. [17] proposed an effective heuristic to estimate the relative size of coverage holes using the distance between each sensor and its furthest Voronoi vertex. Using the same heuristic, a simple approach to heal the Voronoi holes is to move each sensor toward its farthest Voronoi vertex.
The placement problem in SNs is closely related to the observer sitting problem, which has been addressed in the geomatics science literature [18,19]. In this problem, one tries to find the optimal position for a number of observers, required to cover a certain ratio of an area. Methods proposed for this problem have been applied to determine the location of telecommunication base stations [20], to protect endangered species [21] and to determine the location of wind turbines [22]. Therefore, solutions proposed for the placement problem in SNs have great influence in related problems from other domains.
Methods proposed for placement optimization can be classified into two categories: exact methods and heuristic-based approaches. A group of approaches have considered the placement problem as a special case of the maximum coverage problem [23,24]. In these approaches, the problem is formulated so that a greedy algorithm can produce near-optimal results with approximation boundaries. Other algorithms, such as integer linear programming [25] and binary integer programming [26] methods, have also been employed for the placement problem. The shortcoming of these algorithms is that the assumptions about the environment and the sensors are very simplistic (e.g., two-dimensional target environments, binary coverage of sensors, etc.).
Another approach is based on the virtual potential fields [27]. In this strategy, sensors are moved by the repulsive forces that they sense from other sensors and the obstacles in the environment. These repulsive forces tend to spread sensors across the environment. At the same time, sensors sense a viscous friction force, which helps the sensors reach a static equilibrium.
A wide variety of meta-heuristic methods have also been applied to the placement problem, ranging from genetic algorithm [28], evolution strategies [10], evolution algorithm with specialized operators [29–31], swarm optimization [32,33] and simulated annealing [34]. An issue with meta-heuristic algorithms is their high computational cost, because these optimization algorithms usually need many evaluations of candidate solutions through simulations, which requires high processing resources. This issue makes these algorithms unsuitable for on-line applications where the position and orientation of sensors should be adapted after deployment and during utilization. The computational requirement also limits the size of the networks for which a solution can be found in a reasonable time.
In another set of approaches, spatial phenomena are modelled using Gaussian processes (GP). As a solution for the placement problem under this assumption, sensors could be placed in locations with highest entropy [35], or maximum mutual information [36]. Krause et al. [36] have shown a polynomial-time algorithm for the placement problem, which is within a constant factor of the optimal result. Even though the complexity of this algorithm is reduced to O(kn) for k sensors in n possible sensor locations (n ≫ k), it can still remain inapplicable for large environment where n is proportional to the map area.
In this paper, we are proposing to use gradient descent (GD) as an optimization method for the sensor placement problem. At each step of the algorithm, we calculate the analytical derivatives of the coverage function with respect to the position and orientation of each sensor and try to move them in a way that maximizes the overall coverage of the network.
There has been some work conducted on the usage of the classical gradient descent method for the sensor placement problem. Cortes et al. [37] proposed a distributed mechanism for maximal coverage in multi-robot sensor systems. They showed that if the coverage performance between sensor and target is based on Euclidean distance, the optimal coverage could be achieved by moving each omni-directional sensor in the direction of its Voronoi cell centroid. In this approach, authors have assumed an omnidirectional coverage area for each sensor, therefore the “dominance region” of each sensor is simulated by its Voronoi cell. This assumption is not valid for directional sensors, which will be considered in our work.
Recently, Schwager et al. [38] have proposed another gradient descent method for the unmanned aerial vehicle (UAV) placement problem, but their approach relies on a two dimensional view of the environment, and the covered area of each sensor is strictly binary. As the mentioned approach is designed for placement of the UAVs, each pixel of the camera can cover different area sizes depending on the elevation of the UAV. Therefore, the main notion of coverage in the cost function is the pixel per unit area that the optimization method is trying to minimize. In contrast, the elevation of each camera is fixed in our proposed approach, so the pixel per area value is fixed for all cameras. On the other hand, we consider line-of-sight visibility, such that the optimization method is trying to find the position for which the visibility is maximum.
Unlike previous approaches on sensor placement optimization using the gradient descent method [37,38], we use a realistic model for the terrain and a directional probabilistic sensing model for the coverage of each sensor [8]. We show that in addition to its simplicity, our method can produce results comparable to more sophisticated black box optimization methods, without the need for large computational resources.
The rest of this paper is organized as follows. Section 2 presents our sensor model. In Section 3, the gradient descent method is described in the context of our optimization problem. The presentation of the experimental protocol follows in Section 4. Results are presented in Section 5, where our algorithm is compared with two black box optimization methods, before concluding the paper in Section 6.
2. Sensor Model
The proposed sensing model depends on distance, orientation and visibility. Sensors are positioned at a constant height τ above ground level. The sensor position is thus described by a 3D point p = (x, y, z), where (x, y) are free parameters and z = g(x, y) + τ is constrained by the terrain elevation g(x, y) at position (x, y), as defined by a digital elevation model (DEM). We further assume that the anisotropic properties of sensors are fully defined by a pan angle θ around the vertical axis and a tilt angle ξ around the horizontal axis. A sensor network N = {s1, s2,…, sn} of n sensors is thus fully specified by 4n free parameters si = (pi, θi, ξi), i = 1,2,…,n, with pi = (xi, yi).
Now, the coverage C(si, q) of sensor si at point q in the environment can be defined as a function of distance d(si, q) = ‖q − pi‖, pan angle p(si, q) = ∠p (q − pi) − θi, tilt angle t(si, q) = ∠t (q − pi) − ξi and visibility υ(si, q) from the sensor:
The function υ(pi, q) is binary. Given a sensor position pi, if the line-of-sight between sensor si and q is obstructed, then we assume that the coverage cannot be met, that is υ(pi, q) = 0, otherwise the visibility condition is fully respected, that is υ(pi, q) = 1. In our experiments, we assume that all sensors are one meter above the ground (τ = 1). Memberships μd, μp and μt need to be defined according to their parameters.
At each position q of environment ξ, the coverage for a single sensor is thus the multiplication of the above four conditions. Value C = 1 means full coverage, and C = 0 indicates no coverage. Each position q is also attributed to another parameter wq ∈ [0, ∞]. This parameter defines the importance of location q for the coverage task. Therefore, higher values of wq represent higher importance of the location q in the goal coverage problem. If more than one sensor covers q, then a way to compute the local network coverage Cl is:
Given an environment Ξ, the problem statement is thus to determine the sensor network deployment N that maximizes global coverage, that is:
Note that the NP-hardness of the mentioned placement problem could be verified by comparison with the maximum coverage problem, which is known to be NP-hard [39]. In this comparison, each sensor at a specific position and orientation is a sample for a subset that covers a set of locations in the environment, and we want to find the k sensor positions that allow a maximum coverage when used together. In this problem, the assumption we are making is more general, as the position and orientation of sensors are continuous and coverage of a sensor for each location is probabilistic.
The membership functions μd, μp and μt can be defined as crisp functions, with a value of 1 when the position is within a fixed sensing range or angle of view and otherwise zero.
However, such functions used in a coverage function provide essentially a binary 0/1 signal, which is not a good feedback to use for optimizing functions given its lack of information. Moreover, for a method such as gradient descent, derivable coverage functions are needed. For these reasons, we propose real-valued membership functions that provide a monotonically decreasing membership value over distance and relative angle of position to the sensor (see Figure 1). The value of probabilistic coverage at a given position can be interpreted as the probability of detecting objects of interest from the sensed signal with some given pattern recognition system.
Our proposal is thus to use the following function, based on the well-known sigmoid function, to evaluate the distance membership:
As for the pan angle membership functions, we propose another function based on sigmoids:
3. Gradient Descent Method
Gradient descent (GD) is a classical numerical optimization method used to find the local optimum of an error function. At each step of the algorithm, the gradient of the error function (loss function in our formulation) is calculated and the free parameter of the system is updated to make a small step in the opposite direction to the gradient [40]. Next, the gradient is recalculated for the new solution, and this step is repeated until a maximum number of iterations is reached or the size of the gradient falls beneath a threshold.
3.1. Loss Function
Equation (3) defines the objective function for a maximization problem, while the GD method is defined as a minimization method. Therefore, we define the loss function L(N, ξ) as the negative of the coverage function to form a minimization problem. More precisely, the loss function for network N and environment Ξ is given by:
The visible loss is thus defined as:
The visible loss for the whole network comes to one minus the global coverage defined in Equation (3), which is the coverage function used here as the parameter criterion. However, this measure provides no useful feedback for non-visible positions. Still, these positions are as important as the visible positions in the optimization problem, and their effect should be taken into consideration. In order to provide a better signal to the optimization algorithm, we add a non-visible component to the loss function, which adds the effect of the positions in the environment that are not visible by any sensor or poorly covered by some sensors.
Non-visible loss between sensor si and location q is defined as the difference between the current coverage (given by visible loss Lυ (N, q)) of point q and the coverage that it would have if it was visible from sensor si:
Accordingly, the non-visible loss for a network N and location q is:
3.2. Analytical Gradient Descent on Distance, Pan Angle and Tilt Angle
In this section, we calculate the analytical gradient on distance, pan angle and tilt angle for the sensor placement optimization problem.
Given independent variables xi, yi, θi and ξi, we need to obtain partial derivatives of the loss function for all of these variables (see the Appendix for more details). Let:
As there are four free parameters for each sensor, we show the derivative of the overall loss with respect to a generic parameter ψ of sensor si. ψ can be any of the four parameters (i.e., x, y, ψ;, or ξ). The derivations are as follows:
The derivative of the loss function with respect to parameter ψ can be divided into two parts. The visible loss is constant when the position q is not visible from the sensor si, and therefore, the derivative equals zero. Similarly, the non-visible loss has a derivative of zero when sensor si can see position q. Therefore, the derivative was divided into two equations using the gψ (si, q) function. The ν parameter used in the loss function records the weighting of the non-visible component against the visible loss component.
Therefore, in each step of the GD method, all of the gradients are calculated with respect to the free parameters of each sensor (i.e., xi, yi, θi and ξi), and the position and orientation of all sensors are updated using the pseudocode shown in Algorithm 1.
In this algorithm, is a free parameter of sensor i at iteration t and ηψ is the learning rate for the generic parameter ψ. Furthermore, ω is the momentum parameter used to help the algorithm escape from local minima. The momentum is a classical method used for neural network optimization to encourage faster convergence of the gradient descent algorithm [41]. It increases the step sizes taken for a free parameter if the gradient points in the same direction for several iterations. Therefore, the algorithm can ignore small features in the loss function surface and skip shallow local minima.
| Algorithm 1 The proposed gradient descent method for sensor placement optimization. | |
| procedure GD(N, Ξ) | |
| for t = 1,…, max_iter do | |
| for all si ∈ N do | |
| end for | |
| end for | |
| end procedure | |
The gψ(si, q) function needs the value for the derivative of [μdi · μpi · μti] with respect to the free parameters. We have calculated this derivative for all free parameters and reported the result in Equations (21)-(24) (see the Appendix-(24) for more details). In these Equations, dsg(δ, β, α) is an auxiliary function used to simplify the Equations:
To explain the loss function rather informally, the visible loss is the loss incurred by the visible points; similarly the non-visible loss is the loss incurred by the non-visible points. The optimization algorithm tries to maximize the coverage of the visible points through the visible loss and tries to minimize the number of non-visible points through the non-visible loss. Although these two goals seem similar (and they do have similar effects in most of the cases), they are complementary. We will later see in Section 3.3 how they complement each other.
Although we presented the algorithm in a centralized fashion, it is distributed in nature. Each sensor only needs to know its own position, orientation and visible area, in addition to the overlap between its covered area and other sensors in its neighbourhood to calculate its derivatives. Therefore, if we are using mobile sensors capable of communicating with their neighbours (which is essential in most SNs), they can transfer the required information, and each sensor can compute its movement independently.
3.3. Sanity Checks
In order to check the behaviour of the GD optimization algorithm in real settings, we performed some simple experiments to check if the method performs reasonably in these simple settings, so that we can later extend the experiments to more complex experiments.
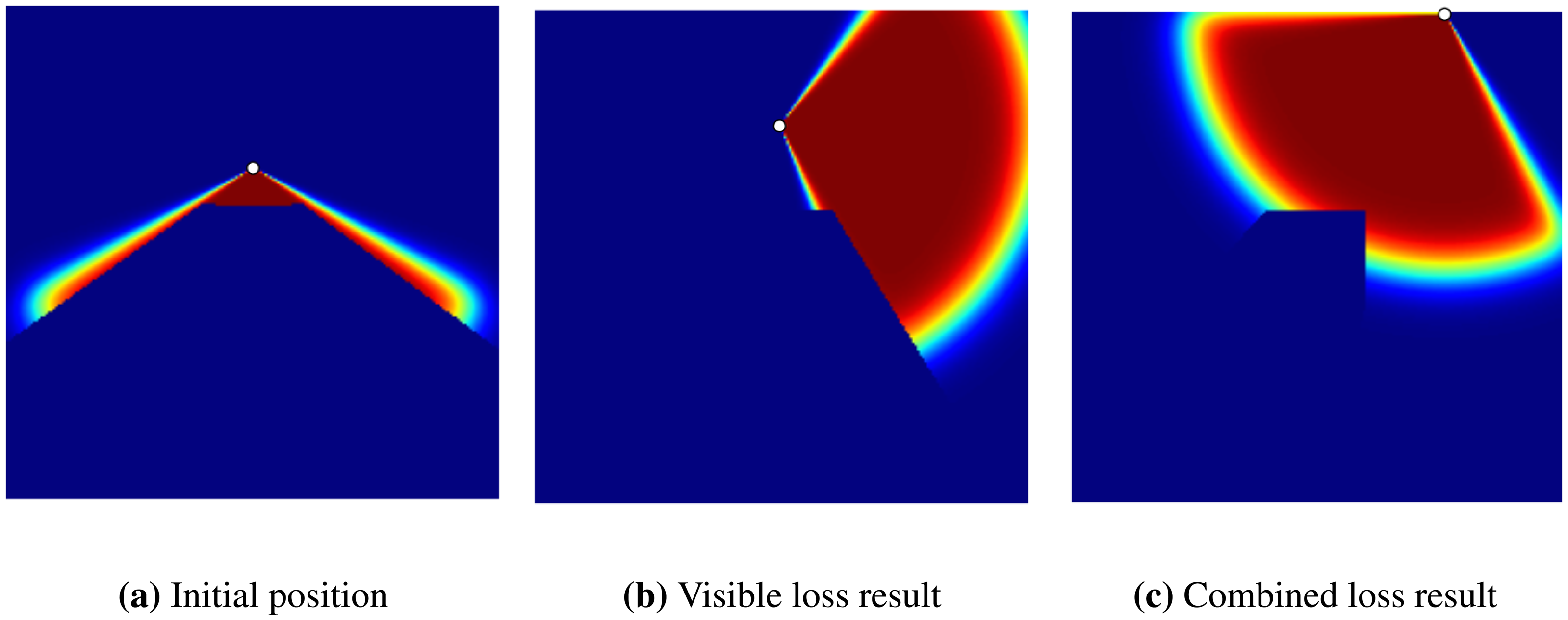
In the first experiment, we examine the effectiveness of the non-visible loss on the overall coverage achieved by the GD algorithm. The setting contains one sensor in a map that has a cube-shaped obstacle in the middle (see Figure 2). Two sets of experiments were performed on the map to optimize the location of the sensors. In the first experiment, we use only the visible loss part of the loss function (Equation (11)). In the second experiment, the combination of both visible and non-visible losses were used for optimization (see Figure 3). In these experiments, the final coverage percentage achieved by the visible and combined loss were 23.29% and 27.47%, respectively. Therefore, we observe that even in the simple example shown, the inclusion of the non-visible loss (in the overall loss function) helps in producing better final results.
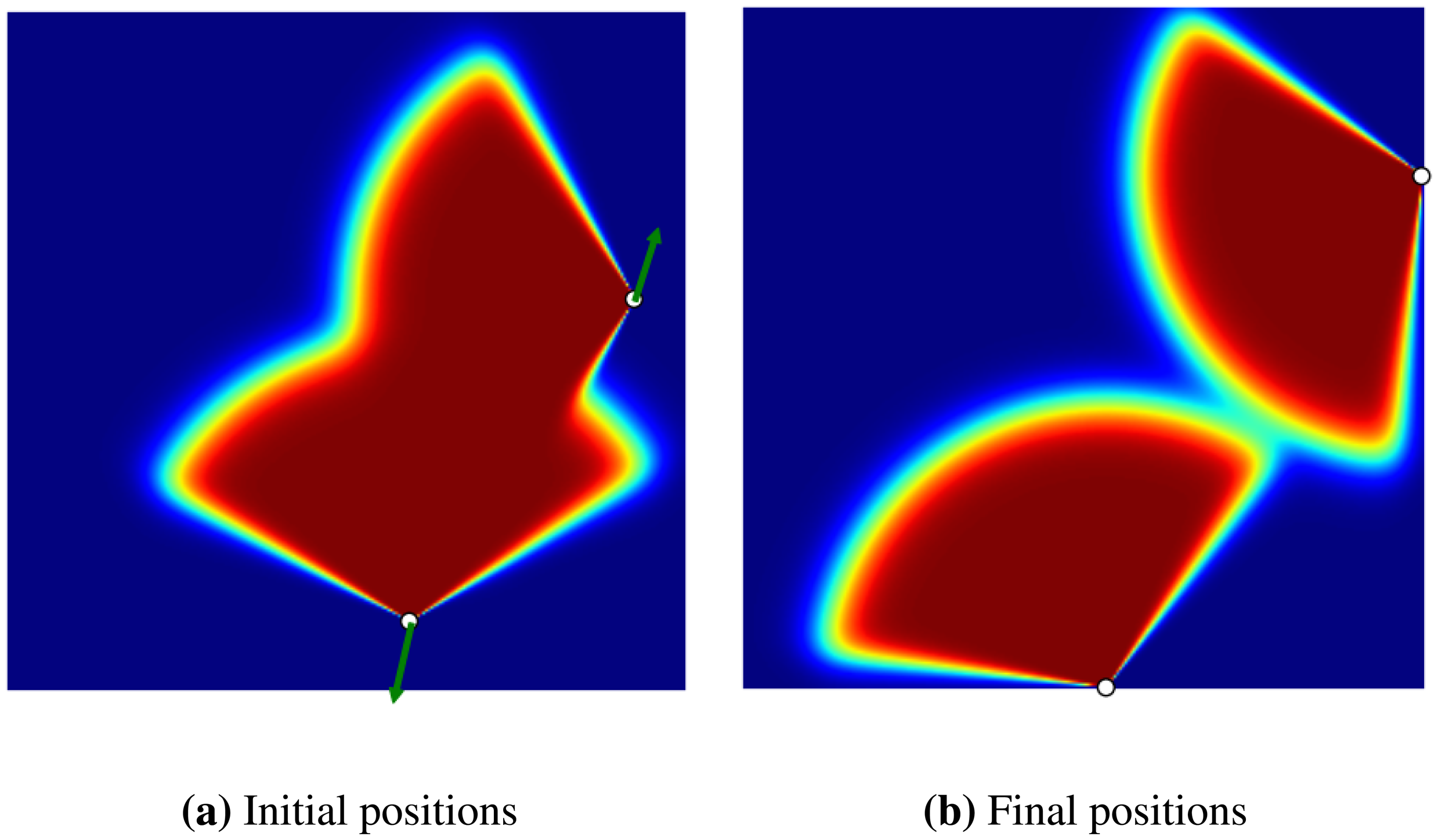
In the second experiment, we evaluated the effect of overlap between the coverages of two sensors over the gradient calculated for each one (see Figure 4). In this experiment, two sensors are initially placed in a flat environment (no obstacle), where there is an overlap between the coverage of the two sensors. The gradient calculated for each sensor makes the sensors move away from each other to reach a final position where the total coverage is maximum.
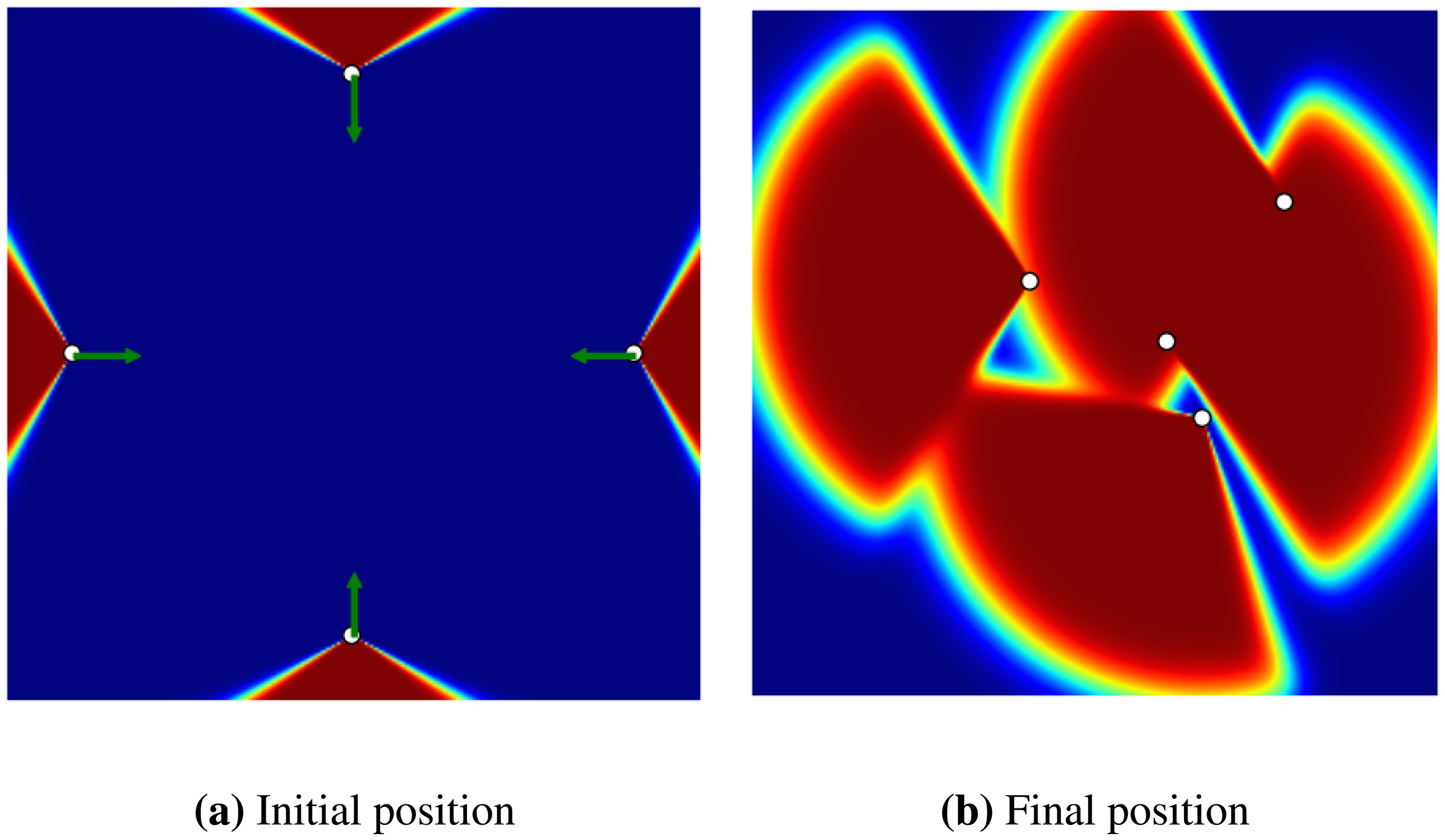
In the final experiment, we show how a coverage gap can be filled with the GD method (see Figure 5). In this experiment, there are four sensors in a flat environment, each heading outward, so creating a coverage gap in the centre. The goal is to determine whether the GD method can detect this gap and displace the sensors in order to cover it. As shown in Figure 5b, the sensors have moved to cover most of the gap.
4. Experiments
In order to evaluate the performance of the proposed method, we compared it with two other optimization methods that we already applied to the sensor placement problem, namely simulated annealing (SA) and covariance matrix adaptation evolution strategy (CMA-ES), which we briefly summarize next. CMA-ES was chosen among different population based stochastic optimization methods, as it was shown several times that it has overall superior performance compared to other optimization methods on a variety of standard continuous black-box optimization benchmarks (as an example in [42]). SA was also chosen as it is a classical stochastic optimization method, widely used for global optimization problems. Interested readers are referred to Akbarzadeh et al. [7] for more detailed explanations on how each method was used for sensor placement optimization.
4.1. Simulated Annealing (SA)
SA [43] is a classical meta-heuristic global optimization method inspired from the annealing process of material in metallurgy. In reality, temperature is the controlling mechanism used to convert material from a high energy state into a low energy, solid condition. This process is imitated in SA, where the temperature controls the number and spread of accessible solutions from a given solution in the search space. SA begins with a high initial temperature to allow a random walk in the search space. As the temperature gradually decreases the system becomes more focused, only allowing moves in the search space which improve the performance of the solution. The process terminates when a temperature close to zero is reached.
SA uses three parameters:
M : the maximum number of iterations for the algorithm.
σsa: the size of the neighbourhood where the subsequent solutions are searched at each iteration of the algorithm.
T(t): the temperature function. This function defines the probability of accepting a random move at each iteration of the algorithm.
4.2. Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
CMA-ES [44] is an optimization method that belongs to the class of evolutionary computation methods. Like classical quasi-Newton optimization methods, CMA-ES attempts to estimate a second order model of the objective function in an iterative procedure. In contrast to quasi-Newton methods, CMA-ES does not need the gradient of the objective function [45].
The algorithm's parameters include the number of parents (μ), the number of offspring (λ), the mutation factor (σ) and the number of generations through which the algorithm runs. At each generation of the algorithm, a collection of the best μ candidate solutions are selected from the set of λ offspring of the previous generation. These solutions are then used to update the distribution parameters, which will eventually generate the offspring for the next generation.
4.3. Maps
To conduct our experiments, we first selected a mountainous area in North Carolina, USA. The data was provided by a raster layer map in the “OSGeo Edu” dataset (Available at http://grass.osgeo.org/download/sample-data/). More specifically, we focused on a portion of the map that covers a small watershed in a rural area near Raleigh, the capital city of North Carolina. The coordinate system of the map is the NC State Plane (Lambert Conformal Conic projection), metric units and North American Datum (NAD83) geodetic datum. We used four portions of the map for our experiments. The information concerning different selected portions of the map is presented in Table 1. Testing the optimization methods with different map sizes, allows the scalability of each method to be verified.
We also tested the optimization algorithms over a map of Université Laval campus, in Quebec City, Canada. The map of the area is shown in Figure 6. In this experiment, which is an example of a surveillance system for the campus, the goal is two-fold. First, we want to test the performance of different methods in the presence of man-made obstacles (i.e., buildings). Second, the target area is weighted, meaning that each pixel is attributed with a different weight (wq) as described in Section 2. For this experiment, we assume that the top of the buildings have low importance in the total coverage (wq = 0.1), the streets have an average importance (wq = 0.4) and the ground level where the pedestrians walk have the highest importance (wq = 0.8). The specifications for the coordinates of the campus maps are also provided in Table 1.
4.4. Settings
Sensors are modelled following a description given in Section 2. For a reasonable model of a sensor, we propose to use the parameters shown in Table 2. With these values, the sensors have 50% of the maximum coverage at 30 m or at a sensing angle of 120°.
For SA, the perturbations for positions and orientations follow a Gaussian distribution with standard deviation σsa. The optimal value for σsa has been established by trial and error (over the range σsa ϵ {0.001,0.005,0.01, 0.05, 0.1, 0.2}), and set to σsa = 0.01 for each map. CMA-ES is run following recommendations of its author [45], with a population of λ = [4 + 3log(N)] offspring and parents. Here, N is the dimensionality of the given problem, determined by the number of sensors in each map. A mutation factor σcma = 0.167 is also used. For the GD method, the list of parameters include the learning rates ηx and ηy for positions, the learning rate ηθ for pan angles, the learning rate ηξ for tilt angles and the weighting parameter υ. The values of these parameters used in the experiments have been found by trial and error, with the same values used over all maps. For that, we performed a grid search for all of the parameters over the NC-A map. More precisely, we had a grid search over parameters η ∈ {0.001, 0.005, 0.01, 0.05, 0.1, 0.5}, υ ∈ {0, 0.5,1,1.5, 2} and ω ∈ {0,0.5,1}. Then, we chose the best five selections of the parameters and among them chose the one that performed best (on average) on all of the other maps. All parameters used for the experiments are summarized in Table 3.
The most computationally demanding part of each algorithm lies in calculating the overall coverage for a candidate solution. Therefore, to allow fair comparison between different optimization methods regarding computation requirements, we put a limit on the number of candidate network coverage calculations each method can do. SA and GD methods perform one coverage calculation per iteration; therefore, the maximum number of iterations for these methods equal the maximum number of coverage calculations for each map. The CMA-ES method calculates coverage for each of its offspring at each generation, so this algorithm proceeds for iterations on each map, where tmax is the maximum number of iterations and A is the number of offspring. We have reported the maximum iteration for each map and algorithm in Table 4. The maximum number of iterations define the stop criterion for each algorithm on each map.
In the GD method, we added another criteria for the termination of the algorithm. In this algorithm, if the fitness of the candidate solution is not improved after a specific number of iterations, the algorithm will stop and report the best solution found so far. In our implementation, this number of iterations is set to be 50.
For the CMA-ES and SA methods, each sensor placement optimization scheme has been run 30 times, from which are estimated the average and the standard deviation of each method. CPU times are also averaged over the 30 runs, in order to compare the resources required by each method to produce a solution. These time values, reported in Table 5, have been evaluated by running the methods on a single Intel i7 core running at 2.8 GHz.
Comparatively, the running time of GD on a specific map is much less than the other two methods. Therefore, we implemented a restart mechanism for our experiments. More precisely, we accomplished this by calculating, on average, how many runs GD is able to perform with restart to be comparable in terms of the number of evaluations calculated. In stochastic optimization, restarting consists in making several runs of the algorithm and using the best solution of these runs as the final result. Joined to a stop criterion that halts the optimization process as soon as it converges, this leads to better results than one single long run. SA and CMA-ES are executed 30 times, so GD is executed for 30 × the average number of runs with restart executed on each map. In Table 5, for the GD method, we have reported the average coverage percentage between the 30 repetitions with restart as “GD with restart” and the average between all runs as “GD single run average”.
Each optimization method begins the optimization process from an initial network setting. We take the random distribution as our initial setting for the optimization methods. Random distribution is the simplest scenario, meaning that all sensors are randomly distributed in the environment.
All optimization programs are implemented in the Python language. The CMA-ES implementation was taken from Distributed Evolutionary Algorithms in Python (DEAP), available at http://deap.gel.ulaval.ca [46]; a Python library for evolutionary algorithms developed at Université Laval.
5. Results
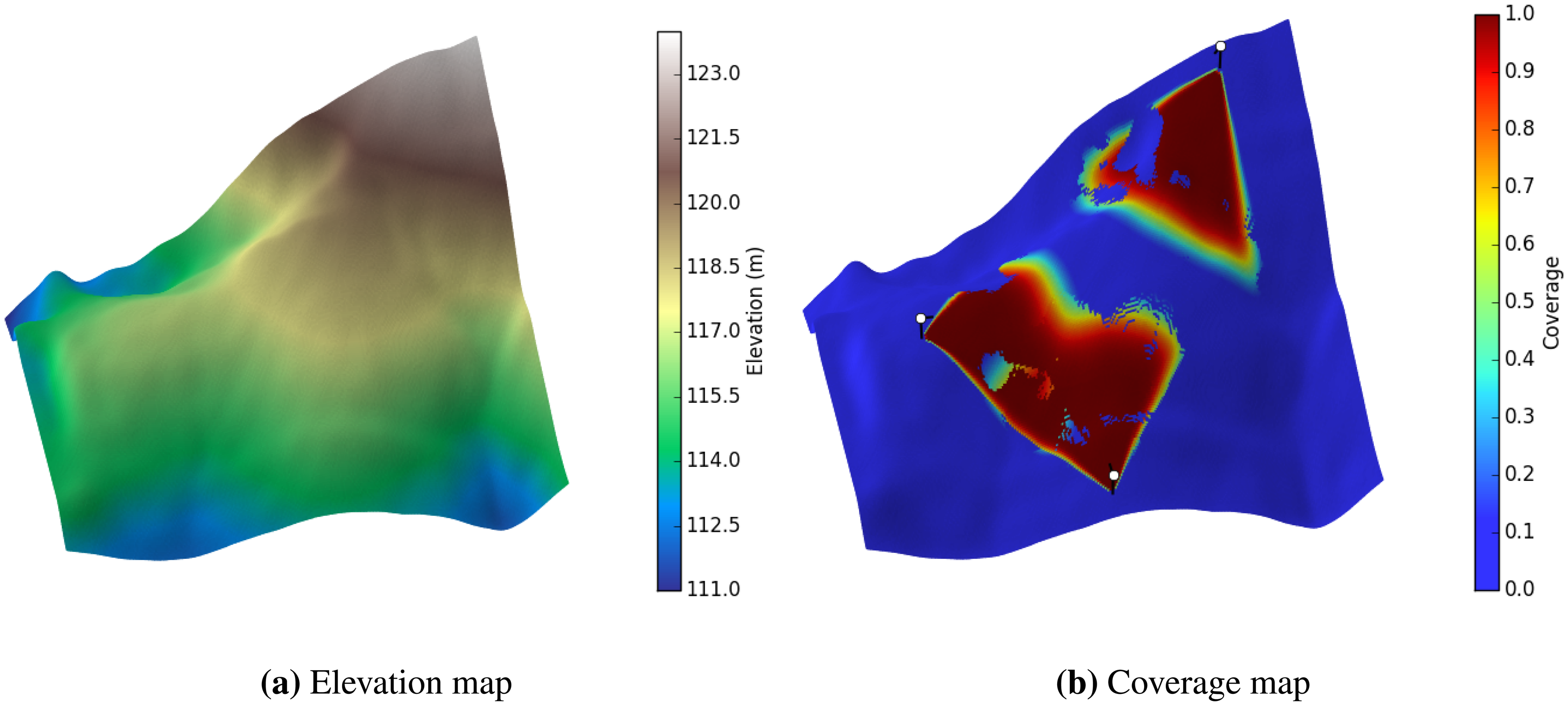
Here, we compare the performance of optimization methods on the mentioned test maps. Each optimization method was run 30 times, except GD, which was run for 30× the average number of runs with restart, from which the average coverage percentage and standard deviation were recorded. A good optimization method should have high coverage and low standard deviation. The results are reported in Table 5. In the experiments, each scheme has been run 30 times, with coverage averages and the corresponding standard deviations reported. Note that 100% coverage is not possible with a finite number of sensors, given its probabilistic nature. Figures 7 and 8 also present the best results obtained by the GD method for each map. There are several aspects that should be pointed out in Figure 7b. First, the coverage of each sensor is scaled by the weight of the area that the sensor is placed on (the same way that the coverage of sensors are weighted in Equation (3)). This gives us the ability to differentiate between areas with different weights. For example, on the top of the buildings (where the weight is smallest), the sensors have blue coverage, or on the roads, the coverage of sensors is green. Next, notice that the area which has lower weights (e.g., the top of the buildings) is not covered as well as the areas with higher weights (e.g., the ground level). This makes sense as the algorithm has balanced the coverage capacity and put more emphasis on the more important areas.
Results indicate that CMA-ES outperformed other methods on three maps and GD performed better on the other three maps. In general, the performance of the three methods is very similar on smaller maps, but on larger maps, the difference is significant. CMA-ES performed better on smaller maps, while GD with restart performed better on larger maps. Still, the difference between the performance of CMA-ES and GD on smaller maps (∼ 1%) is much less than the difference on larger maps (∼ 30%), except for one small map (UL-B) where the difference is larger (∼ 4%). The larger difference of the performance on UL-B map could be related to the abrupt changes of the elevation and visibility on this map, which itself is caused by the abundance of buildings on this map. These changes make the derivative of the objective function discontinuous in the search space; therefore, it will be harder for the GD method to escape local minima. The main difference occurs on the largest map (NC-D) where CMA-ES is unable to obtain a better estimation than the initial random positions. It is well-known that CMA-ES does not scale well in high dimensionality [47]. The reason is that large maps generate high dimensional search spaces (i.e., hundreds of dimensions), and estimating the covariance matrix from a relatively small sample set is brittle. Therefore, the CMA-ES with full covariance matrix is only usable for problems with a small number of sensors (less than 250).
The other major difference is attributed to the computational demand of different algorithms. SA and CMA-ES consume roughly the same amount of computational power, while GD requires between 13- to 165-times less computation time. For example, Figure 9 compares the speed of convergence between different methods on map NC-B.
6. Conclusions
This paper presented an analytical gradient descent (GD) algorithm for optimizing sensor placement. The algorithm was implemented with a realistic model for the environment and a probabilistic model for the sensors. Other optimization methods (CMA-ES and SA) were also implemented and compared with the GD method. In comparison, CMA-ES performed slightly better on smaller maps, while GD performed significantly better on larger maps. Another advantage of the GD method lies in its processing time, as on the tested maps, its performance was between 13- to 165-times superior to that of the other two methods. The final advantage of the algorithm is related to its distributed nature. Although, in this paper, we have tested the algorithm in a centralized fashion, GD has the capability to be executed in a distributed fashion, where each sensor only needs to know the position and coverage of neighbour sensors.
Future work could involve analytically calculating the second order derivative of the objective function to use other gradient-based optimization methods (e.g., Newton's or the quasi-Newton method). Another possible future study could focus on the application of the coverage model to obtain k-coverage over an environment. Therefore, if one sensor fails for any reason, there would be other sensors which could cover the uncovered area.
A. Appendix: Calculation of Derivatives
This section presents the calculation of the analytical derivative of the membership functions (μdi, μpi and μti) with respect to the four free parameters xi, yi, θi and ξi The following function is introduced to simplify the math formulations:
First, let us develop the derivatives of membership functions with respect to xi and yi, that is:
For the term :
To obtain the terms and , we can simply use the chain rule by multiplying the term with additional terms and , respectively:
Consequently, the derivatives of the membership function μdi can be calculated as:
For the term , we first notice that μpi = μp (φpi) where φpi = ∠p (q−pi) − θi. Therefore, we have:
In the term only the pan angle ∠p (q − pi) is a function of xi and yi:
Similarly, the derivative of ∠p (q − pi) with respect to yi can be obtained:
Consequently, we can also develop the terms and as in the following:
For the term , we have μti = μt(φti) where φti = ∠t(q−pi) − ξi:
In the term , only the tilt angle ∠t (q − pi) is a function of xi and yi (indirectly through pi):
By substituting Equations (33), (39) and (45) in Equation (27), we obtain the analytical derivative for the x position of sensor si to the position q in the environment. The derivative to the y position can be calculated in the same way, substituting Equations (34), (40) and (46) in Equation (28).
Let us now develop the derivatives of membership functions with respect to θi:
For the term , the change of θi will not affect the membership functions μdi and μti, hence:
For the term :
By substituting Equations (48) and (49) in Equation (47), we obtain the analytical derivative for pan orientation of sensor si to the position q in the environment.
Now, the developments of the derivatives of membership functions with respect to ξi:
For the term , the change of ξi will not affect the membership functions μdi, and μpi. Hence:
As for the term :
By substituting Equations (51) and (52) in Equation (50), we obtain the analytical derivative for the tilt orientation of sensor si to the position q in the environment.
Acknowledgments
Computational resources have been provided by Calcul Québec/Compute Canada. We thank Anne-Laure Jousselme and Patrick Maupin from Defence Research and Development Canada (DRDC) Valcartier for scientific discussions throughout the project. We also thank Annette Schwerdtfeger for proofreading the manuscript.
Author Contributions
All authors contributed extensively to the work presented in this paper. V.A. and J.-C.L. implemented the system and performed the experiments. Authors wrote the manuscript altogether, and discussed the results and implications and commented on the manuscript at all stages.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yap, F.G.; Yen, H.H. A Survey on Sensor Coverage and Visual Data Capturing/Processing/Transmission in Wireless Visual Sensor Networks. Sensors 2014, 14, 3506–3527. [Google Scholar]
- Marks, M. A Survey of Multi-Objective Deployment in Wireless Sensor Networks. J. Telecommun. Inf. Technol. 2010, 3, 36–41. [Google Scholar]
- Cardei, M.; Wu, J. Energy-efficient coverage problems in wireless ad-hoc sensor networks. Comput. Commun. 2006, 29, 413–420. [Google Scholar]
- Meguerdichian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M. Coverage problems in wireless ad-hoc sensor networks. Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2001), Anchorage, AK, USA, 22–26 April 2001; Volume 3, pp. 1380–1387.
- Huang, C.; Tseng, Y. The coverage problem in a wireless sensor network. Mob. Netw. Appl. 2005, 10, 519–528. [Google Scholar]
- Hefeeda, M.; Ahmadi, H. Energy Efficient Protocol for Deterministic and Probabilistic Coverage in Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2009, 99, 579–593. [Google Scholar]
- Akbarzadeh, V.; Gagné, C.; Parizeau, M.; Mostafavi, M. Black-box optimization of sensor placement with elevation maps and probabilistic sensing models. Proceedings of the International Symposium on Robotic and Sensors Environments (ROSE), Montreal, Canada, 17–18 September 2011; pp. 89–94.
- Akbarzadeh, V.; Gagné, C.; Parizeau, M.; Mostafavi, M.; Argany, M. Probabilistic Sensing Model for Sensor Placement Optimization based on Line-of-sight Coverage. IEEE Trans. Instrum. Meas. 2012, 62, 293–303. [Google Scholar]
- Dhillon, S.; Chakrabarty, K. Sensor placement for effective coverage and surveillance in distributed sensor networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 16–20 March 2003; Volume 3, pp. 1609–1614.
- Akbarzadeh, V.; Ko, A.; Gagné, C.; Parizeau, M. Topography-Aware Sensor Deployment Optimization with CMA-ES. Proceedings of the International Conference on Parallel Problem Solving from Nature (PPSN), KrakÂşw, Poland, 11–15 September 2010; Volume 6239, pp. 141–150.
- Yi, T.H.; Li, H.N. Methodology developments in sensor placement for health monitoring of civil infrastructures. Int. J. Distrib. Sens. Netw. 2012, 2012. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. A new method for optimal selection of sensor location on a high-rise building using simplified finite element model. Struct. Eng. Mech. 2011, 37, 671–684. [Google Scholar]
- Yi, T.H.; Li, H.N.; Gu, M. Optimal sensor placement for structural health monitoring based on multiple optimization strategies. Struct. Des. Tall Spec. Build. 2011, 20, 881–900. [Google Scholar]
- Papadimitriou, C.; Beck, J.L.; Au, S.K. Entropy-based optimal sensor location for structural model updating. J. Vib. Control 2000, 6, 781–800. [Google Scholar]
- Basseville, M.; Benveniste, A.; Moustakides, G.; Rougee, A. Optimal sensor location for detecting changes in dynamical behavior. IEEE Trans. Autom. Control 1987, 32, 1067–1075. [Google Scholar]
- Argany, M.; Mostafavi, M.A.; Karimipour, F. Voronoi-based approaches for geosensor networks coverage determination and optimisation: A survey. Proceedings of the IEEE 2010 International Symposium on Voronoi Diagrams in Science and Engineering (ISVD), Quebec, Canada, 28–30 June 2010; pp. 115–123.
- Wang, G.; Cao, G.; Berman, P.; La Porta, T. Bidding protocols for deploying mobile sensors. IEEE Trans. Mob. Comput. 2007, 6, 563–576. [Google Scholar]
- Lv, P.; Zhang, J.; Lu, M. An optimal method for multiple observers sitting on terrain based on improved simulated annealing techniques. Proceedings of the 19th International Conference on Advances in Applied Artificial Intelligence: Industrial, Engineering and Other Applications of Applied Intelligent Systems (IEA/AIE), Annecy, France, 27–30 June 2006; Springer: Berlin/Heidelberg, Germany. pp. 373–382.
- Franklin, W.; Vogt, C. Multiple observer siting on terrain with intervisibility or lo-res data. Proceedings of the Congress of International Society for Photogrammetry and Remote Sensing (ISPRS), Istanbul, Turkey, 12–23 July 2004; pp. 12–23.
- De Floriani, L.; Marzano, P.; Puppo, E. Line-of-sight communication on terrain models. Int. J. Geogr. Inf. Sci. 1994, 8, 329–342. [Google Scholar]
- Aspbury, A.; Gibson, R. Long-range visibility of greater sage grouse leks: A GIS-based analysis. Animal Behav. 2004, 67, 1127–1132. [Google Scholar]
- Kidner, D.; Sparkes, A.; Dorey, M. GIS Wind Farm Planning. In Geographical Information and Planning; Springer: Berlin, Germany, 1999; pp. 203–223. [Google Scholar]
- Agarwal, P.; Ezra, E.; Ganjugunte, S. Efficient sensor placement for surveillance problems. Proceedings of the 5th IEEE International Conference on Distributed Computing in Sensor Systems Marina Del Rey, CA, USA, 8–10 June 2009; pp. 301–314.
- Johnson, M.; Bar-Noy, A. Pan and scan: Configuring cameras for coverage. Proceedings of the 2011 Proceedings IEEE International Conference on Computer Communications (INFOCOM), Shanghai, China, 10–15 April 2011; pp. 1071–1079.
- Horster, E.; Lienhart, R. Approximating optimal visual sensor placement. Proceedings of the 2006 IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 1257–1260.
- Zhao, J.; Cheung, S.; Nguyen, T. Optimal camera network configurations for visual tagging. IEEE J. Sel. Top. Signal Process. 2008, 2, 464–479. [Google Scholar]
- Howard, A.; Mataric, M.; Sukhatme, G. Mobile sensor network deployment using potential fields: A distributed, scalable solution to the area coverage problem. Distrib. Auton. Robot. Syst. 2002, 5, 299–308. [Google Scholar]
- Jourdan, D.; de Weck, O. Layout optimization for a wireless sensor network using a multi-objective genetic algorithm. Proceedings of the 2004 IEEE 59th Vehicular Technology Conference, Milan, Italy, 17–19 May 2004; Volume 5, pp. 2466–2470.
- Topcuoglu, H.; Ermis, M.; Sifyan, M. Positioning and Utilizing Sensors on a 3-D Terrain Part II; Solving with a Hybrid Evolutionary Algorithm. IEEE Trans. Syst. Man Cybern. Part C 2011, 41, 470–480. [Google Scholar]
- Yi, T.H.; Li, H.N.; Gu, M. Optimal sensor placement for health monitoring of high-rise structure based on genetic algorithm. Math. Probl. Eng. 2011, 2011. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H.; Li, H.N. Wireless Sensor Placement for Bridge Health Monitoring Using a Generalized Genetic Algorithm. Int. J. Struct. Stab. Dyn. 2014, 14. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Ma, J. An improved co-evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment. Sensors 2007, 7, 354–370. [Google Scholar]
- Yi, T.H.; Li, H.N.; Zhang, X.D. Sensor placement on Canton Tower for health monitoring using asynchronous-climb monkey algorithm. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Chiu, P.; Lin, F. A simulated annealing algorithm to support the sensor placement for target location. Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (CCECE/CCGEI), Niagara Falls, Canada, 2–5 May 2004; Volume 2, pp. 867–870.
- Cressie, N. Statistics for Spatial Data; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Krause, A.; Singh, A.; Guestrin, C. Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage control for mobile sensing networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar]
- Schwager, M.; Julian, B.J.; Angermann, M.; Rus, D. Eyes in the Sky: Decentralized Control for the Deployment of Robotic Camera Networks. Proc. IEEE 2011, 99, 1541–1561. [Google Scholar]
- Khuller, S.; Moss, A.; Naor, J.S. The budgeted maximum coverage problem. Inf. Proc. Lett. 1999, 70, 39–45. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rumelhart, D.; McClelland, J. Parallel Distributed Processing: Psychological and Biological Models; The MIT Press: Cambridge, MA, USA, 1986; Volume 2. [Google Scholar]
- Mersmann, O.; Preuss, M.; Trautmann, H. Benchmarking Evolutionary Algorithms: Towards Exploratory Landscape Analysis. Proceedings of the 11th International Conference on Parallel Problem Solving from Nature: Part I, Krakow, Poland, 11–15 September 2010; Volume 6238, pp. 73–82.
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evolut. Comput. 2001, 9, 159–195. [Google Scholar]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. Available online: https://www.lri.fr/hansen/cmatutorial110628.pdf (accessed on 7 May 2014).
- Fortin, F.A.; de Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Ros, R.; Hansen, N. A Simple Modification in CMA-ES Achieving Linear Time and Space Complexity. In Parallel Problem Solving from Nature-PPSN X; Springer: Dortmund, Germany, 2008; pp. 296–305. [Google Scholar]





| Method | Map NC-A | Map NC-B | Map NC-C | Map NC-D | Map UL-A | Map UL-B | |
|---|---|---|---|---|---|---|---|
| West boundary | 638,800 | 638,800 | 638,300 | 638,300 | 245,815 | 245,615 | |
| East boundary | 638,900 | 639,000 | 638,800 | 638,800 | 245,915 | 245,865 | |
| South boundary | 220,000 | 220,500 | 220,500 | 220,000 | 5182,750 | 5,182,550 | |
| North boundary | 220,100 | 220,750 | 220,750 | 220,500 | 5,182,850 | 5182,750 | |
| Highest elevation | 130.65 | 127.81 | 131.6 | 131.55 | 100.0 | 107.3 | |
| Lowest elevation | 125.95 | 109.3 | 103.7 | 103.76 | 85.25 | 82.85 | |
| No. of Columns | 100 | 200 | 500 | 500 | 100 | 250 | |
| No. of Rows | 100 | 250 | 250 | 500 | 100 | 200 | |
| No. of pixels | 10,000 | 50,000 | 125,000 | 250,000 | 10,000 | 50,000 | |
| Parameter | αd | βd | αp | βp | αt | βt |
| Value | 30 | 1 | 60 | 1 | 30 | 1 |
| SA | GD | CMA-ES | ||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | σsa | ηx | ηy | ηθ | ηξ | υ | ω | σcma |
| Value | 0.01 | 0.05 | 0.05 | 0.5 | 0.005 | 1 | 0.5 | 0.167 |
| Method | Map NC-A | Map NC-B | Map NC-C | Map NC-D | Map UL-A | Map UL-B |
|---|---|---|---|---|---|---|
| Simulated Annealing (SA) | 6000 | 30,000 | 103,500 | 144,000 | 6000 | 30,000 |
| Gradient Descent (GD) | 6000 | 30,000 | 103,500 | 144,000 | 6000 | 30,000 |
| CMA-ES | 400 | 1500 | 4500 | 6000 | 400 | 1500 |
| Method | NC-A | NC-B | NC-C | NC-D | UL-A | UL-B | |
|---|---|---|---|---|---|---|---|
| Number of sensors | 12 | 60 | 150 | 300 | 12 | 60 | |
| Search dimension | 48 | 240 | 600 | 1200 | 48 | 240 | |
| SA average | 88.42% | 89.38% | 88.98% | 84.9% | 89.09% | 83.56% | |
| SA SD | 1.56% | 0.58% | 0.43% | 0.53% | 1.69% | 2.47% | |
| SA CPU time | 17.7 m | 10.2h | 4.1 d | 11.1 d | 15.1 m | 10.1 h | |
| CMA-ES average | 90.22% | 92.4% | 91.75% | 60.32 % | 90.44% | 87.63% | |
| CMA-ES SD | 1.89% | 0.73% | 0.65 % | 2.3 % | 1.47% | 1.03% | |
| CMA-ES CPU time | 18.0m | 11.0 h | 4.4 d | 11.4d | 15.9m | 11.1 h | |
| GD with restart | 88.60% | 92.1% | 95.1% | 91.7% | 91.38 % | 83.17% | |
| GD single run average | 84.99% | 90.7% | 94.29% | 90.3% | 86.66% | 76.25% | |
| GD single run SD | 0.90% | 0.23% | 0.12% | 0.26% | 1.05% | 1.64% | |
| GD average # of restart | 13 | 19 | 112 | 165 | 15 | 27 | |
| GD CPU time single run | 85 s | 33.9 m | 52.0 m | 1.5 h | 72 s | 22.2 m | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Akbarzadeh, V.; Lévesque, J.-C.; Gagné, C.; Parizeau, M. Efficient Sensor Placement Optimization Using Gradient Descent and Probabilistic Coverage. Sensors 2014, 14, 15525-15552. https://doi.org/10.3390/s140815525
Akbarzadeh V, Lévesque J-C, Gagné C, Parizeau M. Efficient Sensor Placement Optimization Using Gradient Descent and Probabilistic Coverage. Sensors. 2014; 14(8):15525-15552. https://doi.org/10.3390/s140815525
Chicago/Turabian StyleAkbarzadeh, Vahab, Julien-Charles Lévesque, Christian Gagné, and Marc Parizeau. 2014. "Efficient Sensor Placement Optimization Using Gradient Descent and Probabilistic Coverage" Sensors 14, no. 8: 15525-15552. https://doi.org/10.3390/s140815525
APA StyleAkbarzadeh, V., Lévesque, J.-C., Gagné, C., & Parizeau, M. (2014). Efficient Sensor Placement Optimization Using Gradient Descent and Probabilistic Coverage. Sensors, 14(8), 15525-15552. https://doi.org/10.3390/s140815525




