High Accuracy Localization of Long Term Evolution Based on a New Multiple Carrier Noise Model
Abstract
: A high accuracy localization technique using Long Term Evolution (LTE) based on a new and accurate multiple carrier noise model has been developed. In the noise consideration, the LTE multiple carriers phase noise has been incorporated so that a new and accurate noise model is achieved. An experiment was performed to characterize the phase noise of carriers at 2 GHz. The developed noise model was incorporated into LTE localization analysis in a high traffic area in Hong Kong to evaluate the accuracy of localization. The evaluation and analysis reveals that the new localization method achieves an improvement of about 10% accuracy comparing to existing widely adopted schemes.1. Introduction
One of the prominent methods for localization employs wireless sensor nodes and directional antenna in robots to assist positioning [1,2] and results are encouraging. Since there are increasing numbers of Long Term Evolution (LTE) cellular phone subscribers, in this letter, LTE localization is investigated in an attempt to expedite consumer mobile applications. LTE has become the main-stream in mobile communication since it offers efficient spectrum utilization, cell coverage and handover compared with evolved high speed packet access (HSPA+) [3]. Typical localization algorithms employ received signal strength (RSS) to locate the mobile handset (MH) [4]. Since noise is the key factor influencing the accuracy of localization, a new and accurate noise model should be developed and applied to localization to enhance the localization accuracy.
The phase noise is an inherent property of a carrier that affects transmission performance. Since LTE is a multiple carrier scheme thus the phase noise incurred may affect the accuracy of localization. It is intuitive that the accuracy of localization should be improved if a more accurate noise model is developed. This investigation is dedicated to a new model that incorporates phase noise for multiple carriers. In telecommunication, RSS is an indicative parameter reflecting the strength of the received signal [5–8]. Normally, when the distance between a MH and the base station (BS) is short, the RSS will be large. In general, RSS can be greatly attenuated by tall buildings in dense or populated areas, hence deteriorating the accuracy of localization.
In this Communication, a new noise model dedicated to LTE localization of mobile handsets is proposed. Based on the developed noise model, a new localization model has been developed and an improvement of localization accuracy has been achieved. In mobile telecommunication, broadband Gaussian noise prevails in all circumstances and is incorporated into localization considerations [9]. In general, the Gaussian noise model [10] is adopted. In essence, the phase noise is an inherent property of the signal carrier. Hence the phase noise is an indispensable element in the noise evaluation. The multiple carrier nature of LTE further demands the consideration of the impact of the phase noise. In this investigation, it is proposed that the Gaussian noise co-exists with the phase noise in an LTE orthogonal frequency division multiplexing (OFDM) system.
2. Noise Model
For radio frequency propagation, a path-loss model [4,9] is typically used to determine the distance from BS to MH. The model considers the coordinates of BS and MH as well as the log-normal shadowing [11,12] which is represented by wo. Pt is the transmitted power from BS and Pr is the received power in MH, PL accounts for the reference signal power in one meter. dk is the distance between a BS and a MH and is associated with random Gaussian variable wo. Equation (1) is normally used to locate a handset's coordinates:
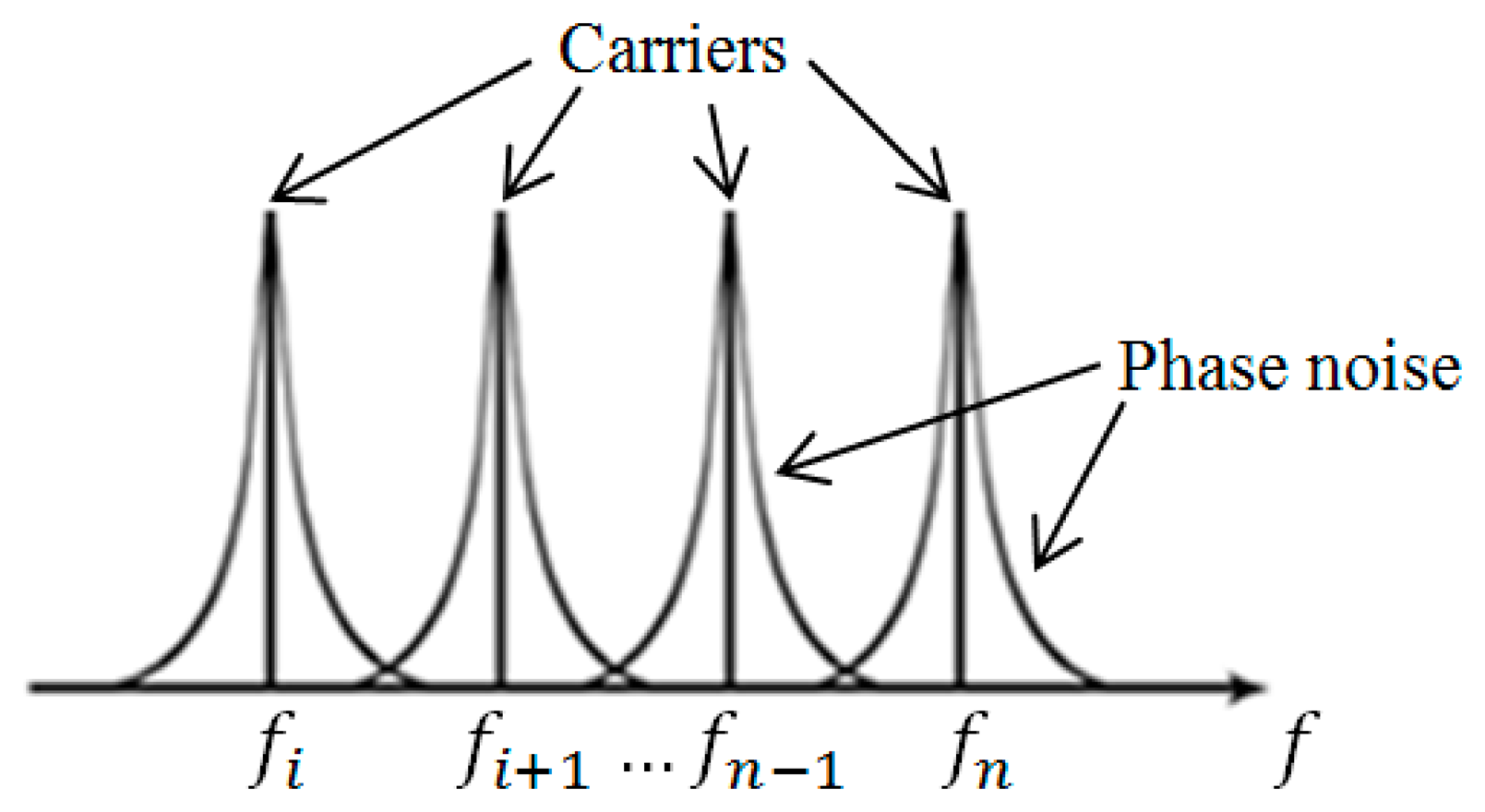
Phase noise is introduced when there is a small deviation of phase of a RF signal in oscillators and such deviation is commonly found in wireless communication systems. In LTE communication from BS to MH, signal transmission is in the form of multiple carriers of OFDM system. The corresponding phase noise [13] associated with multiple carriers in OFDM are shown in Figure 1. From this figure, it is seen that phase noise in neighboring channels may influence one another and is additive in nature.
Phase noise is a spectral density of phase deviation and usually represented as L(f) and expressed in dBc/Hz. The phase noise in a noisy oscillator can be approximated by a Leeson function [14]. In a multi-carrier system, an aggregate effect of phase noise needs to be considered. Assume that an OFDM symbol has n carriers, where fi is the carrier frequency, Δf is the offset frequency, F is the noise factor, Ps is the oscillator signal power level, Q is the quality factor, k is the Boltzmann constant and T is the temperature in Kelvin. By observing the waveform and by intuition, the individual phase noise is represented in Equation (2) where m is to be determined and A is a constant to be characterized. An experiment was performed on the effective offset that should be included at 2 GHz. In the design, it was found from experiment that A/QPs was typically in the range ∼800–1600. In our design, A/QPs = 1200 and F = 10 were chosen. From measurement, it was concluded that an offset frequency Δf of about ±0.00002% at 2 GHz accounted for most of the phase noise effect and that m had the best fitting in the range between 1.5 and 2.5:
Since there are multiple of carriers in LTE, the total phase noise in the system becomes:
By incorporating the phase noise for multiple carriers in LTE, a new noise model has been developed and is shown in Equation (3). The effectiveness of the new model will be investigated in the next section.
3. Experimental Results
In high traffics areas, noise is a particularly prominent factor that may affect the accuracy of localization. The localization method in [9] is implemented by incorporating the developed noise model in Equation (3). The outdoor localization model is then modelled as:
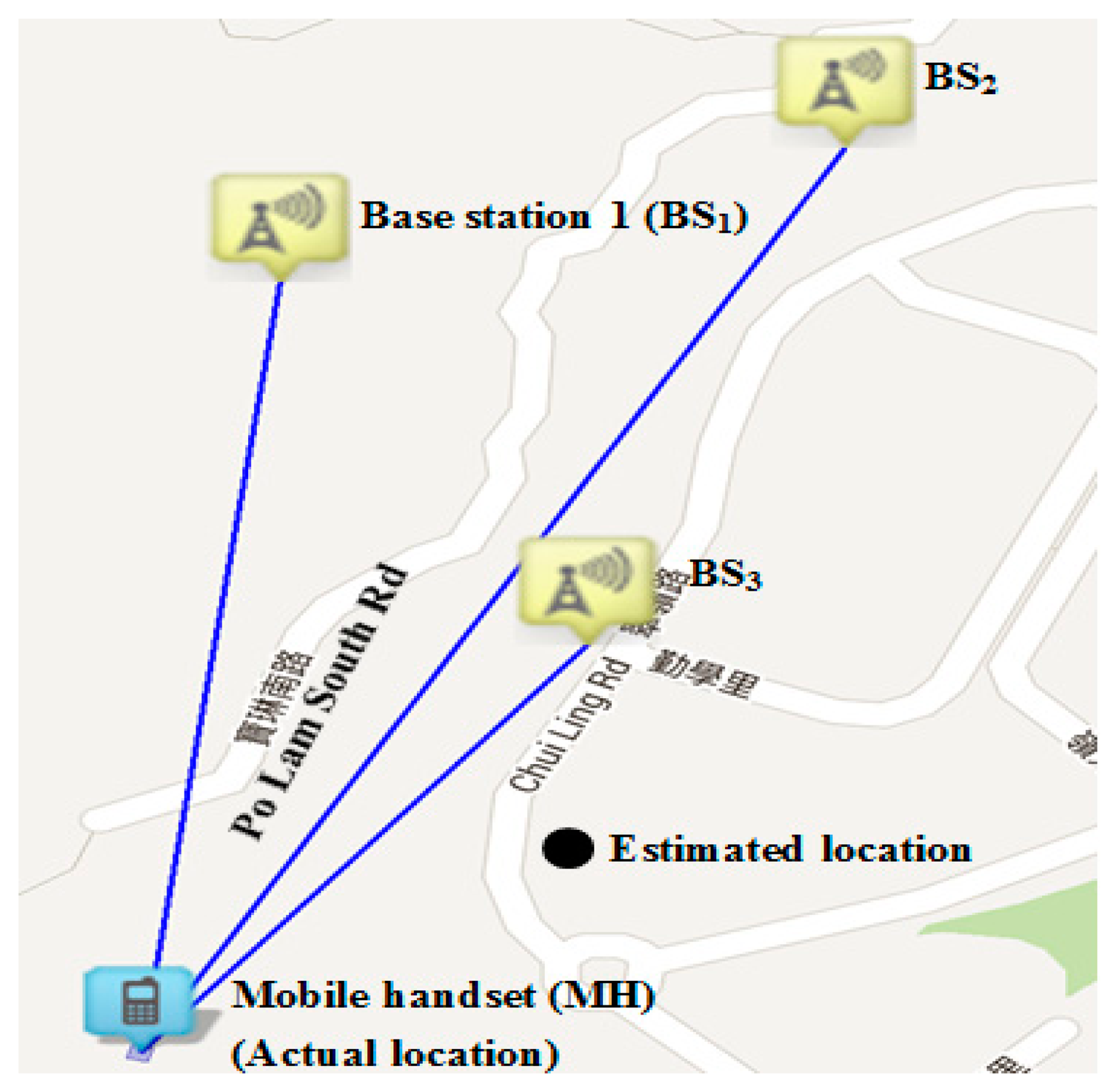
The localization model developed in Equation (4) (referred as the new scheme) is then used to evaluate the localization accuracy and comparison with the existing widely adopted localization scheme (1) (referred to as reference scheme) will be performed. The experiment was carried out in a noisy and yet busy area in the city of Hong Kong where there were more base stations than a typical remote area. During the experiment, a stationary MH was anchored into the actual location to intercept the RSS from neighboring BSs. By substituting the coordinates of all BSs and RSS values into Equation (4), an estimated location as shown in Figure 2 is obtained. The variance of random Gaussian noise typically varies according to condition of the environment under investigation. In our experiment, it was measured that the variance for random Gaussian noise was typically between 5 dB and 13 dB.
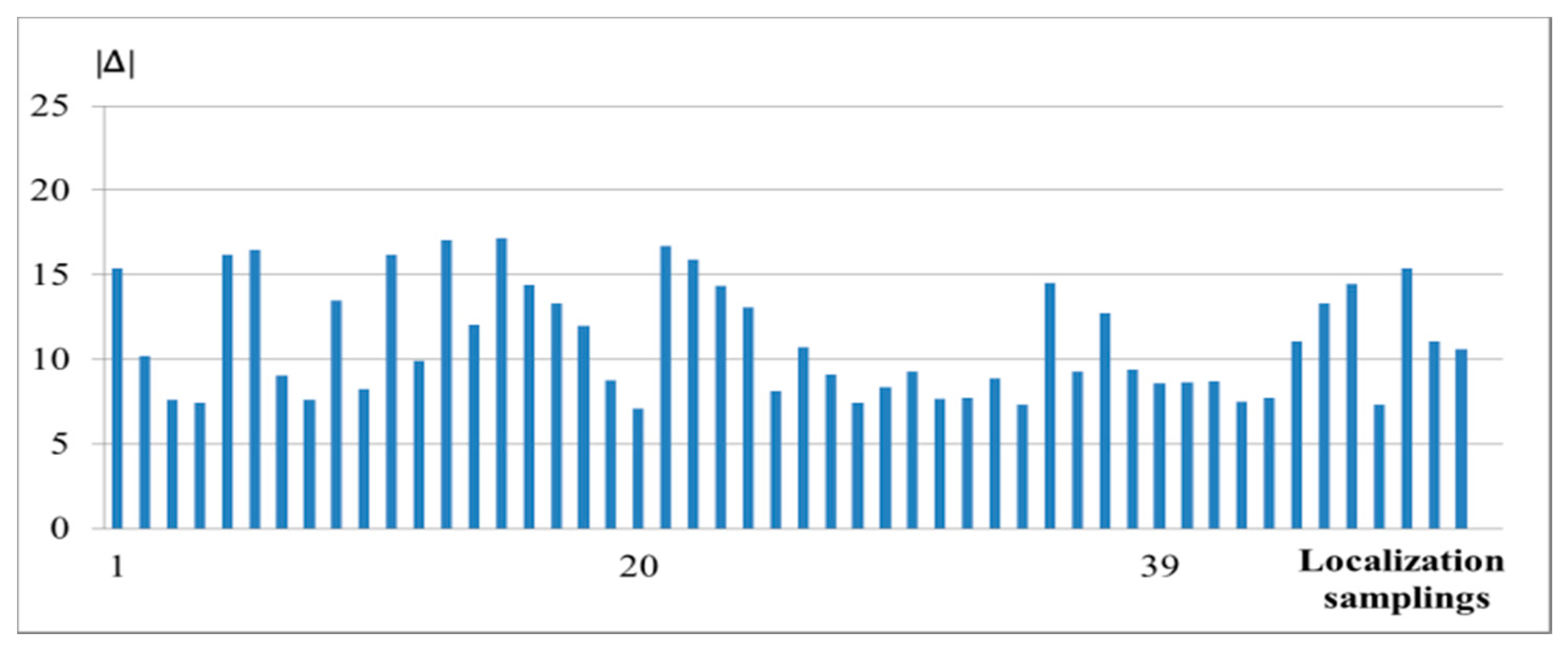
Fifty (50) RSSs data were captured by a MH and used for the RSS localization. Measurement data using the reference scheme are recorded and compared with the new scheme in Figure 3. The percentage improvement of accuracy of the new scheme (4) over the reference scheme (1), |Δ|, based on 50 localization samplings is shown in Figure 4. It is seen that the accuracy has been improved by about 10% on average.
4. Conclusions
An accurate localization model using Long Term Evolution (LTE) has been developed by incorporating a high accuracy noise model. The developed noise model incorporates the multiple carrier effect of the phase noise in LTE. Basic parameters for phase noise of carriers at 2 GHz have been characterized. The new localization model, based on the developed noise model, has been applied to RSS localization of LTE in a busy residential area in Hong Kong. The new localization method achieves on average an accuracy improvement of about 10%.
Acknowledgments
This work was financially supported by the Department of Electronic Engineering, City University of Hong Kong through project GRF116013 from UGC of the government of the Hong Kong SAR, China. The support from the Wireless Sustainability Center of the Department of Electronic Engineering, City University of Hong Kong is gratefully acknowledged.
Author Contributions
Wah Ching Lee contributed to equipment for measurement of noise, mathematical development and paper written. Faan Hei Hung was involved in the mathematical development, experiment setting as well as drafting of the paper. Kim Fung Tsang and Hao Ran Chi have developed part of the mathematical development used and designed some characterization experiments, as well as have participated in the drafting of the paper. Chung Kit Wu, Kwok Tai Chui and Wing Hong Lau carried out the experiments, data analyzing and critically reviewed the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, D.; Kim, C.-Y.; Yi, J. Simultaneous localization of multiple unknown CSMA-based wireless sensor network nodes using a mobile robot with a directional antenna. Intell. Serv Robotics 2009, 2, 219–231. [Google Scholar]
- Song, D.; Kim, C.-Y.; Yi, J. Simultaneous localization of multiple unknown and transient radio sources using a mobile robot. IEEE Trans. Robotics 2012, 28, 668–680. [Google Scholar]
- Elnashar, A.; El-Saidny, M.A. Looking at LTE in Practice: A Performance Analysis of the LTE System Based on Field Test Results. IEEE Veh. Technol. Mag. 2013, 8, 81–92. [Google Scholar]
- Coluccia, A.; Ricciato, F. RSS-Based Localization via Bayesian Ranging and Iterative Least Squares Positioning. IEEE Commun. Lett. 2014, 18, 873–876. [Google Scholar]
- Leu, J.-S.; Tung, N.H.; Liu, C.-Y. Non-Parametric RSS Prediction Based Energy Saving Scheme for Moving Smartphones. IEEE Trans. Comput 2014, 63, 1793–1801. [Google Scholar]
- Jeong, E.-M.; Yang, S.-H.; Kim, H.-S.; Han, S.-K.; Cavalcanti, D. Tilted receiver angle error compensated indoor positioning system based on visible light communication. IEEE Electron. Lett. 2013, 49, 890–892. [Google Scholar]
- Bel, A.; Vicario, J.L.; Seco-Granados, G. Localization Algorithm with On-line Path Loss Estimation and Node Selection. Sensors 2011, 11, 6905–6925. [Google Scholar]
- Zhou, M.; Xu, Y.B.; Ma, L.; Tian, S. On the Statistical Errors of RADAR Location Sensor Networks with Built-In Wi-Fi Gaussian Linear Fingerprints. Sensors 2012, 12, 3605–3626. [Google Scholar]
- Salman, N.; Kemp, A.H.; Ghogho, M. Low Complexity Joint Estimation of Location and Path-Loss Exponent. IEEE Wirel. Commun. Lett. 2012, 1, 364–367. [Google Scholar]
- Wu, Y.; Wang, K.; Sun, Y.; Ji, Y. R2NA: Received Signal Strength (RSS) Ratio-Based Node Authentication for Body Area Network. Sensors 2013, 13, 16512–16532. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-Based Localization in Wireless Sensor Networks Based on Second-Order Cone Programming. Sensors 2014, 14, 18410–18432. [Google Scholar]
- Tarrío, P.; Bernardos, A.M.; Casar, J.R. An Energy-Efficient Strategy for Accurate Distance Estimation in Wireless Sensor Networks. Sensors 2012, 12, 15438–15466. [Google Scholar]
- Ryu, H.-G.; Lee, Y.-S. Phase noise analysis of the OFDM communication system by the standard frequency deviation. IEEE Trans. Consum. Electron. 2003, 49, 41–47. [Google Scholar]
- Leeson, D.B. A simple model of feedback oscillator noise spectrum. Proc. IEEE RFIC Virtual J. 1966, 54, 329–330. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.C.; Hung, F.H.; Tsang, K.F.; Wu, C.K.; Chi, H.R.; Chui, K.T.; Lau, W.H. High Accuracy Localization of Long Term Evolution Based on a New Multiple Carrier Noise Model. Sensors 2014, 14, 22613-22618. https://doi.org/10.3390/s141222613
Lee WC, Hung FH, Tsang KF, Wu CK, Chi HR, Chui KT, Lau WH. High Accuracy Localization of Long Term Evolution Based on a New Multiple Carrier Noise Model. Sensors. 2014; 14(12):22613-22618. https://doi.org/10.3390/s141222613
Chicago/Turabian StyleLee, Wah Ching, Faan Hei Hung, Kim Fung Tsang, Chung Kit Wu, Hao Ran Chi, Kwok Tai Chui, and Wing Hong Lau. 2014. "High Accuracy Localization of Long Term Evolution Based on a New Multiple Carrier Noise Model" Sensors 14, no. 12: 22613-22618. https://doi.org/10.3390/s141222613
APA StyleLee, W. C., Hung, F. H., Tsang, K. F., Wu, C. K., Chi, H. R., Chui, K. T., & Lau, W. H. (2014). High Accuracy Localization of Long Term Evolution Based on a New Multiple Carrier Noise Model. Sensors, 14(12), 22613-22618. https://doi.org/10.3390/s141222613







