Fixed-Base Comb with Window-Non-Adjacent Form (NAF) Method for Scalar Multiplication
Abstract
: Elliptic curve cryptography (ECC) is one of the most promising public-key techniques in terms of short key size and various crypto protocols. For this reason, many studies on the implementation of ECC on resource-constrained devices within a practical execution time have been conducted. To this end, we must focus on scalar multiplication, which is the most expensive operation in ECC. A number of studies have proposed pre-computation and advanced scalar multiplication using a non-adjacent form (NAF) representation, and more sophisticated approaches have employed a width-w NAF representation and a modified pre-computation table. In this paper, we propose a new pre-computation method in which zero occurrences are much more frequent than in previous methods. This method can be applied to ordinary group scalar multiplication, but it requires large pre-computation table, so we combined the previous method with ours for practical purposes. This novel structure establishes a new feature that adjusts speed performance and table size finely, so we can customize the pre-computation table for our own purposes. Finally, we can establish a customized look-up table for embedded microprocessors.1. Introduction
Elliptic curve cryptography (ECC) is a public-key cryptography based on the algebraic structure of elliptic curves over finite fields [1–3]. The use of elliptic curves in cryptography was suggested independently by Koblitz [4] and Miller [5] in 1985. The short key size and various crypto protocols are available in ECC, which enable secure and robust communications. However, scalar multiplication, which multiplies a secret scalar, k, with a point, P, on an elliptic curve, E(


In this paper, we propose an efficient method for fixed-point scalar multiplication, enhancing the method of Mohamed et al. by constructing a novel look-up table structure. This structure generates consecutive zero-sequences more frequently, so we can compute the scalar multiplication with a smaller number of group addition operations. This characteristic is derived from observation of the w-NAF behavior and test secret scalars, k, given by the Blum-Blum-Shub random number generator, which is guaranteed by the National Institute of Standards and Technology (NIST) random number suite [11]. However, straight-forward implementation of our method does not show advantage, due to a large pre-computation table, so we mixed the previous method with ours in various combinations to meet the speed and size requirements. This novel structure has a new feature that can adjust size and speed more accurately, and this is unavailable in the previous method. With this hybrid method, we can construct various pre-computation tables for various purposes, such as the finely-tuned speed and size trade-off model. This method can be implemented on modern microprocessors, such as the ATmega, MSP and ARM series, which provide ROM more than at least 32 Kbytes. Furthermore, even an unknown point is efficiently computable by exploiting the proposed method. The detailed explanations of the unknown point are available in Appendix B. The following are the main contributions of this paper.
Our Contributions
We found zero occurrence characteristic of NAFw representation. This feature is useful to construct a pre-computation table with a high zero occurrence ratio.
We presented a finely-tuned hybrid model, which can adjust size and speed performance more accurately. This can establish a customized look-up table for embedded microprocessors, by adjusting the program size or computation costs.
We applied this method to an unknown point and show high performance enhancement by 12.7% compared to traditional NAFw representation.
The paper is organized as follows. In Section 2, we give an introduction to existing scalar multiplication methods, including those mentioned above. In Section 3, we introduce our proposed method, and in Section 4 we evaluate our proposal. Finally, we conclude our paper in Section 5.
2. Related Work
In this section, we explore scalar multiplication, which is one of the most expensive operations of elliptic curve cryptography. As shown in Algorithm 1, the inputs of the double-and-add algorithm are a random number, k, and a point, P, on an elliptic curve, E, defined over field,

| Algorithm 1. Double-and-add method using left-to-right binary method. | |
Input: k = (kt-1,…, k1, k0)2, P ∈ E(
 q). q). | |
| Output: kP. | |
| 1. | Q ← ∞. |
| 2. | For i from t − 1 down to 0 do |
| 2.1 | Q ← 2Q. |
| 2.2 | If ki = 1, then Q ← Q + P. |
| 3. | Return(Q) |
2.1. (Fixed-Base) Scalar Multiplication Method
To describe scalar multiplication, we assume that #E(

2.1.1. Non-Adjacent Form
If P is given by P = (x, y; ∈ E(

2.1.2. Window Method
The window method efficiently reduces the running time of scalar multiplication, using extra memory for pre-computation by window size. Thus, scalar multiplication time can be decreased by a window method that processes w digits of k at a time.
2.1.3. Zero Occurrence Evaluation
Tables 1 and 2 show the relation of neighbor bit settings under w-NAF. We can find the w-NAF characteristic that, if a certain bit is set or reset, after the window size, the value of that bit has a high probability of being similar to the previous setting. For this reason, grouping the index by window size can obtain a setting with the same values. Finally, our structure efficiently separates zero and non-zero values by gathering the same values.
To improve its performance, the window method can be combined with NAF in a technique known as width-w NAF. NAFw(k) can be computed using Algorithm 2, where k mods 2w denotes the integer, u, satisfying u = k(mod 2w) and −2w-1≤ u < 2w-1. The digits of NAFw(k) are obtained by repeatedly dividing k by two, giving remainders, r, in [−2w−1, 2w−1 − 1]. If k is odd and the remainder, r = k mod 2w, is chosen, then (k − r)/2 will be divisible by 2w−1, ensuring that the next w - 1 digits are zero. Using NAFw(k), the integer, k, is computed by window width, (w), from the left- to right-most bit, following Algorithm 3.
| Algorithm 2. Computing the width-w NAF of a positive integer. | |
| Input: Window width w, positive integer k. | |
| Output: NAFw(k). | |
| 1. | i ← 0. |
| 2. | While k ≥ 1 do |
| 2.1 | If k is odd, then: ki ← k mods 2w, k ← k - ki |
| 2.2 | Else: ki ← 0. |
| 2.3 | k←k/2,i←i + 1 |
| 3. | Return(ki–1, ki–2, …, k1, k0) |
| Algorithm 3. Window NAF method for point multiplication. | |
Input: Window width w, positive integer k, P ∈ E(
 q). q). | |
| Output: kP. | |
| 1. | Use Algorithm 2 to compute w-NAF , |
| 2. | Compute Pi = iP for i ∈ {1, 3, 5,…, 2w-1 − 1}. |
| 3. | Q ← ∞. |
| 4. | For i from l − 1 down to 0 do |
| 4.1 | Q ← 2Q. |
| 4.2 | If ki ≠ 0, then |
| 4.2.1 | If ki> 0 then Q ← Q + Pki. |
| 4.2.2 | Else Q ← Q − Pki. |
| 5. | Return(Q). |
2.1.4. Lim and Lee's Method
Let R be an n-bit exponent, for which we want to compute gR and divide the exponent, R, into h blocks, Ri, for 0 ≤ i ≤ h − 1, of size . We can subdivide each Ri into v smaller blocks, Ri,j, of size, , for 0 ≤ j ≤ v − 1, as follows: Ri = Ri,v-1,…, Ri,1, . Let g0= g and define gi as for 0 < i < h. Then, we can express gR as:
Let Ri = ei,a-1,…, ei,1, ei,0 be the binary representation of Ri(0 ≤ i < h). Then, Ri,j(0 ≤ j < v) is represented in binary as Ri,j= ei,jb+b−1,…, ei,jb+k,… ei,jb+1,ei,jb. Therefore, Expression (2) can be rewritten as follows:
The following values are pre-computed and stored for all 1 ≤ i < 2h and 0 ≤ j < v. The index, i, is equal to the decimal value of eh−1,…, e1, e0.:
| Algorithm 4. Lim and Lee's method for exponentiation. | |
| Input: Exponent R, g(Fixed element of Zn) | |
| Output: gR. | |
| 1. | u = Πki=hgmibi |
| 2. | v = u |
| 3. | For w = h − 1 to 1 by −1 |
| 3.1 | u = u × Πki = wgmibi |
| 3.2 | v = v×u |
| 4. | Return(v). |
2.1.5. Tsaur and Chou's Method
Let k be an l-bit scalar represented in NAF, and we describe the table in two-dimensional form. Divide k into h × v blocks from top-to-bottom and, then, from right-to-left, where . k can then be rewritten as Equation (5).
From right-to-left, the h × a blocks are then divided into h × v blocks, each of size, .
Let P0= P and Pj = 2hbPj−1= 2jhbP for 0 < j < v. Therefore, we can rewrite kP as Equation (6), where cjb+t= eh-1,jb+t,… e1,jb+t, e0,jb+t is the NAF representation.
Suppose that the following values described in expression (7) are pre-computed and stored for all and 0 ≤ j ≤ v − 1, where Ij,t is the decimal representation of eh-1,jb+t, …, e1,jb+t, e0jb+t.
Using expression (7), kP can be rewritten as in Equation (8).
| Algorithm 5. Tsaur and Chou's method for scalar multiplication. | |
Input: Positive integers k, P ∈ E(
 q). q). | |
| Output: Q = kP. | |
| 1. | R=∞ |
| 2. | For k = b - 1 to 0 by −1 do |
| 2.1 | If h = 1, then |
| 2.1.1 | R = 2R. |
| 2.2 | Else |
| 2.2.1 | Compute R = 2hR using Algorithm 6. |
| 2.3 | For j = v - 1 to 0 by −1 do |
| 2.3.1 | If (eh-1,bj+k, …, e0,bj+k)NAF > 0 then |
| 2.3.1.1 | R = R + G[j] [Ij,k] |
| 2.3.2 | Else if (eh-1,bj+k, …, e0,bj+k)NAF < 0 then |
| 2.3.2.1 | |
| 2.3.2.2 | R= R − G[j] [ ] |
| 3. | Return R |
| Algorithm 6. Sakai and Sakurai's method for direct doubling. | |
Input: A positive integer r such that k = 2r and P ∈ E(
 q). q). | |
| Output: k = 2rP. | |
| 1. | A1 = x1,. , C1 = -y1. |
| 2. | For i = 2 to r. |
| 2.1 | |
| 2.2 | |
| 2.2 | |
| 3. | Compute |
| 4. | Compute |
| 5. | Compute |
| 6. | Return x2r, y2r |
| Algorithm 7. Mohamed, Hashim and Hutter's method for scalar multiplication. | |
Input: Positive integers w,v,k = (kl-1,…, k1, k0)NAFw, P ∈ E(
 q). q). | |
| Output: Q = kP. | |
| 1. | , |
| 2. | Compute G[0] [sd], G[j] [sd] for all s ∈ {1,2, 22, 23,…, 2w-1}, 0 < j ≤ v − 1,d ∈ {1,3,5,…, 2w-1 − 1}. |
| 3. | Q = ∞ |
| 4. | For t = b − 1 down to 0 do |
| 4.1 | If w = 1, then |
| 4.1.1 | Q = 2Q. |
| 4.2 | Else |
| 4.2.1 | Use Algorithm 6 to compute Q = 2wQ. |
| 4.3 | For j = v − 1 down to 0 do |
| 4.3.1 | Ij.t=(kjb+t,w-1,…, kjb+t,0)NAFw |
| 4.3.2 | If Ij,t > 0, then |
| 4.3.2.1 | Q = Q + G[j] [Ij,t]. |
| 4.3.3 | Else if Ij,t < 0 |
| 4.3.3.1 | Q = Q − G[j] [−Ij,t]. |
| 5. | Return (Q). |
2.1.6. Direct Doubling Method
Sakai and Sakurai proposed a multi-doubling method for elliptic scalar multiplication. This reduced computational complexity by applying one constant inversion operation, regardless of the number of doubling. The complexity is given as (4r + 1)M + (4r + 1)S + I,, where M, S and I denote a multiplication, a squaring and an inversion in

2.1.7. Mohamed, Hashim and Hutter's Method
This method represents the scalar, k, in width-w NAF. First, k is divided into blocks of equal size, w. k can then be written as follows:
3. (Proposed) Fixed-Base Comb with Window-NAF Method
This method represents the scalar, k, in the width-w NAF used for the previous approach. First, the scalar, k, having length (l), is divided into blocks of equal size, w, and k can be written as follows:
| Algorithm 8. (Proposed) Fixed-base comb with Window-NAF method for scalar multiplication. | |
Input: Positive integers w,v,k = (kl_1, …,k1, k0)NAFW, P ∈ E(
 q). q). | |
| Output: Q = kP. | |
| 1. | , |
| 2. | Compute G[0][sd], G[i][sd] for all s ∈ {1, 2, 22, 23,…, 2w-1}, 0 < i ≤ w-1, d ∈ {20, 2w,…, 2w(a-1)}. |
| 3. | Q = ∞ |
| 4. | For i = 0 to w − 1 do |
| 4.1 | Q = 2Q. |
| 4.2 | For t = z − 1 down to 0 do |
| 4.2.1 | Ii,t=(kzw2+w(w-1),i… kzw2)NAFW. |
| 4.2.2 | If kzw2+w(w-1) > 0, then |
| 4.2.2.1 | Q = Q + G[i] [Ii,t]. |
| 4.2.3 | Else if kzw2+w(w-1) < 0 |
| 4.2.3.1 | Q = Q − G[i] [−Ii,t]. |
| 5. | Return (Q). |
3.1. Comparison of Pre-Computation Table Structures
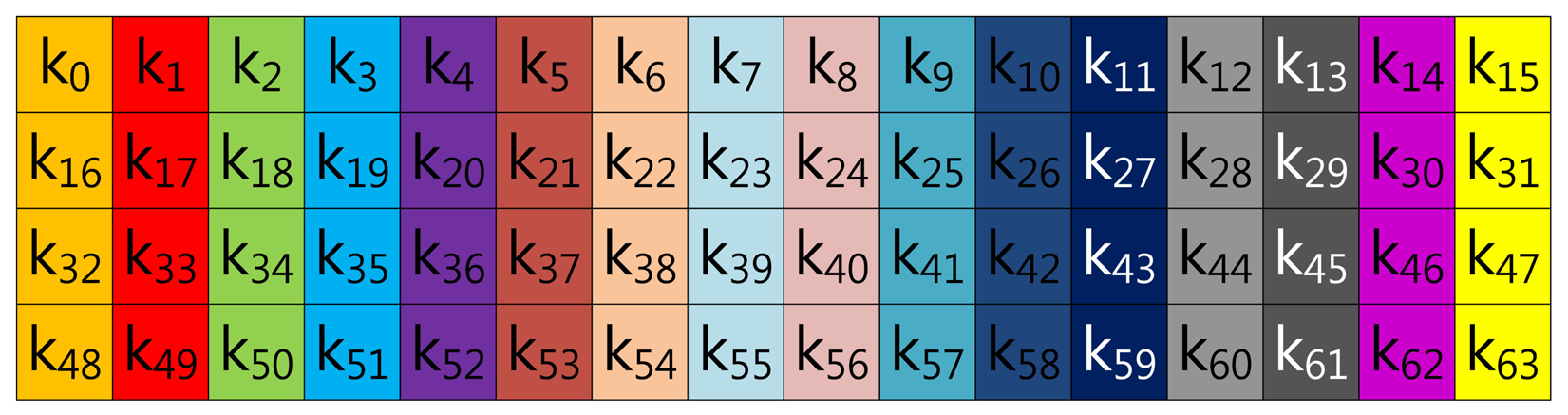
In this section, we demonstrate fixed-base scalar multiplication in a block form to allow a comparison of the table structures. In the example, we use a 64-bit scalar value, k, and a look-up table with width-4 index. To illustrate the look-up table index more vividly, we use the same color for the same group elements. Figure 1 shows the structure of Lim and Lee's method when the width of the block index, (a), is set to 16. In the Figure, elements are grouped in this order: (k0, k16, k32, k48), …, (k15, k31, k47, k63).
In the case of Tsaur and Chou's method described in Figure 2, the look-up table has the same structure as in Lim and Lee's method, so elements are grouped in this order: (n0, n16, n32, n48), …, (n15, n31, n47, n63). However, the scalar value (k) is represented in NAF2(n) to generate frequent consecutive zero sequences, which can reduce the overhead of group addition.
In the case of Mohamed, Hashim and Hutter's method described in Figure 3, the scalar value (k) is represented in window-NAF (w), which replaces the adjacent set values to zero values by window size. The look-up table index is grouped in incremental order by window size, and elements represented in w-NAF are grouped in this order: (w0, w1, w2, w3), …, (w60, w61, w62, w63). This structure is efficiently reducing table size, because within window size, only one element can have a value.
Our proposed method described in Figure 4 represents the scalar value (k) in window-NAF (w). Mohamed et al. grouped values in incremental order of index. On the other hand, we use a different look-up table structure, following the characteristic that the set value in one position will affect the following value's bit setting. For window size, w, the a-th and the (a + w)th sub-windows, e.g., in the case of w = 4, (w0, w4), (w2, w6), (w3, w7) and (w4, w8), exhibit a strong interrelationship. If one value is set, the other has a high probability of being set, and the opposite case shows same results. In Table 1, we give a test on this features by testing all cases. This characteristic can be used to construct a look-up table with a more frequent number of zero occurrences, so our method constructs a table in this order: (w0, w4, w8, w12), …, (w51, w55, w59, w63).
3.2. Size Optimized Method
The size-optimized model has a pre-computation table combining the proposed method and that of Mohamed et al. Therefore, the method constructs the table structure with consecutive elements and elements in distance. The consecutive elements represented in NAF form do not have consecutive values, so the number of cases in the table is smaller than the table constructed with elements in distance. Unlike the consecutive elements, an element selected in distance shows higher zero occurrence, but the table size is much larger than consecutive elements. For this reason, the method combining both table structures reduces the table size, while it degrades speed performance. However, reduction of speed performance is minor, compared to the huge reduction of table size. Examples of 3NAF and 4NAF are illustrated in Figures 5, 6, 7 and 8, respectively. In Figure 5, two elements are selected from a consecutive index, and one element is chosen in distance. The elements are grouped in this order: (w0, w1, w44), (w22, w23, w45) …, (w20, w21, w64), (w42, w43, w65). To compute this structure, elements are added to a result, and then, the result is doubled twice.
In Figure 6, a different 3NAF look-up table, version 2, is illustrated. Elements are grouped in the same structure of that of the previous one, but the index is mixed. This structure combines the elements by window size, so it can group similar characteristic elements, but this structure requires a doubling process three times, because the elements are grouped by window size: three. In this model, the elements are grouped in this order: (w0, w1, w35), (w2, w33, w34) …, (w32, w63, w64), (w30, w31, w65).
In Figure 7, the 4NAF look-up table, version 3, is illustrated. The elements are grouped in two structure, which are placed in a window size distance, and the inner structures of this follow Mohamed et al. To compute scalar multiplication, a grouped element is added, and then, doubling is conducted twice in a row; then, addition is computed. In the example, the elements are grouped in this order: (w0, w1, w4, w5), (w2, w3, w6, w7) …, (w56, w57, w60, w61), (w58, w59, w62, w63).
In Figure 8, a different 4NAF look-up table, named version 4, is introduced. The elements are grouped in two structures, and one inner structure follows Mohamed et al. The other index is placed in distance. This shows a size optimized model, because three elements are consecutively grouped, so this has a small number of table cases. However, compared to version 3, this model needs to compute a doubling process four times. In the example, the elements are grouped in this order: (w0, w1, w3, w35), (w3, w32, w33, w34) …, (w31, w60, w61, w62), (w28, w29, w30, w63).
3.3. Hybrid Method for Fine Tuning
The hybrid method combines two methods, including our size-optimized or speed-optimized model and that of Mohamed et al. The advantage of a combined model is in generating a fine-tuned look-up table, which can adjust speed and size accurately, because both of them have a trade-off relation. By adjusting the look-up table size property, we can generate a proper look-up table more efficiently and accurately. This is based on the previous observation that Mohamed et al. provided a small pre-computation table with low zero occurrence and ours provides a big pre-computation table with high zero occurrence. Therefore, if we represent the table as Mohamed et al., that part shows low zero occurrence and a small table, and if we use the proposed table, this part shows high zero occurrence and a big table. Finally, we draw a trade-off relation by representing a table with the finely-tuned method. This relation is available in Tables 3 and 4.
In Figure 10, a combined look-up table structure is described. From w0 to w23, 3NAF version 1 is used, and the remaining part follows Mohamed et al. The number of elements for each structure model can be adjusted. To compute this model, the addition of Mohamed et al. elements is computed, and then doubling is conducted once. Afterward, then, our size-optimized elements are added, and then direct doubling in a width of two is conducted.
In Figure 11, the hybrid model of 3NAF version 2 is introduced. To compute this model, addition of Mohamed et al.'s and our model's elements are conducted, and then, direct doubling in a width of three is conducted for both structures. For this reason, more simple computation is available than the version 1 model.
In Figure 12, the hybrid model of 4NAF version 3 is introduced. The version 3 model is structured in a width of two elements. To compute scalar multiplication, direct doubling in a width of two is conducted once, and then, our elements are added after. Then, direct doubling in a width of two is conducted.
In Figure 13, the hybrid model of 4NAF version 4 is introduced. This model is conducted with direct doubling in a width of four. Compared to version 3, this model consumes a small-sized look-up table.
4. Results
In this section, we evaluate the proposed method in terms of its look-up table size and computation speed for practical performance evaluation.
4.1. Random Number Generator for Pair Evaluation
Random numbers are needed to evaluate the methods of generating the secret value (k) that is used to construct the look-up tables. For pair comparison, we choose a high-entropy random number algorithm (Blum-Blum-Shub) that is suited to the NIST random number suite. The difficulty of this pseudo-random number generator (PRNG) is based on integer factorization. When the prime is chosen appropriately, predicting the random patterns is at least as difficult as factoring prime. For this reason, using the output from this PRNG is suitable for pair comparison of computation.
4.2. Zero Occurrence of Look-up Table
Table 5 shows the percentage of zero occurrences under various conditions, such as the representation and window size. Lim and Lee use a normal representation, and the other methods are represented in NAF form. In each case, our proposed method shows better performance than previous published works. One interesting result is that the method of Mohamed et al. has a lower performance than that of Tsaur and Chou, but this becomes obvious after referring to the experimental results in this section. Within a given window size, values repeat periodically with high probability. Therefore, the model of Mohamed et al. has a low probability of having a zero sequence index for a given window size. On the other hand, Tsaur and Chou's method has no relation to the index of the look-up table, but shows higher performance.
Our model is perfectly suited to the characteristics of w-NAF, exhibiting a high zero occurrence. We also provide a size-optimized model, because our model requires a huge amount of storage for the look-up table. This model is properly adjusted for demand on speed and size.
The following Figures 14, 15 and 16 show the frequency of the scalar value in the case of 160-bits. The graphical results are generated from the random scalar value derived from Blum-Blum-Shub. In Figure 14, the frequency of 2NAF representation is described. The red graph is Lim et al., and the value range is between one and zero, because this method does not use NAF form. The line in the graph is densely placed. The yellow graph is Tsaur et al., and the value range is between one and minus one after transformation into 2NAF form. Compared to Lim et al., many points are placed in zero value, and this generates consecutive zero values. The green and black graphs are Mohamed et al. and ours. The consecutive zero occurrences in our graph happen frequently, so this represents the efficiency of our method.
In Figure 15, the frequency of 3NAF representation is described. The red graph, Lim et al., has high frequency, so it is hard to find zero occurrence. Unlike Lim et al., other methods show a sparsely drawn graph. After 3NAF transformation, values are placed between three to minus three. At a glance, all representations appear to have a similar frequency. However, Table 5 shows that our method presents higher zero occurrences than any other methods.
In Figure 16, the frequency of 4NAF representation is described. This example describes the strength of our method vividly. The red graph, Lim et al., obtains a higher frequency, so this has a high hamming weight. In the case of Tsaur et al., there are low frequencies and many consecutive zeros. In the case of Mohamed et al., the frequency is much higher than Tsaur et al., so its hamming weight is higher than Tsaur et al. Finally, our method shows an impressive consecutive zero array. Furthermore, a high frequency is gathered in some regions. For this reason, this method is more efficient than other methods.
4.3. Size of Look-up Tables
In this section, we consider the size of the look-up tables, and detailed table size is described in Table 6. Lim and Lee's method has the smallest look-up table, and this can compute a storage size of (2w − 1) × t, where t is the size of a point (in the case of 160-bit, 40 bytes are used, 20 for the x-axis and 20 for the y-axis), because elements consist of two values, zero and one. In the case of Tsaur and Chou's method, the number of elements for w-NAF is 2(w-1) + 1, so the table size is ((2(w-1) + 1)(w-1)(2(w-2) + 1)) × t. Mohamed et al.'s method has a smaller look-up table than that of Tsaur and Chou, because elements do not exist consecutively within each window size, due to the characteristics of w-NAF; so, the table size is w × 2(w-2) × t. Our speed-optimized method is equivalent to Tsaur and Chou's method, because elements in the look-up table are randomly chosen, meaning that we should compute all cases. To reduce the size, while keeping a high zero occurrence, we provide a size-optimized model that has a high probability of zeros with reduced storage size. The size-optimized model combines our speed-optimized model and that of Mohamed et al., so the table size estimation follows both methods partly, and the total table size is ((w − 1) × 2(w-2) × (2(w-1) + 1) + 2(w-2)) × t.
4.4. Computational Efficiency
Table 7 shows the performance results in terms of size and speed factors. For size, we calculate table size depending on the number of points. For speed, we estimated complexity from the number of group operations. In the table, we evaluate two cases, one using a partial look-up table and the other using the full look-up table for fixed point computation. The benefit of full computation is that all doubling computations are removed. Compared to Mohamed et al., our speed-optimized method exhibits the best performance, due to the large number of zero occurrences, but it suffers from having a large look-up table. On the other hand, Mohamed et al.'s method has a small look-up table, but suffers from poor performance, due to the small number of zero occurrences. In the size-optimized model, it provides a proper zero occurrence probability with a much smaller table size than the speed model.
However, in Table 7, we compared performance unfairly, because we did not evaluate performance in the same look-up table size. Computation with a larger look-up table shows higher speed performance than a method with a small look-up table, because in the case of fixed-base point multiplication, a bigger look-up table ensure less point additions, and this directly affects faster scalar multiplication. For clarity, we further evaluate our performance in the same look-up table size and calculate overhead, generalized in multiplication, which is derived from Table 8, describing the relation of each operation in an affine coordinate. There are a number of operation dependencies, so we set our coordinate as affine and multiplication and squaring, and inversion is implemented in the basic method. Additionally, we refer to these basic relations from [2]. First, overheads of finite field squaring and inversion are re-written in the overhead of multiplication. Afterwards, then, group operations, overheads of addition, doubling and direct doubling are re-written in the overheads of multiplication.
In Table 9, we evaluate our model and that of Mohamed et al. under the same condition. Our size-optimized model (version 2) has a 12.3 Kbyte look-up table. Compared to the 4NAF model (partial table) our method outperforms in terms of size and speed factors. However, the 3NAF model (full table) shows much higher performance than ours with small size overheads. For this reason, we cannot confidently say that our method is faster than that of Mohamed et al. under the same condition. However, through this evaluation, we found that our method can be used for size and speed tuning techniques. We named it the hybrid method.
4.5. Hybrid Model Performance Evaluation
Our hybrid model is developed during evaluation of the previous models to overcome the drawbacks of the proposed method. Tables 3, 4 and 10 describe the performance in size and speed. The most interesting feature is that we can adjust performance more finely. In Table 9, using Mohamed et al.'s method, there is no table model in 3.2∼6.4 and 6.5∼12.8 Kbyte. However, the hybrid model can tune the performance in terms of size and speed and provide various size models, including 3.2, 3.36, … 11.6 and 12.9 Kbytes. Various table models generate finely-tuned table structure for user's purposes. However, the hybrid model using 4NAF is not useful, because zero occurrence of 4NAF is far lower than 3NAF, so even 4NAF has a large table, but shows low speed performance. In Figure 17, a finely-tuned look-up table is depicted. In the figure, we found that with the blue dotted line, the method of Mohamed et al. is coarsely-tuned, so there is a large gap between each look-up table. However, our hybrid model can finely tune and fill gaps between each table, which is coarsely-tuned. Finally, we can complete the smooth graph, which means we can adjust our performance more accurately and finely.
5. Conclusions
Recently released novel scalar multiplication by Mohamed et al. reduced the number of addition operations using w-NAF and a novel look-up table structure. However, this method cannot carefully adjust their table structures in terms of speed and size matters, so this does not provide flexibility for selecting table structure, depending on different purposes. In this paper, we presented a novel method for fixed-point scalar multiplication. The new structure is firstly derived from w-NAF characteristics observed in this paper. However, our method shows similar performance when it is tested under the same look-up table size. However, constructing our table in various ways, we found one interesting features that can be used for speed and size performance adjustment. Finally, we presented a novel fine-tuned look-up table structure, which can provide more accurate and fine adjustment than previous methods. This idea can be applied to other combinations using many other table structures for the finely-tuned table model. This method can provide more flexible look-up tables for embedded microprocessors. Furthermore, the proposed method is straight-forwardly implementable on an unknown point, and this shows high performance enhancement compared to traditional NAFw methods.
Acknowledgments
“This work was supported by the Industrial Strategic Technology Development Program (No.10043907, Development of high performance IoT device and Open Platform with Intelligent Software) funded by the Ministry of Science, ICT & Future Planning (MSIF, Korea).”
Appendix. A
Example of Proposed Method
In this section, we give a detailed process of proposed methods, including speed, size and hybrid models. Figure 4 shows the speed-optimized model. This model is constructed after two phases. First, Figure 1 is represented in w-NAF form using Algorithm 2; the corresponding output has the same structure as shown in Figure 3. Second, each element is grouped by window size (four). In our case, it is grouped in this order: [(w0, w4, w8, w12), (w1, w5, w9, w13), (w2, w6, w10, w14), (w3, w7, w11, w15), (w16,w20,w24, w28), (w17,w21,w25,w29), (w18, w22,w26,w30), (w19, w23, w27, w31), (w32,w36,w40,w44), (w33,w37,w41, w45), (w34,w38,w42,w46), (w35, w39,w43,w47), (w48, w52, w56, w60), (w49,w53,w57,w61), (w50, w54, w58, w62), (w51, w55, w59, w63)]. Afterward, then, scalar multiplication is conducted in the following order. Firstly, elements, including (w3, w7, w11, w15), (w19, w23, w27, w31), (w35, w39, w43, w47) and (w51, w55, w59, w63), are added to a point, and then, doubling is conducted. Secondly, elements, including (w2,w6,w10,w14), (w18, w22, w26,w30), (w34, w38, w42, w46) and (w50,w54,w58,w62), are added to the point, and then, doubling is conducted. Thirdly, elements, including (w1, w5, w9, w13), (w17, w21, w25, w29), (w33, w37, w41, w45) and (w49, w53, w57, w61), are added to the point, and then, doubling is conducted. Finally, elements, including (w0, w4, w8, w12), (w16, w20, w24, w28), (w32, w36, w40, w44) and (w48, w52, w56, w60), are added to the point.
For the size-optimized model in Figure 5, scalar multiplication value is represented in 3NAF form. Then, it is grouped in this order: [(w0, w1, w44), (w2, w3, w46), (w4, w5, w48), (w6, w7, w50), (w8, w9, w52), (w10,w11,w54), (w12,w13,w56), (w14,w15,w58), (w16,w17,w60), (w18,w19,w62), (w20,w21,w64), (w22,w23,w45), (w24,w25,w47), (w26,w27,w49), (w28,w29,w50), (w30,w31,w53), (w32,w33,w55), (w34, w35, w57), (w36, w37, w59), (w38, w39, w61), (w40, w41, w63), (w42, w43, w65)] Firstly, elements, including (w2, w3, w46), (w6, w7, w50), (w10, w11, w54), (w14, w15, w58), (w18, w19, w62), (w22, w23, w45), (w26, w27, w49), (w30, w31, w53), (w34, w35, w57), (w38, w39, w61) and (w42, w43, w65), are added to the point, and then, direct doubling by a width of two is conducted. Afterwards, then, elements, including (w0, w1, w44), (w4, w5, w48), (w8, w9, w52), (w12, w13, w56), (w16, w17, w60), (w20, w21, w64), (w24,w25,w47), (w28,w29,w50), (w32,w33,w55), (w36,w37,w59) and (w40,w41,w63), are added for completion.
For the hybrid model in Figure 11, scalar multiplication value is represented in 3NAF form. Then, it is grouped in two different orders. Firstly, elements from zero to 23 are constructed in this order: [(w0,w1,w16), (w2,w3,w18), (w4,w5,w20), (w6,w7,w22), (w8,w9,w17), (w10,w11,w19), (w12,w13,w21), (w14,w15,w23)]. Secondly, elements from 24 to 65 are grouped in this order: [(w24, w25, w26), (w27, w28, w29), (w30, w31, w32), (w33, w34, w35), (w36, w37, w38), (w39, w40, w41), (w42,w43,w44), (w45,w46,w47), (w48,w49,w50), (w51,w52,w53), (w54,w55,w56), (w57,w58,w59), (w60, w61, w62), (w63, w64, w65)]. After table construction, the scalar multiplication process is started. Firstly, elements, including (w27, w28, w29), (w33, w34, w35), (w39, w40, w41), (w45, w46, w47), (w51, w52, w53), (w57, w58, w59) and (w63, w64, w65), are added to the point, and then, doubling is conducted. Secondly, elements, including (w2, w3, w18), (w6, w7, w22) and (w10, w11, w19), are added to the point, and then, direct doubling by a width of two is conducted. Finally, elements, including (w0, w1, w16), (w4, w5, w20), (w8, w9, w17), (w12, w13, w21), (w14, w15, w23), (w24, w25, w26), (w30, w31, w32), (w36, w37, w38), (w42, w43, w44), (w48, w49, w50), (w54, w55, w56) and (w60, w61, w62), are added to the point.
Appendix. B
Proposed Method on an Unknown Point
Throughout this paper, we explored the proposed method on a fixed-point. However, we found that the method is also available for an unknown point. Ordinarily, NAFw representation is used for unknown point computation. By exploiting our structure, we can improve previous methods. The detailed structures of previous and proposed methods are described in Figures 18 and 19, respectively. This example shows the case of 32-bit input. First, the traditional method groups each element by a size of two in ascending order. Unlike the previous method, our method groups element in this order: [(w0, w2), (w1, w3), (w4, w6), (w5, w7), (w8, w10), (w9, w11), (w12, w14), (w13, w15), (w16, w18), (w17, w19), (w20, w22), (w21, w23), (w24, w26), (w25, w27), (w28, w30), (w29, w31)]. This structure shows a higher zero occurrence ratio than previous method, and its result is available in Table 5. After table construction, the scalar multiplication process is started. Firstly, element (w0, w2) is added, and then, one doubling process is conducted. Secondly, element (w1, w3) is added, and then, direct doubling by three is conducted. This process is repeated, until the end of computation.
In the Table 1, we compared the size of the look-up table and the computation costs of previous and proposed methods on an unknown point in the case of 160-bit scalar multiplication with 2NAF representation. In terms of size, the previous method has results for (10) and (01), and the proposed method has results for (101), (100), (10-1) and (001). Each result has 40 byte values, including X and Y values, so the previous method occupies 80 bytes and ours occupies 160 bytes. For look-up table computation, one doubling is required for the traditional method, to compute (10). In the case of ours, two additions and a direct doubling by two are needed to compute (101), (100) and (10-1). After look-up table computation, point computation is conducted. By exploiting high zero occurrence, our method shows a small number of addition computation and our method conducts a doubling and a direct doubling by three. Total computation costs, including pre-computation and point-computation, are listed in the Table 1. Our method shows speed performance enhancement by 12.7% compared to traditional NAF2 representation for an unknown point.
Conflict of Interest
The authors declare no conflict of interest.
References
- Cohen, H.; Frey, G.; Avanzi, R.; Doche, C.; Lange, T.; Nguyen, K.; Vercauteren, F. Handbook of Elliptic and Hyperelliptic Curve Cryptography; Taylor and Francis Group LLC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2004. [Google Scholar]
- Silverman, J.H. The Arithmetic of Elliptic Curves; Springer: Berlin, Germany, 1986; Volume 106. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–220. [Google Scholar]
- Miller, V.S. Use of Elliptic Curves in Cryptography. Proceedings of the International Cryptology Conference (CRYPTO 1985), Santa Barbara, CA, USA, 18–22 August 1985; Williams, H.C., Ed.; Springer: Heidelberg, Germany, 1986; Volume 218, pp. 417–426. [Google Scholar]
- Brickell, E.F.; Gordon, D.M.; McCurley, K.S.; Wilson, D.B. Fast Exponentiation with Precomputation. Extended Abstract. Proceedings of the International Conference on Cryptology in Europe (EUROCRYPT 1992), Balatonfred, Hungary, 24–28 May 1992; Rueppel, R.A., Ed.; Springer: Heidelberg, Germany, 1993; Volume 658, pp. 200–207. [Google Scholar]
- Lim, C.H.; Lee, P.J. More Flexible Exponentiation with Precomputation. Proceedings of the International Cryptology Conference (CRYPTO 1994), Santa Barbara, CA, USA, 21– 25 August 1994; Desmedt, Y.G., Ed.; Springer: Heidelberg, Germany, 1994; LNCS. Volume 839, pp. 95–107. [Google Scholar]
- Tsaur, W.J.; Chou, C.H. Efficient algorithm for speeding up the computations of elliptic curve cryptosystem. Appl. Math. Comput 2005, 168, 1045–1064. [Google Scholar]
- Sakai, Y.; Sakurai, K. Speeding up elliptic scalar multiplication using multidoubling. IEICE Trans. Inf. Syst. 2002, E-84-A, 1075–1083. [Google Scholar]
- Mohamed, N.A.F.; Hashim, M.H.A.; Hutter, M. Improved Fixed-Base Comb Method for Fast Scalar Multiplication. Proceedings of the International Conference on Cryptology in Africa (AFRICACRYPT 2012), Morocco, 10– 12 July 2012; Mitrokotsa, A., Vaudenay, S., Eds.; Springer: Heidelberg, Germany, 2012; LNCS. Volume 7374, pp. 342–359. [Google Scholar]
- A Statistical Test Suite for the Validation of Random Number Generators and Pseudo Random Number Generators for Cryptographic Applications Version sts-2.1. National Institute of Standards and Technology (NIST). Available online: http://csrc.nist.gov/groups/ST/toolkit/rng/index.html (on accessed 22 July 2013).




















| Form | Set | Being set | Occurrence | Prob (%) | |
|---|---|---|---|---|---|
| 2NAF | 1st | 3rd | 16 | 67 | |
| 4th | 8 | 33 | |||
| 2nd | 3rd | 0 | 0 | ||
| 4th | 8 | 100 | |||
| 3NAF | 1st | 4th | 128 | 36 | |
| 5th | 128 | 36 | |||
| 6th | 96 | 28 | |||
| 2nd | 4th | 0 | 0 | ||
| 5th | 64 | 50 | |||
| 6th | 64 | 50 | |||
| 3rd | 4th | 0 | 0 | ||
| 5th | 0 | 0 | |||
| 6th | 32 | 100 | |||
| 4NAF | 1st | 5th | 262,144 | 53 | |
| 6th | 131,072 | 27 | |||
| 7th | 65,536 | 13 | |||
| 8th | 32,768 | 7 | |||
| 2nd | 5th | 0 | 0 | ||
| 6th | 131,072 | 57 | |||
| 7th | 65,536 | 29 | |||
| 8th | 32,768 | 14 | |||
| 3rd | 5th | 0 | 0 | ||
| 6th | 0 | 0 | |||
| 7th | 65,536 | 67 | |||
| 8th | 32,768 | 33 | |||
| 4th | 5th | 0 | 0 | ||
| 6th | 0 | 0 | |||
| 7th | 0 | 0 | |||
| 8th | 32,768 | 100 | |||
| Form | Reset | Being reset | Occurrence | Prob (%) |
|---|---|---|---|---|
| 2NAF | 1st | 3rd | 24 | 55 |
| 4th | 20 | 45 | ||
| 2nd | 3rd | 24 | 40 | |
| 4th | 36 | 60 | ||
| 3NAF | 1st | 4th | 448 | 35 |
| 5th | 416 | 33 | ||
| 6th | 400 | 32 | ||
| 2nd | 4th | 576 | 32 | |
| 5th | 608 | 34 | ||
| 6th | 624 | 34 | ||
| 3rd | 4th | 704 | 34 | |
| 5th | 672 | 32 | ||
| 6th | 720 | 34 | ||
| 4NAF | 1st | 5th | 491,520 | 30 |
| 6th | 376,832 | 22 | ||
| 7th | 385,024 | 23 | ||
| 8th | 421,888 | 25 | ||
| 2nd | 5th | 491,520 | 20 | |
| 6th | 638,976 | 26 | ||
| 7th | 647,168 | 26 | ||
| 8th | 684,032 | 28 | ||
| 3rd | 5th | 622,592 | 22 | |
| 6th | 638,976 | 22 | ||
| 7th | 778,240 | 27 | ||
| 8th | 815,104 | 29 | ||
| 4th | 5th | 688,128 | 23 | |
| 6th | 704,512 | 23 | ||
| 7th | 778,240 | 25 | ||
| 8th | 880,640 | 29 | ||
| Bit | Non-zero P | Total | Size | |
|---|---|---|---|---|
| [10] | Here | Sp | Sp | [KB] |
| 160 | 0 | 52.88 | 591.46 | 3.2 |
| 156 | 4 | 52.05 | 582.60 | 3.36 |
| 152 | 8 | 51.23 | 573.74 | 3.52 |
| 148 | 12 | 50.40 | 564.88 | 3.68 |
| 144 | 16 | 49.58 | 556.02 | 3.84 |
| 140 | 20 | 48.76 | 547.17 | 4 |
| 136 | 24 | 47.93 | 538.31 | 4.16 |
| 132 | 28 | 47.11 | 529.45 | 4.32 |
| 128 | 32 | 46.28 | 520.59 | 4.48 |
| 124 | 36 | 45.46 | 511.73 | 4.64 |
| 120 | 40 | 44.64 | 502.88 | 4.8 |
| 116 | 44 | 43.81 | 494.02 | 4.96 |
| 112 | 48 | 42.99 | 485.16 | 5.12 |
| 108 | 52 | 42.16 | 476.30 | 5.28 |
| 104 | 56 | 41.34 | 467.44 | 5.44 |
| 100 | 60 | 40.52 | 458.59 | 5.6 |
| 96 | 64 | 39.69 | 449.73 | 5.76 |
| 92 | 68 | 38.87 | 440.87 | 5.92 |
| 88 | 72 | 38.04 | 432.01 | 6.08 |
| 84 | 76 | 37.22 | 423.15 | 6.24 |
| 80 | 80 | 36.4 | 414.3 | 6.4 |
| Bit | Non-zero P | Total | Size | |||
|---|---|---|---|---|---|---|
| [10] | Here | V1 | V2 | V1 | V2 | [KB] |
| 162 | 0 | 33.38 | 33.38 | 382.5 | 389.5 | 6.5 |
| 150 | 12 | 33.12 | 32.77 | 378.9 | 386.73 | 7.8 |
| 138 | 24 | 32.86 | 32.16 | 375.32 | 383.96 | 9 |
| 126 | 36 | 32.6 | 31.55 | 371.74 | 381.19 | 10.3 |
| 114 | 48 | 32.35 | 30.93 | 368.15 | 378.42 | 11.6 |
| 102 | 60 | 32.09 | 30.32 | 364.56 | 375.65 | 12.9 |
| 90 | 72 | 31.83 | 29.71 | 360.98 | 372.88 | 14.2 |
| 78 | 84 | 31.57 | 29.1 | 357.39 | 370.11 | 15.4 |
| 66 | 96 | 31.31 | 28.49 | 353.80 | 367.34 | 16.7 |
| Form | [7] | [8] | [10] | SP | V(1,3) | V(2,4) |
|---|---|---|---|---|---|---|
| 2NAF | 24.20 | 44.70 | 33.90 | 50.20 | - | - |
| 3NAF | 11.59 | 48.98 | 38.20 | 50.16 | 46.54 | 44.64 |
| 4NAF | 6.35 | 40.38 | 18.43 | 53.33 | 44.10 | 44.57 |
| Form | [7] | [8] | [10] | Sp | V(1,3) | V(2,4) |
|---|---|---|---|---|---|---|
| 2NAF | 0.12 | 0.16 | 0.08 | 0.16 | - | - |
| 3NAF | 0.28 | 3.00 | 0.24 | 3.00 | 0.88 | 0.88 |
| 4NAF | 0.60 | 145.80 | 0.64 | 145.80 | 4.48 | 5.44 |
| Scheme | Computation Cost No.Operation | Look-up [KB] | Table Size No. |
|---|---|---|---|
| Partial Table Implementation | |||
| [10] | 33 × A + 1 × DD(3) | 6.48 | 27 × 0.24 |
| Speed | 27 × A + 3 × D | 54.00 | 18 × 3.00 |
| V1 | 29 × A + 2 × DD(2) | 15.84 | 18 × 0.88 |
| Full Table Implementation | |||
| [10] | 33 × A | 12.96 | 54 × 0.24 |
| Speed | 27 × A | 162.00 | 54 × 3.00 |
| V1 | 29 ×A | 47.52 | 54 × 0.88 |
| Operation | Computation Cost | ||
|---|---|---|---|
| Inv | Mul | Sqr | |
| Addition | 1 | 2 | 1 |
| Doubling | 1 | 2 | 2 |
| Direct Doubling | 1 | (4r+1) | (4r+1) |
| Op. | No. Op. | Inv | Mul | Sqr | Total | Size [Kbyte] |
|---|---|---|---|---|---|---|
| Our size-optimized model | ||||||
| SZ(V1) | 28.9A+2DD(2) | 30.9 | 75.7 | 46.9 | 357.8 | 15.8 |
| SZ(V2) | 28.9A+3DD(2) | 31.9 | 84.7 | 55.9 | 381.5 | 15.8 |
| Mohamed et al. (partial table implementation) | ||||||
| 2NAF | 52.9A+DD(2) | 53.9 | 114.8 | 61.9 | 591.5 | 3.2 |
| 3NAF | 33.4A+DD(3) | 34.4 | 79.7 | 46.4 | 389.5 | 6.5 |
| 4NAF | 32.6A+DD(4) | 33.6 | 82.3 | 49.6 | 388.5 | 12.8 |
| 5NAF | 28.5A+DD(5) | 29.5 | 78.1 | 49.5 | 351.6 | 25.6 |
| Mohamed et al. (full table implementation) | ||||||
| 2NAF | 52.9A | 52.9 | 105.8 | 52.9 | 568.7 | 6.4 |
| 3NAF | 33.4A | 33.4 | 66.7 | 33.4 | 358.7 | 13 |
| 4NAF | 32.6A | 32.6 | 65.3 | 32.6 | 350.8 | 25.6 |
| 5NAF | 28.5A | 28.5 | 57 | 28.5 | 306.4 | 51.2 |
| Bit | Non-zero P | Total | Size[KB] | ||||
|---|---|---|---|---|---|---|---|
| [10] | Here | V3 | V4 | V3 | V4 | V3 | V4 |
| 160 | 0 | 32.63 | 32.63 | 398.25 | 393.00 | 12.8 | 12.8 |
| 144 | 16 | 31.6 | 31.59 | 387.21 | 381.76 | 20.48 | 22.4 |
| 128 | 32 | 30.57 | 30.54 | 376.17 | 370.52 | 28.16 | 32 |
| 112 | 48 | 29.55 | 29.5 | 365.13 | 359.28 | 35.84 | 41.6 |
| 96 | 64 | 28.52 | 28.45 | 354.09 | 348.04 | 43.52 | 51.2 |
| 80 | 80 | 27.49 | 27.4 | 343.06 | 336.8 | 51.2 | 60.8 |
| 64 | 96 | 26.47 | 26.36 | 332.02 | 325.55 | 58.9 | 70.4 |
| 48 | 112 | 25.44 | 25.31 | 320.98 | 314.31 | 66.6 | 80 |
| 32 | 128 | 24.41 | 24.27 | 309.94 | 303.07 | 74.2 | 89.6 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Seo, H.; Kim, H.; Park, T.; Lee, Y.; Liu, Z.; Kim, H. Fixed-Base Comb with Window-Non-Adjacent Form (NAF) Method for Scalar Multiplication. Sensors 2013, 13, 9483-9512. https://doi.org/10.3390/s130709483
Seo H, Kim H, Park T, Lee Y, Liu Z, Kim H. Fixed-Base Comb with Window-Non-Adjacent Form (NAF) Method for Scalar Multiplication. Sensors. 2013; 13(7):9483-9512. https://doi.org/10.3390/s130709483
Chicago/Turabian StyleSeo, Hwajeong, Hyunjin Kim, Taehwan Park, Yeoncheol Lee, Zhe Liu, and Howon Kim. 2013. "Fixed-Base Comb with Window-Non-Adjacent Form (NAF) Method for Scalar Multiplication" Sensors 13, no. 7: 9483-9512. https://doi.org/10.3390/s130709483
APA StyleSeo, H., Kim, H., Park, T., Lee, Y., Liu, Z., & Kim, H. (2013). Fixed-Base Comb with Window-Non-Adjacent Form (NAF) Method for Scalar Multiplication. Sensors, 13(7), 9483-9512. https://doi.org/10.3390/s130709483





