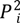Employing Measures of Heterogeneity and an Object-Based Approach to Extrapolate Tree Species Distribution Data
Abstract
:1. Introduction
2. Experimental Section
2.1. Study Area
2.2. Data
2.2.1. Hyperspectral/LiDAR-Derived Tree Species Data

2.2.2. Tree Species Heterogeneity
2.2.3. Tree Species Dominance
2.2.4. Landsat Data
2.3. Landsat Segmentation
2.4. Targeting Segment Features as Independent Variables
| Layer summaries | Geometry/shape |
|---|---|
| mean | area (meters) |
| standard deviation | area (pixels) |
| skewness | border length |
| minimum | length |
| maximum | length/width |
| mean inner border | volume |
| mean outer border | width |
| border contrast | asymmetry |
| contrast to neighbor pixels | border index |
| edge contrast to neighbor pixels | compactness |
| standard deviation to neighbor pixels | density |
| elliptic fit | |
| main direction | |
| radius of largest enclosed ellipse | |
| radius of smallest enclosed ellipse | |
| rectangular fit | |
| roundness | |
| shape index |
2.5. Extraction of Segment-Level Heterogeneity Values (Dependent Variables)
2.6. Model Creation and Validation
2.7. Extrapolation through an Object-Based Approach
3. Results
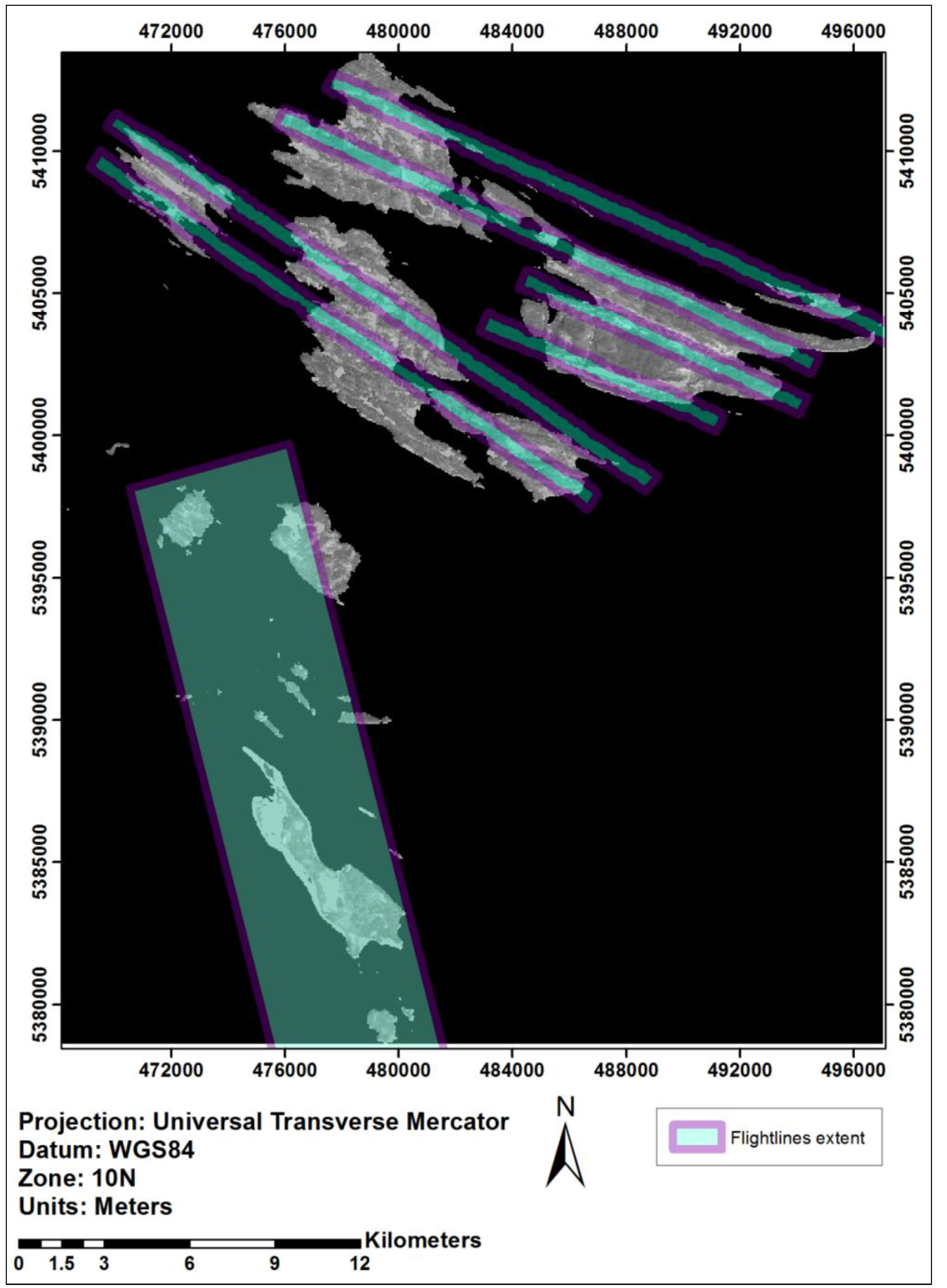
3.1. Impact of Majority Filtering in Tree Species Dominance
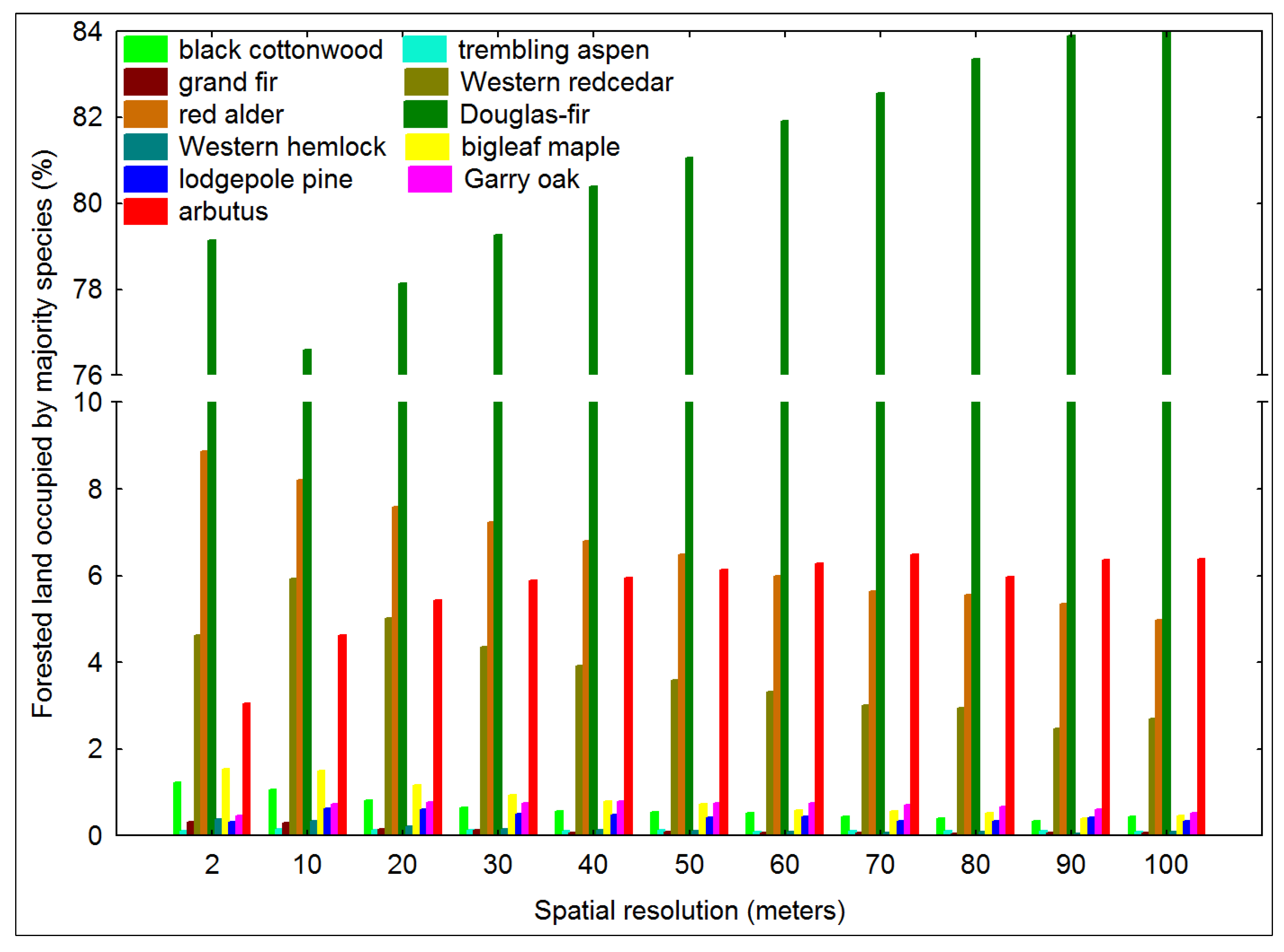
3.2. Tree Species Heterogeneity Calculated at the Pixel-Level
| Spatial Resolution | Heterogeneity | Minimum | Maximum | Mean | Standard deviation |
|---|---|---|---|---|---|
| 10 | Richness | 1 | 7 | 1.48 | 0.71 |
| Diversity | 1 | 5.45 | 1.25 | 0.44 | |
| Evenness | 0.31 | 1 | 0.9 | 0.16 | |
| 20 | Richness | 1 | 9 | 2.04 | 1.08 |
| Diversity | 1 | 6.17 | 1.4 | 0.56 | |
| Evenness | 0.21 | 1 | 0.77 | 0.22 | |
| 30 | Richness | 1 | 10 | 2.5 | 1.33 |
| Diversity | 1 | 5.88 | 1.48 | 0.62 | |
| Evenness | 0.19 | 1 | 0.67 | 0.25 | |
| 40 | Richness | 1 | 9 | 2.94 | 1.5 |
| Diversity | 1 | 5.61 | 1.52 | 0.64 | |
| Evenness | 0.16 | 1 | 0.6 | 0.24 | |
| 50 | Richness | 1 | 10 | 3.33 | 1.64 |
| Diversity | 1 | 5.86 | 1.55 | 0.65 | |
| Evenness | 0.14 | 1 | 0.55 | 0.24 | |
| 60 | Richness | 1 | 10 | 3.67 | 1.76 |
| Diversity | 1 | 5.83 | 1.57 | 0.66 | |
| Evenness | 0.13 | 1 | 0.51 | 0.24 | |
| 70 | Richness | 1 | 10 | 3.96 | 1.86 |
| Diversity | 1 | 5.56 | 1.59 | 0.67 | |
| Evenness | 0.13 | 1 | 0.48 | 0.24 | |
| 80 | Richness | 1 | 11 | 4.21 | 1.95 |
| Diversity | 1 | 5.83 | 1.6 | 0.67 | |
| Evenness | 0.13 | 1 | 0.45 | 0.23 | |
| 90 | Richness | 1 | 10 | 4.45 | 2.02 |
| Diversity | 1 | 6.19 | 1.61 | 0.67 | |
| Evenness | 0.12 | 1 | 0.44 | 0.23 | |
| 100 | Richness | 1 | 11 | 4.68 | 2.1 |
| Diversity | 1 | 5.69 | 1.62 | 0.67 | |
| Evenness | 0.12 | 1 | 0.42 | 0.23 |
3.3. Tree Species Heterogeneity: Comparison of Pixel- To Segment-Level
| Pixel | Segment | Pixel | Segment | Pixel | Segment | |
|---|---|---|---|---|---|---|
| Richness | Diversity | Evenness | ||||
| Minimum | 1 | 1 | 1 | 1 | 0.19 | 0.33 |
| Maximum | 10 | 5.58 | 5.9 | 3.45 | 1 | 1 |
| Mean | 2.6 | 2.66 | 1.48 | 1.48 | 0.66 | 0.64 |
| Standard deviation | 1.33 | 0.9 | 0.61 | 0.4 | 0.24 | 0.12 |
3.4. Model Definition and Validation (Regression Tree Analysis)
| Wavelength (µm) | Minimum (Min) | Maximum (Max) | Mean | Standard deviation (Stdev) | Mean inner border (MIB) | |
|---|---|---|---|---|---|---|
| band 1 | 0.45–0.52 | x | ||||
| band 2 | 0.52–0.60 | x | x | |||
| band 3 | 0.63–0.69 | x | x | |||
| band 4 | 0.76–0.90 | xx | xx | x | xx | |
| band 5 | 1.55–1.75 | xx | xx | xx | xx | x |
| band 7 | 2.08–2.35 | xx | x |
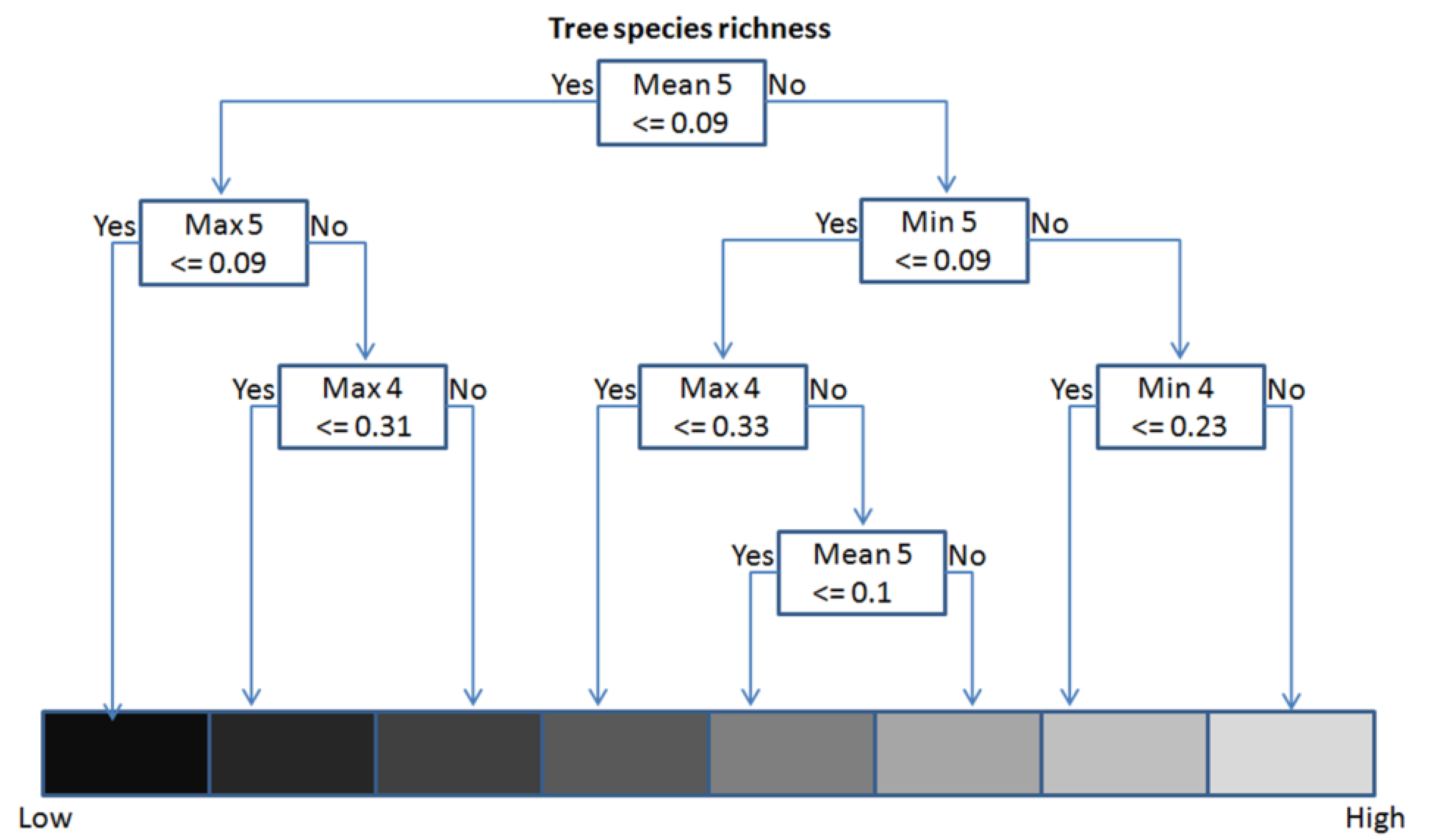
3.5. Extrapolation through an Object-Based Approach
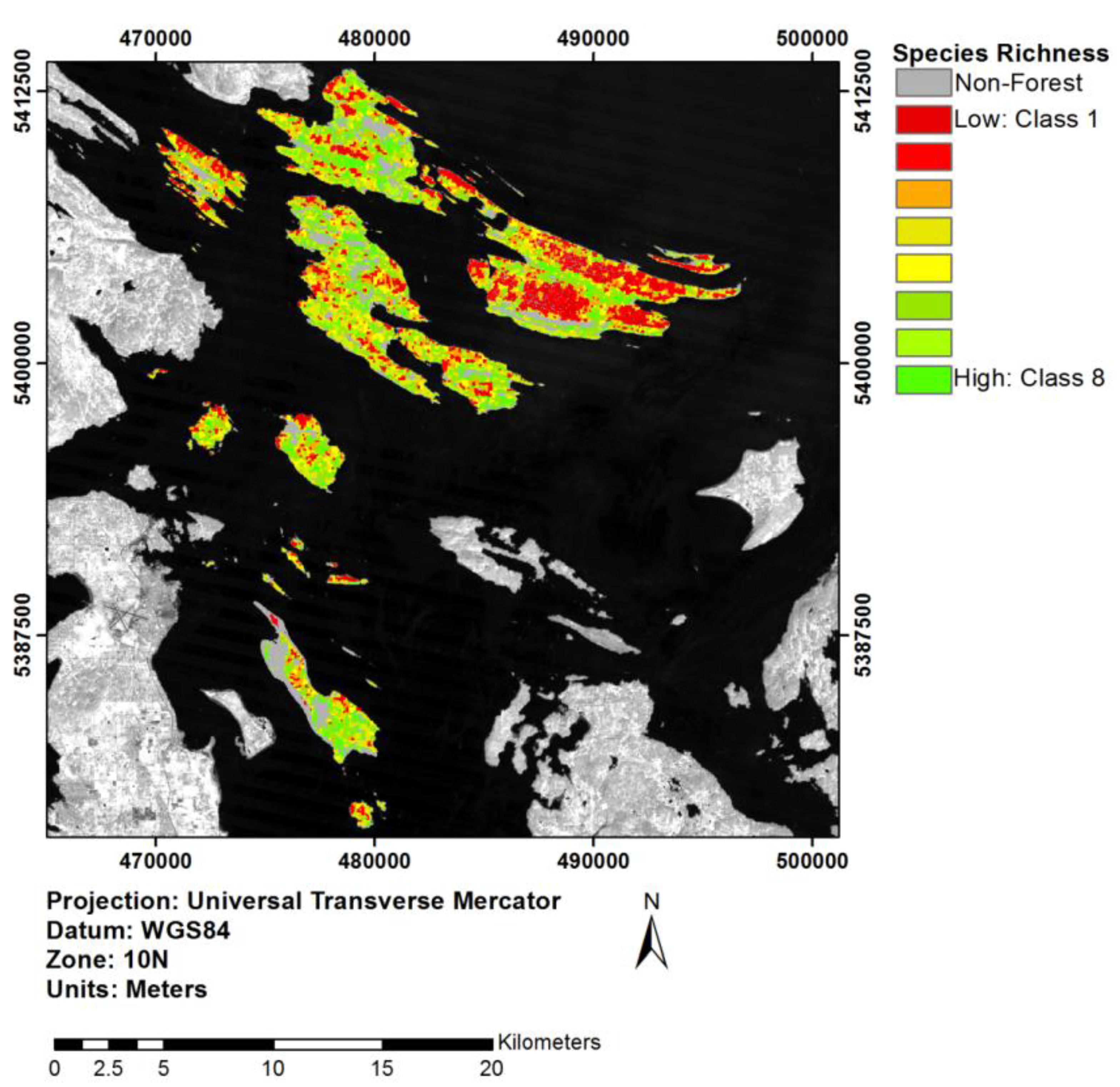
4. Discussion
4.1. Tree Species Heterogeneity Compared with Majority Filtering
4.2. Tree Species Heterogeneity: Comparison of Pixel to Segment-Level
4.3. Regression Tree Results
4.4. Implications of Object-Based Extrapolation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. Bioscience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free Access to Landsat Imagery. Science 2008, 320, 1011. [Google Scholar]
- Huang, C.; Asner, G.P. Applications of Remote Sensing to Alien Invasive Plant Studies. Sensors 2009, 9, 4869–4889. [Google Scholar] [CrossRef]
- Thompson, S.D.; Gergel, S.E. Conservation implications of mapping rare ecosystems using high spatial resolution imagery: Recommendations for heterogeneous and fragmented landscapes. Landsc. Ecol. 2008, 23, 1023–1037. [Google Scholar] [CrossRef]
- Hill, R.A.; Smith, G.N. Land cover heterogeneity in Great Britain as identified in Land Cover Map 2000. Int. J. Rem. Sens. 2005, 26, 5467–5473. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Franklin, J.F.; Fischer, J. General management principles and a checklist of strategies to guide forest biodiversity conservation. Biol. Conserv. 2006, 131, 433–445. [Google Scholar] [CrossRef]
- Morgan, J.L.; Gergel, S.E. Quantifying historic landscape heterogeneity from aerial photographs using object-based analysis. Landsc. Ecol. 2010, 25, 985–998. [Google Scholar] [CrossRef]
- Castilla, G.; Hay, G.J. Image objects and geographic objects. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications Series; Blaschke, T., Lang, S., Hay, G., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 91–110. [Google Scholar]
- Hay, G.J.; Castilla, G. Geographic object-based image analysis (GEOBIA): A new name for a new discipline. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications Series; Blaschke, T., Lang, S., Hay, G., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 75–89. [Google Scholar]
- Chubey, M.S.; Franklin, S.E.; Wulder, M.A. Object-based analysis of Ikonos-2 imagery for extraction of forest inventory parameters. Rem. Sens. Environ. 2006, 72, 383–394. [Google Scholar]
- Wulder, M.A.; White, J.C.; Hay, G.J.; Castilla, G. Pixels to objects to information: Spatial context in forest characterization with remote sensing. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications Series; Blaschke, T., Lang, S., Hay, G., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 345–363. [Google Scholar]
- Definiens Developer 7 User Guide; Definiens: Munchen, Germany, 2010.
- Wulder, M.A.; Seemann, D. Forest inventory height update through the integration of LiDAR data with segmented Landsat imagery. Can. J. Rem. Sens. 2003, 29, 536–543. [Google Scholar] [CrossRef]
- British Columbian Ministry Of Forests and Range. Biogeoclimactic Zones of British Columbia. Available online: http://www.for.gov.bc.ca (accessed on 1 January 2012).
- British Columbia Conservation Data Centre. Available online: http://a100.gov.bc.ca/pub/eswp/ (accessed on 1 January 2012).
- Green, R.N. Terrestrial Ecosystem Mapping of the Southern Gulf Islands; B.A. Blackwell and Associates Ltd.: North Vancouver, BC, Canada, 2007. [Google Scholar]
- Jones, T.G.; Coops, N.C.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest. Rem. Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Chavez, P.S. Image-based atmospheric corrections: Revisited and improved. Photogramm. Eng. Rem. Sens. 1996, 62, 1025–1036. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Wadsworth: Belmont, California, USA, 1984. [Google Scholar]
- Steinberg, D.; Colla, P. CART: Tree-Structured Non-Parametric Data Analysis; Salford Systems: San Diego, CA, USA, 1995; p. 336. [Google Scholar]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Chapman and Hall: London, UK, 1998. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object based detailed vegetation classification with airborne high spatial resolution remote sensing imagery. Photogramm. Eng. Rem. Sens. 2006, 72, 799–811. [Google Scholar] [CrossRef]
- Smith, G.M. The development of integrated object-based analysis of EO data within UK national land cover products. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications Series; Blaschke, T., Lang, S., Hay, G., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 513–528. [Google Scholar]
- Sinclair, T.R.; Hoffer, R.M.; Schreiber, M.M. Reflectance and internal structure of leaves from several crops during a growing season. Agro. J. 1971, 63, 864–868. [Google Scholar] [CrossRef]
- Kumar, L.; Schmidt, K.; Dury, S.; Skidmore, A. Imaging spectrometry in vegetation science. In Imaging Spectroscopy: Basic Principles and Prospective Applications; Van der Meer, F.D., de Jong, S.M., Eds.; Springer Publishers: Dordrecht, Netherlands, 2006; pp. 111–155. [Google Scholar]
- Van der Meer, F.D. 2006. Basic principles of spectrometry. In Imaging Spectroscopy: Basic Principles and Prospective Applications; Van der Meer, F.D., de Jong, S.M., Eds.; Springer Publishers: Dordrecht, Netherlands, 2006; pp. 3–16. [Google Scholar]
- Jones, T.G.; Coops, N.C.; Sharma, T. Exploring the utility of hyperspectral imagery and LiDAR data for predicting Quercus garryana ecosystem distribution and aiding in habitat restoration. Restor. Ecol. 2011, 19, 245–256. [Google Scholar] [CrossRef]
- Jones, T.G.; Coops, N.C.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest, Canada. Rem. Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. Forest. Chron. 2008, 84, 1–19. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jones, T.G.; Coops, N.C.; Gergel, S.E.; Sharma, T. Employing Measures of Heterogeneity and an Object-Based Approach to Extrapolate Tree Species Distribution Data. Diversity 2014, 6, 396-414. https://doi.org/10.3390/d6030396
Jones TG, Coops NC, Gergel SE, Sharma T. Employing Measures of Heterogeneity and an Object-Based Approach to Extrapolate Tree Species Distribution Data. Diversity. 2014; 6(3):396-414. https://doi.org/10.3390/d6030396
Chicago/Turabian StyleJones, Trevor G., Nicholas C. Coops, Sarah E. Gergel, and Tara Sharma. 2014. "Employing Measures of Heterogeneity and an Object-Based Approach to Extrapolate Tree Species Distribution Data" Diversity 6, no. 3: 396-414. https://doi.org/10.3390/d6030396
APA StyleJones, T. G., Coops, N. C., Gergel, S. E., & Sharma, T. (2014). Employing Measures of Heterogeneity and an Object-Based Approach to Extrapolate Tree Species Distribution Data. Diversity, 6(3), 396-414. https://doi.org/10.3390/d6030396