A Different Statistical Perspective on the Evaluation of Ecological Data Sets

Abstract

Statistical significance varies depending on the sample size. Therefore, when the sample size is sufficient, even differences that affect the total variation very little may be statistically significant. For this reason, it is very important to report effect size measures that estimate the share of the difference between groups of samples in the total variation. This study aims to determine the most reliable effect size measures that can be used when evaluating data obtained from ecological studies. The three most popular effect size measures used in practice were compared in terms of their performance in 2700 different experimental conditions. For this purpose, random numbers generated from the multivariate Poisson distribution were used with the Monte Carlo simulation technique. As a result of the simulations, it was determined that Epsilon-squared and Omega-squared were quite unbiased estimators. Therefore, it was concluded that one of these two effect size measures should be reported in addition to the p-value when evaluating ecological studies.

1. Introduction

In ecological studies, groups of samples such as sites, regions, stations, and locations are compared in terms of species abundance to gain information about community structure [1]. To test whether there is a statistically significant difference between such groups, several methods, such as Analysis of Similarity (ANOSIM) [2], Permutational Multivariate Analysis of Variance (PERMANOVA) [3], the Mantel test [4], Pillai’s trace [5], and Permutational Analysis of Multivariate Dispersions (PERMDISP) [6], have been proposed. However, statistical significance is highly influenced by sample size; when the sample size is sufficiently large, even very small differences may become statistically significant [7,8,9]. This may lead to misleading, overinterpreted, or underinterpreted conclusions if statistical significance is considered in isolation. At this point, determining the share of the difference between the groups in the total variation is at least as important as hypothesis testing [10]. The share of groups in the total variation is called effect size, and the statistics that estimate it are called effect size measures [11]. However, it was observed that effect size measures were generally not taken into account when evaluating results in ecological studies. This may be partly because some of the statistical methods used (such as PERMANOVA and db-RDA), although they decompose the variation according to explanatory components, do not provide a summary statistic like ANOSIM which gives an R value that compares the mean similarity between groups to the mean similarity within groups. Although ANOSIM provides a coefficient, it does not show the share of the total variation explained by the groups. In other words, it only tells whether the similarity between groups is greater than within groups, without quantifying the extent of this effect. This limitation highlights the need for separate effect size measures to determine how much variation can actually be attributed to group differences. Therefore, it is necessary to use effect size measures to estimate the share of groups in the total variation. A large number of effect size measures have been developed [10,12,13,14,15,16,17]. Ecological data generally do not meet the assumptions of ANOVA. Therefore, this was taken into account when selecting the effect size measures to be evaluated in the present study. Detailed simulation studies have shown that Epsilon-squared (${\widehat{\epsilon }}^2$) and Omega-squared (${\widehat{\omega }}^2$) are among the most reliable effect size measures even when the assumptions of classical ANOVA are violated [8,18,19]. Given that it is a fundamental and widely recognized measure of effect size, Eta-squared (${\widehat{\eta }}^2$) was also included in this study for reference purposes.

Accordingly, this study aims to evaluate the performance of these three effect size measures in ecological data sets and to identify the most reliable one(s) for ecological applications.

2. Materials and Methods

2.1. Effect Size Measures

In this study, ${\widehat{\eta }}^2$, ${\widehat{\epsilon }}^2$, and ${\widehat{\omega }}^2$ were taken into consideration as effect size measures. In this section, the effect size measures in question are introduced.

$${\widehat{\eta }}^2={\displaystyle \frac{{\mathrm{S}\mathrm{S}}_{\mathrm{b}}}{{\mathrm{S}\mathrm{S}}_{\mathrm{t}}}}$$

(1)

$${\widehat{\epsilon }}^2={\displaystyle \frac{{\mathrm{S}\mathrm{S}}_{\mathrm{b}}-{\mathrm{d}\mathrm{f}}_{\mathrm{b}}\mathrm{M}\mathrm{S}\mathrm{E}}{{\mathrm{S}\mathrm{S}}_{\mathrm{t}}}}$$

(2)

$${\widehat{\omega }}^2={\displaystyle \frac{{\mathrm{S}\mathrm{S}}_{\mathrm{b}}-{\mathrm{d}\mathrm{f}}_{\mathrm{b}}\mathrm{M}\mathrm{S}\mathrm{E}}{{\mathrm{S}\mathrm{S}}_{\mathrm{t}}+\mathrm{M}\mathrm{S}\mathrm{E}}}$$

(3)

where ${\mathrm{S}\mathrm{S}}_{\mathrm{b}}$ is the sum of squares between the groups, ${\mathrm{S}\mathrm{S}}_{\mathrm{t}}$ is the total sum of squares, ${\mathrm{d}\mathrm{f}}_{\mathrm{b}}$ are the degrees of freedom between the groups, and MSE is the mean squared error [8,9]. The sums of squares, mean squares, and degrees of freedom in the above formulas are obtained from PERMANOVA [3].

2.2. Design of the Simulation Study

In this study, bias was used as the criterion for comparing effect sizes. For this purpose, random numbers generated according to the experimental conditions considered were used. These numbers were drawn from the multivariate Poisson distribution, which is suitable for modeling the count of events occurring within a specified time or area, to simulate species counts [20]. In the study, multivariate Poisson distributions with 75 different parameter combinations based on varying lambda (1, 3, 5, 7, and 10), number of variables (p = 2, 3, 4, 5, and 10), and correlation structures (r = 0, 0.3, and 0.6) were used. In order to create differences between groups, the same fixed numbers were added to all observations in one random group (delta = 0.3, 0.9, and 1.5). Finally, the population effect size was estimated for each effect size measure in three different sample sizes (n = 2, 3, and 4) and four different group combinations (k = 2, 3, 4, and 10). This process was repeated 10,000 times and the means were calculated. The absolute difference between the mean of each effect size measure obtained as a result of 10,000 simulations and the true value of the population effect size was considered as bias. The population effect size was calculated as follows.

$${\mathrm{S}\mathrm{S}}_{\mathrm{b}}=\mathrm{N}{\sum }_{\mathrm{i}=1}^{\mathrm{k}}{\sum }_{\mathrm{j}=1}^p{\left({\mathsf{\mu }}_{\mathrm{i}\mathrm{j}}-{\mathsf{\mu }}_{.\mathrm{j}}\right)}^2$$

(4)

$${\mathrm{S}\mathrm{S}}_{\mathrm{w}}=\mathrm{N}{\sum }_{\mathrm{i}=1}^{\mathrm{k}}{\sum }_{\mathrm{j}=1}^p{\sigma }_{ij}^2$$

(5)

$$\mathrm{Population} \mathrm{Effect} \mathrm{Size}={\displaystyle \frac{{\mathrm{S}\mathrm{S}}_{\mathrm{b}}}{{\mathrm{S}\mathrm{S}}_{\mathrm{b}}+{\mathrm{S}\mathrm{S}}_{\mathrm{w}}}}$$

(6)

where k is the number of populations being compared, p is the number of variables (species), and ${\sigma }^2$ is the variance of each population with respect to each variable [11]. Simulation trials were conducted with codes written using the R programming language [21].

As a result of the simulation trials (10,000 simulations for each condition), predictions were made for 2700 different trial conditions for each test. This means a total of 8100 predictions for three tests. Unlike classical simulation studies, regression trees [22] were used to evaluate simulation results. When using the regression tree, the data was randomly divided into two groups: training (70% of all data) and testing (30% of all data). The model that creates the regression tree that is easiest to interpret, with the highest explained variation, was validated on test data. Thus, the factors affecting the predictions were determined more objectively.

3. Results

The variations explained by the regression trees obtained from the training and test data sets are 98.36% and 98.39%, respectively (

Table 1. Model diagnostics for training and test regression trees.

Statistics	Training	Test
R-squared	98.36%	98.39%
Root-mean-squared error (RMSE)	1.7681	1.7553
Mean squared error (MSE)	3.1261	3.0811
Mean absolute deviation (MAD)	1.0819	1.0797
Mean absolute percent error (MAPE)	3.0629	2.6872

). It can be seen that the variation explained and other model selection criteria by both trees are quite close. This shows that the interpretations made from the regression tree created for the test data are reliable.

According to the regression tree results, the factor that most affects bias is the effect size measure used. However, the number of replications and the number of groups are as effective as 16% and 3.8% of the effect size measure, respectively. On the other hand, the shape of the distribution (mean), effect size (delta), number of variables (p), and correlation coefficient (r) between variables did not affect bias at all (Figure 1).

In terms of bias, effect size measures were divided into two groups (Figure 2). The first group included ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$. ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$ were not affected by any factors and their estimates deviated by a mean of 0.42% in all experimental conditions considered. This showed that ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$ were quite unbiased estimators. ${\widehat{\eta }}^2$, which has very high deviations in its estimates, was in the second group. Considering all experimental conditions, there was a mean deviation of 27.14% in ${\widehat{\eta }}^2$’s estimates. The number of replications and the number of groups seriously affected the estimates of ${\widehat{\eta }}^2$. For example, the mean deviations in the estimates were 38.88% when n = 2, 24.47% when n = 3, and 18.05% when n = 4. As in all experimental studies, increasing the number of replications gradually reduced bias. Moreover, the increase in the number of groups also negatively affected the bias of ${\widehat{\eta }}^2$. For example, the bias was 34.58% when n = 2 and k = 2 and 3, and 43.29% when n = 2 and k = 4 and 10. Regardless of the experimental conditions considered, ${\widehat{\eta }}^2$ made highly biased estimates relative to ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$.

4. Discussion

In general, the focus of this research is to investigate the sources of variation. With the widespread use of inferential statistics, the focus in evaluating study results has begun to shift. Results of scientific research have generally been evaluated on the basis of the p-value. As a result, the belief has emerged that as the p-value decreases, the results are considered more significant [23]. However, the p-value indicates the statistical significance of the difference observed between groups. In general, as the number of replications increases, even very small differences begin to become statistically significant, due to the principle that the sample will more accurately represent the population. The reverse is also true. Significant differences observed between groups may not be statistically significant, due to the small number of replications [7,8,9]. To explain this situation more concretely, two different hypothetical examples are given in Appendix A. In the first of these examples, three groups were compared with respect to three variables using PERMANOVA, with four replications for each group. As a result of the analysis, it was seen that the differences between the groups were statistically significant (p = 0.012). However, differences between groups can explain 37.82% (${\widehat{\epsilon }}^2$) of the total variation. As can be noted, although the differences between the groups are statistically significant, they can only explain one third of the total variation. In the other hypothetical example, three groups were compared with two replications in terms of four variables. As a result of PERMANOVA, it was seen that there was no statistically significant difference between the groups (p = 0.067). On the other hand, it was determined that the statistically insignificant difference explained 73.54% of the total variation. This shows that there is a remarkable difference between the groups, but it is not statistically significant, due to the small number of replications. Therefore, evaluating results solely based on the p-value may be misleading. It is essential to report effect size measures alongside the p-value. Thus, reporting how much the differences between groups affect the total variation will eliminate contradictions and misunderstandings in the interpretation of the results [8,9,10,19,24]. However, the effect size measure you report should not be affected by sample size or any other factor. Therefore, the most appropriate effect size measures that can be used need to be determined. In this study, the three most commonly used effect size measures in practice were compared with a detailed simulation study based on ecological data sets. However, the estimates obtained empirically as a result of simulation trials were evaluated not subjectively, but with an objective method such as a regression tree. 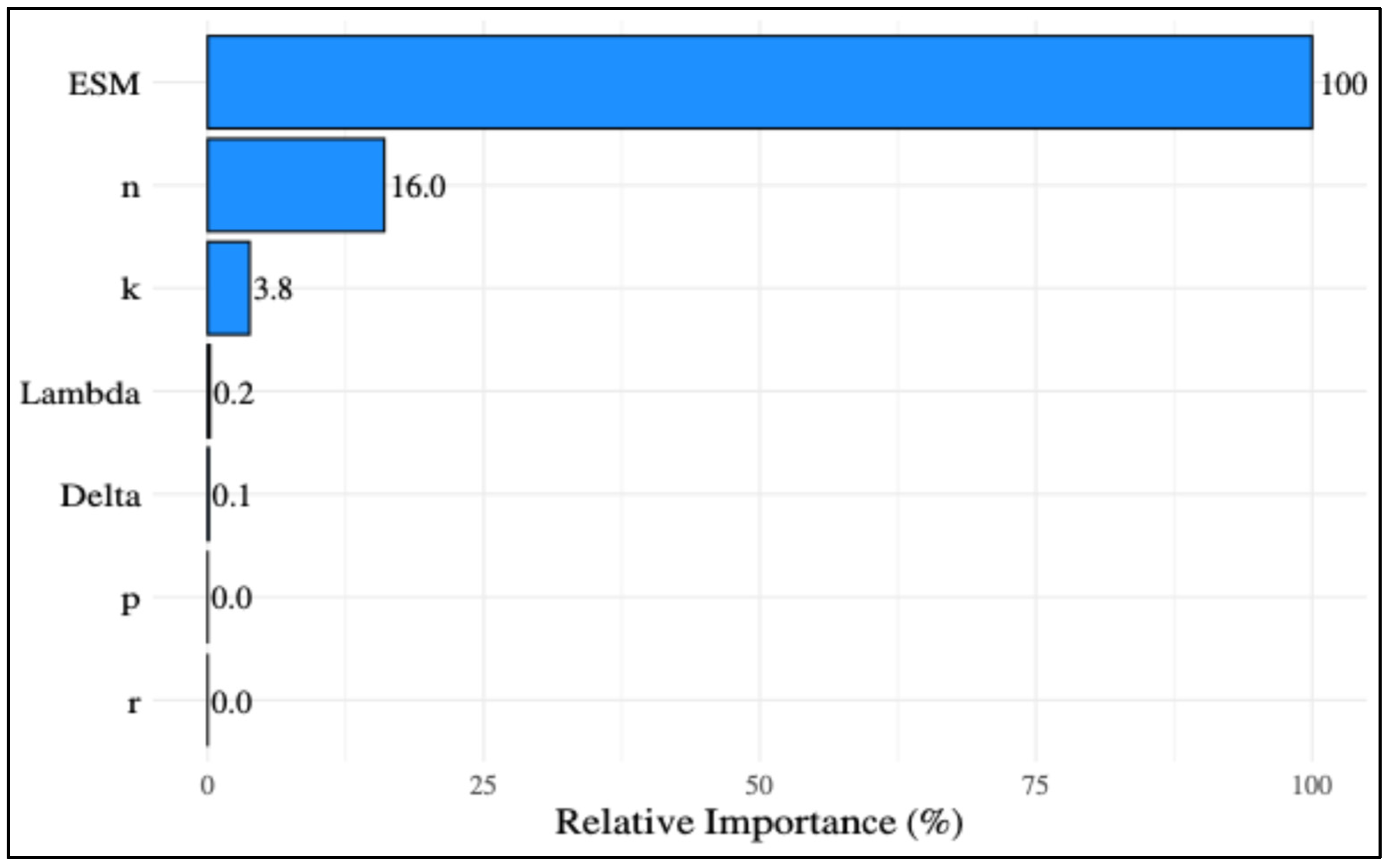As in almost all studies conducted for classical ANOVA, it was observed that ${\widehat{\eta }}^2$ gave quite biased results [8,18,19]. The bias of ${\widehat{\eta }}^2$ gradually increased with the decrease in the number of replications. The shape of the distribution, effect size, number of variables, and correlation between variables generally did not affect the performance of effect size measures in any way. This situation is consistent with the results of other studies comparing effect sizes [8,18]. Regardless of the experimental conditions considered, ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$ produced results that are quite unbiassed compared to ${\widehat{\eta }}^2$. Furthermore, the results of this study confirmed Glass and Hakstian [25] who claimed that the difference between the predictions of ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$ is negligible. On the other hand, this study draws attention to the fact that when evaluating ecological data sets, one should not only focus on the p-value but also evaluate the share of the groups in the total variation. Therefore, it will contribute to making the results of ecological studies more understandable.

5. Conclusions

Particularly, the main goal of ecological studies comparing groups in terms of species abundance should be the separation of the total variation into its components. The p-value does not partition variation; it only indicates statistical significance, as demonstrated by two concrete examples. The most appropriate effect size measures that can be used for this purpose were determined by a detailed simulation study based on ecological data sets. As a result of the simulation study, it was revealed that ${\widehat{\epsilon }}^2$ and ${\widehat{\omega }}^2$ are quite unbiased estimators. It is thought that determining the sources of variation observed in terms of the subject of interest will make significant contributions to the studies conducted. For this, it is recommended to report ${\widehat{\epsilon }}^2$ or ${\widehat{\omega }}^2$ together with the p-value.

This study primarily focused on ecological data sets under certain assumptions, such as multidimensional Poisson distributions and relatively small sample sizes. While the findings provide valuable insights, future research could examine the performance of effect size measures under different distributional scenarios and with larger, more diverse ecological data sets. Such work would help reinforce and broaden the applicability of these estimators across various ecological contexts.