Next Article in Journal
Growth Patterns of Reef-Building Porites Species in the Remote Clipperton Atoll Reef
Previous Article in Journal
Determining Large Trees and Population Structures of Typical Tree Species in Northeast China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Diversity
Volume 17
Issue 7
10.3390/d17070493
diversity-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Allometric Equations for Aboveground Biomass Estimation in Natural Forest Trees: Generalized or Species-Specific?

by
Yuxin Shang
1,
Yutong Xia
1,
Xiaodie Ran
1,
Xiao Zheng
2,
Hui Ding
2 and
Yanming Fang
1,*
1
Key Laboratory of State Forestry and Grassland Administration On Subtropical Forest Biodiversity Conservation, Co-Innovation Center for Sustainable Forestry in Southern China, College of the Life Sciences, Nanjing Forestry University, Nanjing 210037, China
2
State Environmental Protection Key Laboratory On Biosafety, Research Center for Biodiversity Conservation and Biosafety, State Environmental Protection Scientifc Observation and Research Station for Ecological Environment of Wuyi Mountains, Biodiversity Comprehensive Observation Station for Wuyi Mountains, Nanjing Institute of Environmental Sciences, Ministry of Ecology and Environment of China, Nanjing 210042, China
*
Author to whom correspondence should be addressed.
Diversity 2025, 17(7), 493; https://doi.org/10.3390/d17070493
Submission received: 16 June 2025 / Revised: 2 July 2025 / Accepted: 6 July 2025 / Published: 18 July 2025
(This article belongs to the Section Plant Diversity)
Browse Figures
Versions Notes

Abstract

Accurate estimation of aboveground biomass (AGB) in tree–shrub communities is critical for quantifying forest ecosystem productivity and carbon sequestration potential. Although generalized allometric equations offer expediency in natural forest AGB estimation, their neglect of interspecific variability introduces methodological pitfalls. Precise AGB prediction necessitates resolving two biological constraints: phylogenetic conservation of allometric coefficients and ontogenetic regulation of scaling relationships. This study establishes an integrated framework combining the following: (1) phylogenetic signal detection (Blomberg’s K/Pagel’s λ) across 157 species’ allometric equations, revealing weak but significant evolutionary constraints (λ = 0.1249, p = 0.0027; K ≈ 0, p = 0.621); (2) hierarchical error decomposition of 9105 stems in a Mt. Wuyishan forest dynamics plot (15 species), identifying family-level error stratification (e.g., Theaceae vs. Myrtaceae, Δerror > 25%); (3) ontogenetic trajectory analysis of Castanopsis eyrei between Mt. Wuyishan and Mt. Huangshan, demonstrating significant biomass deviations in small trees (5–15 cm DBH, p < 0.05). Key findings resolve the following hypotheses: (1) absence of strong phylogenetic signals validates generalized models for phylogenetically diverse communities; (2) ontogenetic regulation dominates error magnitude, particularly in early developmental stages; (3) differential modeling is recommended: species-specific equations for pure forests/seedlings vs. generalized equations for mixed mature forests. This work establishes an error hierarchy: ontogeny > taxonomy > phylogeny, providing a mechanistic basis for optimizing forest carbon stock assessments.

1. Introduction

Biomass is an important measure of forest ecosystem productivity [1]. It is also a key indicator of forest ecosystem function, and assessments of forest carbon stocks are based upon the estimation of forest biomass [2]. Forest biomass can be measured at both individual tree and stand level [3], or at both individual and stand level [4]. The biomass of individual trees and forest communities is dynamic over time. The process of forest development and community succession can affect forest biomass. The stand development increases biomass [5], while forest succession links biomass dynamics [6]. In addition to being associated with forest ecological processes, forest biomass is also positively correlated with biodiversity indices such as species richness and functional diversity, though context-dependent exceptions exist in degraded ecosystems [7,8,9].
Forest biodiversity is essential to ecosystem function and can provide a variety of ecosystem services, including pollination, seed dispersal, resistance to wind storms, and others [10]. Aboveground biomass (AGB) of trees and shrubs serves as a fundamental basis for evaluating forest ecosystem functions and the value of ecosystem services such as biodiversity and carbon storage [11]. As a proxy for habitat complexity, AGB mediates biodiversity conservation by (i) providing multi-layered niches for canopy specialists and understory taxa, and (ii) enhancing resource partitioning through size-structured allocation patterns. It directly reflects the productivity and health status of the forest [12]. Higher AGB indicates a more complex forest structure including different layers of canopy and vegetation that provide diverse ecological niches [13]. Hence, quantifying natural forest AGB is crucial for assessing global carbon sinks, as well as for developing effective forest management and conservation strategies [14]. By estimating AGB, we can understand the growth patterns of different tree species under various environmental conditions and analyze the productivity and resource use efficiency of forest ecosystems [15].
An allometric equation for aboveground biomass is a model that describes the relationship between aboveground biomass and factors such as tree species diameter at breast height (DBH) and height. The estimation of AGB can be based on a single factor (DBH), or dual factors (DBH and tree height), e.g., biomass–diameter regression and biomass–diameter–height regression [16]. In the allometric model of Y = bxa, b is a constant, indicating y’s value when x = 1, and a is the allometric coefficient, determining the growth rate of y relative to x, e.g., isometric (a = 1), positive (a > 1), and negative allometry (a < 1) [17,18,19]. Allometric equations are widely applied to different forests or geographical regions, such as various ecosystems in USA [20], Douglas-fir plantation in Italy [21], pine stands in Portugal [22], Omo-Gibe woodland species in Ethiopia [23], dry secondary forest trees in Thailand [24], and Atlantic forest species in Brazil [25]. In China, allometric equations have been developed for tree species in both temperate [26,27] and subtropical forests [28,29,30].
The widespread application of allometric equations across biomass presents both opportunities for standardized carbon accounting and challenges in addressing ecological specificity, particularly in hyper-diverse forests. However, in terms of natural forests (especially tropical and subtropical forests), species highly assemble at a local scale. The species density per unit area in long-term forest dynamics plots (FDPs) often reaches a high level, e.g., 1519 (species)/25 ha in Manaus (Brazil), 1114/50 ha in Yasuni (Ecuador), 468/20 ha in Xishuangbanna (Yunnan, China), 299/50 ha in Barro Colorado Island (Panama), and 153/20 ha in Tiantongshan (Zhejiang, China) [31]. In FDPs with abundant species, the estimation of overall forest biomass faces a potential problem: not all species have a specific allometric equation. On the other hand, for natural forests of different ages, sizes, and species, carbon storage is often estimated using a generalized allometric equation [13,30,32,33]. In this context, a similar question arises: is there sufficient scientific basis for estimating biomass using a genenralized allometric equation? There are few reports on such investigations, although some studies have noted between tree species (phylogenetic) [34,35] and between size classes (ontogenetic) [29,36]. Although allometric equations have been widely studied across taxa, our understanding of how phylogenetic history and ontogenetic development shape these relationships remains incomplete. Phylogenetic comparative methods [37,38] have substantially advanced the field, but their integration into allometric studies is still limited. Most empirical studies focus either on interspecific scaling without accounting for developmental changes, or on within-species ontogenetic patterns without considering evolutionary history. As highlighted by Voje et al. [39] and Pélabon et al. [40], there is a lack of studies that jointly analyze both phylogenetic and ontogenetic influences on trait scaling. Moreover, classic work such as Gould [41] and more recent syntheses like Klingenberg [42] emphasize that separating the effects of growth and descent remains a major challenge. These gaps limit our ability to generalize allometric patterns and predict trait variation across lineages and developmental stages.
In this study, we focus on two potential errors, namely phylogenetic and ontogenetic errors, in estimating the biomass of FDPs using a general biomass–DBH allometric equation. The datasets created by our lab from two FDPs at Mt. Wuyishan [43,44] and Mt. Huangshan [43,45] were used to evaluate the two types of errors. We plan to collect parameters of the biomass–DBH allometric equations from different species around the world for phylogenetic signal detection. Based on these, we propose two hypotheses: (1) Since the growth patterns of trees are influenced by evolutionary history, tree species with different phylogenetic locations have distinct allometric equation parameters. Thus, there may be significant phylogenetic errors when using a general allometric equation to estimate AGB in FDPs, compared to using species-specific equations. (2) The growth patterns of trees are influenced by environmental factors, and local environmental factors vary over time. Thus, using general allometric equations to estimate AGB in FDPs with different size classes may introduce ontogenetic errors. The verification of the two hypotheses not only provides a basis of model selection for the determination of AGB in FDPs, but also lays a scientific foundation for ecosystem function evaluation and biodiversity conservation.

2. Materials and Methods

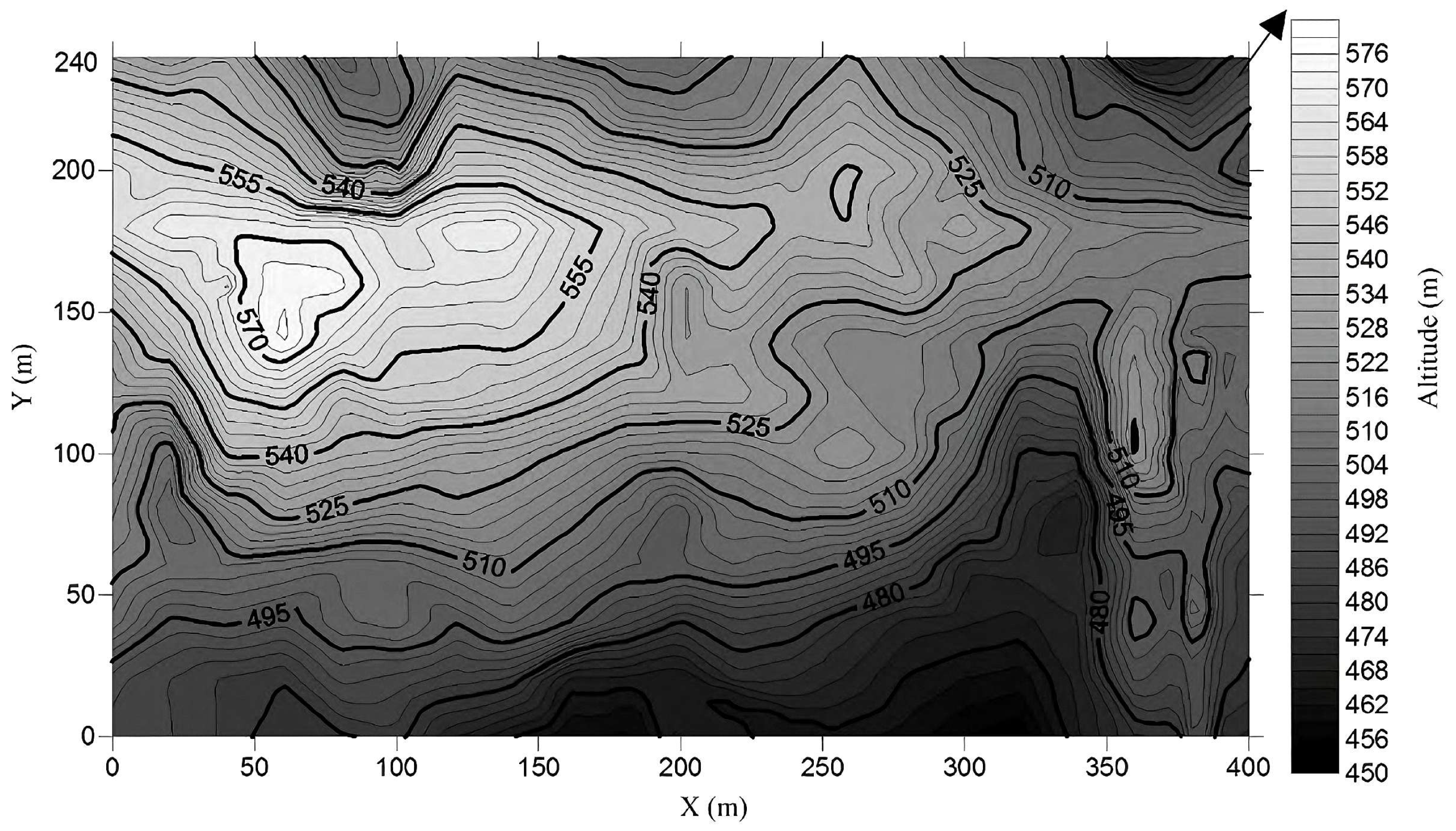
2.1. Site Description

The study site is located near Sixin Village, Xingcun Town, Wuyishan City. This region is characterized by a mid-subtropical monsoon humid climate, with an annual average temperature ranging from 17.0 °C to 18.4 °C, an average relative humidity of 75–84%, annual precipitation of 1800 mm, an average annual sunshine duration of 1910.2 h, and a frost-free period of 227–246 days [43]. The soil type of the sample site is dominated by red soil with pH ranging from 4.5 to 5.0. Evergreen broad-leaved forests represent the zonal forest vegetation of Mt. Wuyishan, covering a vast area and predominantly distributed at elevations between 350 and 1400 m. The plant community is primarily composed of species from families such as Fagaceae, Lauraceae, Ericaceae, Magnoliaceae, Elaeocarpaceae, and Theaceae. Common species include Castanopsis carlesii, Castanopsis fordii, Castanopsis eyrei, and Engelhardia roxburghiana.
A long-term forest dynamics plot (WY) was established at Mt. Wuyishan according to the criteria proposed by the Center for Tropical Forest Sciences (CTFS). All woody plants with DBH (diameter at breast height) ≥ 1 cm in the WY were calibrated and surveyed. WY’s geographic coordinate is 27°35′24.23″ N, 117°45′55.43″ E, with an elevation ranging approximately from 450 to 580 m as it shown in Figure 1. The plot is rectangular, with a projected area of 9.6 ha (400 m × 240 m).

2.2. Data Determination of Biomass

To advance the research, this study collected a total of 157 datasets [Supplementary Materials, Dataset s1: Coefficients of 157 sets of species-specific allometric equations] measured as ln(W) = a + b * ln(DBH) from Web of Science, Google Scholar. The time frame covered the period from 2000 to 2023, and the study objects were limited to woody plants. To ensure data quality, we implemented stringent inclusion criteria. Only peer-reviewed studies with clearly reported ln(W) = a + b × ln(DBH) parameters and associated statistics were included. Studies focusing on herbaceous species, managed forests, or those lacking site metadata were excluded to minimize bias from non-representative conditions. Allometric models without variance estimates were also omitted to maintain statistical integrity [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124]. The search was conducted using keyword combinations such as (“allometric equation” or “biomass equation”) and (“tree” or “woody plant”) and (“coefficient” or “parameter”). The equations were required to explicitly provide coefficients a and b, as well as relevant statistical metrics. The coefficients a and b collected from papers were subjected to descriptive statistical analysis and visualization in Python 3.11 to compare the values across different tree species, where
  • W represents the aboveground biomass of the tree species;
  • DBH represents the diameter at breast height of the tree.
Following the methodology outlined by Anhui Agricultural University [125], phylogenetic signal analysis was conducted on the scaling constant (a) of the allometric equation only. The allometric exponent (b), which reflects the proportional relationship between DBH and AGB, was not included in the phylogenetic analysis due to its higher stability and lower sensitivity to phylogenetic constraints. To verify that the 157 sets of coefficients have a phylogenetic signal, we calculated Blomberg’s K statistic [34] and its corresponding p-value in R 4.2.3 using the phylogenetic-K function. Blomberg’s K is a statistical measure that quantifies the strength of trait signal along a given phylogenetic tree. A K-value < 1 suggests that the trait evolution follows the Brownian motion model, indicating a strong phylogenetic signal. A K-value significantly less than 1 implies that the trait is more randomly distributed across the phylogeny. The p-value is used to evaluate the significance of the phylogenetic signal, with values < 0.05 indicating that the signal is statistically significant.
In this study, 9105 individuals from 15 species in the Mt. Wuyishan dynamics plot were selected as the analysis subjects [Supplementary Materials, Dataset s2: AGB errors calculated by generalized and species-specific allometric equations]. AGB was estimated using both generalized and species-specific equations, and error analysis was conducted in Python 3.9.13. For the error analysis with the generalized and species-specific allometric equations, the generalized equation from the study by Zuo et al. [126] on the subtropical evergreen broadleaf forests of China was used. This study site is located in Nanping, Fujian, China, the same region as the Mt. Wuyishan forest dynamics plot. The species overlap is high, and the climatic and soil conditions are similar, making the equation highly relevant for this study:
ln(W) = −1.9783 + 2.3771 × ln(DBH)
To compare the regional differences in biomass of the dominant species, data from 1319 Castanopsis eyrei individuals in Mt. Wuyishan and 14,216 individuals in Mt. Huangshan were selected. The DBH data were classified into 5 cm intervals to analyze the biomass at different size classes. The allometric equation of C. eyrei in the dataset compiled by Luo Y J et al. [127] was used to calculate the AGB of C. eyrei within each DBH interval. Since there is a large amount of data on Mt. Huangshan and the maximum DBH of the C. eyrei is larger than the maximum DBH of the C. eyrei in Mt. Wuyishan, there is an imbalance problem in the data. A downsampling method is used to limit the data volume of Mt. Huangshan to the level of the Mt. Wuyishan data and limit the DBH to 5~60 cm to ensure that comparability of data between the two places. t-test was performed on different DBH intervals to verify whether there were significant ontogenetic differences.

3. Results

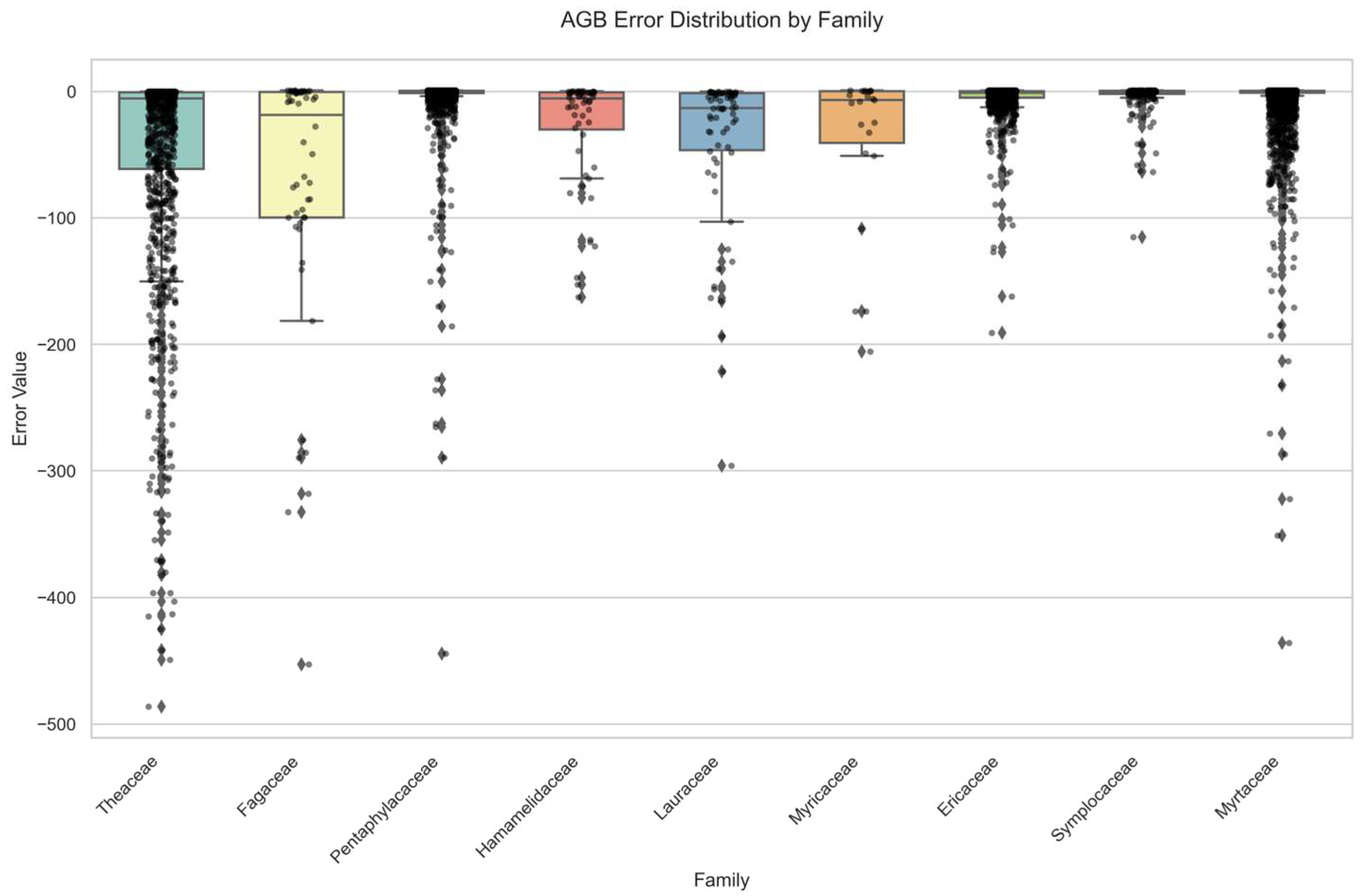
3.1. Analysis of Coefficients of Allometric Equations

Phylogenetic signal detection was conducted on parameters of 157 allometric equations and corresponding phylogenetic tree is presented in Figure 2. Table 1 evaluates the phylogenetic signals and evolutionary trajectories of allometric coefficients through a multi-metric analytical framework. For the empirical dataset (a), Pagel’s Lambda (λ = 0.1249, p = 0.0027) indicates a weak yet statistically significant phylogenetic signal (p < 0.05), suggesting partial dependency of allometric coefficient evolution on phylogenetic history, albeit substantially modulated by non-phylogenetic drivers such as environmental selection pressures. The significant positive spatial autocorrelation (Moran’s I = 0.0764, p = 0.002) further corroborates elevated trait similarity among phylogenetically proximate taxa relative to stochastic expectations. Concurrently, the positive covariance structure (C mean = 0.1106, p = 0.024) reinforces a weak but detectable association between trait variation and phylogenetic distances. Notably, the non-significant Blomberg’s K (K = 0.0427, p = 0.621) implies stochastic evolutionary dynamics, potentially attributable to convergent adaptation or heterogeneous evolutionary rates across clades.

3.2. Analysis of Species Phylogenetic Error

In this study, we applied both generalized and species-specific allometric equations to estimate the AGB of 15 species with a total of 9105 individuals and systematic phylogenetic error analysis was then performed [Supplementary Materials, Dataset s2: AGB errors calculated by generalized and species-specific allometric equations].
In Figure 3, the differences in boxplot width and position between different families indicate that there are certain differences in the error in calculating AGB for each family. The error variation in Figure 3 for Theaceae and Myrtaceae is more pronounced, with some individual errors being extremely large, indicating that these families may be more sensitive to the allometric equations used. In contrast, Pentaphylacaceae and Ericaceae show more concentrated errors, suggesting that AGB estimates for these families are more stable. Theaceae and Symplocaceae exhibit more outliers, meaning that the AGB estimates for these individual plants deviate significantly, which could reflect the unique growth characteristics of these families or limitations in the current equations.

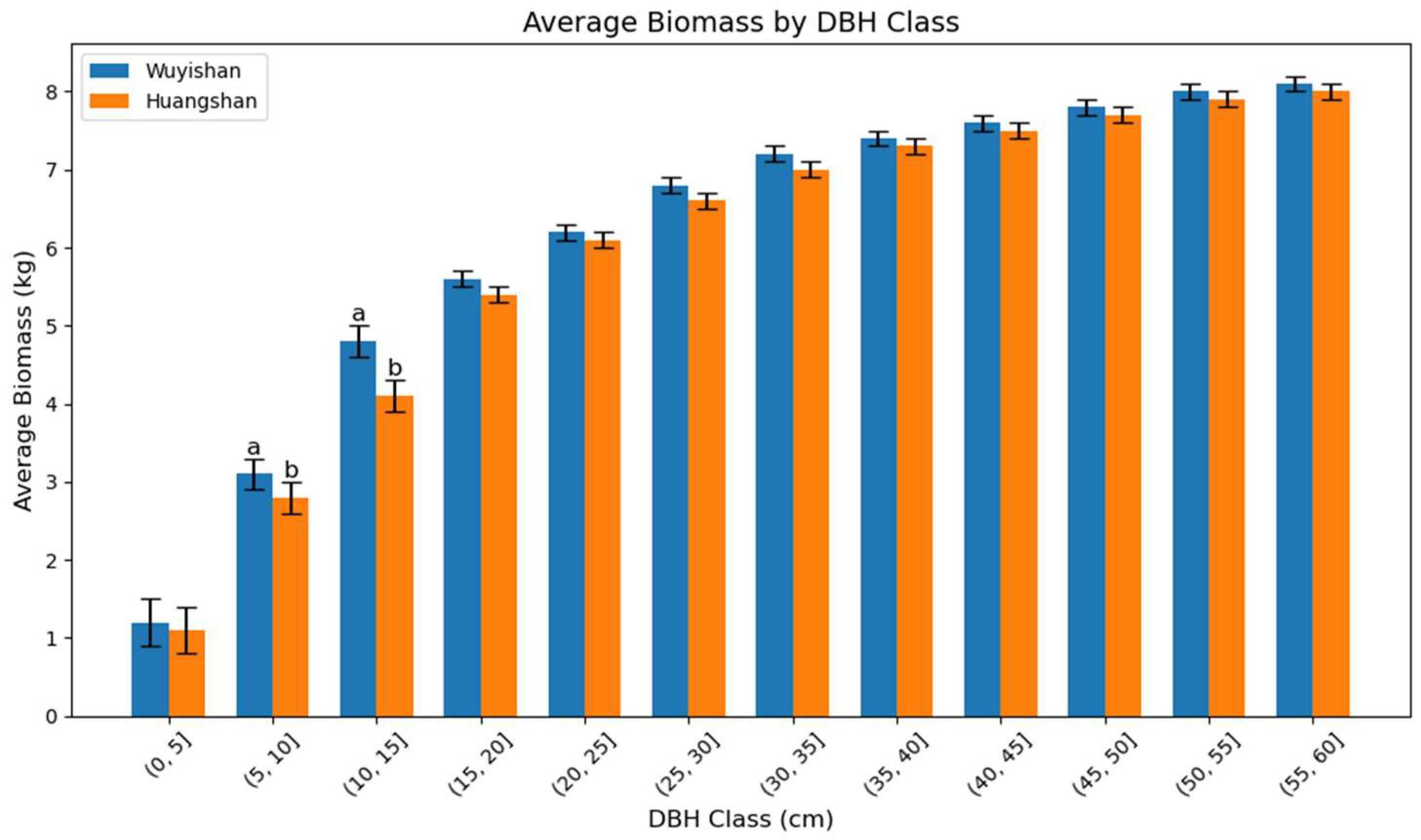
3.3. Analysis of Species Ontogeny Errors

The t-test results (Table A1) show that in the size classes 5–10 cm and 10–15 cm, the biomass difference between C. eyrei in Mt. Huangshan and Mt. Wuyishan is statistically significant; in most size classes, especially 25–30 cm and above, the biomass difference between the two places is not significant. These results show that within the smaller size class of 5–15 cm, there is a large difference (Figure 4) in the AGB of C. eyrei between the two locations. In the larger DBH classes, the aboveground biomass difference becomes smaller and is not significant.

4. Discussion and Conclusion

4.1. Phylogenetic Signal Analysis of Allometric Equations

To the best of our knowledge, it remains unclear how the phylogenetic history affects large-scale variation in tree allometry [128]. The analysis of phylogenetic signals provides a good platform in studies on tree allometry variation. The interpretation of the results in phylogenetic signal analysis of traits (or parameters) is based on the following rules: significant phylogenetic signals indicating trait phylogenetic conservatism, conversely, insignificant phylogenetic signals revealing traits are mainly influenced by the environment [35]. Significant phylogenetic signals in 50 species demonstrated phylogenetic conservation of the crown-to-stem biomass ratio (Pagel’s λ = 0.359, p < 0.05), demonstrating that biomass allocation of crown-to-stem, rather than stem biomass is phylogenetic conservation [35]. However, shoot–root biomass allocation in 20 dry-grassland species varies greatly among closely related species, implying that this biomass allocation pattern is not phylogenetically conservative [129]. Furthermore, in a study of 894 allometric biomass models of 276 tree species, the model parameters of AGB-DBH regressions are not significantly constrained by phylogeny [34]. It was also demonstrated that the scaling relationships for annualized biomass production rates and different measures of body size were indifferent to phylogenetic affiliation [130]. Therefore, based on existing empirical studies, there is no statistically significant impact of phylogenetics on the allometric equation of biomass estimation.
Will there be significant errors in estimating biomass using a generalized allometric equation established with DBH as a single factor? Several investigation results have confirmed that the error is not significant. Based on both generalized and species-specific allometric equations, the correlation coefficients between aboveground biomass and DBH were >0.85 for subtropical Fagaceae species [131] and > 0.80 for understory woody species in northeastern China forest ecosystems [132], and despite the improved fit of biomass after integrating tree height and crown spread data. DBH is an effective estimator in the process of aboveground biomass estimation, and equations considering only DBH can explain component biomass and total biomass with more than 80% variability for tree species in Tibetan Plateau, China [133].
A phylogenetic signal detection was conducted on the parameters a and b of 157 allometric equations, and no significant phylogenetic signal was found, indicating that phylogeny does not impose constraints on allometry. Phylogenetic signal is present but weak, as evidenced by a statistically significant yet low-magnitude λ (λ = 0.1249, p = 0.0027), indicating that allometric coefficients exhibit only partial dependency on phylogenetic relationships. Environmental selective pressures likely drive trait divergence, thereby attenuating phylogenetic conservatism. The non-significant K value (K ≈ 0, p = 0.621) suggests stochastic trait evolution, with patterns indistinguishable from random processes. Notably, comparative analysis with the Brownian motion model (bm) reveals that the empirical K value (0.0427) is significantly lower than the Brownian motion expectation (0.6239; p < 0.05), further supporting non-conservative evolutionary dynamics dominated by environmental filtering or convergent adaptation. More intriguingly, within the range of tree species in the families Theaceae and Myrtaceae, the general allometric equations exhibited substantial errors, suggesting that allometry exhibits intra-familial or intra-generic differentiation rather than being consistent. Despite the quality screening, we acknowledge that site-specific variables such as soil fertility, microclimate, and tree age were not consistently reported in all sources. This introduces potential unexplained variance, a limitation common in meta-analytical studies on allometry [134].

4.2. Ontogeny and Allometric Equations

Evolution and development jointly shape plant architecture. In theory, plant architecture may be subject to both phylogenetic constraints and ontogenetic genetic control. The formation trajectory of plant architecture, growth, branching, axial differentiation, and reproductive organ development is a dynamic and multi-level process of ontogeny, and 23 architectural models and their names were proposed and coined by Halle and his colleagues [135]. As a support of biomass production and partitioning at organ scale, architectural models can simulate individual tree development and stand dynamics, while thinning treatment can alter tree architectural [136]. Thus, morphological transformation and developmental bias exist in plants, although they are modular organisms [137].
Complex ontogenetic rules, e.g., leaf neoformation or polycyclism, result in tree architecture, and both inherent and environmental factors affect biomass formation and allocation of a tree [138]. In a tropical rainforest, wood density explains specific architectural differentiation, light capture strategy and species co-existence. Interestingly, wood density correlates negatively with stem diameter and positively with stem biomass [139]. Interspecific variation in architectural traits (tree diameter, height and crown dimensions) is related to the functional traits (light requirements and wood density) in a Central Africa tropical forest [140]. In the forest, the canopy’s obstruction of light has a substantial impact on the understory small trees. Stem height growth is limited in understory trees, and following canopy release events diameter growth responds more rapidly than tree height, indicating that tree growth is driven by diameter instead of height [141]. In a forest environment with low light and interference from neighboring trees, the biomass allocation of trees is size-dependent, with major allocation resources to leaves for small-diameter trees (DBH < 8 cm), to stems for medium-diameter trees (8 cm < DBH < 20 cm), and branches for large-diameter trees (DBH > 20 cm) [142]. Ontogenetic variation in tree biomass allocation is influenced by several ecological and biophysical factors: (i) Soil Fertility: In nutrient-rich environments, trees tend to allocate more biomass to aboveground parts (e.g., stems), leading to a more pronounced relationship between DBH and AGB. Conversely, in nutrient-poor soils, root allocation may be prioritized, causing deviations in allometric models for small trees. (ii) Light Availability: For understory trees or those in shaded environments, biomass allocation may favor leaf development for light capture, particularly in the early stages of growth. This alters the DBH-to-AGB relationship in small trees. (iii) Climate: Variability in temperature and precipitation regimes influences tree growth and biomass allocation. In drier or harsher climates, trees may allocate more biomass to roots, whereas in more temperate conditions, aboveground growth is often more pronounced. (iv) Anthropogenic Disturbance: Disturbances such as logging or land conversion can modify growth patterns, often resulting in altered biomass allocation strategies. In disturbed environments, trees may focus more on regrowth or survival, further influencing allometric relationships.
Tree architecture or allometry is also influenced by developmental time, e.g., tree age or size [143]. For a given tree species, the allometric model varies with developmental stages or size classes [144,145,146], and even if the stages differ by two years, their allometric coefficients may also be inconsistent [147]. Branches and leaves are more sensitive to environmental changes and are the tree components most influenced by stand age. The intercepts and slopes differ significantly across different stand age classes, indicating that stand age affects allometric growth models [28]. The allometry of Norwegian spruce exhibits an ontogenetic trend, and as age increases (2, 8, and 21 years), the biomass allocated to the stem elevates [148]. Due to the influence of the ontogenetic stage on biomass–diameter relation, allometric equations established based on different age groups or size classes may underestimate or overestimate biomass [149]. Different allometric models should be adopted to estimate the biomass of large and small trees, and applying equations for large trees to saplings results in biased and/or inaccurate estimates [16,132].
Analysis results on Castanopsis eyrei confirm that ontogenetic deviation of biomass estimation occurs among the individuals with different size classes. We also demonstrate that developing species-specific allometric equations for individuals of different ages can provide more robust estimates of aboveground biomass. Although using a generalized allometric equation for aboveground biomass estimation is convenient and effective for mature trees or forests, species-specific allometric equations should be used to reduce individual ontogenetic errors for small trees or young forests.

4.3. Selection of Allometric Equations

In order to reduce the model bias of AGB measurement and improve accuracy, a model needs to be validated before the selection allometric equations [150]. The selection of allometric equations often comes with shortcomings or defects. It is not advisable to replace regional models with national models directly, or vice versa [151]. Integrating more models and complete tree size classes and using a weighted function method is beneficial for selection of the optimal allometric equation [152].
Model selection requires multidimensional thinking, such as phylogenetics, ontogeny, and forest types. Phylogenetically, a reliable method for model selection is to group species based on phylogenetic relationships and determine allometric equations [35]. Genus-specific allometric equations, known as mixed models, can improve the accuracy of tree biomass estimates [153]. In addition, the biomass allometric model established based on the method of phylogenetically weighted regression (PWR) can avoid phylogenetic stationarity and improve the accuracy of biomass measurement [154]. Ontogenetically, the AGB aboveground biomass may be underestimated or overestimated when applying the allometric equations of large trees to small trees [16,29,155,156]. For a single tree species, there are significant differences in the allometric equations between large and small trees [157,158]. The generalized allometric equations for large trees should not be simply applied to understory shrubs, subcanopy small trees, and alpine dwarf forests, and need to be independently developed [158,159,160,161]. From the perspective of forest management, the selection of models needs to consider the diversity of tree species and the values of correlation coefficients [162]. In terms of the biomass allometric equations of Picea abies stands, specific models for pure stands cannot be applied to mixed stands (and vice versa); otherwise it may lead to significant bias [163]. This discrepancy in allometry between pure and mixed stands may be species-dependent. For instance, allometric patterns of biomass in mixed stands are significantly different from those in monospecific stands for Quercus petraea, while those in Pinus sylvestris are similar [164]. In addition, site effects [165,166] and climate effects [167,168] on biomass allometric models were documented in a quite a number of reports.
In the choice of biomass estimation models, there are often methodological mistakes and pitfalls, such as the arbitrary choice of analytical methods, model dredging and inadequate model diagnosis, and ignoring collinearity [134]. Based on the above discussion, if the differences in biological estimation objects and purposes are ignored, the selection of allometric models will also result in errors. Our data confirms that in the cases of forest stands with less species, in a young state, or for yield estimation, species-specific models should be applied as much as possible, while in the cases of forest stands with many tree species, in an old state, or for general biomass estimation, general models cannot be excluded.
This study highlights the need for dynamic AGB modeling strategies. Future research could focus on the following: (i) developing size-class-specific biomass equations to address ontogenetic variance; (ii) applying phylogenetically weighted regression in taxa showing consistent deviations; (iii) integrating functional trait data for more biologically informed allometry; (iv) compiling regional biomass databases with site metadata to improve model transferability.

4.4. Conclusions

This study provides critical insights into the interplay between phylogenetic constraints and allometric variation in forest biomass estimation. Theoretical implications emerge from the decoupling of trait evolution from phylogenetic history: the absence of strong phylogenetic signals (λ = 0.1249, p = 0.0027; K ≈ 0, p = 0.621) challenges the assumption of phylogenetic conservatism in allometric scaling, thereby validating the empirical rationale for employing generalized allometric models in phylogenetically diverse forest plots. Ecological significance lies in the hierarchical differentiation patterns, while family-level disparities (e.g., Theaceae vs. Myrtaceae) reflect divergent ecological strategies, and ontogenetic shifts across size classes highlight the necessity of incorporating life-stage dynamics into biomass prediction frameworks.
Methodologically, the reduced error magnitude when applying generalized equations to large individuals (vs. small individuals) suggests a strategic priority: resource-constrained monitoring programs could optimize accuracy by developing size-specific models for smaller individuals while retaining generalized equations for mature trees. These findings directly address the proposed hypotheses of ontogenetic sensitivity: The detectable size-class differentiation underscores a critical limitation-broad-scale equations may systematically misrepresent biomass allocation trajectories, necessitating error-correction protocols when extrapolating across developmental stages. Using generalized allometric equations to estimate AGB in FDPs with different size classes can results in ontogenetic errors. This study not only provides reference for the development of AGB allometric models, but also helps with AGB estimation in different scenarios.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/d17070493/s1, Dataset s1: Coefficients of 157 sets of species-specific allometric equations; Dataset s2: AGB errors calculated by generalized and species-specific allometric equations.

Author Contributions

Conceptualization, H.D. and Y.F.; methodology, Y.F.; software, Y.S. and Y.X.; formal analysis, Y.S.; investigation, Y.X., Y.S., X.Z. and X.R.; data curation, Y.X., X.R. and X.Z.; writing—original draft preparation, Y.S. and Y.F.; writing—review and editing, Y.F.; visualization, X.R.; supervision, Y.F.; project administration, Y.F. and H.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. t-test results.
Table A1. t-test results.
DBH Class (cm)T-Statisticp-Value
(0–5]1.9600.050 *
(5–10]−6.059<0.001 ***
(10–15]−3.5880.0004 ***
(15–20]−0.5490.584
(20–25]0.5410.589
(25–30]−1.3200.190
(30–35]1.0170.312
(35–40]1.1810.244
(40–45]1.3200.198
(45–50]0.0330.974
(50–55]1.1730.271
(55–60]−1.6340.141
Note: * indicate statistically significant results at the corresponding significance level. *: p < 0.05; ***: p < 0.001.

References

  1. Georgia, G.; Dimitris, Z.; Ioannis, G.; Kalliopi, R.; Vassilia, K.; Maria, T.S.; Iain, W.; Giorgos, M. Vegetation biomass estimation with remote sensing: Focus on forest and other wooded land over the Mediterranean ecosystem. Int. J. Remote Sens. 2017, 38, 1940–1966. [Google Scholar]
  2. Zhao, M.; Yang, J.; Zhao, N.; Liu, Y.; Wang, Y.; Wilson, J.P.; Yue, T. Estimation of China’s forest stand biomass carbon sequestration based on the continuous biomass expansion factor model and seven forest inventories from 1977 to 2013. For. Ecol. Manag. 2019, 448, 528–534. [Google Scholar] [CrossRef]
  3. Cheng, D.; Zhong, Q.; Niklas, K.J.; Ma, Y.; Yang, Y.; Zhang, J. Isometric scaling of above-and below-ground biomass at the individual and community levels in the understorey of a sub-tropical forest. Ann. Bot. 2015, 115, 303–313. [Google Scholar] [CrossRef] [PubMed]
  4. Cheng, Y.; Zhang, C.; Zhao, X.; Gadow, K. Biomass-dominant species shape the productivity-diversity relationship in two temperate forests. Ann. For. Sci. 2018, 75, 97. [Google Scholar] [CrossRef]
  5. Pesola, L.; Cheng, X.; Sanesi, G.; Colangelo, G.; Elia, M.; Lafortezza, R. Linking above-ground biomass and biodiversity to stand development in urban forest areas: A case study in Northern Italy. Landsc. Urban Plan. 2017, 157, 90–97. [Google Scholar] [CrossRef]
  6. Rozendaal, D.M.A.; Chazdon, R.L.; Arreola-Villa, F.; Balvanera, P.; Bentos, T.V.; Dupuy, J.M.; Hernández-Stefanoni, L.J.; Jakovac, C.C.; Lebrija-Trejos, E.E.; Lohbeck, M.; et al. Demographic drivers of aboveground biomass dynamics during secondary succession in neotropical dry and wet forests. Ecosystems 2017, 20, 340–353. [Google Scholar] [CrossRef]
  7. Adler, P.B.; Seabloom, E.W.; Borer, E.T.; Hillebrand, H.; Hautier, Y.; Hector, A.; Harpole, W.S.; O’Halloran, L.R.; Grace, J.B.; Anderson, T.M.; et al. Productivity is a poor predictor of plant species richness. Science 2011, 333, 1750–1753. [Google Scholar] [CrossRef]
  8. Lauchlan, H.F.; Jason, P.; Anke, J.; Marcelo, S.; Martin, Z.; Diana, A.; Sandor, B.; Carl, B.; Jonathan, A.B.; Alex, B.; et al. Worldwide evidence of a unimodal relationship between productivity and plant species richness. Science 2015, 349, 302–305. [Google Scholar] [CrossRef]
  9. Liang, J.; Crowther, T.W.; Picard, N.; Wiser, S.; Zhou, M.; Alberti, G.; Schulze, E.D.; McGuire, A.D.; Bozzato, F.; Pretzsch, H.; et al. Positive biodiversity-productivity relationship predominant in global forests. Science 2016, 354, aaf8957. [Google Scholar] [CrossRef]
  10. Brockerhoff, E.G.; Barbaro, L.; Castagneyrol, B.; Forrester, D.I.; Gardiner, B.; González-Olabarria, J.R.; Lyver, P.O.; Meurisse, N.; Oxbrough, A.; Taki, H.; et al. Forest biodiversity, ecosystem functioning and the provision of ecosystem services. Biodivers. Conserv. 2017, 26, 3005–3035. [Google Scholar] [CrossRef]
  11. Ma, T.; Zhang, C.; Ji, L.; Zuo, Z.; Beckline, M.; Hu, Y.; Li, X.; Xiao, X. Development of forest aboveground biomass estimation, its problems and future solutions: A review. Ecol. Indic. 2024, 159, 111653. [Google Scholar] [CrossRef]
  12. Cai, T.; Chang, C.; Zhao, Y.; Wang, X.; Yang, J.; Dou, P.; Otgonbayar, M.; Zhang, G.; Zeng, Y.; Wang, J. Within-season estimates of 10 m aboveground biomass based on Landsat, Sentinel-2 and PlanetScope data. Sci. Data 2024, 11, 1276. [Google Scholar] [CrossRef]
  13. Ali, A.; Chen, H.Y.; You, W.H.; Yan, E.R. Multiple abiotic and biotic drivers of aboveground biomass shift with forest stratum. For. Ecol. Manag. 2019, 436, 1–10. [Google Scholar] [CrossRef]
  14. Yao, Y. Spatial pattern of forest aboveground biomass and its environmental influencing factors in Qinling-Daba Mountains, central China. Sci. Rep. 2024, 14, 21411. [Google Scholar] [CrossRef] [PubMed]
  15. Gwal, S.; Singh, S.; Gupta, S.; Anand, S. Understanding forest biomass and net primary productivity in Himalayan ecosystem using geospatial approach. Model. Earth Syst. Environ. 2020, 6, 2517–2534. [Google Scholar] [CrossRef]
  16. Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
  17. Meng, Q.; Cieszewski, C.J.; Madden, M.; Borders, B. Linear mixed-effects model of biomass and volume of trees using Landsat ETM+ images. For. Ecol. Manag. 2007, 244, 93–101. [Google Scholar] [CrossRef]
  18. Tošković, D.; Veličković, M. Comparison of allometric relationships and morphological differences in Tilia cordata Mill. outer leaves exposed to different environmental conditions. Plant Biosyst. 2013, 147, 611–619. [Google Scholar] [CrossRef]
  19. Hornung-Leoni, C.; Sosa, V. Morphological variation in Puya (Bromeliaceae):an allometric study. Plant Syst. Evol. 2006, 256, 35–53. [Google Scholar] [CrossRef]
  20. Rudgers, J.A.; Hallmark, A.; Baker, S.R.; Baur, L.; Hall, K.M.; Litvak, M.E.; Muldavin, E.H.; Pockman, W.T.; Whitney, K.D. Sensitivity of dryland plant allometry to climate. Funct. Ecol. 2019, 33, 2290–2303. [Google Scholar] [CrossRef]
  21. Coletta, V.; Menguzzato, G.; Pellicone, G.; Veltri, A.; Marziliano, P.A. Effect of thinning on above-ground biomass accumulation in a Douglas-fir plantation in southern Italy. J. For. Res. 2016, 27, 1313–1320. [Google Scholar] [CrossRef]
  22. Gonçalves, A.C.; Sousa, A.M.O.; Mesquita, P.G. Estimation and dynamics of above ground biomass with very high resolution satellite images in Pinus pinaster stands. Biomass Bioenergy 2017, 106, 146–154. [Google Scholar] [CrossRef]
  23. Aneseyee, A.B.; Soromessa, T.; Elias, E.; Feyisa, G.L. Allometric equations for selected Acacia species (Vachellia and Senegalia genera) of Ethiopia. Carbon Balance Manag. 2021, 16, 34. [Google Scholar] [CrossRef]
  24. Pothong, T.; Elliott, S.; Chairuangsri, S.; Chanthorn, W.; Shannon, D.P.; Wangpakapattanawong, P. New allometric equations for quantifying tree biomass and carbon sequestration in seasonally dry secondary forest in northern Thailand. New For. 2022, 53, 17–36. [Google Scholar] [CrossRef]
  25. Gaui, T.D.; Cysneiros, V.C.; Souza, F.C.; Souza, H.J.; Filho, T.B.S.; Carvalho, D.C.; Pace, J.H.C.; Vidaurre, G.B.; Miguel, E.P. Biomass Equations and Carbon Stock Estimates for the Southeastern Brazilian Atlantic Forest. Forests 2024, 15, 1568. [Google Scholar] [CrossRef]
  26. Wang, C. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
  27. He, H.; Zhang, C.; Zhao, X.; Fousseni, F.; Wang, J.; Dai, H.; Yang, S.; Zuo, Q. Allometric biomass equations for 12 tree species in coniferous and broadleaved mixed forests, Northeastern China. PLoS ONE 2018, 13, e0186226. [Google Scholar] [CrossRef]
  28. Xiang, W.; Li, L.; Ouyang, S.; Xiao, W.; Zeng, L.; Chen, L.; Lei, P.; Deng, X.; Zeng, Y.; Fang, J. ForresterDI Effects of stand age on tree biomass partitioning and allometric equations in Chinese fir (Cunninghamia lanceolata) plantations. Eur. J. For. Res. 2021, 140, 317–332. [Google Scholar] [CrossRef]
  29. Ali, A.; Xu, M.S.; Zhao, Y.T.; Zhang, Q.Q.; Zhou, L.L.; Yang, X.D.; Yan, E.R. Allometric biomass equations for shrub and small tree species in subtropical China. Silva Fenn. 2015, 49, 1275. [Google Scholar] [CrossRef]
  30. Peng, S.; He, N.; Yu, G.; Wang, Q. Aboveground biomass estimation at different scales for subtropical forests in China. Bot. Stud. 2017, 58, 45. [Google Scholar] [CrossRef]
  31. Davies, S.J.; Abiem, I.; Salim, K.A.; David, S.A.; Allen, D.; Alonso, A.; Anderson-Teixeira, K.; Andrade, A.; Arellano, G.; Ashton, P.S.; et al. ForestGEO: Understanding forest diversity and dynamics through a global observatory network. Biol. Conserv. 2021, 253, 108907. [Google Scholar] [CrossRef]
  32. Ji, B.; Yin, J.; Shi, Y.; Xu, L.; Tao, J.; Zhou, Y. Predicting Vegetation Carbon Density Distribution in different Terrains in Subtropical Forests in China. J. Sustain. For. 2021, 40, 473–490. [Google Scholar] [CrossRef]
  33. Xu, L.; Shi, Y.; Fang, H. Vegetation carbon stocks driven by canopy density and forest age in subtropical forest ecosystems. Sci. Total Environ. 2018, 631, 619–626. [Google Scholar] [CrossRef] [PubMed]
  34. Huang, X.Z.; Li, F.B.; Wang, Z.X.; Jin, Y.; Qian, H. Are allometric model parameters of aboveground biomass for trees phylogenetically constrained? Plant Divers. 2023, 45, 229–233. [Google Scholar] [CrossRef]
  35. Yang, M.; Zhou, X.; Peng, C.; Li, T.; Chen, K.; Liu, Z.; Li, P.; Zhang, C.; Tang, J.; Zou, Z. Developing allometric equations to estimate forest biomass for tree species categories based on phylogenetic relationships. For. Ecosyst. 2023, 10, 100130. [Google Scholar] [CrossRef]
  36. Huang, C.; Feng, C.; Ma, Y.; Liu, H.; Wang, Z.; Yang, S.; Wang, W.; Fu, S.; Chen, H.Y.H. Allometric models for aboveground biomass of six common subtropical shrubs and small trees. J. For. Res. 2021, 33, 1317–1328. [Google Scholar] [CrossRef]
  37. Felsenstein, J. Phylogenies and the comparative method. Am. Nat. 1985, 125, 1–15. [Google Scholar] [CrossRef]
  38. Garland, T.; Ives, A.R. Using the past to predict the present: Confidence intervals for regression equations in phylogenetic comparative methods. Am. Nat. 2000, 155, 346–364. [Google Scholar] [CrossRef]
  39. Voje, K.L.; Hansen, T.F.; Egset, C.K.; Bolstad, G.H.; Pélabon, C. Allometric constraints and the evolution of allometry. Evolution 2014, 68, 866–885. [Google Scholar] [CrossRef]
  40. Pélabon, C.; Firmat, C.; Bolstad, G.H.; Voje, K.L.; Houle, D.; Cassara, J.; Rouzic, A.L.; Hansen, T.F. Evolution of morphological allometry. Ann. N. Y. Acad. Sci. 2014, 1320, 58–75. [Google Scholar] [CrossRef]
  41. Gould, S.J. Ontogeny and Phylogeny; Harvard University Press: Cambridge, MA, USA, 1977. [Google Scholar]
  42. Klingenberg, C.P. Size, shape, and form: Concepts of allometry in geometric morphometrics. Dev. Genes Evol. 2016, 226, 113–137. [Google Scholar] [CrossRef]
  43. Ding, H.; Fang, Y.; Yang, X.; Yuan, F.; He, L.; Yao, J.; Wu, J.; Chi, B.; Li, Y.; Chen, S.; et al. Community characteristics of a subtropical evergreen broad-leaved forest in Huangshan, Anhui Province, East China. Biodivers. Sci. 2016, 24, 875. [Google Scholar] [CrossRef]
  44. Chen, S.; Xie, L.; Zhou, W.; Chen, H.; Xu, X.; Jiang, S.; Zang, M.; Peng, Y.; Chen, X.; Duan, Y.; et al. Species diversity has a positive interrelationship with aboveground biomass and a mismatch with productivity in a subtropical broadleaf forest on the Wuyi Mountains, China. Diversity 2022, 14, 952. [Google Scholar] [CrossRef]
  45. Xie, L.; Chen, H.; Wei, L.; Chen, S.; Wang, L.; Xu, B.; Yi, X.; Wang, X.; Ding, H.; Fang, Y. Scale-dependent effects of species diversity on aboveground biomass and productivity in a subtropical broadleaved forest on Mt. Huangshan. Ecol. Evol. 2023, 13, e9786. [Google Scholar] [CrossRef] [PubMed]
  46. Pu, Y.; Li, Z.; Wang, R.; Wang, S.; Hu, Y.; Zhang, L.; Kong, F.; Zhang, L.; Chen, J.; Li, H.; et al. Guidelines for Carbon Measurement and Monitoring Technologies in Economic Forests: T/CSF 012-2023; China Forestry Society: Beijing, China, 2023. [Google Scholar]
  47. Fu, X.; Zhang, Y.; Wang, X. Prediction of Forest Biomass Carbon Pools and Carbon Sequestration Potential in China by 2060. For. Sci. 2022, 58, 32–41. (In Chinese) [Google Scholar]
  48. Li, X. Relative Growth and Allocation of Common Understory Biomass in the Natural Secondary Forest of Mao’er Mountain. Master’s Thesis, Northeast Forestry University, Harbin, China, 2010. (In Chinese). [Google Scholar]
  49. Liu, G.; Fu, B.; Fang, J. Carbon Dynamics of Forests in China and Their Contribution to Global Carbon Balance. Acta Ecol. Sin. 2000, 20, 733–740. (In Chinese) [Google Scholar]
  50. Liu, J.; Ni, J. A Comparative Study on Modeling the General Biomass Relative Growth Equations for Major Tree Species in China. Quat. Res. 2021, 41, 1169–1180. (In Chinese) [Google Scholar]
  51. Ma, X.; Wang, Z. An Estimate of Forest Carbon Sequestration by Province in China. Sci. Bull. 2011, 56, 433–439. (In Chinese) [Google Scholar] [CrossRef]
  52. Wu, S.; Zhu, J.; He, Y. Guidelines for Carbon Stock Measurement in Forest Ecosystems: LY/T 2988—2018; National Forestry and Grassland Administration: Beijing, China, 2018. [Google Scholar]
  53. Yuan, W.; Jiang, B.; Ge, Y.; Zhu, J.; Shen, A. Study on Biomass Models of Key Public Welfare Forests in Zhejiang Province. Zhejiang For. Sci. Technol. 2009, 29, 1–5. (In Chinese) [Google Scholar]
  54. Abdul-Hamid, H.; Mohamad-Ismail, F.N.; Mohamed, J.; Samdin, Z.; Abiri, R.; Tuan-Ibrahim, T.M.; Mohammad, L.S.; Jalil, A.M.; Naji, H.R. Aboveground biomass estimation of mixed mature mangrove forest. Forests 2022, 13, 325. [Google Scholar] [CrossRef]
  55. Abich, A.; Mucheye, T.; Tebikew, M.; Gebremariam, Y.; Alemu, A. Species-specific allometric equations for improving aboveground biomass estimates of dry deciduous woodland ecosystems. J. For. Res. 2019, 30, 1619–1632. [Google Scholar] [CrossRef]
  56. Altanzagas, B.; Luo, Y.; Altansukh, B.; Dorjsuren, C.; Fang, J.; Hu, H. Allometric Equations for Estimating the Above-Ground Biomass of Five Forest Tree Species in Khangai, Mongolia. Forests 2019, 10, 661. [Google Scholar] [CrossRef]
  57. Ameztegui, A.; Rodrigues, M.; Granda, V. Uncertainty of biomass stocks in Spanish forests: A comprehensive comparison of allometric equations. Eur. J. For. Res. 2022, 141, 395–407. [Google Scholar] [CrossRef]
  58. Basuki, T.M.; Leksono, B.; Baral, H.; Andini, S.; Wahyuni, N.S.; Artati, Y.; Choi, E.; Shin, S.; Kim, R.; Yang, A.; et al. Allometric equations for the biomass estimation of Calophyllum inophyllum L. in Java, Indonesia. Forests 2022, 13, 1057. [Google Scholar] [CrossRef]
  59. Bond-Lamberty, B.; Wang, C.; Gower, S.T. Aboveground and belowground biomass and sapwood area allometric equations for six boreal tree species of northern Manitoba. Can. J. For. Res. 2002, 32, 1441–1450. [Google Scholar] [CrossRef]
  60. Cao, L.; Zhang, Z.; Yun, T.; Wang, G.; Ruan, H.; She, G. Estimating tree volume distributions in subtropical forests using airborne LiDAR data. Remote Sens 2019, 11, 97. [Google Scholar] [CrossRef]
  61. Chambers, J.Q.; Dos Santos, J.; Ribeiro, R.J.; Higuchi, N. Tree damage, allometric relationships, and aboveground net primary production in central Amazon forest. For. Ecol. Manag. 2001, 152, 73–84. [Google Scholar] [CrossRef]
  62. Chave, J.; Riéra, B.; Dubois, M.A. Estimation of biomass in a neotropical forest of French Guiana: Spatial and temporal variability. J. Trop. Ecol. 2001, 17, 79–96. [Google Scholar] [CrossRef]
  63. Chave, J.; Condit, R.; Lao, S.; Caspersen, J.P.; Foster, R.B.; Hubbell, S.P. Spatial and temporal variation of biomass in a tropical forest: Results from a large census plot in Panama. J. Ecol. 2003, 91, 240–252. [Google Scholar] [CrossRef]
  64. Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
  65. Chave, J.; Ejou-Mechain, M.; Burquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2015, 20, 3177–3190. [Google Scholar] [CrossRef]
  66. Chen, J.; Fang, X.; Wu, A.; Xiang, W.; Lei, P.; Ouyang, S. Allometric equations for estimating biomass of natural shrubs and young trees of subtropical forests. New Forests 2023, 55, 15–46. [Google Scholar] [CrossRef]
  67. Cushman, K.C.; Muller-Landau, H.C.; Condit, R.S.; Hubbell, S.P. Improving estimates of biomass change in buttressed trees using tree taper models. Methods Ecol. Evol. 2014, 5, 573–582. [Google Scholar] [CrossRef]
  68. Daryaei, A.; Sohrabi, H.; Puerta-Piñero, C. How does light availability afect the aboveground biomass allocation and leaf morphology of saplings in temperate mixed deciduous forests? New For. 2019, 50, 409–422. [Google Scholar] [CrossRef]
  69. Dickinson, Y.; Zenner, E.K. Allometric Equations for the aboveground biomass of selected common eastern hardwood understory species. North. J. Appl. For. 2010, 27, 160–165. [Google Scholar] [CrossRef]
  70. Djomo, A.N.; Ibrahima, A.; Saborowski, J.; Gravenhorst, G. Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa. For. Ecol. Manag. 2010, 260, 1873–1885. [Google Scholar] [CrossRef]
  71. Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
  72. Fang, J.; Guo, Z.; Hu, H.; Kato, T.; Muraoka, H.; Son, Y. Forest biomass carbon sinks in east Asia, with special reference to the relative contributions of forest expansion and forest growth. Glob. Change Biol. 2014, 20, 2019–2030. [Google Scholar] [CrossRef]
  73. Fang, Y.; Leung, L.R.; Koven, C.D.; Bisht, G.; Detto, M.; Cheng, Y.; McDowell, N.; Muller-Landau, H.; Wright, S.J.; Chambers, J.Q. Modeling the topographic influence on aboveground biomass using a coupled model of hillslope hydrology and ecosystem dynamics. Geosci. Model Dev. 2022, 15, 7879–7901. [Google Scholar] [CrossRef]
  74. Feyisa, K.; Beyene, S.; Megersa, B.; Said, M.Y.; Angassa, A. Allometric equations for predicting above-ground biomass of selected woody species to estimate carbon in East African rangelands. Agroforest Syst. 2018, 92, 599–621. [Google Scholar] [CrossRef]
  75. Fayolle, A.; Doucet, J.L.; Gillet, J.F.; Bourland, N.; Lejeune, P. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. For. Ecol. Manag. 2013, 305, 29–37. [Google Scholar] [CrossRef]
  76. He, A.; McDermid, G.J.; Rahman, M.M.; Strack, M.; Saraswati, S.; Xu, B. Developing allometric equations for estimating shrub biomass in a boreal fen. Forests 2018, 9, 569. [Google Scholar] [CrossRef]
  77. Henry, M.; Picard, N.; Trotta, C.; Manlay, R.; Valentini, R.; Bernoux, M.; Saint André, L. Estimating tree biomass of sub-saharan african forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef]
  78. Henry, M.; Bombelli, A.; Trotta, C.; Alessandrini, A.; Birigazzi, L.; Sola, G.; Vieilledent, G.; Santenoise, P.; Longuetaud, F.; Valentini, R.; et al. GlobAllomeTree: International platform for tree allometric equations to support volume, biomass and carbon assessment. iForest 2013, 6, 326–330. [Google Scholar] [CrossRef]
  79. Hughes, R.F.; Kauffman, J.B.; Jaramillo, V.J. Biomass, carbon, and nutrient dynamics of secondary forests in a humid tropical region of México. Ecology 1999, 80, 1897–1907. [Google Scholar]
  80. Huy, B.; Kralicek, K.; Poudel, K.P.; Phuong, V.T.; Van Khoa, P.; Hung, N.D.; Temesgen, H. Allometric equations for estimating tree aboveground biomass in evergreen broadleaf forests of Viet Nam. For. Ecol. Manag. 2016, 382, 193–205. [Google Scholar] [CrossRef]
  81. Ishihara, M.I.; Utsugi, H.; Tanouchi, H.; Aiba, M.; Kurokawa, H.; Onoda, Y.; Nagano, M.; Umehara, T.; Ando, M.; Miyata, R.; et al. Efficacy of generic allometric equations for estimating biomass: A test in Japanese natural forests. Ecol. Appl. 2015, 25, 1433–1446. [Google Scholar] [CrossRef]
  82. Jiang, J.; Lu, Y.C.; Wang, L.; Liu, X.; Cai, D.; Jia, H.; Ming, A.; Chen, B. Facilitation by tree species in variable retention harvesting for the restoration of monoculture plantations in Southern China. Trop. Conserv. Sci. 2019, 12, 1940082918824836. [Google Scholar] [CrossRef]
  83. Kalita, R.M.; Das, A.K.; Nath, A.J. Allometric equations for estimating above- and belowground biomass in Tea (Camellia sinensis (L.) O. Kuntze) agroforestry system of Barak Valley, Assam, northeast India. Biomass Bioenergy 2015, 83, 42–49. [Google Scholar] [CrossRef]
  84. Kenzo, T.; Furutani, R.; Hattori, D.; Kendawang, J.J.; Tanaka, S.; Sakurai, K.; Ninomiya, I. Allometric equations for accurate estimation of above-ground biomass in logged-over tropical rainforests in Sarawak, Malaysia. J. For. Res. 2009, 14, 365–372. [Google Scholar] [CrossRef]
  85. Kim, C.; Baek, G.; Yoo, B.O.; Jung, S.Y.; Lee, K.S.; An, K.W. Comparison of allometric equations and biomass expansion factors for six evergreen broad-leaved trees in subtropical forests in southern Korea. J. Sustain. For. 2019, 38, 199–212. [Google Scholar] [CrossRef]
  86. Kora, S.H.; Guendehou, G.S.; Assogbadjo, A.E.; Sinsin, B.; Goussanou, C.A. Allometric equations from a non-destructive approach for biomass prediction in natural forest and plantation in West Africa. South. For. A J. For. Sci. 2019, 81, 111–122. [Google Scholar] [CrossRef]
  87. Lin, K.; Lyu, M.; Jiang, M.; Chen, Y.; Li, Y.; Chen, G.; Xie, J.; Yang, Y. Improved allometric equations for estimating biomass of the three Castanopsis carlesii H. forest types in subtropical China. New For. 2017, 48, 115–135. [Google Scholar] [CrossRef]
  88. Liu, B.; Bu, W.; Zang, R. Improved allometric models to estimate the aboveground biomass of younger secondary tropical forests. Glob. Ecol. Conserv. 2023, 41, e02359. [Google Scholar] [CrossRef]
  89. Lu, J.; Feng, Z.; Zhu, Y. Estimation of forest biomass and carbon storage in china based on forest resources inventory data. Forests 2019, 10, 650. [Google Scholar] [CrossRef]
  90. Mahmood, H.; Siddique, M.R.H.; Akhter, M. A critical review and database of biomass and volume allometric equation for trees and shrubs of Bangladesh. IOP Conf. Ser. Earth Environ. Sci 2016, 39, 012057. [Google Scholar] [CrossRef]
  91. Martínez-Sánchez, J.L.; Martínez-Garza, C.; Cámara, L.; Castillo, O. Species-specific or generic allometric equations:which optionis better when estimating the biomass of Mexican tropical humid forests? Carbon Manag. 2020, 11, 241–249. [Google Scholar] [CrossRef]
  92. Mascaro, J.; Asner, G.P.; Muller-Landau, H.C.; van Breugel, M.; Hall, J.; Dahlin, K. Controls over aboveground forest carbon density on Barro Colorado Island, Panama. Biogeosciences 2011, 8, 1615–1629. [Google Scholar] [CrossRef]
  93. Meng, S.; Liu, Q.; Zhou, G.; Jia, Q.; Zhuang, H.; Zhou, H. Aboveground tree additive biomass equations for two dominant deciduous tree species in Daxing’anling, northernmost China. J. For. Res. 2017, 22, 233–240. [Google Scholar] [CrossRef]
  94. Mensah, S.; Veldtman, R.; Seifert, T. Allometric models for height and aboveground biomass of dominant tree species in South African Mistbelt forests. South. For. A J. For. Sci. 2017, 79, 19–30. [Google Scholar] [CrossRef]
  95. Ouyang, S.; Xiang, W.; Wang, X.; Zeng, Y.; Lei, P.; Deng, X.; Peng, C. Significant effects of biodiversity on forest biomass during the succession of subtropical forest in south China. For. Ecol. Manag. 2016, 372, 291–302. [Google Scholar] [CrossRef]
  96. Ouyang, S.; Xiang, W.; Wang, X.; Xiao, W.; Chen, L.; Li, S.; Sun, H.; Deng, X.; Forrester, D.I.; Zeng, L.; et al. Effects of stand age, richness and density on productivity in subtropical forests in China. J. Ecol. 2019, 107, 2266–2277. [Google Scholar] [CrossRef]
  97. Carreras Pereira, K.A.; Wolf, A.A.; Kou-Giesbrecht, S.; Akana, P.R.; Funk, J.L.; Meng, D.N.L. Allometric relationships for eight species of 4–5 year old nitrogen-fixing and non-fixing trees. PLoS ONE 2023, 18, e0289679. [Google Scholar] [CrossRef]
  98. Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
  99. Réjou-Méchain, M.; Cornu, G.; Pere, A.; Tanguy, A.; Piponiot, C.; Herault, B.; Chave, J.; Feldpausch, T.; Verley, P. Biomass: An R package for estimating above-ground biomass and its uncertainty in tropical forests. Methods Ecol. Evol. 2017, 8, 1163–1167. [Google Scholar] [CrossRef]
  100. Ren, S.; Yang, Q.; Liu, H.; Shen, H.; Zheng, Z.; Zhou, S.; Liang, M.; Yin, H.; Zhou, Z.; Wang, X. The driving factors of subtropical mature forest productivity: Stand structure matters. Forests 2021, 12, 998. [Google Scholar] [CrossRef]
  101. Rojas-García, F.; De Jong, B.H.J.; Martínez-Zurimendí, P.; Paz-pellat, F. Database of 478 allometric equations to estimate biomass for Mexican trees and forests. Ann. For. Sci. 2015, 72, 835–864. [Google Scholar] [CrossRef]
  102. Romero, F.M.B.; Jacovine, L.A.G.; Ribeiro, S.C.; Ribeiro, S.C.; Torres, C.M.M.E.; Silva, L.F.D.; Gaspar, R.D.O.; Silva Soares da Rocha, S.J.; Staydhammer, C.L.; Fearnside, P.M. Allometric equations for volume, biomass, and carbon in commercial stems harvested in a managed forest in the southwestern amazon: A case study. Forests 2021, 11, 874. [Google Scholar] [CrossRef]
  103. Ruiz-Peinado, R.; del Rio, M.; Montero, G. New models for estimating the carbon sink capacity of Spanish softwood species. For. Syst. 2011, 20, 176–188. [Google Scholar] [CrossRef]
  104. Ruiz-Peinado, R.; Montero, G.; del Rio, M. Biomass models to estimate carbon stocks for hardwood tree species. Forest Systems 2012, 21, 42–52. [Google Scholar] [CrossRef]
  105. Satdichanh, M.; Ma, H.; Yan, K.; Dossa, G.G.O.; Winowiecki, L.; Vagen, T.G.; Gassner, A.; Xu, J.; Harrison, R. Phylogenetic diversity correlated with above-ground biomass production during forest succession: Evidence from tropical forests in Southeast Asia. J. Ecol. 2019, 107, 1419–1432. [Google Scholar] [CrossRef]
  106. Schmidt, A.; Poulain, M.; Klein, D.; Krause, K.; Peña-Rojaset, K.; Schmidt, H.; Schulte, A. Allometric above-belowground biomass equations for Nothofagus pumilio (Poepp. & Endl.) natural regeneration in the Chilean Patagonia. Ann. For. Sci. 2009, 66, 513. [Google Scholar] [CrossRef]
  107. Singh, V.; Tewari, A.; Kushwaha, S.P.S.; Dadhwal, V.K. Formulating allometric equations for estimating biomass and carbon stock in small diameter trees. For. Ecol. Manag. 2011, 261, 1945–1949. [Google Scholar] [CrossRef]
  108. Smith, A.R.; Lukac, M.; Hood, R.; Healey, J.R.; Miglietta, F.; Godbold, D.L. Elevated CO2 enrichment induces a differential biomass response in a mixed species temperate forest plantation. New Phytol. 2013, 198, 156–168. [Google Scholar] [CrossRef] [PubMed]
  109. Sun, H.; Wang, X.; Wu, P.; Han, W.; Xu, K.; Liang, P.; Liu, C.; Yin, W.; Xia, X. What causes greater deviations from predictions of metabolic scaling theory in earlier successional forests? For. Ecol. Manag. 2017, 405, 101–111. [Google Scholar] [CrossRef]
  110. Tang, X.; Fehrmann, L.; Guan, F.; Forrester, D.I.; Guisasola, R.; Pérez-Cruzado, C.; Vor, T.; Lu, Y.; Álvarez-González, J.G.; Kleinn, C. A generalized algebraic difference approach allows an improved estimation of aboveground biomass dynamics of Cunninghamia lanceolata and Castanopsis sclerophylla forests. Ann. For. Sci. 2017, 74, 12. [Google Scholar] [CrossRef]
  111. Tang, X.; Zhao, X.; Bai, Y.; Tang, Z.; Wang, W.; Zhao, Y.; Wan, H.; Xie, Z.; Shi, X.; Wu, B.; et al. Carbon pools in China’s terrestrial ecosystems: New estimates based on an intensive field survey. Proc. Natl. Acad. Sci. USA 2018, 115, 4021–4026. [Google Scholar] [CrossRef]
  112. Tiwari, R.M.; Liu, J.; Xie, Y.; Yao, S.H.; Liu, S.L.; Wu, S.M.; Liu, J.L.; Qian, H.Y.; Lei, Z.P.; Zhang, H.W.; et al. Decoupling the impact of biodiversity and environmental factors on the biomass and biomass growth of trees in subtropical forests. J. Plant Ecol. 2023, 16, rtac040. [Google Scholar] [CrossRef]
  113. Vargas-Larreta, B.; López-Sánchez, C.A.; Corral-Rivas, J.J.; López-Martínez, J.O.; Aguirre-Calderón, C.G.; Álvarez-González, J.G. Allometric equations for estimating biomass and carbon stocks in the temperate forests of North-Western Mexico. Forests 2017, 8, 269. [Google Scholar] [CrossRef]
  114. Wang, G.; Xie, B.; Lv, Y.; Yin, J.; Zhou, Y.; Xu, L.; Shi, Y. Interaction effect of stand age and diversity on aboveground wood carbon accumulation in subtropical mixed forests of the Zhejiang Province (China). Forests 2023, 14, 262. [Google Scholar] [CrossRef]
  115. Wang, X.; Fang, J.; Tang, Z.; Zhu, B. Climatic control of primary forest structure and DBH-height allometry in Northeast China. For. Ecol. Manag. 2006, 234, 264–274. [Google Scholar] [CrossRef]
  116. Xiang, W.; Zhou, J.; Ouyang, S.; Zhang, S.; Lei, P.; Li, J.; Deng, X.; Fang, X.; Forrester, D.I. Species-specific and general allometric equations for estimating tree biomass components of subtropical forests in southern China. Eur. J. For. Res. 2016, 135, 963–979. [Google Scholar] [CrossRef]
  117. Xing, D.; Bergeron, J.A.C.; Solarik, K.A.; Tom, M.B.; Macdonald, S.E.; Spence, J.R.; He, F. Challenges in estimating forest biomass: Use of allometric equations for three boreal tree species. Can. J. For. Res 2019, 49, 1613–1622. [Google Scholar] [CrossRef]
  118. Yang, H.; Wang, Z.; Tan, H.; Gao, Y. Allometric models for estimating shrub biomass in desert grassland in northern China. Rid Land Res. Manag. 2017, 31, 283–300. [Google Scholar] [CrossRef]
  119. Yang, T.; Song, K.; Da, L.; Li, X.; Wu, J. The biomass and aboveground net primary productivity of Schima superba–Castanopsis carlesii forests in east China. Sci. China Life Sci. 2010, 53, 811–821. [Google Scholar] [CrossRef] [PubMed]
  120. Roy, A.D.; Das, S.K.; Debnath, B. A non-destructive approach to develop tree-level allometric equations for estimating aboveground biomass in the forests of Tripura, Northeast India. Trop. Ecol. 2023, 64, 532–542. [Google Scholar]
  121. Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Jugo, I.; Steven, J.; Simon, L.L.; Regis, B.M.; Nathan, G.S.; Michael, C.W.; Jerome, C. Data from: Towards a worldwide wood economics spectrum. Dryad 2009. [Google Scholar] [CrossRef]
  122. Zeng, H.; Liu, Q.; Feng, Z.; Ma, Q. Biomass equations for four shrub species in subtropical China. J. For. Res. 2010, 15, 83–90. [Google Scholar] [CrossRef]
  123. Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Aboveground biomass allometric models for evergreen broad-leaved forest damaged by a serious ice storm in Southern China. Forests 2020, 11, 320. [Google Scholar] [CrossRef]
  124. Zubair, M.; Yasin, G.; Qazlbash, S.K.; Haq, A.U.; Jamil, A.; Yaseen, M.; Rahman, S.U.; Guo, W. Carbon Sequestration by Native Tree Species around the Industrial Areas of Southern Punjab, Pakistan. Land 2022, 11, 1577. [Google Scholar] [CrossRef]
  125. Li, F.; Qian, H.; Sardans, J.; Amishev, D.; Wang, Z.; Zhang, C.; Wu, T.; Tao, X.; Huang, X. Evolutionary history shapes variation of wood density of tree species across the world. Plant Divers. 2024, 46, 283–293. [Google Scholar] [CrossRef]
  126. Zuo, S.Z.; Ren, Y.; Weng, X.; Ding, H.; Luo, Y. Biomass relative growth models of 9 common tree species in subtropical evergreen broad-leaved forests. J. Appl. Ecol. 2015, 26, 356. (In Chinese) [Google Scholar]
  127. Luo, Y.; Wang, X.; Ouyang, Z.; Lu, F.; Feng, L.; Tao, J. A review of biomass equations for China’s tree species. Earth Syst. Sci. Data 2020, 12, 21–40. [Google Scholar] [CrossRef]
  128. Hulshof, C.M.; Swenson, N.G.; Weiser, M.D. Tree height–diameter allometry across the United States. Ecol. Evol. 2015, 5, 1193–1204. [Google Scholar] [CrossRef] [PubMed]
  129. Husáková, I.; Weiner, J.; Münzbergová, Z. Species traits and shoot-root biomass allocation in 20 dry-grassland species. J. Plant Ecol. 2018, 11, 273–285. [Google Scholar] [CrossRef]
  130. Niklas, K.J.; Enquist, B.J. Invariant scaling relationships for interspecific plant biomass production rates and body size. Proc. Natl. Acad. Sci. 2001, 98, 2922–2927. [Google Scholar] [CrossRef]
  131. Meng, S. Species-specific and generalized allometric biomass models for eight Fagaceae species in the understory of evergreen broadleaved forests in subtropical China. J. For. Res. 2024, 35, 69. [Google Scholar] [CrossRef]
  132. Meng, S.; Zhou, G.; Liu, W.; Yu, J.; Zhou, H.; Liu, Q. Species-specific and generalized allometric equations for improving aboveground biomass estimations of 33 understory woody species in northeastern China forest ecosystems. Can. J. For. Res. 2023, 54, 524–542. [Google Scholar] [CrossRef]
  133. Ran, F.; Chang, R.; Yang, Y.; Zhu, W.; Luo, J.; Wang, G. Allometric equations of select tree species of the Tibetan Plateau, China. J. Mt. Sci. 2017, 14, 1889–1902. [Google Scholar] [CrossRef]
  134. Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
  135. Barthélémy, D.; Caraglio, Y. Plant architecture: A dynamic, multilevel and comprehensive approach to plant form, structure and ontogeny. Ann. Bot. 2007, 99, 375–407. [Google Scholar] [CrossRef] [PubMed]
  136. Feng, L.; De Reffye, P.; Dreyfus, P.; Auclair, D. Connecting an architectural plant model to a forest stand dynamics model-application to Austrian black pine stand visualization. Ann. For. Sci. 2012, 69, 245–255. [Google Scholar] [CrossRef]
  137. Petrone-Mendoza, E.; Vergara-Silva, F.; Olson, M.E. Plant morpho evo-devo. Trends Plant Sci. 2023, 28, 1257–1276. [Google Scholar] [CrossRef]
  138. Tondjo, K.; Brancheriau, L.; Sabatier, S.; Kokutse, A.D.; Kokou, K.; Jaeger, M.; De Reffye, P.; Fourcaud, T. Stochastic modelling of tree architecture and biomass allocation: Application to teak (Tectona grandis L. f.), a tree species with polycyclic growth and leaf neoformation. Ann. Bot. 2018, 121, 1397–1410. [Google Scholar] [CrossRef] [PubMed]
  139. Iida, Y.; Poorter, L.; Sterck, F.J.; Kassim, A.R.; Kubo, T.; Potts, M.D.; Kohyama, T.S. Wood density explains architectural differentiation across 145 co-occurring tropical tree species. Funct. Ecol. 2012, 26, 274–282. [Google Scholar] [CrossRef]
  140. Loubota Panzou, G.J.; Ligot, G.; Gourlet-Fleury, S.; Doucet, J.L.; Forni, E.; Loumeto, J.J.; Fayolle, A. Architectural differences associated with functional traits among 45 coexisting tree species in Central Africa. Funct. Ecol. 2018, 32, 2583–2593. [Google Scholar] [CrossRef]
  141. Noyer, E.; Ningre, F.; Dlouhá, J.; Fournier, M.; Collet, C. Time shifts in height and diameter growth allocation in understory European beech (Fagus sylvatica L.) following canopy release. Trees 2019, 33, 333–344. [Google Scholar] [CrossRef]
  142. Xu, Z.; Du, W.; Zhou, G.; Qin, L.; Meng, S.; Yu, J.; Sun, Z.; SiQing, B.; Liu, Q. Aboveground biomass allocation and additive allometric models of fifteen tree species in northeast China based on improved investigation methods. For. Ecol. Manag. 2022, 505, 119918. [Google Scholar] [CrossRef]
  143. Pretzsch, H.; Dauber, E.; Biber, P. Species-specific and ontogeny-related stem allometry of European forest trees: Evidence from extensive stem analyses. For. Sci. 2013, 59, 290–302. [Google Scholar] [CrossRef]
  144. Niklas, K.J. Size-dependent allometry of tree height, diameter and trunk-taper. Ann. Bot. 1995, 75, 217–227. [Google Scholar] [CrossRef]
  145. Weiner, J. Allocation, plasticity and allometry in plants. Perspectives in Plant Ecology. Evol. Syst. 2004, 6, 207–215. [Google Scholar]
  146. Picard, N.; Rutishauser, E.; Ploton, P.; Ngomanda, A.; Henry, M. Should tree biomass allometry be restricted to power models? For. Ecol. Manag. 2015, 353, 156–163. [Google Scholar] [CrossRef]
  147. Huber, J.A.; May, K.; Hülsbergen, K.J. Allometric tree biomass models of various species grown in short-rotation agroforestry systems. Eur. J. For. Res. 2017, 136, 75–89. [Google Scholar] [CrossRef]
  148. Chmura, D.J.; Guzicka, M.; Rożkowski, R.; Chałupka, W. Allometry varies among related families of Norway spruce. Ann. For. Sci. 2017, 74, 36. [Google Scholar] [CrossRef]
  149. Baumert, S.; Khamzina, A. Allometric relations in Jatropha curcas production systems of Burkina Faso. J. Arid Environ. 2015, 120, 95–104. [Google Scholar] [CrossRef]
  150. Manuri, S.; Brack, C.; Noor’an, F.; Rusolono, T.; Anggraini, S.M.; Dotzauer, H.; Kumara, I. Improved allometric equations for tree aboveground biomass estimation in tropical dipterocarp forests of Kalimantan, Indonesia. For. Ecosyst. 2016, 3, 28. [Google Scholar] [CrossRef]
  151. Zhao, F.; Guo, Q.; Kelly, M. Allometric equation choice impacts lidar-based forest biomass estimates: A case study from the Sierra National Forest, CA. Agric. For. Meteorol. 2012, 165, 64–72. [Google Scholar] [CrossRef]
  152. Gonzalez-Akre, E.; Piponiot, C.; Lepore, M.; Herrmann, V.; Lutz, J.A.; Baltzer, J.L.; Dick, C.W.; Gilbert, G.S.; He, F.; Heym, M.; et al. allodb: An R package for biomass estimation at globally distributed extratropical forest plots. Methods Ecol. Evol. 2022, 13, 330–338. [Google Scholar] [CrossRef]
  153. Adhikari, D.; Singh, P.P.; Tiwary, R.; Barik, S.K. Forest carbon stock-based bioeconomy: Mixed models improve accuracy of tree biomass estimates. Biomass Bioenergy 2024, 183, 107142. [Google Scholar] [CrossRef]
  154. Davies, T.J.; Regetz, J.; Wolkovich, E.M.; McGill, B.J. Phylogenetically weighted regression: A method for modelling non-stationarity on evolutionary trees. Glob. Ecol. Biogeogr. 2019, 28, 275–285. [Google Scholar] [CrossRef]
  155. Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
  156. Litton, C.M.; Boone Kauffman, J. Allometric models for predicting aboveground biomass in two widespread woody plants in Hawaii. Biotropica 2008, 40, 313–320. [Google Scholar] [CrossRef]
  157. Adhikari, B.S.; Rawat, Y.S.; Singh, S.P. Structure and function of high altitude forests of central Himalaya I. Dry matter dynamics. Ann. Bot. 1995, 75, 237–248. [Google Scholar] [CrossRef]
  158. BK, R.B.; Sharma, R.P.; Bhandari, S.K. A generalized aboveground biomass model for juvenile individuals of Rhododendron arboreum (SM.) in Nepal. Cerne 2019, 25, 119–130. [Google Scholar]
  159. Elzein, T.M.; Blarquez, O.; Gauthier, O.; Carcaillet, C. Allometric equations for biomass assessment of subalpine dwarf shrubs. Alp. Bot. 2011, 121, 129–134. [Google Scholar] [CrossRef]
  160. Zhang, Q.; Li, J.; Xu, W.; Xiong, G.; Xie, Z. Estimation of biomass allocation and carbon density of Rhododendron simsii shrubland in the subtropical mountainous areas of China. Chin. J. Plant Ecol. 2017, 41, 43. [Google Scholar]
  161. Sun, X.; Wang, X.; Wang, C.; Zhang, Q.; Guo, Q. Filling the “vertical gap” between canopy tree species and understory shrub species: Biomass allometric equations for subcanopy tree species. J. For. Res. 2023, 34, 903–913. [Google Scholar] [CrossRef]
  162. López-Martínez, J.O.; Vargas-Larreta, B.; González, E.J.; Corral-Rivas, J.J.; Aguirre-Calderón, O.A.; Treviño-Garza, E.J.; De los Santos-Posadas, H.M.; Martínez-Salvador, M.; Zamudio-Sánchez, F.J.; Aguirre-Calderón, C.G. Forest Biometric Systems in Mexico: A Systematic Review of Available Models. Forests 2022, 13, 649. [Google Scholar] [CrossRef]
  163. Dutcă, I.; Mather, R.; Ioraş, F. Tree biomass allometry during the early growth of Norway spruce (Picea abies) varies between pure stands and mixtures with European beech (Fagus sylvatica). Can. J. For. Res. 2018, 48, 77–84. [Google Scholar] [CrossRef]
  164. Cudjoe, E.; Bravo, F.; Ruiz-Peinado, R. Allometry and biomass dynamics in temperate mixed and monospecific stands: Contrasting response of Scots pine (Pinus sylvestris L.) and sessile oak (Quercus petraea (Matt.) Liebl.). Sci. Total Environ. 2024, 953, 176061. [Google Scholar] [CrossRef]
  165. Dutcă, I.; Mather, R.; Blujdea, V.N.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-effects on biomass allometric models for early growth plantations of Norway spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
  166. Fortier, J.; Truax, B.; Gagnon, D.; Lambert, F. Allometric equations for estimating compartment biomass and stem volume in mature hybrid poplars: General or site-specific? Forests 2017, 8, 309. [Google Scholar] [CrossRef]
  167. Fu, L.; Lei, X.; Hu, Z.; Zeng, W.; Tang, S.; Marshall, P.; Cao, L.; Song, X.; Yu, L.; Liang, J. Integrating regional climate change into allometric equations for estimating tree aboveground biomass of Masson pine in China. Ann. For. Sci. 2017, 74, 42. [Google Scholar] [CrossRef]
  168. Xu, K.; Jiang, J.; He, F. Climate-based allometric biomass equations for five major Canadian timber species. Can. J. For. Res. 2021, 51, 1633–1642. [Google Scholar] [CrossRef]
Diversity 17 00493 g001
Figure 1. Topographic map of Mt. Wuyishan dynamics plot.
Figure 1. Topographic map of Mt. Wuyishan dynamics plot.
Diversity 17 00493 g001
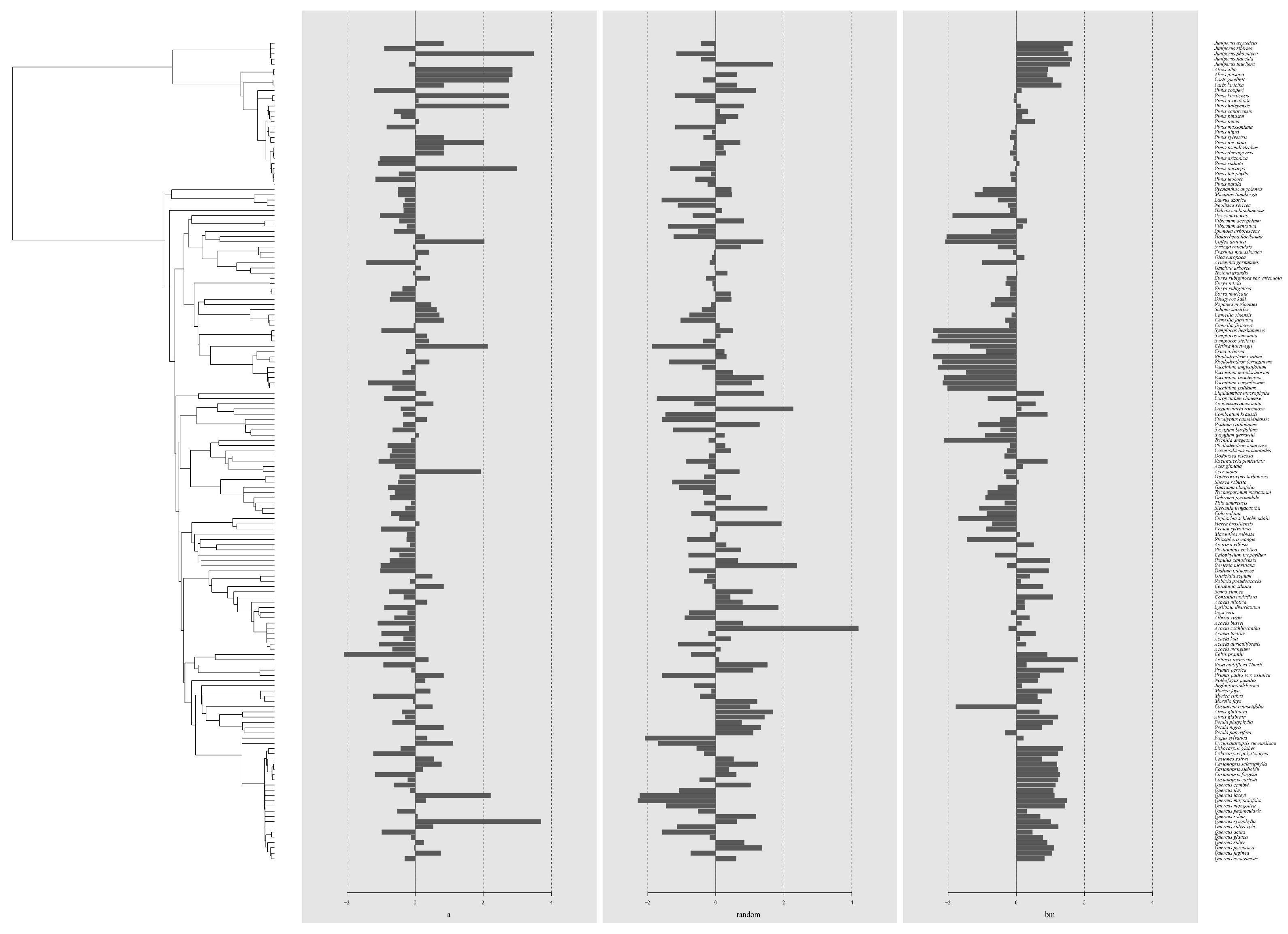
Diversity 17 00493 g002
Figure 2. Phylogenetic tree of the studied 157 species.
Figure 2. Phylogenetic tree of the studied 157 species.
Diversity 17 00493 g002
Diversity 17 00493 g003
Figure 3. AGB error distribution by family.
Figure 3. AGB error distribution by family.
Diversity 17 00493 g003
Diversity 17 00493 g004
Figure 4. AGB distribution across DBH classes. Note: a and b represent the DBH classes that show significant differences in the t-test.
Figure 4. AGB distribution across DBH classes. Note: a and b represent the DBH classes that show significant differences in the t-test.
Diversity 17 00493 g004
Table 1. Statistical results of allometric coefficient analysis across species groups (a, random, bm).
Table 1. Statistical results of allometric coefficient analysis across species groups (a, random, bm).
GroupC meanIKK.starλ
a0.1106 *0.0764 **0.04270.04710.1249 **
(p = 0.024)(p = 0.002)(p = 0.621)(p = 0.749)(p = 0.003)
random−0.0317−0.00640.04700.05760.00007
(p = 0.674)(p = 0.477)(p = 0.475)(p = 0.476)(p = 1.000)
bm0.5201 **0.2709 **0.6239 **0.6012 **1.0010 **
(p = 0.001)(p = 0.001)(p = 0.001)(p = 0.001)(p = 0.001)
Note: Values represent estimated parameters and associated p-values. Significant results are bolded with asterisks (*: p < 0.05, **: p < 0.01). C mean: Mean effect size of covariates; K: Kruskal–Wallis statistic for median comparisons; K.star: Adjusted K-value; λ: Regularization parameter; a: Empirical dataset; bm: Brownian motion model; random: Random null model.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shang, Y.; Xia, Y.; Ran, X.; Zheng, X.; Ding, H.; Fang, Y. Allometric Equations for Aboveground Biomass Estimation in Natural Forest Trees: Generalized or Species-Specific? Diversity 2025, 17, 493. https://doi.org/10.3390/d17070493

AMA Style

Shang Y, Xia Y, Ran X, Zheng X, Ding H, Fang Y. Allometric Equations for Aboveground Biomass Estimation in Natural Forest Trees: Generalized or Species-Specific? Diversity. 2025; 17(7):493. https://doi.org/10.3390/d17070493

Chicago/Turabian Style

Shang, Yuxin, Yutong Xia, Xiaodie Ran, Xiao Zheng, Hui Ding, and Yanming Fang. 2025. "Allometric Equations for Aboveground Biomass Estimation in Natural Forest Trees: Generalized or Species-Specific?" Diversity 17, no. 7: 493. https://doi.org/10.3390/d17070493

APA Style

Shang, Y., Xia, Y., Ran, X., Zheng, X., Ding, H., & Fang, Y. (2025). Allometric Equations for Aboveground Biomass Estimation in Natural Forest Trees: Generalized or Species-Specific? Diversity, 17(7), 493. https://doi.org/10.3390/d17070493

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop