Can a Non-Destructive Method Predict the Leaf Area of Species in the Caatinga Biome?

Abstract

Understanding the leaf area is essential in plant physiology and ecological studies, as it directly influences photosynthesis, transpiration and plant productivity. This study aimed to develop non-destructive allometric models to estimate the leaf area of three species from the Caatinga biome: Cynophalla flexuosa, Libidibia ferrea and Tabebuia aurea. A total of 1293 leaves were collected from these species, scanned, and analysed using ImageJ software to obtain their length, width, and actual leaf area. In addition, the product of length and width was calculated. Linear, power and exponential regression models were used. The best equations were chosen based on the coefficient of determination, Pearson’s linear correlation coefficient, Willmott’s agreement index, mean squared error, root mean squared error, mean absolute error and mean absolute percentage error. The best equations for all species were constructed using linear and power models, which were indicated for accurate prediction of leaf area. These findings confirm the efficiency of allometric equations as a non-destructive method for predicting leaf area, providing an accessible and economical alternative for ecological studies in semi-arid environments.

1. Introduction

Leaves perform vital functions for plants, acting in light interception, carbon fixation, gas exchange and water regulation. These functions make leaf area an indispensable parameter in studies of plant physiology and ecology [1]. Throughout evolution, leaves have developed various shapes and sizes as an adaptive strategy to cope with different environmental conditions [2,3]. This diversity directly reflects on photosynthetic efficiency, water use, and plant productivity, highlighting the importance of investigating leaf area to understand the performance of species [4,5].

Leaf area can be determined by direct methods, such as measuring with graph paper or digital gauges, and by indirect methods, which use mathematical models based on linear measurements of leaves [6]. Although direct methods are accurate, they have disadvantages such as the need to destroy leaves, making repeated analyses in the same growth cycle unfeasible [7]. Indirect methods based on allometric models emerge as practical and economical alternatives, allowing non-destructive and successive measurements throughout the development of the plant, in addition to presenting high accuracy in estimates [8]. Allometric models eliminate expensive equipment [9].

Allometric models that use variables such as the length (L) and width (W) of leaves or the product of these dimensions (LW) have been widely used in the estimation of leaf area (LA) of several species. Salazar et al. [7] demonstrated the efficacy of using the LW product to estimate LA in Theobroma cacao. Similar methods have been successfully applied in species such as Eustoma grandiflorum [10] and Manilkara zapota [11], Dendranthema grandiflora [12], and Euterpe oleracea [13], reinforcing their efficiency in different morphological contexts.

Species such as Cynophalla flexuosa, Libidibia ferrea, and Tabebuia aurea offer unique opportunities to study physiological and ecological adaptations to adverse conditions, such as high salinity and water scarcity, characteristic of the Brazilian semi-arid region. The variation in leaf dimensions across these species is advantageous, as it enhances data representativeness and supports the development of robust allometric models that account for different phenological stages and environmental conditions [14].

Cynophalla flexuosa (L.) J. Presl is a shrub-tree species native to Brazil, widely distributed in different ecosystems, from the Atlantic coastal vegetation to the semi-arid regions of the Caatinga [15]. Belonging to the Capparaceae family, this species has significant ecological and economic relevance, being used as forage, for wood production, for soil recovery and in folk medicine [15,16]. With a height of up to 4 m, C. flexuosa is tolerant to different types of soil and climate, being recognized as a perennial species, and is also used as a source of renewable energy [17]. Libidibia ferrea (Mart. ex Tul.) L.P. Queiroz is a tree species native to Brazil found predominantly in the North and Northeast regions [18]. Valued by indigenous, traditional and urban communities, its wood is widely used; in addition, it is often cultivated as an ornamental tree in Brazil and in tropical regions and has antibacterial and anti-inflammatory activities, in addition to being used in the treatment of parasitic diseases such as leishmaniasis [19]. Traditional communities also use it in folk medicine and religious rituals [20].

Tabebuia aurea (Silva Manso) Benth. & Hook. f. ex S. Moore is a tree species widely distributed in the tropical and subtropical regions of the Americas [21]. This species native to Brazil occurs in all biomes of the country, including the Pantanal, Atlantic Forest, Cerrado, Amazon, and Caatinga [22]. In the Brazilian semi-arid region, T. aurea is notable for its ornamental beauty and the shade provided by its broad canopy. Its drought tolerance makes it valuable for environmental restoration projects, while its durable, high-strength wood is widely used in urban and rural afforestation, civil construction, paper production, and carpentry [23]. Its leaves, bark, and roots are widely used in folk medicine, including anti-anemic, antipyretic, diuretic, vermifuge, and purgative actions, in addition to being used in the treatment of flu and inflammatory processes [24,25].

Studies carried out with Erythroxylum pauferrense [26] and Malus domestica [27] enabled the construction of equations with a high coefficient of determination. Including a large number of samples in studies is essential to reduce errors and increase the representativeness of models [14].

In addition, the equations allow successive analyses throughout the plant development cycle, which are valuable tools in studies of growth, ecology, and sustainable management [28,29]. These methods provide relevant information for management and conservation strategies for species of ecological and economic importance. Previous studies have shown that non-destructive methods are effective for estimating leaf area in tropical crops, promoting greater sustainability and efficiency in agricultural management [30]. However, many species native to or adapted to the semi-arid region still lack scientific approaches that explore their potential.

Given these species’ relevance to semi-arid ecosystems and their adaptability to severe environmental conditions, studies focused on leaf area estimation can help in understanding their ecology and in developing sustainable management practices. Non-destructive allometric methods allow the evaluation of the impact of environmental factors and agricultural practices on the growth of these plants, contributing to their preservation and rational use [5].

These non-destructive models seek to improve foliar analysis techniques, providing valuable tools for agronomic and ecological studies. In addition, this type of work emphasizes the relevance of efficient and accessible methods for the sustainable management of these species in semi-arid climate environments [27]. Therefore, this study aimed to develop allometric equations to estimate the leaf area of Cynophalla flexuosa, Libidibia ferrea, and Tabebuia aurea based on the linear dimensions of the leaves.

2. Materials and Methods

The study was carried out in August 2024 at the Center for Research in Plant Sciences of the Semi-Arid at the Federal Rural University of the Semi-Arid Region, located in the state of Rio Grande do Norte, municipality of Mossoró, Northeast Brazil (5°12′22″ S, 37°19′13″ W, altitude of 21 m). The region has a hot and dry climate, characterized by an arid season and rainfall concentrated in the summer, classified as BSh (hinterland climate) [31]. The average annual rainfall is 555 mm, while the average annual air temperature is around 27.8 °C. The predominant soil in the area is classified as Eutrophic Red-Yellow Ultisol [32].

The samples were collected from mother trees, and healthy leaves and leaflets were selected, free of damage caused by pests and diseases or abiotic and biotic factors. Three hundred sixty-eight leaves of Cynophalla flexuosa, 718 leaflets of Libidibia ferrea, and 207 of Tabebuia aura were used. The leaves were collected from eight mother trees of each species. The number of collected leaves and leaflets varied among species due to differences in leaf morphology and availability in the sampled trees. The leaf samples were collected under similar environmental conditions to minimize external variability and ensure that the observed differences in leaf dimensions were primarily due to genetic and phenological factors rather than environmental influences. This approach enhances the reliability of the allometric models by reducing confounding variables. The samples were collected randomly to search for leaves of different sizes and shapes and to build models and accurate equations to predict the leaf area of these species. After collection, the samples were transported in plastic containers containing ice to prevent water loss through transpiration, seeking to mitigate dehydration. Subsequently, the leaves/leaflets were detached and digitized in a desktop scanner (HP Scanjet G2410, Palo Alto, CA, USA) at a maximum resolution of 600 × 600 dpi. The images were processed and contrasted using ImageJ software version 1.53e in the public domain. Then, the length (L, cm), corresponding to the distance between the insertion of the petiole and the point opposite the central vein, the width (W, cm), obtained as the most significant measurement perpendicular to the length vein (Figure 1), and the actual leaf/leaflet area (LA, cm²) were determined individually. These data were used to calculate the products between length and width (LW, cm²).

According to Equation (1) [33] and Equation (2) [34], the variance inflation factor (VIF) and the tolerance value (T) were calculated to evaluate the presence of multicollinearity in the data. The VIF quantifies how much the variance of a regression coefficient is inflated due to multicollinearity. At the same time, the tolerance value (T) is reciprocal, indicating how much of a variable’s variance is not explained by other predictors in the model. High VIF values (>10) or low T values (<0.1) suggest problematic multicollinearity. When VIF is less than 10 and T is greater than 0.1, length and width data can be used to estimate the area of leaflets using regression models [34].

$$\mathrm{V}\mathrm{I}\mathrm{F}={\displaystyle \frac{1}{1-{\mathrm{r}}^2}}$$

(1)

$$\mathrm{T}={\displaystyle \frac{1}{\mathrm{V}\mathrm{I}\mathrm{F}}}$$

(2)

where r represents the correlation coefficient between L and W.

Linear and nonlinear regression models were tested to estimate LA, considered a dependent variable, as a function of leaf dimensions (L, W, and LW) as independent variables. To construct the allometric equations, linear (ŷ = β₀ + β₁ × x), power (ŷ = β₀ × x^β1) and exponential (ŷ = β₀ × β₁^x) models were used, in which the values of ŷ represent the estimated leaf area, the values of the linear dimensions of the leaves x, and the regression coefficients β₀ and β₁.

The criteria adopted for selecting the best equation for predicting the leaf area of the three species were based on the highest coefficient of determination (R²), Pearson’s linear correlation coefficient (r), and Willmott agreement index (d), and lowest mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE). When VIF is less than 10 and T is greater than 0.1, length and width data can be used to estimate the area of leaflets using regression models [34].

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}{)}^2}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}({{\mathrm{y}}^{\prime }}_{\mathrm{i}}{)}^2}}$$

(3)

$$\mathrm{r}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}})}{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}}\right)}^2}}}$$

(4)

$$d=1-{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}({\widehat{\mathrm{y}}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}{)}^2}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}(\left|{{\hat{\mathrm{y}}}^{\prime }}_{\mathrm{i}}\right|+|{{\mathrm{y}}^{\prime }}_{\mathrm{i}}|{)}^2}}$$

(5)

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}(\widehat{\mathrm{y}}\mathrm{i}-\mathrm{y}\mathrm{i}{)}^2}{\mathrm{n}}}$$

(6)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}(\widehat{\mathrm{y}}\mathrm{i}-\mathrm{y}\mathrm{i}{)}^2}{\mathrm{n}}}}$$

(7)

$$\mathrm{MAE}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}\right|}{\mathrm{n}}}$$

(8)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{100}{\mathrm{n}}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left|{\displaystyle \frac{{\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}}{{\mathrm{y}}_{\mathrm{i}}}}\right|$$

(9)

where $\widehat{\mathrm{y}}\mathrm{i}$ is the estimated values of leaf area; ${\mathrm{y}}_{\mathrm{i}}$ is the observed values of leaf area; $\stackrel{-}{\mathrm{y}}\mathrm{i}$ is the average of observed values; ${\widehat{\mathrm{y}}}^{\prime }\mathrm{i}=\widehat{\mathrm{y}}\mathrm{i}-\stackrel{-}{\mathrm{y}};{\mathrm{y}}^{\prime }\mathrm{i}=\mathrm{y}\mathrm{i}-\stackrel{-}{\mathrm{y}}$; $\mathrm{n}$ is the total observation numbers; $\mathrm{x}\mathrm{i}$ and $\mathrm{y}\mathrm{i}$ are the i-th observations of the independent and dependent variables, respectively; $\stackrel{-}{\mathrm{y}}$ and $\stackrel{-}{\mathrm{x}}$ are averages of the variables y and x.

Initially, a descriptive data analysis was performed, including the minimum, maximum and mean values, total amplitude, asymmetry coefficient, kurtosis and coefficient of variation of the sampled parameters. The criteria adopted for selecting the best equation for predicting the leaf area of the three species were based on statistical performance metrics. The equation with the highest coefficient of determination (R²) and Pearson’s linear correlation coefficient (r) were preferred, indicating a strong relationship between predicted and observed values. The Willmott agreement index (d) was also considered to assess the model’s overall predictive accuracy. To ensure low prediction error, the equation with the lowest mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) was selected. The normality of the data was assessed using the Shapiro–Wilk test. The observed leaf area (actual) and the estimated area were compared using the Student’s t-test for paired samples (p ≤ 0.01). Data analysis was performed using R software (version 4.1.2) [35].

3. Results

The results of the descriptive analysis for the three species evaluated, Cynophalla flexuosa, Libidibia ferrea and Tabebuia aurea, highlight marked differences in leaf characteristics. For C. flexuosa, the length of the leaves varied between 3.482 and 9.690 cm, with an average of 7.303 cm and an amplitude of 6.208 cm, while the width varied from 2.199 to 6.168 cm, with an average of 4.457 cm and an amplitude of 3.969 cm. The product of length and width presented values between 8.545 and 59.768 cm², with a mean of 33.165 cm² and amplitude of 51.223 cm². The leaf area of this species ranged from 6.634 to 47.695 cm², with a mean of 25.754 cm² and a range of 41.061 cm² (

Table 1. Descriptive analysis of length (W), width (L), product of length and width (LW), and leaf area (LA) of Cynophalla flexuosa, Libidibia ferrea, and Tabebuia aurea.

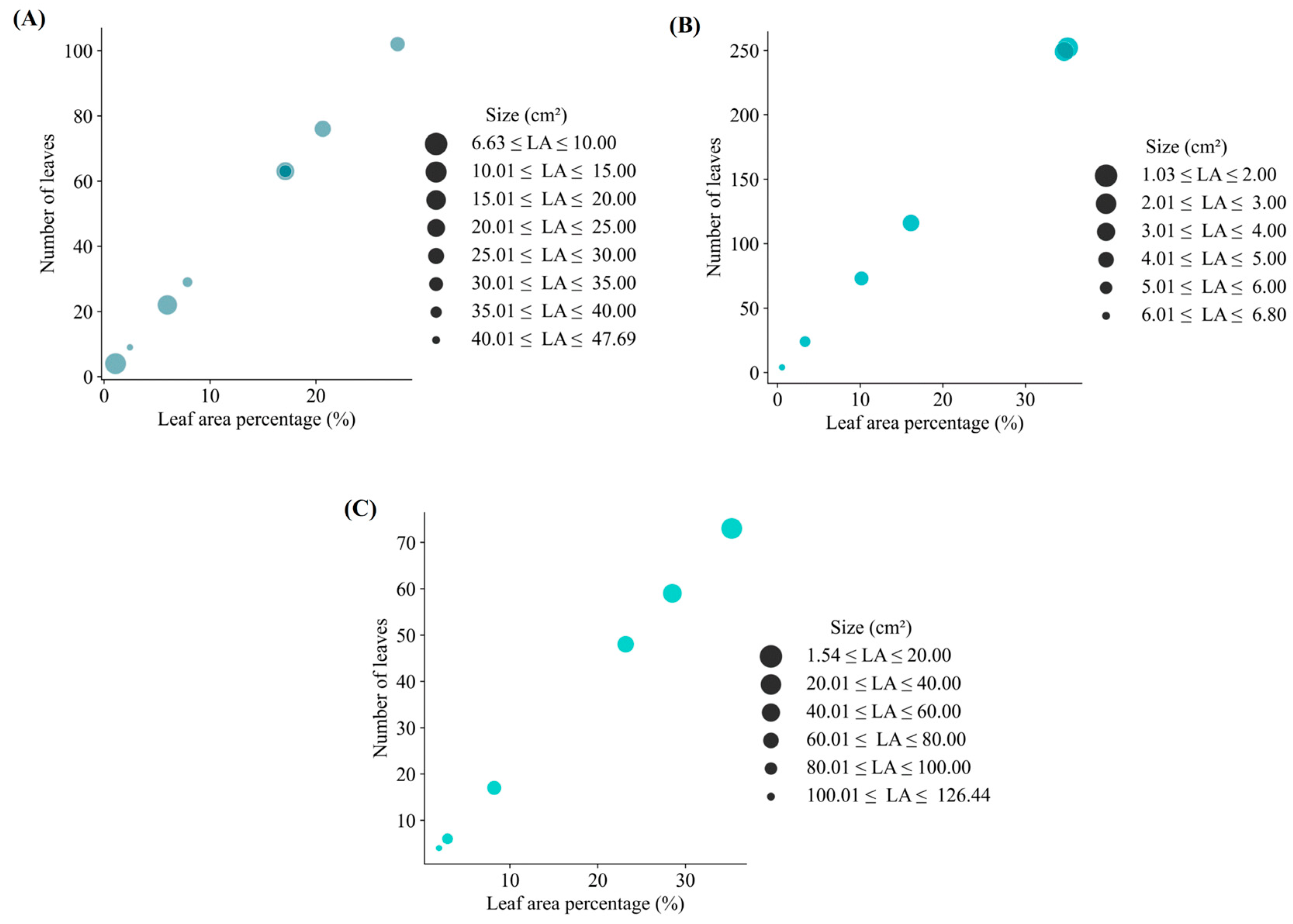
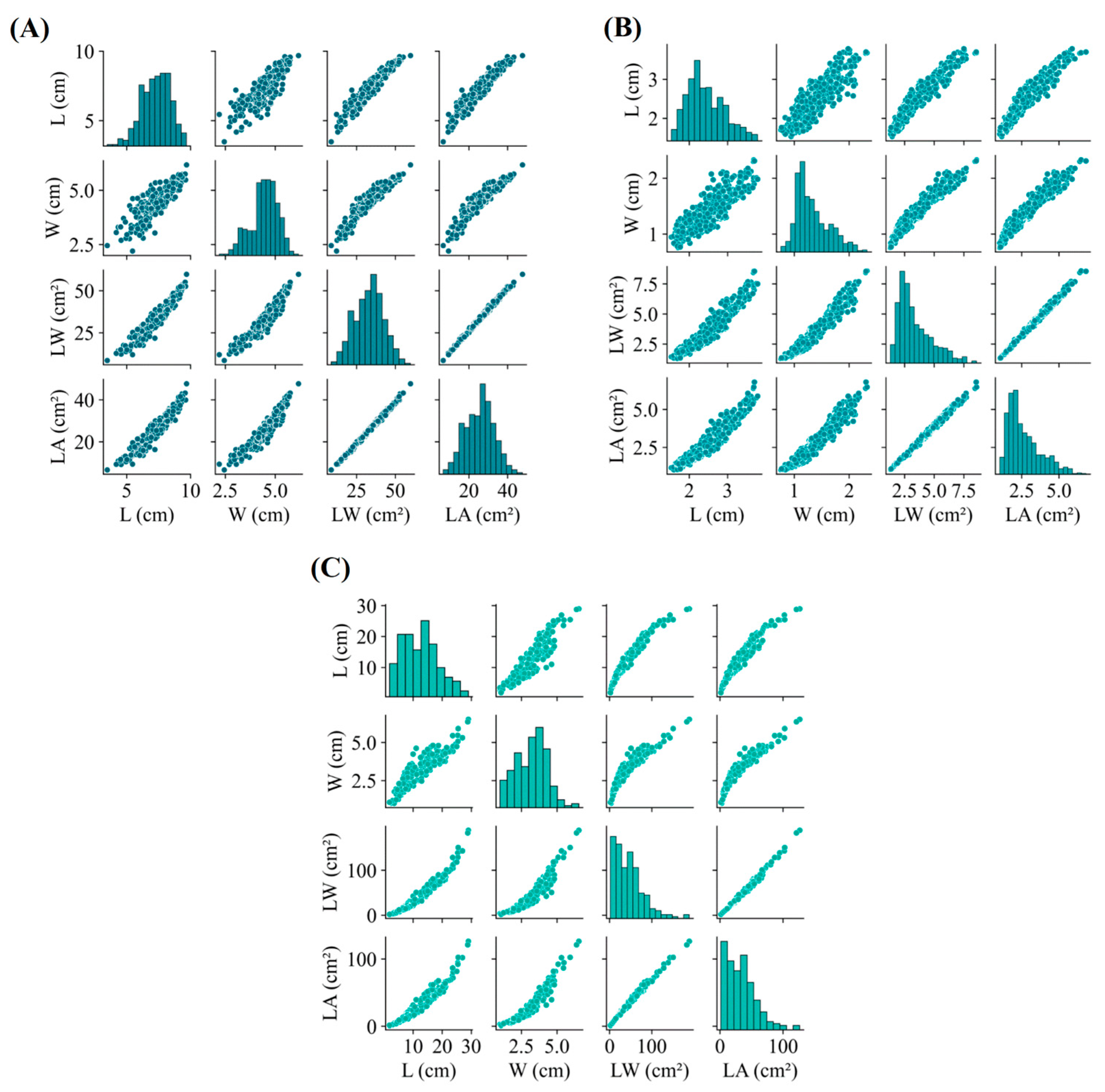
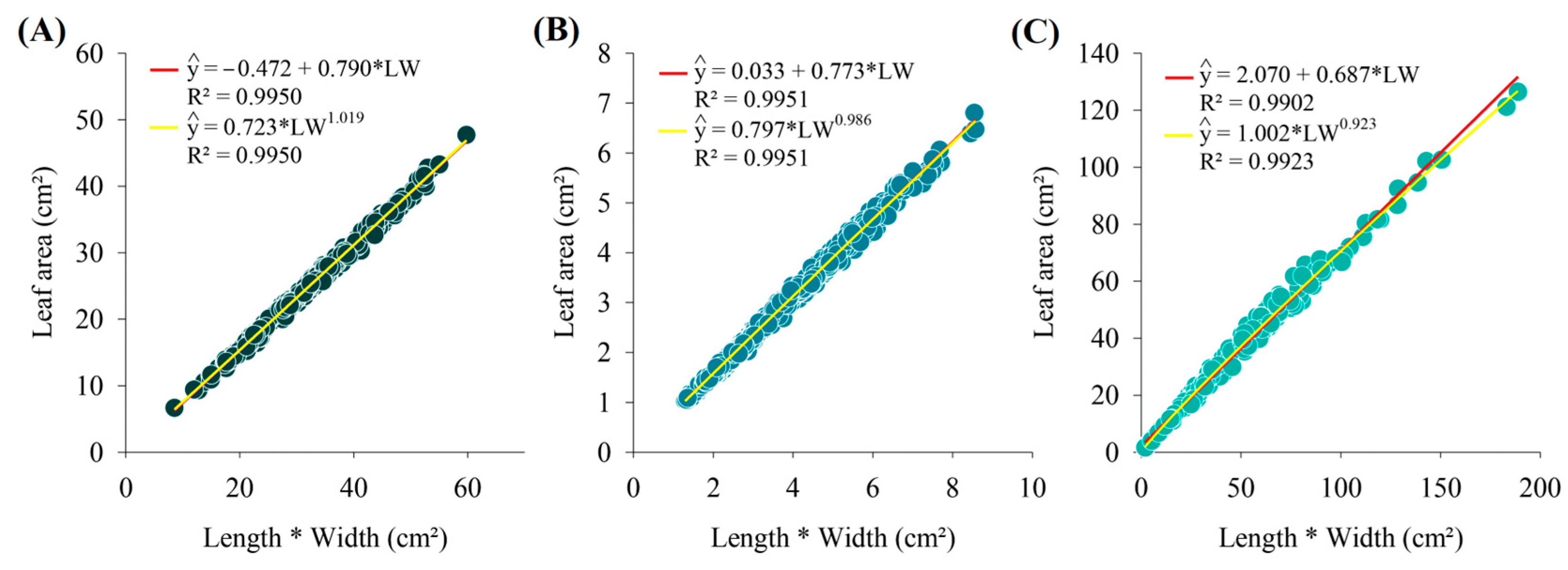
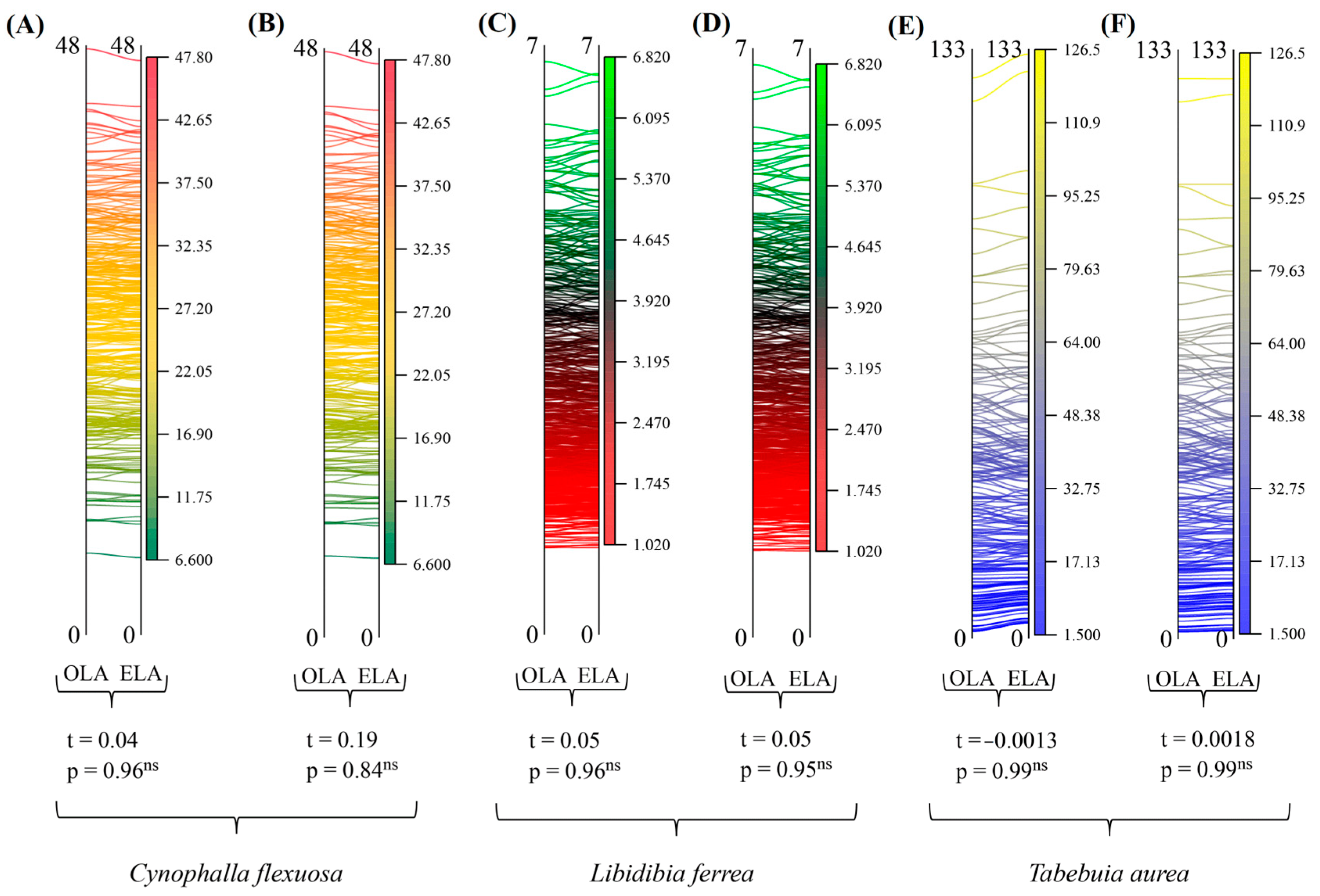
Descriptive Statistic	L	W	LW	LA
Cynophalla flexuosa
Minimum	3.482	2.199	8.545	6.634
Maximum	9.690	6.168	59.768	47.695
Amplitude	6.208	3.969	51.223	41.061
Mean	7.303	4.457	33.165	25.754
Standard deviation	1.098	0.678	9.227	7.315
Coefficient of variation	15.0	15.2	27.8	28.4
Asymmetry a	−0.381	−0.511	−0.012	0.006
Kurtosis + 3 b	2.939	2.965	2.596	2.629
Shapiro–Wilk	0.003 **	<0.0001 **	0.321 ns	0.384 ns
Libidibia ferrea
Minimum	1.534	0.756	1.289	1.030
Maximum	3.784	2.328	8.574	6.803
Amplitude	2.250	1.572	7.285	5.773
Mean	2.438	1.336	3.383	2.651
Standard deviation	0.479	0.298	1.421	1.102
Coefficient of variation	19.6	22.3	42.0	41.6
Asymmetry a	0.558	0.837	1.086	1.049
Kurtosis + 3 b	2.688	3.104	3.652	3.526
Shapiro–Wilk	<0.0001 **	<0.0001 **	<0.0001 **	<0.0001 **
Tabebuia aurea
Minimum	1.898	1.002	2.014	1.546
Maximum	28.967	6.518	188.807	126.440
Amplitude	27.069	5.516	186.793	124.894
Mean	12.468	3.180	45.602	33.396
Standard deviation	6.023	1.091	34.161	23.583
Coefficient of variation	48.3	34.3	74.9	70.6
Asymmetry a	0.360	0.060	1.246	1.027
Kurtosis + 3 b	2.596	2.841	5.160	4.392
Shapiro–Wilk	0.003 **	0.030 *	<0.0001 **	<0.0001 **

^a Asymmetry differs from zero by the t-test at 5% probability; ^b Kurtosis differs from three by the t-test at 5% probability; ** Significant at 1% probability; * Significant at 5% probability; ^ns Not significant.

).

The species T. aurea presented the highest values and the most significant variation. The length of the leaves varied widely between 1.898 and 28.967 cm, with an average of 12.468 cm and a width of 27.069 cm. The width varied between 1.002 and 6.518 cm, with a mean of 3.180 cm and a width of 5.516 cm. The product of length and width ranged from 2.014 to 188.807 cm², with a mean of 45.602 cm² and amplitude of 186.793 cm². The leaf area ranged from 1.546 to 126.440 cm², with a mean of 33.396 cm² and a range of 124.894 cm². Thus, it is noteworthy that T. aurea has the largest leaves with more significant variability in their dimensions, L. ferrea has the most minor and most uniform leaves, while C. flexuosa, in turn, has intermediate values with less dispersion of the data (Figure 2).

The linear and nonlinear association patterns between the independent and dependent variables were used to construct regression models that estimate the leaf area (LA) for C. flexuosa, L. ferrea and T. aurea (Figure 3). These results highlight the importance of using different approaches, linear and nonlinear, depending on the variables under analysis and the species studied, ensuring more robust regression models for leaf area estimation.

The results of the regression models to estimate the leaf area of the species C. flexuosa, L. ferrea and T. aurea highlight the efficiency of different equations as a function of leaf dimensions (

Table 2. Regression model, equations, coefficient of determination (R²), Pearson correlation coefficient (r), Willmott’s concordance index (d), mean squared error (MSE), root mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) obtained as a function of measurements of leaf dimensions of Cynophalla flexuosa, Libidibia ferrea, and Tabebuia aurea.

Equation Code	Model	R2	r	d	MSE	RMSE	MAE	MAPE	$\mathbf{Estimator} \mathbf{of} \mathbf{LA} (\widehat{\mathbf{y}}$)
Cynophalla flexuosa
1	Linear	0.8997	0.9485	0.9729	5.367	2.316	1.862	0.0914	$\widehat{\mathrm{y}}=-20.393+6.319\times \mathrm{L}$
2	Linear	0.9489	0.9005	0.9732	5.322	2.306	1.827	0.0844	$\widehat{\mathrm{y}}=-19.860+10.230\times \mathrm{W}$
3	Linear	0.9950	0.9975	0.9987	0.266	0.516	0.406	0.0164	$\widehat{\mathrm{y}}=-0.472+0.790\times \mathrm{L}\mathrm{W}$
4	Power	0.9108	0.9544	0.9763	4.769	2.184	1.751	0.0758	$\widehat{\mathrm{y}}=0.591\times {\mathrm{L}}^{1.888}$
5	Power	0.9153	0.9567	0.9776	4.532	2.129	1.676	0.0712	$\widehat{\mathrm{y}}=1.477\times {\mathrm{W}}^{1.898}$
6	Power	0.9950	0.9975	0.9987	0.265	0.515	0.405	0.0163	$\widehat{\mathrm{y}}=0.723\times {\mathrm{L}\mathrm{W}}^{1.019}$
7	Exponential	0.9077	0.9527	0.9750	4.946	2.224	1.762	0.0764	$\widehat{\mathrm{y}}=3.903\times {1.288}^{\mathrm{L}}$
8	Exponential	0.9147	0.9564	0.9770	4.567	2.137	1.662	0.0688	$\widehat{\mathrm{y}}=3.808\times {1.522}^{\mathrm{W}}$
9	Exponential	0.9147	0.9564	0.9770	4.567	2.137	1.662	0.0688	$\widehat{\mathrm{y}}=9.480\times {1.095}^{\mathrm{L}\mathrm{W}}$
Libidibia ferrea
1	Linear	0.9146	0.9563	0.9772	0.103	0.322	0.250	0.1060	$\widehat{\mathrm{y}}=-2.715+2.201\times \mathrm{L}$
2	Linear	0.9315	0.9651	0.9819	0.083	0.288	0.220	0.0892	$\widehat{\mathrm{y}}=-2.123+3.573\times \mathrm{W}$
3	Linear	0.9951	0.9975	0.9987	0.005	0.077	0.058	0.0221	$\widehat{\mathrm{y}}=0.033+0.773\times \mathrm{L}\mathrm{W}$
4	Power	0.9314	0.9650	0.9820	0.083	0.288	0.216	0.0841	$\widehat{\mathrm{y}}=0.424\times {\mathrm{L}}^{2.011}$
5	Power	0.9331	0.9660	0.9822	0.081	0.285	0.216	0.0817	$\widehat{\mathrm{y}}=1.560\times {\mathrm{W}}^{1.727}$
6	Power	0.9951	0.9975	0.9987	0.005	0.076	0.058	0.0220	$\widehat{\mathrm{y}}=0.797\times {\mathrm{L}\mathrm{W}}^{0.986}$
7	Exponential	0.9254	0.9620	0.9799	0.090	0.301	0.219	0.0837	$\widehat{\mathrm{y}}=0.412\times {2.090}^{\mathrm{L}}$
8	Exponential	0.9113	0.9546	0.9753	0.108	0.329	0.256	0.0973	$\widehat{\mathrm{y}}=0.567\times {3.039}^{\mathrm{W}}$
9	Exponential	0.9113	0.9546	0.9753	0.108	0.329	0.256	0.0973	$\widehat{\mathrm{y}}=1.176\times {1.253}^{\mathrm{L}\mathrm{W}}$
Tabebuia aurea
1	Linear	0.9223	0.9603	0.9794	43.190	6.572	4.958	0.6849	$\widehat{\mathrm{y}}=-13.491+3.761\times \mathrm{L}$
2	Linear	0.8926	0.9447	0.9709	59.706	7.727	5.752	0.6037	$\widehat{\mathrm{y}}=-31.560+20.430\times \mathrm{W}$
3	Linear	0.9902	0.9950	0.9975	5.459	2.336	1.856	0.0877	$\widehat{\mathrm{y}}=2.070+0.687\times \mathrm{L}\mathrm{W}$
4	Power	0.9424	0.9708	0.9850	32.011	5.657	4.375	0.1460	$\widehat{\mathrm{y}}=0.675\times {\mathrm{L}}^{1.511}$
5	Power	0.9394	0.9692	0.9838	33.837	5.817	4.241	0.1497	$\widehat{\mathrm{y}}=2.562\times {\mathrm{W}}^{2.114}$
6	Power	0.9923	0.9961	0.9980	4.295	2.072	1.591	0.0594	$\widehat{\mathrm{y}}=1.002\times {\mathrm{L}\mathrm{W}}^{0.923}$
7	Exponential	0.9167	0.9574	0.9758	48.088	6.934	5.655	0.2393	$\widehat{\mathrm{y}}=9.280\times {1.096}^{\mathrm{L}}$
8	Exponential	0.8973	0.9472	0.9677	61.331	7.831	6.408	0.2431	$\widehat{\mathrm{y}}=6.159\times {1.641}^{\mathrm{W}}$
9	Exponential	0.8973	0.9472	0.9677	61.331	7.831	6.408	0.2431	$\widehat{\mathrm{y}}=18.671\times {1.012}^{\mathrm{L}\mathrm{W}}$

). The analyses were performed based on criteria such as coefficient of determination (R²), Pearson’s correlation coefficient (r), Willmott agreement index (d), mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE).

For C. flexuosa, the linear (ŷ = −0.472 + 0.790 × LW) and power (ŷ = 0.723 × LW^1.019) models were the most accurate, presenting R² of 0.9950, r of 0.9975, and d of 0.9987, indicating that approximately 99.5% of the variation in leaf area could be explained by the adjusted equations. The RMSE and MAE of these models were low (0.516 and 0.406 for the linear model and 0.515 and 0.405 for the power model), reinforcing the accuracy of the estimates. In the species L. ferrea, linear (ŷ = 0.033 + 0.773 × LW) and power (ŷ = 0.797 × LW^0.986) models also stood out, with R² of 0.9951, r of 0.9975 and d of 0.9987. The RMSE and MAE values were the lowest recorded (0.077 and 0.058 for the linear model and 0.076 and 0.058 for the power model), suggesting high reliability in the predictions of these equations.

For T. aurea, the linear (ŷ = 2.070 + 0.687 × LW) and power (ŷ = 1.002 × LW^0.923) models again showed better performance, with R² of 0.9902 and 0.9923, r of 0.995 and 0.9961, and d of 0.9975 and 0.998, respectively. The associated errors (RMSE and MAE) were significantly low (2.336 and 1.856 in the linear model and 2.072 and 1.591 in the power model), indicating high accuracy in the estimation of leaf area. Models based on linear equations without intercept (model 3) and power (model 6) were the most appropriate to estimate these species’ leaf area, regardless of their morphological differences.

Figure 4 shows the relationship between leaf area (LA) and the product of length and width (LW) for the species C. flexuosa, L. ferrea, and T. aurea. Visual analysis of the residuals’ dispersion and the application of the best models confirmed the accuracy of the adjusted equations.

For C. flexuosa, a well-defined positive relationship between LA and LW was observed, with low data dispersion and homogeneity of the residuals. The best models identified were the linear non-intercept and power models with R² values of 0.995, indicating that LW could explain 99.50% of the variation in LA. These models demonstrated high efficiency in predicting leaf area for this species. In the case of L. ferrea, the same models (linear without intercept and power) also showed a good fit, with a clear positive relationship between LA and LW. The residuals were homogeneous, and the dispersion was minimal, reinforcing the applicability of the proposed equations. The R² value was also high (0.9951), showing high explanatory capacity.

For T. aurea, the results showed similar behavior, with the linear non-intercept and power models providing the best fits. Despite the greater amplitude in the LW and LA values, the positive relationship between these variables was consistent. The R² values were slightly lower (0.9923 and 0.9902), but it still indicates that the variation in LA can be explained by the LW product. The linear non-intercept and power models demonstrated high applicability and precision in estimating LW leaf area (LA) from the three species studied. The data’s low dispersion and the residuals’ homogeneity validate the use of these models in practical applications and comparative studies.

The models chosen (linear and power) to estimate the leaf area (LA) of C. flexuosa, L. ferrea and T. aurea showed a high correlation with the observed LA values (R² close to 0.99, Figure 5). For C. flexuosa, the linear model (Figure 5A) showed a strong relationship between the observed leaf area (OLA) and the estimated leaf area (ELA), with a high coefficient of determination (R² = 0.9950), indicating that the model was highly effective for representing the relationship between the variables. The power model (Figure 5D) also showed a high correlation, with R² comparable to the linear model (R² = 0.9950), reinforcing its applicability.

In the analysis of L. ferrea, the linear (Figure 5B) and power (Figure 5E) regression models also showed excellent performance, with high R² (R² = 0.9951 and 0.9952, respectively) and consistency between estimates and observations. The data distribution along the regression curves demonstrated a reliable fit, validating the models as accurate options for this species. In turn, T. aurea showed similar results. The linear regression model (Figure 5C) showed a high relationship between the observed and estimated values of LA (R² = 0.9902), while the power regression model (Figure 5F) revealed a comparable adjustment capacity (R² = 0.9923). The linear and power models proved to be robust tools for estimating LA in the three species, with high precision and consistent correlation with the observed values.

The comparison between the observed leaf area (OLA) and the estimated leaf area (ELA) for the species C. flexuosa, L. ferrea and T. aurea demonstrated the high precision of the adjusted models (Figure 6). There were no significant differences between the observed and estimated values of leaf area in the selected models, confirming the similarity of the values and the significant relationships between the variables. Therefore, the results confirm that the models can be used with high accuracy to estimate the leaf area of these species, evidencing their applicability in agronomic and ecological studies.

4. Discussion

The high variability in the variables L, W, LW and LA (Table 1) reflects the diversity of shapes and sizes of the leaves of the species analyzed (C. flexuosa, L. ferrea and T. aurea). This variability is crucial for building reliable and accurate models and equations, as it covers small, medium, and large leaves, ensuring the representativeness of the models under different conditions [29]. This diversity allows the application of the models in leaves of different sizes and shapes, including different phenological stages of the plants [36,37].

The significant variability in leaf dimensions among the species analyzed reflects the survival strategies of native plants of the Brazilian semi-arid region, such as C. flexuosa, L. ferrea and T. aurea. This variability confers greater resilience under biotic and abiotic stress [38]. In addition, the diversity of leaf sizes and shapes contributes to obtaining representative and accurate models covering varied conditions [39,40]. The relationship between L, W, and LW proved to be fundamental for the constitution of leaf area (LA) since the size and shape of the leaves directly impact the active photosynthetic area and, consequently, the species’ photosynthetic capacity [41]. The linearity observed in the relationship between LW and LA confirms the applicability of the linear and nonlinear models, which is consistent with the results of Ribeiro et al. [26] in studies with E. pauferrense.

Leaf dimensions impact physiological processes, such as the exchange of heat, water vapor and carbon, as a function of the thickness of the boundary layer [42]. This relationship reinforces the need to include wide variability in the data [12] to ensure that the models generated are widely applicable. The large number of leaves collected (>200 per plant) was essential to ensure the representativeness of the models, corroborating studies such as those by Cargnelutti Filho et al. [28] and Montelatto et al. [43], which highlight the importance of extensive samples to avoid bias in allometric models. Collecting from different parts of the plants allows for capturing a wide range of leaf sizes, which contributes to constructing robust models applicable to various conditions.

The patterns of association between the variables L, W, LW and LA (Figure 3) require linear and nonlinear models to adjust and validate the leaf dimension data [44]. These parameters, therefore, are suitable for use in regression models [45]. This approach is essential to properly adjust the data and validate leaf area estimation models [11]. Analyzing the collinearity patterns between L and W reflects that these parameters can be used together in regression models. This validation is particularly relevant in research that seeks to estimate leaf area in a non-destructive way, providing greater efficiency and accuracy in obtaining data. The association patterns reinforce the complexity inherent in the estimation of leaf area, especially in species with significant variability in leaf dimensions. The choice of different regression models is crucial to ensure the validity and applicability of the results in various phenological conditions and stages [44,46,47].

Regression models based on the product of the length (L) and width (W) of the leaves (LW) are the most suitable for estimating the leaf area of the studied species (C. flexuosa, L. ferrea and T. aurea). These models presented the best-fit criteria, such as high coefficients of determination (R²), low variability of residuals, and high precision in the estimates, corroborating previous studies that point to the superiority of equations that use LW compared to those that consider only one leaf dimension [4,37,48].

Although it is possible to estimate LA using a single leaf dimension (L or W), this approach can reduce the accuracy of the models and underestimate the leaf area, as Santos et al. [49] discussed. Previous studies have also shown that equations using LW provide more excellent reliability and are widely applicable in different species, such as Crotalaria juncea [50], E. pauferrense [26], Chrysanthemum morifolium [45], Erythrina velutina [51], Phaseolus vulgaris [52], Psidium guajava [53], Dendranthema grandiflora [12], and Euterpe oleracea [13]. In the case of this study, the linear models without intercept and power were the best indicated, presenting R² values greater than 0.99 and a homogeneous distribution of the residuals, reinforcing their robustness.

The adequacy of the models was evaluated not only by the high R² values but also by the homoscedasticity of the residuals, which confirms the normality and accuracy of the estimates [13,30]. These criteria are key to validating regression models, ensuring they can be used confidently for future studies on the growth, development, and propagation of the species analyzed.

Power regression models, such as the one obtained in the present study, have also been widely recommended in research with other species, such as Manihot esculenta [54], Arachis hypogaea [55], and Chrysanthemum morifolium [45]. The high correlation between LW and LA reinforces that the product between L and W is an essential parameter for estimating leaf area accurately [3,29].

The results obtained in this study also corroborate the equations’ applicability to species from different habitats, such as the semi-arid climate, where leaf morphological variability is an important adaptive strategy. Choosing the most appropriate models not only improves the accuracy of estimates but also contributes to the conservation and sustainable management of native species [37,56,57].

5. Conclusions

This study developed allometric models to accurately estimate the leaf area of Cynophalla flexuosa, Libidibia ferrea and Tabebuia aurea based on non-destructive measurements (leaf dimensions). The relationships between actual leaf area and the product between leaf length and width demonstrate the reliability of these models, with equations obtained with the linear and power models providing greater accuracy across all species. The results highlight the practicality of these models for repeated measurements without damaging plants, making them valuable tools for physiological and ecological studies. Furthermore, the findings contribute to sustainable plant management strategies in semi-arid environments, where monitoring plant development is important.