Strong Philopatry, Isolation by Distance, and Local Habitat Have Promoted Genetic Structure in Heermann’s Gull
Abstract
1. Introduction
2. Materials and Methods
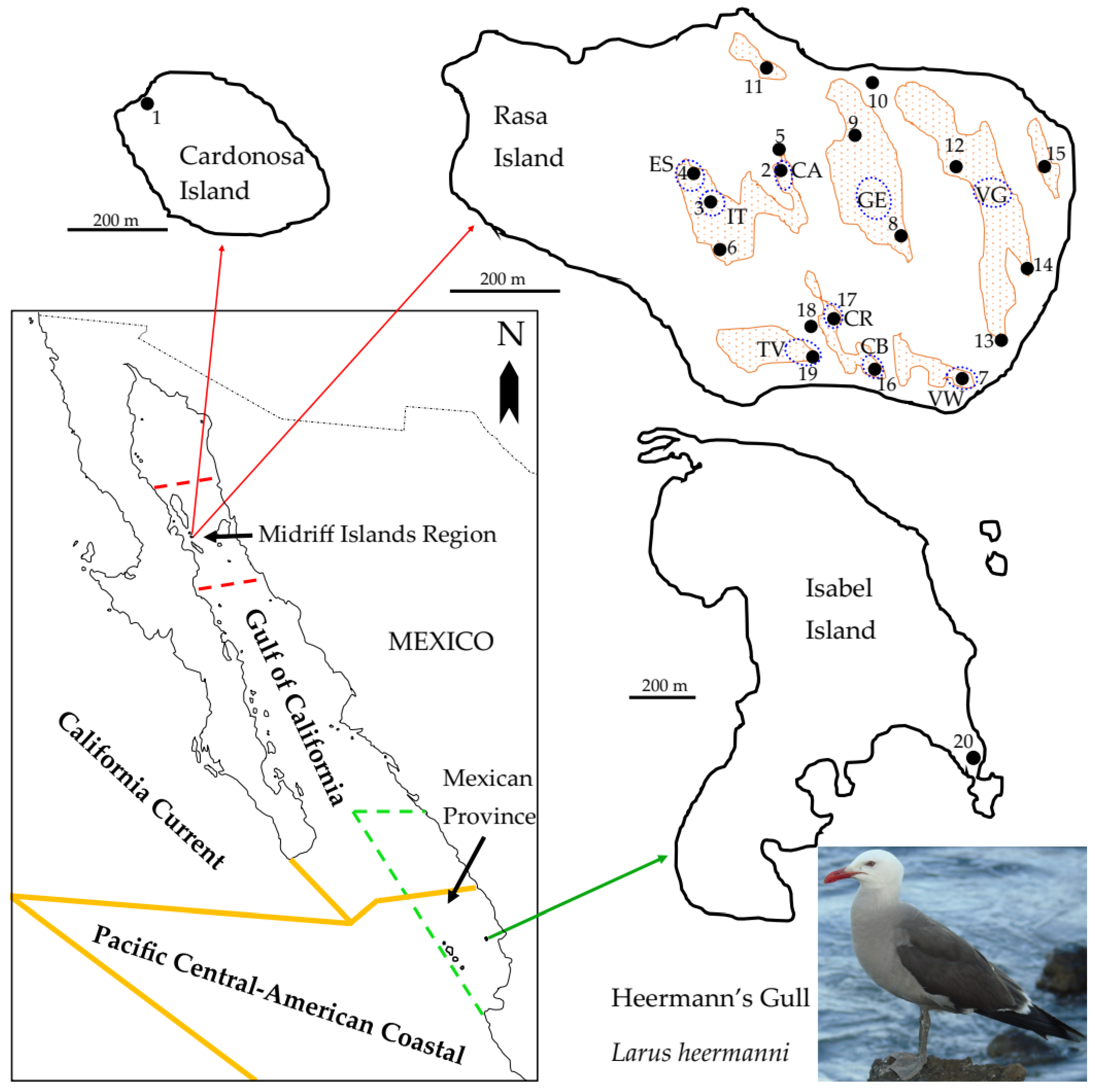
2.1. Study Area
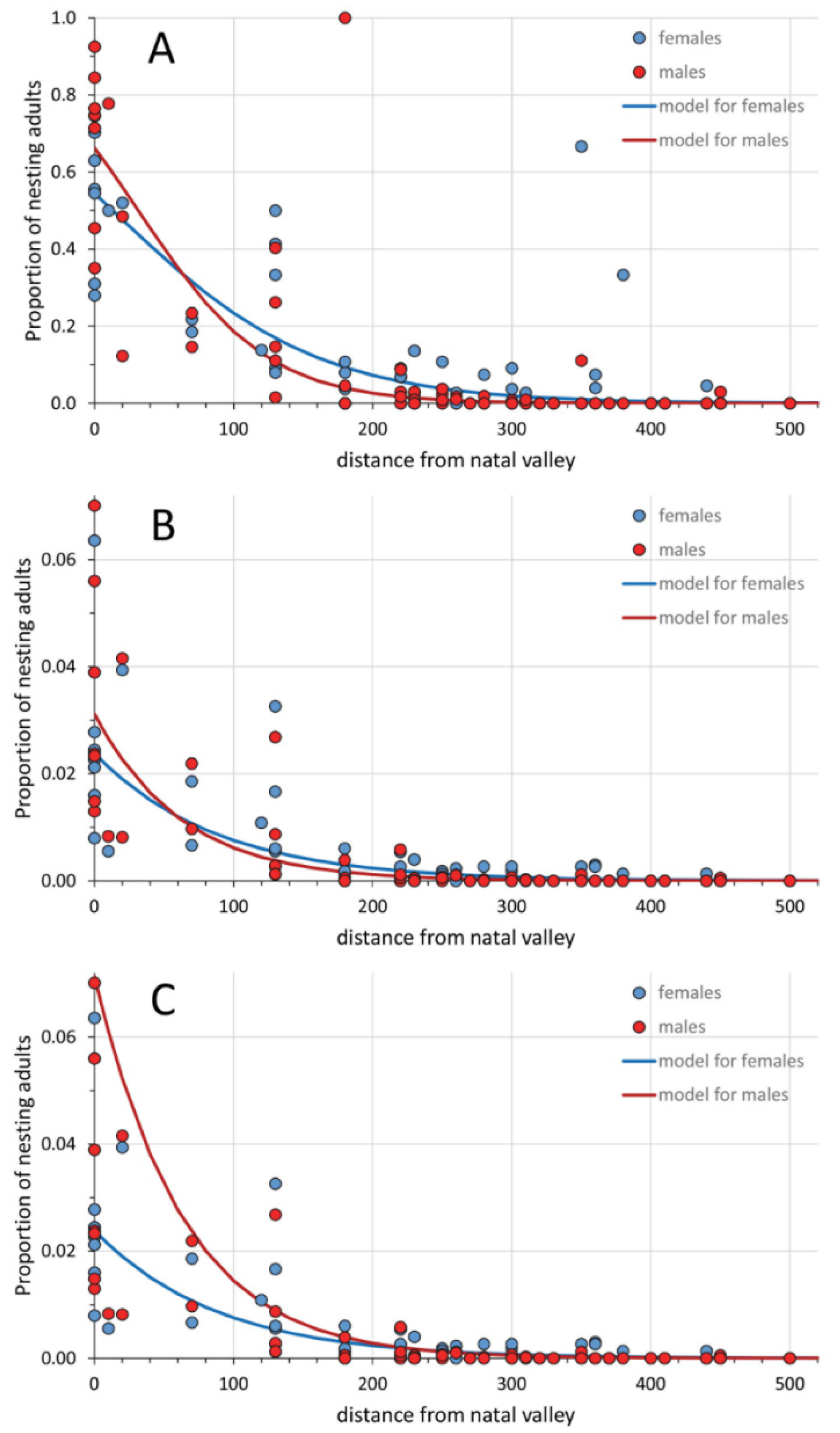
2.2. Analyses of Philopatry and Dispersal by Banding Data
2.3. DNA Extraction, PCR Amplification, Sequencing, and Analyses of Genetic Diversity
2.4. Genetic Differentiation
2.5. Genetic Structure
2.6. Gene Flow
2.7. Correlation of Genetic Differentiation with Geographic Distances
3. Results
3.1. Philopatry and Dispersal Behavior
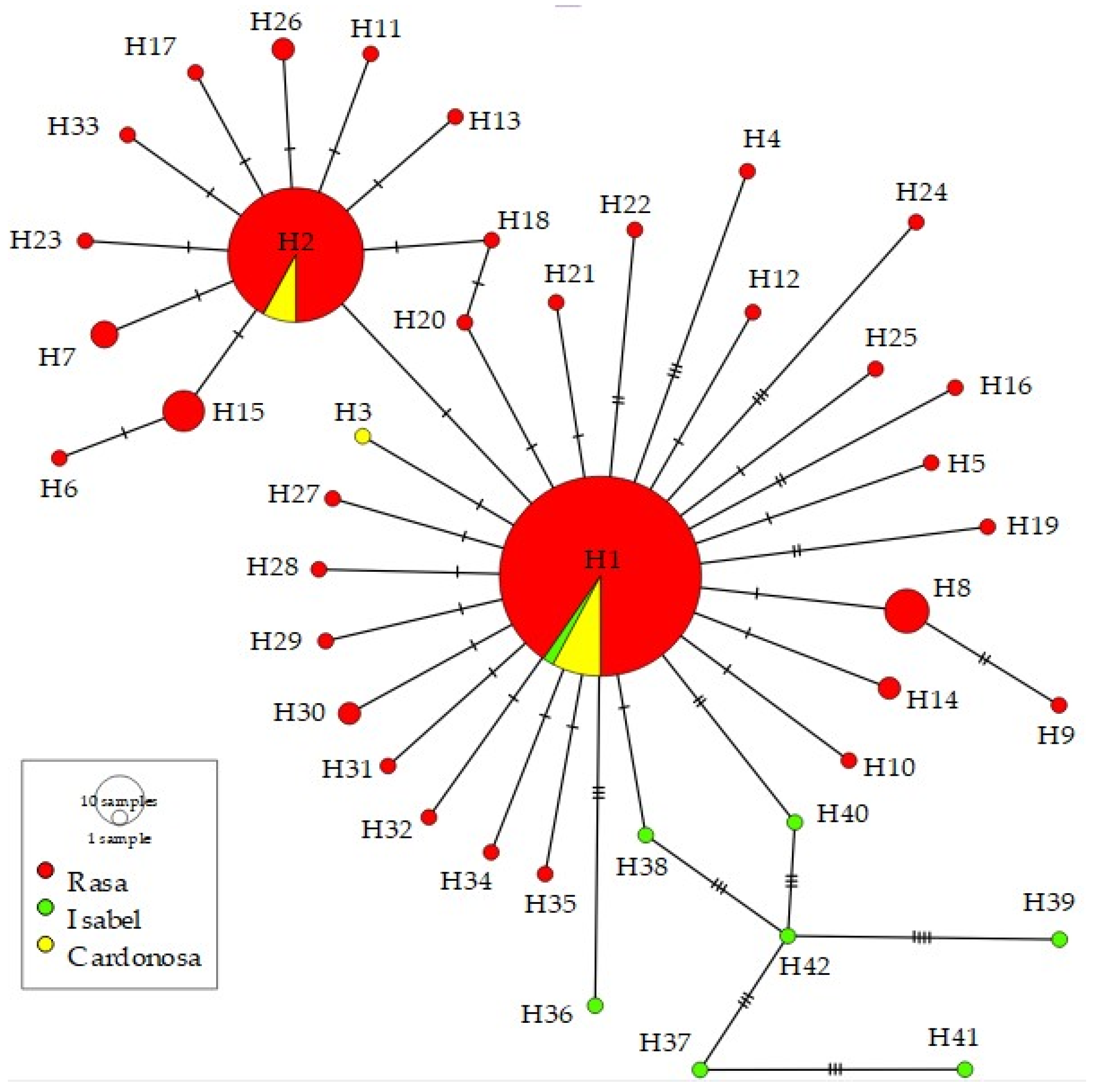
3.2. Genetic Diversity
3.3. Genetic Differentiation
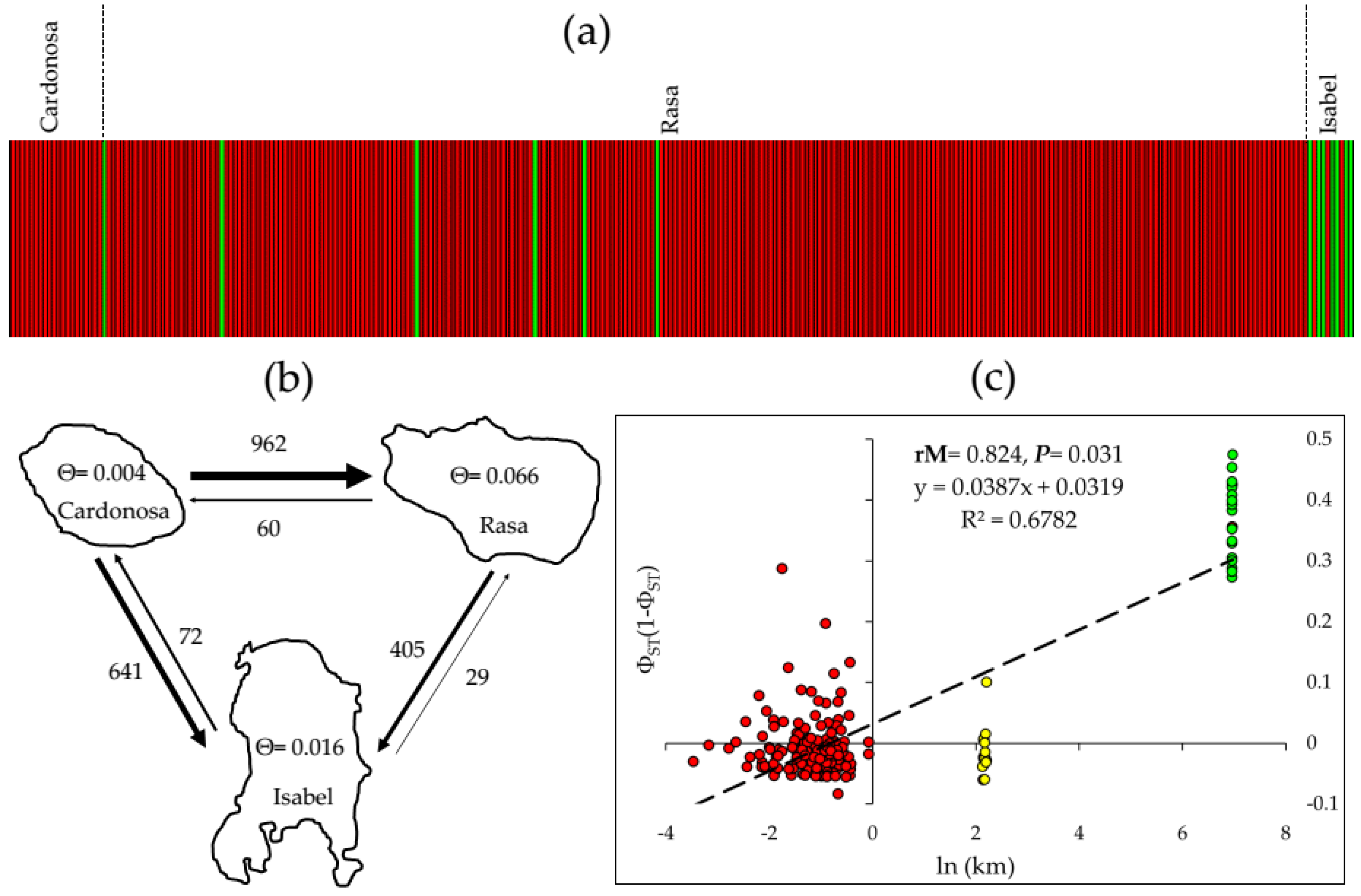
3.4. Genetic Structure
3.5. Estimation of Gene Flow between Islands
3.6. Isolation by Distance
4. Discussion
4.1. Philopatry and Dispersal Behavior
4.2. Gene Diversity, Genetic Structure, and Gene Flow
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Greenwood, P.J. Mating systems, philopatry and dispersal in birds and mammals. Anim. Behav. 1980, 28, 1140–1162. [Google Scholar] [CrossRef]
- Cury, P. Obstinate nature: An ecology of individuals. Thoughts on reproductive behavior and biodiversity. Can. J. Fish Aquat. Sci. 1994, 51, 1664–1673. [Google Scholar] [CrossRef]
- Pearce, J.M. Philopatry: A return to origins. Auk 2007, 124, 1085. [Google Scholar] [CrossRef]
- Hedgecock, D. Population genetics of marine organisms. Ocean Sci. 2019, 778–783. [Google Scholar] [CrossRef]
- Friesen, V.L. Speciation in seabirds: Why are there so many species… and why aren’t there more? J. Ornithol. 2015, 156, 27–39. [Google Scholar] [CrossRef]
- Cristofari, R.; Plaza, P.; Fernández, C.E.; Trucchi, E.; Gouin, N.; Le Bohec, C.; Luna-Jorquera, G. Unexpected population fragmentation in an endangered seabird: The case of the Peruvian diving-petrel. Sci. Rep. 2019, 9, 2021. [Google Scholar] [CrossRef]
- Dantas, G.P.M.; Oliveira, L.R.; Santos, A.M.; Flores, M.D.; De Melo, D.R.; Simeone, A.; Vianna, J.A. Uncovering population structure in the Humboldt penguin (Spheniscus humboldti) along the Pacific coast at South America. PLoS ONE 2019, 14, e0215293. [Google Scholar] [CrossRef]
- Milot, E.; Weimerskirch, H.; Bernatchez, L. The seabird paradox: Dispersal, genetic structure and population dynamics in a highly mobile, but philopatric albatross species. Mol. Ecol. 2008, 17, 1658–1673. [Google Scholar] [CrossRef]
- Cristofari, R.; Trucchi, E.; Whittington, J.D.; Vigetta, S.; Gachot-Neveu, H.; Stenseth, N.C.; Le Bohec, C. Spatial heterogeneity as a genetic mixing mechanism in highly philopatric colonial seabirds. PLoS ONE 2015, 10, e0117981. [Google Scholar] [CrossRef][Green Version]
- Coulson, J.C.A. Review of Philopatry in Seabirds and Comparisons with Other Waterbird Species. Waterbirds 2016, 39, 229–240. [Google Scholar] [CrossRef]
- Peters, J.L.; Bolender, K.A.; Pearce, J.M. Behavioural vs. molecular sources of conflict between nuclear and mitochondrial DNA: The role of male-biased dispersal in a Holarctic sea duck. Mol. Ecol. 2012, 21, 3562–3575. [Google Scholar] [CrossRef] [PubMed]
- Schjørring, S. Ecologically determined natal philopatry within a colony of great cormorants. Behav. Ecol. 2001, 12, 287–294. [Google Scholar] [CrossRef]
- Griesser, M.; Halvarsson, P.; Sahlman, T.; Ekman, J. What are the strengths and limitations of direct and indirect assessment of dispersal? Insights from a long-term field study in a group-living bird species. Behav. Ecol. Sociobiol. 2014, 68, 485–497. [Google Scholar] [CrossRef]
- Mabry, K.E.; Shelley, E.L.; Davis, K.E.; Blumstein, D.T.; Van Vuren, D.H. Social Mating System and Sex-Biased Dispersal in Mammals and Birds: A Phylogenetic Analysis. PLoS ONE 2013, 8, e57980. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Lloyd, P.; Feldheim, K.A.; Bowie, R.C.K. Microgeographic socio-genetic structure of an African cooperative breeding passerine revealed: Integrating behavioural and genetic data. Mol. Ecol. 2012, 21, 662–672. [Google Scholar] [CrossRef]
- Beck, N.R.; Peakall, R.; Heinsohn, R. Social constraint and an absence of sex-biased dispersal drive fine-scale genetic structure in white-winged choughs. Mol. Ecol. 2008, 17, 4346–4358. [Google Scholar] [CrossRef]
- Berg, E.C.; Eadie, J.M.; Langen, T.A.; Russell, A.F. Reverse sex-biased philopatry in a cooperative bird: Genetic consequences and a social cause. Mol. Ecol. 2009, 18, 3486–3499. [Google Scholar] [CrossRef]
- Lecomte, N.; Gauthier, G.; Giroux, J.F.; Milot, E.; Bernatchez, L. Tug of war between continental gene flow and rearing site philopatry in a migratory bird: The sex-biased dispersal paradigm reconsidered. Mol. Ecol. 2009, 18, 593–602. [Google Scholar] [CrossRef]
- Rocha-Olivares, A.; González-Jaramillo, M. Population genetic structure of Mexican Magnificent Frigatebirds: An integrative analysis of the influence of reproductive behavior and sex-biased dispersal. Rev. Mex. Biodivers. 2014, 85, 532–545. [Google Scholar] [CrossRef]
- Clucas, G.V.; Younger, J.L.; Kao, D.; Emmerson, L.; Southwell, C.; Wienecke, B.; Hart, T. Comparative population genomics reveals key barriers to dispersal in Southern Ocean penguins. Mol. Ecol. 2018, 27, 4680–4697. [Google Scholar] [CrossRef]
- Quillfeldt, P.; Moodley, Y.; Weimerskirch, H.; Cherel, Y.; Delord, K.; Phillips, R.A.; Masello, J.F. Does genetic structure reflect differences in non-breeding movements? A case study in small, highly mobile seabirds. BMC Evol. Biol. 2017, 17, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Guerrero, J.A.; Piña-Ortiz, A.; Enríquez-Paredes, L.; van der Heiden, A.M.; Hernández-Vázquez, S.; Saavedra-Sotelo, N.C.; Fernández, G. Low genetic structure and diversity of Red-billed Tropicbirds in the Mexican Pacific. J. Field Ornithol. 2020, 91, 142–155. [Google Scholar] [CrossRef]
- Perez, G.S.; Goodenough, K.S.; Horn, M.H.; Patton, R.T.; Ruiz, E.A.; Velarde, E.; Aguilar, A. High Connectivity among Breeding Populations of the Elegant Tern (Thalasseus elegans) in Mexico and Southern California Revealed Through Population Genomic Analysis. Waterbirds 2020, 43, 17–27. [Google Scholar] [CrossRef]
- Ibarguchi, G.; Gaston, A.J.; Friesen, V.L. Philopatry, morphological divergence, and kin groups: Structuring in thick-billed murres Uria lomvia within a colony in Arctic Canada. J. Avian Biol. 2011, 42, 134–150. [Google Scholar] [CrossRef]
- Mancilla-Morales, M.D.; Romero-Fernández, S.; Contreras-Rodríguez, A.; Flores-Martínez, J.J.; Sánchez-Cordero, V.; Herrera, M.G.; López, M.F.; Ruiz, E.A. Diverging Genetic Structure of Coexisting Populations of the Black Storm-Petrel and the Least Storm-Petrel in the Gulf of California. Trop. Conserv. Sci. 2020, 13, 1–12. [Google Scholar] [CrossRef]
- Sexton, J.P.; Hangartner, S.B.; Hoffmann, A.A. Genetic isolation by environment or distance: Which pattern of gene flow is most common? Evolution 2014, 68, 1–15. [Google Scholar] [CrossRef]
- Pertierra, L.R.; Segovia, N.I.; Noll, D.; Martinez, P.A.; Pliscoff, P.; Barbosa, A.; Vianna, J.A. Cryptic speciation in gentoo penguins is driven by geographic isolation and regional marine conditions: Unforeseen vulnerabilities to global change. Divers. Distrib. 2020, 26, 958–975. [Google Scholar] [CrossRef]
- Nunes, G.T.; Mancini, P.L.; Bugoni, L. When Bergmann’s rule fails: Evidences of environmental selection pressures shaping phenotypic diversification in a widespread seabird. Ecography 2017, 40, 365–375. [Google Scholar] [CrossRef]
- Wallace, S.J.; Wolf, S.G.; Bradley, R.W.; Harvey, L.L.; Friesen, V.L. The influence of biogeographical barriers on the population genetic structure and gene flow in a coastal Pacific seabird. J. Biogeogr. 2015, 42, 390–400. [Google Scholar] [CrossRef]
- Martínez-Abraín, A.; Viedma, C.; Ramón, N.; Oro, D. A note on the potential role of philopatry and conspecific attraction as conservation tools in Audouin’s Gull Larus auduoii. Bird Conserv. Int. 2001, 11, 143–147. [Google Scholar] [CrossRef]
- Oro, D.; Tavecchia, G.; Genovart, M. Comparing demographic parameters for philopatric and immigrant individuals in a long-lived bird adapted to unstable habitats. Oecologia 2011, 165, 935–945. [Google Scholar] [CrossRef] [PubMed]
- Piper, W.H. Making habitat selection more “familiar”: A review. Behav. Ecol. Sociobiol. 2011, 65, 1329–1351. [Google Scholar] [CrossRef]
- Chalfoun, A.D.; Schmidt, K.A. Adaptive breeding-habitat selection: Is it for the birds? Auk 2012, 129, 589–599. [Google Scholar] [CrossRef]
- Oro, D.; Pradel, R.; Lebreton, J.D. Food availability and nest predation influence life history traits in Audouin’s gull, Larus audouinii. Oecologia 1999, 118, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Wrege, P.H.; Shuford, W.D.; Winkler, D.W.; Jellison, R. Annual variation in numbers of breeding California Gulls at Mono Lake, California: The importance of natal philopatry and local and regional conditions. Condor 2006, 108, 82–96. [Google Scholar] [CrossRef]
- Ellis, J.C.; Shulman, M.J.; Jessop, H.; Suomala, R.; Morris, S.R.; Seng, V.; Mach, K. Impact of Raccoons on breeding success in large colonies of Great Black-backed Gulls and Herring Gulls. Waterbirds 2007, 30, 375–383. [Google Scholar] [CrossRef]
- Bolton, M.; Conolly, G.; Carroll, M.; Wakefield, E.D.; Caldow, R. A review of the occurrence of inter-colony segregation of seabird foraging areas and the implications for marine environmental impact assessment. Ibis 2019, 161, 241–259. [Google Scholar] [CrossRef]
- Antaky, C.C.; Young, L.; Ringma, J.; Price, M.R. Dispersal under the seabird paradox: Probability, life history, or spatial attributes? Mar. Ornithol. 2021, 49, 1–8. Available online: https://www.marineornithology.org/PDF/49_1/49_1_1-8.pdf (accessed on 16 June 2021).
- Stacey, P.B.; Ligon, J.D. The benefits-of-philopatry hypothesis for the evolution of cooperative breeding: Variation in territory quality and group size effects. Am. Nat. 1991, 137, 831–846. [Google Scholar] [CrossRef]
- Navarro, J.; Votier, S.C.; Aguzzi, J.; Chiesa, J.J.; Forero, M.G.; Phillips, R.A. Ecological Segregation in Space, Time and Trophic Niche of Sympatric Planktivorous Petrels. PLoS ONE 2013, 8, e62897. [Google Scholar] [CrossRef]
- O’Connor, E.A.; Hasselquist, D.; Nilsson, J.Å.; Westerdahl, H.; Cornwallis, C.K. Wetter climates select for higher immune gene diversity in resident, but not migratory, songbirds. Proc. R. Soc. B Biol. Sci. 2020, 287, 20192675. [Google Scholar] [CrossRef] [PubMed]
- Barbraud, C.; Delord, K. Selection against immigrants in wild seabird populations. Ecol. Lett. 2021, 24, 84–93. [Google Scholar] [CrossRef]
- Case, T.J.; Cody, M.L.; Ezcurra, E. A New Island Biogeography of the Sea of Cortés; Oxford University Press: Oxford, UK, 2002; 690p. [Google Scholar]
- Velarde, E. Breeding biology of Heermann’s Gulls on Isla Rasa, Gulf of California, Mexico. Auk 1999, 116, 513–519. [Google Scholar] [CrossRef]
- Velarde, E.; Ezcurra, E.; Cisneros-Mata, M.A.; Lavín, M.F. Seabird ecology, El Niño anomalies, and prediction of sardine fisheries in the Gulf of California. Ecol. Appl. 2004, 14, 607–615. [Google Scholar] [CrossRef]
- Velarde, E.; Ezcurra, E.; Anderson, D.W. Seabird diets provide early warning of sardine fishery declines in the Gulf of California. Sci. Rep. 2013, 3, 1332. [Google Scholar] [CrossRef]
- Boswall, J.; Barrett, M. Notes on the breeding birds of Isla Rasa, Baja California. West Birds 1978, 9, 93–108. [Google Scholar]
- Mellink, E. History and status of colonies of Heermann’s Gull in Mexico. Waterbirds 2001, 24, 188–194. [Google Scholar] [CrossRef]
- Ruiz, E.A.; Velarde, E.; Aguilar, A. Demographic history of Heermann’s Gull (Larus heermanni) from late Quaternary to present: Effects of past climate change in the Gulf of California. Auk 2017, 134, 308–316. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Rueda-Roa, D.; Chavez, F.P.; Kavanaugh, M.T.; Roffer, M.A. Megaregions among the large marine ecosystems of the Americas. Environ. Dev. 2017, 22, 52–62. [Google Scholar] [CrossRef]
- Mercado-Santana, J.A.; Santamaría-del-Ángel, E.; González-Silvera, A.; Sánchez-Velasco, L.; Gracia-Escobar, M.F.; Millán-Núñez, R.; Torres-Navarrete, C. Productivity in the Gulf of California large marine ecosystem. Environ. Dev. 2017, 22, 18–29. [Google Scholar] [CrossRef]
- Lluch-Cota, S.E.; Parés-Sierra, A.; Magaña-Rueda, V.O.; Arreguín-Sánchez, F.; Bazzino, G.; Herrera-Cervantes, H.; Lluch-Belda, D. Changing climate in the Gulf of California. Prog. Oceanogr. 2010, 87, 114–126. [Google Scholar] [CrossRef]
- Espinosa-Carreón, T.L.; Escobedo-Urías, D. South region of the gulf of California large marine ecosystem upwelling, fluxes of CO2 and nutrients. Environ. Dev. 2017, 22, 42–51. [Google Scholar] [CrossRef]
- Velarde, E.; Wilder, B.T.; Felger, R.S.; Ezcurra, E. Floristic diversity and dynamics of Isla Rasa, Gulf of California—A globally important seabird island. Bot. Sci. 2014, 92, 89–101. [Google Scholar] [CrossRef][Green Version]
- Flores-Martínez, J.J.; Herrera, L.G.; Arroyo-Cabrales, J.; Alarcón, I.; Ruiz, E.A. Seasonal dietary differences of the Yellow-footed Gull (Charadriiformes: Laridae) in Isla Partida Norte, Gulf of California, Mexico. Rev. Mex. Biodivers. 2015, 86, 412–418. [Google Scholar] [CrossRef]
- Velarde, E. Predation of Nesting Larids by Peregrine Falcons at Rasa Island, Gulf of California, Mexico. Condor 1993, 95, 706–708. [Google Scholar] [CrossRef]
- Velarde, E. Predation of Heermann’s Gull (Larus heermanni) Chicks by Yellow-footed Gulls (Larus livens) in Dense and scattered nesting sites. Colon. Waterbird 1992, 15, 8–13. [Google Scholar] [CrossRef]
- Lozano, E.; Carmona, R.; Brabata, G. Reproductive success of Heermann’s (Larus heermanni) and Yellow-footed (L. livens) gulls in the south of the Gulf of California, Mexico. Ornitol. Neotrop. 2004, 15, 237–246. Available online: https://sora.unm.edu/sites/default/files/journals/on/v015n02/p0237-p0246.pdf (accessed on 27 October 2020).
- Housh, T.B.; Aranda-Gómez, J.J.; Luhr, J.F. Isla Isabel (Nayarit, México): Quaternary alkalic basalts with mantle xenoliths erupted in the mouth of the Gulf of California. J. Volcanol. Geotherm. Res. 2010, 197, 85–107. [Google Scholar] [CrossRef]
- Vieyra, L.; Velarde, E.; Ezcurra, E. Effects of Parental Age and Food Availability on the Reproductive Success of Heermann’s Gulls in the Gulf of California. Ecology 2009, 90, 1084–1094. [Google Scholar] [CrossRef]
- Dwight, J. The gulls (Laridae) of the world; their plumages, moults, variations, relationships, and distribution. Bull. AMNH 1925, 52, 63–408. Available online: http://digitallibrary.amnh.org/handle/2246/1245 (accessed on 4 May 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.R-project.org (accessed on 13 October 2021).
- Gouy, M.; Guindon, S.; Gascuel, O. Sea view version 4: A multiplatform graphical user interface for sequence alignment and phylogenetic tree building. Mol. Biol. Evol. 2010, 27, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Darriba, D.; Taboada, G.L.; Doallo, R.; Posada, D. JModelTest 2: More models, new heuristics and parallel computing. Nat. Methods 2012, 9, 772. [Google Scholar] [CrossRef] [PubMed]
- Rozas, J.; Ferrer-Mata, A.; Sanchez-DelBarrio, J.C.; Guirao-Rico, S.; Librado, P.; Ramos-Onsins, S.E.; Sanchez-Gracia, A. DnaSP 6: DNA sequence polymorphism analysis of large data sets. Mol. Biol. Evol. 2017, 34, 3299–3302. [Google Scholar] [CrossRef] [PubMed]
- Leigh, J.W.; Bryant, D. POPART: Full-feature software for haplotype network construction. Methods Ecol. Evol. 2015, 6, 1110–1116. [Google Scholar] [CrossRef]
- Crochet, P.-A.; Desmaris, E. Slow rate of Evolution in the Mitochondrial Region of Gulls (Aves: Laridae). Mol. Biol. Evol. 2000, 17, 1797–1806. [Google Scholar] [CrossRef] [PubMed]
- Crochet, P.-A.; Bonhomme, F.; Lebreton, J.-D. Molecular phylogeny and plumage evolution in gulls (Larini). J. Evol. Biol. 2000, 13, 47–57. Available online: http://gull-research.org/papers/16crochet.pdf (accessed on 25 January 2022).
- Lefort, V.; Longueville, J.E.; Gascuel, O. SMS: Smart Model Selection in PhyML. Mol. Biol. Evol. 2017, 34, 2422–2424. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Gascuel, O. Improving the efficiency of SPR moves in phylogenetic tree search methods based on maximum likelihood. Bioinformatics 2005, 21, 4338–4347. [Google Scholar] [CrossRef]
- Anisimova, M.; Gascuel, O. Approximate likelihood-ratio test for branches: A fast, accurate, and powerful alternative. Syst. Biol. 2006, 55, 539–552. [Google Scholar] [CrossRef]
- Guindon, S.; Dufayard, J.F.; Lefort, V.; Anisimova, M.; Hordijk, W.; Gascuel, O. New Algorithms and Methods to Estimate Maximim-Likelihood Phylogenies Assessing the Performance of PhyML 3.0. Syst. Biol. 2010, 59, 307–321. [Google Scholar] [CrossRef]
- Pearse, D.E.; Crandall, K.A. Beyond FST: Analysis of population genetic data for conservation. Conserv. Genet. 2004, 5, 585–602. Available online: https://link.springer.com/content/pdf/10.1007/s10592-004-1863-z.pdf (accessed on 25 March 2021). [CrossRef]
- Ryman, N.; Palm, S.; André, C.; Carvalho, G.R.; Dahlgren, T.G.; Jorde, P.E.; Ruzzante, D.E. Power for detecting genetic divergence: Differences between statistical methods and marker loci. Mol. Ecol. 2006, 15, 2031–2045. [Google Scholar] [CrossRef] [PubMed]
- Friesen, V.L.; Burg, T.M.; McCoy, K.D. Mechanisms of population differentiation in seabirds: Invited review. Mol. Ecol. 2007, 16, 1765–1785. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R.; Boos, D.D.; Kaplan, N.L. A statistical test for detecting geographic subdivision. Mol. Biol. Evol. 1992, 9, 138–151. [Google Scholar] [CrossRef]
- Hudson, R.R. A new statistic for detecting genetic differentiation. Genetics 2000, 155, 2011–2014. [Google Scholar] [CrossRef] [PubMed]
- Nei, M. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 1973, 70, 3321–3323. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Crease, T.J. The analysis of population survey data on DNA sequence variation. Mol. Biol. Evol. 1990, 7, 377–394. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. The genetical structure of populations. Ann. Eugen. 1951, 15, 323–354. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R.; Slatkin, M.; Madisson, W.P. Estimation of levels of gene flow from DNA sequence data. Genetics 1992, 132, 583–589. [Google Scholar] [CrossRef]
- Slatkin, M. A comparison of three indirect methods for estimating average levels of gene flow. Evolution 1989, 43, 1349–1368. [Google Scholar] [CrossRef]
- Excoffier, L.; Lischer, H.E.L. Arlequin suite ver 3.5: A new series of programs to perform population genetics analyses under Linux and Windows. Mol. Ecol. Resour. 2010, 10, 564–567. [Google Scholar] [CrossRef]
- Dupanloup, I.; Schneider, S.; Excoffier, L. A simulated annealing approach to define the genetic structure of populations. Mol. Ecol. 2002, 11, 2571–2581. [Google Scholar] [CrossRef] [PubMed]
- Manel, S.; Gaggiotti, O.E.; Waples, R.S. Assignment methods: Matching biological questions with appropriate techniques. Trends Ecol. Evol. 2005, 20, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Corander, J.; Cheng, L.; Marttinen, P.; Tang, J. BAPS: Bayesian Analysis of Population Structure; Manual v 6.0; Department of Mathematics and Statistics, University of Helsinki: Helsinki, Finland, 2013; (Latest Update of This Manual on 14 February 2013). [Google Scholar]
- Beerli, P.; Palczewski, M. Unified framework to evaluate panmixia and migration direction among multiple sampling locations. Genetics 2010, 185, 313–326. [Google Scholar] [CrossRef] [PubMed]
- Mantel, N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967, 27, 209–220. [Google Scholar]
- Rousset, F. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 1997, 145, 1219–1228. [Google Scholar] [CrossRef]
- Weir, B.S.; Cockerman, C.C. Estimating F-statistics for the analysis of population structure. Evolution 1984, 38, 1358–1370. [Google Scholar] [CrossRef]
- Lento, G.M.; Haddon, M.; Chambers, G.K.; Baker, C.S. Genetic Variation of Southern Hemisphere Fur Seals (Arctocephalus spp.): Investigation of population structure and species identity. J. Hered. 1997, 88, 202–208. [Google Scholar] [CrossRef]
- Hajizadeh, M.; Sokhandan-Bashir, N. Population genetic analysis of potato virus X based on the CP gene sequence. VirusDisease 2017, 28, 93–101. [Google Scholar] [CrossRef]
- Wang, J. Application of the one-migrant-per-generation rule to conservation and management. Conserv. Biol. 2004, 18, 332–343. [Google Scholar] [CrossRef]
- Mills, L.S.; Allendorf, F.W. The One-Migrant-per-Generation Rule in Conservation and Management. Conserv. Biol. 1996, 10, 1509–1518. [Google Scholar] [CrossRef]
- Nathan, L.R.; Kanno, Y.; Vokoun, J.C. Population demographics influence genetic responses to fragmentation: A demogenetic assessment of the ‘one migrant per generation’ rule of thumb. Biol. Conserv. 2017, 210, 261–272. [Google Scholar] [CrossRef]
- Ortiz-Ramírez, M.F.; Sánchez-González, L.A.; Castellanos-Morales, G.; Ornelas, J.F.; Navarro-Sigüenza, A.G. Concerted Pleistocene dispersal and genetic differentiation in passerine birds from the Tres Marías Archipelago, Mexico. Auk 2018, 135, 716–732. [Google Scholar] [CrossRef]
- Müller, W.; Groothuis, T.G.G.; Eising, C.M.; Dijkstra, C. An experimental study on the causes of sex-biased mortality in the black-headed gull—The possible role of testosterone. J. Anim. Ecol. 2005, 74, 735–741. [Google Scholar] [CrossRef]
- Kalmbach, E.; Nager, R.G.; Griffiths, R.; Furness, R.W. Increased reproductive effort results in male-biased offspring sex ratio: An experimental study in a species with reversed sexual size dimorphism. Proc. R. Soc. B 2001, 268, 2175–2179. [Google Scholar] [CrossRef] [PubMed]
- Merkling, T.; Welcker, J.; Hewison, A.J.M.; Hatch, S.A.; Kitaysky, A.S.; Speakman, J.R.; Blanchard, P. Identifying the selective pressures underlying offspring sex-ratio adjustments: A case study in a wild seabird. Behav. Ecol. 2015, 26, 916–925. [Google Scholar] [CrossRef]
- Becker, P.H.; Ezard, T.H.G.; Ludwigs, J.D.; Sauer-Gürth, H.; Wink, M. Population sex ratio shift from fledging to recruitment: Consequences for demography in a philopatric seabird. Oikos 2008, 117, 60–68. [Google Scholar] [CrossRef]
- Becker, P.H.; Erdelen, M. Egg Size in Herring Gulls (Larus argentatus) on Mellum Island, North Sea, West Germany: The Influence of Nest Vegetation, Nest Density, and Colony Development. Colon. Waterbirds 1986, 9, 68–80. [Google Scholar] [CrossRef]
- Skórka, P.; Martyka, R.; Wójcik, J.D.; Babiarz, T.; Skórka, J. Habitat and nest site selection in the Common Gull Larus canus in southern Poland: Significance of man-made habitats for conservation of an endangered species. Acta Ornithol. 2006, 41, 137–144. [Google Scholar] [CrossRef]
- Kramer, J.; Meunier, J. Kin and multilevel selection in social evolution: A never-ending controversy? [version 1; peer review: 4 approved]. F1000Research 2016, 5, 1–13. [Google Scholar] [CrossRef]
- Humeau, L.; Le Corre, M.; Reynolds, S.J.; Wearn, C.; Hennicke, J.C.; Russell, J.C.; Gomard, Y.; Magalon, H.; Pinet, P.; Gélin, P.; et al. Genetic structuring among colonies of a pantropical seabird: Implication for subspecies validation and conservation. Ecol. Evol. 2020, 10, 11886–11905. [Google Scholar] [CrossRef]
- Thanou, E.; Sponza, S.; Nelson, E.J.; Perry, A.; Wanless, S.; Daunt, F.; Cavers, S. Genetic structure in the European endemic seabird, Phalacrocorax aristotelis, shaped by a complex interaction of historical and contemporary, physical and nonphysical drivers. Mol. Ecol. 2017, 26, 2796–2811. [Google Scholar] [CrossRef] [PubMed]
- Lombal, A.J.; O’dwyer, J.E.; Friesen, V.; Woehler, E.J.; Burridge, C.P. Identifying mechanisms of genetic differentiation among populations in vagile species: Historical factors dominate genetic differentiation in seabirds. Biol. Rev. 2020, 95, 625–651. [Google Scholar] [CrossRef] [PubMed]
- Sauve, D.; Patirana, A.; Chardine, J.W.; Friesen, V.L. Mitochondrial DNA reveals population genetic structure within Atlantic but not Pacific populations of a holarctic seabird, the Black-legged Kittiwake Rissa tridactyla. Mar. Ornithol. 2019, 2, 199–208. Available online: https://www.marineornithology.org/content/get.cgi?rn=1318 (accessed on 21 January 2021).
| Natal Valley | Recapture Valley | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sex | IT | CA | GE | TV | CR | CB | VW | Total | |
| ES | males | 7 | 1 | 1 | 1 | 0 | 0 | 0 | 9 |
| females | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 4 | |
| IT | males | 98 | 17 | 0 | 0 | 0 | 0 | 0 | 116 |
| females | 17 | 5 | 2 | 1 | 0 | 2 | 0 | 27 | |
| CA | males | 66 | 211 | 0 | 2 | 3 | 0 | 0 | 282 |
| females | 24 | 82 | 1 | 0 | 3 | 0 | 0 | 110 | |
| GE | males | 2 | 4 | 99 | 1 | 0 | 1 | 0 | 107 |
| females | 0 | 4 | 26 | 1 | 4 | 1 | 1 | 37 | |
| VG | males | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| females | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 3 | |
| TV | males | 1 | 0 | 0 | 30 | 11 | 0 | 0 | 42 |
| females | 1 | 1 | 0 | 15 | 9 | 1 | 0 | 27 | |
| CR | males | 5 | 1 | 0 | 23 | 20 | 7 | 1 | 57 |
| females | 2 | 0 | 0 | 12 | 9 | 4 | 2 | 29 | |
| CB | males | 0 | 0 | 0 | 3 | 32 | 30 | 1 | 66 |
| females | 1 | 0 | 0 | 2 | 13 | 7 | 2 | 25 | |
| VW | males | 1 | 0 | 1 | 0 | 1 | 5 | 26 | 34 |
| females | 0 | 1 | 3 | 2 | 2 | 2 | 12 | 22 | |
| All natal valleys | males | 180 | 234 | 102 | 60 | 67 | 43 | 28 | 714 |
| females | 47 | 97 | 32 | 33 | 40 | 18 | 17 | 284 | |
| Total | 227 | 331 | 134 | 93 | 107 | 61 | 45 | 998 | |
| Model 1: Binomial ANOVA for Recaptured/Total Recaptured | |||||
| df | Deviance | r2 | p | Signif. | |
| distance | 1 | 2564.1 | 0.8331 | <10−70 | *** |
| effort | 1 | 9.8 | 0.0032 | 0.001717 | *** |
| natal place | 8 | 93.0 | 0.0302 | 1.12 × 10−16 | *** |
| breeding place | 5 | 95.2 | 0.0309 | 5.32 × 10−19 | *** |
| natal × breed. pl. | 47 | 208.4 | 0.0677 | 3.4 × 10−22 | *** |
| sex | 1 | 0.1 | 0.0000 | 0.740144 | ns |
| sex × distance | 1 | 43.1 | 0.0140 | 5.23 × 10−11 | *** |
| residuals | 61 | 64.1 | |||
| null model | 125 | 3077.9 | |||
| Model 2: Binomial ANOVA for Recaptured/Total Banded (Assuming Sex Ratios as in Recaptured) | |||||
| df | Deviance | r2 | p | Signif. | |
| distance | 1 | 2436.6 | 0.7626 | <10−70 | *** |
| effort | 1 | 140.7 | 0.0440 | 1.88 × 10−32 | *** |
| natal place | 8 | 330.0 | 0.1033 | 1.67 × 10−66 | *** |
| breeding place | 5 | 52.8 | 0.0165 | 3.68 × 10−10 | *** |
| natal × breed. pl. | 47 | 141.0 | 0.0441 | 2.51 × 10−11 | *** |
| sex | 1 | 1.2 | 0.0004 | 0.277356 | ns |
| sex × distance | 1 | 34.6 | 0.0108 | 4.13 × 10−09 | *** |
| residuals | 61 | 58.2 | |||
| null model | 125 | 3195.0 | |||
| Model 3: Binomial ANOVA for Recaptured/Total Banded (Assuming Sex Ratios to be 50:50%) | |||||
| df | Deviance | r2 | p | Signif. | |
| distance | 1 | 2436.6 | 0.7180 | < 0−70 | *** |
| effort | 1 | 140.7 | 0.0415 | 1.88 × 10−32 | *** |
| natal place | 8 | 331.4 | 0.0976 | 8.54 × 10−67 | *** |
| breeding place | 5 | 53.0 | 0.0156 | 3.32 × 10−10 | *** |
| natal × breed. pl. | 47 | 141.0 | 0.0415 | 2.51 × 10−11 | *** |
| sex | 1 | 196.4 | 0.0579 | 1.31 × 10−44 | *** |
| sex × distance | 1 | 36.4 | 0.0107 | 1.63 × 10−09 | *** |
| residuals | 61 | 58.3 | |||
| null model | 125 | 3393.7 | |||
| Region | Island | Cluster | Location | Lat (N)/Long (W) | n (M, F) | h | S | k | Hd | π | Haplotypes |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MIR | Cardonosa | I | 1 | 28°53′16″/113°01′51″ | 20 (8, 12) | 3 | 2 | 0.54 | 0.51 | 0.00053 | H1(13), H2(6), H3 |
| Rasa | II | 2 | 28°49′29″/112°58′50″ | 19 (9, 10) | 7 | 9 | 1.30 | 0.70 | 0.00126 | H1(10), H2(4), H4, H5, H6, H7, H8 | |
| 3 | 28°49′27″/112°58′50″ | 16 (8, 8) | 8 | 8 | 1.31 | 0.70 | 0.00127 | H1(9), H2, H8, H9, H10, H11, H12, H13 | |||
| 4 | 28°49′28″/112°58′55″ | 12 (6, 6) | 2 | 1 | 0.49 | 0.49 | 0.00047 | H1(8), H2(4) | |||
| 5 | 28°49′30″/112°58′50″ | 18 (8, 10) | 4 | 3 | 0.65 | 0.58 | 0.00063 | H1(11), H2(5), H8, H14 | |||
| 6 | 28°49′26″/112°58′53″ | 11 (5, 6) | 5 | 5 | 1.38 | 0.78 | 0.00134 | H1(5), H2 (2), H8, H15(2), H16 | |||
| III | 7 | 28°49′16′″/112°58′37″ | 13 (4, 9) | 6 | 5 | 0.77 | 0.77 | 0.00109 | H1(3), H2(6), H8, H14, H17, H18 | ||
| IV | 8 | 28°49′24″/112°58′41″ | 23(12, 11) | 7 | 8 | 1.01 | 0.65 | 0.00098 | H1(13), H2(5), H19, H20, H21, H22, H23 | ||
| 9 | 28°49′29″/112°58′46″ | 8 (4, 4) | 3 | 2 | 0.82 | 0.68 | 0.00080 | H1(4), H2(3), H7 | |||
| 10 | 28°49′32″/112°58′42″ | 11 (3, 8) | 4 | 5 | 1.16 | 0.60 | 0.00113 | H1(7), H2(2), H15, H24 | |||
| V | 11 | 28°49′34″/112°58′50″ | 19 (7, 12) | 3 | 2 | 0.52 | 0.49 | 0.00050 | H1(13), H2(5), H25 | ||
| VI | 12 | 28°49′27″/112°58′37″ | 12 (4, 8) | 2 | 1 | 0.49 | 0.49 | 0.00047 | H1(8), H2(4) | ||
| 13 | 28°49′19″/112°58′35″ | 20 (13, 7) | 6 | 5 | 0.88 | 0.68 | 0.00085 | H1(10), H2 (6), H8, H26, H27, H28 | |||
| 14 | 28°49′22″/112°58′33″ | 13 (7, 6) | 4 | 3 | 0.69 | 0.60 | 0.00067 | H1(8), H2 (3), H29, H30 | |||
| VII | 15 | 28°49′27″/112°58′31″ | 14 (6, 8) | 5 | 4 | 0.99 | 0.59 | 0.00096 | H1(9), H2, H7, H8, H15(2) | ||
| VIII | 16 | 28°49′17″/112°58′43″ | 15 (11, 4) | 3 | 2 | 0.38 | 0.36 | 0.00037 | H1(12), H2(2), H31 | ||
| 17 | 28°49′20″/112°58′46″ | 16 (5, 11) | 5 | 4 | 0.86 | 0.68 | 0.00085 | H1(8), H2(5), H30, H32, H33 | |||
| 18 | 28°49′20″/112°58′47″ | 11 (1, 10) | 4 | 4 | 1.13 | 0.60 | 0.00019 | H1(7), H15(2), H26, H34 | |||
| IX | 19 | 28°49′17″/112°58′47″ | 15 (7, 8) | 4 | 3 | 0.78 | 0.66 | 0.00076 | H1(7), H2(6), H8, H35 | ||
| MP | Isabel | X | 20 | 21°50′40″/105°52′49″ | 10 (4, 6) | 8 | 12 | 4.13 | 0.93 | 0.00401 | H1(3), H36, H37, H38, H39, H40, H41, H42 |
| All | 296 | 42 | 53 | 1.01 | 0.62 | 0.00098 | - |
| Level | χ2 | HST | KST* | Z* | Snn | GST | Nm1 | NST | Nm2 | FST | Nm3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regions | 206 *** | 0.009 ** | 0.047 *** | 9.795 ** | 0.96 9 *** | 0.028 | 17.56 | 0.227 | 1.70 | 0.226 | 1.71 |
| Islands | 224 *** | 0.062 ns | 0.046 *** | 9.797 ** | 0.842 *** | 0.018 | 27.31 | 0.206 | 1.93 | 0.205 | 1.94 |
| Clusters | 470 *** | 0.068 ns | 0.032 *** | 9.922 * | 0.156 * | 0.012 | 41.77 | 0.119 | 3.70 | 0.118 | 3.70 |
| Locations | 815 ns | 0.005 ns | 0.040 *** | 9.80 ns | 0.064 *** | 0.003 | 145.24 | 0.061 | 7.73 | 0.060 | 7.75 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | 8.57 | 8.62 | 8.48 | 8.54 | 8.57 | 9.08 | 8.83 | 8.61 | 8.60 | 8.43 | 8.81 | 9.06 | 9.01 | 8.91 | 8.97 | 8.84 | 8.83 | 8.89 | 1063.42 |
| 2 | −0.02 | - | 0.06 | 0.18 | 0.07 | 0.12 | 0.44 | 0.25 | 0.10 | 0.25 | 0.18 | 0.36 | 0.47 | 0.47 | 0.48 | 0.37 | 0.26 | 0.24 | 0.30 | 1054.96 |
| 3 | 0.01 | −0.01 | - | 0.14 | 0.10 | 0.07 | 0.45 | 0.28 | 0.17 | 0.30 | 0.22 | 0.41 | 0.50 | 0.51 | 0.53 | 0.36 | 0.23 | 0.22 | 0.25 | 1054.92 |
| 4 | −0.06 | −0.05 | −0.01 | - | 0.15 | 0.09 | 0.58 | 0.42 | 0.27 | 0.39 | 0.21 | 0.51 | 0.64 | 0.65 | 0.66 | 0.50 | 0.37 | 0.35 | 0.35 | 1055.07 |
| 5 | −0.04 | −0.03 | −0.02 | −0.06 | - | 0.14 | 0.51 | 0.31 | 0.12 | 0.24 | 0.12 | 0.37 | 0.54 | 0.53 | 0.52 | 0.44 | 0.32 | 0.31 | 0.36 | 1054.99 |
| 6 | 0.01 | −0.03 | 0.00 | −0.02 | −0.01 | - | 0.50 | 0.35 | 0.23 | 0.36 | 0.24 | 0.45 | 0.56 | 0.58 | 0.60 | 0.41 | 0.32 | 0.26 | 0.27 | 1054.98 |
| 7 | 0.09 | 0.04 | 0.10 | 0.04 | 0.08 | 0.02 | - | 0.23 | 0.44 | 0.51 | 0.60 | 0.33 | 0.13 | 0.23 | 0.37 | 0.13 | 0.22 | 0.25 | 0.30 | 1054.45 |
| 8 | −0.03 | −0.01 | 0.00 | −0.04 | −0.03 | 0.01 | 0.08 | - | 0.22 | 0.27 | 0.40 | 0.18 | 0.23 | 0.23 | 0.28 | 0.22 | 0.17 | 0.21 | 0.31 | 1054.69 |
| 9 | 0.01 | −0.04 | 0.04 | −0.03 | 0.01 | −0.03 | −0.05 | 0.00 | - | 0.14 | 0.18 | 0.25 | 0.45 | 0.42 | 0.40 | 0.40 | 0.29 | 0.30 | 0.37 | 1054.90 |
| 10 | −0.02 | −0.03 | −0.01 | −0.04 | −0.03 | −0.04 | 0.06 | −0.02 | −0.01 | - | 0.23 | 0.21 | 0.47 | 0.41 | 0.34 | 0.49 | 0.40 | 0.42 | 0.50 | 1054.90 |
| 11 | −0.04 | −0.02 | 0.00 | −0.06 | −0.04 | 0.01 | 0.12 | −0.03 | 0.03 | −0.02 | - | 0.44 | 0.63 | 0.60 | 0.56 | 0.56 | 0.43 | 0.43 | 0.48 | 1055.08 |
| 12 | −0.06 | −0.05 | −0.01 | −0.09 | −0.06 | −0.02 | 0.04 | −0.04 | −0.03 | −0.04 | −0.06 | - | 0.27 | 0.20 | 0.15 | 0.37 | 0.35 | 0.37 | 0.45 | 1054.68 |
| 13 | −0.03 | −0.03 | 0.00 | −0.06 | −0.03 | −0.01 | 0.03 | −0.01 | −0.03 | −0.02 | −0.02 | −0.06 | - | 0.11 | 0.27 | 0.24 | 0.31 | 0.35 | 0.41 | 1054.46 |
| 14 | −0.03 | −0.03 | −0.02 | −0.04 | −0.04 | 0.00 | 0.11 | −0.03 | 0.03 | −0.03 | −0.04 | −0.04 | −0.02 | - | 0.16 | 0.32 | 0.36 | 0.40 | 0.48 | 1054.49 |
| 15 | −0.01 | −0.04 | −0.01 | −0.04 | −0.03 | −0.06 | 0.07 | −0.01 | −0.02 | −0.05 | −0.01 | −0.04 | −0.02 | −0.02 | - | 0.45 | 0.45 | 0.49 | 0.57 | 1054.57 |
| 16 | 0.01 | 0.01 | −0.01 | 0.03 | 0.00 | 0.06 | 0.22 | −0.01 | 0.16 | 0.00 | −0.01 | 0.03 | 0.03 | −0.02 | 0.02 | - | 0.13 | 0.15 | 0.18 | 1054.57 |
| 17 | −0.03 | −0.02 | 0.02 | −0.06 | −0.02 | −0.01 | 0.02 | −0.01 | −0.05 | −0.02 | −0.02 | −0.06 | −0.03 | −0.03 | −0.01 | 0.05 | - | 0.04 | 0.13 | 1054.70 |
| 18 | 0.00 | −0.03 | 0.00 | −0.02 | −0.01 | −0.05 | 0.08 | −0.01 | 0.01 | −0.05 | 0.00 | −0.02 | −0.01 | −0.01 | −0.06 | 0.03 | 0.00 | - | 0.09 | 1054.72 |
| 19 | −0.03 | −0.03 | 0.01 | −0.06 | −0.03 | −0.03 | 0.00 | −0.01 | −0.06 | −0.02 | −0.01 | −0.06 | −0.04 | −0.01 | −0.02 | 0.07 | −0.04 | 0.00 | - | 1054.67 |
| 20 | 0.32 | 0.26 | 0.23 | 0.26 | 0.30 | 0.22 | 0.30 | 0.29 | 0.23 | 0.21 | 0.31 | 0.26 | 0.30 | 0.25 | 0.25 | 0.28 | 0.28 | 0.22 | 0.29 | - |
| Grouping | Source of Variation | d.f. | S.S. | %V | Φ-Statistics |
|---|---|---|---|---|---|
| Regions | among regions (ΦCT) | 1 | 9.11 | 48.57 | 0.49 * |
| among populations within regions (ΦSC) | 18 | 6.72 | −0.80 | −0.02 | |
| within populations (ΦST) | 276 | 133.67 | 52.23 | 0.48 *** | |
| Islands | among islands (ΦCT) | 2 | 9.18 | 24.16 | 0.24 |
| among populations within islands (ΦSC) | 17 | 6.61 | −1.02 | −0.01 | |
| within populations (ΦST) | 276 | 133.5 | 76.86 | 0.23 *** | |
| Clusters | among clusters (ΦCT) | 9 | 12.16 | 6.95 | 0.070 |
| among populations within clusters (ΦSC) | 10 | 3.64 | −1.65 | −0.018 | |
| within populations (ΦST) | 276 | 133.5 | 94.71 | 0.053 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancilla-Morales, M.D.; Velarde, E.; Aguilar, A.; Contreras-Rodríguez, A.; Ezcurra, E.; Rosas-Rodríguez, J.A.; Soñanez-Organis, J.G.; Ruiz, E.A. Strong Philopatry, Isolation by Distance, and Local Habitat Have Promoted Genetic Structure in Heermann’s Gull. Diversity 2022, 14, 108. https://doi.org/10.3390/d14020108
Mancilla-Morales MD, Velarde E, Aguilar A, Contreras-Rodríguez A, Ezcurra E, Rosas-Rodríguez JA, Soñanez-Organis JG, Ruiz EA. Strong Philopatry, Isolation by Distance, and Local Habitat Have Promoted Genetic Structure in Heermann’s Gull. Diversity. 2022; 14(2):108. https://doi.org/10.3390/d14020108
Chicago/Turabian StyleMancilla-Morales, Misael Daniel, Enriqueta Velarde, Andres Aguilar, Araceli Contreras-Rodríguez, Exequiel Ezcurra, Jesús A. Rosas-Rodríguez, José G. Soñanez-Organis, and Enrico A. Ruiz. 2022. "Strong Philopatry, Isolation by Distance, and Local Habitat Have Promoted Genetic Structure in Heermann’s Gull" Diversity 14, no. 2: 108. https://doi.org/10.3390/d14020108
APA StyleMancilla-Morales, M. D., Velarde, E., Aguilar, A., Contreras-Rodríguez, A., Ezcurra, E., Rosas-Rodríguez, J. A., Soñanez-Organis, J. G., & Ruiz, E. A. (2022). Strong Philopatry, Isolation by Distance, and Local Habitat Have Promoted Genetic Structure in Heermann’s Gull. Diversity, 14(2), 108. https://doi.org/10.3390/d14020108








