Respiration Rates, Metabolic Demands and Feeding of Ephyrae and Young Medusae of the Rhizostome Rhopilema nomadica
Abstract
:1. Introduction
- Basal respiration rate—oxygen consumption (measured) and CO2 production (estimated). The prediction for these measures in R. nomadica is to be relatively low.
- Basal/minimum carbon demand, needed to cover the estimated CO2 production, accordingly also predicted to be low.
- Ingestion rate (measured) and carbon input (estimated), predicted to be high when compared to similarly sized individuals of other species.
- Carbon budget—input versus required, when evaluated in terms of required feeding duration to satisfy daily demands, predicted to be relatively low in R. nomadica.
2. Materials and Methods
2.1. Respiration Experiments
2.2. Respiration Measuring Equipment and Procedure
2.3. Regression Analyses of Respiration Rates
2.4. Minimum Daily Carbon Demand
2.5. Feeding Experiments
2.6. Predation Rates
Feeding Trials
2.7. Conversion Factors
2.8. Statistical Analysis
3. Results
3.1. Respiration Trials
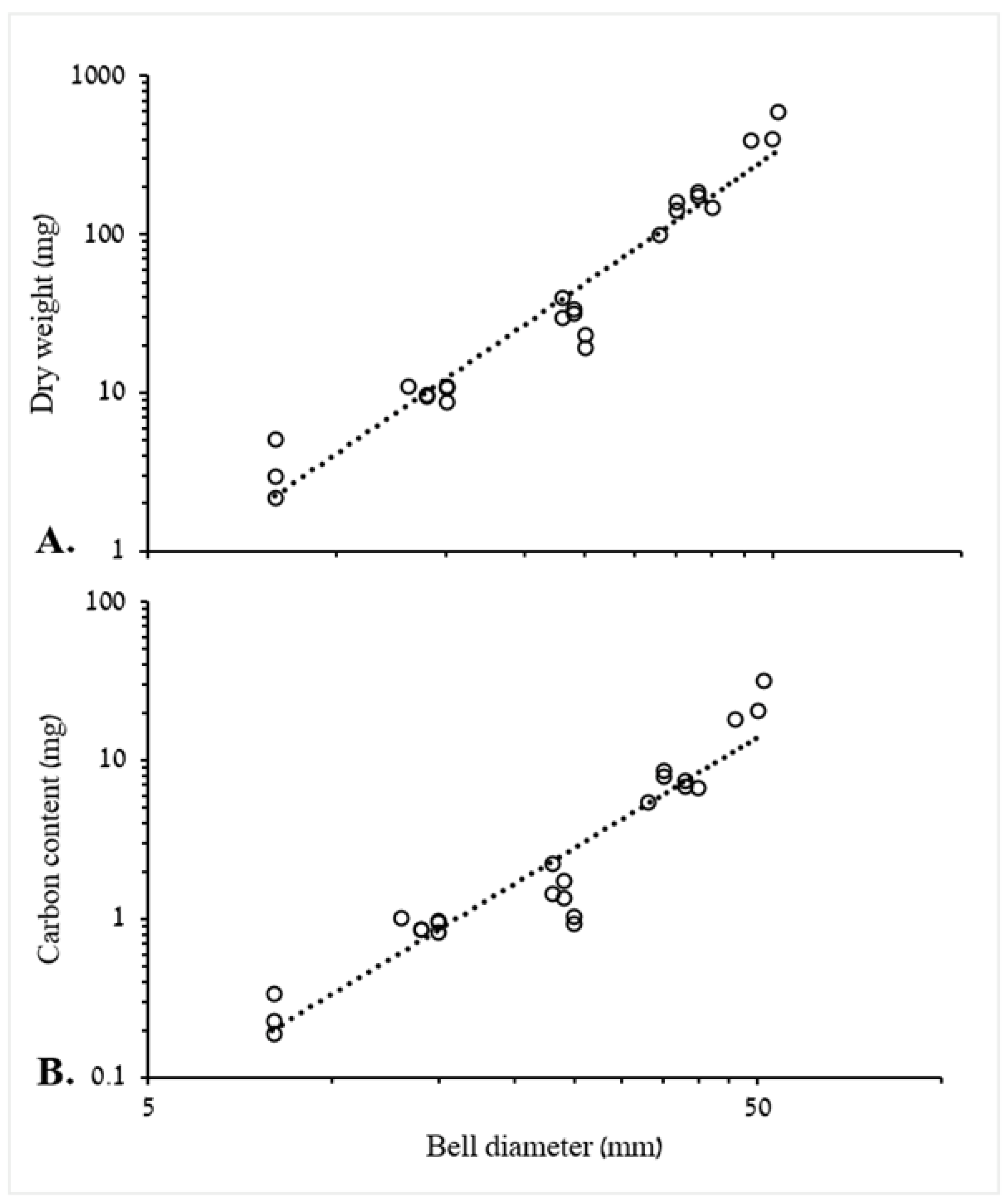
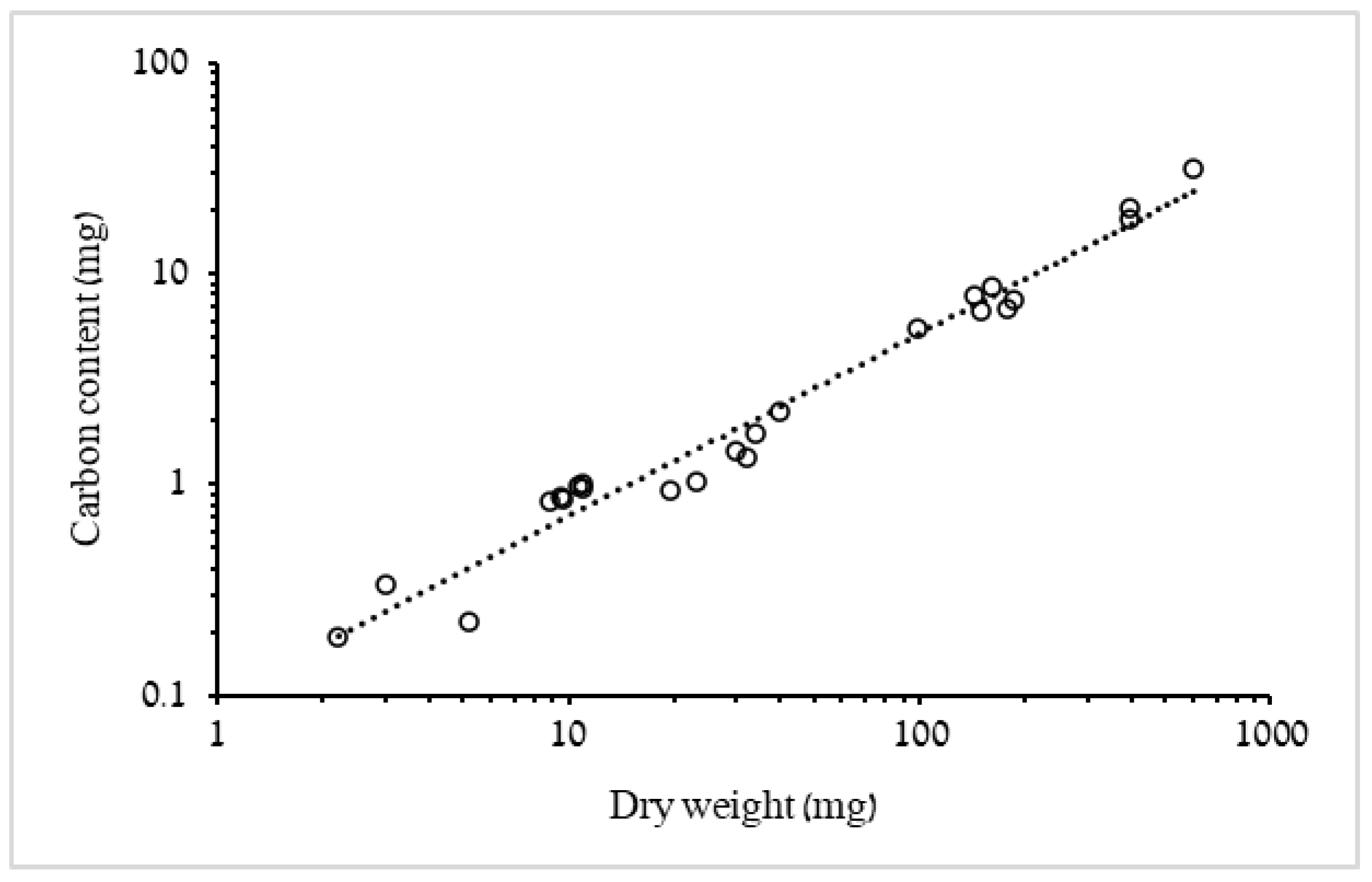
3.1.1. Biometric Relationships of Bell Diameter and Mass
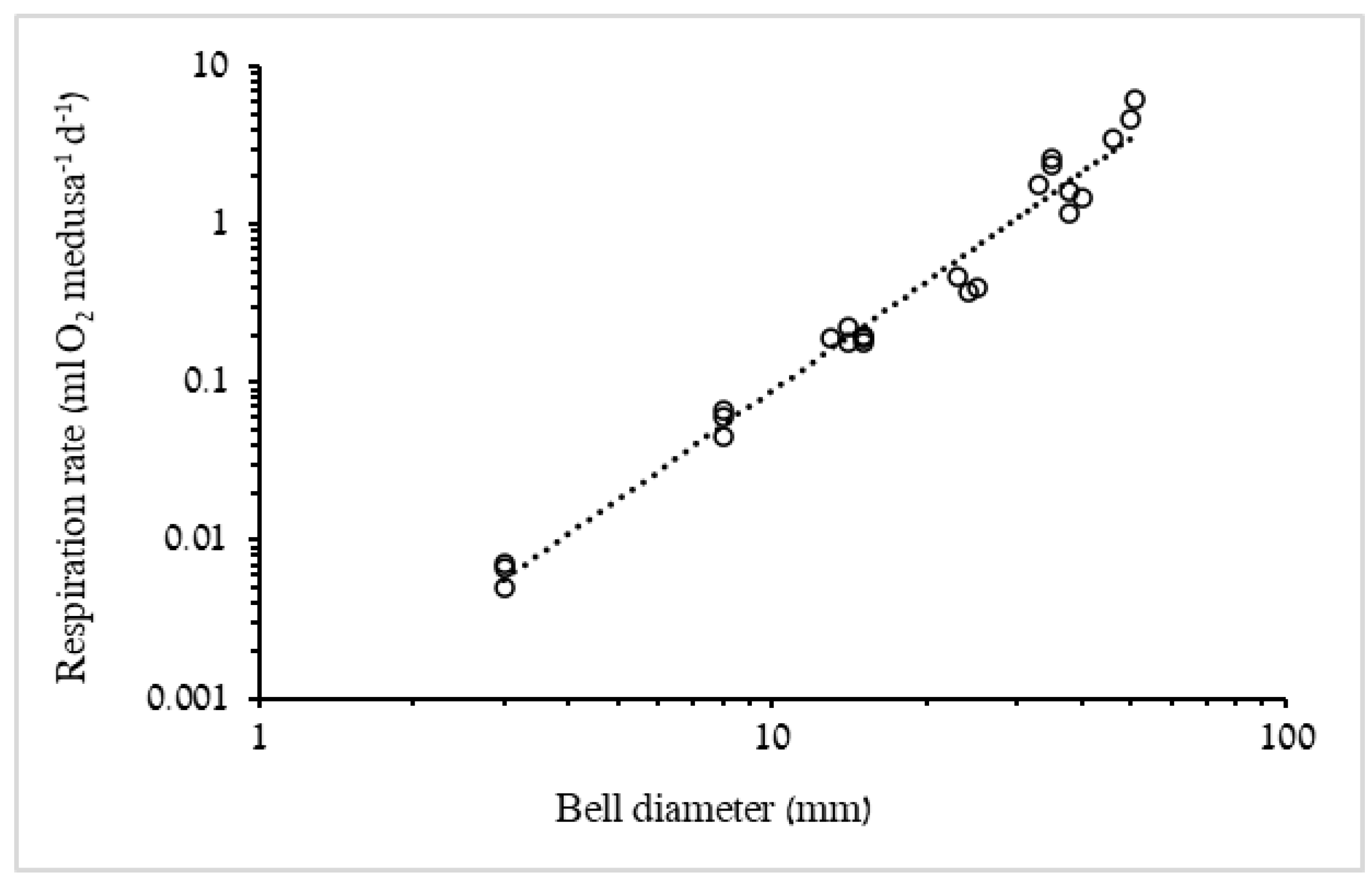
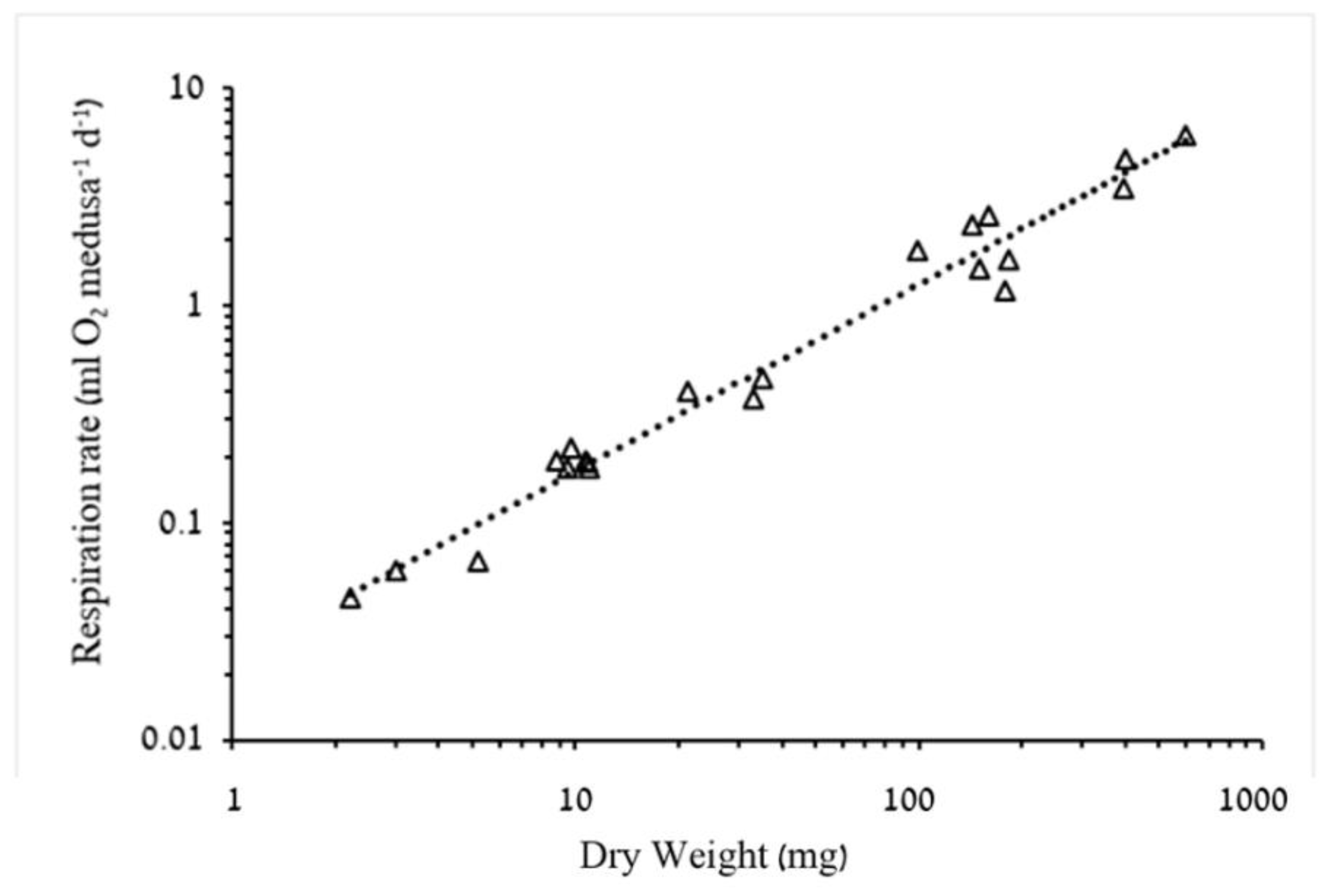
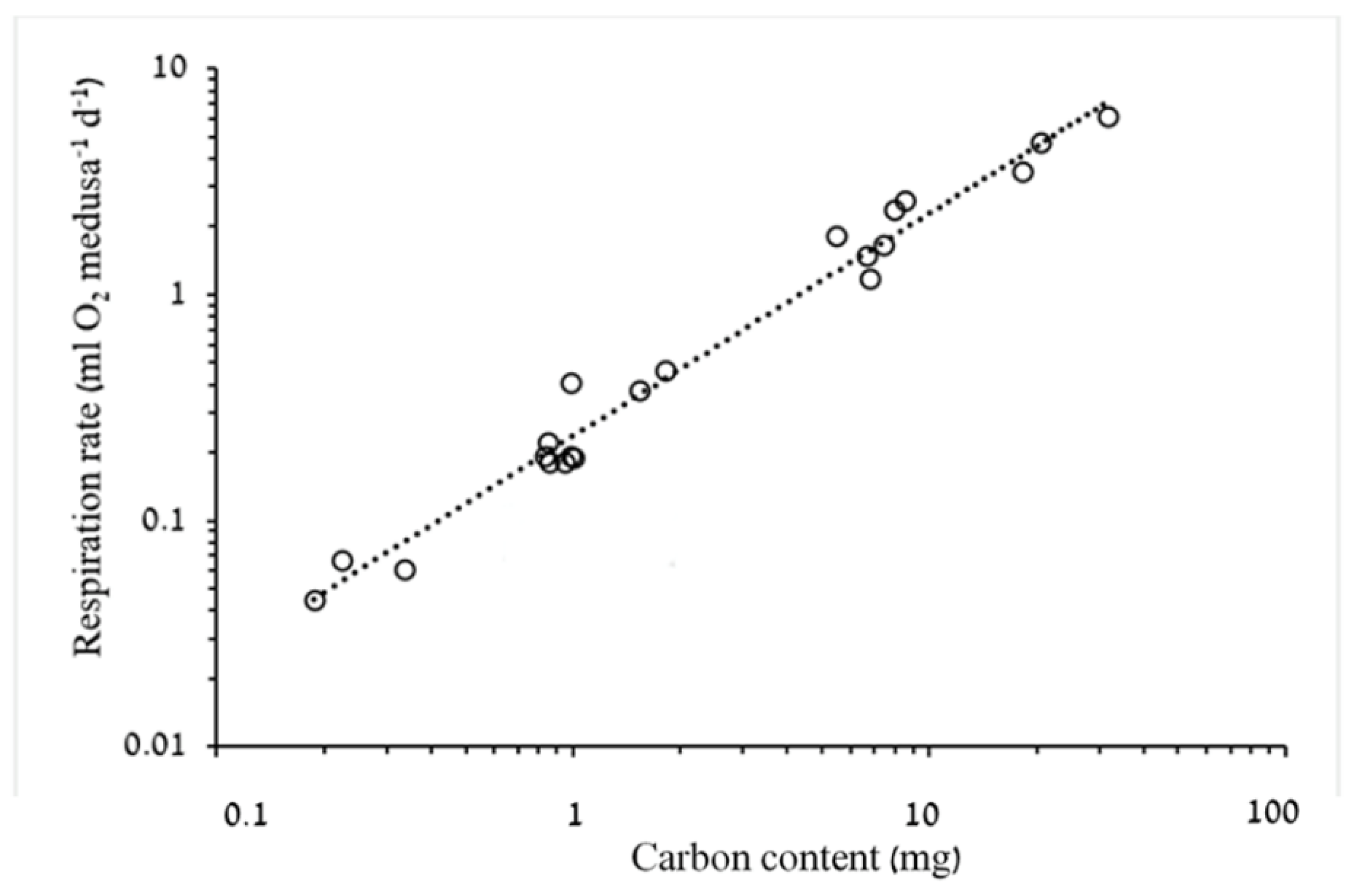
3.1.2. Respiration Rate and Carbon Demand
3.2. Feeding Experiments
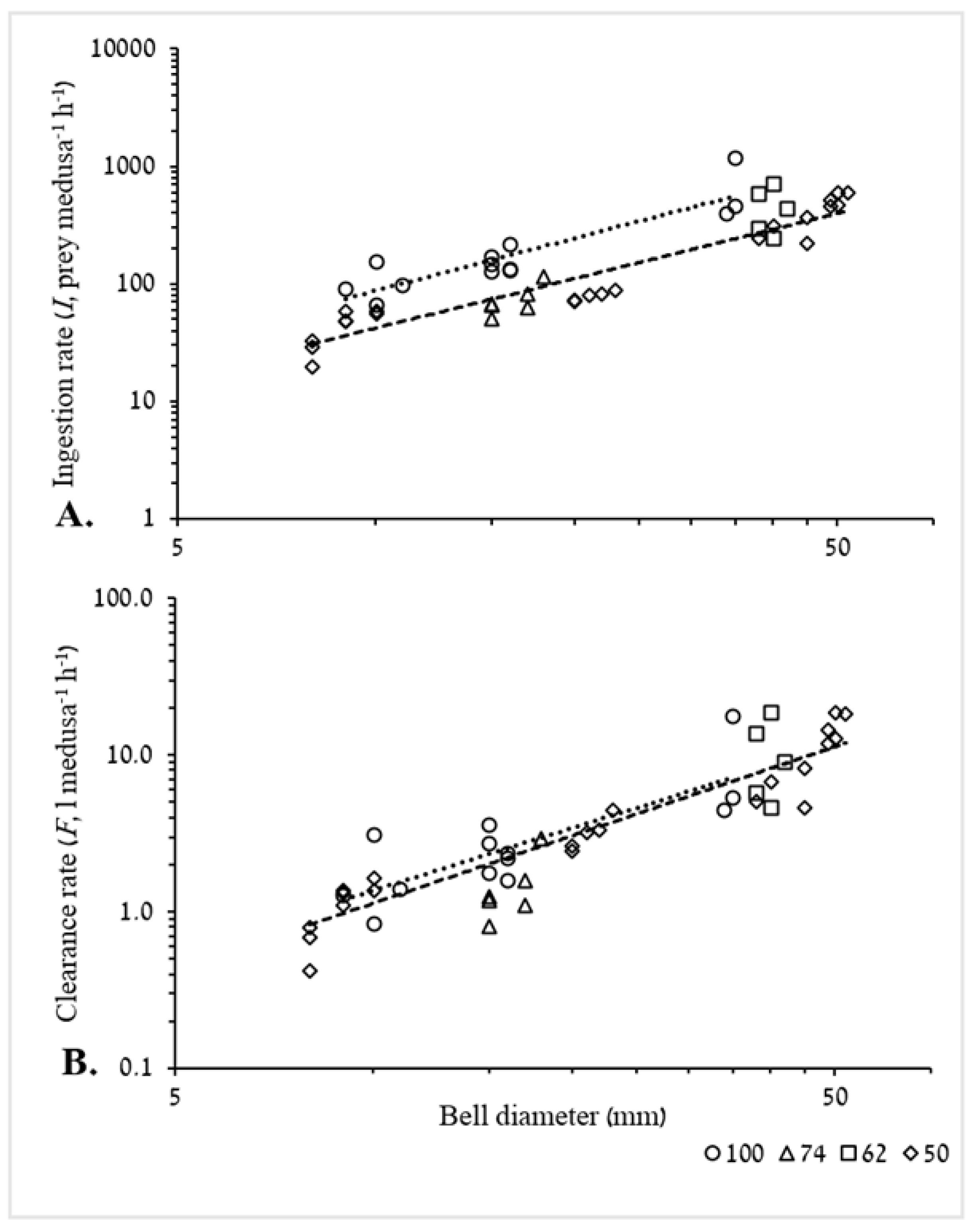
3.2.1. Ingestion and Clearance Rates
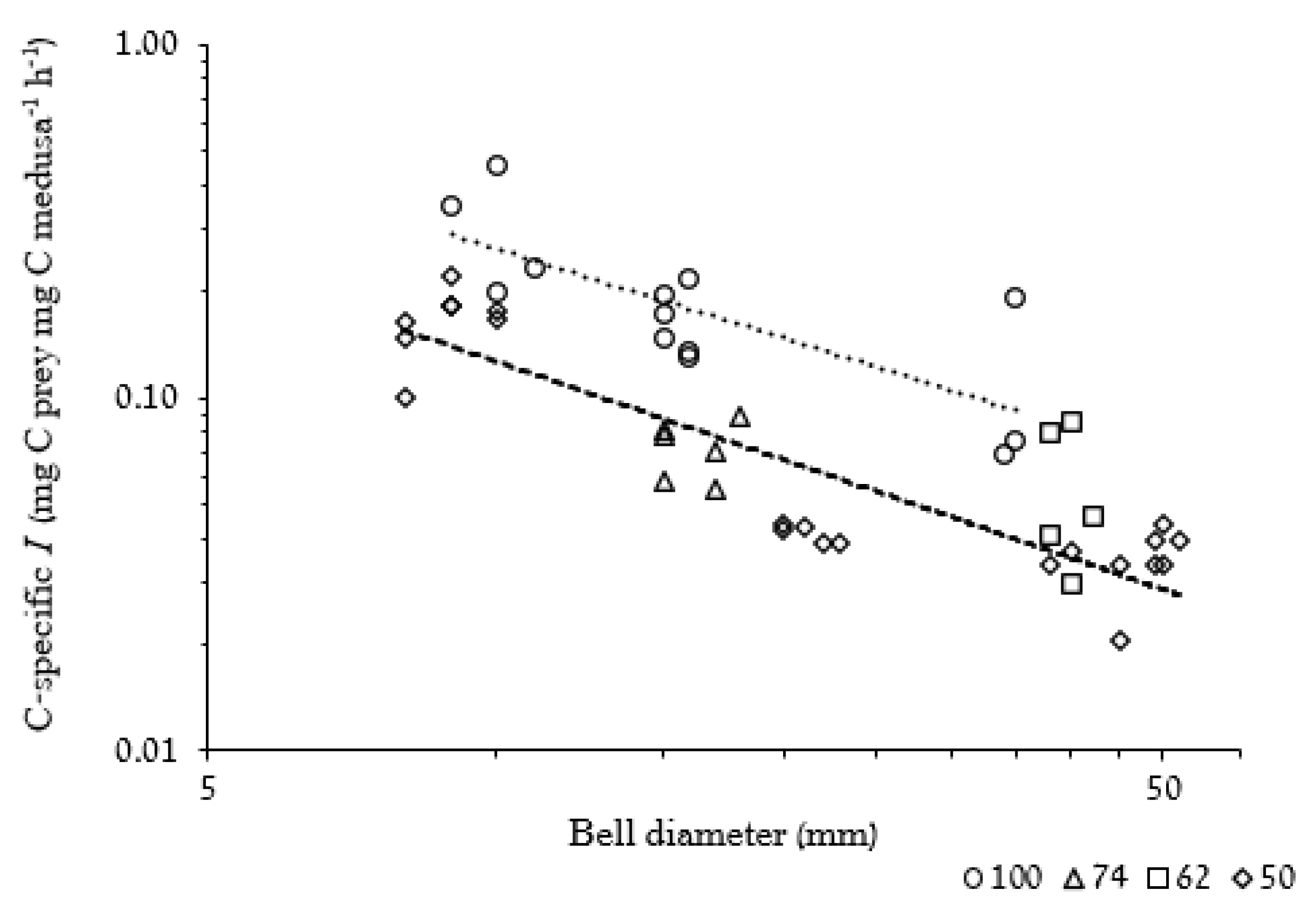
3.2.2. Weight-Specific Ingestion Rate
4. Discussion
4.1. Biometric Relationships
4.2. Respiration Rates
4.3. Carbon Demand
4.4. Feeding Experiments
4.4.1. Ingestion and Clearance Rates
4.4.2. Carbon Budget
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fraser, J.H. Experimental feeding of some medusae and chaetognatha. J. Fish. Res. Board Can. 1969, 26, 1743–1762. [Google Scholar] [CrossRef]
- Purcell, J.E.; Tilves, U.; Fuentes, V.L.; Milisenda, G.; Olariaga, A.; Sabates, A. Digestion times and predation potentials of Pelagia noctiluca eating fish larvae and copepods in the NW Mediterranean Sea. Mar. Ecol. Prog. Ser. 2014, 510, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Purcell, J.E. Extension of methods for jellyfish and ctenophore trophic ecology to large-scale research. Hydrobiologia 2009, 616, 23–50. [Google Scholar] [CrossRef] [Green Version]
- Haury, L.; McGowan, J.; Wiebe, P. Patterns and processes in the time-space scales of plankton distributions. In Spatial Pattern in Plankton Communities; Springer: Boston, MA, USA, 1978; pp. 277–327. [Google Scholar]
- Kuplik, Z. Proliferation of the Scyphomedusa Rhopilema nomadica in the Eastern Mediterranean: Efficiency in Resource Exploitation in an Oligotrophic Environment? Ph.D. Thesis, University of Haifa, Haifa, Israel, 2017. [Google Scholar]
- Pitt, K.A.; Clement, A.L.; Connolly, R.M.; Thibault-Botha, D. Predation by jellyfish on large and emergent zooplankton: Implications for benthic-pelagic coupling. Estuar. Coast. Shelf Sci. 2008, 76, 827–833. [Google Scholar] [CrossRef] [Green Version]
- Kress, N.; Herut, B. Hyper-nutrification in the oligotrophic Eastern Mediterranean. A study in Haifa Bay, Israel. Estuar. Coast. Shelf Sci. 1998, 46, 645–656. [Google Scholar] [CrossRef]
- Larson, R.J. Respiration and carbon turnover rates of medusae from the NE Pacific. Comp. Biochem. Physiol. Part A Physiol. 1987, 87, 93–100. [Google Scholar] [CrossRef]
- Han, C.H.; Chae, J.; Jin, J.; Yoon, W. Estimation of the minimum food requirement using the respiration rate of medusa of Aurelia aurita in Sihwa Lake. Ocean Sci. J. 2012, 47, 155–160. [Google Scholar] [CrossRef]
- Lilley, M.K.; Elineau, A.; Ferraris, M.; Thiery, A.; Stemmann, L.; Gorsky, G.; Lombard, F. Individual shrinking to enhance population survival: Quantifying the reproductive and metabolic expenditures of a starving jellyfish, Pelagia noctiluca. J. Plankton Res. 2014, 36, 1585–1597. [Google Scholar] [CrossRef] [Green Version]
- Hamner, W.M. Design developments in the plankton kreisel, a plankton aquarium for ships at sea. J. Plankton Res. 1990, 12, 397–402. [Google Scholar] [CrossRef]
- International Council for the Exploration of the Sea (ICES). Available online: https://www.ices.dk (accessed on 1 January 2021).
- Kremer, P. Respiration and excretion by ctenophore Mnepiopsis leidyi. Mar. Biol. 1977, 44, 43–50. [Google Scholar] [CrossRef]
- Purcell, J.E.; Fuentes, V.; Atienza, D.; Tilves, U.; Astorga, D.; Kawahara, M.; Hays, G.C. Use of respiration rates of scyphozoan jellyfish to estimate their effects on the food web. Hydrobiologia 2010, 645, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Hansson, L.J.; Moeslund, O.; Kiørboe, T.; Riisgård, H.U. Clearance rates of jellyfish and their potential predation impact on zooplankton and fish larvae in a neritic ecosystem (Limfjorden, Denmark). Mar. Ecol. Prog. Ser. 2005, 304, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Moller, L.F.; Riisgard, H.U. Feeding, bioenergetics and growth in the common jellyfish Aurelia aurita and two hydromedusae, Sarsia tubulosa and Aequorea vitrina. Mar. Ecol. Prog. Ser. 2007, 346, 167–177. [Google Scholar] [CrossRef]
- Olesen, N.J.; Frandsen, K.; Riisgard, H.U. Population dynamics, growth and energetics of jellyfish Aurelia aurita in a shallow fjord. Mar. Ecol. Prog. Ser. 1994, 105, 9–18. [Google Scholar] [CrossRef]
- Ohman, M.D. Energy sources for recruitment of the sub-antarctic copepod neocalanus tonsus. Limnol. Oceanogr. 1987, 32, 1317–1330. [Google Scholar] [CrossRef] [Green Version]
- Osinga, R.; Charko, F.; Cruzeiro, C.; Janse, M.; Grymonpre, D.; Sorgeloos, P.; Verreth, J.A.J. Feeding corals in captivity: Uptake of four Artemia-based feeds by Galaxea fascicularis. In Proceedings of the 11th International Coral Reef Symposium, Fort Lauderdale, FL, USA, 7–11 July 2008; pp. 149–153. [Google Scholar]
- Evjemo, J.O.; Olsen, Y. Effect of food concentration on the growth and production rate of Artemia franciscana feeding on algae (T-iso). J. Exp. Mar. Biol. Ecol. 1999, 242, 273–296. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.L. The effect of temperature and food supply on the growth and ontogeny of Aurelia. sp 1 ephyrae. Hydrobiologia 2015, 754, 157–167. [Google Scholar] [CrossRef]
- Szyper, J.P. Nutritional depletion of the aquaculture feed organisms Euterpina acutifrons, Artemia sp. and Brachionus plicatilis during starvation. J. World Aquac. Soc. 1989, 20, 162–169. [Google Scholar] [CrossRef]
- Larson, R.J. Water content, organic content, and carbon and nitrogen composition of medusae from the northeast Pacific. J. Exp. Mar. Biol. Ecol. 1986, 99, 107–120. [Google Scholar] [CrossRef]
- Uye, S.; Shimauchi, H. Population biomass, feeding, respiration and growth rates, and carbon budget of the scyphomedusa Aurelia aurita in the Inland Sea of Japan. J. Plankton Res. 2005, 27, 237–248. [Google Scholar] [CrossRef] [Green Version]
- Shenker, J.M. Carbon content of the neritic scyphomedusa Chrysaora fuscescens. J. Plankton Res. 1985, 7, 169–173. [Google Scholar] [CrossRef]
- Purcell, J.E. Effects of predation by the scyphomedusan Chrysaora quinquecirrha on zooplankton populations in Chesapeake Bay, USA. Mar. Ecol. Prog. Ser. 1992, 87, 65–76. [Google Scholar] [CrossRef]
- Graham, W.; Martin, D.; Felder, D.; Asper, V.; Perry, H. Ecological and economic implications of a tropical jellyfish invader in the Gulf of Mexico. In Marine Bioinvasions: Patterns, Processes and Perspectives; Springer: Dordrecht, The Netherlands, 2003; pp. 53–69. [Google Scholar]
- Lucas, C.H.; Pitt, K.A.; Purcell, J.E.; Lebrato, M.; Condon, R.H. What's in a jellyfish? Proximate and elemental composition and biometric relationships for use in biogeochemical studies. ESA Ecol. 2011, 92, 1704. [Google Scholar] [CrossRef] [Green Version]
- Hirst, A.G.; Lucas, C.H. Salinity influences body weight quantification in the scyphomedusa Aurelia aurita: Important implications for body weight determination in gelatinous zooplankton. Mar. Ecol. Prog. 1998, 165, 259–269. [Google Scholar] [CrossRef]
- Kogovsek, T.; Tinta, T.; Klun, K.; Malej, A. Jellyfish biochemical composition: Importance of standardised sample processing. Mar. Ecol. Prog. Ser. 2014, 510, 275–288. [Google Scholar] [CrossRef]
- Lucas, C.H. Biochemical composition of Aurelia aurita in relation to age and sexual maturity. J. Exp. Mar. Biol. Ecol. 1994, 183, 179–192. [Google Scholar] [CrossRef]
- Kleiber, M. Body size and metabolism. Hilgardia 1932, 6, 315–353. [Google Scholar] [CrossRef] [Green Version]
- Savage, V.M.; Gillooly, J.F.; Woodruff, W.H.; West, G.B.; Allen, A.P.; Enquist, B.J.; Brown, J.H. The predominance of quarter-power scaling in biology. Funct. Ecol. 2004, 18, 257–282. [Google Scholar] [CrossRef]
- Bonner, J.T. Size, function, and life-history. Calder, WA. Nature 1984, 312, 475–476. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: Towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S. The 3/4-power law is not universal: Evolution of isometric, ontogenetic metabolic scaling in pelagic animals. Biosci. 2006, 56, 325–332. [Google Scholar] [CrossRef] [Green Version]
- Bokma, F. Evidence against universal metabolic allometry. Funct. Ecol. 2004, 18, 184–187. [Google Scholar] [CrossRef]
- White, C.R.; Cassey, P.; Blackburn, T.M. Allometric exponents do not support a universal metabolic allometry. Ecology 2007, 88, 315–323. [Google Scholar] [CrossRef]
- Glazier, D.S. Beyond the '3/4-power law': Variation in the intra- and interspecific scaling of metabolic rate in animals. Biol. Rev. 2005, 80, 611–662. [Google Scholar] [CrossRef] [PubMed]
- Reeve, M.R.; Walter, M.A. Laboratory studies of ingestion and food utilization in lobate and tentaculate ctenophores. Limnol. Oceanogr. 1978, 23, 740–751. [Google Scholar] [CrossRef]
- Larson, R.J. Trophic Ecology of Gelatinous Predators (Cnidaria and Ctenophora) in Saanich Inlet, Vancouver Is., B.C., Canada. Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 1985. [Google Scholar]
- McHenry, M.J.; Jed, J. The ontogenetic scaling of hydrodynamics and swimming performance in jellyfish (Aurelia aurita). J. Exp. Biol. 2003, 206, 4125–4137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinoshita, J.; Hiromi, J.; Kadota, S. Do respiratory metabolic rates of the scyphomedusa Aurelia aurita scale isometrically throughout ontogeny in a sexual generation? Hydrobiologia 1997, 347, 51–55. [Google Scholar] [CrossRef]
- Moller, L.F.; Riisgard, H.U. Respiration in the scyphozoan jellyfish Aurelia aurita and two hydromedusae (Sarsia tubulosa and Aequorea vitrina): Effect of size, temperature and growth. Mar. Ecol. Prog. Ser. 2007, 330, 149–154. [Google Scholar] [CrossRef]
- Ikeda, T. Metabolic rates of epipelagic marine zooplankton as a function of body-mass and temperature. Mar. Biol. 1985, 85, 1–11. [Google Scholar] [CrossRef]
- Schneider, G. A comparison of carbon-specific respiration rates in gelatinous and nongelatinous zooplankton: A search for general rules in zooplankton metabolism. Helgol. Meeresunters. 1992, 46, 377–388. [Google Scholar] [CrossRef] [Green Version]
- Shanks, A.L.; Graham, W.M. Orientated swimming in the jellyfish Stomolopus meleagris L-Agassiz (Scyphozoan, Rhizostomida). J. Exp. Mar. Biol. Ecol. 1987, 108, 159–169. [Google Scholar] [CrossRef]
- D'Ambra, I.; Costello, J.H.; Bentivegna, F. Flow and prey capture by the scyphomedusa Phyllorhiza punctata von Lendenfeld, 1884. Hydrobiologia 2001, 451, 223–227. [Google Scholar] [CrossRef]
- Uye, S.I. Blooms of the giant jellyfish Nemopilema nomurai: A threat to the fisheries sustainability of the East Asian Marginal Seas. Plankton Benthos Res. 2008, 3, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Vernon, H.M. The respiratory exchange of the lower invertebrates. J. Physiol. 1895, 19, 18–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yakovleva, K.K. Respiration intensity of some Black Sea medusae. Proc. Sevas. Biol. Stn. (Fish. Res. Board Can. Trans. Ser. No 2218) 1964, 17, 364–637. [Google Scholar]
- Kruger, F. Metabolism and growth in scyphomedusae. Helgol. Wiss. Meeresunters. 1968, 18, 367–383. [Google Scholar]
- Nemazie, D.A.; Purcell, J.E.; Glibert, P.M. Ammonium excretion by gelatinous zooplankton and their contribution to the ammonium requirements of microplankton in Chesapeake Bay. Mar. Biol. 1993, 116, 451–458. [Google Scholar] [CrossRef]
- Dawson, M.N.; Martin, L.E. Geographic variation and ecological adaptation in Aurelia (Scyphozoa, Semaeostomeae): Some implications from molecular phylogenetics. Hydrobiologia 2001, 451, 259–273. [Google Scholar] [CrossRef]
- Larson, R.J. Diet, prey selection and daily ration of Stomolophus meleagris, a filter-feeding scyphomedusa from the NE Gulf of Mexico. Estuar. Coast. Shelf Sci. 1991, 32, 511–525. [Google Scholar] [CrossRef]
- Schneider, G. Estimation of food demands of Aurelia aurita medusae populations in the Kiel Bight western Baltic. Ophelia 1989, 31, 17–27. [Google Scholar] [CrossRef]
- Ishii, H.; Tanaka, F. Respiration rates and metabolic demands of Aurelia aurita in Tokyo Bay with special reference to large medusae. Plankton Benthos Res. 2006, 1, 64–67. [Google Scholar] [CrossRef] [Green Version]
- Fancett, M.S. Diet and prey selectivity of scyphomedusae from Port Phillip Bay, Australia. Mar. Biol. 1988, 98, 503–509. [Google Scholar] [CrossRef]
- Perez-Ruzafa, A.; Gilabert, J.; Gutierrez, J.M.; Fernandez, A.I.; Marcos, C.; Sabah, S. Evidence of a planktonic food web response to changes in nutrient input dynamics in the Mar Menor coastal lagoon, Spain. Hydrobiologia 2002, 475, 359–369. [Google Scholar] [CrossRef]
- Morand, P.; Carre, C.; Biggs, D.C. Feeding and metabolism of the jellyfish Pelagia noctiluca (Scyphomedusae, Semaeostomae). J. Plankton Res. 1987, 9, 651–665. [Google Scholar] [CrossRef]
- Riisgard, H.U.; Madsen, C.V. Clearance rates of ephyrae and small medusae of the common jellyfish Aurelia aurita offered different types of prey. J. Sea Res. 2011, 65, 51–57. [Google Scholar] [CrossRef]
- Kramp, P. Zoogeographical studies on Rhizostomeae (Scyphozoa). Vidensk. Medd. Fra Dan. Nat. Foren. 1970, 133, 7–30. [Google Scholar]
- Hamner, W.M.; Hauri, I.R. Long distance horizontal migrations of zooplankton (Scyphomedusae, Mastigias). Limnol. Oceanogr. 1981, 26, 414–423. [Google Scholar]
- Kuplik, Z.; Angel, D. Diet composition and some observations on the feeding ecology of the rhizostome Rhopilema nomadica in Israeli coastal waters. J. Mar. Biol. Assoc. UK 2020, 100, 681–689. [Google Scholar] [CrossRef]
- Pasternak, A.; Wassmann, P.; Riser, C.W. Does mesozooplankton respond to episodic P inputs in the Eastern Mediterranean? Deep. Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 2975–2989. [Google Scholar] [CrossRef]
- Costello, J.H.; Colin, S.P. Morphology, fluid motion and predation by the scyphomedusa Aurelia aurita. Mar. Biol. 1994, 121, 327–334. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.E.; Yoon, W.D.; Lim, D. Description of feeding apparatus and mechanism in Nemopilema nomurai kishinouye (Scyphozoa: Rhizostomeae). Ocean. Sci. J. 2008, 43, 61–65. [Google Scholar] [CrossRef]
- Buskey, E.J.; Lenz, P.H.; Hartline, D.K. Escape behavior of planktonic copepods in response to hydrodynamic disturbances: High speed video analysis. Mar. Ecol. Prog. Ser. 2002, 235, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Hansson, L.J.; Norrman, B. Release of dissolved organic carbon (dog) by the scyphozoan jellyfish Aurelia aurita and its potential influence on the production of planktic bacteria. Mar. Biol. 1995, 121, 527–532. [Google Scholar] [CrossRef]
- Reeve, M.R.; Syms, M.A.; Kremer, P. Growth dynamics of a ctenophore (Mnemiopsis) in relation to variable food-supply. I. carbon biomass, feeding, egg-production, growth and assimilation efficiency. J. Plankton Res. 1989, 11, 535–552. [Google Scholar] [CrossRef]
- Daan, R. Food-intake and growth of Sarsia tubulosa (sars, 1835), with quantitative estimates of predation on copepod populations. Neth. J. Sea Res. 1986, 20, 67–74. [Google Scholar] [CrossRef]
- Kiorboe, T.; Hirst, A.G. Shifts in Mass Scaling of Respiration, Feeding, and Growth Rates across Life-Form Transitions in Marine Pelagic Organisms. Am. Nat. 2014, 183, E118–E130. [Google Scholar] [CrossRef] [Green Version]
- Larson, R.J. Daily ration and predation by medusae and ctenophores in Saanich Inlet, BC, Canada. Neth. J. Sea Res. 1987, 21, 35–44. [Google Scholar] [CrossRef]
| Date | Water Temperature (°C) | N | n | BD (mm) | V (L) | t (min) |
|---|---|---|---|---|---|---|
| 3 September 2014 | 29.8 | 3 | 10 | 3 | 0.02 | 180 |
| 10 September 2014 | 29 | 3 | 1 | 14 ± 1 | 0.02 | 120 |
| 14 September 2014 | 29 | 3 | 1 | 15 ± 1 | 0.02 | 130 |
| 1 October 2014 | 27.5 | 3 | 1 | 8 ± 0 | 0.02 | 180 |
| 15 October 2014 | 26.5 | 3 | 1 | 34 ± 1 | 1 | 380 |
| 23 October 2014 | 26 | 3 | 1 | 49 ± 3 | 1 | 230 |
| 19 November 2014 | 23 | 3 | 1 | 39 ± 1 | 0.4 | 130 |
| 2 December 2014 | 21 | 3 | 2 | 24 ± 1 | 0.4 | 130 |
| Date | Temperature (°C) | N | BD (mm) | V (L) | C (Artemia L−1) | t (min) |
|---|---|---|---|---|---|---|
| 28 September 2014 | 28 | 3 | 15 ± 1 | 2 | 100 | 60 |
| 1 October 2014 | 28 | 4 | 10 ± 1 | 2 | 97 | 60 |
| 9 October 2014 | 28 | 3 | 16 ± 1 | 2 | 100 | 30 |
| 13 October 2014 | 27.5 | 3 | 35 ± 1 | 20 | 99 | 60 |
| 18 October 2014 | 27 | 4 | 9 ± 1 | 2 | 50 | 60 |
| 18 October 2014 | 27 | 4 | 9 ± 1 | 2 | 50 | 30 |
| 20 October 2014 | 25.5 | 5 | 50 ± 1 | 20 | 50 | 60 |
| 24 October 2014 | 25 | 5 | 21 ± 1 | 2 | 50 | 60 |
| 31 October 2014 | 24.5 | 6 | 16 ± 1 | 2 | 74 | 60 |
| 1 November 2014 | 24.2 | 4 | 42 ± 4 | 17 | 53 | 45 |
| 18 November 2014 | 23 | 5 | 40 ± 2 | 17 | 62 | 60 |
| Artemia spp. | Carbon Content (µg) of Newly Hatched Nauplii | Reference |
|---|---|---|
| A. salina | 0.5 | [18] |
| A. salina | 0.3 | [19] |
| A. franciscana | 0.93 | [20] |
| A. sp. | 1 | [21] |
| A. sp. | 0.69–1.63 | [22] |
| N | BD (mm) | Dry Weight (mg) | Carbon Content (mg) | C%/DW | RR (mL O2 ind−1 d−1) | DW-RR (mL O2 mg DW−1 d−1) | C-RR (mL O2 mg C−1 d−1) | Carbon Demand (%) of Body C d−1 |
|---|---|---|---|---|---|---|---|---|
| 30 † | 3 | 0.21 ± 0.04 | 0.03 ± 0.00 | 12.2 ± 0.3 | 0.006 ± 0.001 | 0.030 ± 0.001 | 0.249 ± 0.001 | 10.7 ± 0.0 |
| 3 | 8 | 3.47 ± 1.55 | 0.25 ± 0.08 | 8.0 ± 3.5 | 0.057 ± 0.011 | 0.018 ± 0.004 | 0.238 ± 0.058 | 10.2 ± 2.4 |
| 3 | 14 ± 1 | 10.47 ± 0.84 | 0.94 ± 0.07 | 9.0 ± 0.3 | 0.183 ± 0.006 | 0.018 ± 0.001 | 0.194 ± 0.012 | 8.3 ± 0.5 |
| 3 | 15 ± 1 | 9.73 ± 0.95 | 0.89 ± 0.08 | 9.2 ± 0.3 | 0.203 ± 0.016 | 0.021 ± 0.002 | 0.229 ± 0.032 | 9.8 ± 1.4 |
| 6 †† | 24 ± 1 | 29.78 ± 7.45 | 1.46 ± 0.48 | 4.8 ± 0.5 | 0.413 ± 0.045 | 0.014 ± 0.004 | 0.301 ± 0.093 | 12.9 ± 4.0 |
| 3 | 34 ± 1 | 134 ± 31.48 | 7.37 ± 1.64 | 5.5 ± 0.1 | 2.252 ± 0.401 | 0.017 ± 0.001 | 0.308 ± 0.018 | 13.2 ± 0.8 |
| 3 | 39 ± 1 | 170.67 ± 18.15 | 7.01 ± 0.40 | 4.1 ± 0.3 | 1.437 ± 0.237 | 0.008 ± 0.002 | 0.205 ± 0.029 | 8.8 ± 1.3 |
| 3 | 49 ± 3 | 465 ± 118.65 | 23.64 ± 7.24 | 5.0 ± 0.4 | 4.760 ± 1.305 | 0.010 ± 0.001 | 0.203 ± 0.021 | 8.7 ± 0.9 |
| N | BD (mm) | Carbon Content (mg) | Prey Concentration (ind L−1) | Minimum Prey Requirement (ind d−1) | I (ind Medusa−1 h−1) | F (L Medusa−1 h−1) | Required Number of 1 h Feeding Sessions |
|---|---|---|---|---|---|---|---|
| 8 | 9 ± 1 | 0.255 ± 0.060 | Low | 26 | 44 ± 15.5 | 1.1 ± 0.4 | 0.60 |
| 5 | 21 ± 1 | 1.906 ± 0.274 | Low | 191 | 78 ± 7.2 | 3.2 ± 0.8 | 2.45 |
| 5 | 40 ± 2 | 8.089 ± 0.798 | Low | 809 | 451 ± 192 | 10.3 ± 5.9 | 1.79 |
| 4 | 42 ± 4 | 9.326 ± 1.804 | Low | 933 | 286 ± 66.9 | 6.2 ± 1.7 | 3.26 |
| 5 | 50 ± 1 | 13.867 ± 0.797 | Low | 1387 | 528 ± 72.8 | 15.2 ± 3.1 | 2.62 |
| 3 | 16 ± 1 | 0.942 ± 0.079 | Med | 94 | 74 ± 22.4 | 1.6 ± 1.0 | 1.24 |
| 4 | 10 ± 1 | 0.335 ± 0.063 | High | 34 | 102 ± 36.2 | 2.8 ± 0.7 | 0.33 |
| 3 | 15 ± 1 | 0.897 ± 0.079 | High | 90 | 149 ± 17 | 1.5 ± 0.8 | 0.60 |
| 6 | 16 ± 1 | 1.021 ± 0.195 | High | 102 | 157 ± 51.2 | 1.9 ± 0.4 | 0.65 |
| 3 | 35 ± 1 | 5.931 ± 0.227 | High | 593 | 674 ± 425 | 9.1 ± 7.4 | 0.87 |
| Species | Carbon Mass (mg) | Temperature (°C) | Carbon-Specific Respiration Rate * | Reference |
|---|---|---|---|---|
| Rhopilema nomadica | 0.25–23.64 | 21–29 | 0.24 ± 0.06 | Present study |
| Rhizostoma pulmo | 36.3 | 16, 20 | 0.17 | [50,51] |
| Rhizostoma octopus | 100, 1 × 106 | 15 | 0.16 | [52] |
| Nemopilema nomurai | 1.89 × 103–1.89 × 104 | not specified | 0.12 | [49] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuplik, Z.; Kerem, D.; Angel, D.L. Respiration Rates, Metabolic Demands and Feeding of Ephyrae and Young Medusae of the Rhizostome Rhopilema nomadica. Diversity 2021, 13, 320. https://doi.org/10.3390/d13070320
Kuplik Z, Kerem D, Angel DL. Respiration Rates, Metabolic Demands and Feeding of Ephyrae and Young Medusae of the Rhizostome Rhopilema nomadica. Diversity. 2021; 13(7):320. https://doi.org/10.3390/d13070320
Chicago/Turabian StyleKuplik, Zafrir, Dani Kerem, and Dror L. Angel. 2021. "Respiration Rates, Metabolic Demands and Feeding of Ephyrae and Young Medusae of the Rhizostome Rhopilema nomadica" Diversity 13, no. 7: 320. https://doi.org/10.3390/d13070320
APA StyleKuplik, Z., Kerem, D., & Angel, D. L. (2021). Respiration Rates, Metabolic Demands and Feeding of Ephyrae and Young Medusae of the Rhizostome Rhopilema nomadica. Diversity, 13(7), 320. https://doi.org/10.3390/d13070320







