Building a Robust, Densely-Sampled Spider Tree of Life for Ecosystem Research
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Collection
2.2. Species Identification and Community Composition
2.3. Laboratory Protocols and Molecular Data
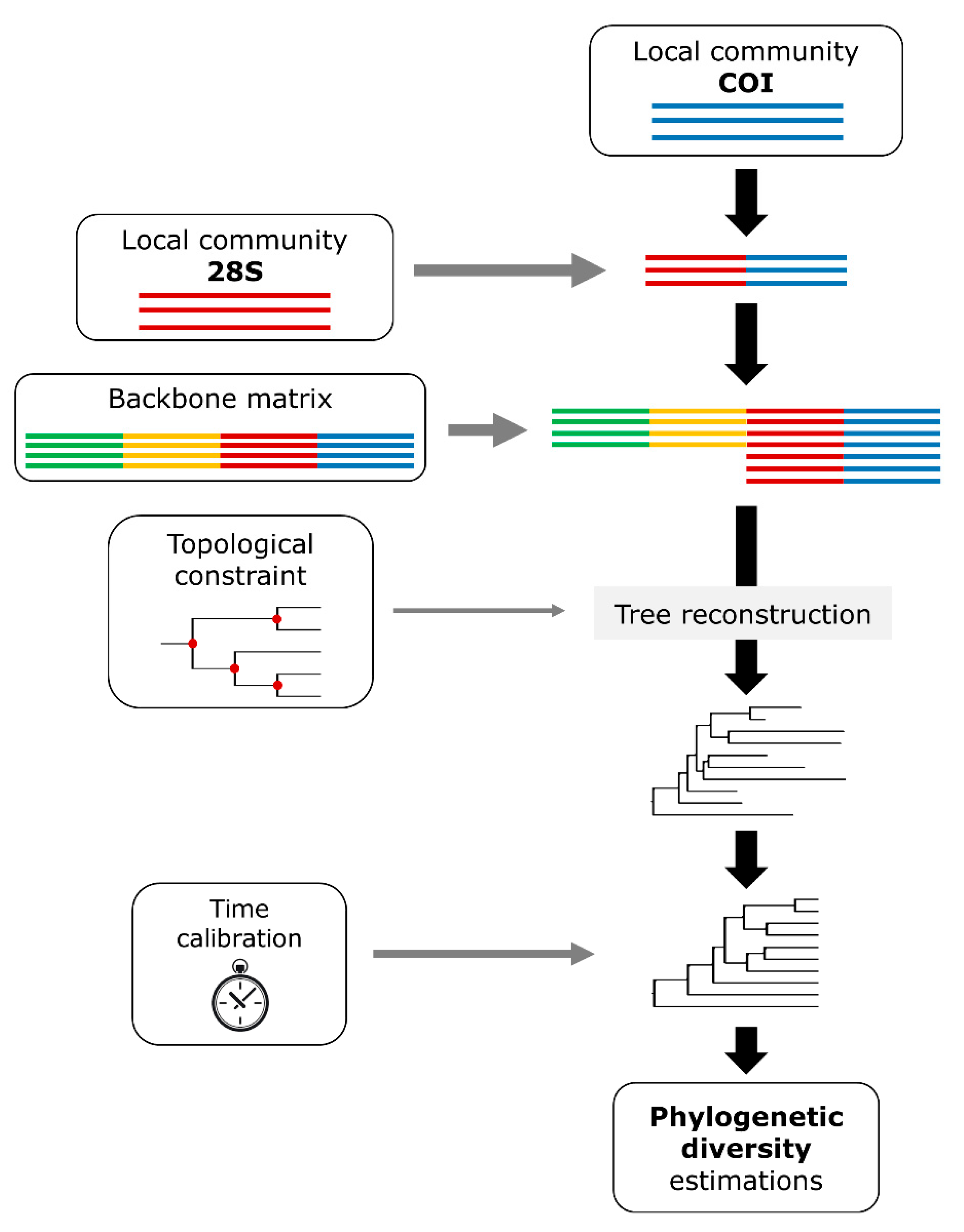
2.4. Phylogenetic Analyses
2.4.1. Ibercoding and NetBiome-MacDiv Matrices
2.4.2. Topological Constraint
2.4.3. Backbone Matrix
2.4.4. Maximum Likelihood Analyses
2.4.5. Inferring Ultrametric Trees
2.4.6. Tree Similarity and Monophyly Levels
2.5. Phylogenetic Community Metrics and Statistical Analyses
2.6. Null Models and Ecological Patterns
3. Results
3.1. COI and 28S Sequences
3.2. Phylogenetic Trees
3.3. Phylogenetic Community Metrics
3.4. Null Models and Ecological Patterns
4. Discussion
4.1. Tree Topology
4.2. Phylogenetic Diversity (PD)
4.3. Use of Time-Stamped vs. Non-Ultrametric Trees in PD Estimation
4.4. Recommendations and Suggested Workflow
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cavender-Bares, J.; Kozak, K.H.; Fine, P.V.A.; Kembel, S.W. The merging of community ecology and phylogenetic biology. Ecol. Lett. 2009, 12, 693–715. [Google Scholar] [CrossRef] [PubMed]
- Mittelbach, G.G.; Schemske, D.W. Ecological and evolutionary perspectives on community assembly. Trends Ecol. Evol. 2015, 30, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Devictor, V.; Mouillot, D.; Meynard, C.; Jiguet, F.; Thuiller, W.; Mouquet, N. Spatial mismatch and congruence between taxonomic, phylogenetic and functional diversity: The need for integrative conservation strategies in a changing world. Ecol. Lett. 2010, 13, 1030–1040. [Google Scholar] [CrossRef] [PubMed]
- Morlon, H. Phylogenetic approaches for studying diversification. Ecol. Lett. 2014, 17, 508–525. [Google Scholar] [CrossRef] [PubMed]
- Mouquet, N.; Devictor, V.; Meynard, C.N.; Munoz, F.; Bersier, L.F.; Chave, J.; Couteron, P.; Dalecky, A.; Fontaine, C.; Gravel, D.; et al. Ecophylogenetics: Advances and perspectives. Biol. Rev. 2012, 87, 769–785. [Google Scholar] [CrossRef]
- Vamosi, S.M.; Heard, S.B.; Vamosi, J.C.; Webb, C.O. Emerging patterns in the comparative analysis of phylogenetic community structure. Mol. Ecol. 2009, 18, 572–592. [Google Scholar] [CrossRef]
- Gerhold, P.; Cahill, J.F.; Winter, M.; Bartish, I.V.; Prinzing, A. Phylogenetic patterns are not proxies of community assembly mechanisms (they are far better). Funct. Ecol. 2015, 29, 600–614. [Google Scholar] [CrossRef]
- Narwani, A.; Matthews, B.; Fox, J.; Venail, P. Using phylogenetics in community assembly and ecosystem functioning research. Funct. Ecol. 2015, 29, 589–591. [Google Scholar] [CrossRef]
- Speed, J.D.M.; Skjelbred, I.Å.; Barrio, I.C.; Martin, M.D.; Berteaux, D.; Bueno, C.G.; Christie, K.S.; Forbes, B.C.; Forbey, J.; Fortin, D.; et al. Trophic interactions and abiotic factors drive functional and phylogenetic structure of vertebrate herbivore communities across the Arctic tundra biome. Ecography 2019, 42, 1152–1163. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.; Qiao, L.; Dietrich, C.H.; Matsumura, M.; Qin, D. Population structure and genetic differentiation of tea green leafhopper, Empoasca (Matsumurasca) onukii, in China based on microsatellite markers. Sci. Rep. 2019, 9, 1202. [Google Scholar] [CrossRef]
- Winter, M.; Devictor, V.; Schweiger, O. Phylogenetic diversity and nature conservation: Where are we? Trends Ecol. Evol. 2013, 28, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Grab, H.; Branstetter, M.G.; Amon, N.; Urban-Mead, K.R.; Park, M.G.; Gibbs, J.; Blitzer, E.J.; Poveda, K.; Loeb, G.; Danforth, B.N. Agriculturally dominated landscapes reduce bee phylogenetic diversity and pollination services. Science 2019, 363, 282–284. [Google Scholar] [CrossRef] [PubMed]
- Kembel, S.W. Disentangling niche and neutral influences on community assembly: Assessing the performance of community phylogenetic structure tests. Ecol. Lett. 2009, 12, 949–960. [Google Scholar] [CrossRef] [PubMed]
- Schweiger, O.; Klotz, S.; Durka, W.; Kühn, I. A comparative test of phylogenetic diversity indices. Oecologia 2008, 157, 485–495. [Google Scholar] [CrossRef]
- Miller, E.T.; Farine, D.R.; Trisos, C.H. Phylogenetic community structure metrics and null models: A review with new methods and software. Ecography 2017, 40, 461–477. [Google Scholar] [CrossRef]
- Tucker, C.M.; Cadotte, M.W.; Carvalho, S.B.; Jonathan Davies, T.; Ferrier, S.; Fritz, S.A.; Grenyer, R.; Helmus, M.R.; Jin, L.S.; Mooers, A.O.; et al. A guide to phylogenetic metrics for conservation, community ecology and macroecology. Biol. Rev. 2017, 92, 698–715. [Google Scholar] [CrossRef]
- Faith, D.P. Conservation evaluation and phylogenetic diversity. Biol. Conserv. 1992, 61, 1–10. [Google Scholar] [CrossRef]
- Qian, H.; Zhang, J. Are phylogenies derived from family-level supertrees robust for studies on macroecological patterns along environmental gradients? J. Syst. Evol. 2016, 54, 29–36. [Google Scholar] [CrossRef]
- Park, D.S.; Worthington, S.; Xi, Z. Taxon sampling effects on the quantification and comparison of community phylogenetic diversity. Mol. Ecol. 2018, 27, 1296–1308. [Google Scholar] [CrossRef]
- Patrick, L.E.; Stevens, R.D. Investigating sensitivity of phylogenetic community structure metrics using North American desert bats. J. Mammal. 2014, 95, 1240–1253. [Google Scholar] [CrossRef]
- Li, D.; Trotta, L.; Marx, H.E.; Allen, J.M.; Sun, M.; Soltis, D.E.; Soltis, P.S.; Guralnick, R.P.; Baiser, B. For common community phylogenetic analyses, go ahead and use synthesis phylogenies. Ecology 2019, 100, e02788. [Google Scholar] [CrossRef]
- Molina-Venegas, R.; Roquet, C. Directional biases in phylogenetic structure quantification: A Mediterranean case study. Ecography 2014, 37, 572–580. [Google Scholar] [CrossRef]
- Swenson, N.G. Phylogenetic resolution and quantifying the phylogenetic diversity and dispersion of communities. PLoS ONE 2009, 4, e4390. [Google Scholar] [CrossRef]
- Cadotte, M.W. Phylogenetic diversity-ecosystem function relationships are insensitive to phylogenetic edge lengths. Funct. Ecol. 2015, 29, 718–723. [Google Scholar] [CrossRef]
- Jantzen, J.R.; Whitten, W.M.; Neubig, K.M.; Majure, L.C.; Soltis, D.E.; Soltis, P.S. Effects of taxon sampling and tree reconstruction methods on phylodiversity metrics. Ecol. Evol. 2019, 9, 9479–9499. [Google Scholar] [CrossRef]
- Allen, J.M.; Germain-Aubrey, C.C.; Barve, N.; Neubig, K.M.; Majure, L.C.; Laffan, S.W.; Mishler, B.D.; Owens, H.L.; Smith, S.A.; Whitten, W.M.; et al. Spatial Phylogenetics of Florida Vascular Plants: The Effects of Calibration and Uncertainty on Diversity Estimates. iScience 2019, 11, 57–70. [Google Scholar] [CrossRef]
- Boyle, E.E.; Adamowicz, S.J. Community phylogenetics: Assessing tree reconstruction methods and the utility of DNA barcodes. PLoS ONE 2015, 10, e0126662. [Google Scholar] [CrossRef]
- Hebert, P.D.N.; Ratnasingham, S.; DeWaard, J.R. Barcoding animal life: Cytochrome c oxidase subunit 1 divergences among closely related species. Proc. R. Soc. B Biol. Sci. 2003, 270 (Suppl. 1), S96–S99. [Google Scholar] [CrossRef]
- Cardoso, P. Diversity and community assembly patterns of epigean vs. troglobiont spiders in the Iberian Peninsula. Int. J. Speleol. 2012, 41, 83–94. [Google Scholar] [CrossRef]
- Crozier, R.H.; Dunnett, L.J.; Agapow, P.-M. Phylogenetic Biodiversity Assessment Based on Systematic Nomenclature. Evol. Bioinforma. 2005, 1, 11–36. [Google Scholar] [CrossRef]
- Purschke, O.; Schmid, B.C.; Sykes, M.T.; Poschlod, P.; Michalski, S.G.; Durka, W.; Kühn, I.; Winter, M.; Prentice, H.C. Contrasting changes in taxonomic, phylogenetic and functional diversity during a long-term succession: Insights into assembly processes. J. Ecol. 2013, 101, 857–866. [Google Scholar] [CrossRef]
- Erickson, D.L.; Jones, F.A.; Swenson, N.G.; Pei, N.; Bourg, N.; Chen, W.; Davies, S.J.; Ge, X.; Hao, Z.; Howe, R.W.; et al. Comparative evolutionary diversity and phylogenetic structure across multiple forest dynamics plots: A mega-phylogeny approach. Front. Genet. 2014, 5, 358. [Google Scholar] [CrossRef] [PubMed]
- Kress, W.J.; Erickson, D.L.; Swenson, N.G.; Thompson, J.; Uriarte, M.; Zimmerman, J.K. Advances in the use of DNA barcodes to build a community phylogeny for tropical trees in a puerto rican forest dynamics plot. PLoS ONE 2010, 5, e15409. [Google Scholar] [CrossRef]
- Uriarte, M.; Swenson, N.G.; Chazdon, R.L.; Comita, L.S.; John Kress, W.; Erickson, D.; Forero-Montaña, J.; Zimmerman, J.K.; Thompson, J. Trait similarity, shared ancestry and the structure of neighbourhood interactions in a subtropical wet forest: Implications for community assembly. Ecol. Lett. 2010, 13, 1503–1514. [Google Scholar] [CrossRef]
- Schmitz, O.J.; Hambäck, P.A.; Beckerman, A.P. Trophic cascades in terrestrial systems: A review of the effects of carnivore removals on plants. Am. Nat. 2000, 155, 141–153. [Google Scholar] [CrossRef]
- Cardoso, P.; Pekár, S.; Jocqué, R.; Coddington, J.A. Global patterns of guild composition and functional diversity of spiders. PLoS ONE 2011, 6, e21710. [Google Scholar] [CrossRef]
- Carvalho, J.C.; Cardoso, P.; Crespo, L.C.; Henriques, S.; Carvalho, R.; Gomes, P. Determinants of beta diversity of spiders in coastal dunes along a gradient of mediterraneity. Divers. Distrib. 2011, 17, 225–234. [Google Scholar] [CrossRef]
- Carvalho, J.C.; Malumbres-Olarte, J.; Arnedo, M.A.; Crespo, L.C.; Domènech, M.; Cardoso, P. Taxonomic divergence and functional convergence in Iberian spider forest communities: Insights from beta diversity partitioning. J. Biogeogr. 2019, 47, 288–300. [Google Scholar] [CrossRef]
- Ulrich, W.; Hajdamowicz, I.; Zalewski, M.; Stańska, M.; Ciurzycki, W.; Tykarski, P. Species assortment or habitat filtering: A case study of spider communities on lake islands. Ecol. Res. 2010, 25, 375–381. [Google Scholar] [CrossRef]
- Ridel, A.; Lafage, D.; Devogel, P.; Lacoue-labarthe, T.; Petillion, J. Habitat filtering differentially modulates phylogenetic vs functional diversity relationships between dominant ground-dwelling arthropods in salt marshes. bioRxiv 2020. [Google Scholar] [CrossRef]
- Barrett, R.D.H.; Hebert, P. Identifying spiders through DNA barcodes. Can. J. Zool. 2005, 83, 481–491. [Google Scholar] [CrossRef]
- Blagoev, G.A.; DeWaard, J.R.; Ratnasingham, S.; DeWaard, S.L.; Lu, L.; Robertson, J.; Telfer, A.C.; Hebert, P. Untangling taxonomy: A DNA barcode reference library for Canadian spiders. Mol. Ecol. Resour. 2016, 16, 325–341. [Google Scholar] [CrossRef]
- Wheeler, W.C.; Coddington, J.A.; Crowley, L.M.; Dimitrov, D.; Goloboff, P.A.; Griswold, C.E.; Hormiga, G.; Prendini, L.; Ramírez, M.J.; Sierwald, P.; et al. The spider tree of life: Phylogeny of Araneae based on target-gene analyses from an extensive taxon sampling. Cladistics 2016, 33, 574–616. [Google Scholar] [CrossRef]
- Fernández, R.; Kallal, R.J.; Dimitrov, D.; Ballesteros, J.A.; Arnedo, M.A.; Giribet, G.; Hormiga, G. Phylogenomics, Diversification Dynamics, and Comparative Transcriptomics across the Spider Tree of Life. Curr. Biol. 2018, 28, 1489–1497.e5. [Google Scholar] [CrossRef]
- Crespo, L.C.; Domènech, M.; Enguídanos, A.; Malumbres-Olarte, J.; Moya-Laraño, J.; Frías-López, C.; Macías-Hernández, N.; De Mas, E.; Mazzuca, P.; Mora, E.; et al. A DNA barcode-assisted annotated checklist of the spider (Arachnida, Araneae) communities associated to white oak woodlands in Spanish National Parks. Biodivers. Data J. 2018, 6, e29443. [Google Scholar] [CrossRef]
- Malumbres-olarte, J.; Cardoso, P.; Crespo, L.C. Standardised inventories of spiders (Arachnida, Araneae) of Macaronesia I: The native forests of the Azores (Pico and Terceira islands). Biodivers. Data J. 2019, 7, e32625. [Google Scholar] [CrossRef]
- Malumbres-Olarte, J.; Boieiro, M.; Cardoso, P.; Carvalho, R.; Crespo, L.C.F.; Gabriel, R.; Hernández, N.M.; Paulo, O.S.; Pereira, F.; Rego, C.; et al. Standardised inventories of spiders (Arachnida, Araneae) of Macaronesia II: The native forests and dry habitats of Madeira archipelago (Madeira and Porto Santo islands). Biodivers. Data J. 2020, 8, e47502. [Google Scholar] [CrossRef]
- Emerson, B.C.; Casquet, J.; López, H.; Cardoso, P.; Borges, P.A.V.; Mollaret, N.; Oromí, P.; Strasberg, D.; Thébaud, C. A combined field survey and molecular identification protocol for comparing forest arthropod biodiversity across spatial scales. Mol. Ecol. Resour. 2016, 17, 694–707. [Google Scholar] [CrossRef]
- Folmer, O.; Black, M.; Hoeh, W.; Lutz, R.; Vrijenhoek, R. DNA primers for amplification of mitochondrial cytochrome c oxidase subunit I from diverse metazoan invertebrates. Mol. Mar. Biol. Biotechnol. 1994, 3, 294–299. [Google Scholar] [CrossRef]
- Simon, C.; Frati, F.; Beckenbach, A.; Crespi, B.; Liu, H.; Flook, P. Evolution, Weighting, and Phylogenetic Utility of Mitochondrial Gene Sequences and a Compilation of Conserved Polymerase Chain Reaction Primers. Ann. Entomol. Soc. Am. 1994, 87, 651–701. [Google Scholar] [CrossRef]
- Hedin, M.C.; Maddison, W.P. A combined molecular approach to phylogeny of the jumping spider subfamily Dendryphantinae (Araneae: Salticidae). Mol. Phylogenet. Evol. 2001, 18, 386–403. [Google Scholar] [CrossRef] [PubMed]
- Whiting, M.F.; Carpenter, J.C.; Wheeler, Q.D.; Wheeler, W.C. The strepsiptera problem: Phylogeny of the holometabolous insect orders inferred from 18S and 28S ribosomal DNA sequences and morphology. Syst. Biol. 1997, 46, 1–68. [Google Scholar] [CrossRef] [PubMed]
- Giribet, G.; Rambla, M.; Carranza, S.; Baguñà, J.; Riutort, M.; Ribera, C. Phylogeny of the Arachnid Order Opiliones (Arthropoda) Inferred from a Combined Approach of Complete 18S and Partial 28S Ribosomal DNA Sequences and Morphology. Mol. Phylogenet. Evol. 1999, 11, 296–307. [Google Scholar] [CrossRef] [PubMed]
- Edgecombe, G.D.; Giribet, G. A century later-A total evidence re-evaluation of the phylogeny of scutigeromorph centipedes (Myriapoda: Chilopoda). Invertebr. Syst. 2006, 20, 503–525. [Google Scholar] [CrossRef]
- Kearse, M.; Moir, R.; Wilson, A.; Stones-Havas, S.; Cheung, M.; Sturrock, S.; Buxton, S.; Cooper, A.; Markowitz, S.; Duran, C.; et al. Geneious Basic: An integrated and extendable desktop software platform for the organization and analysis of sequence data. Bioinformatics 2012, 28, 1647–1649. [Google Scholar] [CrossRef] [PubMed]
- World Spider Catalog. Version 21.0. Natural History Museum Bern. Available online: http://wsc.nmbe.ch (accessed on 3 March 2020). [CrossRef]
- Stöver, B.C.; Müller, K.F. TreeGraph 2: Combining and visualizing evidence from different phylogenetic analyses. BMC Bioinform. 2010, 11, 7. [Google Scholar] [CrossRef]
- R Core Research Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2004; Volume 2, ISBN 3-900051-07-0. [Google Scholar]
- Grabherr, M.G.; Haas, B.J.; Yassour, M.; Levin, J.Z.; Thompson, D.A.; Amit, I.; Adiconis, X.; Fan, L.; Raychowdhury, R.; Zeng, Q.; et al. Trinity: Reconstructing a full-length transcriptome without a genome from RNA-Seq data. Nat. Biotechnol. 2013, 29, 644–652. [Google Scholar] [CrossRef]
- Haas, B.J.; Papanicolaou, A.; Yassour, M.; Grabherr, M.; Blood, P.D.; Bowden, J.; Couger, M.B.; Eccles, D.; Li, B.; Lieber, M.; et al. De novo transcript sequence reconstruction from RNA-seq using the Trinity platform for reference generation and analysis. Nat. Protoc. 2013, 8, 1494–1512. [Google Scholar] [CrossRef]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Katoh, K.; Rozewicki, J.; Yamada, K.D. MAFFT online service: Multiple sequence alignment, interactive sequence choice and visualization. Brief. Bioinform. 2018, 20, 1160–1166. [Google Scholar] [CrossRef]
- Stamatakis, A. RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 2014, 30, 1312–1313. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.A.; Pfeiffer, W.; Schwartz, T. Creating the CIPRES Science Gateway for inference of large phylogenetic trees. In 2010 Gateway Computing Environments Workshop (GCE); IEEE: Piscataway, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Harmon, L.J.; Weir, J.T.; Brock, C.D.; Glor, R.E.; Challenger, W. GEIGER: Investigating evolutionary radiations. Bioinformatics 2008, 24, 129–131. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.A.; O’Meara, B.C. treePL: Divergence time estimation using penalized likelihood for large phylogenies. Bioinformatics 2012, 28, 2689–2690. [Google Scholar] [CrossRef] [PubMed]
- Magalhaes, I.L.F.; Azevedo, G.H.F.; Michalik, P.; Ramírez, M.J. The fossil record of spiders revisited: Implications for calibrating trees and evidence for a major faunal turnover since the Mesozoic. Biol. Rev. 2020, 95, 184–217. [Google Scholar] [CrossRef]
- Schliep, K.P. Phangorn: Phylogenetic analysis in R. Bioinformatics 2011, 27, 592–593. [Google Scholar] [CrossRef]
- Robinson, D.F.; Foulds, L.R. Comparison of phylogenetic trees. Math. Biosci. 1981, 53, 131–147. [Google Scholar] [CrossRef]
- Schwery, O.; O’Meara, B.C. MonoPhy: A simple R package to find and visualize monophyly issues. PeerJ Comput. Sci. 2016, 2, e56. [Google Scholar] [CrossRef]
- Cardoso, P.; Rigal, F.; Carvalho, J.C. BAT-Biodiversity Assessment Tools, an R package for the measurement and estimation of alpha and beta taxon, phylogenetic and functional diversity. Methods Ecol. Evol. 2015, 6, 232–236. [Google Scholar] [CrossRef]
- De Queiroz, A.; Gatesy, J. The supermatrix approach to systematics. Trends Ecol. Evol. 2007, 22, 34–41. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Team, R.C. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 2020, 3, 111. [Google Scholar]
- Barton, K. MuMIn: Multi-model inference. R Package Version 2020, 1, 18. [Google Scholar]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Hardy, O.J. Testing the spatial phylogenetic structure of local communities: Statistical performances of different null models and test statistics on a locally neutral community. J. Ecol. 2008, 96, 914–926. [Google Scholar] [CrossRef]
- Heath, T.A.; Hedtke, S.M.; Hillis, D.M. Taxon sampling and the accuracy of phylogenetic analyses. J. Syst. Evol. 2008, 46, 239–257. [Google Scholar] [CrossRef]
- Zwickl, D.J.; Hillis, D.M. Increased Taxon Sampling Greatly Reduces Phylogenetic Error. Oxford Journals 2020, 51, 588–598. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Shan, Y.X.; Ge, X.J.; Burgess, K.S. The use of DNA barcodes to estimate phylogenetic diversity in forest communities of southern China. Ecol. Evol. 2019, 9, 5372–5379. [Google Scholar] [CrossRef]
- Brown, W.M.; George, M.; Wilson, A.C. Rapid evolution of animal mitochondrial DNA. Proc. Natl. Acad. Sci. USA 1979, 76, 1967–1971. [Google Scholar] [CrossRef]
- Bidegaray-Batista, L.; Arnedo, M.A. Gone with the plate: The opening of the Western Mediterranean basin drove the diversification of ground-dweller spiders. BMC Evol. Biol. 2011, 11, 317. [Google Scholar] [CrossRef]
- Hillis, D.M. Molecular versus morphological approaches to systematics. Annu. Rev. Ecol. Syst. 1987, 18, 23–42. [Google Scholar] [CrossRef]
- Davies Jonathan, T.; Buckley, L.B. Phylogenetic diversity as a window into the evolutionary and biogeographic histories of present-day richness gradients for mammals. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 2414–2425. [Google Scholar] [CrossRef] [PubMed]
- Mazel, F.; Davies, T.J.; Gallien, L.; Renaud, J.; Groussin, M.; Münkemüller, T.; Thuiller, W. Influence of tree shape and evolutionary time-scale on phylogenetic diversity metrics. Ecography 2016, 39, 913–920. [Google Scholar] [CrossRef]
- Elliott, M.J.; Knerr, N.J.; Schmidt-Lebuhn, A.N. Choice between phylogram and chronogram can have a dramatic impact on the location of phylogenetic diversity hotspots. J. Biogeogr. 2018, 45, 2190–2201. [Google Scholar] [CrossRef]
- Thornhill, A.H.; Baldwin, B.G.; Freyman, W.A.; Nosratinia, S.; Kling, M.M.; Morueta-Holme, N.; Madsen, T.P.; Ackerly, D.D.; Mishler, B.D. Spatial phylogenetics of the native California flora. BMC Biol. 2017, 15, 96. [Google Scholar] [CrossRef] [PubMed]
- Faith, D.P.; Lozupone, C.A.; Nipperess, D.; Knight, R. The cladistic basis for the phylogenetic diversity (PD) measure links evolutionary features to environmental gradients and supports broad applications of microbial ecology’s “phylogenetic beta diversity” framework. Int. J. Mol. Sci. 2009, 10, 4723–4741. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.M.; Shaw, J.; Olff, H. Ecology’s cruel dilemma, phylogenetic trait evolution and the assembly of Serengeti plant communities. J. Ecol. 2011, 99, 797–806. [Google Scholar] [CrossRef]
- Hinchliff, C.E.; Smith, S.A.; Allman, J.F.; Burleigh, J.G.; Chaudhary, R.; Coghill, L.M.; Crandall, K.A.; Deng, J.; Drew, B.T.; Gazis, R.; et al. Synthesis of phylogeny and taxonomy into a comprehensive tree of life. Proc. Natl. Acad. Sci. USA 2015, 112, 12764–12769. [Google Scholar] [CrossRef]
- Webb, C.O.; Donoghue, M.J. Phylomatic: Tree assembly for applied phylogenetics. Mol. Ecol. Notes 2005, 5, 181–183. [Google Scholar] [CrossRef]
- Leray, M.; Knowlton, N.; Ho, S.L.; Nguyen, B.N.; Machida, R.J. GenBank is a reliable resource for 21st century biodiversity research. Proc. Natl. Acad. Sci. USA 2019, 116, 22651–22656. [Google Scholar] [CrossRef]
- Bennett, D.J.; Hettling, H.; Silvestro, D.; Zizka, A.; Bacon, C.D.; Faurby, S.; Vos, R.A.; Antonelli, A. Phylotar: An automated pipeline for retrieving orthologous DNA sequences from GenBank in R. Life 2018, 8, 20. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Dimitrov, D.; Rahbek, C.; Wang, Z. NCBIminer: Sequences harvest from Genbank. Ecography 2015, 38, 426–430. [Google Scholar] [CrossRef]
- Smith, S.A.; Walker, J.F. PyPHLAWD: A python tool for phylogenetic dataset construction. Methods Ecol. Evol. 2019, 10, 104–108. [Google Scholar] [CrossRef]
- Fenker, J.; Tedeschi, L.G.; Pyron, R.A.; Nogueira, C. de C. Phylogenetic diversity, habitat loss and conservation in South American pitvipers (Crotalinae: Bothrops and Bothrocophias). Divers. Distrib. 2014, 20, 1108–1119. [Google Scholar] [CrossRef]


| Matrix Name | Taxa | Genes | Topology | Time | Terminals | %missing | COI | 28S | 12S | 16S | 18S | H3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | Backbone matrix | NA | Unconst. | no | 964 | 58.88 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| B_tc | Backbone matrix | NA | Const. | no | 964 | 58.88 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| BLc1_tc | Backbone matrix + local species | c1 | Const. | no | 1453 | 70.62 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| BLc1_tc_cal | Backbone matrix + local species | c1 | Const. | yes | 1453 | 70.62 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| BLc1 | Backbone matrix + local species | c1 | Unconst. | no | 1453 | 70.62 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| BLc1_cal | Backbone matrix + local species | c1 | Unconst. | yes | 1453 | 70.62 | 1079 | 4369 | 769 | 1031 | 2608 | 318 |
| BLc128_tc | Backbone matrix + local species | c1 + 28s | Const. | no | 1456 | 68.36 | 1079 | 4364 | 769 | 1031 | 2608 | 318 |
| BLc128_tc_cal | Backbone matrix + local species | c1 + 28s | Const. | yes | 1456 | 68.36 | 1079 | 4364 | 769 | 1031 | 2608 | 318 |
| BLc128 | Backbone matrix + local species | c1 + 28s | Unconst. | no | 1456 | 68.36 | 1079 | 4364 | 769 | 1031 | 2608 | 318 |
| BLc128_cal | Backbone matrix + local species | c1 + 28s | Unconst. | yes | 1456 | 68.36 | 1079 | 4364 | 769 | 1031 | 2608 | 318 |
| Lc1 | Local species | c1 | Unconst. | no | 489 | 3.61 | 658 | |||||
| Lc128 | Local species | c1 + 28s | Unconst. | no | 492 | 32.23 | 658 | 1300 |
| GLMM | Topology | Time | Genes | Taxa | R2 | Varimp | Mean Varimp |
|---|---|---|---|---|---|---|---|
| BLc1_tc_cal~BLc1_cal | const vs. unconst | yes | c1 | all | 0.889 | 0.111 | 0.113 |
| BLc1_tc~BLc1 | const vs. unconst | no | c1 | all | 0.889 | 0.111 | |
| BLc128_tc_cal~BLc128_cal | const vs. unconst | yes | c1 + 28s | all | 0.886 | 0.114 | |
| BLc128_tc~BLc128 | const vs. unconst | no | c1 + 28 s | all | 0.886 | 0.114 | |
| BLc1_tc_cal~BLc1_tc | constrained | yes vs. no | c1 | all | 0.909 | 0.091 | 0.093 |
| BLc1_cal~BLc1 | unconstrained | yes vs. no | c1 | all | 0.901 | 0.099 | |
| BLc128_tc_cal~BLc128_tc | constrained | yes vs. no | c1 + 28 s | all | 0.910 | 0.090 | |
| BLc128_cal~BLc128 | unconstrained | yes vs. no | c1 + 28 s | all | 0.907 | 0.093 | |
| BLc128_tc_cal~BLc1_tc_cal | constrained | yes | c1 vs. c1 + 28 s | all | 0.891 | 0.109 | 0.102 |
| BLc128_cal~BLc1_cal | unconstrained | yes | c1 vs. c1 + 28 s | all | 0.891 | 0.109 | |
| BLc128_tc~BLc1_tc | constrained | no | c1 vs. c1 + 28 s | all | 0.913 | 0.087 | |
| BLc128~BLc1_cal | unconstrained | no | c1 vs. c1 + 28 s | all | 0.896 | 0.104 | |
| BLc1~Lc1 | unconstrained | no | c1 | all vs. set | 0.898 | 0.102 | 0.103 |
| BLc128~Lc128 | unconstrained | no | c1 + 28s | all vs. set | 0.896 | 0.104 | |
| Lc128~Lc1 | unconstrained | no | c1 vs. c1 + 28 s | set | 0.915 | 0.085 | 0.085 |
| B_tc | BLc1_tc | BLc1 | BLc128_tc | BLc128 | Lc1 | Lc128 | |
|---|---|---|---|---|---|---|---|
| B | 400 (0.208) | 402 (0.209) | 204 (0.106) | 552 (0.287) | 462 (0.222) | NA | NA |
| B_tc | 364 (0.189) | 404 (0.211) | 414 (0.215) | 516 (0.268) | NA | NA | |
| BLc1_tc | 782 (0.27) | 1240 (0.427) | 1262 (0.435) | 454 (0.467) | 516 (0.531) | ||
| BLc1 | 1266 (0.436) | 1158 (0.399) | 434 (0.446) | 518 (0.533) | |||
| BLc128_tc | 544 (0.187) | 508 (0.522) | 284 (0.290) | ||||
| BLc128 | 526 (0.541) | 266 (0.272) | |||||
| Lc1 | 508 (0.522) |
| Number of Taxa | B | B_tc | BLc1_tc | BLc1 | BLc128_tc | BLc128 | Lc1 | Lc128 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Species | 964 | 964 | 1453 | 964 | 489 | 1453 | 964 | 489 | 1456 | 964 | 492 | 1456 | 964 | 492 | 489 | 492 |
| Families | 117 | 117 | 117 | 117 | 39 | 117 | 117 | 39 | 117 | 117 | 39 | 117 | 117 | 39 | 39 | 39 |
| Genera | 761 | 761 | 884 | 761 | 215 | 884 | 761 | 215 | 884 | 761 | 215 | 884 | 761 | 215 | 215 | 215 |
| Monophyletic/Total | ||||||||||||||||
| Families | 0.58 | 0.62 | 0.49 | 0.59 | 0.54 | 0.47 | 0.57 | 0.46 | 0.59 | 0.62 | 0.67 | 0.58 | 0.61 | 0.64 | 0.41 | 0.54 |
| Genera | 0.16 | 0.15 | 0.20 | 0.15 | 0.34 | 0.20 | 0.16 | 0.33 | 0.21 | 0.16 | 0.35 | 0.21 | 0.15 | 0.34 | 0.34 | 0.35 |
| Monophyletic/Total (excluding monotypic) | ||||||||||||||||
| Families | 0.67 | 0.71 | 0.56 | 0.68 | 0.70 | 0.54 | 0.66 | 0.60 | 0.68 | 0.71 | 0.87 | 0.67 | 0.70 | 0.83 | 0.53 | 0.70 |
| Genera | 0.79 | 0.78 | 0.67 | 0.79 | 0.73 | 0.66 | 0.80 | 0.70 | 0.72 | 0.79 | 0.74 | 0.71 | 0.79 | 0.73 | 0.72 | 0.74 |
| BLc128_tc_cal against | R2 | BLc128_tc Against | R2 |
| BLc128_cal | 0.786 | BLc128 | 0.810 |
| BLc1_tc_cal | 0.683 | Lc128 | 0.519 |
| BLc1_cal | 0.660 | BLc1_tc | 0.475 |
| Lc1 | 0.575 | BLc1 | 0.459 |
| BLc128 | 0.545 | Lc1 | 0.422 |
| Lc128 | 0.521 | ||
| BLc1 | 0.503 | ||
| BLc128_tc | 0.502 | ||
| BLc1_tc | 0.493 |
| Phylogenetic Tree | TSS |
|---|---|
| BLc128_cal | 1.000 |
| BLc1_tc_cal | 0.918 |
| BLc1_cal | 0.870 |
| BLc1_tc | 0.603 |
| BLc128_tc | 0.536 |
| BLc128 | 0.519 |
| BLc1 | 0.511 |
| Lc128 | 0.417 |
| Lc1 | 0.374 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macías-Hernández, N.; Domènech, M.; Cardoso, P.; Emerson, B.C.; Borges, P.A.V.; Lozano-Fernandez, J.; Paulo, O.S.; Vieira, A.; Enguídanos, A.; Rigal, F.; et al. Building a Robust, Densely-Sampled Spider Tree of Life for Ecosystem Research. Diversity 2020, 12, 288. https://doi.org/10.3390/d12080288
Macías-Hernández N, Domènech M, Cardoso P, Emerson BC, Borges PAV, Lozano-Fernandez J, Paulo OS, Vieira A, Enguídanos A, Rigal F, et al. Building a Robust, Densely-Sampled Spider Tree of Life for Ecosystem Research. Diversity. 2020; 12(8):288. https://doi.org/10.3390/d12080288
Chicago/Turabian StyleMacías-Hernández, Nuria, Marc Domènech, Pedro Cardoso, Brent C. Emerson, Paulo Alexandre Vieira Borges, Jesús Lozano-Fernandez, Octávio S. Paulo, Ana Vieira, Alba Enguídanos, François Rigal, and et al. 2020. "Building a Robust, Densely-Sampled Spider Tree of Life for Ecosystem Research" Diversity 12, no. 8: 288. https://doi.org/10.3390/d12080288
APA StyleMacías-Hernández, N., Domènech, M., Cardoso, P., Emerson, B. C., Borges, P. A. V., Lozano-Fernandez, J., Paulo, O. S., Vieira, A., Enguídanos, A., Rigal, F., Amorim, I. R., & Arnedo, M. A. (2020). Building a Robust, Densely-Sampled Spider Tree of Life for Ecosystem Research. Diversity, 12(8), 288. https://doi.org/10.3390/d12080288







