Testing Hypotheses of Diversification in Panamanian Frogs and Freshwater Fishes Using Hierarchical Approximate Bayesian Computation with Model Averaging
Abstract
1. Introduction
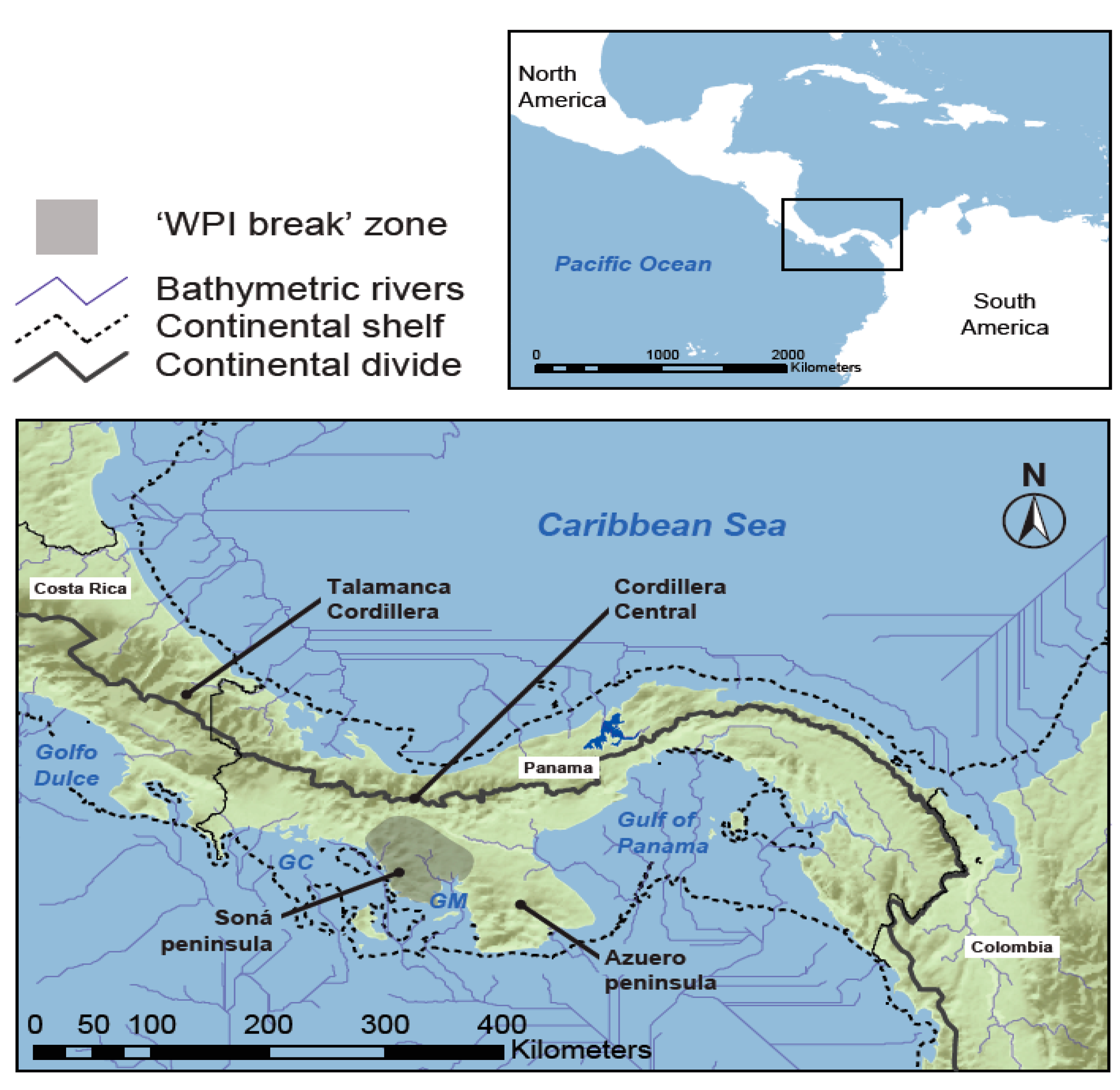
2. Materials and Methods
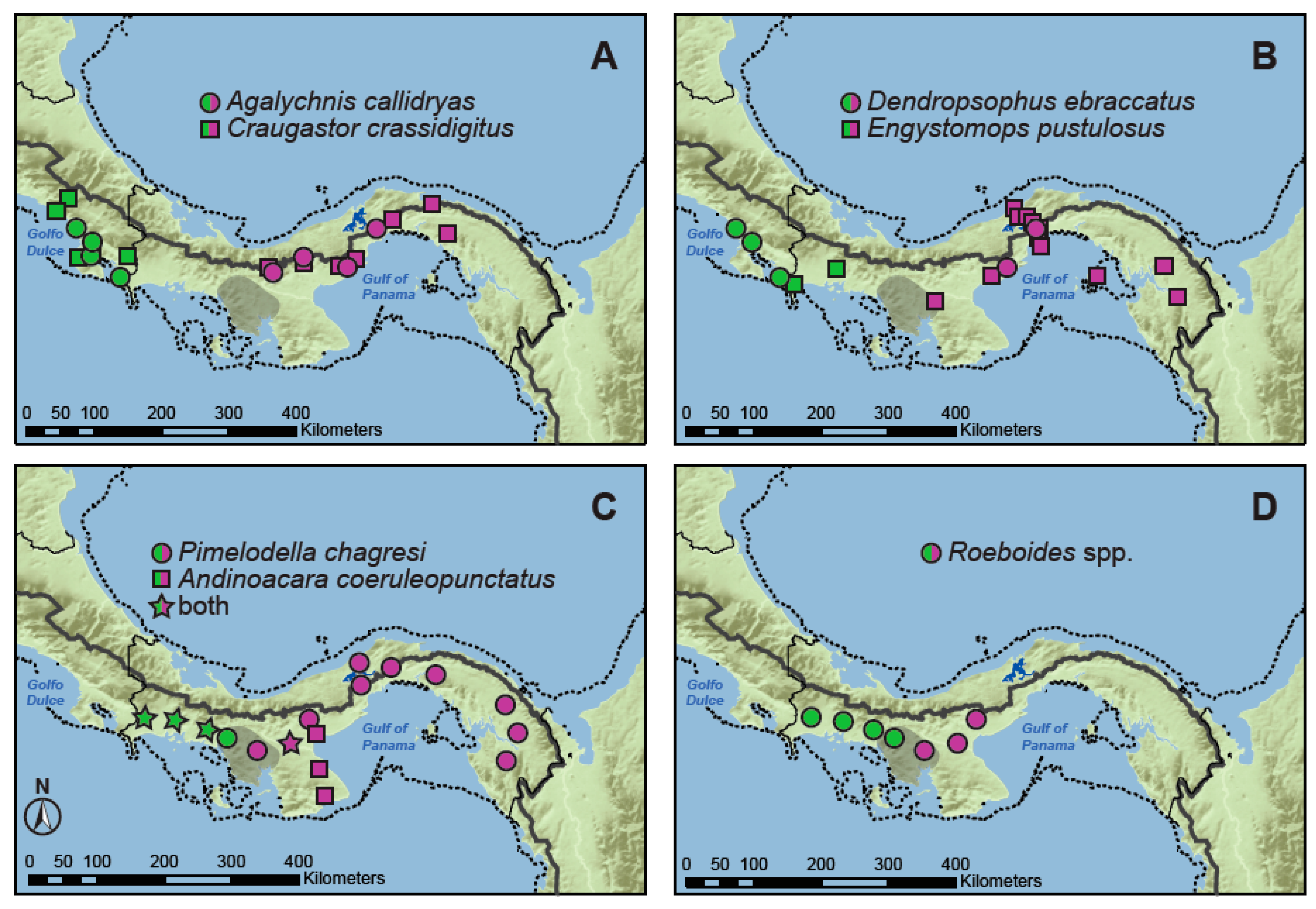
2.1. Taxon Sampling and Molecular Data
2.2. Genetic Diversity and Neutrality
2.3. Estimating Gene-Tree Depths Using Bayesian Dating
2.4. Tests for Synchronous Diversification
3. Results
3.1. Genetic Diversity and Neutrality
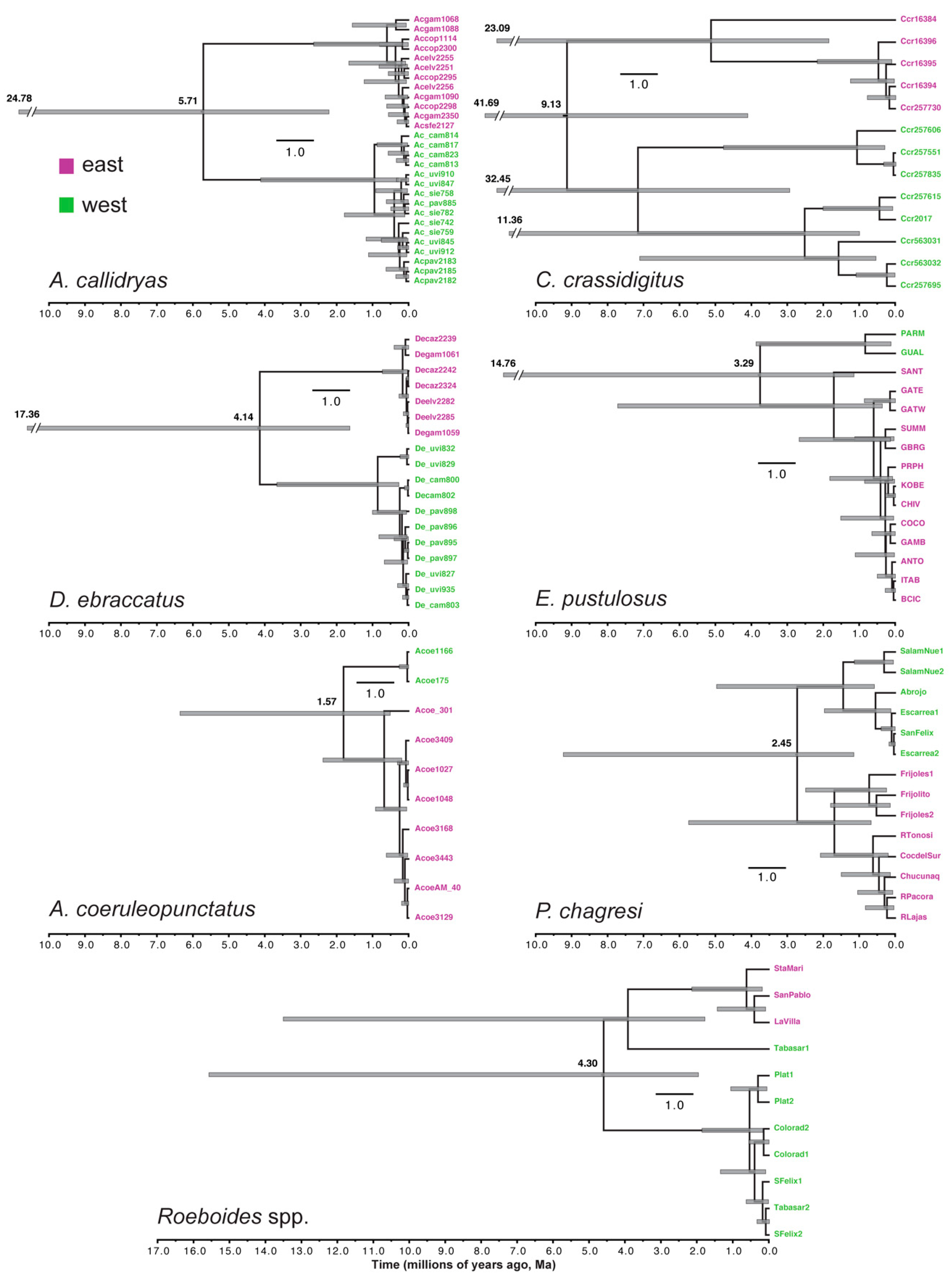
3.2. Estimating Gene-Tree Depths Using Bayesian Dating
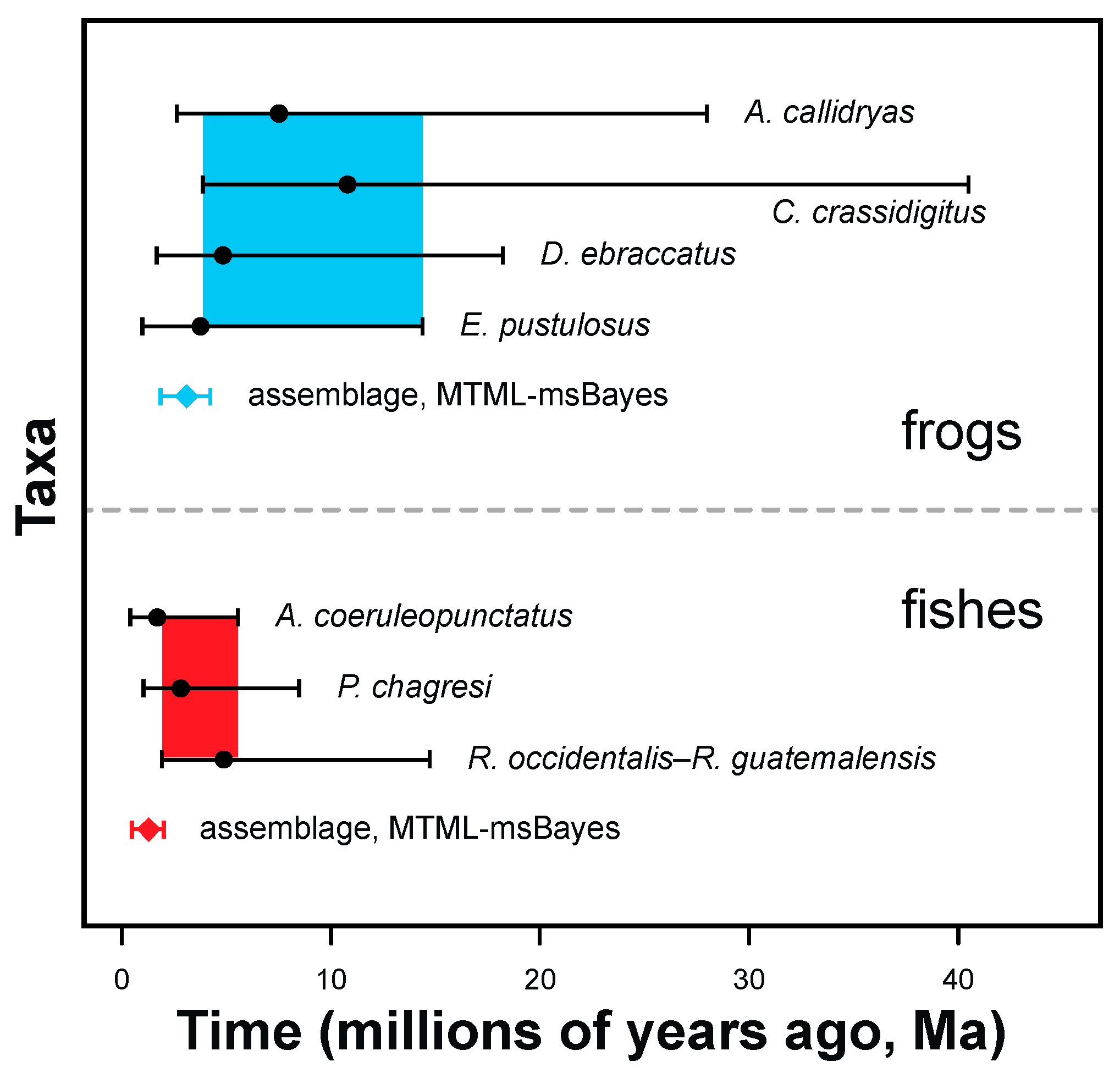
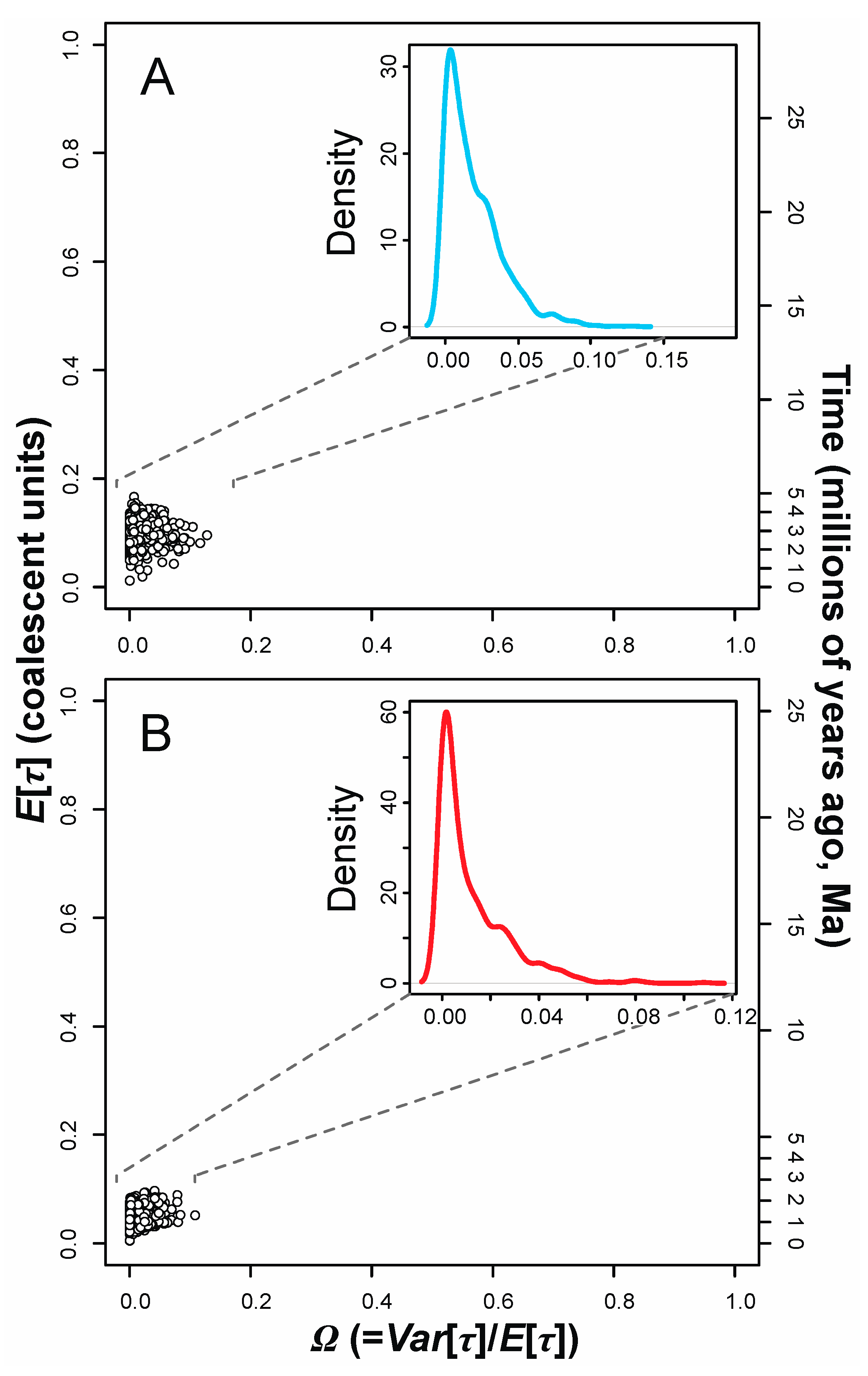
3.3. Tests for Synchronous Diversification
4. Discussion
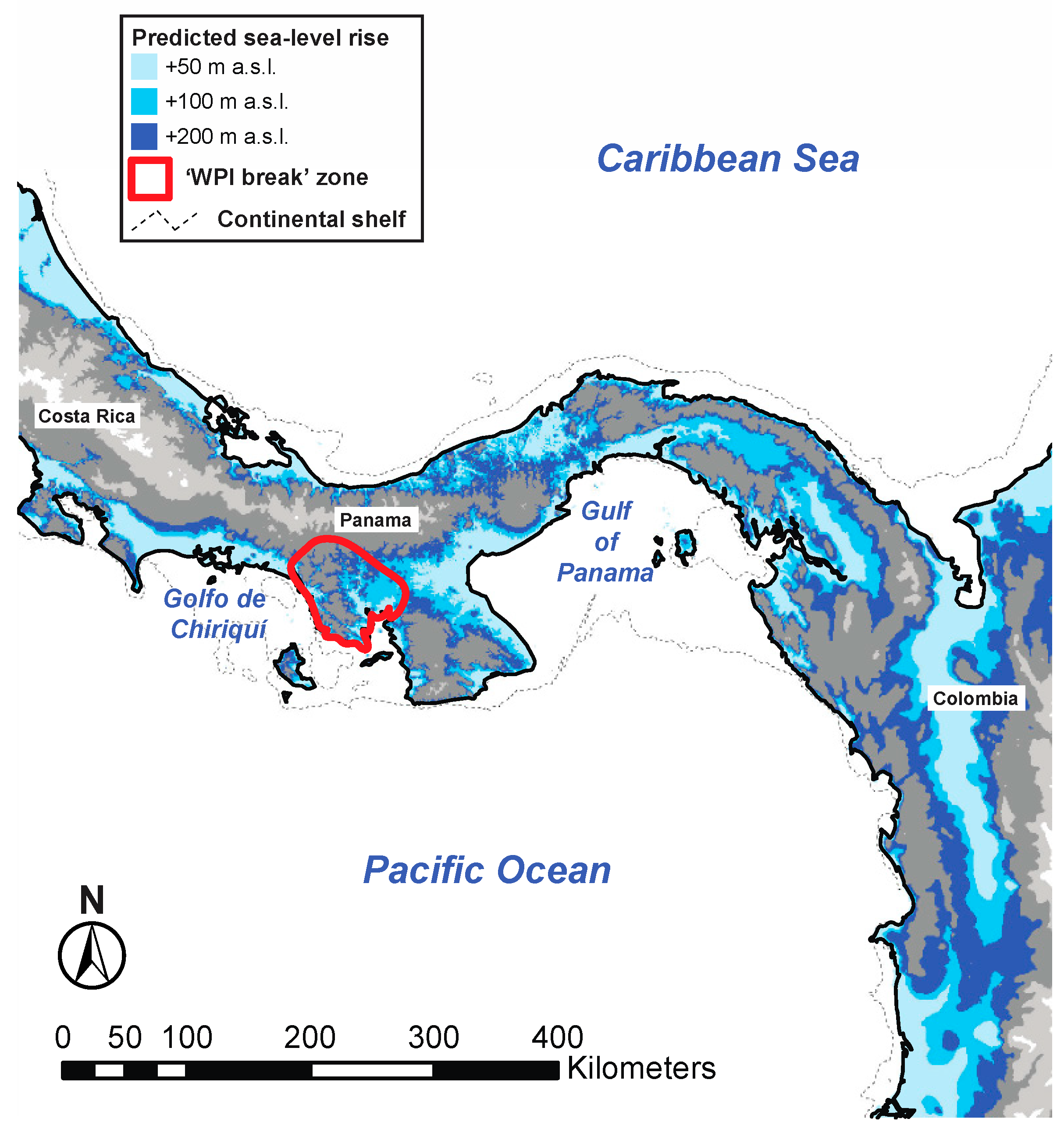
4.1. Comparative Phylogeography of Panamanian Frog and Fish Assemblages
4.2. Caveats and Potential Limitations
4.2.1. Mitochondrial DNA
4.2.2. Migration and “Secondary Contact”
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Supplementary Methods
Appendix A.1.1. Taxon Sampling, Molecular Data, and Outgroup Details
Appendix A.1.2. Supplementary MTML-msBayes Methods
Appendix A.2. Supplementary Results
Appendix A.2.1. Additional Genetic Diversity and Neutrality Results and Discussion
Appendix A.2.2. Additional MTML-msBayes Results and Discussion
| Parameter | Description | Prior Distribution |
|---|---|---|
| A. Hyperparameters | ||
| Ω | Dispersion index of divergence times, Var[τ]/E[τ] (ratio of variance to mean), across Y taxon/population-pairs | Set by Y, τmax, and Ψ |
| E[τ] | Mean multi-species (i.e., assembly-wide) divergence time across Y | Set by Y, τmax, and Ψ |
| Ψ | Number of distinct divergence times across Y | Discrete uniform [1, Y] |
| S | Vector of mutation rate scalars to accommodate among-locus mutation rate heterogeneity | Gamma (with shape and scale parameters α and 1/α, respectively) |
| α | Shape parameter of the gamma distribution | Uniform (1, 20) |
| B. Parameters | ||
| τ | Divergence time in units of 4N generations | Uniform (0.0, τmax) |
| θ = 4Nµ | Population size (mutation) parameter where N is average population size of two daughter populations, µ is the per-site mutation rate | Uniform (θmin, θmax) |
| θA | Ancestral effective population size (mutation) parameter | Uniform (0.01, θmax Nanc-max) |
| θA1, θA2 | Ancestral effective population size (mutation) parameters for daughter populations 1 and 2 over ancestral period (from time τ to τB) | Uniform (0.01, θB1), (0.01, θB2) |
| θB1, θB2 | Effective population size (mutation) parameters for daughter populations 1 and 2 over recent period (from time τB to 0.0, the present time) | Uniform (0.01 θ, 1.99θ), and where θB2 = 2θ − θB1 |
| τB1, τB2 | Times at which θA1 and θA2 experience exponential growth into populations with sizes of θB1 and θB2 | Uniform (0.0, τ), with τB1 = τB2 |
| M = Nm | Effective migration rate, where m is the probability of symmetric migration between pairs of daughter populations | Uniform (0.0, Mmax) |
| r | Per-locus mutation rate scalar | fixed |
| p | Per-locus ploidy and/or generation time scalar | p |
References
- Avise, J.C.; Arnold, J.; Ball, R.M.; Bermingham, E.; Lamb, T.; Neigel, J.E.; Reeb, C.A.; Saunders, N.C. Intraspecific phylogeography: The mitochondrial DNA bridge between population genetics and systematics. Annu. Rev. Ecol. Syst. 1987, 18, 489–522. [Google Scholar] [CrossRef]
- Avise, J.C. Phylogeography: The History and Formation of Species; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Kidd, D.M.; Ritchie, M.G. Phylogeographic information systems: Putting the geography into phylogeography. J. Biogeogr. 2006, 33, 1851–1865. [Google Scholar] [CrossRef]
- Soltis, D.E.; Morris, A.B.; Jason, M.; McLachlan, S.; Manos, P.S.; Soltis, P.S. Comparative phylogeography of unglaciated eastern North America. Mol. Ecol. 2006, 15, 4261–4293. [Google Scholar] [CrossRef] [PubMed]
- Bagley, J.C.; Johnson, J.B. Phylogeography and biogeography of the lower Central American Neotropics: Diversification between two continents and between two seas. Boil. Rev. 2014, 89, 767–790. [Google Scholar] [CrossRef] [PubMed]
- Arbogast, B.S.; Kenagy, G.J. Comparative phylogeography as an integrative approach to historical biogeography. J. Biogeogr. 2001, 28, 819–825. [Google Scholar] [CrossRef]
- Hickerson, M.J.; Carstens, B.C.; Cavender-Bares, J.; Crandall, K.A.; Graham, C.H.; Johnson, J.B.; Rissler, L.; Victoriano, P.F.; Yoder, A.D. Phylogeography’s past; present; and future: 10 years after Avise. 2000. Mol. Phylogenet. Evol. 2010, 54, 291–301. [Google Scholar] [CrossRef] [PubMed]
- Bermingham, E.; Avise, J.C. Molecular zoogeography of freshwater fishes in the south-eastern United States. Genetics 1986, 113, 939–965. [Google Scholar] [PubMed]
- Bermingham, E.; Martin, A.P. Comparative mtDNA phylogeography of Neotropical freshwater fishes: Testing shared history to infer the evolutionary landscape of lower Central America. Mol. Ecol. 1998, 7, 499–517. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, J.; Arellano, E.; Rogers, D. Comparative phylogeography of Mesoamerican highland rodents: Concerted versus independent response to past climatic fluctuations. Am. Nat. 2000, 155, 755–768. [Google Scholar] [CrossRef] [PubMed]
- Avise, J.C. Gene trees and organismal histories: A phylogenetic approach to population biology. Evolution 1989, 43, 1192–1208. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.V.; Beerli, P. Perspective: Gene divergence; population divergence; and the variance in coalescence time in phylogeographic studies. Evolution 2000, 54, 1839–1854. [Google Scholar] [CrossRef] [PubMed]
- Hey, J.; Machado, C.A. The study of structured populations—New hope for a difficult and divided science. Nat. Rev. Genet. 2003, 4, 535–543. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.H.; Avise, J.C. Phylogeographic breaks in low-dispersal species: The emergence of concordance across gene trees. Genetica 2005, 124, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Irwin, D.E. Local adaptation along smooth ecological gradients causes phylogeographic breaks and phenotypic clustering. Am. Nat. 2012, 180, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Zink, R.M.; Barrowclough, G.F. Mitochondrial DNA under siege in avian phylogeography. Mol. Ecol. 2008, 17, 2107–2121. [Google Scholar] [CrossRef] [PubMed]
- Kubatko, L.S.; Carstens, B.C.; Knowles, L.L. STEM: Species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics 2009, 25, 971–973. [Google Scholar] [CrossRef] [PubMed]
- Heled, J.; Drummond, A.J. Bayesian inference of species trees from multilocus data. Mol. Boil. Evol. 2010, 27, 570–580. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R. Gene genealogies and the coalescent process. Oxf. Surv. Evol. Boil. 1990, 7, 1–44. [Google Scholar]
- Riddle, B.R.; Hafner, D.J. A step-wise approach to integrating phylogeographic and phylogenetic biogeographic perspectives on the history of a core North American warm desert biota. J. Arid. Environ. 2006, 66, 435–461. [Google Scholar] [CrossRef]
- Beaumont, M.A.; Zhang, W.; Balding, D.J. Approximate Bayesian computation in population genetics. Genetics 2002, 162, 2025–2035. [Google Scholar] [PubMed]
- Hickerson, M.J.; Stahl, E.; Takebayashi, N. msBayes: A pipeline for testing comparative phylogeographic histories using hierarchical approximate Bayesian computation. BMC Bioinform. 2007, 8, 268. [Google Scholar] [CrossRef] [PubMed]
- Hickerson, M.J.; Stahl, E.; Lessios, H.A. Test for simultaneous divergence using Approximate Bayesian Computation. Evolution 2006, 60, 2435–2453. [Google Scholar] [CrossRef] [PubMed]
- Hickerson, M.J.; Stone, G.N.; Lohse, K.; Demos, T.C.; Xie, X.; Landerer, C.; Takebayashi, N. Recommendations for using msBayes to incorporate uncertainty in selecting an ABC model prior: A response to Oaks et Al. Evolution 2014, 68, 284–294. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Takebayashi, N.; Qi, Y.; Hickerson, M.J. MTML-msBayes: Approximate Bayesian comparative phylogeographic inference from multiple taxa and multiple loci with rate heterogeneity. BMC Bioinform. 2011, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Leaché, A.D.; Crews, S.C.; Hickerson, M.J. Two waves of diversification in mammals and reptiles of Baja California revealed by hierarchical Bayesian analysis. Boil. Lett. 2007, 3, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Barber, B.R.; Klicka, J. Two pulses of diversification across the Isthmus of Tehuantepec in a montane Mexican bird fauna. Proc. R. Soc. Lond. B Boil. Sci. 2010, 277, 2675–2681. [Google Scholar] [CrossRef] [PubMed]
- Bell, R.C.; MacKenzie, J.B.; Hickerson, M.J.; Chavarría, K.L.; Cunningham, M.; Williams, S.; Moritz, C. Comparative multi-locus phylogeography confirms multiple vicariance events in co-distributed rainforest frogs. Proc. R. Soc. Lond. B Boil. Sci. 2011, 279, 991–999. [Google Scholar] [CrossRef] [PubMed]
- Dolman, G.; Joseph, L. A species assemblage approach to comparative phylogeography of birds in southern Australia. Ecol. Evol. 2012, 2, 354–369. [Google Scholar] [CrossRef] [PubMed]
- Bagley, J.C.; Johnson, J.B. Testing for shared biogeographic history in the lower Central American freshwater fish assemblage using comparative phylogeography: Concerted, independent, or multiple evolutionary responses? Ecol. Evol. 2014, 4, 1686–1705. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.T.; Harvey, M.G.; Faircloth, B.C.; Glenn, T.C.; Brumfield, R.T. Target capture and massively parallel sequencing of ultraconserved elements for comparative studies at shallow evolutionary time scales. Syst. Boil. 2013, 63, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Oaks, J.R.; Sukumaran, J.; Esselstyn, J.A.; Linkem, C.W.; Siler, C.D.; Holder, M.T.; Brown, R.M. Evidence for climate-driven diversification? A caution for interpreting ABC inferences of simultaneous historical events. Evolution 2013, 67, 991–1010. [Google Scholar] [CrossRef] [PubMed]
- Bagley, J.C. Understanding the Diversification of Central American Freshwater Fishes Using Comparative Phylogeography and Species Delimitation; Brigham Young University: Provo, UT, USA, 2014. [Google Scholar]
- Oaks, J.R. An improved approximate-Bayesian model-choice method for estimating shared evolutionary history. BMC Evol. Boil. 2014, 14, 150. [Google Scholar] [CrossRef] [PubMed]
- Oaks, J.R.; Linkem, C.W.; Sukumaran, J. Implications of uniformly distributed; empirically informed priors for phylogeographical model selection: A reply to Hickerson et al. Evolution 2014, 68, 3607–3617. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, A.; Knowles, L.L. Species-specific responses to island connectivity cycles: Refined models for testing phylogeographic concordance across a Mediterranean Pleistocene Aggregate Island Complex. Mol. Ecol. 2015, 24, 4252–4268. [Google Scholar] [CrossRef] [PubMed]
- Overcast, I.; Bagley, J.C.; Hickerson, M.J. Improving approximate Bayesian computation tests for synchronous diversification by buffering divergence time classes. BMC Evol. Boil. 2017, 17, 203. [Google Scholar]
- Savage, J.M. The origins and history of the Central American herpetofauna. Copeia 1966, 1966, 719–766. [Google Scholar] [CrossRef]
- Savage, J.M. The enigma of the Central American herpetofauna: Dispersals or vicariance? Ann. Mol. Bot. Gard. 1982, 69, 464–547. [Google Scholar] [CrossRef]
- Savage, J.M. The Amphibians and Reptiles of Costa Rica: A Herpetofauna between Two Continents, Between Two Seas; University of Chicago Press: Chicago, IL, USA, 2002. [Google Scholar]
- Vanzolini, P.E.; Heyer, W.R. The American herpetofauna and the interchange. In The Great American Biotic Interchange; Stehli, F.G., Webb, S.D., Eds.; Plenum Press: New York, NY, USA, 1985; pp. 475–487. [Google Scholar]
- Crawford, A.J.; Bermingham, E.; Polania, C. The role of tropical dry forest as a long-term barrier to dispersal: A comparative phylogeographical analysis of dry forest tolerant and intolerant frogs. Mol. Ecol. 2007, 16, 4789–4807. [Google Scholar] [CrossRef] [PubMed]
- Wang, I.J.; Crawford, A.J.; Bermingham, E. Phylogeography of the pygmy rain frog (Pristimantis ridens) across the lowland wet forests of isthmian Central America. Mol. Phylogenet. Evol. 2008, 47, 992–1004. [Google Scholar] [CrossRef] [PubMed]
- Graham, A.; Dilcher, D. The Cenozoic record of tropical dry forest in northern Latin America and the southern United States. In Seasonally Dry Tropical Forests; Bullock, S.H., Mooney, H.A., Medina, E., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 124–145. [Google Scholar]
- Piperno, D.R.; Pearsall, D.M. The Origins of Agriculture in the Lowland Neotropics; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Coates, A.G.; Obando, J.A. The geologic evolution of the Central American isthmus. In Evolution and Environment in Tropical America; Jackson, J.B.C., Budd, A.F., Coates, A.G., Eds.; University of Chicago Press: Chicago, IL, USA, 1996; pp. 21–56. [Google Scholar]
- Cronin, T.M.; Dowsett, H.J. (Eds.) Pliocene climates. Quat. Sci. Rev. 1991, 10, 115–296. [Google Scholar]
- Zeh, J.A.; Zeh, D.W.; Bonilla, M.M. Phylogeography of the harlequin beetle-riding pseudoscorpion and the rise of the Isthmus of Panama. Mol. Ecol. 2003, 12, 2759–2769. [Google Scholar] [CrossRef] [PubMed]
- Perdices, A.; Bermingham, E.; Montilla, A.; Doadrio, I. Evolutionary history of the genus Rhamdia (Teleostei: Pimelodidae) in Central America. Mol. Phylogenet. Evol. 2002, 25, 172–189. [Google Scholar] [CrossRef]
- Perdices, A.; Doadrio, I.; Bermingham, E. Evolutionary history of the synbranchid eels (Teleostei: Synbranchidae) in Central America and the Caribbean islands inferred from their molecular phylogeny. Mol. Phylogenet. Evol. 2005, 37, 460–473. [Google Scholar] [CrossRef] [PubMed]
- Weigt, L.A.; Crawford, A.J.; Rand, A.S.; Ryan, M.J. Biogeography of the túngara frog; Physalaemus pustulosus: A molecular perspective. Mol. Ecol. 2005, 14, 3857–3876. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.M.; Zamudio, K.R. Genetic diversification; vicariance; and selection in a polytypic frog. J. Hered. 2009, 100, 715–731. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.M.; Duryea, M.C.; Zamudio, K.R. Discordant patterns of evolutionary differentiation in two Neotropical treefrogs. Mol. Ecol. 2009, 18, 1375–1395. [Google Scholar] [CrossRef] [PubMed]
- McCafferty, S.S.; Martin, A.; Bermingham, E. Phylogeographic diversity of the lower Central American cichlid Andinoacara coeruleopunctatus (Cichlidae). Int. J. Evol. Boil. 2012, 2012, 780169. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.P.; Bermingham, E. Regional endemism and cryptic species revealed by molecular and morphological analysis of a widespread species of Neotropical catfish. Proc. R. Soc. Lond. B 2000, 267, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Bussing, W.A. Geographic distribution of the San Juan ichthyofauna of Central America with remarks on its origin and ecology. In Investigations of the Ichthyofauna of Nicaraguan Lakes; Thorson, T.B., Ed.; University of Nebraska, Lincoln: Lincoln, NE, USA, 1976; pp. 157–175. [Google Scholar]
- Bussing, W.A. Freshwater Fishes of Costa Rica, 2nd ed.; Editorial de la Universidad de Costa: Rica San José, Costa Rica, 1998. [Google Scholar]
- Crawford, A.J.; Smith, E.N. Cenozoic biogeography and evolution in direct developing frogs of Central America (Leptodactylidae: Eleutherodactylus) as inferred from a phylogenetic analysis of nuclear and mitochondrial genes. Mol. Phylogenet. Evol. 2005, 35, 536–555. [Google Scholar] [CrossRef] [PubMed]
- Picq, S.; Alda, F.; Krahe, R.; Bermingham, E. Miocene and Pliocene colonization of the Central American Isthmus by the weakly electric fish Brachyhypopomus occidentalis (Hypopomidae; Gymnotiformes). J. Biogeogr. 2014, 41, 1520–1532. [Google Scholar] [CrossRef]
- Hasegawa, M.; Kishino, H.; Yano, T. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 1985, 22, 160–174. [Google Scholar] [CrossRef] [PubMed]
- Nei, M. Molecular Evolutionary Genetics; Columbia University Press: New York, NY, USA, 1987. [Google Scholar]
- Swofford, D.S. PAUP*: Phylogenetic Analysis Using Parsimony (*and Other Methods); Version 4.0a; Sinauer: Sunderland, MA, USA, 2002. [Google Scholar]
- McDonald, J.H.; Kreitman, M. Adaptive protein evolution at the Adh locus in Drosophila. Nature 1991, 351, 652–654. [Google Scholar] [CrossRef] [PubMed]
- Librado, P.; Rozas, J. DnaSP v5: A software for comprehensive analysis of DNA polymorphism data. Bioinformatics 2009, 25, 1451–1452. [Google Scholar] [CrossRef] [PubMed]
- Drummond, A.J.; Suchard, M.A.; Xie, D.; Rambaut, A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Boil. Evol. 2012, 29, 1969–1973. [Google Scholar] [CrossRef] [PubMed]
- Kingman, J. The coalescent. Stoch. Process. Their Appl. 1982, 13, 235–248. [Google Scholar] [CrossRef]
- Drummond, A.J.; Ho, S.Y.W.; Phillips, M.J.; Rambaut, A. Relaxed phylogenetics and dating with confidence. PLoS Boil. 2006, 4, e88. [Google Scholar] [CrossRef] [PubMed]
- Macey, J.R.; Schulte, J.A., II; Larson, A.; Fang, Z.; Wang, Y.; Tuniyev, B.S.; Papenfuss, T.J. Phylogenetic relationships of toads in the Bufo bufo species group from the Eastern Escarpment of the Tibetan Plateau: A case of vicariance and dispersal. Mol. Phylogenet. Evol. 1998, 9, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Waters, J.M.; Burridge, C.P. Extreme intraspecific mitochondrial DNA sequence divergence in Galaxias maculatus (Osteichthys: Galaxiidae); one of the world’s most widespread freshwater fish. Mol. Phylogenet. Evol. 1999, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Burridge, C.P.; Craw, D.; Fletcher, D.; Waters, J.M. Geological dates and molecular rates: Fish DNA sheds light on time dependency. Mol. Boil. Evol. 2008, 18, 624–633. [Google Scholar] [CrossRef] [PubMed]
- Bagley, J.C. PIrANHA. Justincbagley/PIrANHA: PIrANHA version 0.1.4 [Data Set]. Zenodo 2017. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Clarendon: Oxford, UK, 1961. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Bagley, J.C.; Hickerson, M.J. Data for: Testing hypotheses of diversification in Panamanian frogs and freshwater fishes using hierarchical approximate Bayesian computation with model averaging [Data Set]. Mendeley Data 2018. [Google Scholar] [CrossRef]
- Lambeck, K.; Esat, T.M.; Potter, E.K. Links between climate and sea levels for the past three million years. Nature 2002, 419, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.G.; Kominz, M.A.; Browning, J.V.; Wright, J.D.; Mountain, G.S.; Katz, M.E.; Sugarman, P.J.; Cramer, B.S.; Christie-Blick, N.; Pekar, S.F. The Phanerozoic record of global sea-level change. Science 2005, 310, 1293–1298. [Google Scholar] [CrossRef] [PubMed]
- O’Dea, A.; Lessios, H.A.; Coates, A.G.; Eytan, R.I.; Restrepo-Moreno, S.A.; Cione, A.L.; Collins, L.S.; de Queiroz, A.; Farris, D.W.; Norris, R.D.; et al. Formation of the Isthmus of Panama. Sci. Adv. 2016, 2, e1600883. [Google Scholar] [CrossRef] [PubMed]
- Montes, C.; Cardona, A.; Jaramillo, C.; Pardo, A.; Silva, J.C.; Valencia, V.; Ayala, C.; Pérez-Angel, L.C.; Rodriguez-Parra, L.A.; Ramirez, V.; et al. Middle Miocene closure of the Central American seaway. Science 2015, 348, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Nores, M. The implications of Tertiary and Quaternary sea level rise events for avian distribution patterns in the lowlands of northern South America. Glob. Ecol. Biogeogr. 2004, 13, 149–161. [Google Scholar] [CrossRef]
- Smith, S.A.; Bermingham, E. The biogeography of lower Mesoamerican freshwater fishes. J. Biogeogr. 2005, 32, 1835–1854. [Google Scholar] [CrossRef]
- Hearty, P.J.; Kindler, P.; Cheng, H.; Edwards, R.L. A +20 m middle Pleistocene sea-level highstand (Bermuda and the Bahamas) due to partial collapse of Antarctic ice. Geology 1999, 27, 375–378. [Google Scholar] [CrossRef]
- Crawford, A.J. Huge populations and old species of Costa Rican and Panamanian dirt frogs inferred from mitochondrial and nuclear gene sequences. Mol. Ecol. 2003, 12, 2525–2540. [Google Scholar] [CrossRef] [PubMed]
- Gibbard, P.L.; Head, M.J.; Walker, M.J.C. The Subcommission on Quaternary Stratigraphy. Formal ratification of the Quaternary System/Period and the Pleistocene Series/Epoch with a base at 2.58 Ma. J. Quat. Sci. 2010, 25, 96–102. [Google Scholar] [CrossRef]
- Gibbard, P.; van Kolfschoten, T. The Pleistocene and Holocene epochs. In A Geologic Time Scale 2004; Gradstein, F.M., Ogg, J.G., Smith, A.G., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 441–452. [Google Scholar]
- Arbogast, B.S.; Edwards, S.V.; Wakeley, J.; Beerli, P.; Slowinski, J.B. Estimating divergence times from molecular data on phylogenetic and populations genetic timescales. Annu. Rev. Ecol. Syst. 2002, 33, 707–740. [Google Scholar] [CrossRef]
- Nielsen, R.; Beaumont, M.A. Statistical inferences in phylogeography. Mol. Ecol. 2009, 18, 1034–1047. [Google Scholar] [CrossRef] [PubMed]
- Wakeley, J. Inferences about the structure and history of populations: Coalescents and intraspecific phylogeography. In The Evolution of Population Biology; Singh, R.S., Uyenoyama, M.K., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 193–215. [Google Scholar]
- Xue, A.T.; Hickerson, M.J. The aggregate site frequency spectrum for comparative population genomic inference. Mol. Ecol. 2015, 24, 6223–6240. [Google Scholar] [CrossRef] [PubMed]
- Xue, A.T.; Hickerson, M.J. Multi-DICE: R package for comparative population genomic inference under hierarchical co-demographic models of independent single-population size changes. Mol. Ecol. Resour. 2017, 17, E212–E224. [Google Scholar] [CrossRef] [PubMed]
- Peterson, B.K.; Weber, J.N.; Kay, E.H.; Fisher, H.S.; Hoekstra, H.E. Double digest RADseq: An inexpensive method for de novo SNP discovery and genotyping in model and non-model species. PLoS ONE 2012, 7, e37135. [Google Scholar] [CrossRef] [PubMed]
- Kimura, M. The Neutral Theory of Molecular Evolution; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Faivovich, J.; Haddad, C.F.B.; Baêta, D.; Jungfer, K.-H.; Álvares, G.F.R.; Brandão, R.A.; Sheil, C.; Barrientos, L.S.; Barrio-Amorós, C.L.; Cruz, C.A.G.; et al. The phylogenetic relationships of the charasmatic poster frogs, Phyllomedusinae (Anura, Hylidae). Cladistics 2010, 26, 227–261. [Google Scholar] [CrossRef]
- Wiens, J.J.; Fetzner, J.W., Jr.; Parkinson, C.L.; Reeder, T.W. Hylid frog phylogeny and sampling strategies for speciose clades. Syst. Boil. 2005, 54, 778–807. [Google Scholar] [CrossRef] [PubMed]
- Musilová, Z.; Říčan, O.; Janko, K.; Novák, J. Molecular phylogeny and biogeography of the Neotropical cichlid fish tribe Cichlasomatini (Teleostei: Cichlidae: Cichlasomatinae). Mol. Phylogenet. Evol. 2008, 46, 659–672. [Google Scholar] [CrossRef] [PubMed]
- Musilová, Z.; Říčan, O.; Janko, K.; Novák, J. Phylogeny of the neotropical cichlid fish tribe Cichlasomatini (Teleostei: Cichlidae) based on morphological and molecular data, with the description of a new genus. J. Zool. Syst. Evol. Res. 2009, 47, 234–247. [Google Scholar] [CrossRef]
| Taxon | mtDNA Genes | Length (bp) | ntotal (West/East) | π | Ti/Tv | % div | Source |
|---|---|---|---|---|---|---|---|
| Frogs | |||||||
| Agalychnis callidryas | 16S, ND1 | 1149 (118, 1031) | 28 (16/12) | 0.0337 | 11.373 | 8.0 | Robertson & Zamudio (2009) |
| Craugastor crassidigitus | cytb, cox1 | 1353 (714, 639) | 13 (5/8) | 0.0645 | 14.55 | 13.9 | Crawford et al. (2007) |
| Dendropsophus ebraccatus | ND1, tRNAs | 1877 | 18 (11/7) | 0.0245 | 12.04 | 5.9 | Robertson et al. (2009) |
| Engystomops pustulosus | cox1 | 564 | 15 (2/13) | 0.0139 | 31.67 | 4.6 | Weigt et al. (2005) |
| Freshwater Fishes | |||||||
| Andinoacara coeruleopunctatus | ATP6/8 | 842 | 10 (2/8) | 0.0093 | 20.77 | 2.4 | McCafferty et al. (2012) |
| Pimelodella chagresi | ATP6/8, cox1 | 1471 (842, 629) | 14 (6/8) | 0.0210 | 12.19 | 3.5 | Bermingham & Martin (1998) |
| Roeboides occidentalis–R. guatemalensis | ATP6/8, cox1 | 1493 (842, 651) | 11 (8/3) | 0.0311 | 10.36 | 6.4 | Bermingham & Martin (1998) |
| Prior | P(τ) | P(θD) | P(θA) | P(Mk|D)1000 | Ω Mode | Ω 95% HPDs |
|---|---|---|---|---|---|---|
| WPI frogs (Y = 4) | 0.0036 | [0.000, 0.0565] | ||||
| M1 | ~U(0, 1.75) | ~U(0, 0.1) | ~U(0, 0.25) | 0.2666 | – | – |
| M2 | ~U(0, 1.75) | ~U(0, 0.1) | ~U(0, 0.5) | 0.4990 | – | – |
| M3 | ~U(0, 1.75) | ~U(0, 0.4) | ~U(0, 0.25) | 0.0000 | – | – |
| M4 | ~U(0, 0.875) | ~U(0, 0.1) | ~U(0, 0.25) | 0.2344 | – | – |
| WPI fishes (Y = 3) | 0.0017 | [0.000, 0.0423] | ||||
| M1 | ~U(0, 0.8) | ~U(0, 0.1) | ~U(0, 0.25) | 0.3124 | – | – |
| M2 | ~U(0, 0.8) | ~U(0, 0.1) | ~U(0, 0.5) | 0.3766 | – | – |
| M3 | ~U(0, 0.8) | ~U(0, 0.4) | ~U(0, 0.25) | 0.0000 | – | – |
| M4 | ~U(0, 0.4) | ~U(0, 0.1) | ~U(0, 0.25) | 0.3110 | – | – |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagley, J.C.; Hickerson, M.J.; Johnson, J.B. Testing Hypotheses of Diversification in Panamanian Frogs and Freshwater Fishes Using Hierarchical Approximate Bayesian Computation with Model Averaging. Diversity 2018, 10, 120. https://doi.org/10.3390/d10040120
Bagley JC, Hickerson MJ, Johnson JB. Testing Hypotheses of Diversification in Panamanian Frogs and Freshwater Fishes Using Hierarchical Approximate Bayesian Computation with Model Averaging. Diversity. 2018; 10(4):120. https://doi.org/10.3390/d10040120
Chicago/Turabian StyleBagley, Justin C., Michael J. Hickerson, and Jerald B. Johnson. 2018. "Testing Hypotheses of Diversification in Panamanian Frogs and Freshwater Fishes Using Hierarchical Approximate Bayesian Computation with Model Averaging" Diversity 10, no. 4: 120. https://doi.org/10.3390/d10040120
APA StyleBagley, J. C., Hickerson, M. J., & Johnson, J. B. (2018). Testing Hypotheses of Diversification in Panamanian Frogs and Freshwater Fishes Using Hierarchical Approximate Bayesian Computation with Model Averaging. Diversity, 10(4), 120. https://doi.org/10.3390/d10040120





