Density Functionals of Chemical Bonding
Abstract
:1. Introduction
2. Primary Density Functional Theory Concepts
2.1. Hohenberg-Kohn theorems
2.2. Optimized energy-electronegativity connection
- It starts with a trial electronic density (20) satisfying the N-contingency conditions (14) and (15);
- With trial density the effective potential (31) containing exchange and correlation is calculated;
- With the set of functions the new density (20) is recalculated;
- The procedure is repeated until the difference between two consecutive densities approaches zero;
- Once the last condition is achieved one retains the last set ;
- The electronegativity orbital observed contributions are summed up from (33) with the expression:
3. Electronic Localization Problem
3.1. From global functional to localization function. Localization in solids
3.2. Localization in atoms and molecules
- Choosing the basis of the atomic functions [65]:
- Generating the orthonormal orbital eigen-waves, here according with the Gram-Schmidt algorithm among shells and sub-shells:
- Generating the working overall electronic density
4. Popular Energetic Density Functionals
4.1. Density functionals of kinetic energy
- the Gaussian resummation uses:
- the trigonometric (uniform gas) approximation looks like:
- in Gaussian resummation:
- whereas in trigonometric approximation
4.2. Density functionals of exchange energy
- in Gaussian resummation:
- and in trigonometric approximation (recovering the Dirac formula):
4.3. Density functionals of correlation energy
- The open-shell (OS) case provides the functional [98]:
- Finally, Perdew and Zunger (PZ) recommend the working functional [106]:
4.4. Density functionals of exchange-correlation energy
5. Testing (χ, η) Quadratic Dependency Among Several Energetic Density Functionals
5.1. Proof of the E=E(χ,η) quadratic dependency
5.2. Atomic and molecular analysis of the energetic quadratic bilinear (χ, η) dependency
- the degree of correlation itself between the employed energy functional and the couple of electronegativity-chemical hardness structural indices; this is measured by the standard correlation factor [113]:
- the degree of parabolic dependency by checking whether the chemical hardness coefficient (c) is the square of the electronegativity coefficient (b) thus giving the opportunity of introducing the so-called sigma-pi reactivity index
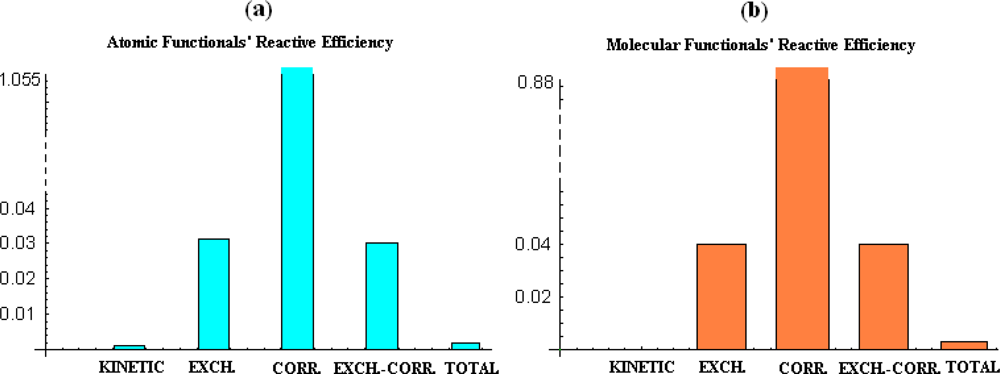
- the correlation energy appears to provide acceptable parabolic shapes in both atomic and molecular cases, with better bilinear regression for molecular analysis, while strongly depending on the electronegativity and chemical hardness atomic models and scales;
- the kinetic energy, while displaying poor parabolic shape at atomic level behaves with negative chemical hardness in molecular systems, probably due the positive contribution in bonding that compete with stabilization (localization) of the electrons within internuclear basin;
- exchange and exchange-correlation functionals reveal similar reactive (parabolic) efficiency as well as close bivariate regression correlation factors for both atomic and molecular cases, leaving with the impression that the exchange contribution is dominant in exchange-correlation functionals since cancelling somehow the behavior of the correlation part of the functional.
- overall, the total energy, although with correlation factors in the range of its components’ regressions does not fit with parabolic reactive theoretical prescription (189), at least for present employed set of atoms and molecules.
6. Conclusions
Acknowledgements
References
- Kohn’s Nobel Prize: http://nobelprize.org/nobel_prizes/chemistry/laureates/1998/index.html.
- Hohenberg, P; Kohn, W. Inhomogeneous Electronic Gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [Green Version]
- Kohn, W; Sham, LJ. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [Green Version]
- Kohn, W; Becke, AD; Parr, RG. Density Functional Theory of Electronic Structure. J. Phys. Chem. 1996, 100, 12974–12980. [Google Scholar] [Green Version]
- Keller, J. On the Formulation of the Hohenberg-Kohn-Sham Theory. Int. J. Quantum Chem. 1986, 20, 767–768. [Google Scholar] [Green Version]
- Ernzerhof, M. Density-Functional Theory as an Example for the Construction of Stationarity Principles. Phys. Rev. A 1994, 49, 76–79. [Google Scholar] [Green Version]
- DePristo, AE. Hohenberg-Kohn Density-Functional-Theory as an Implicit Poisson equation for Density Changes from Summed Fragment Densities. Phys. Rev. A 1996, 54, 3863–3869. [Google Scholar] [Green Version]
- Bamzai, AS; Deb, BM. The Role of Single-Particle Density in Chemistry. Rev. Mod. Phys. 1981, 53, 95–126. [Google Scholar] [Green Version]
- Parr, RG; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, 1989. [Google Scholar]
- Dreizler, RM; Gross, EKU. Density Functional Theory; Springer Verlag: Heidelberg, 1990. [Google Scholar]
- March, NH. Electron Density Theory of Many-Electron Systems; Academic Press: New York, 1991. [Google Scholar]
- Putz, MV. Contributions within Density Functional Theory with Applications to Chemical Reactivity Theory and Electronegativity; Disertation. Com; Parkland: Florida, 2003; http://www.dissertation.com/book.php?method=ISBN&book=1581121849.
- Putz, MV; Chiriac, A; Mracec, M. Foundations for a Theory of the Chemical Field. II. The Chemical Action. Rev. Roum. Chimie 2001, 46, 1175–1181. [Google Scholar] [Green Version]
- Putz, MV. Unifying Absolute and Chemical Electronegativity and Hardness Density Functional Formulations through the Chemical Action Concept. In “Progress in Quantum Chemistry Research”; Hoffman, Erik O, Ed.; Nova Science Publishers Inc.: New York, 2007; pp. 59–121. [Google Scholar]
- Chen, J; Stott, MJ. V-Representability for Systems of a Few Fermions. Phys. Rev. A 1991, 44, 2809–2814. [Google Scholar] [Green Version]
- Chen, J; Stott, MJ. V-Representability for Systems with Low Degeneracy. Phys. Rev. A 1991, 44, 2816–2821. [Google Scholar] [Green Version]
- Kryachko, ES; Ludena, EV. Formulation of N-and V-Representable Density-Functional Theory. I. Ground States. Phys. Rev. A 1991, 43, 2179–2192. [Google Scholar] [Green Version]
- Kryachko, ES; Ludena, EV. Formulation of N-and V-Representable Density-Functional Theory. II. Spin-Dependent Systems. Phys. Rev. A 1991, 43, 2194–2198. [Google Scholar] [Green Version]
- Levy, M; Perdew, J. The Constrained Search Formulation of Density Functional Theory. In ”Density Functional Methods in Physics”; Dreizler, RM, da Providencia, J, Eds.; NATO ASI Series B: Physics; Volume 123, Plenum Press: New York, 1985; pp. 11–31. [Google Scholar] [Green Version]
- Putz, MV. Can Quantum-Mechanical Description of Chemical Bond Be Considered Complete? In ”Quantum Chemistry Research Trends”; Mikas, P. Kaisas, Ed.; Nova Science Publishers Inc.: New York, 2007; Expert Commentary. [Google Scholar]
- Janak, JF. Proof that ∂E / ∂ni = εi in Density Functional Theory. Phys. Rev. B 1978, 18, 7165–7168. [Google Scholar] [Green Version]
- Moscardo, F; San-Fabian, E. Density-Functional Formalism and the Two-Body Problem. Phys. Rev. A 1991, 44, 1549–1553. [Google Scholar] [Green Version]
- Neal, HL. Density Functional Theory of One-Dimension Two-Particle Systems. Am. J. Phys. 1998, 66, 512–516. [Google Scholar] [Green Version]
- Putz, MV; Chiriac, A. Quantum Perspectives on the Nature of the Chemical Bond. In “Advances in Quantum Chemical Bonding Structures”; Putz, MV, Ed.; Transworld Research Network: Kerala, India, 2008; pp. 1–43. [Google Scholar]
- Flores, JA; Keller, J. Differential Equations for the Square Root of the Electronic Density in Symmetry-Constrained Density-Functional Theory. Phys. Rev. A 1992, 45, 6259–6262. [Google Scholar] [Green Version]
- Nagy, A. Kohn-Sham Equations for Multiplets. Phys. Rev. A 1998, 57, 1672–1677. [Google Scholar] [Green Version]
- Garcia-Gonzales, P; Alvarellos, JE; Chacon, E. Kinetic-Energy Density Functional: Atoms and Shell structure. Phys. Rev. A 1996, 54, 1897–1905. [Google Scholar] [Green Version]
- Chan, GKL; Handy, NC. Kinetic-Energy Systems, Density Scaling, and Homogeneity Relations in Density Functional Theory. Phys. Rev. A 1999, 59, 2670–2679. [Google Scholar] [Green Version]
- Bartolotti, LJ; Acharya, PK. On the Functional Derivative of the Kinetic Energy Density Functional. J. Chem. Phys. 1982, 77, 4576–4585. [Google Scholar] [Green Version]
- Dawson, KA; March, NH. Slater Sum in One Dimension: Explicit Kinetic Energy Functional. Phy. Lett. 1984, 106A, 158–160. [Google Scholar] [Green Version]
- Baltin, R. The Three-Dimensional Kinetic Energy Density Functional Compatible with the Exact Differential Equation for its Associated Tensor. J. Chem. Phys. 1987, 86, 947–952. [Google Scholar] [Green Version]
- Becke, AD. Correlation Energy of an Inhomogeneous Electron Gas: A Coordinate-Space. J. Chem. Phys. 1988, 88, 1053–1062. [Google Scholar] [Green Version]
- Ayers, PW; Levy, M. Sum Rules for Exchange and Correlation Potentials. J. Chem. Phys. 2001, 115, 4438–4443. [Google Scholar] [Green Version]Koch, W; Holthausen, MC. A Chemist's Guide to Density Functional Theory; Wiley-VCH: Weinheim, 2000. [Google Scholar] [Green Version]
- Ponec, R; Cooper, DL. Anatomy of bond formation. Bond length dependence of the extent of electron sharing in chemical bonds from the analysis of domain-averaged Fermi holes. Faraday Discuss. 2007, 135, 31–42. [Google Scholar] [Green Version]Matito, E; Solà, M; Salvador, P; Duran, M. Electron sharing indexes at the correlated level. Application to aromaticity calculations. Faraday Discuss. 2007, 135, 325–345. [Google Scholar] [Green Version]March, NH; Howard, IA; Van Doren, VE. Recent Progress in Constructing Nonlocal Energy Density Functionals. Int. J. Quantum Chem. 2003, 92, 192–204. [Google Scholar] [Green Version]
- Zhao, Q; Morrison, RC; Parr, RG. From Electron Densities to Kohn-Sham Kinetic Energies, Orbital Energies, Exchange-Correlation Potentials, and Exchange-Correlation Energies. Phys. Rev. A 1994, 50, 2138–2142. [Google Scholar] [Green Version]
- Gritsenko, OV; Schipper, PRT; Baerends, EJ. Ensuring Proper Short-Range and Asymptotic Behavior of the Exchange-Correlation Kohn-Sham Potential by Modeling with a Statistical Average of Different Orbital Model Potential. Int. J. Quantum Chem. 2000, 76, 407–419. [Google Scholar] [Green Version]
- Zhao, Q; Parr, RG. Local Exchange-Correlation Functional: Numerical Test for Atoms and Ions. Phys. Rev. A 1992, 46, R5320–R5323. [Google Scholar] [Green Version]
- Lam, KC; Cruz, FG; Burke, K. Viral Exchange-Correlation Energy Density in Hooke’s Atom. Int. J. Quantum Chem. 1998, 69, 533–540. [Google Scholar] [Green Version]
- Gaspar, R; Nagy, A. Local-Density-Functional Approximation for Exchange-Correlation Potential. Application of the Self-Consistent and Statistical Exchange-Correlation Parameters to the Calculation of the Electron Binding Energies. Theor. Chim Acta 1987, 72, 393–401. [Google Scholar] [Green Version]
- Levy, M. Density-Functional Exchange Correlation Through Coordinate Scaling in Adiabatic Connection and Correlation Hole. Phys. Rev. A 1991, 43, 4637–4645. [Google Scholar] [Green Version]
- Guo, Y; Whitehead, MA. Generalized Local-Spin-Density-Functional Theory. Phys. Rev. A 1991, 43, 95–108. [Google Scholar] [Green Version]
- Dunlap, BI. Symmetry and Spin Density Functional Theory. Chem. Phys. 1988, 125, 89–97. [Google Scholar] [Green Version]
- Harrison, JG. Electron Affinities in the Self-Interactions-Corrected Local Spin Density Approximation. J. Chem. Phys. 1987, 86, 2849–2853. [Google Scholar] [Green Version]
- Becke, AD. Completely Numerical Calculations on Diatomic Molecules in the Local-Density Approximation. Phys. Rev. A 1986, 33, 2786–2788. [Google Scholar] [Green Version]
- Manoli, SD; Whitehead, MA. Generalized Exchange Local-Spin-Density-Functional Theory: One-Electron Energies and Eigenvalues. Collection Czechoslovak Chem. Commun. 1988, 53, 2279–2307. [Google Scholar] [Green Version]
- Filippeti, A. Electron Affinity in Density-Functional Theory in the Local Spin-Density Approximation. Phys. Rev. A 1998, 57, 914–919. [Google Scholar] [Green Version]
- Guo, Y; Whitehead, MA. Application of Generalized Exchange Local-Spin-Density-Functional Theory: Electronegativity, Hardness, Ionization Potential, and Electron Affinity. Phys. Rev. A 1989, 39, 2317–2323. [Google Scholar] [Green Version]
- Dunlap, BI; Andzelm, J. Second Derivatives of the Local-Density-Functional Total Energy when the Local Potential is Fitted. Phys. Rev. A 1992, 45, 81–86. [Google Scholar] [Green Version]
- Dunlap, BI; Andzelm, J; Mintmire, JW. Local-Density-Functional Total Energy Gradients in the Linear Combination of Gaussian-type Orbitals Method. Phys. Rev. A 1990, 42, 6354–6358. [Google Scholar] [Green Version]
- Liu, S. Local-Density Approximation, Hierarchy of Equations, Functional Expansion, and Adiabatic Connection in Current-Density-Functional Theory. Phys. Rev. A 1996, 54, 1328–1336. [Google Scholar] [Green Version]
- Romera, E; Dehesa, JS. Weizsäcker Energy of Many-Electron Systems. Phys. Rev. A 1994, 50, 256–266. [Google Scholar] [Green Version]
- Murphy, DR. Sixth-Order Term of the Gradient Expansion of the Kinetic-Energy Density Functional. Phys. Rev. A 1981, 24, 1682–1688. [Google Scholar] [Green Version]
- Dufek, P; Blaha, P; Sliwko, V; Schwarz, K. Generalized-Gradient-Approximation Description of Band Splittings in Transition-Metal Oxides and Fluorides. Phys. Rev. B 1994, 49, 10170–10175. [Google Scholar] [Green Version]
- Becke, AD; Edgecombe, KE. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [Green Version]
- Silvi, B; Gatti, C. Direct Space Representation of the Metallic Bond. J. Phys. Chem. A 2000, 104, 947–953. [Google Scholar] [Green Version]
- Bader, RFW; Gillespie, RJ; MacDougall, PJ. A Physical Basis for the VSEPR Model of Molecular Geometry. J . Am. Chem. Soc. 1988, 110, 7329–7336. [Google Scholar] [Green Version]
- Silvi, B; Savin, A. Classification of the Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371, 683–686. [Google Scholar] [Green Version]
- Cioslowski, J. Nonnuclear Attractors in the LI2 Molecule. J. Phys. Chem. 1990, 94, 5496–5498. [Google Scholar] [Green Version]
- Liu, S; Ayers, PW; Parr, RG. Alternative Definition of Exchange-Correlation Charge in Density Functional Theory. J. Chem. Phys. 1999, 111, 6197–6203. [Google Scholar] [Green Version]
- Putz, MV. Markovian Approach of the Electron Localization Functions. Int. J. Quantum Chem. 2005, 105, 1–11. [Google Scholar] [Green Version]
- Santos, JC; Tiznado, W; Contreras, R; Fuentealba, P. Sigma-pi Separation of the Electron Localization Function and Aromaticy. J. Chem. Phys. 2000, 120, 1670–1673. [Google Scholar] [Green Version]Scemama, A; Chaquin, P; Caffarel, M. Electron Pair Localization Function: A Practical Tool to Visualize Electron Localization in Molecules from Quantum Monte Carlo Data. J. Chem. Phys. 2000, 121, 1725–1735. [Google Scholar] [Green Version]Soncini, A; Lazzeretti, P. Nuclear Spin-Spin Coupling Density Functions and the Fermi Hole. J. Chem. Phys. 2003, 119, 1343–1349. [Google Scholar] [Green Version]Silvi, B. The Spin-Pair Compositions as Local Indicators of the Nature of the Bonding. J. Phys. Chem. 2003, 107, 3081–3085. [Google Scholar] [Green Version]
- Matito, E; Silvi, B; Duran, M; Solà, M. Electron Localization Function at the Correlated Level. J. Chem. Phys. 2006, 125, 024301. [Google Scholar] [Green Version]
- Kohout, M; Pernal, K; Wagner, FR; Grin, Y. Electron Localizability Indicator for Correlated Wavefunctions. I. Parallel-Spin Pairs. Theor. Chem. Acc. 2004, 112, 453–459. [Google Scholar] [Green Version]
- Jensen, F. On the Accuracy of Numerical Hartree–Fock Energies. Theor. Chem. Acc. 2005, 113, 187–190. [Google Scholar] [Green Version]
- Gombás, P; Szondy, T. Solutions of the Simplified Self-Consistent Field for All Atoms of the Periodic System of elements from Z=2 to Z=92; Adam Hilger Ltd.: London, 1970. [Google Scholar]
- Putz, MV; Ionaşcu, C; Hulesch, O. Global and Local Indicators of Chemical Bonding. “Proceedings of the VIII-th International Symposium Young People and Multidisciplinary Research”, Timişoara; Welding Publishing House, Association of Multidisciplinary Research of the West Zone of Romania: Timişoara, Romania, 11–12 Mai 2006; pp. 632–641, (ISBN-10 973-8359-39-2, ISBN-13 978-8359-39-0). [Google Scholar]
- Antolin, J; Zarzo, A; Angulo, JC. Maximum Entropy Analysis of the Electron-Pair Density in Many-Electron Systems. Phys. Rev. A 1994, 50, 240–246. [Google Scholar] [Green Version]
- Lee, C; Parr, RG. Gaussian and Other Approximations to the First-Order Density Matrix of Electronic System, and the Derivation of Various Local-Density-Functional-Theories. Phys. Rev. A 1987, 35, 2377–2383. [Google Scholar] [Green Version]
- Zhao, Q; Parr, RG. Quantities Ts[n] and Tc[n] in Density-Functional Theory. Phys. Rev. A 1992, 46, 2337–2342. [Google Scholar] [Green Version]
- Ou-Yang, H; Levy, M. Nonuniform Coordinate Scaling Requirements in Density-Functional Theory. Phys. Rev. A 1990, 42, 155–159. [Google Scholar] [Green Version]
- DePristo, AE; Kress, JD. Kinetic-Energy Functionals via Padé Approximations. Phys. Rev. A 1987, 35, 438–441. [Google Scholar] [Green Version]
- Liberman, DA; Albritton, JR; Wilson, BG; Alley, WE. Self-Consistent-Field Calculations of Atoms and Ions Using a Modified Local-Density Approximation. Phys. Rev. A 1994, 50, 171–176. [Google Scholar] [Green Version]
- Levy, M; Ernzerhof, M; Gorling, A. Exact Local Exchange Potential from Fock Equations at Vanishing Coupling Constant, and δTc / δn from Wave-Function Calculations at Full Coupling Constant. Phys. Rev. A 1996, 53, 3963–3973. [Google Scholar] [Green Version]
- Cedillo, A; Robles, J; Gazquez, JL. New Nonlocal Exchange-Energy Functional from a Kinetic-Energy-Density Padé-Approximant Model. Phys. Rev. A 1988, 38, 1697–1701. [Google Scholar] [Green Version]
- Perdew, JP; Yue, W. Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation. Phys. Rev. B 1986, 33, 8800–8802. [Google Scholar] [Green Version]
- Manoli, SD; Whitehead, MA. Generalized-Exchange Local-Spin-Density-Functional Theory: Calculation and Results for Non-Self-Interaction-Corrected and Self-Interaction-Corrected Theories. Phys. Rev. A 1988, 38, 3187–3199. [Google Scholar] [Green Version]
- Becke, AD. Density Functional Calculations of Molecular Bond Energies. J. Chem. Phys. 1986, 84, 4524–4529. [Google Scholar] [Green Version]
- Ghosh, SK; Parr, RG. Phase-Space Approach to the Exchange Energy Functional of Density-Functional Theory. Phys. Rev. A 1986, 34, 785–791. [Google Scholar] [Green Version]
- Bartolotti, LJ. A new Gradient Expansion of the Exchange Energy to Be Used in Density Functional Calculations on Atoms. J. Chem. Phys. 1982, 76, 6057–6059. [Google Scholar] [Green Version]
- Perdew, JP; Chevary, JA; Vosko, SH; Jackson, KA; Pederson, MR; Singh, DJ; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [Green Version]
- Wang, Y; Perdew, JP; Chevary, JA; Macdonald, LD; Vosko, SH. Exchange Potentials in Density-Functional Theory. Phys. Rev. A 1990, 41, 78–85. [Google Scholar] [Green Version]
- Alonso, JA; Girifalco, LA. Nonlocal Approximation to the Exchange Potential and Kinetic Energy of an Inhomogeneous Electron Gas. Phys. Rev. B 1978, 17, 3735–3743. [Google Scholar] [Green Version]
- Levy, M; Gorling, A. Density-Functional Exchange Identity from Coordinate Scaling. Phys. Rev. A 1996, 53, 3140–3150. [Google Scholar] [Green Version]
- Becke, AD. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [Green Version]
- Taut, M. Generalized Gradient Correction for Exchange: Deduction from the Oscillator Model. Phys. Rev. A 1996, 53, 3143–3150. [Google Scholar] [Green Version]
- Slater, JC. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [Green Version]
- Slater, JC; Johnson, KH. Self-Consistent-Field Xα Cluster Method for Polyatomic Molecules and Solids. Phys. Rev. B 1972, 5, 844–853. [Google Scholar] [Green Version]
- Lee, C; Zhou, Z. Exchange-Energy Density Functional: Reparametrization of Becke’s Formula and Derivation of Second-Order Gradient Correction. Phys. Rev. A 1991, 44, 1536–1539. [Google Scholar] [Green Version]
- Senatore, G; March, NH. Recent Progress in the Field of Electron Correlation. Rev. Mod. Phys. 1994, 66, 445–479. [Google Scholar] [Green Version]
- Liu, S; Nagy, A; Parr, RG. Expansion of the Density-Functional Energy Components Ec and Tc in Terms of Moments of the Electron Density. Phys. Rev. A 1999, 59, 1131–1134. [Google Scholar] [Green Version]
- Ou-Yang, H; Levy, M. Theorem for Functional Derivatives in Density-Functional Theory. Phys. Rev. A 1991, 44, 54–58. [Google Scholar] [Green Version]
- Nagy, A; Liu, S; Parr, RG. Density-Functional Formulas for Atomic Electronic Energy Components in Terms of Moments of the Electron Density. Phys. Rev. A 1999, 59, 3349–3354. [Google Scholar] [Green Version]
- Perdew, JP. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824, with Erratum, Phys. Rev. B 1986, 34, 7406. [Google Scholar] [Green Version]
- Wang, Y; Perdew, JP. Spin Scaling of the Electron-Gas Correlation Energy in the High-Density Limit. Phys. Rev. B 1989, 43, 8911–8916. [Google Scholar] [Green Version]
- Seidl, M; Perdew, JP; Levy, M. Strictly Correlated Electrons in Density-Functional Theory. Phys. Rev. A 1999, 59, 51–54. [Google Scholar] [Green Version]
- Perdew, JP; Burke, K; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [Green Version]Zhang, Y; Yang, W. Comment on: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [Green Version](c)Perdew, Burke, and Ernzerhof Replay, idem, 891. [Green Version]
- Perdew, JP; Ernzerhof, M; Zupan, A; Burke, K. Nonlocality of the Density Functional for Exchange and Correlation: Physical Origins and Chemical Consequences. J. Chem. Phys. 1998, 108, 1522–1531. [Google Scholar] [Green Version]
- Wilson, LC; Levy, M. Nonlocal Wigner-Like Correlation-Energy Density Functional Through Coordinate Scaling. Phys. Rev. B 1990, 41, 12930–12932. [Google Scholar] [Green Version]
- Vosko, SJ; Wilk, L; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [Green Version]
- Perdew, JP. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [Green Version]
- Savin, A; Stoll, H; Preuss, H. An Application of Correlation Energy Density Functionals to Atoms and Molecules. Theor Chim Acta 1986, 70, 407–419. [Google Scholar] [Green Version]
- Savin, A; Preuss, H; Stoll, H. Non-Local Effects on Atomic and Molecular Correlation Energies Studies with a Gradient-Corrected Density Functional. In “Density Matrices and Density Functionals”; Erhahy, R, Smith, VH, Eds.; Reidel Publishing Company, 1987; pp. 457–465. [Google Scholar]
- Rasolt, M; Geldart, DJW. Exchange and Correlation Energy in a Nonuniform Fermion Fluid. Phys. Rev. B 1986, 34, 1325–1328. [Google Scholar] [Green Version]
- Savin, A; Wedig, U; Preuss, H; Stoll, H. Molecular Correlation Energies Obtained with a Nonlocal Density Functional. Phys. Rev. Lett. 1984, 53, 2087–2089. [Google Scholar] [Green Version]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [Green Version]
- Perdew, JP; Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron System. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [Green Version]
- Lee, C; Parr, RG. Exchange-Correlation Functional for Atoms and Molecules. Phys. Rev. A 1990, 42, 193–199. [Google Scholar] [Green Version]
- Berkowitz, M. Exponential Approximation for the Density Matrix and the Wigner’s Distribution. Chem Phys. Lett. 1986, 129, 486–488. [Google Scholar] [Green Version]
- Lee, H; Bartolotti, LJ. Exchange and Exchange-Correlation Functionals Based on the Gradient Correction of the Electron Gas. Phys. Rev. A 1991, 44, 1540–1542. [Google Scholar] [Green Version]
- Tozer, DJ; Handy, NC. The Development of New Exchange-Correlation Functionals. J. Chem. Phys. 1998, 108, 2545–2555. [Google Scholar] [Green Version]
- Mandl, F. Quantum Mechanics; John Wiley & Sons: Chichester, 1992. [Google Scholar]
- Miller, JN; Miller, JC. Statistics and Chemometrics for Analytical Chemistry, fourth edition; Prentice Hall: Harlow, 2000. [Google Scholar]
- Lyons, L. A Practical Guide to Data Analysis for Physical Science Students; Cambridge University Press: Cambridge, 1993. [Google Scholar]
- Koopmans, T. Uber die Zuordnung von Wellen Funktionen und Eigenwerter zu den Einzelnen Elektronen Eines Atom. Physica 1934, 1, 104–113. [Google Scholar] [Green Version]
- Parr, RG; Donnelly, RA; Levy, M; Palke, WE. Electronegativity: the Density Functional Viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. [Google Scholar] [Green Version]
- Parr, RG; Pearson, RG. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [Green Version]
- Chattaraj, PK; Liu, GH; Parr, RG. The Maximum Hardness Principle in the Gyftpoulos-Hatsopoulos Three-Level Model for an Atomic or Molecular Species and Its Positive and Negative Ions. Chem. Phys. Lett. 1995, 237, 171–176. [Google Scholar] [Green Version]
- Ayers, PW; Parr, RG. Variational Principles for Describing Chemical Reactions: the Fukui Function and Chemical Hardness Revisited. J. Am. Chem. Soc. 2000, 122, 2010–2018. [Google Scholar] [Green Version]
- Putz, MV. Maximum Hardness Index of Quantum Acid-Base Bonding. MATCH Commun. Math. Comput. Chem. accepted.
- Grabo, T; Gross, EKU. Density-Functional Theory Using an Optimized Exchange-Correlation Potential. Chem. Phys. Lett. 1995, 240, 141–150. [Google Scholar] [Green Version]
- Mulliken, RS. A New Electroaffinity Scale: Together with Data on Valence States and An Ionization Potential and Electron Affinities”. J. Chem. Phys. 1934, 2, 782–793. [Google Scholar] [Green Version]
- Lackner, KS; Zweig, G. Introduction to the Chemistry of Fractionally Charged Atoms: Electronegativity. Phys. Rev. D. 1983, 28, 1671–1691. [Google Scholar] [Green Version]
- Putz, MV. Systematic Formulation for Electronegativity and Hardness and Their Atomic Scales within Density Functional Softness Theory. Int. J. Quantum Chem. 2006, 106, 361–386. [Google Scholar] [Green Version]
- Putz, MV. Semiclassical Electronegativity and Chemical Hardness. J. Theor. Comp. Chem. 2007, 6, 33–47. [Google Scholar] [Green Version]
- Bratsch, SG. A Group Electronegativity Method with Pauling Units. J. Chem. Educ. 1985, 62, 101–103. [Google Scholar] [Green Version]
- Putz, MV; Russo, N; Sicilia, E. On The Applicability of The HSAB Principle through The Use of Improved Computational Schemes for Chemical Hardness Evaluation. J. Comput. Chem. 2004, 25, 994–1003. [Google Scholar] [Green Version]
- Gross, EKU; Oliveira, LN; Kohn, W. Density-Functional Theory for Ensembles of Fractionally Occupied States.I. Basic Formalism. Phys. Rev. A 1988, 37, 2809–2820. [Google Scholar] [Green Version]
- Oliviera, LN; Gross, EKU; Kohn, W. Density-Functional Theory for Ensembles of Fractionally Occupied States. II. Applications to the He Atom. Phys. Rev. A 1988, 37, 2821–2833. [Google Scholar] [Green Version]
- Nesbet, RK. Fractional Occupation Numbers in Density-Functional Theory. Phys. Rev. A 1997, 56, 2665–2668. [Google Scholar] [Green Version]
- Putz, MV. Absolute and Chemical Electronegativity and Hardness; Nova Publishers Inc.: New York, USA, 2008; https://www.novapublishers.com/catalog/product_info.php?products_id=7678.
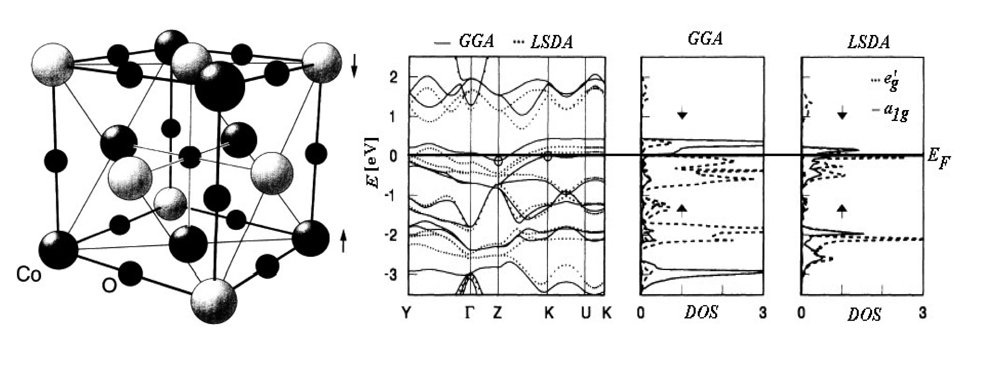
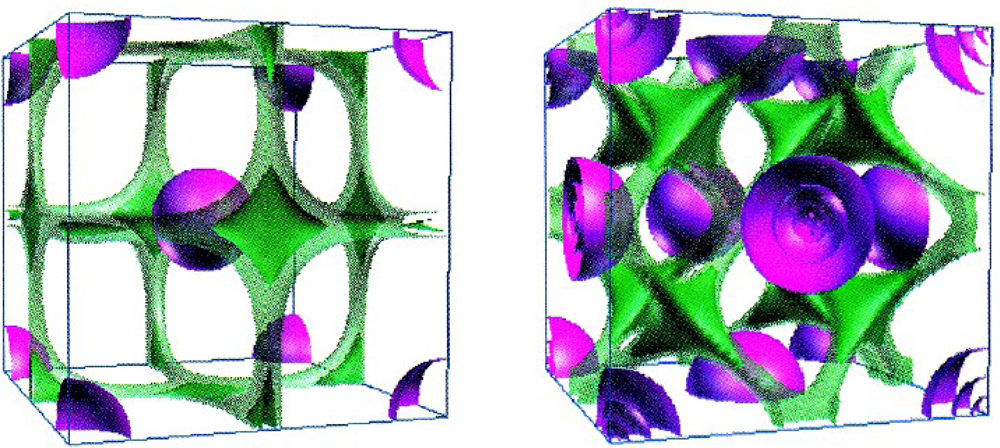
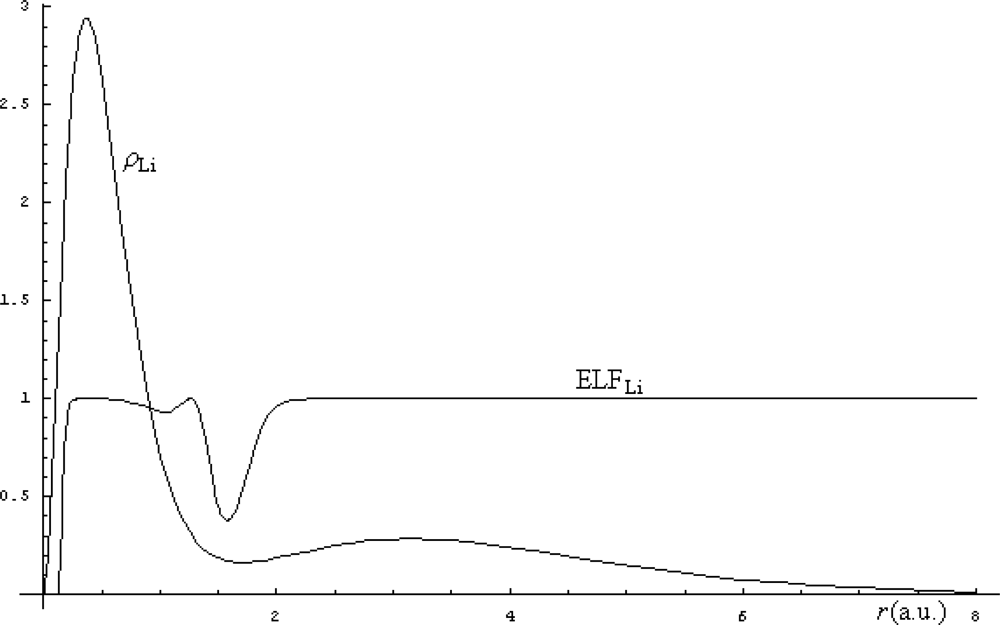
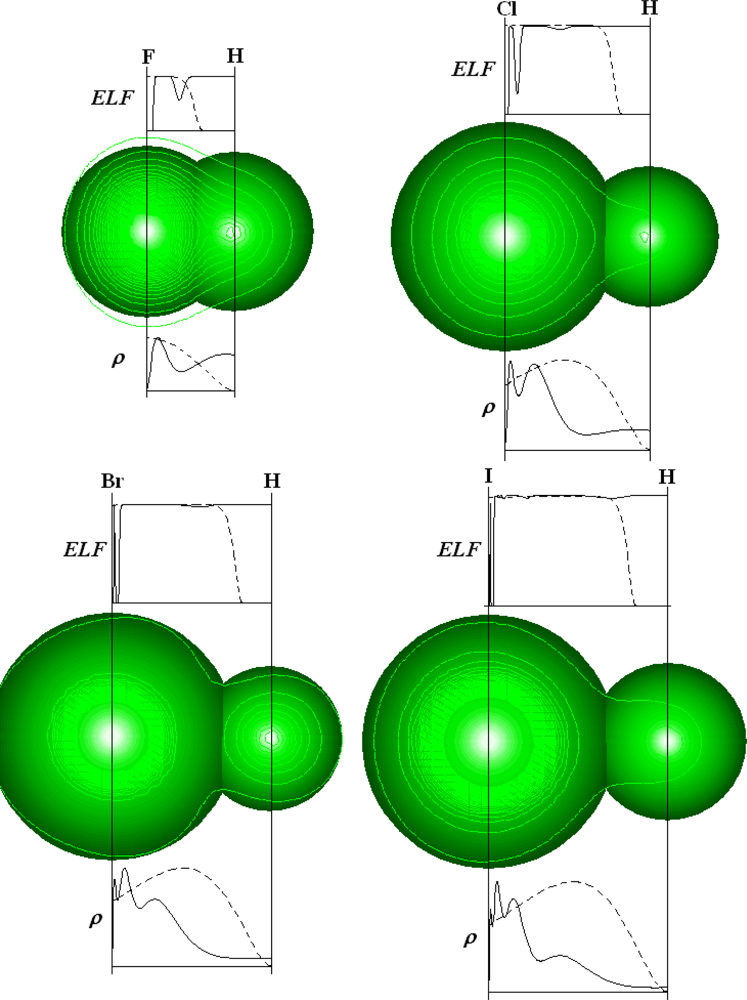
| Atoms | Kinetic energy | Exchange energy | Correlation energy | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Texact♣ | T0♣ | T0+T2♣ | TPadé♣ | Kexact♦ | K0♥ | KB88♥ | Ecexact♦ | Ec(139)♠ | Ec• | |
| He | 2.86168 | 2.56054 | 2.87850 | 2.87639 | −1.0260 | −0.884 | −1.025 | −0.0425 | −0.0215 | −0.0681 |
| Li | 7.43273 | 6.70062 | 7.50504 | 7.44941 | −1.7812 | −1.538 | −1.775 | −0.0454 | −0.0486 | −0.0815 |
| Be | 14.5730 | 13.1286 | 14.6466 | 14.4223 | −2.6669 | −2.312 | −2.658 | −0.0945 | −0.0820 | −0.1192 |
| B | 24.5291 | 22.0720 | 24.5228 | 24.2089 | −3.7438 | −3.272 | −3.728 | −0.1247 | −0.1197 | −0.1625 |
| C | 37.6886 | 34.0144 | 37.5988 | 37.2533 | −5.0444 | −4.459 | −5.032 | −0.1566 | −0.1609 | −0.2091 |
| N | 54.4009 | 49.4771 | 54.3852 | 54.0643 | −6.5971 | −5.893 | −6.589 | −0.1850 | −0.2050 | −0.2567 |
| O | 74.8094 | 67.8965 | 74.3573 | 74.1625 | −8.1752 | −7.342 | −8.169 | −0.2579 | −0.2512 | −0.3035 |
| F | 99.4093 | 90.4598 | 98.6429 | 98.6959 | −10.003 | −9.052 | −10.02 | −0.332 | −0.2996 | −0.3510 |
| Ne | 128.547 | 117.761 | 127.829 | 128.221 | −12.108 | −11.03 | −12.14 | −0.390 | −0.3498 | −0.3987 |
| Na | 161.859 | 148.809 | 161.093 | 161.718 | −14.017 | −12.79 | −14.03 | −0.398 | −0.3892 | −0.4137 |
| Mg | 199.614 | 184.017 | 198.749 | 199.578 | −15.994 | −14.61 | −16.00 | −0.443 | −0.4351 | −0.4491 |
| Al | 241.877 | 223.443 | 240.868 | 242.008 | −18.069 | −16.53 | −18.06 | −0.480 | −0.4809 | −0.4863 |
| Si | 288.854 | 267.315 | 287.659 | 289.139 | −20.280 | −18.59 | −20.27 | −0.521 | −0.5308 | −0.5308 |
| Cl | 459.482 | 426.865 | 457.321 | 460.117 | −27.512 | −25.35 | −27.49 | −0.714 | −0.6901 | −0.6710 |
| Ar | 526.817 | 490.017 | 524.289 | 527.617 | −30.185 | −27.86 | −30.15 | −0.787 | −0.7459 | −0.7190 |
| Atoms | Exchange-Correlation energy | Total energy | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Excexact♣ | ExcI(Xα)♦ | ExcII(Xα)♦ | ExcI(Wig)♦ | ExcII(Wig)♦ | Etotexact♥ | Etotxc(RG)♥ | Etotxc(LDA)♥ | EtotBLYP♠ | EtotPW91♠ | |
| He | −1.0685 | −1.0604 | −1.0566 | −1.0633 | −1.0654 | −2.9042 | −3.0317 | −2.8601 | −2.9071 | −2.9000 |
| Li | −1.8266 | −1.8048 | −1.8134 | −1.8093 | −1.8108 | −7.4781 | −7.6473 | −7.3704 | −7.4827 | −7.4742 |
| Be | −2.7614 | −2.7260 | −2.7522 | −2.7325 | −2.7342 | −14.6675 | −14.8911 | −14.4966 | −14.6615 | −14.6479 |
| B | −3.8685 | −3.8126 | −3.8415 | −3.8215 | −3.8177 | −24.6538 | −24.9158 | −24.4097 | −24.6458 | −24.6299 |
| C | −5.2010 | −5.1127 | −5.1338 | −5.1248 | −5.1121 | −37.8163 | −38.1305 | −37.5095 | −37.8430 | −37.8265 |
| N | −6.7821 | −6.6400 | −6.6440 | −6.6558 | −6.6321 | −54.4812 | −54.8681 | −54.1287 | −54.5932 | −54.5787 |
| O | −8.4331 | −8.3599 | −8.3405 | −8.3796 | −8.3450 | −75.0271 | −75.4597 | −74.5979 | −75.0786 | −75.0543 |
| F | −10.325 | −10.327 | −10.277 | −10.350 | −10.305 | −99.741 | −100.235 | −99.247 | −99.7581 | −99.7316 |
| Ne | −12.498 | −12.551 | −12.466 | −12.579 | −12.524 | −128.937 | −129.522 | −128.403 | −128.9730 | −128.9466 |
| Na | −14.415 | −14.462 | −14.382 | −14.488 | −14.445 | −162.257 | −162.862 | −161.624 | −162.293 | −162.265 |
| Mg | −16.437 | −16.482 | −16.424 | −16.504 | −16.484 | −200.058 | −200.705 | −199.340 | −200.093 | −200.060 |
| Al | −18.549 | −18.566 | −18.542 | −18.583 | −18.593 | −242.357 | −243.028 | −241.533 | −242.380 | −242.350 |
| Si | −20.801 | −20.774 | −20.791 | −20.784 | −20.830 | −289.356 | −290.063 | −288.435 | −289.388 | −289.363 |
| Cl | −28.226 | −28.115 | −28.272 | −28.092 | −28.281 | −460.196 | −461.005 | −458.963 | −460.165 | −460.147 |
| Ar | −30.972 | −30.827 | −31.037 | −30.789 | −31.035 | −527.605 | −528.452 | −526.267 | −527.551 | −527.539 |
| Level | Finite-Difference | Functional | Semiclassical | |||
|---|---|---|---|---|---|---|
| Atoms | χFD | ηFD | χDFT | ηDFT | χSC | ηSC |
| He | 0.45094 | 0.45866 | 1.21132 | 1.66189 | 0.57038 | 0.2172 |
| Li | 0.11099 | 0.16134 | 0.15105 | 0.08784 | 0.00412 | 0.00334 |
| Be | 0.12606 | 0.21794 | 0.44248 | 0.44579 | 0.00893 | 0.0047 |
| B | 0.15656 | 0.14921 | 1.15362 | 1.34105 | 0.01526 | 0.00588 |
| C | 0.22933 | 0.18339 | 2.76332 | 2.9695 | 0.02279 | 0.00684 |
| N | 0.25616 | 0.27894 | 5.79566 | 4.91363 | 0.03139 | 0.0076 |
| O | 0.27894 | 0.22566 | 10.6505 | 5.91694 | 0.04072 | 0.00816 |
| F | 0.38221 | 0.25983 | 16.9129 | 4.37707 | 0.05061 | 0.00849 |
| Ne | 0.39361 | 0.40132 | 23.7119 | −0.08747 | 0.06079 | 0.00864 |
| Na | 0.10290 | 0.10621 | 0.23153 | 0.18743 | 0.00011 | 0.00005 |
| Mg | 0.09555 | 0.18339 | 0.49871 | 0.53142 | 0.00018 | 0.00007 |
| Al | 0.11834 | 0.10327 | 1.04631 | 1.19882 | 0.00026 | 0.00008 |
| Si | 0.17200 | 0.12606 | 2.10805 | 2.30724 | 0.00036 | 0.00009 |
| Cl | 0.30577 | 0.17120 | 11.5766 | 7.7692 | 0.00074 | 0.00012 |
| Ar | 0.28299 | 0.29806 | 17.8831 | 9.08857 | 0.00088 | 0.00013 |
| Molecules | Kinetic | Exchange | Correlation | Exch.-corr. | Total energy | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| T0♣ | T0+T2♣ | Kexact♣ | KPBE♣ | EcVWN♦ | EcGCP♦ | Excexact♣ | ExcPBE♣ | EtotBLYP♥ | EtotTH♥ | |
| H2 | 1.140 | 1.125 | −0.657 | −0.648 | −95·10−3 | −47·10−3 | −0.698 | −0.691 | −1.169 | −1.178 |
| LiH | 7.978 | 8.003 | −2.125 | −2.105 | −219·10−3 | −93·10−3 | −2.212 | −2.188 | −8.068 | −8.070 |
| CH4 | 40.050 | 40.141 | −6.576 | −6.536 | −593·10−3 | −328·10−3 | −6.883 | −6.836 | −40.502 | −40.515 |
| H2O | 76.150 | 75.477 | −8.910 | −8.917 | −664·10−3 | −365·10−3 | −9.292 | −9.241 | −76.448 | −76.433 |
| HF | 100.137 | 99.242 | −10.378 | −10.385 | −704·10−3 | −380·10−3 | −10.779 | −10.720 | −100.48 | −100.455 |
| N2 | 109.115 | 108.242 | −13.094 | −13.128 | −945·10−3 | −506·10−3 | −13.665 | −13.580 | −109.559 | −109.54 |
| O2 | 149.843 | 148.369 | −16.290 | −16.358 | −1110·10−3 | −599·10−3 | −16.958 | −16.887 | −150.384 | −150.337 |
| F2 | 198.892 | 196.729 | −19.872 | −19.951 | −1302·10−3 | −697·10−3 | −20.661 | −20.564 | −199.599 | −199.533 |
| Level Molecule s | Finite-Difference | Functional | Semiclassical | |||
|---|---|---|---|---|---|---|
| χFD | ηFD | χDFT | ηDFT | χSC | ηSC | |
| H2 | 0.26387 | 0.2370 | 0.26384 | 0.23704 | 0.26387 | 0.23705 |
| LiH | 0.15626 | 0.192 | 0.19212 | 0.12818 | 0.00811 | 0.006596 |
| CH4 | 0.25616 | 0.2239 | 0.32216 | 0.29051 | 0.08468 | 0.03064 |
| H2O | 0.26871 | 0.2331 | 0.39097 | 0.34859 | 0.09335 | 0.0229 |
| HF | 0.3077 | 0.2479 | 0.51964 | 0.44974 | 0.08493 | 0.01639 |
| N2 | 0.25616 | 0.2789 | 5.79566 | 4.91363 | 0.03139 | 0.00761 |
| O2 | 0.27894 | 0.2257 | 10.6505 | 5.91694 | 0.04072 | 0.00816 |
| F2 | 0.36898 | 0.2598 | 16.9129 | 4.37707 | 0.05061 | 0.00849 |
| Method of
| QSPR results
| Method of
| QSPR results
| ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Energ y | (χ, η) | a | b | c | σπ | r | Energy | (χ, η) | a | b | c | σπ | r |
| Texact | FD | 194.59 | 741.55 | −951.38 | −0.0017 | 0.33 | Excexact | FD | −15.30 | −44.80 | 60.89 | −0.0303 | 0.37 |
| DFT | 51.73 | 2.09 | 31.51 | 7.2 | 0.62 | DFT | −6.56 | −0.19 | −1.53 | 40.84 | 0.58 | ||
| SC | 186.38
| −2315.7
| 5147.4
| −0.001
| 0.35
| SC | −13.76
| 73.07
| −128.0
| −0.024
| 0.38
| ||
| T0 | FD | 179.67 | 687.26 | −881.14 | −0.0019 | 0.33 | ExcI(Xα) | FD | −15.28 | −44.56 | 60.69 | −0.0306 | 0.37 |
| DFT | 46.99 | 1.91 | 29.41 | 8.07 | 0.62 | DFT | −6.56 | −0.2 | −1.51 | 39.11 | 0.57 | ||
| SC | 172.42
| −2185.3
| 4874.1
| −0.001
| 0.35
| SC | −13.72
| 72.04
| −125.5
| −0.024
| 0.38
| ||
| T0+T2 | FD | 193.83 | 736.94 | −946.29 | −0.0017 | 0.33 | ExcII(Xα) | FD | −15.28 | −44.81 | 60.92 | −0.0303 | 0.37 |
| DFT | 51.59 | 2.07 | 31.36 | 7.33 | 0.62 | DFT | −6.52 | −0.19 | −1.53 | 40.81 | 0.57 | ||
| SC | 185.59
| −2312.1
| 5142
| −0.001
| 0.35
| SC | −13.75
| 74.72
| −132.4
| −0.024
| 0.38
| ||
| TPadé | FD | 194.61 | 741.17 | −951.43 | −0.0017 | 0.33 | ExcI(Wig) | FD | −15.29 | −44.53 | 60.67 | −0.0306 | 0.37 |
| DFT | 51.54 | 2.08 | 31.58 | 7.3 | 0.62 | DFT | −6.58 | −0.2 | −1.50 | 38.78 | 0.57 | ||
| SC | 186.42
| −2334.4
| 5197.4
| −0.001
| 0.35
| SC | −13.72
| 71.4
| −123.8
| −0.024
| 0.38
| ||
| Kexact | FD | −14.91 | −43.62 | 59.38 | −0.0312 | 0.37 | ExcII(Wig) | FD | −15.30 | −44.80 | 60.95 | −0.0304 | 0.37 |
| DFT | −6.37 | −0.19 | −1.49 | 43.17 | 0.57 | DFT | −6.54 | −0.2 | −1.52 | 39.98 | 0.57 | ||
| SC | −13.4
| 72.74
| −128.78
| −0.0243
| 0.38
| SC | −13.76
| 74.1
| −130.7
| −0.024
| 0.38
| ||
| K0 | FD | −13.59 | −40.29 | 54.69 | −0.0337 | 0.37 | Etotexact | FD | −194.98 | −742.7 | 952.91 | −0.0017 | 0.33 |
| DFT | −5.72 | −0.17 | −1.39 | 46.96 | 0.58 | DFT | −51.91 | −2.10 | −31.54 | 7.15 | 0.62 | ||
| SC | −12.24
| 68.77
| −123.42
| −0.026
| 0.38
| SC | −186.73
| 2316
| −5148
| −0.001
| 0.35
| ||
| KB88 | FD | −14.89 | −43.61 | 59.33 | −0.0312 | 0.37 | Etotxc(RG) | FD | −195.55 | −743.9 | 954.5 | −0.0017 | 0.33 |
| DFT | −6.37 | −0.19 | −1.49 | 42.35 | 0.57 | DFT | −52.27 | −2.11 | −31.56 | 7.1 | 0.62 | ||
| SC | −13.39
| 71.88
| −126.54
| −0.0245
| 0.38
| SC | −187.24
| 2315.
| −5143.
| −0.001
| 0.35
| ||
| Ecexact | FD | −0.39 | −1.20 | 1.52 | −1.055 | 0.38 | Etotxc(LDA) | FD | −194.26 | −740.7 | 950.13 | −0.0017 | 0.33 |
| DFT | −0.19 | −0.0075 | −0.03 | 595.98 | 0.59 | DFT | −51.59 | −2.09 | −31.47 | 7.18 | 0.62 | ||
| SC | −0.362
| 0.232
| 0.997
| 18.528
| 0.38
| SC | −186.1
| 2313.
| −5142.
| −0.001
| 0.35
| ||
| Ec(139)♠ | FD | −0.40 | −1.13 | 1.55 | −1.207 | 0.39 | EtotBLYP | FD | −194.99 | −742.7 | 952.86 | −0.0017 | 0.33 |
| DFT | −0.19 | −0.0056 | −0.03 | 1081.3 | 0.57 | DFT | −51.94 | −2.1 | −31.53 | 7.15 | 0.62 | ||
| SC | −0.356
| 0.851
| −0.563
| −0.778
| 0.41
| SC | −186.74
| 2315.
| −5145
| −0.001
| 0.35
| ||
| Ec• | FD | −0.41 | −1.10 | 1.44 | −1.1808 | 0.40 | EtotPW91 | FD | −194.97 | −742.7 | 952.81 | −0.0017 | 0.33 |
| DFT | −0.22 | −0.0063 | −0.03 | 735.5 | 0.59 | DFT | −51.92 | −2.1 | −31.54 | 7.15 | 0.62 | ||
| SC | −0.374 | −0.224 | 2.113 | −42.24 | 0.42 | SC | −186.7 | 2315. | −5145. | −0.001 | 0.35 | ||
| Method of
| QSPR results
| Method of
| QSPR results
| ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Energy y | χ & η | a | b | c | σπ | r | Energy y | χ & η | a | b | c | σπ | r |
| T0 | FD | −192.71 | 821.61 | 238.59 | 0.00035 | 0.77 | T0+T2 | FD | −190.58 | 811.48 | 237.96 | 0.0004 | 0.77 |
| DFT | 40.446 | 8.125 | 4.501 | 0.068 | 0.89 | DFT | 40.199 | 8.012 | 4.497 | 0.07 | 0.89 | ||
| SC | 82.14
| 542.16
| −977.9
| −0.0033
| 0.56
| SC | 81.4
| 537.74
| −969.47
| −0.003
| 0.56
| ||
| Kexact | FD | 18.18 | −70.1 | −38.02 | 0.0077 | 0.74 | KPBE | FD | 18.324 | −70.48 | −38.25 | 0.0077 | 0.74 |
| DFT | −5.234 | −0.646 | −0.805 | 1.93 | 0.89 | DFT | −5.219 | −0.65 | −0.811 | 1.92 | 0.89 | ||
| SC | −9.78
| −48.27
| 94.96
| −0.04
| 0.61
| SC | −9.81
| −48.15
| 95.
| −0.04
| 0.61
| ||
| EcVWN | FD | 1.039 | −4.06 | −2.74 | 0.167 | 0.71 | EcGCP | FD | 0.59 | −2.27 | −1.496 | 0.289 | 0.72 |
| DFT | −0.423 | −0.035 | −0.06 | 47.83 | 0.87 | DFT | −0.225 | −0.019 | −0.033 | 94.08 | 0.86 | ||
| SC | −0.71
| −3.13
| 6.22
| −0.63
| 0.64
| SC | −0.36 | −2.1 | 3.7 | −0.88 | 0.64 | ||
| Excexact | FD | 18.95 | −72.63 | −40.1 | 0.0076 | 0.74 | ExcPBE | FD | 18.85 | −72.45 | −39.62 | 0.0075 | 0.74 |
| DFT | −5.457 | −0.668 | −0.846 | 1.897 | 0.89 | DFT | −5.421 | −0.666 | −0.84 | 1.898 | 0.89 | ||
| SC | −10.19 | −50.16 | 98.71 | −0.039 | 0.61 | SC | −10.13 | −49.97 | 98.28 | −0.04 | 0.61 | ||
| EtotBLYP | FD | 193.12
| −824.17
| −238.96
| 0.00035
| 0.77
| EtotTH | FD | 193.06
| −823.8
| −239.04
| 0.0004
| 0.77
|
| DFT | −40.67 | −8.149 | −4.514 | 0.068 | 0.89 | DFT | −40.67 | −8.145 | −4.514 | 0.068 | 0.89 | ||
| SC | −82.48 | −544.35 | 981.7 | −0.003 | 0.56 | SC | −82.46 | −544.3 | 981.5 | −0.003 | 0.56 | ||
Share and Cite
Putz, M.V. Density Functionals of Chemical Bonding. Int. J. Mol. Sci. 2008, 9, 1050-1095. https://doi.org/10.3390/ijms9061050
Putz MV. Density Functionals of Chemical Bonding. International Journal of Molecular Sciences. 2008; 9(6):1050-1095. https://doi.org/10.3390/ijms9061050
Chicago/Turabian StylePutz, Mihai V. 2008. "Density Functionals of Chemical Bonding" International Journal of Molecular Sciences 9, no. 6: 1050-1095. https://doi.org/10.3390/ijms9061050
APA StylePutz, M. V. (2008). Density Functionals of Chemical Bonding. International Journal of Molecular Sciences, 9(6), 1050-1095. https://doi.org/10.3390/ijms9061050




