Next Article in Journal
A Fragment-Based Scoring Function to Re-rank ATP Docking Results
Previous Article in Journal
Threading Cyclodextrins in Chloroform: A [2]Pseudorotaxane
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 8
Issue 11
10.3390/i8111064
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Molecular Structure and Vibrational Spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene

by
Hakan Arslan
1,* and
Aydın Demircan
2
1
Department of Chemistry, Faculty of Arts and Science, Mersin University, 33343-Mersin, Turkey
2
Department of Chemistry, Faculty of Arts and Science, Niğde University, 51100-Niğde, Turkey
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2007, 8(11), 1064-1082; https://doi.org/10.3390/i8111064
Submission received: 6 September 2007 / Revised: 15 September 2007 / Accepted: 19 September 2007 / Published: 29 October 2007
(This article belongs to the Section Physical Chemistry, Theoretical and Computational Chemistry)
Browse Figures
Versions Notes

Abstract

:
Geometric parameters and FT-IR spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene were computed by the HF, B3LYP, B3PW91 and mPW1PW91 methods in conjunction with the 6-31G(d,p) basis set. The calculated IR spectra are in a good agreement with the observed FT-IR spectrum. A general better performance of B3LYP, B3PW91 and mPW1PW91 versus HF was quantitatively characterized by using PAVF 1.0 program. Optimal uniform scaling factors calculated for the title compound are 0.8952, 0.9552, 0.9520 and 0.9456 for HF, B3LYP, B3PW91 and MPW1PW91 methods, respectively.

1. Introduction

Heterocycles such as furan, thiophene and pyrrole undergo Diels-Alder reactions despite their stabilized 6π-aromatic electronic configuration [1]. In fact proclivity of furans to undergo [2–4] cycloaddition with various π-bonds has attracted the attention of many research groups, as it allows for the rapid construction of valuable synthetic intermediates [2–4]. In view of furans electron-rich constitution and electron donor properties they have been involved mostly as the diene component in the cycloaddition process [5,6]. In this context, we have been studying on synthesis of heterotricyclicfused compounds [7,8]. Sulphure containing rigid tricycle, 2, was obtained from 2-{[(2-bromoprop-2- en-1-yl)thio]methyl}furan, 1, under solvent free condition in a commercial microwave (Scheme 1).
The precursor of intramolecular Diels-Alder (IMDA) cycloadditon, 1, was obtained from the treatment of furfurylmercaptanol with 2,3-dichloropropene by employing Williamson ether synthesis method [9]. The IMDA cycloaddition reaction of 1 was carried out in a commercially available microwave oven (2450 MHz) for 12 min irradiation. This stereoselective cycloaddition process take place over facile exo transition state and is promoted by Thorpe-Ingold (Scissor) effect as previously show in similar studies [10]. Aromatic furan rings and inactivated diene & dienophile sides make such cycloaddition reaction reversible and could give modest yield [11].
Although semi-empirical methods proved its usefulness in practice to facilitate the IR identifications, the performance of semi-empirical methods can not satisfy modern criteria of theoretical FT-IR spectral predictions. The IR spectra computed with Hartree-Fock (HF) and density functional theory (DFT) methods were in much better agreement with the observed IR spectrum: the correlation between the calculated and experimental vibration frequencies was characterized by the coefficients for all DFT methods higher than HF method [12–24]. The calculated absolute band intensities were satisfactorily matched with the observed relative intensities as well. Also, the new local density functionals (M05, M05-2X, M06 and M06-2X) with a very broad applicability were recently developed by the Truhlar group [25,26]. These new hybrid meta exchange-correlation functionals are parametrized including both nonmetallic and metallic compounds. Also, these functionals give the best overall performance for a combination of main-group thermochemistry, thermochemical kinetics, and organic, organometallic, biological, and noncovalent interactions as well as the other popular functionals (B3LYP, BLYP, and BP86) [25–28].
In the present work, we have calculated the vibrational frequencies and geometric parameters of the title compound in the ground state to distinguish the fundamentals from the experimental vibrational frequencies and geometric parameters. Furthermore, we interpreted the calculated spectra of in terms of potential energy distributions (PEDs) and made the assignment of the experimental bands due to PED analysis results. In continuation of our theoretical studies, in the present work we checked the relative performance of B3LYP, B3PW91 and mPW1PW91 methods, as well as of HF for comparison, at the 6-31G(d,p) level taking as a test compound 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene.

2. Experimental

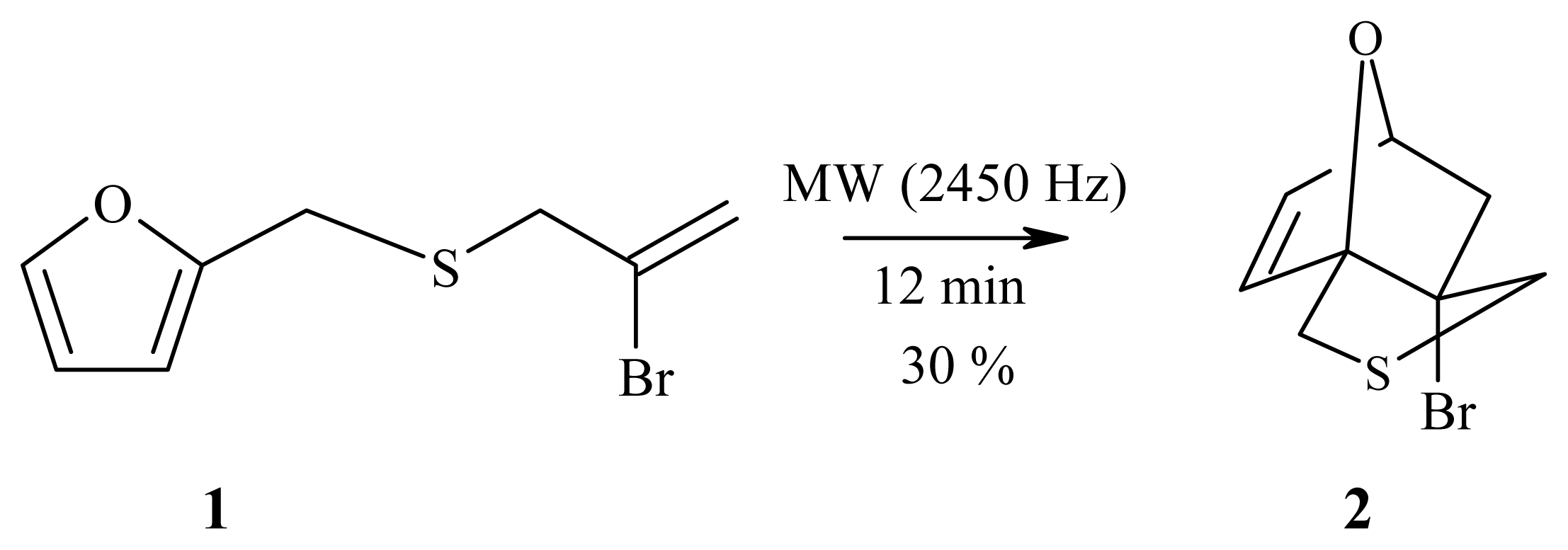
2.1. Synthesis of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene

2-{[(2-bromoprop-2-en-1-yl)thio]methyl}furan, 1, (1.17 g, 5 mmol) was placed in a 5 mL vial and irradiated in a commercial microwave (2450 MHz) for 12 min. Resulting, cyclic and acyclic mixture was subjected to flash column chromatography to afford the title compound as yellow crystal, 0.36 g (30 %), m.p.: 64–66 °C; TLC, (Hexane:Diethylether; (9 : 1), Rf :0.28; δH (300 MHz, CDCl3): 6.55 (dd, 1H, J1 5.8 Hz, J2 1.8 Hz), 6.46 (d, 1H, J 5.8 Hz), 5.10 (dd, 1H, J1 1.8 Hz, J2 4.6 Hz), 3.44 (d, 2H, J 12.5 Hz), 3.38 (d, 2H, J 12.5 Hz), 2.56 (dd, 1H, J1 4.8 Hz, J2 12.5 Hz), 1.90 (d, 1H, J 12.5 Hz). δC (75.5 MHz): 139.1, 138.5, 103.8, 82.6, 71.8, 49.9, 46.2, 31.8. m/z (EI, 70 eV): 234 [M+(81Br), 10%], 232 [M+(79Br), 8%], 93 [M+-(81Br+CH2SCH2), 100%]. EA (C8H9BrOS): Requires: 41.22%, H. 3.89 %, Found: C 41.51, H 3.63 % [11].

2.2. Instrumentation

The room temperature attenuated total reflection Fourier transform infrared (FT-IR ATR) spectrum of the 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene was registered using Varian FTS1000 FT-IR spectrometer with Diamond/ZnSe prism (4000–525 cm−1; number of scans: 250; resolution: 1 cm−1) (Figure 1).

2.2. Calculations details

All the calculations were performed with the Gaussian 03W program package on a double Xeon/3.2 GHz processor with 8 GB Ram [29]. The molecular structure of the 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene, in the ground state is optimized by using the Hartree-Fock (HF) [30], density functional using Becke’s three-parameter hybrid method [31] with the Lee, Yang, and Parr correlation functional methods [32] (B3LYP), the Barone and Adamo’s Becke-style one-parameter functional using the modified Perdew–Wang exchange and Perdew–Wang 91 correlation method, (mPW1PW91) [33,34], Becke’s three parameter exchange functional combined with gradient corrected correlation functional of Perdew and Wang’s 1991 (B3PW91) [35,36], and 6-31G(d,p) basis set. The vibrational frequencies were also calculated with these methods. The frequency values computed at these levels contain known systematic errors [37]. Therefore, we have used the scaling factor values of 0.8992, 0.9614, 0.9573 and 0.9500 for HF, B3LYP, B3PW91 and mPW1PW91, respectively [23,38]. We have also calculated optimal scaling factors for all investigated methods by PAVF 1.0 program [39]. The assignment of the calculated wavenumbers is aided by the animation option of GaussView 3.0 graphical interface for gaussian programs, which gives a visual presentation of the shape of the vibrational modes [40]. Furthermore, theoretical vibrational spectra of the title compound were interpreted by means of PEDs using VEDA 4 program [41].

3. Results and Discussion

Sulfones have always been in interest as a core functional group in both organic and medicinal chemistry because of their versatile synthetic utility and as inhibitors of various types of enzymatic processes [42]. More specifically, alkenyl sulfones are well known for their ability to inhibit many types of cycteine proteases [43,44]. The alkenyl sulfones are reversible inhibitors of these enzymes through conjugated addition of the thiol of the active site cysteine residue. In the synthetic sense, the alkenyl sulfone has come to play important role, acting as an efficient Michael acceptor and as a π donor in cycloadditon reactions [45,46]. We have recently been studying IMDA reaction of furans, since having seen the sulfones are great interest in medicinal chemistry, then we focused onto synthesis of tricyclic sulfones, 2, as parameter of the compound gave negative charge on sulphure and bromine atoms (Atomic polar tensor: S, −0.137; Br, −0.293) [47]. The issue of the further study is to research the biologic activity test of these sulfones.

3.1. Geometry optimization

The crystal and molecular structure of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene have been reported [11]. The structure parameters is triclinic, the space group P1, with the cell dimensions a = 6.6508 (10) Å, b = 7.9576 (12) Å, c = 8.4012 (12) Å, α= 81.030 (12) °, β= 88.572 (12) °, γ = 81.179 (12) ° and V = 434.00 (11) Å3. In this work, we performed full geometry optimization of the title compound. The crystal and optimized structure of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-en with the labelling of atoms are given in Figure 2. The optimized geometrical parameters (bond length and angles) by HF, B3LYP, B3PW91 and mPW1PW91 methods with 6–31G(d,p) as basis set are listed in Table 1. Also, Table 1 compares the calculated geometrical parameters with the experimental data. As follows from this comparison, the bond lengths and angles calculated for the title compound show quite good agreement with experimental values. Owing to our calculations, DFT/mPW1PW91 method correlates well for the bond length in comparison to the other DFT methods and HF method according to RMS values (RMS = 0.014, 0.018, 0.012 and 0.010 Å for HF, B3LYP, B3PW91 and mPW91PW91 levels, respectively). The largest difference between experimental and calculated DFT/mPW1PW91 bond length and angle is about 0.018 Å (R(C10–C12)) and 1.1 ° (A(C5-C8-C10)). As a result, the optimized bond lengths and angles by DFT/mPW1PW91 method show the best agreement with the experimental values.
The importance of relativistic effects in properly describing the electronic structure of molecules containing heavy atoms is frequently stressed in the literature [25,28,48,49]. The relativistic effects lead to an increase of vibrational frequencies and shortening of bond lengths [48,49]. Although the title compound contains one heavy atom “Br”, we cannot observe this effect in the obtained results. The difference between calculated and experimental C-Br bond length is nearly within the experimental error range of the single crystal X-ray diffraction data.

3.2. Vibrational frequencies

Vibration frequencies calculated by HF, B3LYP, B3PW91 and mPW1PW91 for the title compounds are listed in Table 2–5, respectively. All the calculated spectra are in a good agreement with the experimental one, including the calculated absolute band intensities that well match the experimental relative intensities. All three hybrid functions are superior to HF in terms of realistic reproduction of both band intensity distribution and general spectral features.
A general better performance of B3LYP, B3PW91 and mPW1PW91 versus HF can be quantitatively characterized by using the mean deviation, mean absolute deviation, average absolute error, root mean square values and coefficients of correlation (cc) between the calculated and observed vibration frequencies and given in Table 2–5. The root mean square (RMSmol and RMSover) values were calculated in this study by PAVF 1.0 program [39] according to Scott and Radom [38]. The cc values for all three DFT methods were bigger than 0.9998, whereas for HF it was 0.9997: these values are very close to those reported for the literature data [12–24].
These results indicate that the DFT calculations approximate the observed fundamental frequencies much better than the HF results. The small difference between experimental and calculated vibrational modes is observed. This discrepancy can come from the formation of intermolecular hydrogen bonding. Also, we note that the experimental results belong to solid phase and theoretical calculations belong to gaseous phase.
Finally, one should mention scaling factors, which are crucial for IR spectral predictions. To calculate optimal scaling factors, we used PAVF 1.0 program [39]. Only single (uniform) scaling factors were calculated, without discrimination for different vibrations (as, for example, for CH and non-CH stretching vibrations in Ref. [50]). The values obtained are 0.8952, 0.9456, 0.9520 and 0.9552 for HF, mPW1PW91, B3PW91 and B3LYP, respectively. They are very close to those recommended by Scott and Radom and Kuppens et al. [23,38] for the same levels of theory (0.8992, 0.9500, 0.9573 and 0.9614, respectively) and increase in the same order of HF, mPW1PW91, B3PW91 and B3LYP. Thus, for future IR spectral predictions for unknown derivatives of the title compound, one can recommend scaling factors of 0.895, 0.946, 0.952 and 0.955 for HF, mPW1PW91, B3PW91 and B3LYP, respectively.
The IR bands at 3140 and 3077 cm−1 in FT-IR spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene have been designated to symmetric and asymmetric νCH stretching fundamentals of C10 and C12 atoms, respectively [51,52]. The wavenumbers corresponding to the aliphatic νCH stretching are listed in Table 2. All the calculated values in each method are overestimated, as well known in theoretical quantum mechanic assignment concerning hydrocarbons. After we were applied the scale factor both calculated in this research and given by Scott and Radom [38] and Kuppens et al. [23] for all the methods, we observed a good concordance between the experimental and the calculated values. The vibrational spectra show four bands in the aliphatic νCH stretching region and are evident overlap between the different C-H stretching modes. Seven bands at 3015, 3011, 3007, 3007, 2954, 2952 and 2946 cm−1 were calculated in this research. First three is asymmetric νC-H stretching band and the last three bands symmetric νC-H stretching band for –CH2-group. These assignments were also supported by the literature [51].
The vibrational modes concerning the bond angle bending (HCH): scissoring, wagging, twisting and rocking are well defined in all the calculations. As seen from Table 2, the bands observed at 1447, 1439 and 1418 cm−1 in FT-IR spectrum correspond to scissoring deformation of -C(5)H2-, -C(15)H2- and -C(1)H2- group in the title compound [51,52]. The theoretically computed values of scissoring deformation vibration modes show a good agreement with the experimental values. The wagging, twisting and rocking vibrational modes are distributed in a wide range [51–54]. Twisting and wagging vibrational modes of the -CH2- groups were assigned in the range of 1250–1100 cm−1. The above result is in close agreement with the literature values [55]. These vibrational modes are described in the tables by mean of the general symbol δCH2. The rocking -CH2- is assigned in the wavenumber range of 950–800 cm−1 and the wavenumber shift of these bands is due to the atom nature in which the -CH2- group is bonded. The -CH2- rocking vibrational modes are intensive bands in which can be appreciating the vibrational coupling with other vibrational modes [52,53]. These bands are assigned using calculated potential energy distribution.
The bands observed at 722, 701 and 688 cm−1 in FT-IR spectrum corresponds to C-S stretching vibrations in the title compound. The calculated DFT/B3LYP/6-31G(d,p) scaled values for the title compound are: 718, 698 and 690 cm−1, these values are in agreement with the experimental wavenumbers. These results were confirmed by Bensebaa et al. [56].
The C–C stretching vibrations in cyclic alkanes appeared as weak bands in the region 1200–800 cm−1 and consequently are of little importance for structural study [57]. Hence, in the present study, the FT-IR bands observed at 1193 and 1189 cm−1 in title compound have been assigned to C–C stretching vibrations. These results were confirmed by Gunasekaran et al. [58].

4. Conclusions

The IR spectrum of the title compound computed by the HF, B3LYP, B3PW91 and mPW1PW91 methods in conjunction with the 6-31G(d) basis set are in a good agreement with its observed FT-IR spectrum. The correlation between the calculated and experimental vibration frequencies is characterized by the coefficients of bigger than 0.9998 for all three DFT methods and 0.9997 for HF. Optimal uniform scaling factors calculated for the title compound are 0.8952, 0.9456, 0.9520 and 0.9552 for HF, mPW1PW91, B3PW91 and B3LYP, respectively. For IR spectrum predictions for the title compound type derivatives, any of the three hybrid functions can be equally successfully used. Taking into account small variations of the scaling factors for the derivatives of the title compound, for future IR spectral predictions for unknown compounds of this class, one can recommend scaling factors of 0.895, 0.946, 0.952 and 0.955 for HF, mPW1PW91, B3PW91 and B3LYP, respectively.
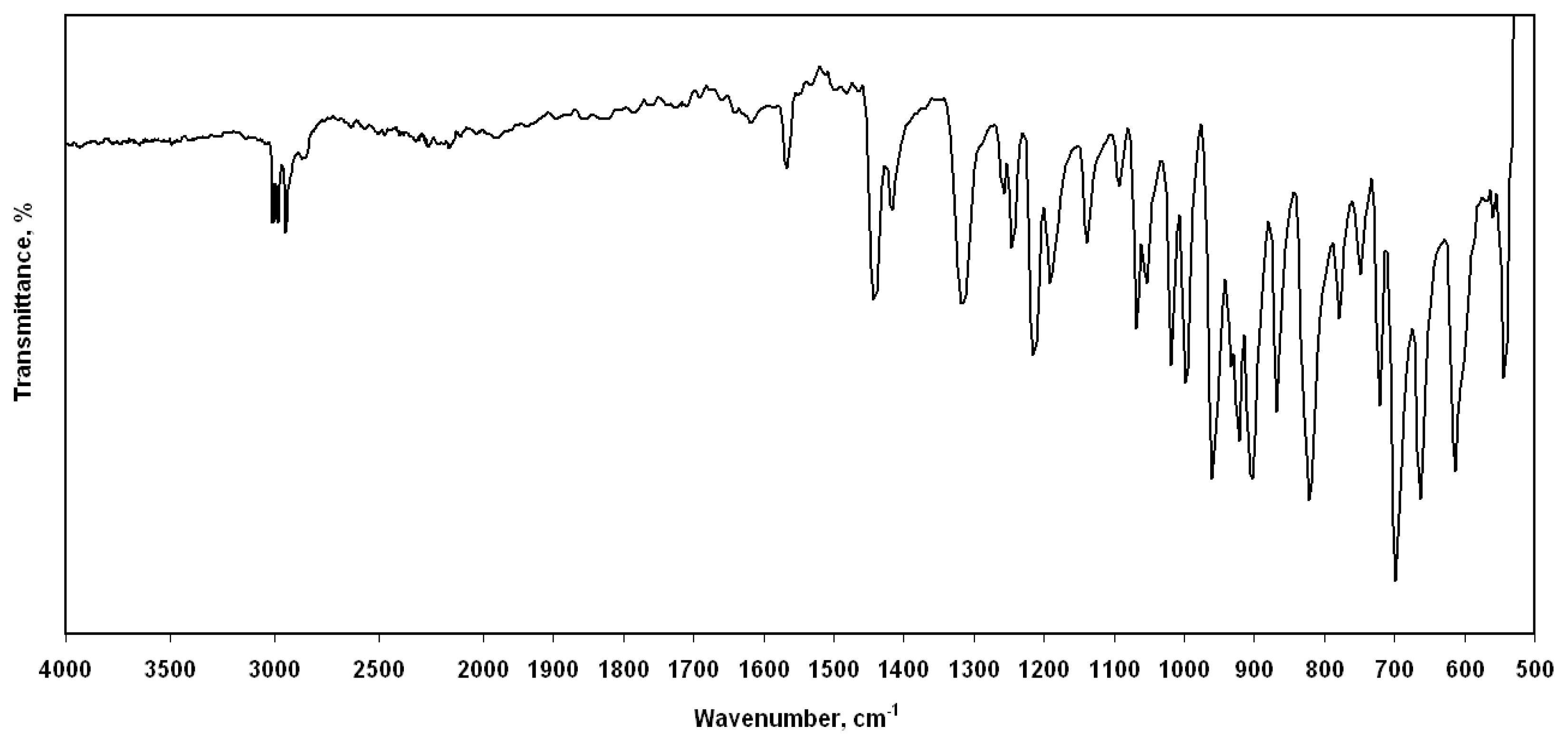
Ijms 08 01064f1 1024
Figure 1. FT-IR spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene recorded at room temperature.
Figure 1. FT-IR spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene recorded at room temperature.
Ijms 08 01064f1
Ijms 08 01064f2 1024
Figure 2. The optimized molecular structure (a) and ORTEP-3 view (50 % probability displacement ellipsoids) of the title compound, with the atom numbering scheme (b).
Figure 2. The optimized molecular structure (a) and ORTEP-3 view (50 % probability displacement ellipsoids) of the title compound, with the atom numbering scheme (b).
Ijms 08 01064f2
Ijms 08 01064f3 1024
Scheme 1.
Scheme 1.
Ijms 08 01064f3
Table
Table 1. Optimized and experimental geometries of the title compound in the ground state.
Table 1. Optimized and experimental geometries of the title compound in the ground state.
ParametersExperimentalCalculated
HFDFT
B3LYPB3PW91mPW1PW91
Bond lengths (Å)
R(1,4)1.508(6)1.5291.5291.5241.522
R(1,19)1.813(4)1.8241.8441.8291.825
R(4,5)1.533(5)1.5481.5511.5441.541
R(4,14)1.552(5)1.5571.5751.5691.566
R(4,20)1.965(3)1.9641.9891.9671.959
R(5,8)1.554(6)1.5561.5701.5641.561
R(8,10)1.512(8)1.5201.5221.5171.515
R(8,18)1.436(5)1.4151.4431.4351.431
R(10,12)1.314(7)1.3171.3351.3341.332
R(12,14)1.508(6)1.5211.5241.5201.517
R(14,15)1.502(5)1.5131.5151.5121.510
R(14,18)1.444(4)1.4141.4431.4351.430
R(15,19)1.829(4)1.8291.8521.8391.834
r0.99710.99940.99900.9988
Bond angles (°)
A(4,1,19)107.7(3)107.53107.69107.49107.44
A(1,4,5)115.5(3)115.02115.45115.30115.15
A(1,4,14)106.5(3)105.48105.63105.26105.16
A(1,4,20)109.1(3)109.46109.41109.62109.72
A(5,4,14)102.3(3)101.62101.98101.95101.93
A(5,4,20)113.0(3)113.10112.78113.15113.31
A(14,4,20)109.9(2)111.68111.12111.01110.97
A(4,5,8)100.0(3)99.5999.8799.7799.73
A(5,8,10)107.1(4)107.56107.32106.98106.87
A(5,8,18)100.9(3)101.13101.13101.34101.41
A(10,8,18)102.0(4)101.42101.89102.11102.10
A(8,10,12)105.9(4)105.45105.53105.39105.37
A(10,12,14)105.7(4)105.38105.55105.33105.28
A(4,14,12)109.9(3)110.24109.59109.24109.22
A(4,14,15)111.0(3)110.96111.01110.77110.72
A(4,14,18)97.3(3)97.6497.5197.7397.79
A(12,14,15)121.4(3)120.76121.16121.23121.20
A(12,14,18)102.1(3)101.60102.02102.27102.30
A(15,14,18)112.3(3)112.88112.69112.81112.86
A(14,15,19)107.4(3)107.52107.97107.99107.94
A(8,18,14)95.7(3)97.3996.3796.3896.44
A(1,19,15)94.58(18)94.5093.7593.8193.86
r0.99430.99750.99650.9961
Table
Table 2. Vibrational wavenumbers obtained for the title compound at B3LYP/6-31G(d,p) level a.
Table 2. Vibrational wavenumbers obtained for the title compound at B3LYP/6-31G(d,p) level a.
NoWave numberIR intensityRed massForce Const.Assignments, PED (%)d
Exp.Unscal.ScalbScalcAbs.Rel.
131403261311531354121.116.93νCH, C10,12, sym (98)
23077323330883109281.096.71νCH, C10,12, asym (100)
330083156301530353111.116.49νCH, C1, asym (88)
430083153301130318261.106.46νCH, C5, asym (82)
52983314930073027151.116.48νCH, C15, asym (100)
6298331483007302630991.096.37νCH, C8, (92)
7294830932954297312401.065.96νCH, C15, sym (100)
8294830912952297129951.065.98νCH, C1,5, sym (90)
92933308429462965141.065.95νCH, C1,5, sym (93)
101568165715831593286.4010.36νC=C (83)
1114471503143514455151.091.45δCH2, scis, C5 (92)
12143914861420142911371.101.44δCH2, scis, C15 (74)
1314181476141014195161.091.40δCH2, scis, C1 (78)
14131813521292130012401.972.13δ=CH, ipb (64)
1513101346128512946202.042.18δOCH(22)+δCH, ipb (11)
+ νCC, C14,15(13)
161259132012601269011.491.53δOCH (40) + δCH2, wagg, C5 (34)
1712461294123612446191.341.33δCH2, wagg, C1,15 (59)
18121812791222123014471.461.40δ=CH, ipb (12)
+ δCH2, wagg, C1,15 (27)
19121112501194120218591.491.37δCH2, wagg, C5 (42) + δOCH (12)
2011931237118211905171.671.51νCC, C14,15 (14)
+ δCH2, wagg, C15 (20)
21118912131158116613441.571.36δCH2, twist, C1,5 (36)
+ νCC, C1,4 (14)
221140120711521160391.391.19δCH2, twist, C15 (45)
2310941162111011185151.230.98δCH2, twist, C1 (34)
241068111410641071281.671.22νCC (25) + δCH (37)
2510551094104510529301.481.04δ=CH, ipb (47)
26101910711023103012382.611.76νCC, (21) + δCCC (12)
27998103799199719622.961.88νCC, C4,5 (28) + δ=CH, ipb (28)
28962102197598119612.251.38δCH2, rock, C1,5,15 (24)
29934981937943301002.301.30δCH2, rock, C15 (23) + δCOC (13)
3092395291091520672.961.58δCH2, rock, C1 (34)
319099388959015171.530.79δCH2, opb (71)
3290392888689222732.111.07νCC, (47) + δ=CC, opb (33)
3387091287187711362.091.02νCC, (19) + δCH2, rock, C1,5 (42)
348308808418466212.371.08νCC(16) + δCOC,(20)
+ δCH2,rock, C1,5 (10)
358228408038083112.581.07νCC(10) + δCOC,(27)
+ δCH2,rock, C15 (41)
3678083679980415503.571.47νCO (25) + δ=CC, (33)
377507867517563113.551.29δCCC, (26) + νCC (10)
387227527187235154.211.40νCS (28) + γC, C14, (15)
397017306987023112.740.86νCS (10) + δCCS, (10)
+ γCH, C10,12 (26)
406887236906959294.801.48νCS (14) + δCCC, (24)
+ γCH, C14 (28)
4166670967768130972.210.65γCH, C10,12 (35)
426506726416465174.111.09νCC (17) + γCH (13) + δCCO, (16)
4361762159359713434.771.08δOCC, (21) + τCO, (14)
445435445205236212.960.52τCH (39)
45-505482485394.790.72νCC (11) + νCS (14) + δSCC, (16)
46-402384387282.570.25δCCO, (11) + τCO, (13)
47-387370372135.340.47δSCC, (13) + νCS (10) + νCO (13)
48-345329331144.190.29τCC, (27) + γC (10)
49-325311313153.550.22νCBr (44) + δCCO, (18)
50-282269271142.440.11γC, C4 (43) + δCCC, (17)
51-262250252283.930.16νCBr (27) + δCCC, (12)
52-144138139265.710.07δCCBr, (25) + γC, C4 (36)
53-116110111135.970.05δCCBr, (28) + τCC (43)
54-787575265.110.02τCC (52)
r0.99990.99990.9999
Mean dev.63.71−2.83−57.54
Mean abs. deviation63.7112.2257.54
Ave. absolute error4.271.094.25
RMSmol78.814.665.3
RMSover71.113.258.9
Sca. Factor1.00000.95520.9614
aHarmonic frequencies (in cm−1), IR intensities (km mol−1), reduced masses (amu) and force constants (m dyn Å−1).
bScaling Factor calculated in this research.
cScaling factor obtained from Ref. [38].
dν, stretching; δ, bending; ipb, in-plane bending; γ, out-of-plane bending; τ, torsion; sym, symmetric; asym, asymmetric; wagg, wagging; twist, twisting; rock, rocking; sciss; scissoring; PED less than 10% are not shown.
Table
Table 3. Vibrational wavenumbers obtained for the title compound at HF/6-31G(d,p) level a.
Table 3. Vibrational wavenumbers obtained for the title compound at HF/6-31G(d,p) level a.
NumberWave numberIR intensityRed MassForce Constant
Exp.UnscaledScaledbScaledcAbs.Rel.
131403423306430784111.117.66
23077339330373051371.097.39
33008331929712984491.117.20
43008331229642978421001.097.06
529833309296229764101.117.16
629833307296029739221.107.10
7294832572916292925591.066.62
8294832512910292322531.066.60
9293332392900291312281.076.59
101568181616251633376.2812.19
111447163014591466491.091.71
12143916151445145212301.111.71
131418161014421448261.101.68
14131814861330133618432.242.91
1513101481132613327161.832.36
161259145813051311121.551.94
17124614321282128711261.391.68
18121814091261126712291.461.71
19121113921246125223551.561.78
2011931355121312195131.932.09
2111891331119211974111.421.48
22114013271188119322541.621.67
2310941274114111467161.241.19
2410681214108710925131.661.44
25105512051079108426622.271.94
2610191182105810639222.522.08
2799811601039104315371.831.45
2896211301012101638912.461.85
29934110398799128682.051.47
309231070958963251.390.94
31909104593593927662.541.63
32903102391692020472.181.34
33870100089589914332.011.18
348309558558595112.511.35
3582293283583817412.191.12
36780914818822243.101.53
377508717807837173.511.57
38722837749753384.721.95
3970181572973327651.690.66
4068880171772010254.431.67
4166679471171426623.751.39
426507286526554104.251.33
4361768160961214334.771.30
445435935315338192.890.60
45-548491493364.920.87
46-440394396252.610.30
47-418375376135.310.55
48-373334335244.060.33
49-355318319253.530.26
50-307275276132.510.14
51-288258259373.920.19
52-160143144255.460.08
53-128114115135.380.05
54-898080246.010.03
r0.99970.99970.9997
Mean deviation181.5713.64−130.89
Mean absolute deviation181.5730.20130.89
Average absolute error13.832.578.38
RMSmol196.034.0169.6
RMSover177.030.7153.1
Scaling Factor1.00000.89520.8992
aHarmonic frequencies (in cm−1), IR intensities (km mol−1), reduced masses (amu) and force constants (m dyn Å−1).
bScaling Factor calculated in this research.
cScaling factor obtained from Ref. [38].
Table
Table 4. Vibrational wavenumbers obtained for the title compound at B3PW91/6-31G(d,p) level a.
Table 4. Vibrational wavenumbers obtained for the title compound at B3PW91/6-31G(d,p) level a.
NumberWave numberIR intensityRed massForce Constant
Exp.UnscaledScaledbScaledcAbs.Rel.
13140327431173134381.116.99
23077324630903107261.096.76
330083167301530316171.116.53
43008316430133029271.116.52
52983316130103026131.116.53
6298331593007302429831.096.41
7294831012952296913361.066.00
8294830992950296621611.066.01
929333091294329595151.065.97
101568166615861595376.5310.67
1114471493142114296171.091.43
12143914781407141513381.111.43
1314181466139514037191.091.38
14131813561291129916472.532.75
1513101350128512924121.872.01
161259132012571264001.571.61
1712461293123112384121.391.37
18121812771216122312341.461.41
19121112521192119819551.651.52
2011931239117911864121.541.39
21118912161158116415431.641.43
221140120911511157391.411.21
2310941161110511115151.240.98
241068111810651071131.691.24
25105510981045105116441.611.14
2610191080102810349252.271.56
279981047997100217492.571.66
28962103098198624702.341.47
2993499394595027782.311.34
3092396191592020572.801.52
3190994389890317491.931.01
3290393488989411331.570.81
3387091987588012352.151.07
348308868438486162.171.00
3582284780781112352.621.11
36780845805809123.131.32
37750794756760273.421.27
387227677307344114.731.64
397017437077118234.871.58
406887377017053102.850.91
41666715681684351001.980.60
426506766446476174.051.09
4361762559559810304.601.06
445435465205226172.930.51
45-508484487374.810.73
46-402382385372.670.25
47-389370372135.230.47
48-348331333254.250.30
49-329313315133.370.21
50-282268270132.400.11
51-264251253263.790.16
52-144137138255.690.07
53-115110110126.470.05
54-767273264.750.02
r0.99980.99980.9998
Mean deviation69.36−2.08−62.63
Mean absolute deviation69.3613.9862.63
Average absolute error4.791.264.50
RMSmol84.616.472.3
RMSover76.414.865.2
Scaling Factor1.00000.95200.9573
aHarmonic frequencies (in cm−1), IR intensities (km mol−1), reduced masses (amu) and force constants (m dyn Å−1).
bScaling Factor calculated in this research.
cScaling factor obtained from Ref. [38].
Table
Table 5. Vibrational wavenumbers obtained for the title compound at mPW1PW91/6-31G(d,p) level a.
Table 5. Vibrational wavenumbers obtained for the title compound at mPW1PW91/6-31G(d,p) level a.
NumberWave numberIR intensityRed massForce Constant
Exp.UnscaledScaledbScaledcAbs.Rel.
13140329331143129261.117.08
23077326630883102241.096.84
330083185301230266171.116.61
43008318330103024261.116.60
52983318130083022121.116.61
6298331793006302027741.096.50
7294831192949296312331.066.07
8294831172947296120561.066.08
929333109294029535141.066.04
101568168015891596376.5510.90
1114471500141814256171.091.44
12143914861406141214381.111.44
1314181474139414007191.091.40
14131813691294130017472.733.02
1513101360128612924121.832.00
161259133112591265001.601.67
1712461303123212384121.401.40
18121812871217122211301.481.44
19121112631195120019531.691.59
2011931248118011864121.521.40
21118912261159116516441.651.46
221140121911521158391.421.25
2310941169110611115151.241.00
241068112710661071121.681.26
25105511071047105219521.761.27
2610191091103210377182.151.51
2799810581001100517452.361.56
28962104198598926722.371.52
29934100595095426712.251.34
3092397091792120542.721.51
3190995390190517471.911.02
3290394489389711311.560.82
3387092887888213342.151.09
348308938448485152.141.00
3582285681081411292.671.15
36780852806810122.941.26
37750803759763263.331.27
38722777735738394.811.71
397017547137168224.791.60
40688744703707392.880.94
41666723684687371001.950.60
426506826456486164.071.11
4361763159759910264.571.07
445435505205236162.920.52
45-513485487374.830.75
46-405383385372.700.26
47-392371372135.180.47
48-350331333254.240.31
49-332314315133.330.22
50-283268269132.400.11
51-266252253263.740.16
52-146138138255.650.07
53-116110110126.480.05
54-777273264.760.02
r0.99980.99980.9998
Mean deviation80.69−0.93−71.89
Mean absolute deviation80.6914.0071.89
Average absolute error5.681.305.06
RMSmol96.216.684.1
RMSover86.914.975.9
Scaling Factor1.00000.94560.9500
aHarmonic frequencies (in cm−1), IR intensities (km mol−1), reduced masses (amu) and force constants (m dyn Å−1).
bScaling Factor calculated in this research.
cScaling factor obtained from Ref. [23].

Acknowledgements

This work was supported by the Mersin University Research Fund (Project no: BAP.ECZ.F.TB.(HA).2007-1) and The Scientific & Research Council of Turkey (TUBITAK, PN: 2377 (103T121)).

References

  1. Lipshutz, B.H. 5-Membered Heteroaromatic Rings as Intermediates in Organic-Synthesis. Chem. Rev 1986, 86(5), 795–819. [Google Scholar]
  2. Dean, F.M. Recent advances in furan chemistry I. Adv. Heterocycl. Chem 1982, 30, 167–238. [Google Scholar]
  3. Dean, F.M.; Sargent, M.V. Furans and Their Benzo Derivatives. In Comprehensive Heterocyclic Chemistry; Bird, C.W., Cheesman, G.W.H., Eds.; Pergamon Press: London, 1984. [Google Scholar]
  4. Vogel, P.; Cossy, J.; Plumet, J.; Arjona, O. Derivatives of 7-oxabicyclo[2.2.1]heptane in nature and as useful synthetic intermediates. Tetrahedron 1999, 55(48), 13521–13642. [Google Scholar]
  5. Kappe, C.O.; Murphree, S.S.; Padwa, A. Synthetic applications or furan Diels-Alder chemistry. Tetrahedron 1997, 53(42), 14179–14233. [Google Scholar]
  6. Grinsteiner, T.J.; Kishi, Y. Synthetic Studies Towards Batrachotoxin.1. A Furan-Based Intramolecular Diels-Alder Route to Construct the a-D Ring-System. Tetrahedron Lett 1994, 35(45), 8333–8336. [Google Scholar]
  7. Demircan, A.; Parsons, P.J. Preparation of tricyclic nitrogen heterocycle via Intramolecular Diels-Alder reaction. Heterocycl. Commun 2002, 8(6), 531–536. [Google Scholar]
  8. Demircan, A.; Karaarslan, M.; Turac, E. A facile synthesis of heterotricycles from furfurylbromoalkenes using thermal IMDA cycloaddition. Heterocycl. Commun 2006, 3–4, 233– 240. [Google Scholar]
  9. Williamson, A.W. XXII.-On etherification. Q. J. Chem. Soc 1852, 4, 229–239. [Google Scholar]
  10. Adamchuk, K.A.; Parker, K.A. Intramolecular Diels-Alder reactions of the furan diene. Tetrahedron Lett 1978, 19, 1689–1692. [Google Scholar]
  11. Buyukgungor, O.; Kosar, B.; Demircan, A.; Turac, E. 6-Bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene. Acta Crystallog E 2005, 61, O1441–O1442. [Google Scholar]
  12. Arslan, H.; Florke, U.; Kulcu, N. Theoretical studies of molecular structure and vibrational spectra of O-ethyl benzoylthiocarbamate. Spectrochim. Acta A 2007, 67(3–4), 936–943. [Google Scholar]
  13. Arslan, H.; Algül, Ö.; Dündar, Y. Structural and spectral studies on 3-(6-benzoyl-5-chloro-2-benzoxazolinon-3-yl) propanoic acid. Vib. Spectrosc 2007, 44, 248–255. [Google Scholar]
  14. Arslan, H.; Emen, F.M.; Kulcu, N. Structure and vibrational spectra of N,N-dimethyl-N′-(2-chlorobenzoyl)thiourea: Hartree-Fock and density functional theory studies. Asian J. Chem 2007, 19, 1888–1896. [Google Scholar]
  15. Arslan, H.; Algul, O. Theoretical studies of molecular structure and vibrational spectra of 2-ethyl-1H-benzo[d]imidazole. Asian J. Chem 2007, 19, 2229–2235. [Google Scholar]
  16. Arslan, H.; Algül, Ö. Synthesis and Ab Initio/DFT Studies on 2-(4-methoxyphenyl) benzo[d]thiazole. Int. J. Mol. Sci 2007, 8, 760–776. [Google Scholar]
  17. Arslan, H.; Flörke, U.; Külcü, N.; Binzet, G. The molecular structure and vibrational spectra of 2-chloro-N-(diethylcarbamothioyl)benzamide by Hartree–Fock and density functional methods. Spectrochim. Acta A 2007. [Google Scholar] [CrossRef]
  18. Arslan, H.; Algul, Ö.; Önkol, T. Vibrational spectroscopy investigation using ab-initio and density functional theory analysis on the structure of 3-(6-benzoyl-2-oxobenzo[d]oxazol-3(2H)-yl)propanoic acid. Spectrochim. Acta A 2007. [Google Scholar] [CrossRef]
  19. Arslan, H.; Demircan, A.; Göktürk, E. Vibrational spectroscopy investigation using ab initio and density functional theory analysis on the structure of 5-chloro-10-oxa-3-thiatricyclo[ 5.2.1.01,5]dec-8-ene-3,3-dioxide. Spectrochim. Acta A 2007. [Google Scholar] [CrossRef]
  20. Arslan, H.; Algül, Ö. Vibrational spectrum and assignments of 2-(4-methoxyphenyl)-1H-benzo[d]imidazole by ab initio Hartree–Fock and density functional methods. Spectrochim. Acta A 2007. [Google Scholar] [CrossRef]
  21. Kupka, T.; Wrzalik, R.; Pasterna, G.; Pasterny, K. Theoretical DFT and experimental Raman and NMR studies on thiophene, 3-methylthiophene and selenophene. J. Mol. Struct 2002, 616, 17–32. [Google Scholar]
  22. Wysokinski, R.; Kuduk-Jaworska, J.; Michalska, D. Electronic structure, Raman and infrared spectra, and vibrational assignment of carboplatin. Density functional theory studies. J. Mol. Struc-Theochem 2006, 758, 169–179. [Google Scholar]
  23. Kuppens, T.; Vandyck, K.; VanderEycken, J.; Herrebout, W.; VanderVeken, B.; Bultinck, P.A. DFT conformational analysis and VCD study on methyl tetrahydrofuran-2-carboxylate. Spectrochim. Acta A 2007, 67, 402–411. [Google Scholar]
  24. Hanuza, J.; Sasiadek, W.; Michalski, J.; Lorenc, J.; Maczka, M.; Kaminskii, A.A.; Butashin, A.V.; Klapper, H.; Hulliger, J.; Mohmed, A.F.A. Polarized Raman and infrared spectra of the salol crystal - chemical quantum calculations of the vibrational normal modes. Vib. Spectrosc 2004, 34, 253–268. [Google Scholar]
  25. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc 2007. [Google Scholar] [CrossRef]
  26. Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions. J. Chem. Phys 2005, 123. [Google Scholar]
  27. Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theory. Comput 2006, 2(2), 364–382. [Google Scholar]
  28. Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys 2006, 125. [Google Scholar]
  29. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; Millam, J.M.; Iyengar, S.S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G.A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Ayala, P.Y.; Morokuma, K.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.; Strain, M.C.; Farkas, O.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Ortiz, J.V.; Cui, Q.; Baboul, A.G.; Clifford, S.; Cioslowski, J.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Gonzalez, C.; Pople, J.A. Gaussian 03, Revision C.02; Gaussian, Inc: Wallingford CT, 2004. [Google Scholar]
  30. Moller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev 1934, 46, 618–622. [Google Scholar]
  31. Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A 1988, 38(6), 3098–3100. [Google Scholar]
  32. Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37(2), 785–789. [Google Scholar]
  33. Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys 1998, 108(2), 664–675. [Google Scholar]
  34. Burke, K.; Perdew, J.P.; Wang, Y. Electronic Density Functional Theory: Recent Progress and New Directions; Dobson, J.F., Vignale, G., Das, M.P., Eds.; Plenum: New York, 1998. [Google Scholar]
  35. Becke, A.D. Density-Functional Thermochemistry .3. The Role of Exact Exchange. J. Chem. Phys 1993, 98(7), 5648–5652. [Google Scholar]
  36. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar]
  37. Foresman, J.B.; Frisch, E. Exploring Chemistry with Electronic Structure Methods: A Guide to Using Gaussian; Gaussian: Pitttsburg, PA, 1993. [Google Scholar]
  38. Scott, A.P.; Radom, L. Harmonic vibrational frequencies: An evaluation of Hartree-Fock, Moller-Plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors. J. Phys. Chem.-US 1996, 100, 16502–16513. [Google Scholar]
  39. Arslan, H. Performance Analysis of Vibrational Frequencies, PAVF 1.0; Mersin: Turkey, 2007. [Google Scholar]
  40. GaussView, Version 3.07; Dennington, Roy, II; Keith, Todd; Millam, John; Eppinnett, Ken; Hovell, W Lee; Gilliland, Ray. Semichem, Inc: Shawnee Mission, KS, 2003. [Google Scholar]
  41. Jamróz, M.H. Vibrational Energy Distribution Analysis VEDA 4; Warsaw, 2004. [Google Scholar]
  42. Supuran, C.T.; Casini, A.; Scozzafava, A. Protease inhibitors of the sulfonamide type: Anticancer, antiinflammatory, and antiviral agents. Med. Res. Rev 2003, 23, 535–558. [Google Scholar]
  43. Palmer, J.T.; Rasnick, D.; Klaus, J.L.; Bromme, D. Vinyl Sulfones as Mechanism-Based Cysteine Protease Inhibitors. J. Med. Chem 1995, 38, 3193–3196. [Google Scholar]
  44. Roush, W.R.; Gwaltney, S.L.; Cheng, J.M.; Scheidt, K.A.; McKerrow, J.H.; Hansell, E. Vinyl sulfonate esters and vinyl sulfonamides: Potent, irreversible inhibitors of cysteine proteases. J. Am. Chem. Soc 1998, 120, 10994–10995. [Google Scholar]
  45. Simpkins, N.S. The Chemistry of Vinyl Sulfones. Tetrahedron 1990, 46, 6951–6984. [Google Scholar]
  46. Kosar, B.; Gokturk, E.; Demircan, A.; Buyukgungor, O. 5-bromo-10-oxa-3-thiatricyclo[5.2.1.0(1,5)]-dec-8-ene 3,3-dioxide. Acta Cryst. E 2006, 62, O3868–O3869. [Google Scholar]
  47. Cioslowski, J. A New Population Analysis Based on Atomic Polar Tensors. J. Am. Chem. Soc 1989, 111, 8333–8336. [Google Scholar]
  48. Visscher, L.; Dyall, K.G. Relativistic and correlation effects on molecular properties.1. The dihalogens F-2, Cl-2, Br-2, I-2, and At-2. J. Chem. Phys 1996, 104(22), 9040–9046. [Google Scholar]
  49. Xiao, C.Y.; Kruger, S.; Belling, T.; Mayer, M.; Rosch, N. Relativistic effects on geometry and electronic structure of small Pd-n species (n=1, 2, 4). Int. J. Quant. Chem 1999, 74(4), 405–416. [Google Scholar]
  50. Bauschlicher, C.W.; Langhoff, S.R. The calculation of accurate harmonic frequencies of large molecules: The polycyclic aromatic hydrocarbons, a case study. Spectrochim. Acta A 1997, 53(8), 1225–1240. [Google Scholar]
  51. Bayari, S.; Saglam, S.; Ustundag, H.F. Experimental and theoretical studies of the vibrational spectrum of 5-hydroxytryptamine. J. Mol. Struc.-Theochem 2005, 726(1–3), 225–232. [Google Scholar]
  52. Silverstein, M.; Basseler, C.G.; Morill, C. Spectrometric Identification of Organic Compounds; Wiley: New York, 1981. [Google Scholar]
  53. Kimmelma, R.; Hotokka, M. Structure-stability relationships in unsaturated sulfur compounds VI. An ab initio study of the stable conformations of (E)- and (Z)-2-methylthio-, methylsulfinyl-and methylsulfonyl-2-butenes. J. Mol. Struct.-Theochem 1997, 418(2–3), 89–196. [Google Scholar]
  54. Sundaraganesan, N.; Meganathan, C.; Anand, B.; Lapouge, C. FT-IR, FT-Raman spectra and ab initio DFT vibrational analysis of p-bromophenoxyacetic acid. Spectrochim. Acta A 2007, 66(3), 773–780. [Google Scholar]
  55. Cabral, O.V.; Tellez, C.A.; Giannerini, T.; Felcman, J. Fourier-transform infrared spectrum of aspartate hydroxo-aqua nickel(II) complex and DFT-B3LYP/3-21G and 6-311G structural and vibrational calculations. Spectrochim. Acta A 2005, 61(1–2), 337–345. [Google Scholar]
  56. Bensebaa, F.; Zhou, Y.; Brolo, A.G.; Irish, D.E.; Deslandes, Y.; Kruus, E.; Ellis, T.H. Raman characterization of metal-alkanethiolates. Spectrochim. Acta A 1999, 55(6), 1229–1236. [Google Scholar]
  57. Mohan, J. Organic Spectroscopy Principles and Applications; Narosa Publishing House: New Delhi, 2001. [Google Scholar]
  58. Gunasekaran, S.; Kumar, R.T.; Ponnusamy, S. Vibrational spectra and normal coordinate analysis of diazepam, phenytoin and phenobarbitone. Spectrochim. Acta A 2006, 65, 1041–1052. [Google Scholar]

Share and Cite

MDPI and ACS Style

Arslan, H.; Demircan, A. The Molecular Structure and Vibrational Spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene. Int. J. Mol. Sci. 2007, 8, 1064-1082. https://doi.org/10.3390/i8111064

AMA Style

Arslan H, Demircan A. The Molecular Structure and Vibrational Spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene. International Journal of Molecular Sciences. 2007; 8(11):1064-1082. https://doi.org/10.3390/i8111064

Chicago/Turabian Style

Arslan, Hakan, and Aydın Demircan. 2007. "The Molecular Structure and Vibrational Spectrum of 6-bromo-8-thia-1,4-epoxybicyclo[4.3.0]non-2-ene" International Journal of Molecular Sciences 8, no. 11: 1064-1082. https://doi.org/10.3390/i8111064

Article Metrics

Back to TopTop