1 Introduction
It is generally assumed that standard Kohn-Sham density functional theory (DFT) [
1,
2,
3,
4] carried out with approx- imate exchange-correlation functionals (
approximate DFT) as they are currently in use covers beside exchange correlation effects just short-range Coulomb correlation (dynamic electron correlation). Nevertheless, approximate Kohn-Sham DFT performs astonishingly well for electronic systems that have been identified by wave function theory (WFT) to represent notorious multi-reference problems. Of course, this observation has to be qualified in a number of ways: a) One cannot expect approximate KS-DFT to be always successful in the case of multi-reference systems. Dramatic failures are also known. [
3,
4,
5,
6,
7,
8] b) One has to specify whether a satisfactory performance is obtained by the restricted, unrestricted or broken-symmetry unrestricted version of DFT: RDFT, UDFT or BS- UDFT. Multi-reference systems can often bebetterdescribedbyBS-UDFTratherthanRDFTorUDFT.[
9]c) The performance of DFT in the case of a multi-reference system depends on the choice of the exchange-correlation functional. Local density approximation (LDA) functionals perform significantly different from GGA (generalized gradient approximation) or hybrid functionals in the case of multi-reference systems. [
2,
3,
4]
The essence of KS-theory is that if the exactexchange-correlationfunctionalwouldbeknown(leadingto
exact KS DFT), any electronic system, whether multi-reference or single-reference in nature could be accurately described. [
10] Obviously, it is the approximate nature of the current exchange-correlation functionals which leads to the varying performance of KS-DFT in the case of multi-reference problems. In this work, we will critically discuss the question to which extent DFT can be used to reliably describe molecules with distinct multi-reference character. We will show that approximate DFT already incorporates some multi-reference effects via the form of its exchange functional [
11,
12,
13] and that this is inherently connected to the self-interaction error, [
14,
15,
16] from which all current exchange functionals suffer. [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26] This will be referred to as
implicit coverage of multi-reference effects, which has serious implications for the
explicit account of multi-reference effects via an extension of standard KS-DFT. For the explicit account of multi-reference effects, DFT offers today two major routes, namely a) the extension of standard DFT to ensemble DFT [
27,
28,
29,
30] and b) the merging of DFT with techniques used in WFT. The latter possibility includes methods such as two-configurational DFT (GVB-DFT) [
31] and multi-configurational DFT such as CAS-DFT. [
32] The former route is realized in REKS(spin-
Restricted
Ensemble-referenced
KS)-DFT. Both approaches will be discussed where the focus of the discussion will be on the principal question on how multi-reference systems can be described in the best way using these methods.
If one discusses multi-reference effects, one should specify what effects are actually addressed by this term. According to a general scheme of classifying multi-reference systems suggested by Gr¨afenstein and Cremer [
9,
32] one can distinguish between a) closed shell and high-spin open-shell systems that are satisfactorily described by a single configurational state function (CSF) represented by a single determinant (type 0 systems), b) low-spin open-shell systems such as singlet biradicals that require two- or multi-determinantal descriptions where these determinants form still one CSF (type I systems), genuine two- and multi-configurational systems where each CSF can be represented by asingledeterminant(typeIIsystemssuchasozone(
1A1), C
2 (
),dissociating A-A molecules, etc.), and finally systems with multi-determinantal, multi-configurational wave functions (type III systems such as the Myer’s biradical). [
9] The current article will concentrate on the correct description of type II and type III systems because this implies the inclusion of long-range Coulomb correlation effects (
non-dynamicor
static electron correlation) into DFT. It will not consider type I systems although their correct description is already problematic at the DFT level and requires methods such as ROSS [
33] or ROKS [
34].However, type I systemsdonotpossess(bydefinition)anylong-rangecorrelationandthereforearenotconsideredtorepresent multi-referenceproblems.
The objectives of this work are threefold: a) First, we will clarify what types of correlation effects are intro- duced by approximate exchange functionals under different conditions, i.e. RDFT, UDFT or BS-UDFT. In this connection, difference densities and representations of the exchange hole will be used to support the discussion. b) Then, we will test the performance of LDA, GGA, and hybrid functionals in combination with two-configurational DFT in the case of singlet biradicals with significant multireference character. For this purpose, a new program was developed, which can carry out energy calculations and geometry optimizations with hybrid functionals. c) Implicit and explicit coverage of multireference effects is analyzed for different situations and the possibility of double-counting of electron correlation effects in multi-configurational DFT is discussed.
Results of this work are presented in the following way. In
section 2, we will analyze the implicit coverage of multi-reference effects by DFT. In the following sections, explicit coverage of multi-reference effects either by ensemble DFT (
section 3 and
section 4) or WFT-DFT methods (
section 5) will be discussed. Conclusions are summarized in
section 6.
2 Implicit Account of Multi-reference Effects by Standard DFT
The exchange-correlation hole
hXCis defined by Eq. (1) (see, e.g., Ref.2):
where
is the pair density distribution,
is the one-electron density distribution,
r1 denotes the position of the first electron (reference electron), and
r2 the position of the second electron. The exchange-correlation hole can be split up into exchange hole
hX and correlation hole
hC , which are related to exchange and Coulomb correlation, respectively.The exchange hole is negative or equal to zero everywhere and fulfills the sum rule [
2]:
Exchange decreases the probability of finding two electrons with the same spin at the same position to zero, however does not affect the corresponding probability for opposite-spin electrons. For a closed shell system, the HF exchange hole is exact. It reflects the electronic structure of the molecule provided the reference electron is positioned in the bonding or lone-pair region. In the first case, the HF exchange holeisdelocalizedoverthebondregionandthe regions of the bonded atoms (reflecting the form of the bond orbital) while in the second case its structure can be deduced from the form of the lone-pair orbital and the overlap of the latter with other orbitals. A deeper exchange hole corresponds to a more negative exchange energy.
The structure of the exchange hole is influenced by two factors, namely a) the self-exchange of the electrons (intraelectronic exchange) and b) the Fermi exchange correlation between different electrons possessing the same spin. The intraelectronic part of the HF exchange hole fulfills Eq.s (2) and (3) while the interelectronic exchange hole can be both positive and negative and
sums to zero. The former takes care of the self-interaction problem in the way that the corresponding self-exchange energy exactly annihilates the self-repulsion energy of an electron with itself. This however is not true in the case of the DFT exchange hole, which leads to the self-interaction error (SIE) of DFT. Approximate DFT, contrary to HF, does not fulfill Eq.s (4) and (5)
which require that for the ground-state density of a system containing just one
α-spin electron, i.e. ∫
ϱα (
r)
dr = 1, and
ϱβ(
r) = 0, the self-exchange energy
EX [
ϱα, 0] exactly cancels the self-repulsion
EJ [
ϱ] of the electron and that there is no correlation of an electron with itself. All commonly used approximate exchange functionalsviolate condition (3) and lead to a relatively large exchange SIE. The SIE of approximate correlation functionals is smaller and even zero in the case of those correlation functionals, which were derived from WFT methods as for example theLYP functional.Therefore,wewillconsiderinthefollowingjusttheexchangeSIE.
While the HF exchange hole is often delocalized, the DFT exchange hole is always localized and concentrated at the position of the reference electron (LDA exchange holes) or in the vicinity of the reference electron (GGA exchange holes). One can consider the differences between HF and DFT exchange hole in two ways:
- a)
The SIE converts the delocalized HF exchange hole into a localized DFT exchange hole.Although it is an error by nature, it introduces in this way some useful electron correlation effects (to be discussed in the following), which significantly influence the performance of DFT. Self-interaction corrected DFT (SIC-DFT) annihilates the SIE and in this way also destroys the electron correlation effects mimicked by the SIE. Accordingly, SIC-DFT is closer to HF as directly reflected by the exchange holes generated by the two methods.
- b)
The LDA and GGA exchange approximations are constructed to genuinely describe both exchange and left- right correlation. The self-interaction correction brings the DFT model closer to HF and destroys the left-right correlation LDA (or GGA) has built in (see, e.g. Ref. 12a).
Reasoning a) partitions the correlation effects covered by the exchange-correlation functional to have a better basis for analyzing these effects in detail and to have a basis for developing better exchange-correlation functionals. Along this line, the necessity of describing first exchange correctly as the larger and more important effect is emphasized and in so far the conversion of the delocalized HF into a localized DFT exchange hole is considered as an error.
Reasoning b) is based on the original DFT strategy, namely all electron interaction effects difficult to describe are contracted in one functional, which, if correctly parametrisized, leads to the true energy. Only in those cases where this approach seriously fails, one has to use methods such as SIC-DFT, which describe the exchange interactions of the electrons more correctly.
In this work, we follow reasoning a) because we are interested to analyze how various correlation effects are covered by the exchange-correlation functional. Therefore, we emphasize the SIE of DFT although it is clear that the latter may be considered as wanted or needed.This becomes obvious by defining the SIE as the difference DFT - SIC/DFT rather than the difference SIC/DFT - DFT as oneshoulddoifonespeaksofanerror.However,the former alternative is preferable because the SIE is related to an electron correlation effect thus suggesting the following correspondence:
and
The DFT energy E(DFT,X-only) obtained from an exchange-only calculation is considered as a correlation- corrected energy approximating the true energy E(true), which is the sum of the HF energy E(HF) (corresponding to E(SIC-DFT,X-only)) and the correct correlation energy E(corr) where the latter term is approximated by the self-interaction energy E(SIE,X-only)) in an exchange-only DFT calculation. It is of course still the question which correlation effects are included into DFT via the SIE of the exchange functional.
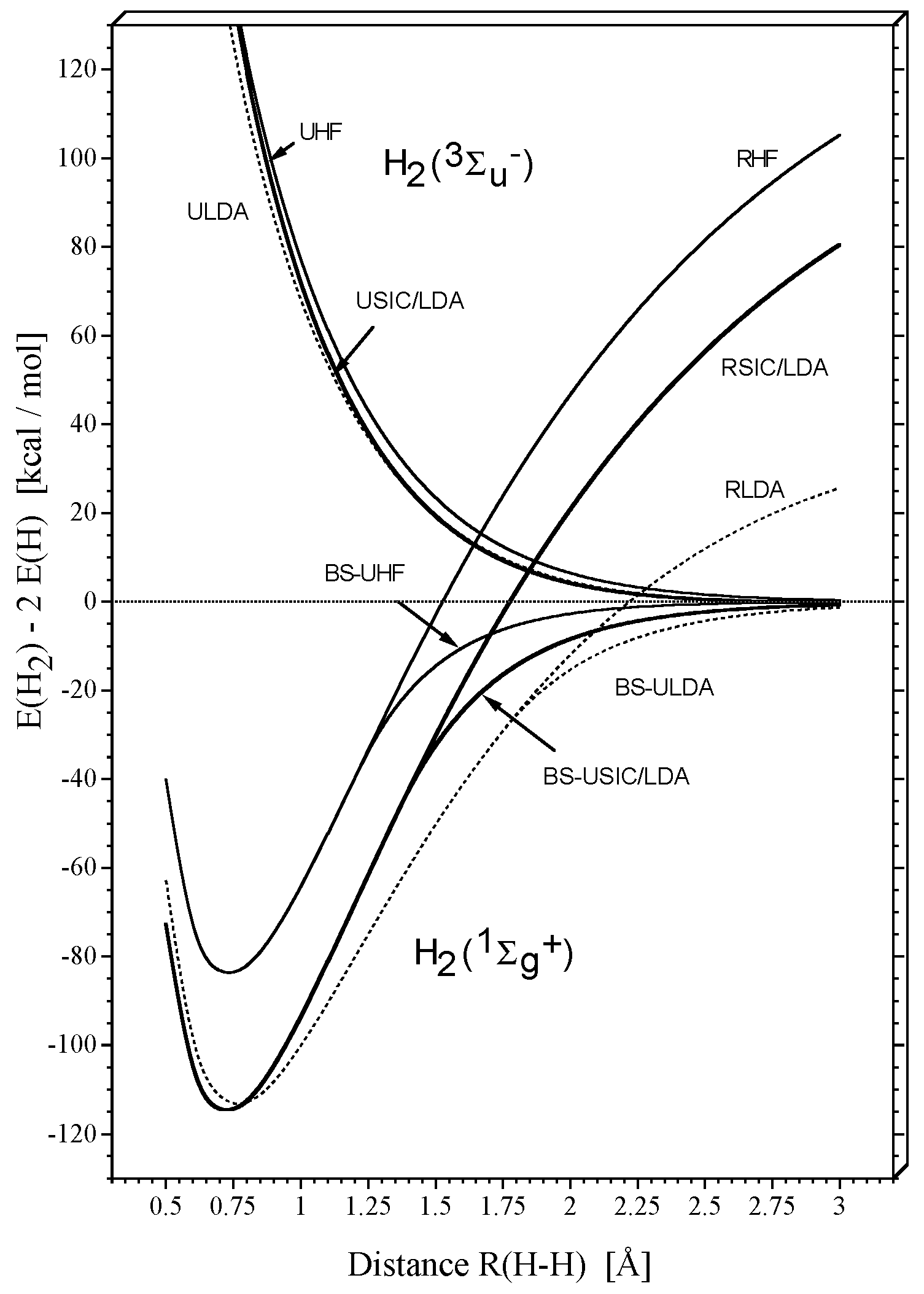
Figure 1 shows the potential curves for H
2 in its
ground state and its
excited state as calculated at different levels of theory with Dunning’s cc-pVTZ basis set [
35]: RHF (restricted Hartree-Fock), UHF (unrestricted Hartree-Fock), and BS(broken-symmetry)-UHF, RLDA, UDLA, and BS-ULDA, RSIC/LDA, USIC/LDA, and BS- USIC/LDA where for the exchange-correlation functional SVWN5 was used (S: Slater exchange [
36]; VWN5: Vosko- Wilk-Nusair correlation [
37]). The self-interaction corrected DFT (SIC-DFT) was obtained using the method of Perdew and Zunger [
17,
18] in a self-consistent-field version. [
19,
20,
21,
22,
38]
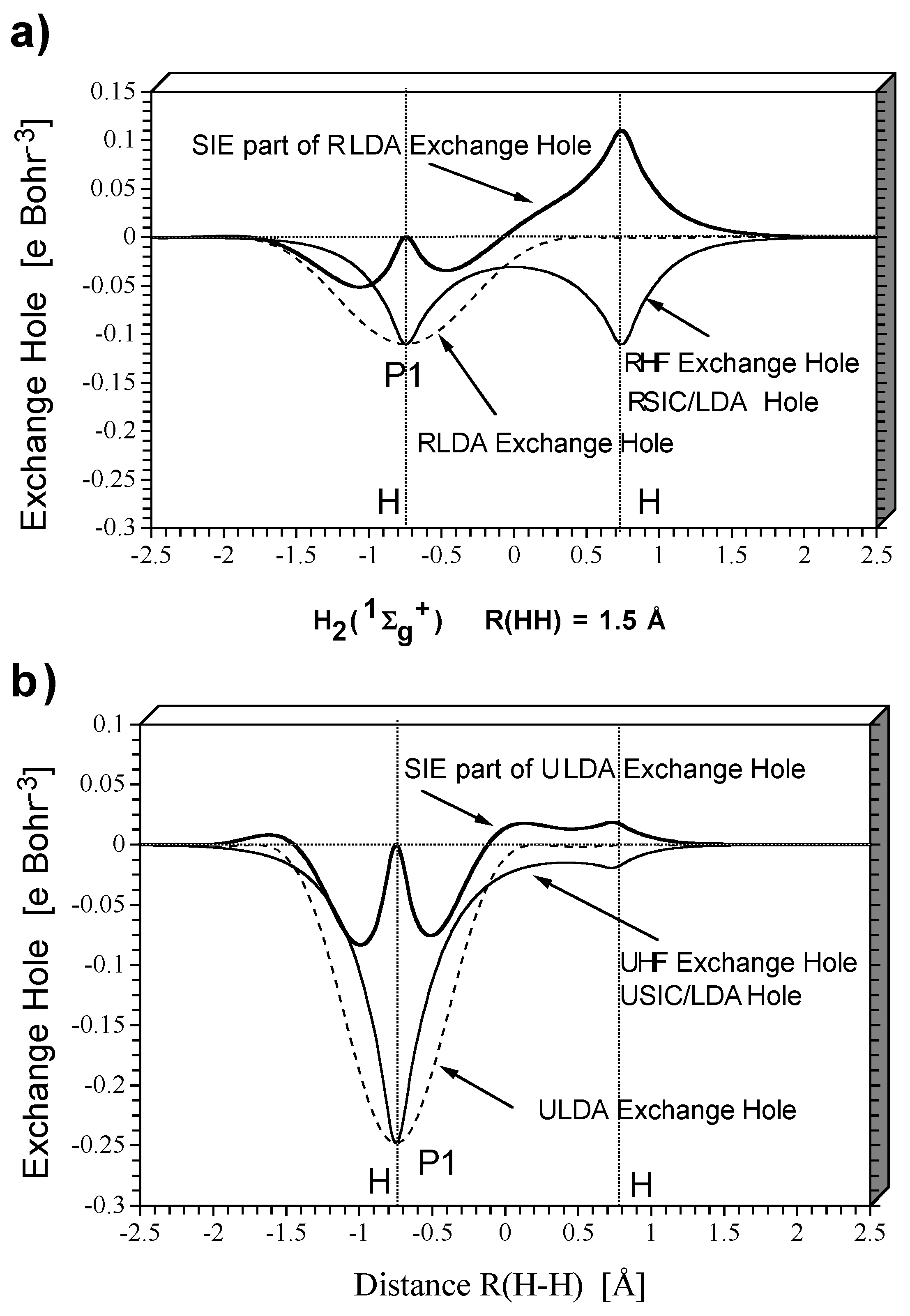
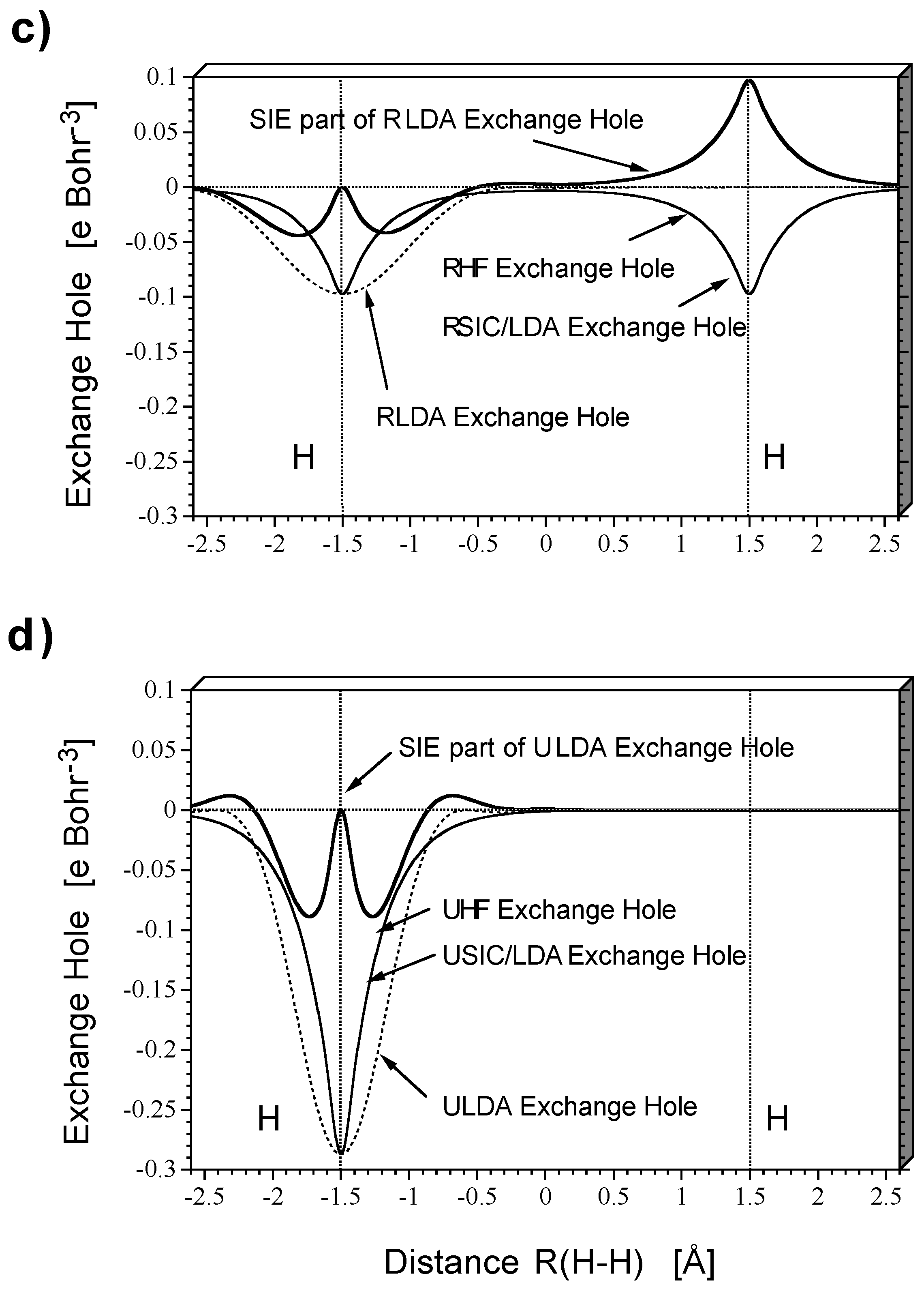
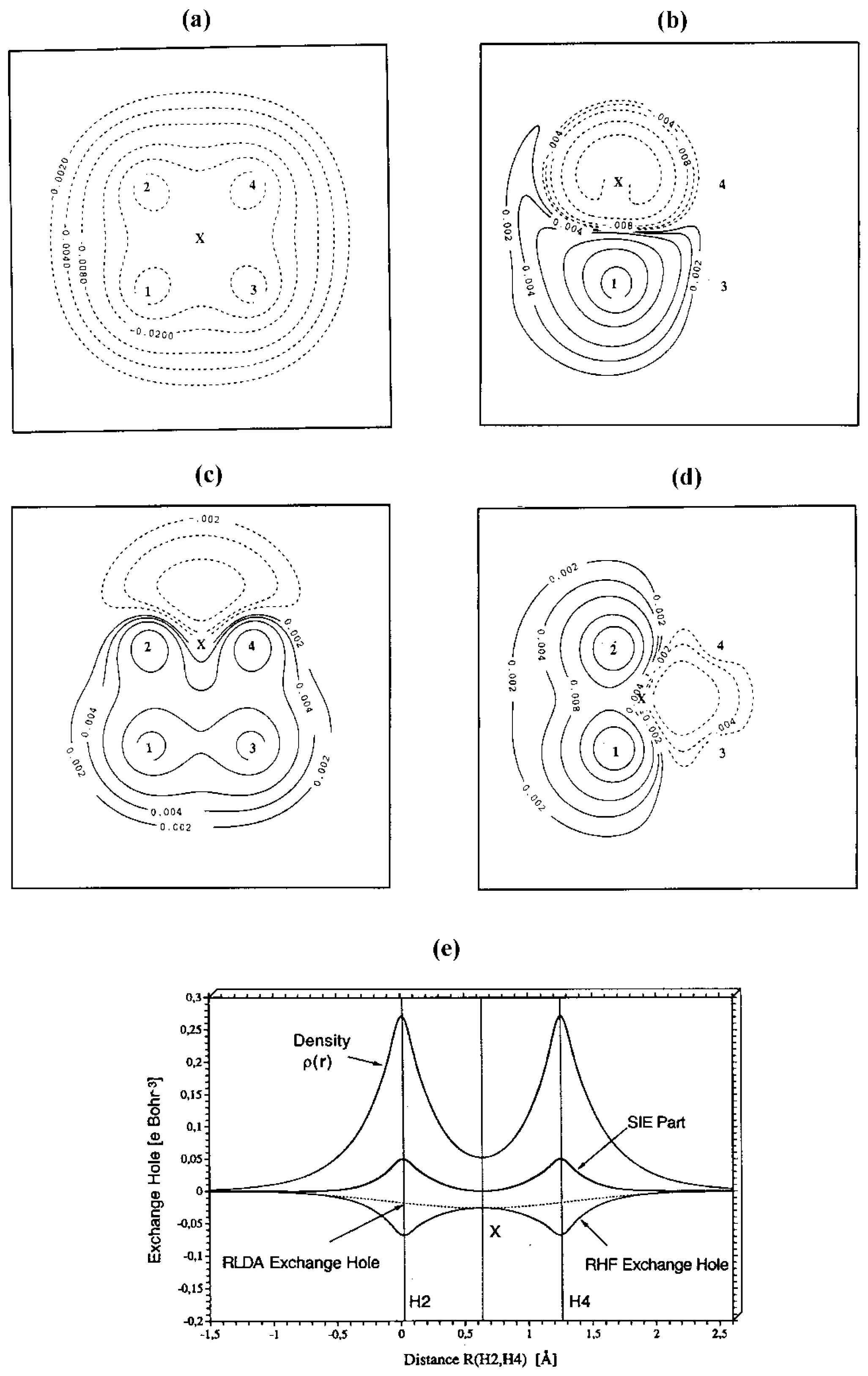
Figure 2 shows HF and DFT exchange holes in a one-dimensional representation along the internuclear axis for the dissociating
molecule at a distance of 1.5 (
Figure 2a and
Figure 2b) and 3.0 Å (
Figure 2c and
Figure 2d) between the nuclei as obtained with a restricted description (
Figure 2a and
Figure 2c) and an unrestricted description (
Figure 2b and
Figure 2d). The exchange holes were calculated with the same density (taken from the HF calculations) to simplify the comparison so that just differences in the electron correlation effects covered by HF and DFT, respectively, need to be discussed. In
Figure 2a to
Figure 2d, the exchange hole functions relate to the probability of finding the second electron when the reference electron is positioned at the left H nucleus.
Restricted theory is not able to describe dissociation correctly, which has been amply discussed and analyzed during the past 5 decades. [
39] Unrestricted theory in its broken-symmetry form qualitatively corrects restricted theory by mixing the first doubly excited state with the ground state configuration thus lending HF some two- configurational character at the expense of spin contamination and the inclusion of higher spin states. [
9] Close to the equilibrium geometry of
, the two electrons are equally shared by the two H atoms thus establishing the H-H bond. In this situation, the only Coulomb correlation effects are of the short-range, dynamic nature. HF does not cover any dynamic electron correlation effects and, therefore, it underestimates the strength of the HH bond (
Figure 1) as documented by a dissociation energy
De of 83.7 kcal/mol (calculated relative to twice the UHF energy of
H(
2S)).
The LDA description at the equilibrium geometry leads to a more stable HH bond (
De = 113.3 kcal/mol) where this difference is caused by a) the VWN5 correlation functional (major effect) and b) the self-interaction error of the Slater exchange functional (minor effect). [
14,
15,
16] The two effects can be separated carrying out a SIC-LDA calculation, again using the HF density. The SIC-LDA calculation leads to the same exchange energy as the HF calculation and since the same correlation functional is used, [
40] the difference between LDA and SIC- LDA (
Figure 1) reflects the consequences of the self-interaction error of Slater exchange. Although differences are relatively small, the self-interaction error causes a) the HH bond length to increase from 0.727 Å (SIC-LDA) to 0.766 Å (LDA) and b) the
De value to decrease from 114.7 to 113.3 kcal/mol (
Figure 1).
If
dissociates, the error caused by the lack of dynamic electron correlation will decrease slightly from its relatively large value of 31 kcal/mol at the equilibrium distance to about 25 kcal/mol at 3 Å as is documented by the RHF and the RSIC-LDA dissociation curves (
Figure 1). The self-interaction error given by the difference RLDA - RSIC/LDA changes in a different way: With increasing distance R(H-H), it rapidlyincreasesfrom0 (R(H-H) = 0.766 Å) to about 55 kcal/mol (3 Å). However, the self-interaction error of the unrestricted description given by the difference BS-ULDA - BS-USIC/LDA decreases beyond the bifurcation point (SIC/LDA: 1.363; LDA: 1.745 Å,
Figure 1) rapidly to zero for increasing R(H-H).
These relationships can be easily explained based on the known properties of restricted and unrestricted theory as well as the structure of the exchange holes given by HF or DFT (
Figure 2). Restricted theory erroneously describes cleavage of the HH bond partially homolytic, partially heterolytic. Dynamic electron correlation decreases with increasing R(H-H) because of the expansion of the doubly occupied
σg orbital. - The consequences of the self- interaction error of the exchange functional can be assessed by inspection of
Figure 2.Exact RHF exchange implies a delocalized exchange hole with deep pockets at the positions of the nuclei and a shallow (close to zero) depression in the internuclear region (
Figure 2a).Since, for
or any other spin-coupled 2-electron system, exchange is equal to the self-exchange (
intra-electronic exchange), the exchange hole is static (independent of the position of the reference electron) and equal to -1/2 the electron density distribution
ρ(
r). When SIC-LDA is calculated with the same density, it leads to exactly the same delocalized, static exchange hole. In this way, the form of both the HF and the SIC-LDA exchange hole provides electronic structure information.
The LDA exchange hole itself is localized rather than delocalized, depends on the position of the reference electron, and adopts a spherically symmetric form.At its deepest point it is equal to -1/2ρ(r), but otherwise it does not contain any electronic structure information. Since the sum rule implies that both LDA and HF exchange hole integrate to -1, a deep LDA exchange hole is narrow while a shallow LDA exchange hole is much more diffuse.
Clearly,the enforced spherically symmetric form of the LDA exchange hole can only be obtained from the correct SIC-LDA delocalized exchange hole by adding the hole due to the self-interaction error. The self-exchange hole of LDA is obtained by subtracting the SIC-LDA from the LDA exchange hole (
Figure 2).It shows that for the reference electron being at the left H nucleus, the self-interaction error drastically increases the probability of finding the second electron at the right H nucleus. Hence, it leads to left-right long-range electron correlation and explains why the RLDA description apart from the fact that it covers dynamic electron correlation (difference RHF - RSIC/LDA) does not suffer so much from the basic failure of restricted theory when describing bond dissociation.
Based on
Figure 2 the following conclusions can be drawn.
- 1)
With increasing distance R(H-H), the exchange hole becomes more and more delocalized. Accordingly the self-interaction error of the LDA exchange functional increases in magnitude and mimics more strongly left-right correlation.
- 2)
As a consequence of 1), the RLDA solution becomes more stable than the RHF solution for the dissociating
molecule. The bifurcation point, at which RLDA becomes unstable relative to ULDA is shifted to a larger R(H-H) value (from 1.212 to 1.745 Å,
Figure 1).The more long-range correlation effects are covered by a given method, the more stable it becomes.
- 3)
The energy difference between RLDA and RSIC/LDA is increased due to the increase of the self-interaction error.
Broken-symmetry unrestricted theory corrects restricted theory by the mixing of HOMO and LUMO thereby leading to an effective separation of the bonding electrons of the dissociating H2 molecule. Homolytic dissociation is qualitatively described in the correct way. This is also reflected by the exchange hole of unrestricted theory (
Figure 2b). The BS-UHF exchange hole is localized at the position of the reference electron (taken to be at the left nucleus,
Figure 2) indicating that there is a low probability of finding the second electron at the left H atom. Hence the situation of an isolated H atom with one electron is approached as required by homolytic dissociation. The LDA exchange hole, which is actually optimized for the situation of the isolated atom, now provides a more accurate description of exchange than it could do in the case of
at its equilibrium geometry.SIC-LDA and LDA exchange hole do no longer differ significantly, and their difference mimics more short-range rather than long-range electron correlation. Accordingly, the self-interaction error is rather small.
- 4)
The explicit two-configurational description of long-range electron correlation as introduced by the BS-UDFT solution reduces the self-interaction error for increasing distance R(H-H) to a small value, i.e. the self-interaction error for the isolated H atoms is close to zero. This is reflected by the difference BS-ULDA - BS-USIC/LDA (
Figure 1).
- 5)
With increasing R(H-H), the self-interaction error mimics more short-range rather than long-range electron correlation. In the region of spin-recoupling from a closed-shell to an open-shell singlet, both long-range and short-range correlation effects are simulated by the exchange functional.
In the triplet state, both the UHF and ULDA exchange hole are localized and, consequently, the self-interaction error is small. USIC/LDA and ULDA hardly differ while however remaining differences become slightly larger for smaller R(H-H) values (
Figure 1). The self-interaction error simulates small amounts of dynamic rather than non-dynamic electron correlation.Hence, one can focus primarily on the description of the singlet state when analyzing singlet-triplet splittings as described by various DFT approaches.
The relationships demonstrated here for in the case of a LDA functional are also true for other multi- reference systems. As a second example, we take the symmetry-forbidden H2 + D2 cycloaddition reaction via a D4h-symmetrical transition state leading to 2 HD molecules (for reasons of simplicity we discuss the degenerate reaction H2 + H2). This is a well-known example for the failure of standard Kohn-Sham DFT as was demonstrated by Baerends and co-workers. [5b] The reaction barrier can only be described by mixing the CSF of the ground state A1g [(a1g)2(b2u)2] with the CSF of the doubly excited state A1g [(a1g)2(b3u)2].
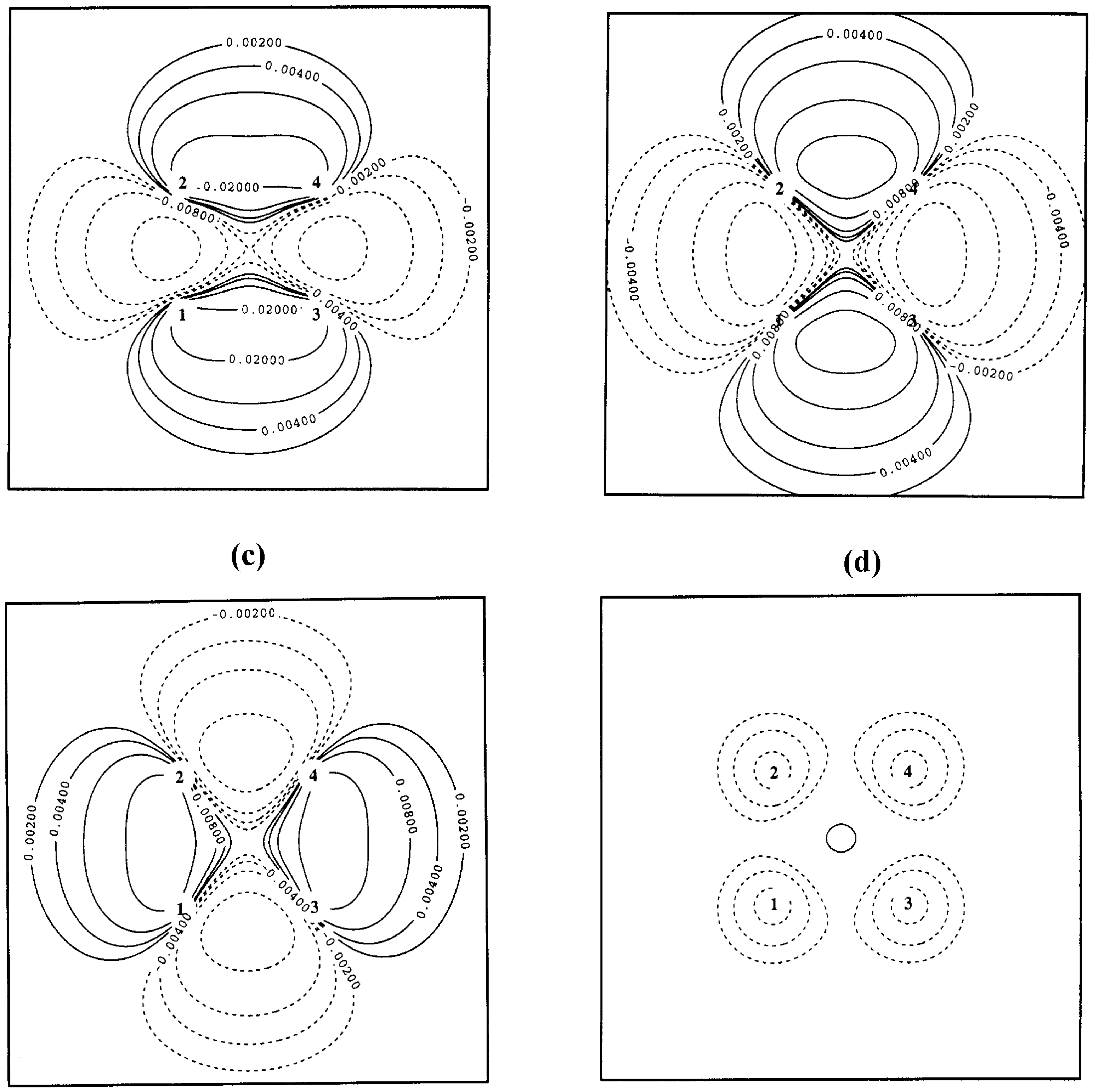
In
Figure 3 and
Figure 4, the electronic structure of the reaction complex {H1-H2 ··· H3-H4} is described at HF and LDA theory with Dunning’s cc-pVTZ basis set using difference densities (
Figure 3) and one- or two-dimensional representations of the exchange hole (
Figure 4) for a situation close to the transition state (R(H1-H2) = 1.212; R(H2-H4) = 1.244 Å). In the transition state, the bonds H1-H2 and H3-H4 are cleaved, while new bonds are formed between H1 and H3 as well as H2 and H4.
The difference density distribution ∆
ρ(BS-UHF,RHF) =
ρ(BS-UHF)-
ρ(RHF) (
Figure 3a) indicates the changes in the density due to the multi-reference effects included via the two-configurational approach of BS-UHF. [
9] Density is shifted from the bonding regions H1-H2 and H3-H4 to the nonbonded regions H1-H3 and H2-H4 to support the formation of the new bonds. We can quantify this effect by calculating the fractional occupation numbers (FON) of the
b2u-symmetrical HOMO and the
b3u-symmetrical LUMO obtained in the BS-UHF calculations: 0.931 and 0.068, respectively.
As found in the case of the dissociating H2 molecule the exchange functional mimics multi-reference effects. Ac- cordingly, the same pattern of density changes is obtained for the difference density distribution ∆
ρ(
RLDA, RHF) =
ρ(
RLDA)
− ρ(
RHF ) (
Figure 3b) as in the case of the BS-UHF/RHF comparison (
Figure 3a).Hence, RLDA plays the roleof theBS-UHF, onlythat thelong-range correlationeffects mimickedby theexchange functionalare clearly stronger (
Figure 3a and
Figure 3b) than those incorporated via the two-configurational form of the wave-function. Although BS-U theory does not use a two-configurational wave function directly it is correct to say that the multi- reference effects implicitly introduced via the self-interaction error of the exchange functional are stronger than the multi-reference effects explicitly included via the form of the wave function.
Figure 3c shows the difference density distribution ∆
ρ(BS-ULDA,RLDA) =
ρ(BS-ULDA)-
ρ(RLDA), which gives a reversed pattern of density changes. Long-range electron correlation mimicked by the BS-ULDA approach is weaker than that covered by the RLDA approach thus increasing the density in bond regions H1-H2 and H3-H4 but decreasing it in the nonbonded regions H1-H3 and H2-H4 relative to the RLDA description. This is contrary to the expectation that account of multi-reference effects by both the exchange functional and the two-configurational form of the wave function should be stronger than those accounted by one of these effects alone. This seeming contradiction is resolved when considering that the BS-UDFT solution mimics via its exchange functional less long-range correlation than RDFT does (see above). In addition, the long-range effects simulated by the exchange functional suppress the long-range effects that should be explicitly included via the wave function. Accordingly, the calculated FON values for HOMO and LUMO are 1.0913 and 0.9087, respectively, indicating a smaller admixture of the LUMO (or the doubly excited state) than obtained at the BS-UHF level of theory (FON: 1.0685 and 0.9315).
The explicit inclusion of long-range correlation effects is largest at the HF level, second largest at the SIC/LDA level, and smallest at the LDA level of theory as one can verify by comparing energy differences RHF-UHF, RSIC/LDA-BS-USIC/LDA, and RLDA - BS-ULDA for the same R(H-H) value (> bifurcation distance) in
Figure 1. Hence, the difference density distribution ∆
ρ(BS-ULDA,BS-UHF) =
ρ(BS-ULDA)-
ρ(BS-UHF) (
Figure 3d) indicates depletion of density in the nuclear regions.
In
Figure 4a, the RHF exchange hole is shown in a two-dimensional (contour-line) representation again for the geometry close to the transition state of the H
2 + H
2 cycloaddition reaction.The reference electron (denoted by X) is at the center of the reaction complex. The exchange hole is delocalized possessing deep pockets at the positions of the four nuclei. For a vertical movement (toward the center of the H1,H3-distance or toward the center of the H2,H4 distance) of the reference electron, the RHF exchange hole is static while for a horizontal movement (toward the center of the H1-H2 bond or toward the center of the H3-H4 bond) of the reference electron the RHF exchange hole of the dissociating H1-H2 or the dissociating H3-H4 molecule is approached (see
Figure 2a).
The RLDA exchange hole follows the reference electron and is always localized. It becomes very shallow and large in diameter in the nonbonded regions between H1 (H2) and H3 (H4) because of the smaller density in these regions (the outer dashed lines in
Figure 4c provide an impression of the radius of the RLDA exchange hole). Hence, the self-interaction error part of the RLDA exchange hole adopts the forms shown in
Figure 4b,
Figure 4c, and
Figure 4d. When the reference electron is at nucleus H2 (
Figure 4b), there is a large probability of finding the second electron close to nucleus H1, i.e. strong left-right correlation effects are mimicked in bond H1-H2.
When the reference electron adopts a central position in the non-bonded region between H2 and H4 (
Figure 4c), the probability of finding the second electron is large at H2 and H4, even larger at H1 and H3, but also in the nonbonded region between them. Again, the structure of the self-interaction part of the exchange hole suggests strong long-range left-right correlation effects in line with those found for the dissociating H
2 molecule. Any movement of the reference electron from the central position adopted in
Figure 4a to the left or right (
Figure 4d) changes the situation to that of the corresponding H
2 molecule approached, i.e. the part of the exchange hole due to the self-interaction error becomes identical to that shown in
Figure 2a. Hence, RLDA with the SVWN5 exchange- correlation functional can provide an improved, although not correct description of the H
2 + H
2 cycloaddition reaction because multi-reference effects are simulated by the Slater exchange functional.
The observations made for the LDA exchange functional are equally valid for GGA exchange functionals. However, long-range correlation effects mimicked by the latter functionals are smaller because the self-interaction error is smaller in this case. [
14] Also, the GGA exchange hole does not follow the reference electron in the region of low density so that the self-interaction part of the exchange hole differs significantly from the structure shown in
Figure 4c. Nevertheless, the self-interaction error determines the stability of an RDFT solution and influences the extent of multi-reference effects incorporated explicitly via the form of the wave function into DFT. Therefore, we have to consider next whether implicit and explicit inclusion of multi-reference effects can lead to a conflicting description of long-range electron correlation, for example by a double-counting of correlation effects.
3 Explicit Coverage of Multi-reference Effects: Ensemble DFT
Since the advent of DFT [
1] it was tacitly assumed that
any ground state density can be represented by a single Slater determinant constructed from the N
lowest eigenfunctions of a certain non-interacting Hamiltonian (10)
where the first term on the right side represents the kinetic energy part and the second the external potential. This assumption is embodied into the Kohn-Sham formulation of DFT [1b] where an auxiliary system of
non- interactingelectrons, which possesses the ground state density
identical to the density of a target system, plays a crucial role. The existence of the corresponding potential,
Vs in eq. (10), hasbeendemonstratedutilizingthe adiabatic connection between the real system of interacting electrons and a fictitious system with the interelectronic interaction switched off [
41,
42]. Such an adiabatic route does exist only if the corresponding density at the intermediate or zero electron-electron coupling strength is the
ground state density [
27].
However, it may well be that certain atomic or molecular electron density situations cannot be described by the ground state of a certain non-interacting Hamiltonian as was discussed early in the literature [
27,
28]. To circumvent the problem of
V -representability it was suggested [
27,
28] to use the ensemble density (11)
(
wi: weighting factor for state
i with density
ρi) rather than the density of a single Slater determinant. Indeed, theoretical arguments were given that the ensemble representation of the density is the only one that guarantees the existence of the corresponding potential
Vs in eq. (10). In terms of the one-electron orbitals, the ensemble representation translates to the fractional occupation numbers of the orbitals
φk(
r),
i. e.However, despite the formal exactness of the ensemble representation of the density, until recently it was considered to be of purely academic interest. Recently, the long-standing assumptionthatanynon-degenerate ground state density can be described by a single
ground state determinant was rejected by the results of accurate numeric Kohn-Sham simulations of the exact densities by Baerends and co-workers [
5]. These authors demonstrated that for the
ground state of the
C2 molecule and for the
1 Ag ground state of the
H2 +
H2 system it is impossible to fit the KS density to the exact one unless fractional occupation numbers are invoked for certain KS orbitals. Taken together with the theoretical arguments, these results showed unambiguously that the ensemble representation has practical relevance andis theonly
rigorous representation for thedensity ofa systemwith strong multi-reference character.
Ensemble DFT has a number of advantages. First of all, it enables one to calculate systems with strong multi- reference effects on the same footing as systems without these effects. In the latter case, the ensemble representation merely collapses to the single determinant as in the conventional Kohn-Sham method. For systems with strong non- dynamic electron correlation, the ground state density is represented by more than one Kohn-Sham determinant within the ensemble DFT approach. In principle, the selection of the determinants for the ensemble is performed automatically when minimizing the ensemble DFT energy functional with respect to the ensemble DFT density. Only the Kohn-Sham orbitals, which are degenerate at the Fermi level will be fractionally populated and the FONs will be obtained. However, this implies the use of the exact Kohn-Sham energy functional constructed for the ensemble densities. Such a functional should conform with the sum rules for the exchange-correlation hole and the on-top pair densities valid for the ensemble densities. The conventional approximate density functionals are based on the single determinant density representation and can not directly be used in the ensemble KS method.
Formally, the ensemble DFT approach can be formulated for a treatment of excited states as well. However, special density functionals must also be used in this case. Thus, it is the lack of the density functionals conforming with the ensemble representation of the density that hinders the practical implementation of ensemble DFT. It must be stressed that, contrary to general belief, the knowledge of the exact density functionals for the exchange- correlation energy would not guarantee an exact description of systems with strong multi-reference effects within standard single determinant DFT.
The REKS method [
29,
30] fills this gap in computational DFT. The method combines some ideas from WFT for constructing the energy functional in case of an ensemble while keeping the exact ensemble representation for the density. The density in REKS is represented as an average over densities of several configurations described by single determinants. In case of the REKS(2,2) method, there are two configurations: one with doubly occupied orbital
φr and another with doubly occupied orbital
φs, where
φr and
φs can be the HOMO and the LUMO from the conventional single determinant Kohn-Sham calculation. The inactive core orbitals are occupied with 2 electrons each, such that the ground state density is given by eq. (13).
The total ground state energy for a state with two fractionally occupied orbitals is represented as a weighted sum of Kohn-Sham energies,
EKS(...
...) and
EKS(...
...) of the two configurations described above and a coupling term
D(
φr,
φs) which is expressed as a linear combination of KS energies of the singly excited configurations generated within the same (2,2) active space.
The dependence of the weighting factors in eq. (5) on the fractional occupation numbers of the active orbitals was derived from model considerations, [
29] which are similar to those used by von Barth [
8] when developing DFT forthe multiplet states. Special care was taken to guarantee that at thetwo limiting situations,namely the ’normal’ system with
nr ≈ 2 and
ns ≈ 0 and open-shell singlet system with
nr =
ns = 1, the results of the conventional spin-restricted Kohn-Sham calculations are reproduced by REKS. [
29] The one-electron orbitals and the FON values are obtained in REKS variationally from minimization of the REKS total energy (14). [
29]
The model nature of the REKS energy expression makes it possible to use standard density functionals in a REKS calculation. Thus, REKS has an advantage of not being bound to a certain specific densityfunctional. However, the same model nature of REKS makes further extension of the ’active’ space quite difficult. While the REKS concept can be relatively easy extended to include the case of three electrons in three orbitals, i.e. REKS(3,3), [
29] the treatment of more complicated situations such as double bond dissociation, which includes four electrons in four orbitals, is not as easy. Furthermore, there is no automatic way of extending the REKS ’active’ space, like in CASSCF theory, and one needs to derive the energy expressions separately for every case of interest.
The fractional occupation numbers of the orbitals in REKS are analogous to the
natural orbital occupation numbers (NOONs) in conventional multi-reference theory. Thus, the concepts developed in WFT for the analysis of the multi-reference wavefunctions can be applied to the analysis of the REKS density and energy.The one- electron properties in REKS can be straightforwardly obtained from the density given by Eq. (13). The energy gradient with respect to atomic coordinates is also obtained easily from differentiation of Eq. (14). Thus, it is the feasibility of the REKS method that makes it anattractive alternative to the conventional multi-reference methods in WFT, especially in application to large molecular systems. Therefore, we will consider in the next section how REKS adjusts the explicit account of multi-reference effects to the implicit introduction of the latter via the exchange functional. For this purpose, we present for the first time REKS calculations based on the use of an hybrid functional, which were not possible with the previous version of the program. [
29]
4 Implicit and Explicit Coverage of multi-reference Effects: The Problem of Double Counting of Electron Correlation
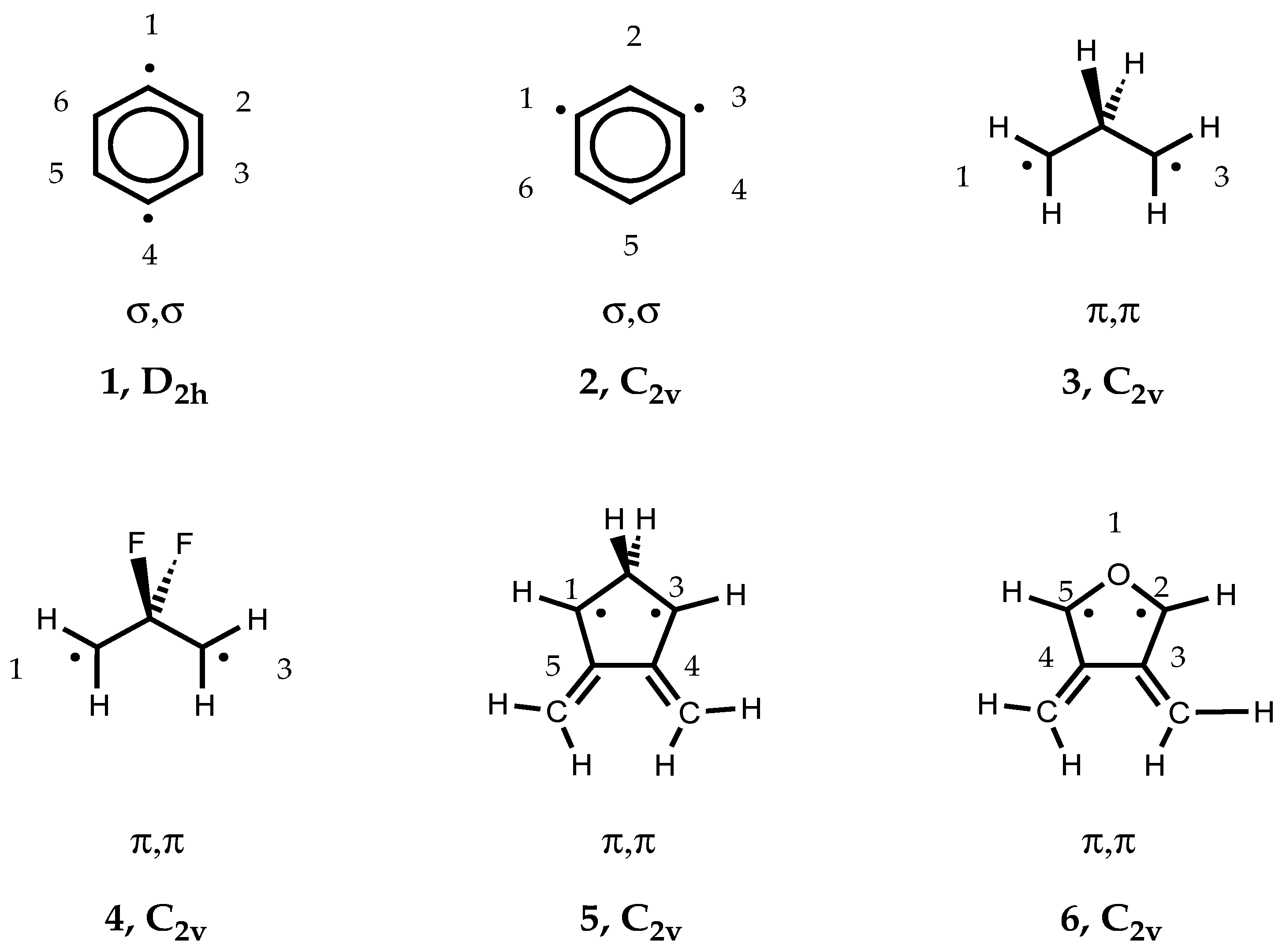
Singlet-triplet splittings ∆
EST were calculated for a number of biradicals with distinct multi-reference character both with restricted Kohn-Sham DFT, BS-UDFT, and the ensemble DFT REKS(2,2) method. The biradicals investigated (see
Scheme 1) include p-didehydrobenzene (p-benzyne,
1),m-didehydrobenzene (m-benzyne,
2), propane-1,3-diyl (trimethylene,
3), 2,2-difluoropropane-1,3-diyl (
4), 4,5-dimethylene-cyclopentane-1,3-diyl (
5), and 3,4-dimethylene-oxolane-2,5-diyl (
6). The open-shell singlet states of these molecules represent type II systems, which can be described by mixing the ground state with the doubly-excited state formed by exciting two electrons from the HOMO to the LUMO, i.e.the biradical character obtained by this two-configurational description can be assessed from the FON values of HOMO and LUMO. The triplet states are high-spin systems without anymulti- reference character (type 0 systems). They constitute appropriate reference systems, which are needed to assess the multi-reference effects of the singlet biradicals. Note that forsomeofthesemolecules,REKS/BLYPcalculations based on the 6-31G(d) basis set were previously published. [
29]
Pople’s 6-31G(d) basis [
43] and Dunning’s cc-pVTZ basis [
35] were used in connection with three different function- als, namely a) BLYP [
44,
45] as an example for a GGA functional characterized by a relatively large self-interaction error in the exchange part, b) B3LYP [
46] as an example for a hybrid functional with a considerably reduced self-interaction error due to the admixture of 20 % HF exchange, and c) BH&HLYP [
47] as an example for a hybrid functional with a relatively small self-interaction error due to an admixture of 50 % HF exchange. In addition, some reference calculations were carried out with the LDA functional SVWN5 [
36,
37]. In cases a), b), c) the corre- lation functional LYP is without a self-interaction error which for other correlation functionals such as VWN, [
37] VWN5 [
37] or PW91 [
48] lead to a negative correlation energy in the case of a single electron. The LYP correlation functional [
45] was constructed from the Colle-Salvetti functional [
49] that as a WFT-based functional is free of any residual self-interaction terms. - All calculations were carried out with the program packages COLOGNE2001 [
50] and Gaussian98. [
51]
In
Table 1 and
Table 2, calculated singlet-triplet splittings are listed for biradicals
1 -
6. Also given are the FON values of HOMO and LUMO (
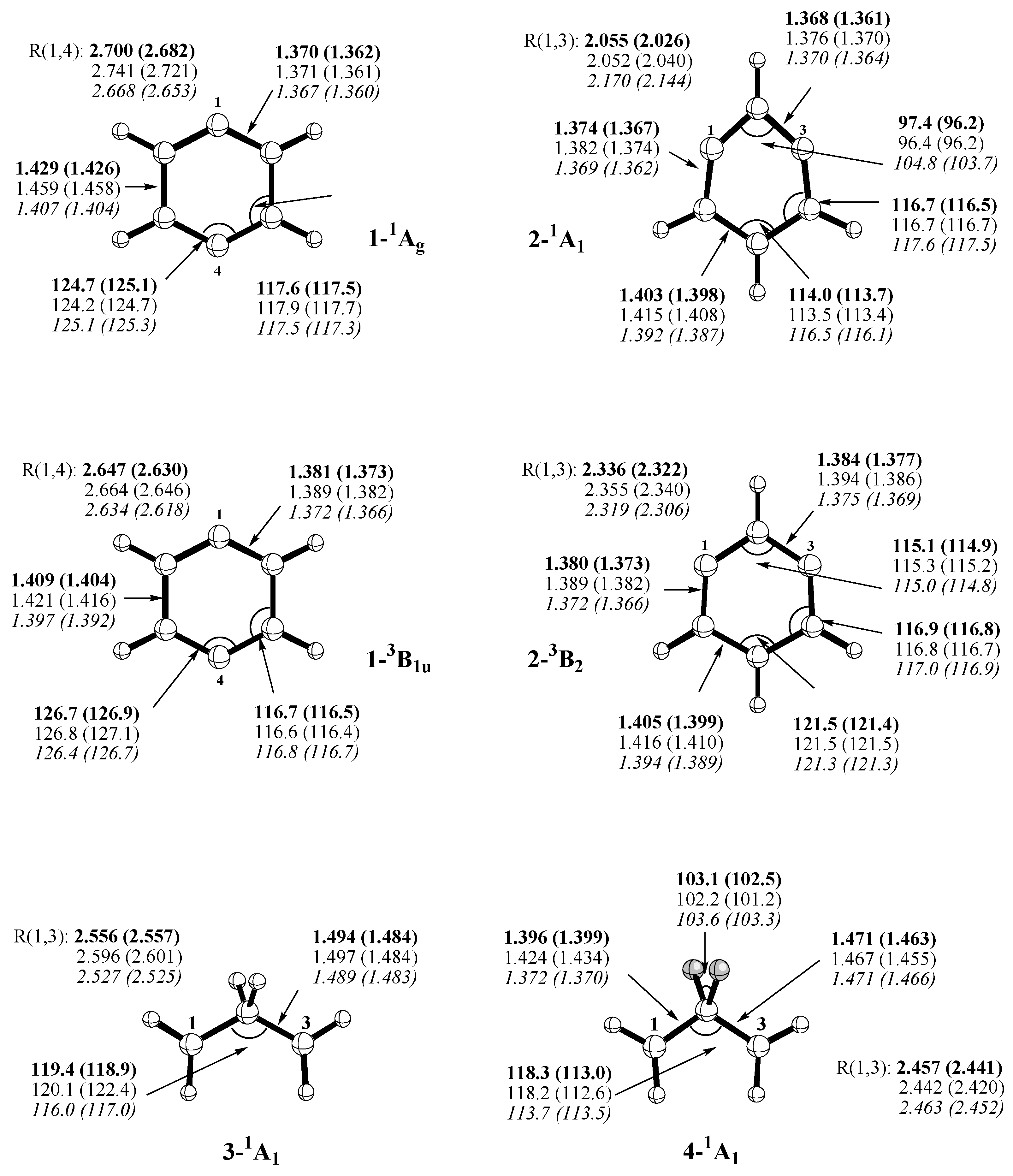
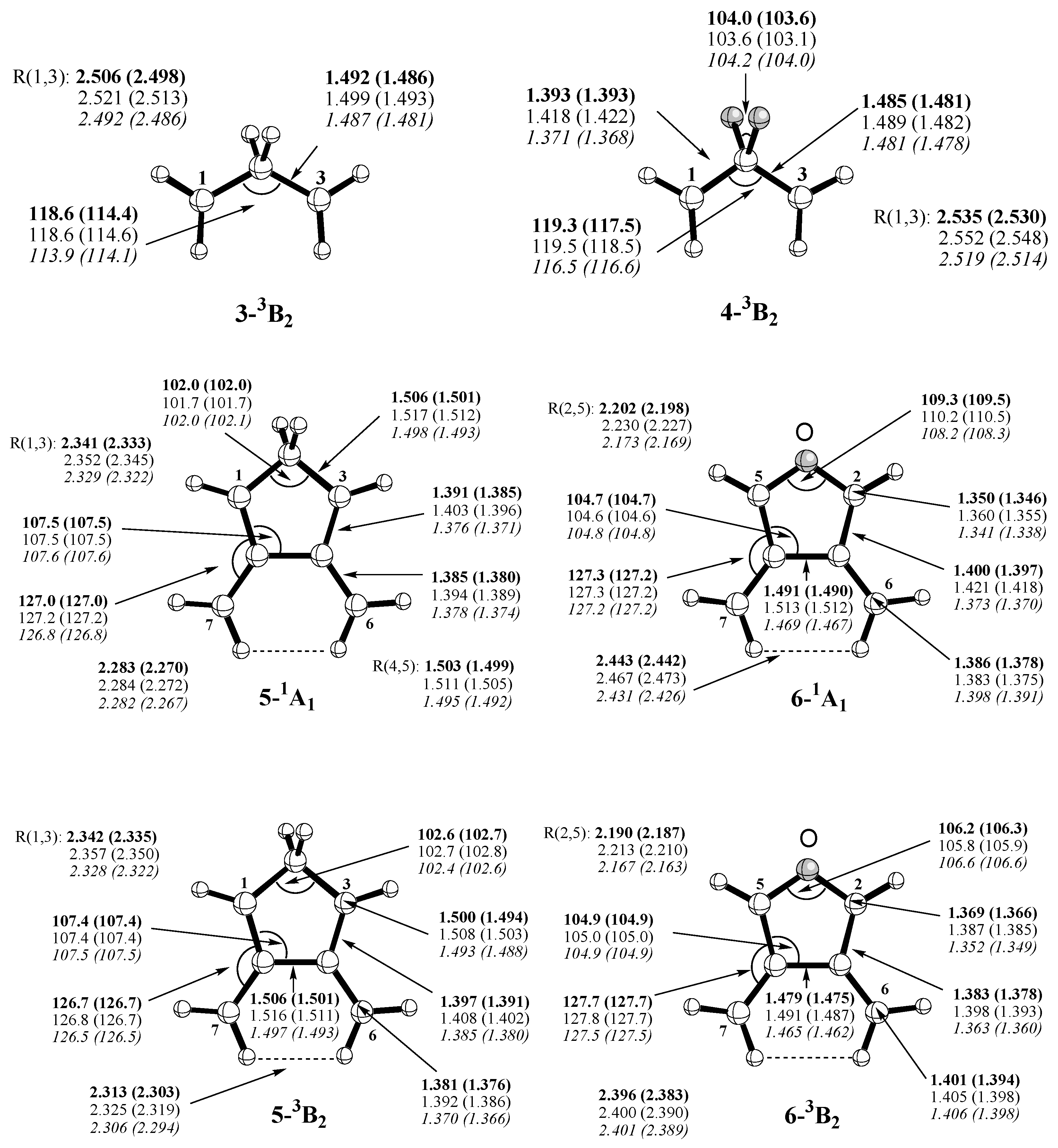
Table 2), which reflect the biradical character and, by this, the amount of long-range correlation effects introduced by REKS(2,2). Calculated REKS geometries are given in
Figure 5.
The exchange functionals of DFT cover long-range correlation effects, which keep the two unpaired electrons apart and thereby reduce the need for spin-coupling via through-bond interactions. Accordingly, the parameter ∆ increases for restricted theory in the series (
Table 1)
since the long-range effects mimicked by the exchange functional decrease in this order. Enforced through-bond coupling implies strained geometries that convert
1 into two allyl units hold together by two long C2-C3/C5-C6 bonds that disturb
π-delocalization and destabilize the molecule. Consequently, the singlet state is higher in energy than the triplet state, which benefits from the exchange interactions of the two unpaired electrons with aligned spin (thus reducing Coulomb repulsion).This is reflected by the calculated singlet-triplet splittings of -3.7 (SVWN5), 1.3 (BLYP), 14.9 (B3LYP), and 36.7 kcal/mol (BH&HLYP; all calculations with the 6-31G(d) basis; for cc-pVTZ results, see
Table 1), respectively where the triplet state was calculated at the UDFT level of theory.
Restricted HF and SIC-DFT theory predict with regard to the two unpaired electrons a delocalized exchange hole stretching from C1 to C4 (2.7 Å). Hence, the self interaction error of the localized RDFT hole is relatively large as are the long-range effects mimicked by it. REKS-DFT leads to a localized exchange hole similar to that shown in
Figure 2b. The self-interaction error of the exchange functional simulates short-range correlation, which is added to that of the LYP correlation functional. Hence, a double-counting of dynamic electron correlation cannot be excluded. This, however, should not be the case for the long-range correlation effects, which may also be simulated by the exchange functional according to the analysis of the H2 case given above.
Implicit coverage of long-range effects via the exchange functional leads to a stabilization of the singlet state and a corresponding increase of ∆
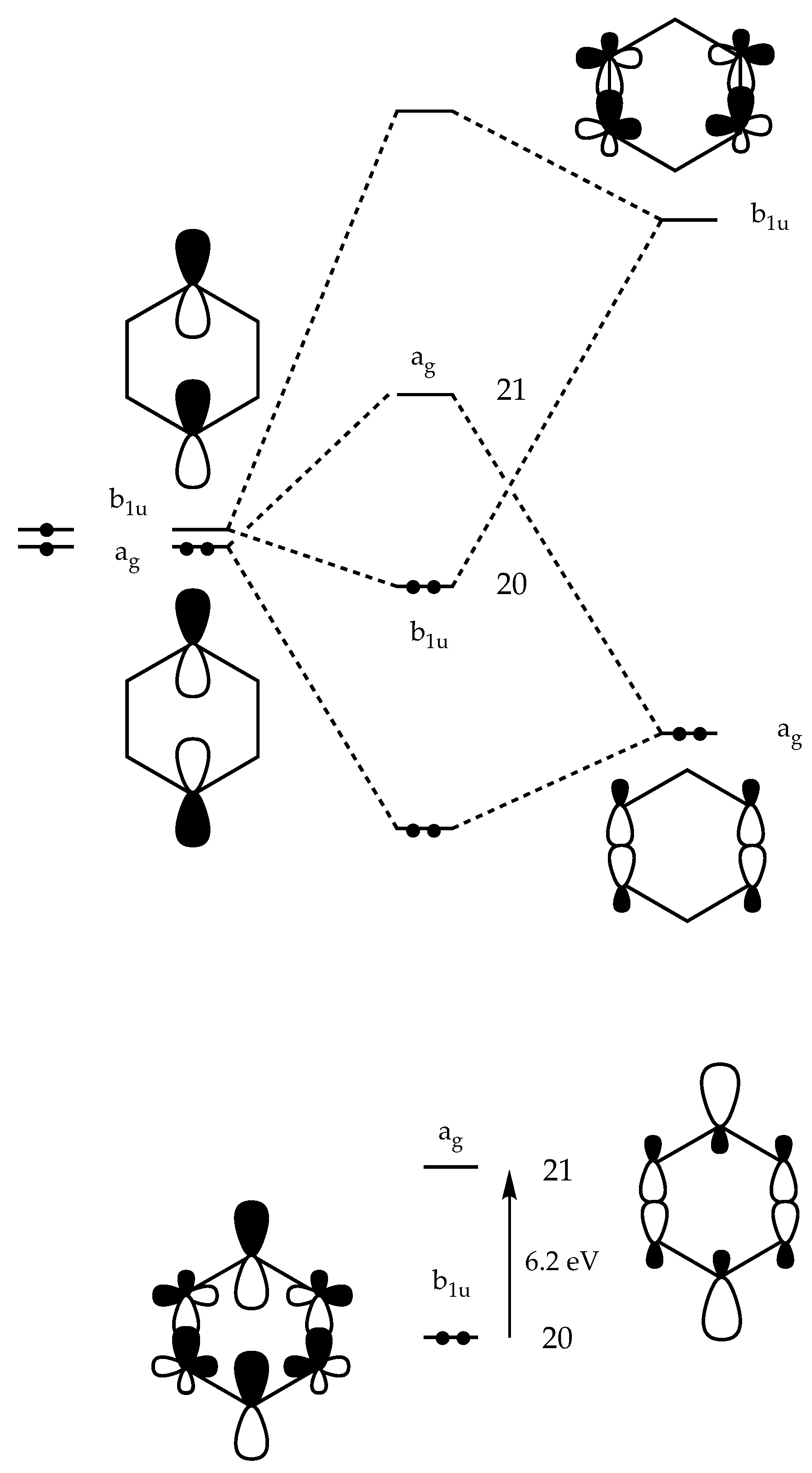
EST . The energy difference between singlet ground state and the doubly excited state increasesand,bythis,thepossibilityofstatemixingisreduced.StatemixinginensembleDFTleads to an occupation of the
ag-symmetrical LUMO (
Scheme 2) which is C2-C3 and C5-C6 bonding thus reducing the influence of through-bond coupling. Thus, the parameter ∆ reflects the amount of CSF-mixing and the corresponding reduction of through-bond coupling.
Clearly, these effects are moderate when using a BLYP functional (FON value for LUMO: 0.32), but increase when reducing the self-interaction error of the Becke exchange functional by admixing in HF exchange: Less long- range correlation effects are mimicked, the singlet energy increases (as documented by a more positive singlet-triplet splittings), the energy difference between singlet state and doubly-excited state decreases, and REKS leads to a larger admixture of the doubly-excited state as reflected by the FON values and the percent biradical character given by them: 59% (B3LYP), 77% (BH&HLYP; 6-31G(d) basis,
Table 1).Ensemble DFT leads to a stabilization of the singlet state relative to the triplet state by 6.2 kcal/mol (BLYP), 16.9 kcal/mol (B3LYP), and 37.3 kcal/mol (BH&HLYP,
Table 1). The stabilization energies caused by the explicit coverage of multi-reference effects increase in the same way as implicit effects are decreased due to a reduced self-interaction error of the exchange functional.
The trends observed for REKS(2,2) are parallel to those obtained with BS-UDFT as both approaches lead to two-configurational descriptions (
Table 1). Singlet-triplet splittings close to the experimental ∆
EST value of -3.5 kcal/mol [
60,
53] are obtained with B3LYP using a larger basis set (BS/UDFT/cc-pVTZ: -2.6), REKS(2,2)/cc- pVTZ: -2.5kcal/mol,
Table 1) while with the BLYP functional values of singlet-triplet splittings are themore exaggerated the larger the basis set used (-4.5 and -5.7 kcal/mol,
Table 1). Since a larger basis set should lead to the better results, we conclude that B3LYP provides the more reliable description. The biradical character predicted by REKS(2,2)/B3LYP (ca60%,
Table 1) is comparable to that suggested on the basis of CCSD(T) calculations (65% [52b]) while the corresponding REKS(2,2)/BLYP value (32%,
Table 1) is much smaller.
For
2, a through-space 1,3-bond can be establishedto avoid a biradical structure. [
52,
57,
58,
59] Hence, restricted theory with HF or hybrid functional falsely predicts bicyclo [3.1.0] hexatriene to be the only isomer of
2. [
58,
59] This is also true for those functionals that exaggerate the strength of abond. Hence, LDA functionals, despite of the multi-reference effects mimicked by the Slater exchange functional, predict a bicyclic rather than biradical form thus indicating that the nature of the functional dominates.
GGA functionals such as BLYP predict weaker bonds and, by this, the long-range correlation effects mimicked by the Becke exchange functional can play a dominant role: They lead to a lengthening to the C1-C3 bond to ca. 2 Å [
58,
59]. The energy differences involved are relatively small: The stretching of the CC bond from 1.6 to 2 Å leads to a 2.5 kcal/mol gain in energy at RBLYP, but a 1 kcal/mol loss in energy at RB3LYP, hence the difference in the two descriptions being about 3.5 kcal/mol. [
58]
When multi-reference effects are included via REKS(2,2), they are smaller for
2 than for
1 by at least a factor of five (see FON values for B3LYP in
Table 2), which reflects the fact that the biradical (multi-reference) character of
2 is considerably reduced compared to that of
1. Thus, the (absolute) corrections in the singlet-triplet splitting of
2 caused by REKS are smaller: a) BH&HLYP: -4 kcal/mol (from -7.4 to -11.4 kcal/mol,
Table 2); b) B3LYP: -2.3 kcal/mol (from -14.3 to -16.6 kcal/mol); c) BLYP: -2.2 kcal/mol (from -19.7 to -21.9 kcal/mol).
Again, the changes in the singlet-triplet splitting caused by REKS increase with decreasing account of implicit multi-reference effects introduced by the exchange functional. However, when the latter correlation effects are not simulated by the exchange functional, the singlet-triplet splitting is largely underestimated.TheREKS/BLYP results are just 1 kcal/mol more negative than the experimental value of -21.1 kcal/mol for the singlet-triplet splitting [
60] (the thermochemical corrections are just 0.4 kcal/mol) while the corresponding REKS/B3LYP energy differences are 4 kcal/mol too positive. Therefore, one could draw the conclusion that the implicit account of long- range correlation improves the BLYP results relative to the B3LYP results. However, two additional considerations have to be made:
- a)
The error in the REKS/B3LYP singlet-triplet splitting of -17 kcal/mol (cc-pVTZ basis,
Table 2) corresponds to the B3LYP destabilization energy of 3.5 kcal/mol caused by stretching the C1-C3 bond. Since the B3LYP functional [
46] was optimized to reproduce the thermochemistry of suitable reference molecules and, by this, the strength of the bonds in these compounds, it makes little sense to draw the conclusion that the B3LYP functional, because of its local contributions, exaggerates the strength of the C1C3 interactions and therefore has to be reoptimized.
- b)
A (2,2) active space provides a poor description of the multi-reference effects of
2 which can only be correctly described if the
π-space is included thus leading to a (8,8) active space (see Ref. 58). This will lead to a stabilization of the singlet state and, by this, an increase of the singlet-triplet splitting. For the B3LYP functional, the (absolute) experimental value of 21.1 kcal/mol would be approached in this way from above. In contrast, for the BLYP functional the singlet-triplet splitting would be significantly more exaggerated than with the (2,2) description (
Table 2).
We conclude that the seemingly better performance of BLYP is fortuitous. A more reliable description is obtained with the B3LYP functional because in this way a double-counting of correlation effects is avoided, which can lead to an exaggeration of the stability of the singlet biradical state. It seems preferable to include multi-reference effects explicitly via ensemble DFT or BS-UDFT than implicitly via the exchange functional. This is reasonable because in the latter case long-range correlation effects enter the description in a more unspecified, not necessarily optimal way while in the former case they are fine-tuned via the active space orbitals. In the following, we have to see whether these preliminary conclusions are also valid for biradicals
3 -
6.
Biradicals 3 - 6. The biradical character of the singlet states of
1 -
6 can be assessed by the FON values of the LUMO. It increases with the value of the singlet-triplet splitting. If the latter is significantly negative (strong stabilization of the singlet state relative to the triplet state by spin-coupling), the biradical character is small while a singlet state of comparable or even higher energy than that of the corresponding triplet state possesses high biradical character. This is reflected by
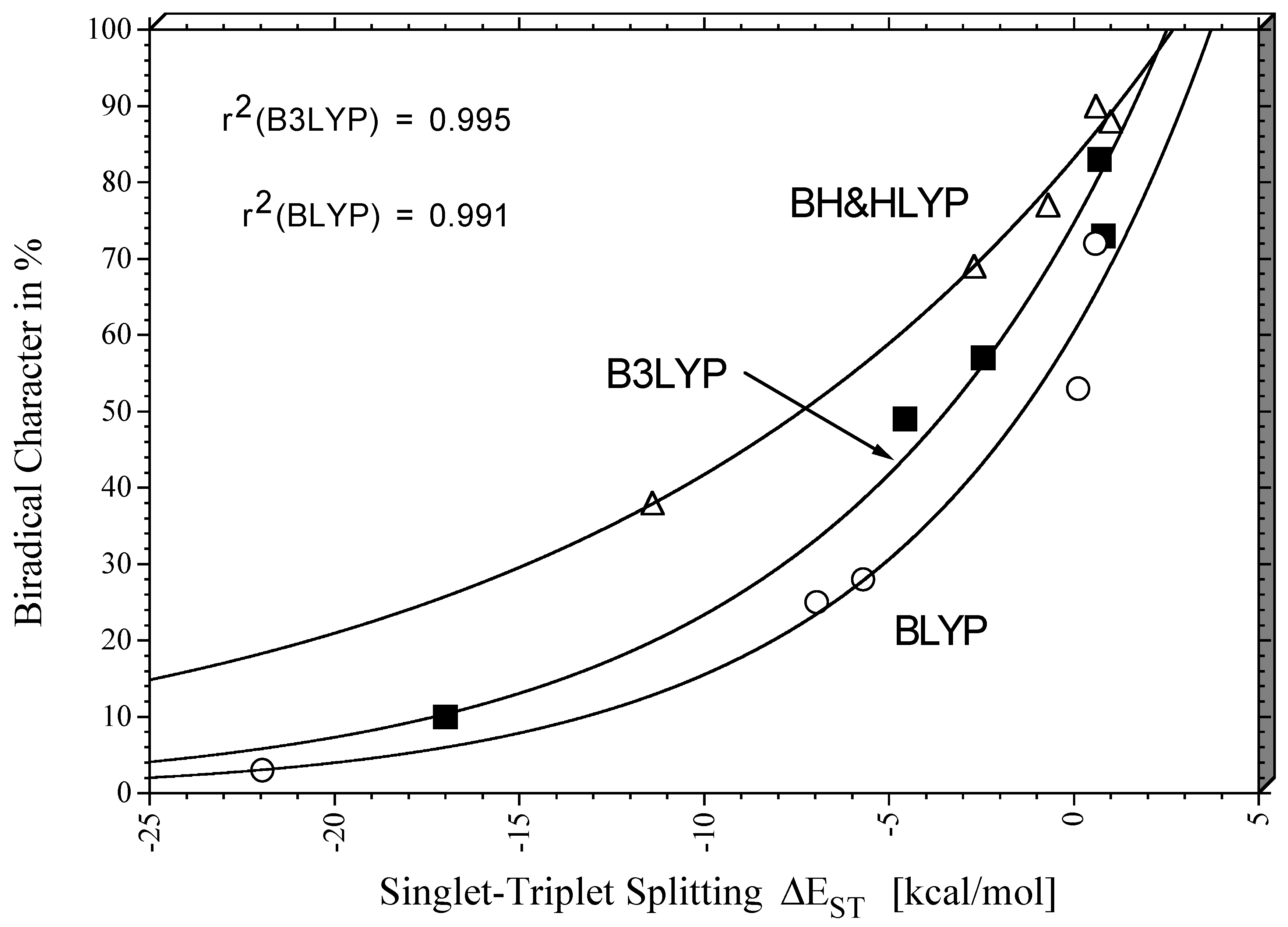
Figure 6 which suggests that the biradical character increases exponentially with the singlet triplet splitting in the range
−25
≤ ∆
EST ≤ 5 kcal/mol.The REKS and BS-UDFT ∆
EST values reproduce the trend in the experimental (or CASPT2) reference value of the splittings [
60,
61,
62,
63,
64,
65] where in the case of
5 and
6 no exact values are known.
In the
π, π-biradical
3 (
Scheme 1), the single electrons can only interact by hyperconjugation via the CH
2 group, which leads to little stabilization and, therefore a singlet energy slightly above the triplet energy (0.7 kcal/mol,
Table 2) results. Substitution of the H atoms by F atoms (
4) increases hyperconjugation due to a lowering of the pseudo-
π*(CF
2) (or
σ*(CF)) orbitals thus coupling the single electrons more effectively and stabilizing the singlet state; the biradical character is reduced from 79 to 55 % (B3LYP; BLYP: from 64 to 34 %,
Table 2).
For the
π, π-biradical
5 (
Scheme 1), the situation is similar to that in
3: Now two allyl units are connected by a CH
2group so that again spin-coupling can only be mediated by hyperconjugation.Bond C4-C5 is relatively long (1.50 to 1.51 Å,
Figure 5) indicating that
π-conjugation via this bond is moderate.Steric repulsion between the exocyclic CH
2-groups plays an important role in this connection (
Figure 5). The singlet-triplet splitting for
5 is larger than zero. [
64] Calculations indicate that it has a similar value (0.7 kcal/mol, REKS/B3LYP,
Table 2) as biradical
3 because of the same coupling mechanism between the unpaired electrons.
If the CH
2 group is replaced by an oxygen atom as in
6, the two allyl units can conjugate via the
π orbital of the heteroatom thus leading to an effective coupling of the single electrons. The singlet state is stabilized below the triplet state and the singlet-triplet splitting becomes -2.5 kcal/mol (REKS/B3LYP/cc-pVTZ,
Table 2). This is in agreement with the experimental observation that the singlet-triplet splitting is negative for
6. [
66]
The data in
Table 2 together with the information provided by
Figure 6 confirm what was discussed in the case of the benzyne biradicals. The hybrid functionals always lead to a stronger explicit account of multi-reference effects, which is clearly due to the fact that the self-interaction error is reduced by the admixture of exact exchange and, by this, also the long-range correlation effects simulated by the exchange functional. Accordingly, a larger biradical character is predicted for the singlet states
1 -
6 (
Table 2,
Figure 6).
The question whether implicit or explicit account of multi-reference effects leads to a better description can be answered by considering the calculated singlet-triplet splittings. Due to additional implicit account of electron correlation effects via the exchange functional, BLYP stabilizes the singlet state stronger than B3LYP thereby increasing absolute splittings (∆
EST < 0) beyond or reducing them (∆
EST > 0) below the experimental value (
Table 2).
The implicit account of multi-reference effects is the more economic way to describe biradicals and other type II systems. However, an unspecified coverage of these effects as provided by the presently availableapproximate exchange functionals cannot guarantee sufficient accuracy. Hence, one has to explicitly add multi-reference effects to get the correct state ordering and accurate relative energies. An explicit addition of multi-reference effects, however, will only be efficient if implicit coverage of multi-reference effects via the exchange functional is largely suppressed, i.e. if one works with partially (or fully) self-interaction corrected functionals such as the hybrid functionals. Hence, B3LYP rather than BLYP has to be used when BS-UDFT, REKS or other multi-configurational methods should be applied in an efficient and economic way.
But even in the case of a hybrid functional such as B3LYP, one cannot exclude a double counting of electron correlation effects. This double counting refers to dynamic rather than non-dynamic electron correlation effects as was discussed above. The variational nature of the REKS orbitals and orbital occupation numbers enables one to separate the non-dynamic correlation effects included explicitly and those included implicitly via the exchange functional. Thus, the double counting of the non-dynamic correlation energy is largely avoided by REKS. The same can not be guaranteed for the dynamic correlation energy. While for the two limiting cases, ’normal’ closed-shell system and open-shell singlet system, REKS reproduces the conventional KS results (i. e., no double counting), the description of intermediate situations depends on the approximations made in the REKS energy expression (Eq. 14). Hopefully, the extent of an extra dynamic correlation energy covered by the 2 × 2 secular problem in REKS is mitigated by the inclusion of the dynamic correlation terms into the coupling term D(φr, φs) of Eq. (14). However, a more precise knowledge is necessary of the dependence of the weighting factor in front of the coupling term D(φr, φs) of Eq. (14) on the fractional occupation numbers of orbitals to avoid precisely the double counting of the dynamic correlation in REKS.
5 Explicit Coverage of Multi-reference Effects: Merging of DFT and WFT
The problem of an accurate or at least a reasonable description of a multi-reference system has been satisfactorily solved for WFT using multi-configurational techniques. [
67] Therefore, it is attractive to combine a correct multi- configurational description of non-dynamic electron correlation effects with the DFT coverage of dynamic electron correlation effects. Various steps in this direction have been made and a review on the topic was given by one of us. [
13] Therefore, we summarize here only the essentials of the CAS(complete active space)-DFT method [
32] while other approaches to the problem can be found in the literature [
13] (for some recent references, see [
68,
69,
70]).
In view of the discussions in
section 2, the combination of WFT and DFT methods must imply that the exchange part is calculated exactly at the WFT level and that a self-interaction free correlation functional such as the LYP [
45] or the Colle-Salvetti functional [
49] is used.Considering these two aspects, CAS-DFT was derived by Gra¨fenstein and Cremer [
32] utilizing results of Miehlich and co-workers for the homogeneous electron gas. [
71]
For CAS-DFT, the standard Kohn-Sham approach is changed in the way that the minimization procedure is done over all properly antisymmetric CAS wave functions for a given size of the active space.Also, the Hartree energy
EJ is replaced by the full electron interaction energy
Vee of the CAS trial wave function, which covers exact exchange and the non-dynamic electron correlation effects.Hence, the CAS-DFT functional is given by Eq.(15):
Adding to (15) the dynamic correlation energy
as determined with a suitable correlation functional for the CAS density leads to Eq. (16):
Of course, one cannot use spin densities
ρα and
ρβ to determine
F[
ρ] because they lead to errors in the description of state multiplets.Therefore, these densities are replaced by the total CAS density
ρ(
r) and the CAS on-top pair density
P (
r,
r) (the second electron is on-top of the reference electron thus leading to a simplified pair density distribution) as input quantities for the correlation functional [
32] as was originally suggested by Moscardo and SanFabian. [
72] In this way, differences between states with different multiplicity can be distinguished. By em- ploying the Colle-Salvetti functional [
49], which uses the total density and pair density directly as input quantities, there is no need for a conversion of the functional as would be the case for any other gradient-corrected correlation functional based on spin densities
ρα and
ρβ.
Although the construction of a suitable CAS-DFT method seems to be straightforward, its realization is ham-pered by the fact that the CASSCF description includes beside non-dynamic electron correlation also an unknown amount of dynamic correlation effects and, accordingly, the functional
F[
ρ] of Eq. (16) leads to some double- counting of short-range correlation effects. A way out of this dilemma is to estimate the amount of dynamic electron correlation covered by the CASSCF description utilizing the homogeneous electron gas as an appropriate reference system. [
32,
68] A reference density
ρref(
r) is determined by considering all core orbitals and active space orbitals to be doubly occupied so that the magnitude of
ρref(
r) reflects the size of the active space.If compared with the true density of the system in question,
ρ(
r), the ratio
ρref(
r)
/ρ(
r)
≥ 1 will increase with the size of the active space as will the amount of dynamic electron correlation already covered by the CASSCF wave function. Hence, one has to scale the DFT correlation energy locally by a scaling factor
f (0
≤ f ≤ 1) to avoid this double counting.
For this purpose, one calculates the correlation energy of the homogeneous electron gas (HEG) with the density
ρ in a way that is comparable to the CASSCF description: Excitations are allowed from the occupied orbitals only into virtual orbitals up to a certain energy limit, which is adjusted in the way that the active space has just the reference density
ρref. For the determination of the scaling factor f, the resulting correlation energy
is related to the value
for all virtual orbitals being included.[
32] The correlation energy is defined by Eq. (17).
where the correlation energy per electron,
εC depends on the total and the on-top pair density as well as on their gradients (apart from higher terms in the most general case).
Although the scaling procedure eliminates the most serious errors due to a double-counting of dynamic electron correlation, the uniform treatment of core and active space orbitals can still jeopardize a successful application of CAS-DFT. For example, the core part of a CASSCF description of a chemical reaction may change, which can only be covered if core and active space orbitals are explicitly distinguished in the scaling procedure based on the homogeneous electron gas. [
73] Also, one has to differentiate between singly and doubly occupied orbitals in the scaling procedure if one wants to get reliable energy differences between ground and excited states having different orbital occupancies. For example in the case of a singlet-triplet energy difference a scaling procedure not differentiating between singly and doubly occupied orbitals will predict the triplet stability too small thus underestimating (∆
EST > 0) or overestimating (∆
EST < 0) the singlet-triplet splitting because of an exaggerated down-scaling of dynamic electron correlation in the triplet. [
73] However, once these problems are solved, CAS-DFT can provide a reliable and computationally feasible account of both non-dynamic and dynamic electron correlation effects.