Abstract
I present a personal viewpoint on multi-reference coupled-cluster theory, its pros and cons. I also suggest some criteria that should be satisfied by multi-reference CC, not the least of which is to develop a tool that will be (almost!) as easy to apply as today’s powerful array of single reference coupled-cluster methods. Some approaches like the equation of motion CC method offers a multi-reference description of some target states, while being entirely single reference in execution. Perhaps it offers a model for further generalization to a wider array of multi-reference problems.
1 INTRODUCTION
In this contribution I thought I would discuss the issue of multireference coupled-cluster (CC) theory from my viewpoint, a viewpoint developed by many years of effort directed toward both single reference and multi-reference CC methods [1,2,3,4,5]. The title question is one that I do not think enough people seriously consider. Instead, conditioned by years of multi-reference CI, most think that if single reference CC is good, then multi-reference CC has to be that much better, and would say that in many cases it is absolutely essential. However, there is another point that needs to be considered. Arguably, the most significant contribution of ab initio quantum chemistry to chemistry might be putting easily applied software into the hands of practicing chemists, who now see ’Computational Chemistry’ as another readily applicable tool for their inexpert use like NMR, IR, and X-ray structure determinations. Quantum chemists can take pride in this development, where applied theory is now used instead of difficult experiments to get essential information about molecules; while commiserating with all the problems this introduces into the literature! However, I think for any MRCC method to have a real impact in the field, a quasi-blackbox element is highly desirable. It facilitates essential calibration, too. Adding this condition tends to make a case for some inventive CC methods that are essentially single reference in application, even while embracing some multi-reference aspects in execution. Hence, this contribution is mainly an editorial, and in no sense is meant to be a review or to cite all the pertinent references. Many excellent reviews of MRCC exist [6,7,8,9,10], and these should be consulted for that kind of information. Instead I present an overview while using few equations to try to maintain a focus and a conversational tone, without undue detail. The references should provide the detailed equations for those interested. I assume the reader is more interested in some of the philosophy of approaches to MRCC than in its detailed formulation.
2 NATURE OF THE PROBLEM
To begin, we have to realize that in an AO basis set, |χ›, the full CI is the right answer. So, our first objective is to achieve that answer. (A second objective is the basis set itself, which is a topic for a different discussion.) With any reference function, and any set of orbitals, |ϕ› = |χ›T we know that we can get the ’exact’ answer in the basis by doing the full CI. Hence, the question we have to address is whether we get to that limit quicker and more efficiently when we introduce a ’multi-reference’ description.
However, the latter term is often ill-used in the field. I think its proper use should include five elements: (I) ’Multi-reference’ should mean that the configuration reference space involved, spanned by the functions, |φ› = |φ1,φ2,...φm› referred to as the P space, where P is a projec-tor, P=|φ›‹φ|φ›−1‹φ|, improves the description as m is increased. Hence, the total (full CI) wavefunction for any state, k, Ψk = (P + Q)Ψk, leads to a model state reference,
with Q the projector for the orthogonal complement, Q=|h›‹h|h›−1‹h|. Ω(k) is the wave operator that takes the model function into the exact result. It might be universal, where it will not depend explicitly upon (k), or it might be k dependent in some approaches. The better Φk, the better the approximation to Ψk (II) The subset of energies and model functions with coefficients, {cµ}, should typically be the eigenvalues and eigenvectors to an effective Hamiltonian matrix, = ‹φ|HΩ|φ›c = cEk, whose precise definition depends upon the particular ansatz for the wave operator of the eigenstate. The determination of the coefficients in Φk should be accomplished in an unbiased way, i.e., typically the solution of an eigenvalue problem as here, where each cµ can immediately assume any weight it wants rather than have to ’grow’ into that weight very slowly via some poor initial, typically perturbative, approximation. The latter is what single reference CC typically does. The equation of Ω(k), the Bloch equation, HΩ − ΩHΩ = Ω necessarily introduces coupling with , which adds substantial complications to the theory. (III) In less than a full CI approximation, the orthogonal complement to |φ› should consist of some category of excitations like all single and double excitations out of |φ› that expands |h› from what would be included if only a single function were in |φ› .The above three desiderata are obviously characteristic of MRCI, but are not all satisfied by what are called MRCC methods. IV, if we are to speak of MRCC, then we should insist upon size-extensivity, or that the approximations obtained from the method only consist of linked diagrams, since the latter is the principal rationale for CC theory, itself; and fundamentally distinguishes it from CI. Other issues of correct separation (size-consistency), size-intensivity, etc. are also highly desirable, but typically require further considerations than simply linked-ness. A fifth point (V) that is worth bearing in mind, is the distinction between achieving spin eigenfunction character and the necessity of a MR description that introduces ’non-dynamic’ correlation. I usually consider the spin (or symmetry) eigenfunction issue to be ’static’ correlation [5,6,7,8]. All correlation is in the full CI, so static, non-dynamic, and dynamic are nebulous terms that only attain relevance in distinguishing among approximations.
In the special case of single reference (SRCC), we replace |φ› by just one |φ0›, which makes its c0 chosen to be 1, irrelevant; and write the wavefunction as
where Ω = exp(T). The effective Hamiltonian reduces to just the energy, so there are no coupling terms on the right side of the equations for Ω (or T). The orthogonal complement does not depend as much on the truncation of T as it does in CI, e.g., since the product excitations are included from the orthogonal complement, |h›, however their weighting in the final wavefunction is limited by the truncation. If we limit ourselves to T2, eg, we have doubles, quadruples, sextuples, or all even excitations in our wavefunction until exceeds the number of electrons. This, of course, is the enormous power of CC theory compared to CI. Not only does the theory recognize that disconnected double excitations in electronic structure theory are more important than connected ones, like T4 and T6, but we also ensure the size-extensive property that is absolutely essential in accurate applications.
T = T1 + T2 + T3 ...
Once we include T1 and T2, we add single, disconnected triple, etc excitations. We also add a very important property of CC theory that is not shared by CI, namely that
where |ψ0›represents a determinant composed of rotated orbitals. This feature, coupled with the introduction of higher excitations via the disconnected cluster operators, makes CCSD and beyond, highly insensitive to orbital choice. Both CCSD and CISD are invariant to transformations among just the occupied or excited orbitals, but only the full CI is invariant to any orbital transformation. However, the above equation permits occupied-excited mixing, causing additional insensitivity. Much of the traditional education in electronic structure theory emphasizes orbital choice as being essential, as in MCSCF and MCSCF+CI. However, the insensitivity to the choice of orbitals in CC theory enables many convenient approximations to be introduced that would never be contemplated by CI aficionados, and this has a pivotal role in providing easily applied, but effectively multi-reference descriptions to be achieved in various CC approaches.
exp(T1)|φ0› = |ψ0›
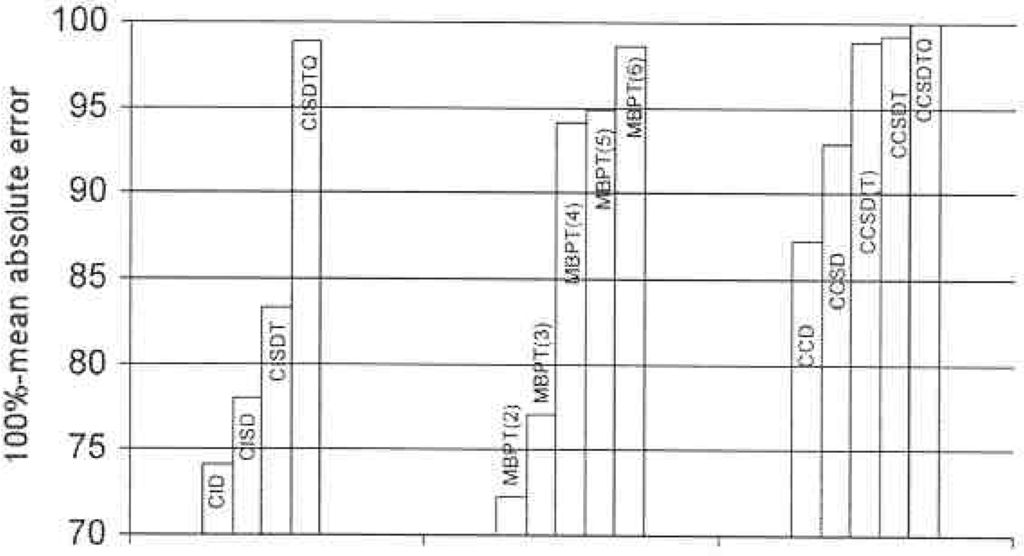
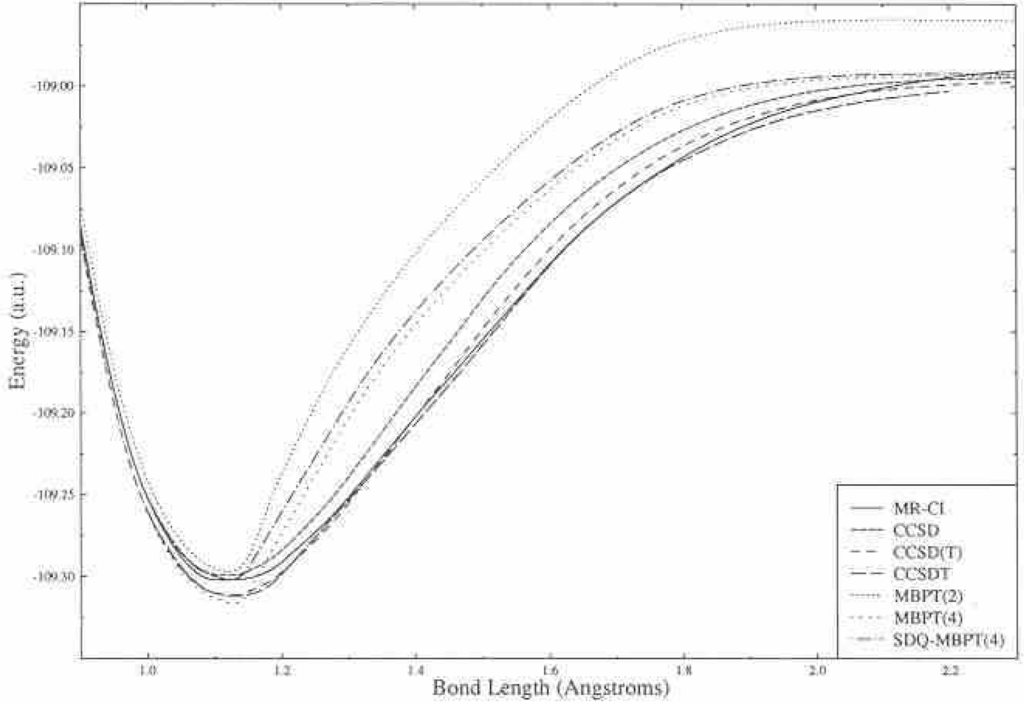
Obviously, if we include higher excited clusters in CC theory we will rapidly reach the full CI as shown in Figure 1. So, from the beginning, the need for a multi-reference CC method is less important than it would be in CI. However, we are aware of bond breaking situations, transition states, transition metal systems that might have many nearly degenerate open shell forms; and excited states, where there would seem to be a need for multi-determinant methods, as in all examples several determinants are especially important in their wavefunction description. However, even here, we need a caveat. It is well known (see Fig 2) that a UHF based CCSDT correctly describes bond breaking in even the triply bonded N2 molecule, so the prime example cited as requiring a multi-reference description has to include the necessity of its being done with a wavefunction that is an exact eigenfunction of S2 and potentially other operators like that due to inversion symmetry. See Fig 3 for RHF based results. Of course, all bond breaking cannot be adequately described by a UHF (O2 is a case in point), but many can. Besides condemning
 the symmetry breaking of UHF, and its various possible solutions; the purist will also point to the discontinuity when the RHF function changes to the UHF function, which has to affect the CC results with the two references until the full CI is reached, but its effect is far smaller at the correlated level. From a coupled-cluster variational viewpoint, as we suggested long ago [11], optimizing the orbitals at the CC level has to pick the lower of the RHF-CC and UHF-CC solutions, or another solution leading to a presumably smooth, and excellent curve as a function of R. As such, a ’variational’ CC would still be, operationally, a single reference CC description of the bond breaking. This is an existence proof that there is a SRCC curve that provides the right curve for SRCC. This basic idea has paid dividends in orbital optimized (OO-CC) applications [12, 13], for example. (I recognize that ’variational’ CC is almost an oxymoron (although XCC [3, 14] and UCC [3, 15] have some of those aspects) but at least at the full CI level we can see some of the consequences [16].)
the symmetry breaking of UHF, and its various possible solutions; the purist will also point to the discontinuity when the RHF function changes to the UHF function, which has to affect the CC results with the two references until the full CI is reached, but its effect is far smaller at the correlated level. From a coupled-cluster variational viewpoint, as we suggested long ago [11], optimizing the orbitals at the CC level has to pick the lower of the RHF-CC and UHF-CC solutions, or another solution leading to a presumably smooth, and excellent curve as a function of R. As such, a ’variational’ CC would still be, operationally, a single reference CC description of the bond breaking. This is an existence proof that there is a SRCC curve that provides the right curve for SRCC. This basic idea has paid dividends in orbital optimized (OO-CC) applications [12, 13], for example. (I recognize that ’variational’ CC is almost an oxymoron (although XCC [3, 14] and UCC [3, 15] have some of those aspects) but at least at the full CI level we can see some of the consequences [16].)

Figure 1.
Differences in correlation energies for various CI, MBPT, and CC methods with respect to the full CI (average of BH, HF, H2O at Re, 1.5Re, 2.0Re, DZP basis).
We know that as higher and higher clusters are added, we have to rapidly approach the full CI; but adding the conditions that we have pure symmetry eigenstates, using a full CI program to extract very high order CC results, Hirata in my lab among others, has shown that the correct bond-breaking in N2 requires essentially the full CI solution [17], and especially through hextuple excitations as one would expect. Hence, it is true that we need a way to accelerate the convergence
 of CC theory for this problem. (Recognize that this is still a somewhat artificial problem in chemistry, since reactions are accomplished by breaking one bond at a time, even for triply bonded systems as in nitrogen fixation, e.g. Furthermore, ensuring correct spin eigenstates for many problems, such as a Ni cluster, is almost inconceivable.)
of CC theory for this problem. (Recognize that this is still a somewhat artificial problem in chemistry, since reactions are accomplished by breaking one bond at a time, even for triply bonded systems as in nitrogen fixation, e.g. Furthermore, ensuring correct spin eigenstates for many problems, such as a Ni cluster, is almost inconceivable.)

Figure 2.
Various potential energy curves for N2 with a UHF reference.
I should also mention the use of GVB based CC for N2 [18]. We reported some GVB based MRCC results a few years ago [19, 20], and before that, there was pertinent work from Dykstra’s group [21], who observed that simply using GVB orbitals in CCD gave improved potential curves. Recognizing that the perfect-paired GVB wavefunction arises from a restricted exp(T2)|φ0› ansatz [22], using such a CCD procedure coupled to orbital optimization to get the GVB solution, Head-Gordon and co-workers have been able to obtain a qualitatively correct N2 potential curve [18]. So this is another type of operationally single reference CC solution for this problem.
Before saying more about MRCC, we should be aware of the two basic categories: direct and indirect MR methods. Direct means to me picking a multireference P space and introducing its complement, Q, and deriving MRCC equations subject to those choices. This might be called a Hilbert space method, and it typically starts from the Jeziorski-Monkhorst ansatz [23]. Ω = exp(T(µ))|Φµ›‹Φµ|. Except in the limit of a complete space, unlike MRCI, there is a manifold
 of configurations associated with every T(µ), which is difficult to manage. Some realizations of this approach for special cases have been achieved. One was the open-shell singlet work of Balkova and me [24], which is easy, since the effective Hamiltonian matrix when implemented in spin-orbitals, can be block diagonalized by symmetry into two essentially single reference problems. The next level of difficulty is to use a GVB reference. Unlike the former, we do not know the values of cµ just by symmetry, so we have to develop a more general structure[19, 20, 24]. Even more complete methods were implemented by Kaldor and co-workers who report N2 results [25].
of configurations associated with every T(µ), which is difficult to manage. Some realizations of this approach for special cases have been achieved. One was the open-shell singlet work of Balkova and me [24], which is easy, since the effective Hamiltonian matrix when implemented in spin-orbitals, can be block diagonalized by symmetry into two essentially single reference problems. The next level of difficulty is to use a GVB reference. Unlike the former, we do not know the values of cµ just by symmetry, so we have to develop a more general structure[19, 20, 24]. Even more complete methods were implemented by Kaldor and co-workers who report N2 results [25].

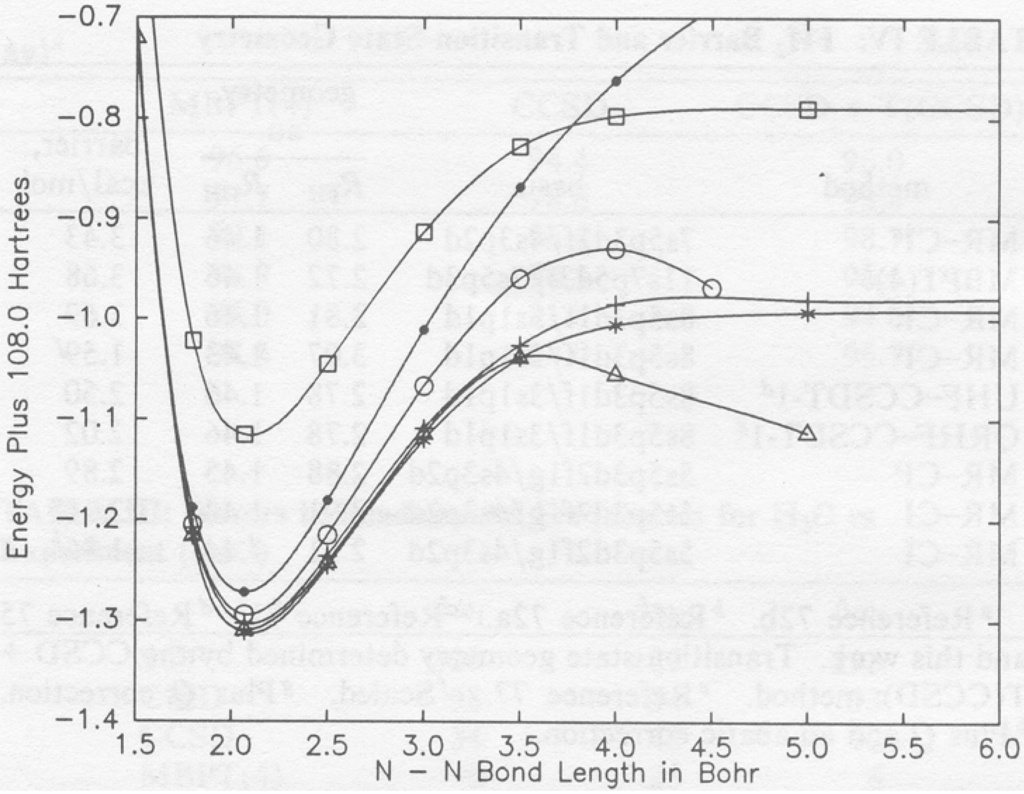
Figure 3.
RHF-based CISD, CCSD, CCSDT-1, MCSCF, MR-CISD, and MR-LCCM potential curves for N2 (absolute scale). The various curves are identified as follows: (•) CISD, (◦) CCSD, (△) CCSDT-1, (☐) MCSCF, (+) MR-CISD, and (*) MR-LCCM.
However, even within different Hilbert space methods, we can derive in principle ’a state-specific’ method meaning our objective is just a single state [26], like that in most MRCI calcula-tions [27]. In normal Hilbert space approaches in MRCC, we are forced to obtain more than one state from diagonalizing the effective Hamiltonian matrix. For quasi-degenerate cases, this makes perfect sense, as there could even be doubt which of several states is the lowest at some geometry, and the order might change as the geometry is changed; so a proper description should include this multi-state capability. But once the quasi-degenerate aspect is lost, the potential for intruder states is extreme; and having one prohibits getting results for any state. The best solution for general purpose applications for multiple states would probably be the ’intermediate Hamiltonian’ approach of Malrieu [28], as has been discussed for MRCC [29]. The basic idea is to introduce a buffer region and define the operators accordingly. However, a single state specific formulation [26] will overcome much of the intruder state problem since we only want one state, as in most MRCI studies.
We should also address the nature of the P space in Hilbert space MRCC. If it corresponds to a complete active space, as in FORS [30] or CASSCF [31], then we know the space has all the properties of full CI. So, among other things, it provides a size-extensive reference for size-extensive CC while being orbital invariant among the active orbitals. But in practice, this is largely impossible. Consider the problem of dissociation of some molecule ABCD into all its fragments: AB + CD, ABC + D, A + B + C + D, ADC + B, etc. Such an active space would be recommended for equivalent descriptions of the dissociation paths for this molecule, but, of course, is far beyond anything that could realistically be used. Some more restrictive incomplete model space choices can sometimes maintain extensivity [32], but CAS choices are severely limited [33].
Indirect methods can be in Hilbert space form, as in the equation-of-motion (EOM-CC) [34,35,36,37], (see also [38] and [39] for the CC-LRT view point), or using a Fock space viewpoint [6, 25] which is usually associated with a valence universal operator, Ω exp{S}, where {} indicate normal order, and S=S(m,n)=T(k.l), with (k,l) starting from (0,0) being the sectors of Fock space up to (m,n). Ω = exp(T(0,0)){exp((m,n)}, after separating T(0,0), which is the usual SRCC T. EOM and Fock space have many aspects in common. Basic to both is that some reference state defines T=T(0.0), a SRCC solution, defines a new reference function from which all other states can be extracted. This gives us the opportunity to introduce some multi-reference character into the target state, even if the reference state comes from SRCC. More interconnections and distinctions will become apparent below.
3 EQUATION-OF-MOTION CC METHODS
One very convenient way to retain the ease of application of SRCC methods is the EOM-CC philosophy. The basic idea is very simple. Given two Schroedinger equations for a state, k, and for the state g, which is a reference state that is not necessarily the ground state, we have
where
from which a little manipulation gives the EOM-CC equation,
where |Ψg› = exp(T)|φ0›. A similar equation provides the left-hand eigenfunction, ‹φ0|Lk to = e−T HeT, a non-Hermitian Hamiltonian, but has the same eigenvalue. It is not connected to like the right-hand eigenfunction. We can allow the electron put into orbital |a› by the operator a† to be a continuum function, giving us a net ionization, and reducing the operators in eqn. 6 accordingly. That is R(i)k = r0 + ∑iri{i} + ∑i<j,b {ib†j} + ... We can obviously do the same kind of thing to describe electron attachment [40], or to describe double ionizations, etc. So EOM is enormously flexible in this regard.
|Ψk› = Rk|Ψg›
Rk = Rk0 + Rk1 + Rk2 + ...
...
H|Ψk› = Ek|Ψk›
H|Ψg› = Eg|Ψg›
[e−T HeT Rk]c|φ0› = ωkRk|φ0›
EOM-CC is multi-reference in the space created by the Rk operator. The eigenfunctions are obtained from the generalized CI-like matrix, so any determinant can assume any weight it needs in the ’target’ eigenstate. The reference CC state, however, is still considered to be described by a SRCC solution. Failing that for some reference state, EOM-CC can be subject to error. For closed shell reference states, all the EOM ’excited’ eigenstates are spin eigenfunctions. If we use a symmetry broken CC reference state, like a UHF based one, this does not follow, and special attention needs to be paid to the resultant EOM-CC eigenvalues and eigenfunctions, where even their spin eigenvalues may be difficult to discern. Although excited states for many cases involving simple open shells are about as accessible [36, 41] as ground states typically are with UHF, ROHF or quasirestricted (QRHF) reference determinants. I might add that all of these reference determinants result in breaking spin symmetry in the reference CC solution even if the single determinant itself, like ROHF or QRHF, is a spin eigenfunction.
In terms of our three desiderata for MRCC methods, in EOM-CC the eigenstate for the target state is Rk exp(T)|φ0› = exp(T)Rk|φ0›, since [T,Rk] = 0. The first viewpoint suggests taking excitations out of a correlated reference state which is clearly MR, while the second suggests first make the ’CI’ like excitations and then operate with exp(T); but, of course, T does not depend upon this choice, as it might with some generalized MRCC ansatz. So we have conditions II and III satisfied, but subject to the underlying limitations in the SRCC reference solution. Condition I, though formally satisfied, is less relevant, since for this part EOM-CC is a single reference theory, where the P function is the reference SRCC state, which is what gives its ease of application. However, as the ansatz shows, it is a correlated reference state, so it is multi-reference in that regard, and will be improved as more functions are added in describing the P space for the underlying SRCC. (The degree of dependence of EOM-CC results on the P space of the reference CC has been considered by independently varying it and the complementary configuration (Rk) space [42].) (If we partition the EOM matrix, we can formally introduce another P’ and a Q’ space, that is pertinent to Fock space, discussed below.) However, for condition IV, strictly speaking, EOM-CC is not a fully linked method [43, 44]. This should not be surprising, as we are diagonalizing a CI-like matrix for the excited states, and they are not generally described by an exponential operator. They are, however, in the [1,0] and [0,1] sectors, since in those cases we can show the equivalence with an exponential ansatz [7, 45] (see below). This raises the issue of ’size-intensivity’ between two eigenstates, which would follow automatically if both states were described in a fully linked way. EOM-CC does have the property that the excited states for AB go smoothly into those for A + B, but not those for A+ and B− [7, 43]. (Fock space CC does.) In an infinite system, the difference due to one electron is meaningless, so for that situation there is no problem.
In EOM-CC, we also have one set of orbitals for the whole problem, so there is no opportunity, like in MRCI, to tailor the orbital choice to optimize a state. As discussed above, this is far less important in CC methods, but also recognize that unlike the reference CC state solution, because of the CI-like operator, Rk ,we do not have an exp(R1) so we cannot expect the same insensitivity to orbital choice that we can for the ground state. For condition V, we know that as long as the reference SRCC state is a closed shell, all eigenstates are spin-eigenfunctions. Of course, the overwhelming advantage of the EOM-CC approach is its ease of application. Essentially, no more decisions are required in doing EOM-CC than in doing SRCC, so EOM-CC methods are suited to black-box application and calibration. Hence, EOM-CC has most of the desiderata we want.
It is often thought that Fock space CC, built upon a valence universal wave operator [7, 8], is ’multi-reference.’ However, like EOM-CC, it is built upon a solution for a reference SRCC state, while in Fock space, the P’ space consists of suitable determinants for the particular sector, like all 1h determinants for the [0,1] sector, while Q’ would include contributions from operators like ia†j. For the [0,1] and [1,0] sectors, the principal ionization eigenvalues (electron attached energies) of the Fock space problem are precisely those for the IP-EOM-CC (EA-EOM-CC) methods (the proof by partitioning is presented elsewhere [40]), so increasing the target space (adding more 1h configurations does not change their values, but does permit more to be obtained. Hence, item I is not really satisfied. The Fock space wave operator is fully exponential, however, unlike that in EOM-CC. Hence, the equations consist solely of linked diagrams and have all of the consequent properties, being size-extensive and size-intensive, which is not shared by EOM-CC for the higher sectors. For [0,1] and [1,0] the exponential operator reduces to a linear form which corresponds to the EOM-CC ansatz. FS-MRCC has properties II, III, and V, as does EOM-CC, and as we go to other sectors like [1,1], there is also benefit from increasing the P’ space. Importantly, FS-CC adds IV, and can do so for even incomplete P’ spaces [32]. In fact, one of the best ways to introduce triple excitations into EOM-CCSD, is to add selective elements missing that would arise from triples in a Fock space method, and that also ensures that the resulting equations are fully linked. Such an approach has been offered by Meissner [46, 47].
A further improvement upon EOM-CC is its similarity transformed version, STEOM-CC [48, 49]. Here, in addition to the similarity transformation above, we make a second one using the information that can be obtained from solving the EOM ionization and electron attached problems, first. This gives us a set of eigenfunctions that defines a new Sk operator [49]. Then by building the double similarity transformed Hamiltonian,
and projecting it into configuration space, we can approximately block diagonalize the matrix form, , to decouple the single excitation block from the double and triple excitation ones. For example, this gives a rigorous, many-body equivalent of CIS for excited states [49, 48]. Similarly, the doubly excited states can be conveniently described by decoupling them from the higher excitation contributions [50]. Though developed quite differently from the Fock space approach, the numerical results for excited states, i.e., the [1,1] sector, are quite similar to those from Fock space [49], and presumably the same will apply in the [2,1], [1,2], [2,2] sectors of which the latter has proven to be very difficult to implement, computationally, within the Fock space structure, while STEOM-CC for double excitations has been implemented [50]. It should be apparent that when we address double ionizations or double electron attachment processes, as we discuss below for O3, we will benefit from the double transformations above.
The general ansatz for the wavefunction in STEOM-CC is
Such a wavefunction can serve as a basis for a multi-reference approach, where Rk creates some linear combination of determinants and at least static correlations, {exp(S)} introduces non-dynamic correlation, and finally exp(T) introduces dynamic correlation. Such a MRCC approach has been pursued by Nooijen [51]. Such a form will satisfy all five of the conditions above, but does not appear to be able to offer the same ease of implementation as the SRCC, EOM-CC, or FS-CC since an active space selection will probably be a necessity. If that selection can be made unambiguously, as discussed in the last section, then there would be hope.
|Ψ› = exp(T){exp(S)}Rk|φ0›
4 THE CI COMPROMISE
Not to view this as a heresy in the sense of the gnostics, but CI has a way of insidiously embedding itself into efforts toward a MRCC, and some generalized SRCC methods. A few examples from the CC world, whether SR or MR include renormalized R-CCSD(T), completely renormalized, CR-CCSD(T), etc. [52,53,54]; the externally corrected CC methods of Paldus et al. [55], where the additional information is taken from CI; BW-CC of Pittner, Carsky and Hubac [56, 57]; and our work on MR-LCCM and MR-AQCC e.g., [58,59,60,61,62,63,64]. Because of the CI aspect, none of these methods are rigorously size-extensive, and in some cases, again because of the unlinked diagrams in CI, a quasi-variational behavior is introduced into the calculations that can appear to be beneficial [52,53,54].
There is a different origin of the CI element for each of these examples. To illustrate, we’ll use SRCC concepts as a special case of the MRCC problem, unless the distinction becomes important. The renormalized approximations to non-iterative triples and quadruples can be viewed to be based upon an expression like,
following some truncation of exp(T)|φ0 >. This introduces unlinked diagrams, because it is not built upon a fully connected expression like,
where the denominator has been removed to all order giving a fully connected structure. Eqns. (17) and (18) are the same in the limit, but not necessarily order by order. Using the connected expressions as a basis for perturbative approximations has been done for many years [65,66,67,68] to yield fully connected expressions like CCSD[T], CCSD(T), CCSD(TQf) and their Λ based alter-natives [69]. However, for some truncation of the exp(T)|φ0 >, the expectation value in Eqn 17, could be used instead, which leads to “renormalization”. We recognize that once a perturbative approximation is made before insisting upon a fully connected structure as in Eqn. 18, a consistent cancellation of terms will not completely remove unlinked diagrams [70]. So a more flexible ap-proach might be thought to be obtained from their retention. Certainly when it comes to potential energy curves where there can be pathological consequences of the non-variational character of SRCC, having a few unlinked terms greatly aids in getting bounded curves, as they are ultimately responsible for the variational bound of truncated CI theory. In fact renormalized CC is a hybrid of CC and CI. So as the CC result turns over due to perturbation theory failures, the variation-aly bounded CI can take over! Hence, there is a CI compromise; but it might be recommended because we get better curves. On the other hand, it has not yet been shown that these kind of renormalized approximations actually converge to the right answer in a satisfactory way [70], as you can get quite a variety of results, short of putting in so many higher excitations that the dis-tinction between CI and CC is moot. Without systematic convergence we threaten the paradigm of converging CC methods CCD<CCSD<CCSD(T)<CCSDT<CCSDT(Qf) < CCSDTQ < Full CI that is responsible for their predictive quality, a cornerstone of the theory.
E = ‹φ0|[exp(T†)H exp(T)]C|φ0› = ‹φ0|(1 + Λ) exp(−T)H exp(T)|φ0›
In externally corrected CC [10], the comparative simplicity of exploiting CI to do higher ex-citation contributions than can be easily accomplished in CC theory itself, makes it possible to identify through a cluster expansion of the CI wavefunction, approximations for the higher exci-tation cluster operators. Once the full CI values for T3 and T4 are included in the determination of T1,T2, eg, then we have an exact expression for the energy from the latter. Hence, a God-given T3 and T4 offers a great deal. Paldus et al. have shown the often spectacular results that emerge from such a method [55], so it is telling us a lot about higher order correlation. However, the CI calculation should be more time-consuming that the corresponding CC one, as it is affected by unlinked diagrams. Furthermore, I cannot see how such a method would be very widely applicable because of an inability to get analytical gradients easily.
BW-CC is a clever way of solving the CC equations with just one critical distinction; by using a BWPT structure, no RSPT denominators arise, and this avoids many problems with strict MRCC methods including the renormalization terms that involve the effective Hamiltonian equation in the equation for Ω. But just as one learns the necessity of doing RSPT to have a linked diagram theorem, and one can do CI calculations readily in a BWPT way [71], the truncated CI and BW-CC retain unlinked diagrams. So this, too, effects a CI compromise. The principal remaining element in BWCC is to introduce an estimate for the effect of the unlinked diagrams remaining in the calculation, and there are less than in a straight-forward CI. Also, such corrections are embedded into an iterative formulae rather than being just a ’tack on’ correction like that due to Davidson [72, 73] to try to fix CI results for unlinked diagrams a posteriori. On the other hand, such BWCC methods are being routinely applied for GVB-reference CC and other multi-reference examples [56, 57], and gradients can be developed making them quasi-black box in implementation.
The methods MR-LCCM (multireference linearized CC method) [74] and MR-AQCC (multi-reference averaged quadratic CC method) [59] arise from a somewhat different consideration than the above. The CI compromise is accepted at the beginning at the program level, because we wanted to use a MRCI program to do some approximate CC calculations (which could be viewed as unlinked diagram corrected MRCI), to investigate some possibilities without writing a lot of new code. The MRCI code provides the evaluation of matrix elements, typically using the graphical unitary group framework. The MR-LCCM method was influenced by some comments of Paldus [75]. The second, its approximate quadratic extension, has much in common with MR-ACPF (multi-reference averaged coupled-pair) method [76], but uses a different way of counting pairs due to Meissner [77]. Both are examples of approximate state-specific MRCC, as our objective is a single state as in the other examples discussed in this section. In MR-AQCC, we insist upon a functional that allows us to simultaneously obtain the energies and the analytical forces in molecules. The importance of having both can hardly be overemphasized for chemistry. We make an approximation to EPV-like quadratic terms, that we hope will account for most of the quadratic correction to MR-LCCM. Even the latter already gives an excellent potential curve for N2, e.g., as shown in Fig. 3. Also, even in 1986 we were already using a quite extensive reference space (P space of 176 determinants) compared to those that have actually been considered computationally in other variants of state-specific, or Hilbert space CC. This, of course, was made possible by the extensive work and experience devoted to MRCI methods. MR-AQCC, as implemented into the COLUMBUS program system [78], has obtained a following, with several investigators who obtain their best results from the method [60]. It has been further extended by Szalay and co-workers to fine-tune the EPV-like approximation with further improvements [58].
Any of the above single state methods could be used, in principle, as a basis to develop an EOM-CC approach for multiple states, albeit retaining the ”CI compromise.” Among other elements, this would allow properly dissociating reference state curves in the determination of excited states, which should assist in correct dissociation for the excited state. This should be a focus for future work.
Each of these methods, as used in a Hilbert space MRCC approach, has properties I, II, III, and V, but lacks IV. Only the last already offers analytical gradient evaluation, while MR-BWCC should permit it without too much difficulty (the extensivity correction has to be incorporated into the gradient equations), as should the R-CCSD(T), etc methods if attention is devoted to that issue. If there is a well-defined way to evaluate the energy, then it should be differentiable. But what made it possible to routinely do analytical gradients for even SRCC techniques, was the realization of the Λ based functional above as satisfying a generalized Hellman-Feynman theorem [79, 80, 81],
or equivalently, that all ∂T/∂Xα could be replaced by solving for only one Λ operator, PΛQ − PEΛQ = 0 [81]. This is a necessity for realistic gradient evaluation for non-variational MRCC methods, too.
∂E/∂Xα = ‹φ0|(1 + Λ) exp(−T)Hα exp(T)|φ0›
From a CC viewpoint, a CI compromise is severe. But for pragmatists, if a method can be created that is almost size-extensive, systematically improvable, and that permits convenient analytical force evaluation, the compromise is justified.
5 NUMERICAL RESULT
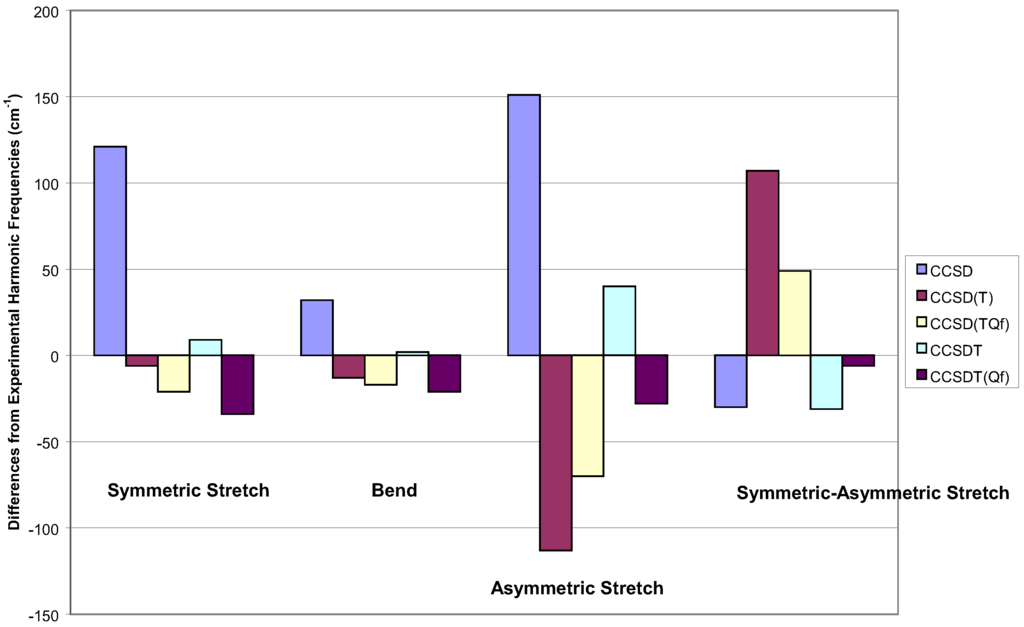
There are few comparative results for MR problems, but one old one that is still informative because it has been studied by many methods, is the vibrational frequencies of O3. The prob-lem is well known. The two symmetric, a1, vibrations of O3 are qualitatively correct, while the asymmetric stretch vibration of a2 symmetry is not. In Figure 4 and Figure 5, I show the results of many single and multi-reference methods in a DZP basis set. In Figure 6, I show some results in the large cc-pVTZ basis Unfortunately, the full CI result is not known, so we cannot provide an unambiguous comparison. We have to appeal to experimental harmonic frequencies. The essence of the problem, is that for the asymmetric stretch, certain configurations are allowed to mix, which cannot contribute to the symmetric displacements [82]. So the normal single reference function is a lesser part of the whole wavefunction for asymmetric displacements, causing a misbalance that affects the vibrational frequency. Consequently, it is usually thought that a proper multi-reference P space will resolve all these issues. Naively, there are two quasi-degenerate orbitals in O3, so we need at least a two-determinant reference space. For asymmetric displacements, we would have a third determinant in the complete active space that could not mix for symmetric displacements, but excitations can be created out of it that should be in the Q space manifold.
Starting with SRCC methods, looking at Figure 4, the reduced scatter for the first two sym-metric modes is apparent, though CCSD is a bit poorer than the others. However, the real issue here is the difference between the frequencies for the symmetric and asymmetric stretch. For this criteria, the worst result is CCSD(T), since it is comparatively poor for the latter mode. The best result for the symmetric modes are given by CCSDT [83], with the quadruple corrected CCSD(TQf) and CCSDT(Qf) close behind [84]. For the difference, the latter is the best result, and the most theoretically complete method.
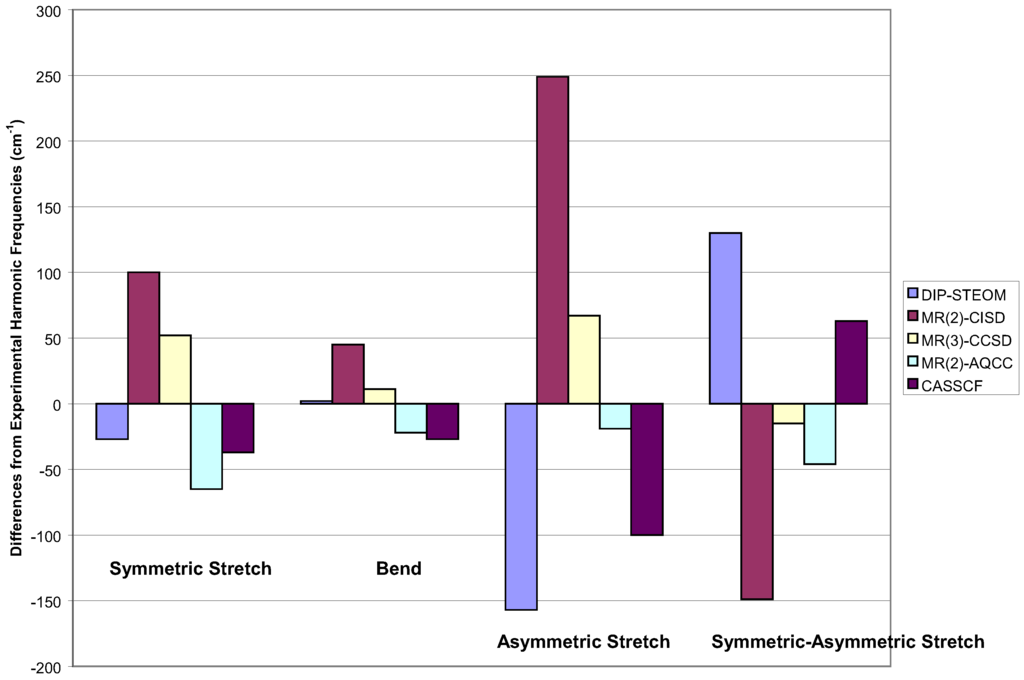
In Figure 5, I show some multi-reference results. The worst in all respects is the two-reference CI [85]. The two-reference MR-AQCC is quite good [58], but the best result overall would appear to be the three determinant reference, MR-CC of Li and Paldus [86]. I would say this is the most theoretically complete result of those here. But note, it is not the full MRCC and the program had to be written by computer to make the calculations possible. I recognize that such computer generated programs are likely to be the wave of the future, but the necessity of having to do it here, attests to the complexity of the formulae.
The DIP-STEOM-CC [48] approaches the problem indirectly. We evaluate a CCSD result for , which of course doesn’t exist, but we can make it bound by using an effective, Vn−1 potential.
 Then, we use our STEOM philosophy to delete two electrons from the reference to give us O3. But notice what this does for us. Since we have at least two important orbital levels in O3, of which one is doubly occupied in its SCF reference with the other nearby in energy, by filling that orbital too, and then kicking two electrons out with our EOM operator, Rk = ∑ rij{ij} + ∑ {ija†}+ ... we create a CC wavefunction that treats the two quasi-degenerate orbitals completely equivalently; the essence of MR theory, but done is a operationally SR way. The CASSCF is presented for comparative purposes [87].
Then, we use our STEOM philosophy to delete two electrons from the reference to give us O3. But notice what this does for us. Since we have at least two important orbital levels in O3, of which one is doubly occupied in its SCF reference with the other nearby in energy, by filling that orbital too, and then kicking two electrons out with our EOM operator, Rk = ∑ rij{ij} + ∑ {ija†}+ ... we create a CC wavefunction that treats the two quasi-degenerate orbitals completely equivalently; the essence of MR theory, but done is a operationally SR way. The CASSCF is presented for comparative purposes [87].

Figure 4.
Vibration frequencies of ozone for various single reference methods within a DZP basis.
Of course, a DZP basis is hardly adequate for us to compare to experiment, so a larger basis set might give us a rather different behavior for these methods. Results for a cc-pVTZ basis are shown in Figure 6. DIP-STEOM-CC is spectacular for the two symmetric modes, but not very good for the difference between the stretches, CCSDT gets the latter exactly right, but only because of a convenient cancellation of error. CCSDT(Qf) is very good, but is slightly poorer than the simpler CCSD(TQf). Of course, this is still far from the basis set limit, though a fairly extensive basis set study [88] pointed to the cc-pVTZ basis as having the best combination of quality and applicability. The fact that I only have one MRCC method, DIP-STEOM-CC, on this figure attests to the difficulty in obtaining these for most MRCC methods. Obviously, we can apply
 the MR(3)-AQCC and its improved versions, because that uses a highly efficient unitary group based MRCI code, but unlike MRCI, also offers analytical gradients. I hope serious applications of MRCC in this basis can be made in the near future. Just as O3 has proven to be an outstanding example to illustrate failures of theories, the ground and excited states of (NO)2 offers another demanding example. See Tobita, et al. [89], for a recent comparative study of DIP-STEOM, MR-AQCC, MR-BWCC, and other methods applied to this highly difficult system.
the MR(3)-AQCC and its improved versions, because that uses a highly efficient unitary group based MRCI code, but unlike MRCI, also offers analytical gradients. I hope serious applications of MRCC in this basis can be made in the near future. Just as O3 has proven to be an outstanding example to illustrate failures of theories, the ground and excited states of (NO)2 offers another demanding example. See Tobita, et al. [89], for a recent comparative study of DIP-STEOM, MR-AQCC, MR-BWCC, and other methods applied to this highly difficult system.

Figure 5.
Vibrational frequencies of ozone for various multi-reference methods within a DZP basis.
6 EXPECTATIONS FOR MRCC
When the many issues are considered, the framework of what I believe would be a desirable MRCC method emerges. It should have the following elements:
- Size-extensivity
- Unambiguous active orbital space
- Single state(SS) MRCC as a special case of multi state (MS) MRCC
- SRCC as a special case of (SS)-MRCC and (MS)-MRCC
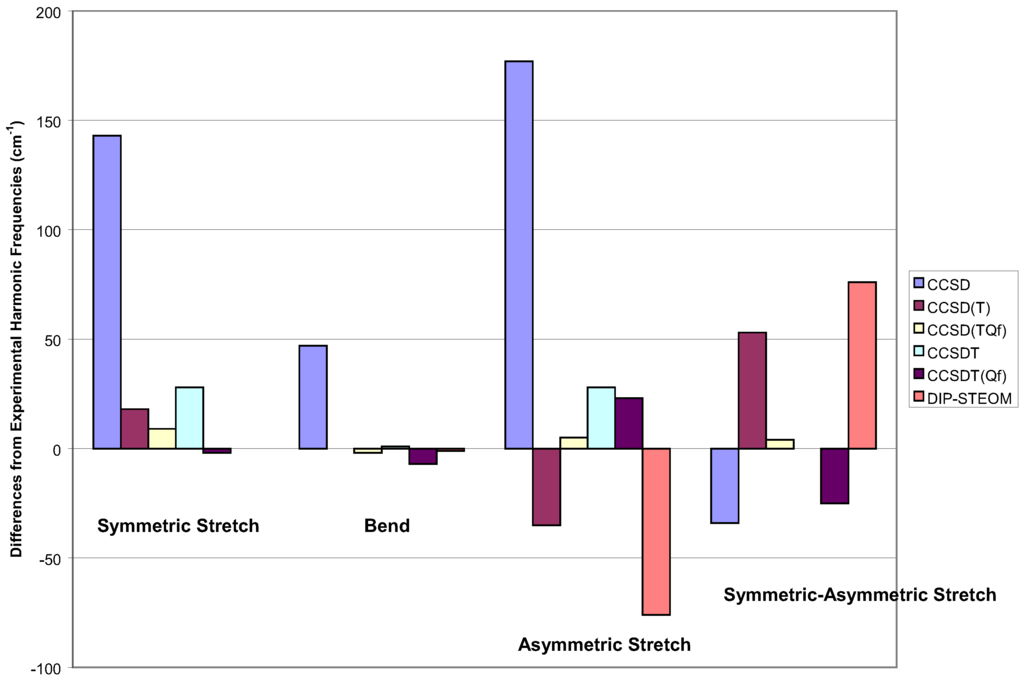
Figure 6.
Vibrational frequencies of ozone for various methods within a cc-pVTZ basis.
- (SS) and (MS) MRCC functional analogous to that for SRCC, to facilitate analytical gradi-ents and properties
- Reference for EOM approach to obtain all other states than obtained in the MRCC itself, with appropriate correspondence when a (SS) MRCC is used plus EOM to give a state that could also be obtained from (MS) MRCC.
- Automatic avoidance of intruder states possibly via an intermediate Hamiltonian framework
- Spin and spatial symmetry adapted
- Routine applicability for non expert use and calibration
- Satisfy conditions, I, II, and III from text.
Perhaps the most difficult of these to ensure is the unambiguous choice of reference space, yet this is particularly important if the method is suited to quasi-black-box application. It is clearly impossible to generally use a CAS space. What other prospects are there? One I like is the GVB space that comes from the perfect paired GVB equations. Since these (natural orbital) GVB orbitals can be determined within a CCD structure, subject to orbital rotation, they are a kind of restricted active space that has highly desirable properties. They facilitate correct separation while being size-extensive because of their representation as an exponential [22]. This is a kind of coherent state [90]. Because of the close correspondence with single reference theory, the smooth transition from SRCC to MRCC is apparent, as is the EOM generalization and the treatment of properties.
Another possible choice related to the first, is the Bardeen-Cooper-Schrieffer (BCS) state [91], also closely related to the antisymmetrized geminal power (AGP) function [92, 93]. This function has been considered as a reference for higher correlated methods, and it, too, has many desirable properties while also sharing the coherent state aspect.
In developing a MRCC method that has all the desiderata above, working from the existing SRCC framework is pertinent. One success of this approach is due to Oliphant and Adamowicz [94, 95], who simply augmented standard SRCC based upon |φ0› by higher excitations chosen from the consideration that if a second double excitation function, | ν›, that is actually treated in the Q space in CCSD, e.g., had been in the P space in a MR approach, then it would logically add new triples and quadruple excitations at its single and double excitation level that would not be included in the usual Q space for the SR-CCSD problem. In this way, some augmentation of the Q space, consistent with condition III, effects somewhat more balance indicative of a MR treatment. However, all operations are still those of SRCC. Of course, there is still substantial misbalance between treating the |ν› in Q space while the |φ0› is the real reference function. Some of this misbalance can be further ameliorated if we also fix the coefficient for |ν› to be what it should become based upon independent (or symmetry) considerations. I refer to this as a ’coefficient restricted’ approach, and for static correlation cases like open-shell singlets, or triplets, such a restriction to make both φ0 and ν be constrained to have the same (±) coefficient could be easily incorporated to accelerate convergence of the CC equations. Generalizations to low-spin doublets, etc. also can be made. If we already have CCSDT or CCSDTQ, then there would be little to gain from such an augmentation, except convergence, which is where the ’coefficient restricted’ approach still has merit.
Since including higher excitations can greatly increase the time for the SRCC calculation, it is logical to limit such terms to an active set of orbitals. This step has much in common with choosing active orbitals in MRCC, and will benefit, too, from an unambiguous choice. We considered several such variants on this basic idea in CCSDt, and CCSDtq methods [96], and in their further generalization to EOM-CCSDt, eg [52]. Such active orbital based single reference theory has an important role to play in our field, as gradients, properties, and excited states can be routinely obtained with very little change from the usual SRCC implementations. Yet, they will give improved results while the rate determining step in the computation is still that for CCSD itself. These methods serve an important role in bridging the gap between SRCC and MRCC.
Pertinent recent efforts toward this goal are the ’CI’ oriented CC equations that have been developed by Hirata et al. [42], Olsen, et al. [97], and Kallay and Surjan [98]. The main potential advantage that these methods have over other implementations is the flexibility of inclusion of selected higher excitations with appropriate spin adaptation. These methods might well yield a smooth transition not only between single and multi-reference theory, but between MRCC and MRCI. In that respect, regaining a practical (SS)-MRCC should follow.
Another such generalized SRCC method offers a different way of introducing higher excitation cluster operators while keeping the rate determining step of the calculation modest. These are the factorizied methods of Kucharski and me [99], which exploit the fact that we can ’force’ a factorization of T4, which would normally require an ∼ n10 algorithm, and similar higher connected terms at the cost of introducing terms. The factorization is beyond that of ordinary CC theory, like C4 ≈ (T2)2/2, eg. The T4 operator shows an exact factorization in its fifth-order energy expression, but does not in the corresponding amplitude expression. However, we have observed that we can force the latter at no significant cost in accuracy. This means that we can evaluate most of the effect of T4 with only an ∼n6 procedure, and if we insist upon including the initial T3, a ∼ n7 method, or ∼ n8 for the full T3. Hence we have a series of approximations including CCSDTQf, CCSDT(Qf), CCSD(TQf) etc. We have suggested a possible ansatz Ψ = exp(Tf) exp(Tu) where we separate the amplitude diagrams that are factorizable, Tf, from those that are not, Tu. If the effect of the latter could be shown to be bound in its consequences for calculations, then we could introduce the fully factorized terms without changing the asymptotic dependence of the computation. Clearly, such tricks can be combined with the active orbital methods above and should also be possible in the MRCC framework.
7 ACKNOWLEDGMENTS
This work has been supported by the U.S. AFOSR, under grant No. F49620-01-1-0072. I appre-ciate M. Nooijen, J. Pittner, P. Carsky and A. Perera reading the manuscript prior to publication and their helpful comments. I also want to thank so many of the scientists who I have cited in this paper, that I also had the pleasure of having in my group for extended periods of time. Nearly all! Their work made mine possible.
References
- Bartlett, R. J. Annu. Rev. Phys. Chem. 1981, 32, 359.
- Bartlett, R. J.; Dykstra, C. E.; Paldus, J. Coupled Cluster Methods for Molecualar Calcu-lations. In Advanced Theories and Compuatational Approaches to the Electronic Structure of Molecules; Dykstra, C. E., Ed.; Reidel: Dordrecht, Holland, 1984. [Google Scholar]
- Bartlett, R. J. J. Phys. Chem. 1989, 93, 1697.
- Bartlett, R. J.; Stanton, J. F. Application of Post-Hartree-Fock Methods: A Tutorial. In Reviews in Computational Chemistry; Vol. 5, Lipkowitz, K. B., Boyd, D. B., Eds.; VCH Publishers, Inc.: New York, 1994. [Google Scholar]
- Bartlett, R. J. Coupled-cluster Theory: An Overview of Recent Developments. In Modern Electronic Structure Theory, Part I; Yarkony, D. R., Ed.; World Scientific Publishing: Sin-gapore, 1995. [Google Scholar]
- Lindgren, I.; Mukherjee, D. Phys. Rep. 1987, 151, 93.
- Mukherjee, D.; Pal, S. Adv. Quantum Chem. 1989, 20, 291.
- Lindgren, I.; Morrison, J. Atomic Many-Body Theory; Springer: Berlin, 1982. [Google Scholar]
- Paldus, J. Methods in Computational Molecular Physics. In NATO Advanced Study Institute, Series B: Physics; Wilson, S., Diercksen, G. H. F., Eds.; Plenum Press: New York, 1992. [Google Scholar]
- Paldus, J.; Pylypow, I.; Jeziorski, B. Many-Body Methods in Quantum Chemistry. In Lecture Notes in Quantum Chemistry; Volume 52, Kaldor, U., Ed.; Springer: Berlin, 1989. [Google Scholar]
- Purvis, G. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76, 1910.
- Sherrill, C. D.; Krylov, A. I.; Byrd, E. F. C.; Head-Gordon, M. J. Chem. Phys. 1998, 109, 4171.
- Krylov, A. I.; Sherrill, C. D.; Head-Gordon, M. J. Chem. Phys. 2000, 113, 6509.
- Bartlett, R. J.; Noga, J. Chem. Phys. Lett. 1988, 150, 29.
- Bartlett, R. J.; Kucharski, S. A.; Noga, J. Chem. Phys. Lett. 1989, 155, 133.
- Olsen, J. Private communication.
- Hirata, S. unpublished.
- Voorhis, T. V.; Head-Gordon, M. J. Chem. Phys. 2001, 115, 7814.
- Balkova, A.; Bartlett, R. J. J. Chem. Phys. 1994, 101, 8972.
- Balkova, A.; Bartlett, R. J. J. Chem. Phys. 1995, 102, 7116.
- Dykstra, C. E. Chem. Phys. Lett. 1982, 88, 202.
- Cullen, J. Chem. Phys. 1996, 202, 217.
- Jeziorski, B.; Monkhorst, H. J. Phys. Rev. A 1981, 24, 1668.
- Balkova, A.; Bartlett, R. J. Chem. Phys. Lett. 1992, 193, 364.
- Berkovic, S.; Kaldor, U. J. Chem. Phys. 1993, 98, 3090.
- Mahapatra, U. S.; Datta, B.; Mukherjee, D. Mol. Phys. 1998, 94, 157.
- Shavitt, I. Mol. Phys. 1998, 94, 3.
- Malrieu, J. P.; Durand, P.; Dauday, J. P. J. Phys. B 1985, 18, 809.
- Meissner, L. J. Chem. Phys. 1998, 108, 9227.
- Feller, D. F.; Schmidt, M. W.; Ruedenburg, K. J. Am. Chem. Soc. 1982, 104, 960.
- Roos, B. O.; Siegbahn, P. E. M. Inter. J. Quantum Chem. 1980, 17, 485.
- Mukhopadhyay, D., Jr.; Mukherjee, D. Chem. Phys. Letts. 1991, 177, 441.
- Olsen, J.; Roos, B. O.; Jorgensen, P.; Jensen, H. J. A. J. Chem. Phys. 1988, 89, 2185.
- Sekino, H.; Bartlett, R. J. Int. J. Quantum Chem. Symp. 1984, 18, 255.
- Geertsen, J.; Rittby, M.; Bartlett, R. J. Chem. Phys. Lett. 1989, 164, 57.
- Comeau, D.; Bartlett, R. J. Chem. Phys. Lett. 1993, 207, 414.
- Stanton, J.; Bartlett, R. J. J. Chem. Phys. 1993, 98, 7029.
- Monkhorst, H. Int. J. of Quantum Chem. Symp. 1977, 11, 421.
- Mukhopadhyay, S. K.; Sinha, D.; Prasad, M. D.; Mukherjee, D. Chem. Phys. Letts. 1985, 111, 437.
- Nooijen, M.; Bartlett, R. J. J. Chem. Phys. 1995, 102, 3629.
- Stanton, J. F.; Gauss, J. J. Chem. Phys. 1995, 103, 8931.
- Hirata, S.; Nooijen, M.; Bartlett, R. J. Chem. Phys. Lett. 2000, 326, 255.
- Meissner, L.; Bartlett, R. J. J. Chem. Phys. 1990, 92, 561.
- Mukhopadhyay, S. K.; Chaudhuri, R.; Mukhopadhyay Jr., D.; Mukherjee, D. Chem. Phys. Letts. 1990, 173, 181.
- Pal, S.; Rittby, M.; Bartlett, R. J.; Sinha, D.; Mukherjee, D. Chem. Phys. Lett. 1987, 137, 273.
- Meissner, L.; Bartlett, R. J. J. Chem. Phys. 1995, 102, 7490.
- Meissner, L. J. Chem. Phys. 1998, 108, 9227.
- Nooijen, M.; Bartlett, R. J. J. Chem. Phys. 1997, 106, 6441.
- Nooijen, M.; Bartlett, R. J. J. Chem. Phys. 1997, 107, 6812.
- Nooijen, M.; Lotrich, V. J. Chem. Phys. 2000, 113, 494.
- Nooijen, M. Int. J. Mol. Sci. 2002, 4. this issue.
- Kowalski, K.; Piecuch, P. J. Chem. Phys. 2001, 115, 643.
- Kowalski, K.; Piecuch, P. Chem. Phys. Lett. 2001, 344, 165.
- Kowalski, K.; Piecuch, P. Chem. Phys. Lett. 2001, 347, 237.
- Peris, G.; Planelles, J.; Malrieu, J. P.; Paldus, J. J. Chem. Phys. 1999, 110, 11708.
- Pittner, J.; Nachtigall, P.; Carsky, P.; Masik, J.; Hubac, I. J. Chem. Phys. 1999, 110, 10275.
- Hubac, I.; Pittner, J.; Carsky, P. J. Chem. Phys. 2000, 112, 8779.
- Szalay, P. G.; Bartlett, R. J. Chem. Phys. Lett. 1993, 214, 481.
- Szalay, P. G.; Bartlett, R. J. J. Chem. Phys. 1995, 103, 3600.
- Lischka, H.; Shepard, R.; Pitzer, R. M.; Shavitt, I.; Dallos, M.; Muller, T.; Szalay, P. G.; Seth, M.; Kedziora, G. S.; Yabushita, S.; Zhang, Z. Phys. Chem. Chem. Phys. 2001, 3, 664.
- Szalay, P. G.; Muller, T.; Lischka, H. Phys. Chem. Chem. Phys. 2000, 2, 2067.
- Szalay, P. G.; Muller, T.; Lischka, H. Phys. Chem. Chem. Phys. 2001, 3, 2190.
- Muller, T.; Dallos, M.; Lischka, H.; Dubrovay, Z.; Szalay, P. G. Theo. Chem. Acc. 2001, 105, 227.
- Dallos, M.; Muller, T.; Lischka, H.; Shepard, R. J. Chem. Phys. 2001, 114, 746.
- Urban, M.; Noga, J.; Cole, S. J.; Bartlett, R. J. J. Chem. Phys. 1985, 83, 4041.
- Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157, 479.
- Kucharski, S. A.; Noga, J.; Bartlett, R. J. J. Chem. Phys. 1989, 90, 7282.
- Kucharski, S. A.; Bartlett, R. J. Chem. Phys. Lett. 1993, 206, 574.
- Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1998, 108, 5243.
- Meissner, L.; Bartlett, R. J. J. Chem. Phys. 2001, 115, 50.
- Löwdin, P. O. J. J. Mol. Struct. 1963, 10, 12.
- Langhoff, S. R.; Davidson, E. R. Int. J. Quantum Chem. 1974, 8, 61.
- Bartlett, R. J.; Shavitt, I. Int. J. Quantum Chem. Symp. 1977, 11, 165.
- Laidig, W. D.; Saxe, P.; Bartlett, R. J. J. Chem. Phys. 1987, 86, 887.
- Paldus, J.; Wormer, P. E. S.; Visser, F.; Vanderavoird, A. J. Chem. Phys. 1982, 76, 2458.
- Gdanitz, R. J.; Ahlrich, R. Chem. Phys. Lett. 1988, 143, 413.
- Meissner, L.; Jankowski, K.; Wasilewski, J. Int. J. Quantum Chem. 1988, 34, 535.
- Lischka, H.; Shepard, R.; Shavitt, I.; Pitzer, R. M.; Dallos, M.; Muller, Th.; Szalay, P. G.; Brown, F.B.; Ahlrichs, R.; Bohm, H. J.; Chang, A.; Comeau, D. C.; Gdanitz, R.; Dachsel, H.; Ehrhardt, C.; Ernzerhof, M.; Hochtl, P.; Irle, S.; Kedziora, G.; Kovar, T.; Parasuk, V.; Pepper, M. J. M.; Scharf, P.; Schiffer, H.; Schindler, M.; Schuler, M.; Seth, M.; Stahlberg, E. A.; Zhao, J.-G.; Yabushita, S.; Zhang, Z. COLUMBUS, an ab initio electronic structure program. release 5.8 (2001).
- Adamowicz, L.; Laidig, W. D.; Bartlett, R. J. Int. J. Quantum Chem., Supp 1984, 18, 245.
- Bartlett, R. J. Analytical evaluation of gradients in coupled-cluster and many-body per-turbation theory. In Geometrical Derivatives of Energy Surfaces and Molecular Properties; Jorgensen, P., Simons, J., Eds.; Reidel: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Salter, E. A.; Trucks, G. W.; Bartlett, R. J. J. Chem. Phys. 1989, 90, 1752.
- Stanton, J. F.; Lipscomb, W. N.; Magers, D. H.; Bartlett, R. J. J. Chem. Phys. 1989, 90, 1077.
- Watts, J. D.; Stanton, J. F.; Bartlett, R. J. Chem. Phys. Lett. 1991, 178, 471.
- Kucharski, S.; Bartlett, R. J. J. Chem. Phys. 1999, 110, 8233.
- Lee, T. J.; Allen, W. D.; Schaefer, H. F., III. J. Chem. Phys. 1987, 87, 7062.
- Li, X.; Paldus, J. J. Chem. Phys. 1999, 110, 2844.
- Alder-Golden, M.; Langhoff, S. R.; Bauschlicker, C. W.; Carney, G. D. J. Chem. Phys. 1985, 83, 255.
- Watts, J. D.; Bartlett, R. J. J. Chem. Phys. 1998, 108, 2511.
- Tobita, M.; Perera, S. A.; Nooijen, M.; Bartlett, R. J. J. Chem. Phys. In Press.
- Klauder, J. R.; Skagerstam, B. S. Coherent States: Applications to Physics and Mathematic Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Sorensen, T. E.; England, W. B. Int. J. Quantum Chem. 2000, 76, 259.
- Linderberg, J.; Ohrn, Y. Int. J. Quantum Chem. 1977, 12, 161.
- Ohrn, Y.; Linderberg, J. Int. J. Quantum Chem. 1979, 15, 343.
- Oliphant, N.; Adamowicz, L. J. Chem. Phys. 1991, 94, 1229.
- Oliphant, N.; Adamowicz, L. J. Chem. Phys. 1992, 96, 3739.
- Piecuch, P.; Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1999, 110, 6103.
- Olsen, J. J. Chem. Phys. 2000, 113, 7140.
- Kallay, M.; Surjan, P. R. J. Chem. Phys. 2001, 115, 2945.
- Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1998, 108, 9221.
©2002 by MDPI, Basel, Switzerland. Reproduction for noncommercial purposes permitted.