Implications of Isomorphism in the Family of Apatite Compounds
Abstract
1. Introduction
2. Results
2.1. Checking the Triple Way of Isomorphism in Apatites
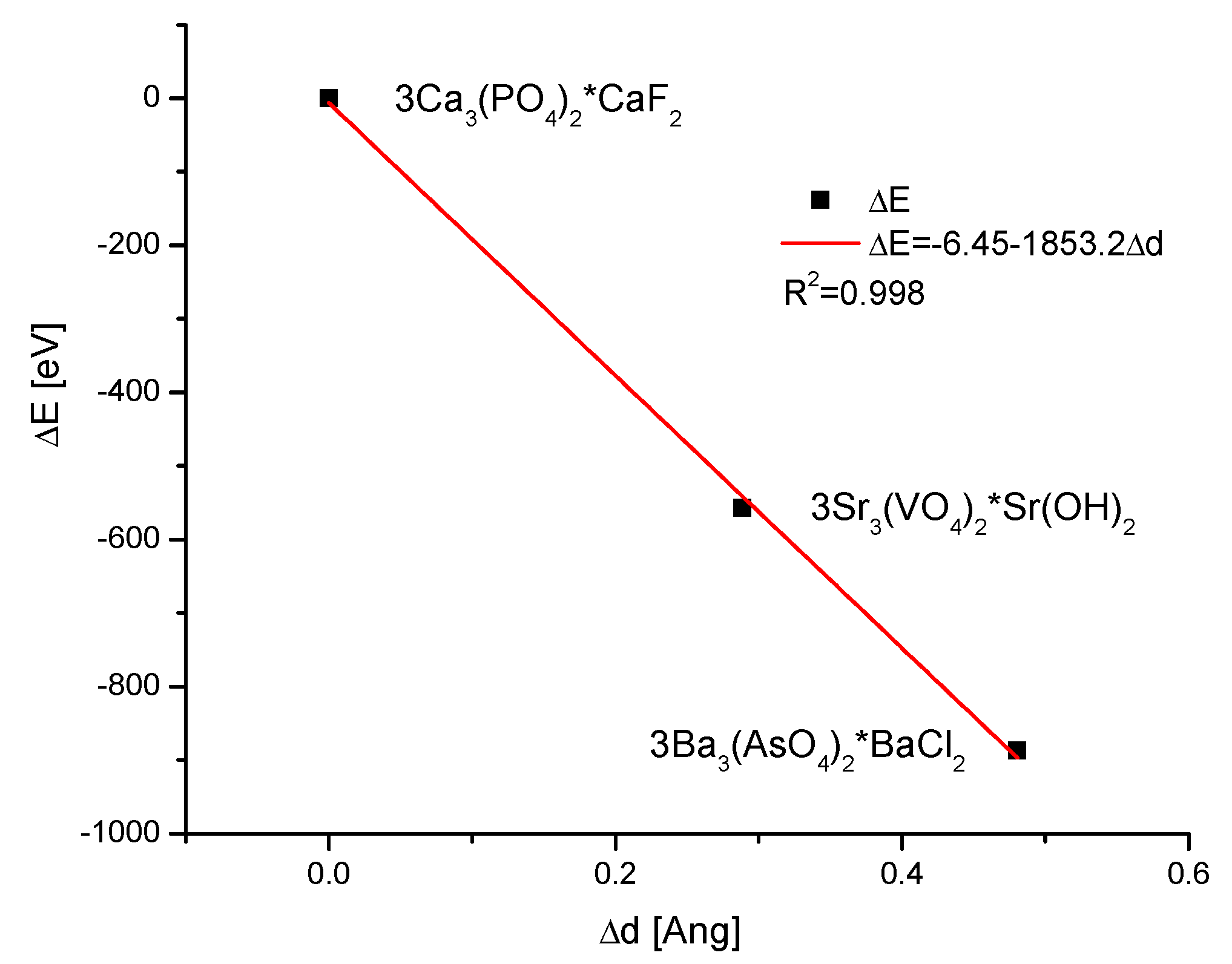
2.2. Swelling of Apatites Due to Ion Exchanges
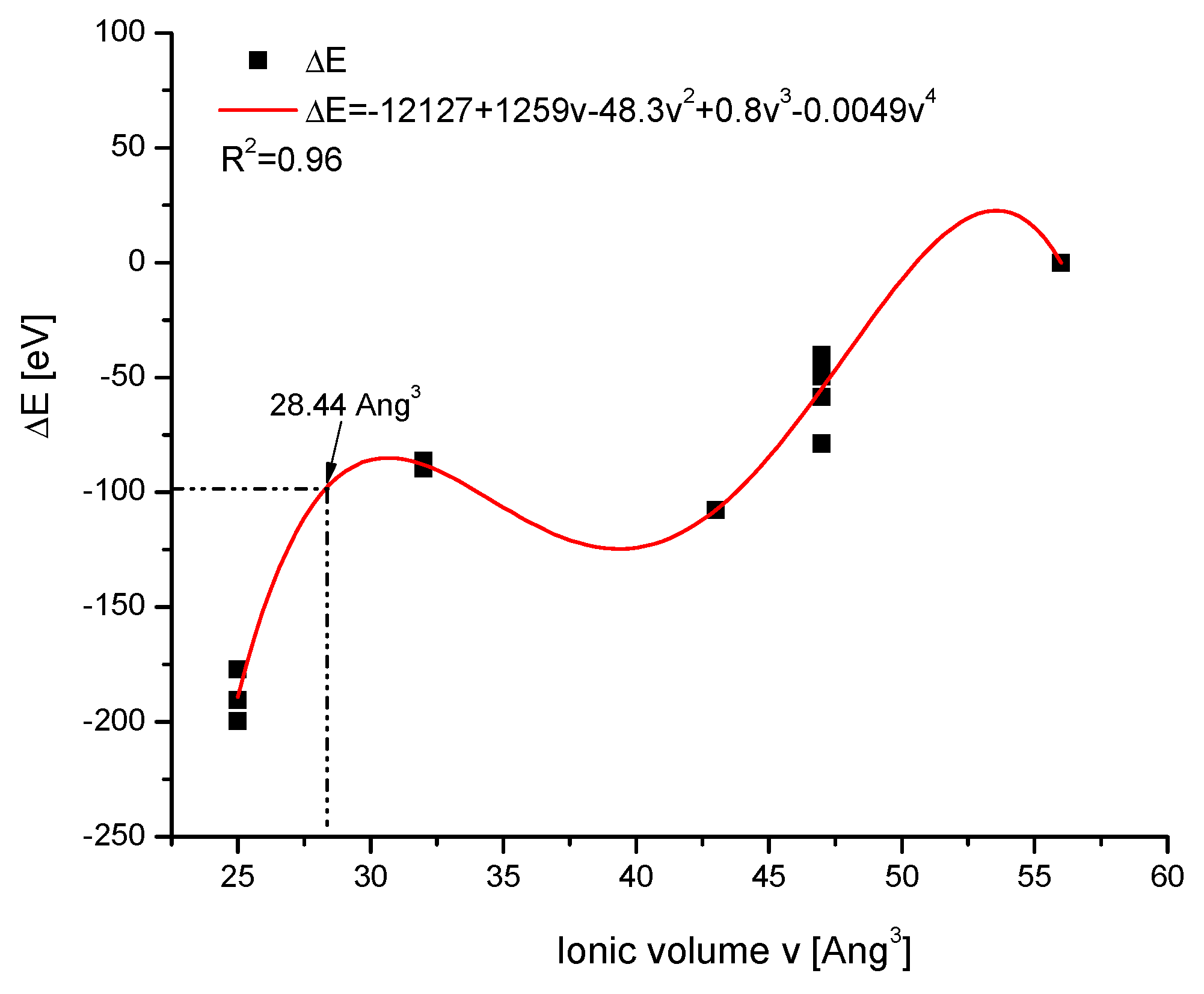
2.3. Vacancies
- whether or not the apatites with the proven presence of vacancies belong to relevant isomorphic series;
- whether there is a possibility of finding the volume of the vacancy-ion agglomerate;
- whether the vacancy influences the behaviour of the rest of the apatite molecule.
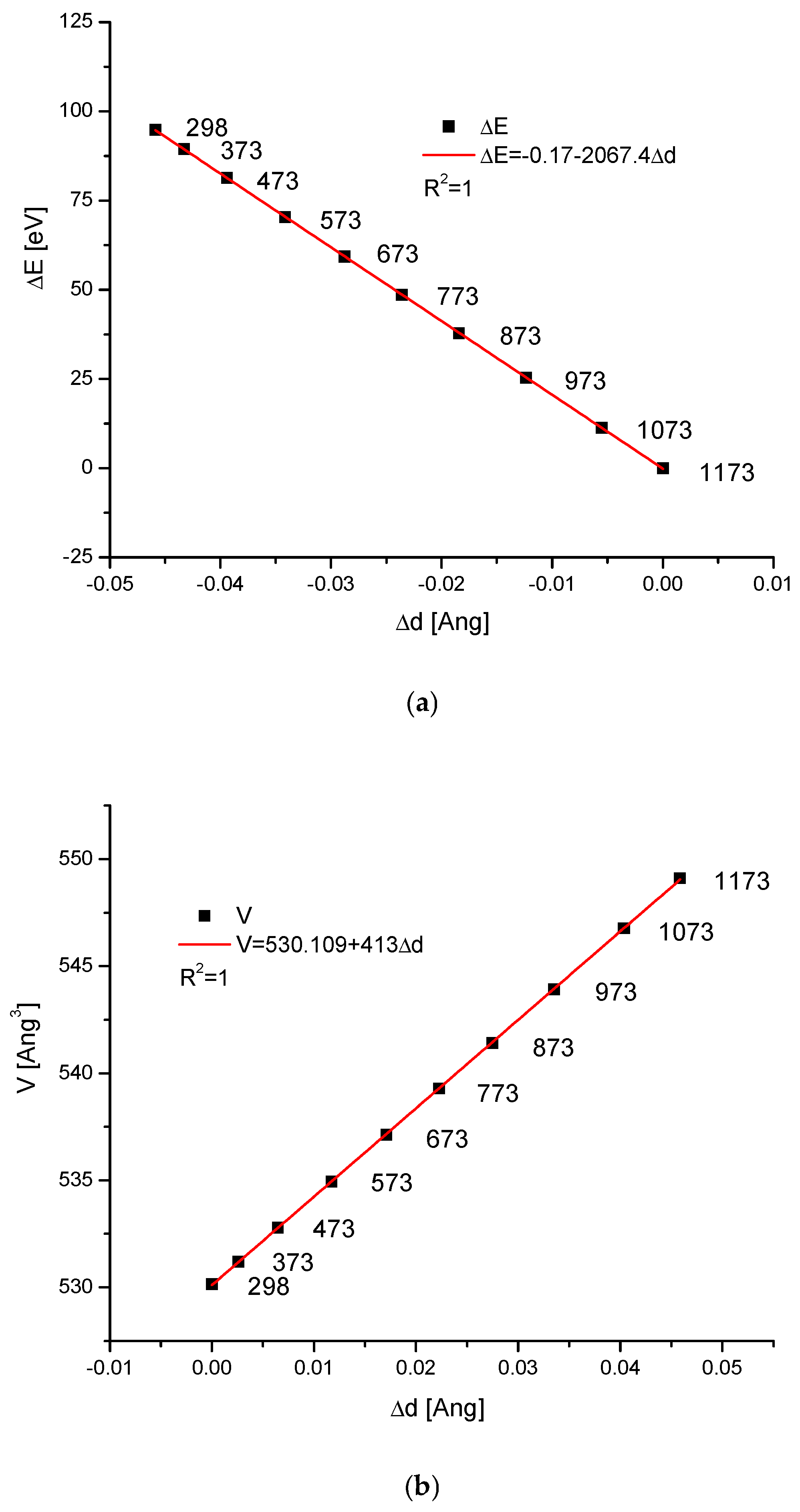
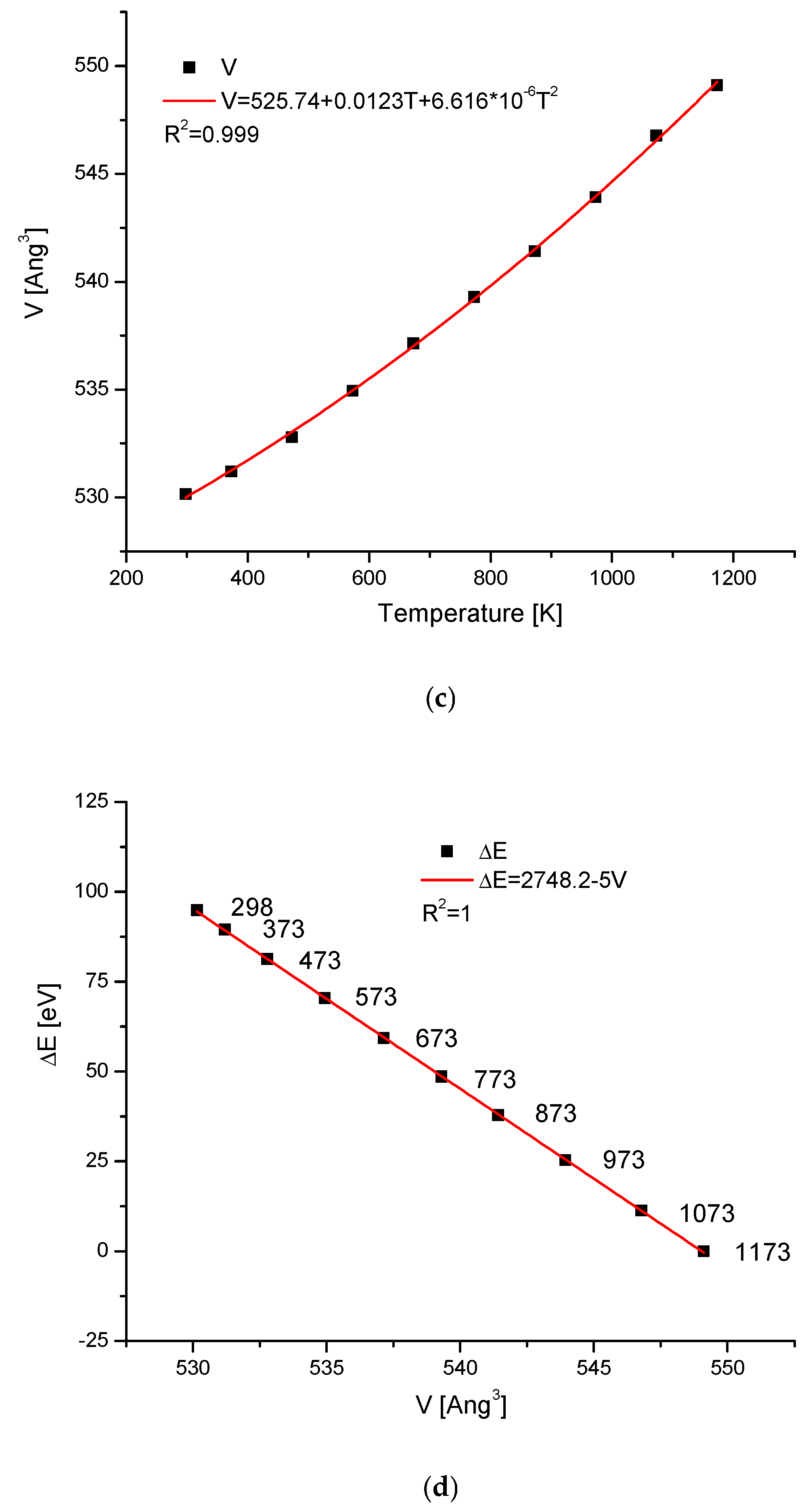
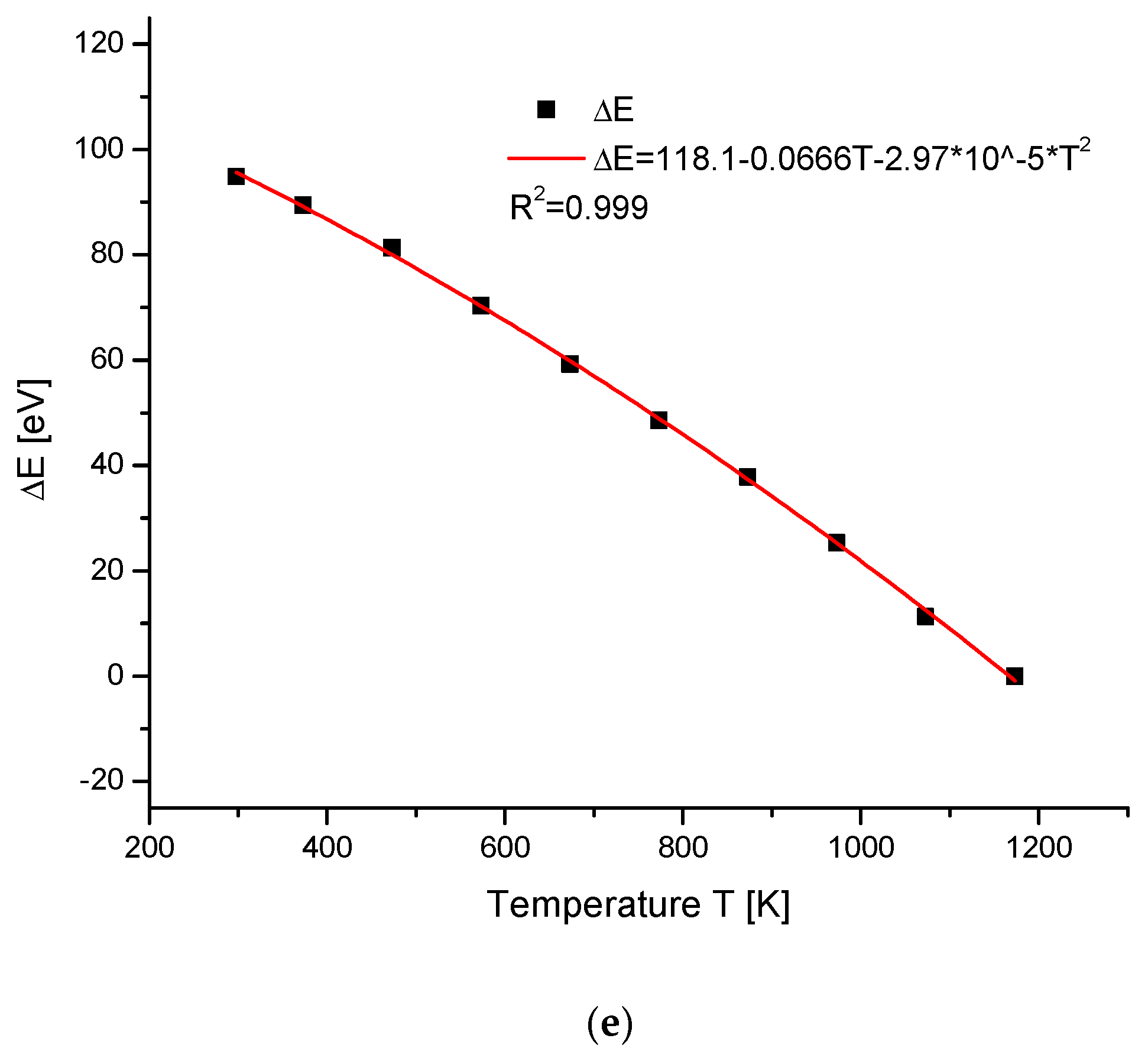
2.4. Temperature Changes of Hydroxyapatite Cells
3. Discussion
Future Directions
- Is it possible to expand our method on other substances forming the series in other crystallographic systems, as e.g., the calcite series?
- Is it possible to split the somewhat strange results from Figure 9b on more detailed components?
4. Materials and Methods
4.1. Materials
4.2. Methods
- E, ΔE—energy and the change of energy;
- d, Δd—Braggs’ crystallographic dimension and its change;
- Θ—the angle between the wave vector and the crystallographic plane.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hughes, J.M.; Nekvasil, H.; Ustunisik, G.; Lindsley, D.H.; Coraor, A.E.; Vaughn, J.; Phillips, B.L.; McCubbin, F.M.; Woerner, W.R. Solid solution in the fluorapatite-chlorapatite binary system: High-precision crystal structure refinements of synthetic F-Cl apatite. Am. Miner. 2014, 99, 369–376. [Google Scholar] [CrossRef]
- Ptáček, P. Apatites and Their Synthetic Analogues—Synthesis, Structure, Properties and Applications; InTech: Rijeka, Croatia, 2016; ISBN 978-953-51-2265-4. [Google Scholar]
- Shepherd, J.H.; Shepherd, D.V.; Best, S.M. Substituted hydroxyapatites for bone repair. J. Mater. Sci. Mater. Med. 2012, 23, 2335–2347. [Google Scholar] [CrossRef] [PubMed]
- Ratnayake, J.T.B.; Mucalo, M.; Dias, G.J. Substituted hydroxyapatites for bone regeneration: A review of current trends. J. Biomed. Mater. Res. Part B Appl. Biomater. 2017, 105, 1285–1299. [Google Scholar] [CrossRef] [PubMed]
- White, T.J.; ZhiLi, D. Structural derivation and crystal chemistry of apatites. Acta Crystallogr. Sect. B Struct. Sci. 2003, 59, 1–16. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die Gesetze der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Sato, T.; Takagi, S.; Deledda, S.; Hauback, B.C.; Orimo, S. Extending the applicability of the Goldschmidt tolerance factor to arbitrary ionic compounds. Sci. Rep. 2016, 6, 23592. [Google Scholar] [CrossRef]
- White, T.; Ferraris, C.; Kim, J.; Srinivasan, M. Apatite—An Adaptive Framework Structure. Rev. Miner. Geochem. 2005, 57, 307–401. [Google Scholar] [CrossRef]
- Ruby, M.V.; Davis, A.; Nicholson, A. In Situ Formation of Lead Phosphates in Soils as a Method to Immobilize Lead. Environ. Sci. Technol. 1994, 28, 646–654. [Google Scholar] [CrossRef]
- Luo, Y.; Hughes, J.M.; Rakovan, J.; Pan, Y. Site preference of U and Th in Cl, F, and Sr apatites. Am. Miner. 2009, 94, 345–351. [Google Scholar] [CrossRef]
- Ciosek, Ż.; Kot, K.; Kosik-Bogacka, D.; Łanocha-Arendarczyk, N.; Rotter, I. The Effects of Calcium, Magnesium, Phosphorus, Fluoride, and Lead on Bone Tissue. Biomolecules 2021, 11, 506. [Google Scholar] [CrossRef]
- Cacciotti, I. Cationic and Anionic Substitutions in Hydroxyapatite. In Handbook of Bioceramics and Biocomposites; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–68. [Google Scholar]
- Castiglioni, S.; Cazzaniga, A.; Albisetti, W.; Maier, J. Magnesium and Osteoporosis: Current State of Knowledge and Future Research Directions. Nutrients 2013, 5, 3022–3033. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Tamilselvan, A. Lattice energy and mechanical stiffness of hydroxyapatite. J. Mater. Sci. Mater. Med. 2007, 18, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Skalny, A.V.; Aschner, M.; Silina, E.V.; Stupin, V.A.; Zaitsev, O.N.; Sotnikova, T.I.; Tazina, S.I.; Zhang, F.; Guo, X.; Tinkov, A.A. The Role of Trace Elements and Minerals in Osteoporosis: A Review of Epidemiological and Laboratory Findings. Biomolecules 2023, 13, 1006. [Google Scholar] [CrossRef]
- Li, Z.Y.; Lam, W.M.; Yang, C.; Xu, B.; Ni, G.X.; Abbah, S.A.; Cheung, K.M.C.; Luk, K.D.K.; Lu, W.W. Chemical composition, crystal size and lattice structural changes after incorporation of strontium into biomimetic apatite. Biomaterials 2007, 28, 1452–1460. [Google Scholar] [CrossRef]
- Lasota, A.; Gorzelak, M.; Turżańska, K.; Kłapeć, W.; Jarzębski, M.; Blicharski, T.; Pawlicz, J.; Wieruszewski, M.; Jabłoński, M.; Kuczumow, A. The Ways of Forming and the Erosion/Decay/Aging of Bioapatites in the Context of the Reversibility of Apatites. Int. J. Mol. Sci. 2024, 25, 11297. [Google Scholar] [CrossRef]
- Leventouri, T.; Antonakos, A.; Kyriacou, A.; Venturelli, R.; Liarokapis, E.; Perdikatsis, V. Crystal Structure Studies of Human Dental Apatite as a Function of Age. Int. J. Biomater. 2009, 2009, 698547. [Google Scholar] [CrossRef]
- Kuczumow, A.; Gorzelak, M.; Kosiński, J.; Lasota, A.; Szabelska, A.; Blicharski, T.; Gągała, J.; Wawrzyniak, J.; Jarzębski, M.; Jabłoński, M. Quantitative Description of Isomorphism in the Series of Simple Compounds. Int. J. Mol. Sci. 2023, 24, 11324. [Google Scholar] [CrossRef]
- Patel, P.N. Mangnesium calcium hydroxylapatite solid solutions. J. Inorg. Nucl. Chem. 1980, 42, 1129–1132. [Google Scholar] [CrossRef]
- O’Donnell, M.D.; Fredholm, Y.; de Rouffignac, A.; Hill, R.G. Structural analysis of a series of strontium-substituted apatites. Acta Biomater. 2008, 4, 1455–1464. [Google Scholar] [CrossRef]
- Bigi, A.; Foresti, E.; Marchetti, F.; Ripamonti, A.; Roveri, N. Barium calcium hydroxyapatite solid solutions. J. Chem. Soc. Dalton Trans. 1984, 6, 1091–1093. [Google Scholar] [CrossRef]
- Bigi, A.; Gandolfi, M.; Gazzano, M.; Ripamonti, A.; Roveri, N.; Thomas, S.A. Structural modifications of hydroxyapatite induced by lead substitution for calcium. J. Chem. Soc. Dalton Trans. 1991, 11, 2883–2886. [Google Scholar] [CrossRef]
- Bigi, A.; Boanini, E.; Gazzano, M. Ion substitution in biological and synthetic apatites. In Biomineralization and Biomaterials; Elsevier: Amsterdam, The Netherlands, 2016; pp. 235–266. [Google Scholar]
- Bigi, A.; Gazzano, M.; Ripamonti, A.; Foresti, E.; Roveri, N. Thermal stability of cadmium–calcium hydroxyapatite solid solutions. J. Chem. Soc. Dalton Trans. 1986, 2, 241–244. [Google Scholar] [CrossRef]
- Bauer Boechat, C.; Eon, J.-G.; Malta Rossi, A.; Andre’ de Castro Perez, C.; Aguiar da Silva San Gil, R. Structure of vanadate in calcium phosphate and vanadate apatite solid solutions. Phys. Chem. Chem. Phys. 2000, 2, 4225–4230. [Google Scholar] [CrossRef]
- Lee, Y.J.; Stephens, P.W.; Tang, Y.; Li, W.; Phillips, B.L.; Parise, J.B.; Reeder, R.J. Arsenate substitution in hydroxylapatite: Structural characterization of the Ca5(PxAs1−xO4)3OH solid solution. Am. Miner. 2009, 94, 666–675. [Google Scholar] [CrossRef]
- Wilhelmi, K.-A.; Jonsson, O.; Karvonen, P.; Kjær, A.; Shapiro, R.H.; Westerdahl, A. X-Ray Studies on Some Alkali and Alkaline-Earth Chromates(V). Acta Chem. Scand. 1965, 19, 177–184. [Google Scholar] [CrossRef]
- Kim, J.Y.; Fenton, R.R.; Hunter, B.A.; Kennedy, B.J. Powder diffraction studies of synthetic calcium and lead apatites. Aust. J. Chem. 2000, 53, 679. [Google Scholar] [CrossRef]
- Elliott, J.C.; Dykes, E.; Mackie, P.E. Structure of bromapatite and the radius of the bromide ion. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1981, 37, 435–438. [Google Scholar] [CrossRef]
- Elliott, J.C. Structure and Chemistry of the Apatites and Other Calcium Orthophosphates, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 1994; ISBN 9780444815828. [Google Scholar]
- Suitch, P.R.; Taitai, A.; Lacout, J.L.; Young, R.A. Structural consequences of the coupled substitution of Eu,S in calcium sulfoapatite. J. Solid State Chem. 1986, 63, 267–277. [Google Scholar] [CrossRef]
- Henning, P.A.; Adolfsson, E.; Grins, J. The chalcogenide phosphate apatites Ca10(PO4)6S, Sr10(PO4)6S, Ba10(PO4)6S and Ca10(PO4)6Se. Z. Krist. Cryst. Mater. 2000, 215, 226–230. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Jenkins, H.D.B.; Roobottom, H.K.; Passmore, J.; Glasser, L. Relationships among Ionic Lattice Energies, Molecular (Formula Unit) Volumes, and Thermochemical Radii. Inorg. Chem. 1999, 38, 3609–3620. [Google Scholar] [CrossRef] [PubMed]
- Roobottom, H.K.; Jenkins, H.D.B.; Passmore, J.; Glasser, L. Thermochemical Radii of Complex Ions. J. Chem. Educ. 1999, 76, 1570. [Google Scholar] [CrossRef]
- Jenkins, H.D.B.; Thakur, K.P. Reappraisal of thermochemical radii for complex ions. J. Chem. Educ. 1979, 56, 576. [Google Scholar] [CrossRef]
- Glasser, L.; Jenkins, H.D.B. Internally Consistent Ion Volumes and Their Application in Volume-Based Thermodynamics. Inorg. Chem. 2008, 47, 6195–6202. [Google Scholar] [CrossRef]
- Chickerur, N.S.; Tung, M.S.; Brown, W.E. A mechanism for incorporation of carbonate into apatite. Calcif. Tissue Int. 1980, 32, 55–62. [Google Scholar] [CrossRef]
- Engel, G.; Pretzsch, J.; Gramlich, V.; Baur, W.H. The crystal structure of hydrothermally grown manganese chlorapatite, Mn5(PO4)3Cl0.9(OH)0.1. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1975, 31, 1854–1860. [Google Scholar] [CrossRef]
- Wondratschek, H. Untersuchungen zur kristallchemie der blei-apatite (pyromorphite). N. Jahrb. Miner. Abh. 1963, 99, 113–160. [Google Scholar]
- Trombe, J.-C.; Montel, G. Sur les conditions de preparation d’une nouvelle apatite contenant des ions sulfure. Compt. Rend. Acad. Sci. 1975, 280, 567–570. [Google Scholar]
- Hata, M.; Marumo, F.; Iwai, S.-I.; Aoki, H. Structure of a lead apatite Pb9(PO4)6. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1980, 36, 2128–2130. [Google Scholar] [CrossRef]
- Brückner, S.; Lusvardi, G.; Menabue, L.; Saladini, M. Crystal structure of lead hydroxyapatite from powder X-ray diffraction data. Inorganica Chim. Acta 1995, 236, 209–212. [Google Scholar] [CrossRef]
- Dai, Y.; Hughes, J.M. Crystal-structure refinements of Vanidinite and Pyromorphite. Can. Miner. 1989, 27, 189–192. [Google Scholar]
- Hendricks, S.B.; Jefferson, M.E.; Mosley, V.M. The Crystal Structures of some Natural and Synthetic Apatite-Like Substances. Z. Krist. Cryst. Mater. 1932, 81, 352–369. [Google Scholar] [CrossRef]
- Hashimoto, H.; Matsumoto, T. Structure refinements of two natural pyromorphites, Pb5(PO4)3Cl, and crystal chemistry of chlorapatite group, M5(PO4)3Cl. Z. Krist. Cryst. Mater. 1998, 213, 585–590. [Google Scholar] [CrossRef]
- Akao, A.; Aoki, H.; Innami, Y.; Minamikata, S.; Yamada, T. Flux Growth and Crystal Structure of Pyromorphite; Tokyo Ika Shika Daigaku Iyo Kizai Kenkyujo Hokoku: Tokyo, Japan, 1989; Volume 23, pp. 25–29. [Google Scholar]
- Grisafe, D.A.; Hummel, F.A. Pentavalent ion substitutions in the apatite structure part A. Crystal chemistry. J. Solid State Chem. 1970, 2, 160–166. [Google Scholar] [CrossRef]
- Belokoneva, E.; Troneva, E.; Dem’yanets, L.; Duderov, N.; Belov, N. Crystal structure of synthetic fluoropyromorphite Pb5(PO4)3F. Sov. Phys. Crystallogr. 1982, 27, 476–477. [Google Scholar]
- Goldenberg, J.E.; Wilt, Z.; Schermerhorn, D.V.; Pasteris, J.D.; Yoder, C.H. Structural effects on incorporated water in carbonated apatites. Am. Miner. 2015, 100, 274–280. [Google Scholar] [CrossRef]
- Knyazev, A.V.; Chernorukov, N.G.; Bulanov, E.N. Apatite-structured compounds: Synthesis and high-temperature investigation. Mater. Chem. Phys. 2012, 132, 773–781. [Google Scholar] [CrossRef]
- Kuczumow, A.; Blicharski, T.; Gorzelak, M.; Kosiński, J.; Lasota, A.; Gągała, J.; Nowak, J.; Jarzębski, M.; Jabłoński, M. Measurements of Energetic States Resulting from Ion Exchanges in the Isomorphic Crystals of Apatites and Bioapatites. Molecules 2022, 27, 8913. [Google Scholar] [CrossRef]
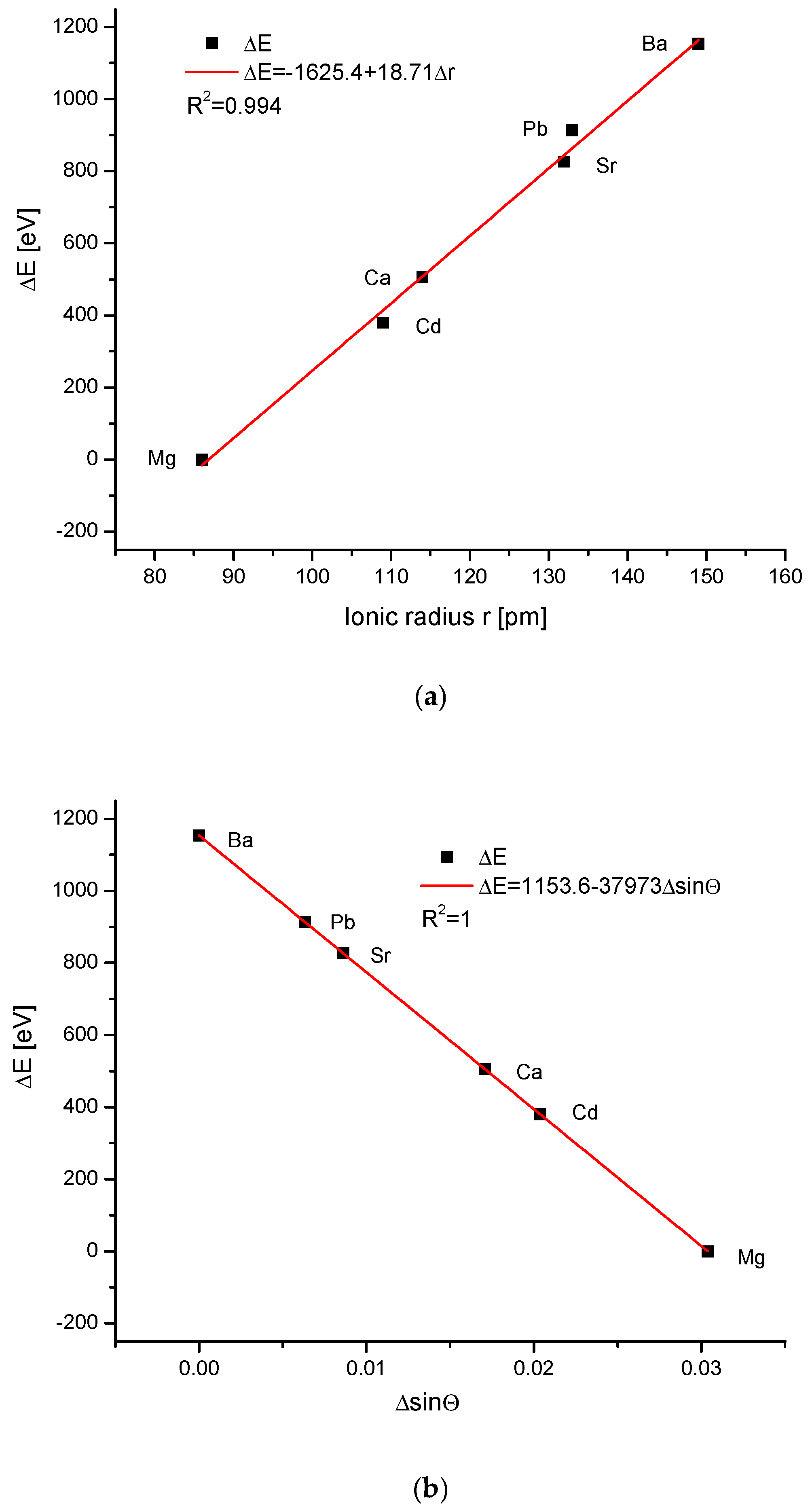
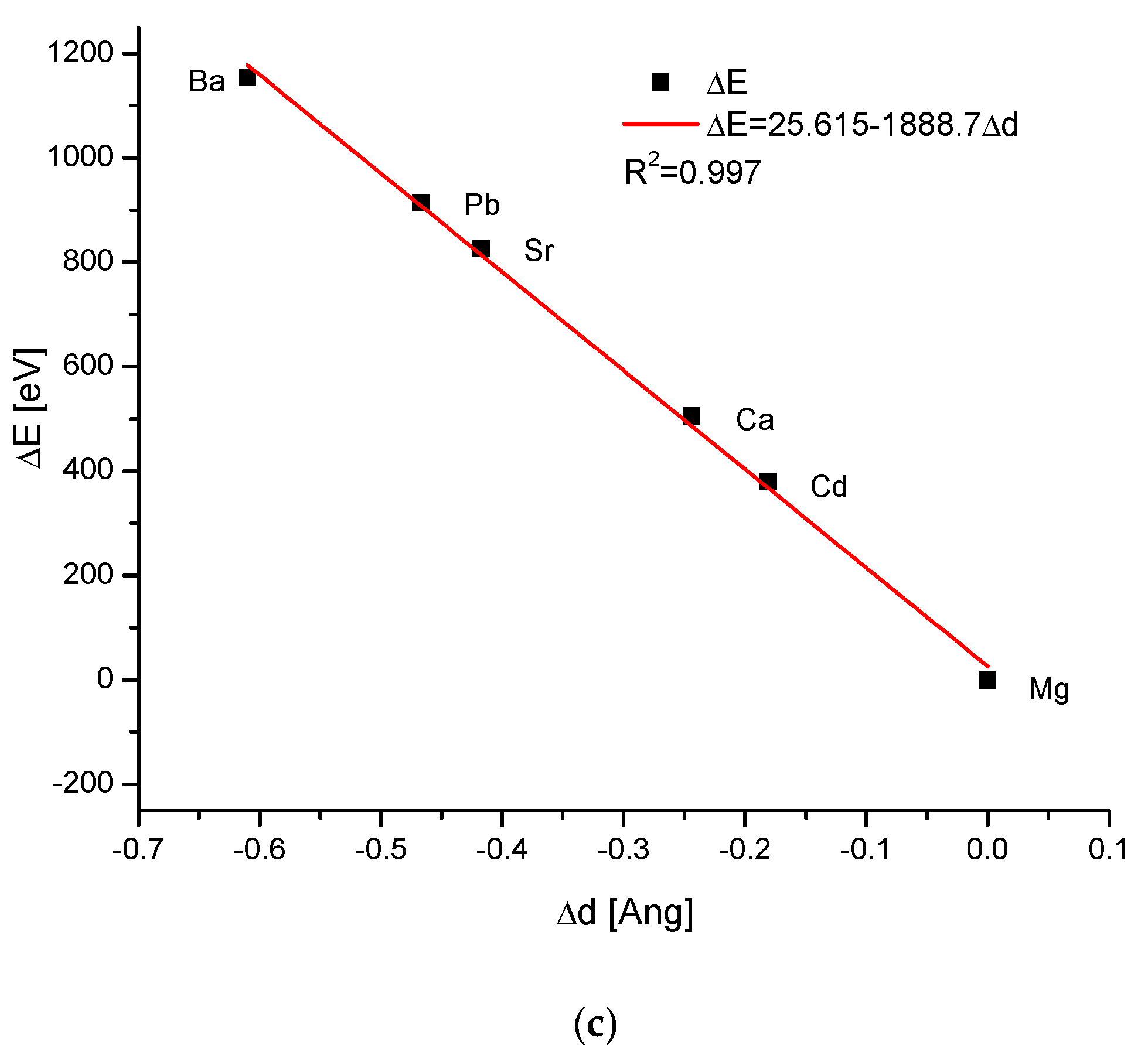
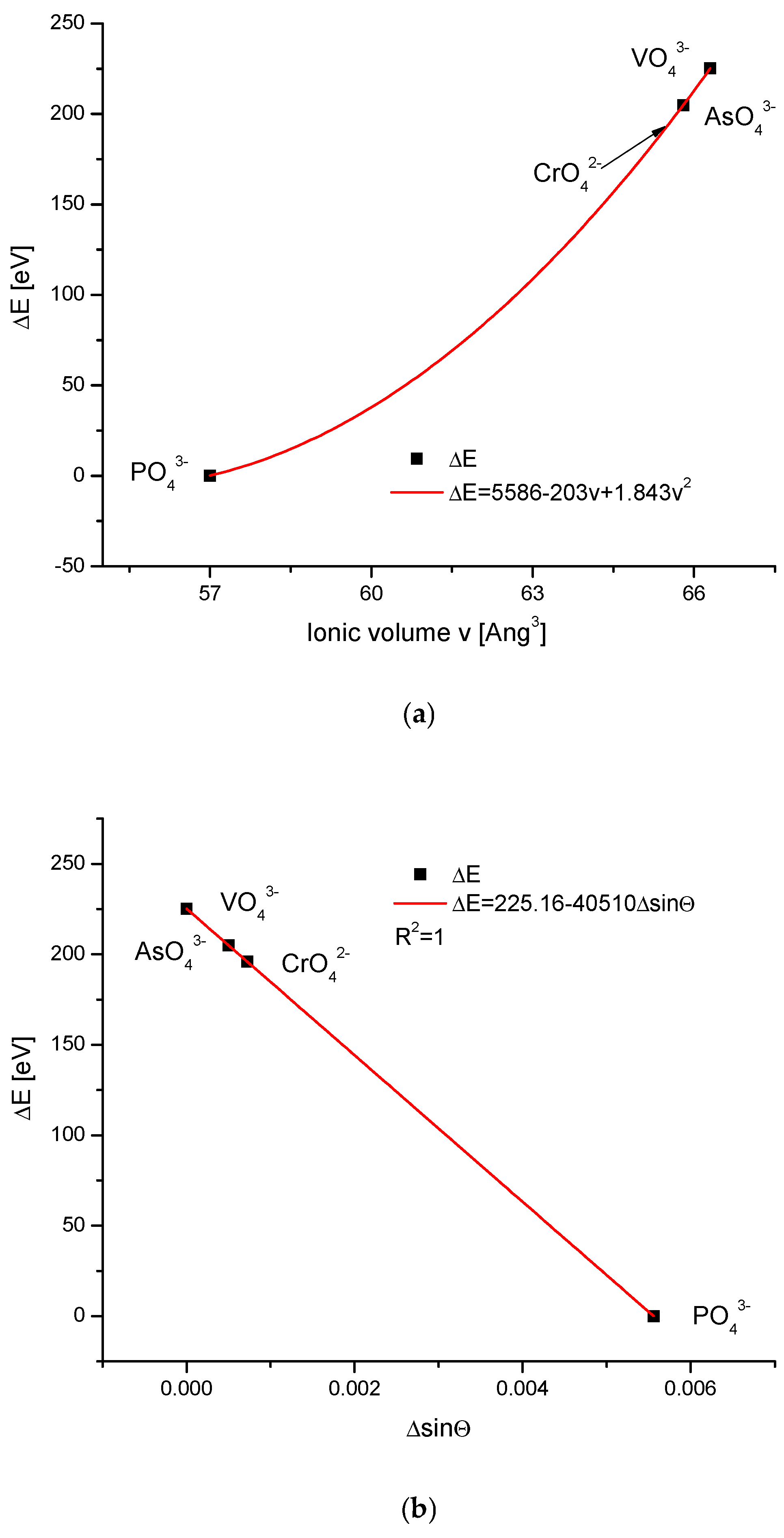
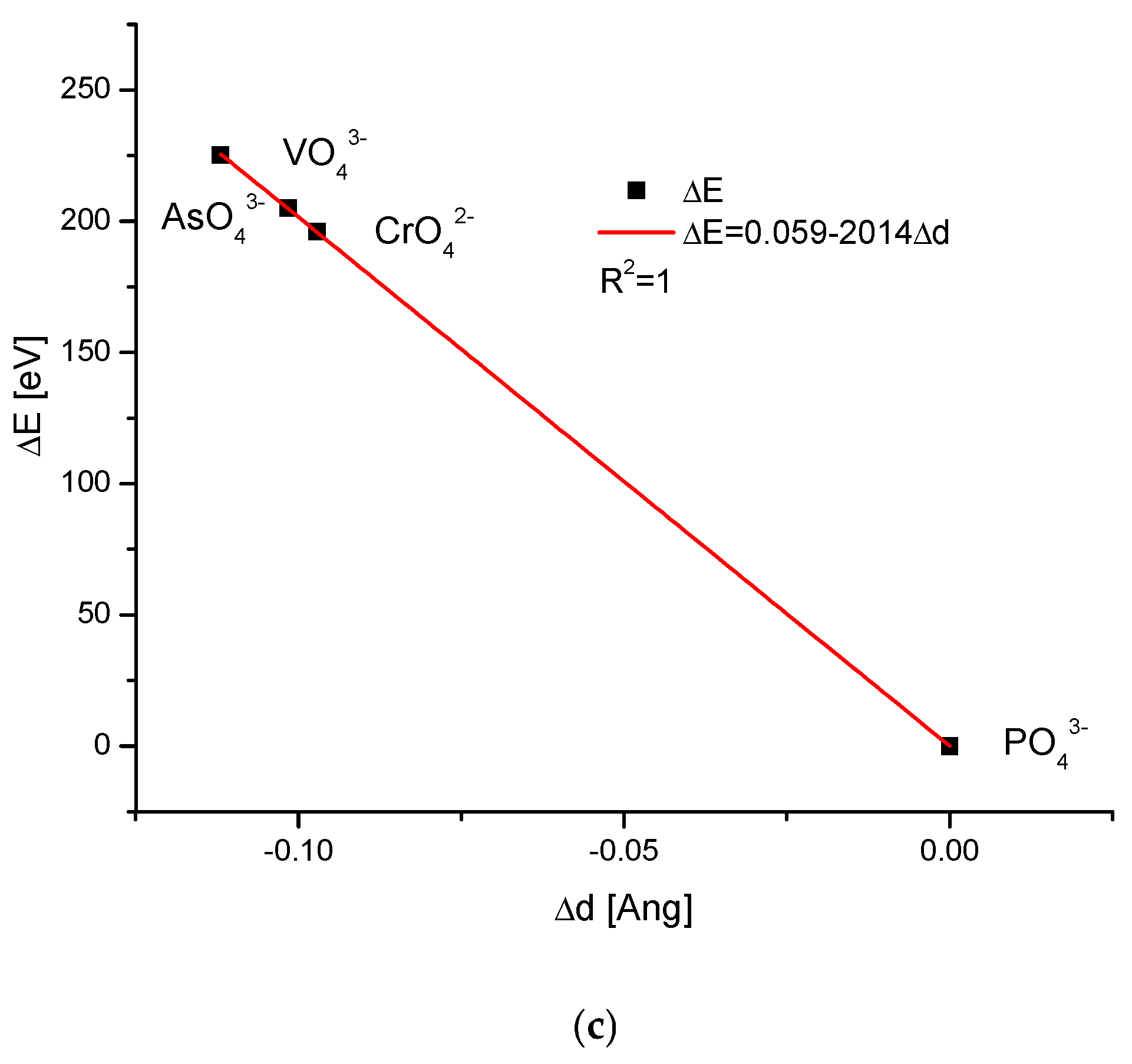
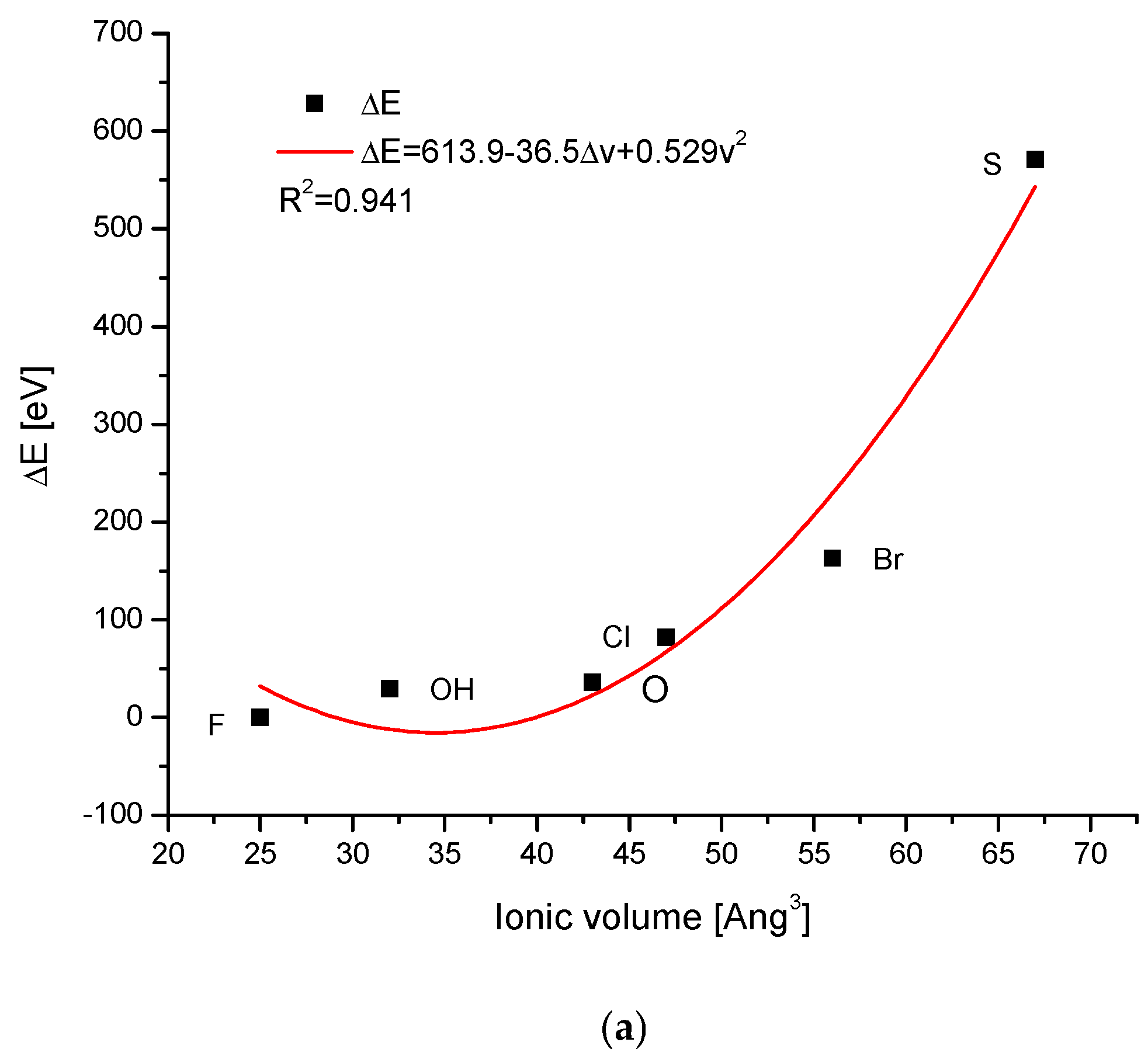
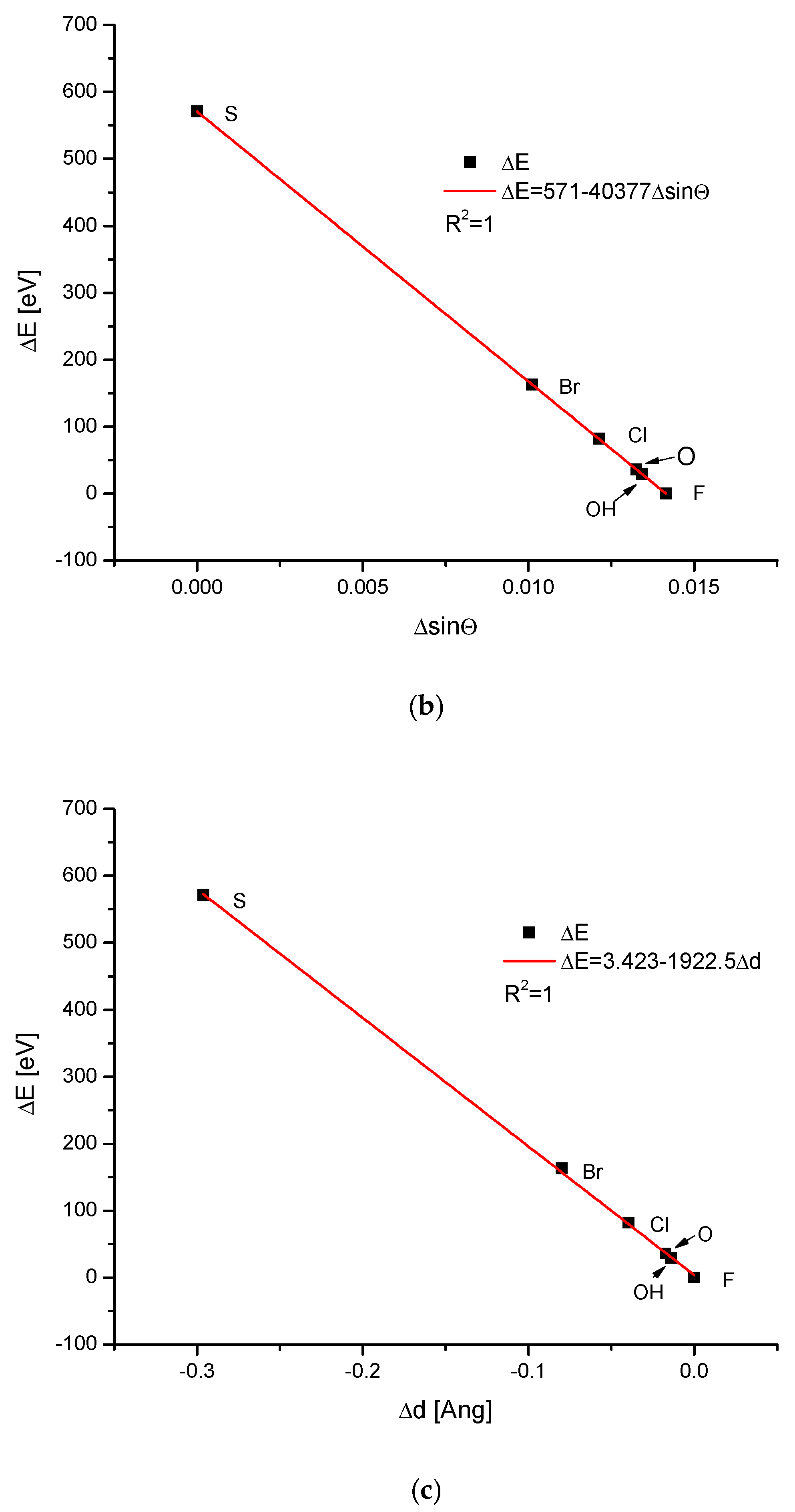

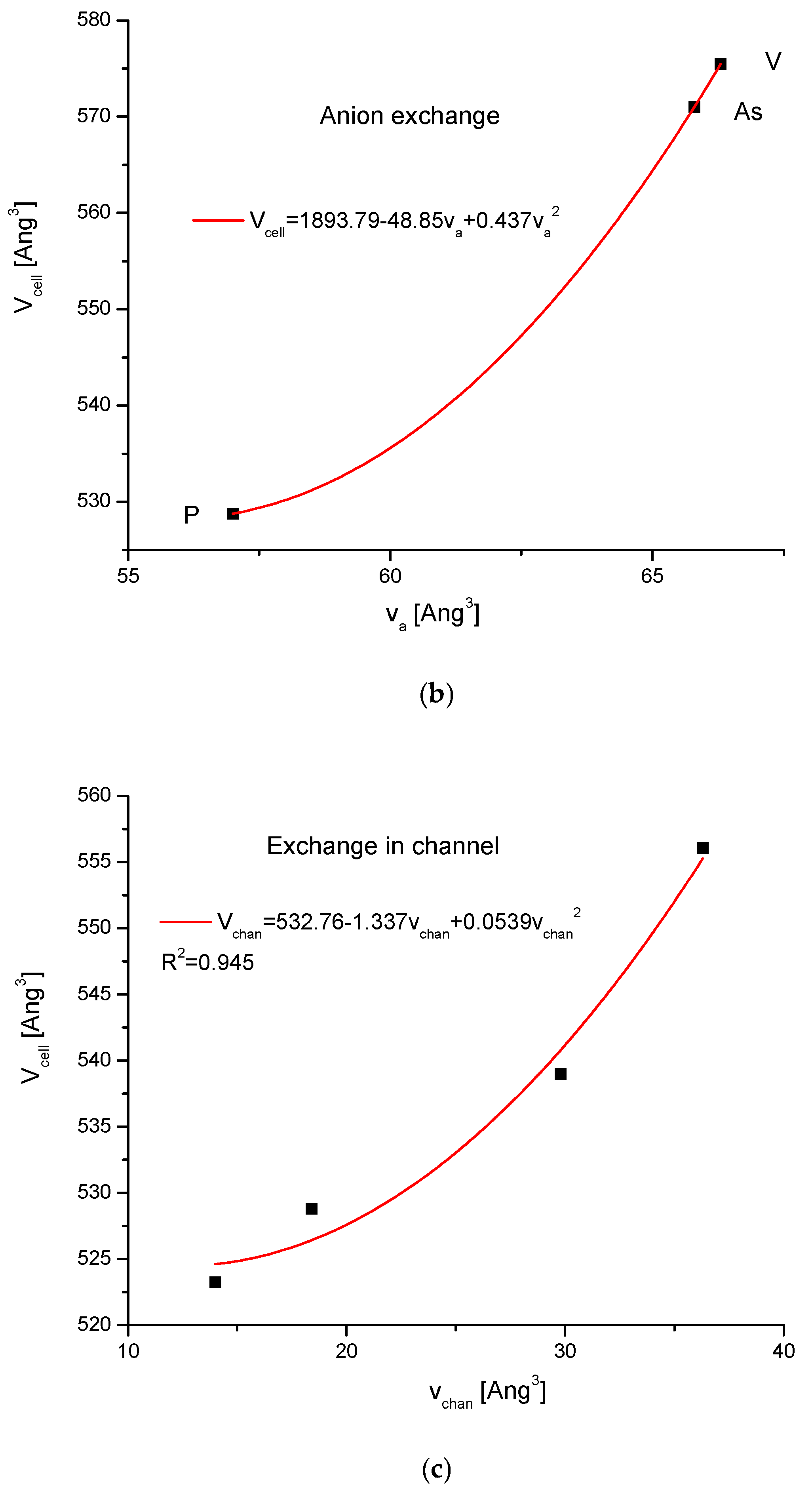

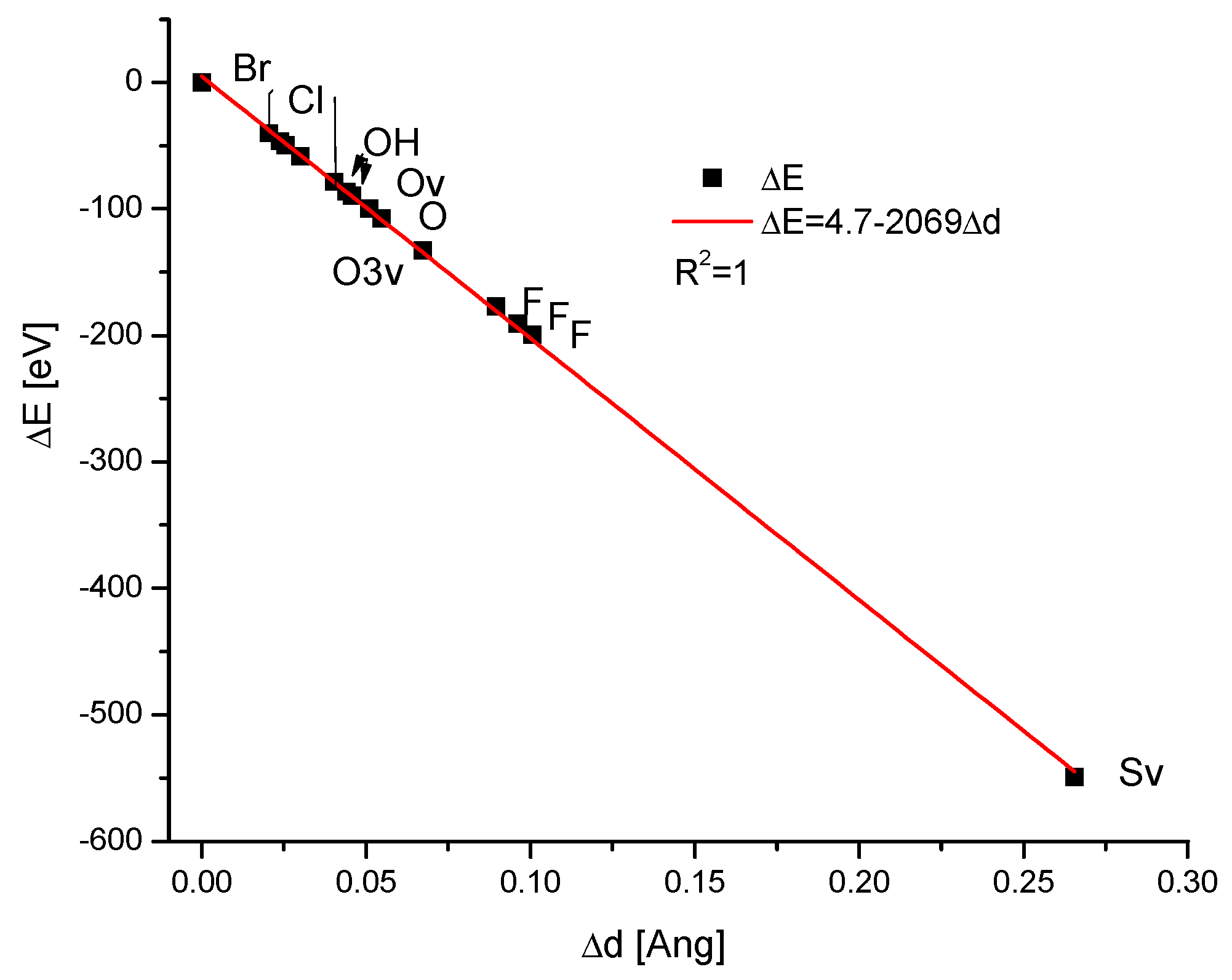

| Kind of Ion Exchange | Formula | a (Å) | c (Å) | a/c | Ionic Radii (pm)/Volumes (Å3) | References |
|---|---|---|---|---|---|---|
| Cationic | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 1.368 | 114 | ICDD 09-0432 |
| Mg10(PO4)6(OH)2 | 8.722 | 6.624 | 1.317 | 86 | [20] | |
| Sr10(PO4)6(OH)2 | 9.777 | 7.288 | 1.342 | 132 | [21] | |
| Ba10(PO4)6(OH)2 | 10.1901 | 7.7212 | 1.320 | 149 | [22] | |
| Pb10(PO4)6(OH)2 | 9.8663 | 7.4262 | 1.329 | 133 | [23,24] | |
| Cd10(PO4)6(OH)2 | 9.3352 | 6.6643 | 1.401 | 109 | [25] | |
| Anionic | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 1.368 | 90 | ICDD 09-0432 |
| Ca10(VO4)6(OH)2 | 9.7405 | 7.0041 | 1.391 | 83 | [26] | |
| Ca10(AsO4)6(OH)2 | 9.7156 | 6.9857 | 1.391 | 88 | [27] | |
| Ca10(CrO4)6(OH)2 | 9.683 | 7.010 | 1.381 | 97 | [28] | |
| Anionic in the channel | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 1.368 | 32 | ICDD 09-0432 |
| Ca10(PO4)6F2 | 9.3684 | 6.8841 | 1.361 | 25 | ICDD 15-0876 | |
| Ca10(PO4)6Cl2 | 9.5903 | 6.7666 | 1.417 | 47 | [29] | |
| Ca10(PO4)6Br2 | 9.7611 | 6.7391 | 1.448 | 56 | [30] | |
| Ca10(PO4)6O | 9.432 | 6.881 | 1.371 | 43 | [31] | |
| Ca10(PO4)6S | 9.455 | 8.84 | 1.070 | 67 | [32] | |
| Ca10(PO4)6Se | 9.5007 | 6.8406 | 1.339 | 181 | [33] |
| Kind of Ion Exchange | Formula | a (Å) | c (Å) | Cell Volume V (Å3) | Ionic Volumes V (Å3) | References |
|---|---|---|---|---|---|---|
| Cationic | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 528.8 | 20.1 | ICDD 09-0432 |
| Mg10(PO4)6(OH)2 | 8.722 | 6.624 | 436.4 | 4.9 | [34] | |
| Sr10(PO4)6(OH)2 | 9.777 | 7.288 | 603.3 | 21.3 | [30] | |
| Ba10(PO4)6(OH)2 | 10.1901 | 7.7212 | 694.3 | 27 | [31] | |
| Anionic | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 528.8 | 57 | ICDD 09-0432 |
| Ca10(VO4)6(OH)2 | 9.7405 | 7.0041 | 575.5 | 66.3 | [29] | |
| Ca10(AsO4)6(OH)2 | 9.7156 | 6.9857 | 523.2 | 65.8 | [28] | |
| Anionic in the channel | Ca10(PO4)6(OH)2 | 9.418 | 6.884 | 528.8 | 18.4 | ICDD 09-0432 |
| Ca10(PO4)6F2 | 9.3684 | 6.8841 | 523.2 | 14 | ICDD 15-0876 | |
| Ca10(PO4)6Cl2 | 9.5903 | 6.7666 | 539.0 | 29.8 | [30] | |
| Ca10(PO4)6Br2 | 9.761 | 6.739 | 556.1 | 36.3 | [30] |
| Kind of Ion Exchange | Formula | a (Å) | c (Å) | Ionic Radii (pm) /Volumes (Å3) | References |
|---|---|---|---|---|---|
| Channel exchanges | Pb10(PO4)6O | 9.826 | 7.431 | 43 | [41] |
| Pb10(PO4)6O□ | 9.84 | 7.43 | [42] | ||
| Pb10(PO4)6S□ | 9.45 | 6.84 | [43] | ||
| Pb9□(PO4)6O□2 | 9.826 | 7.357 | [44] | ||
| Pb10(PO4)6OH2 | 9.866 | 7.426 | 32 | [45] | |
| Pb3(PO4)2 | 9.826 | 7.357 | [44] | ||
| Pb10(PO4)6((OH)2 | 9.8612 | 7.4242 | 32 | [30] | |
| Pb10(PO4)6Br2 | 10.0618 | 7.3592 | 56 | [30] | |
| Pb10(PO4)6Cl2 | 9.9767 | 7.3255 | 47 | [30] | |
| Pb10(PO4)6Cl2 | 9.9764 | 7.3511 | 47 | [46] | |
| Pb10(PO4)6Cl2 | 9.95 | 7.31 | 47 | [47] | |
| Pb10(PO4)6Cl2 | 9.993 | 7.334 | 47 | [48] | |
| Pb10(PO4)6Cl2 | 9.9981 | 7.344 | 47 | [49] | |
| Pb10(PO4)6F2 | 9.7547 | 7.2832 | 25 | [30] | |
| Pb10(PO4)6F2 | 9.777 | 7.310 | 25 | [50] | |
| Pb10(PO4)6F2 | 9.760 | 7.300 | 25 | [51] |
| Compound | Temperature (K) | a (Å) | c (Å) | V (Å3) | References |
|---|---|---|---|---|---|
| Ca10(PO4)6(OH)2 | 298 | 9.4273 | 6.8882 | 530.2 | [53] |
| 373 | 9.4354 | 6.89 | 531.2 | ||
| 473 | 9.444 | 6.898 | 532.7 | ||
| 573 | 9.4589 | 6.904 | 535 | ||
| 673 | 9.4727 | 6.9122 | 537.15 | ||
| 773 | 9.4833 | 6.9245 | 539.3 | ||
| 873 | 9.4986 | 6.9294 | 541.43 | ||
| 973 | 9.514 | 6.939 | 544 | ||
| 1073 | 9.53 | 6.952 | 546.8 | ||
| 1173 | 9.54 | 6.967 | 549.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lasota, A.; Gorzelak, M.; Bis, E.; Biliński, P.; Gieburowski, K.; Kłapeć, W.; Tymczyna-Borowicz, B.; Łobacz, M.; Pawlicz, J.; Jarzębski, M.; et al. Implications of Isomorphism in the Family of Apatite Compounds. Int. J. Mol. Sci. 2025, 26, 4397. https://doi.org/10.3390/ijms26094397
Lasota A, Gorzelak M, Bis E, Biliński P, Gieburowski K, Kłapeć W, Tymczyna-Borowicz B, Łobacz M, Pawlicz J, Jarzębski M, et al. Implications of Isomorphism in the Family of Apatite Compounds. International Journal of Molecular Sciences. 2025; 26(9):4397. https://doi.org/10.3390/ijms26094397
Chicago/Turabian StyleLasota, Agnieszka, Mieczysław Gorzelak, Emanuela Bis, Przemysław Biliński, Krzysztof Gieburowski, Wojciech Kłapeć, Barbara Tymczyna-Borowicz, Michał Łobacz, Jarosław Pawlicz, Maciej Jarzębski, and et al. 2025. "Implications of Isomorphism in the Family of Apatite Compounds" International Journal of Molecular Sciences 26, no. 9: 4397. https://doi.org/10.3390/ijms26094397
APA StyleLasota, A., Gorzelak, M., Bis, E., Biliński, P., Gieburowski, K., Kłapeć, W., Tymczyna-Borowicz, B., Łobacz, M., Pawlicz, J., Jarzębski, M., Wieruszewski, M., Turżańska, K., Jabłoński, M., & Kuczumow, A. (2025). Implications of Isomorphism in the Family of Apatite Compounds. International Journal of Molecular Sciences, 26(9), 4397. https://doi.org/10.3390/ijms26094397









