EMitool: Explainable Multi-Omics Integration for Disease Subtyping
Abstract
1. Introduction
2. Results
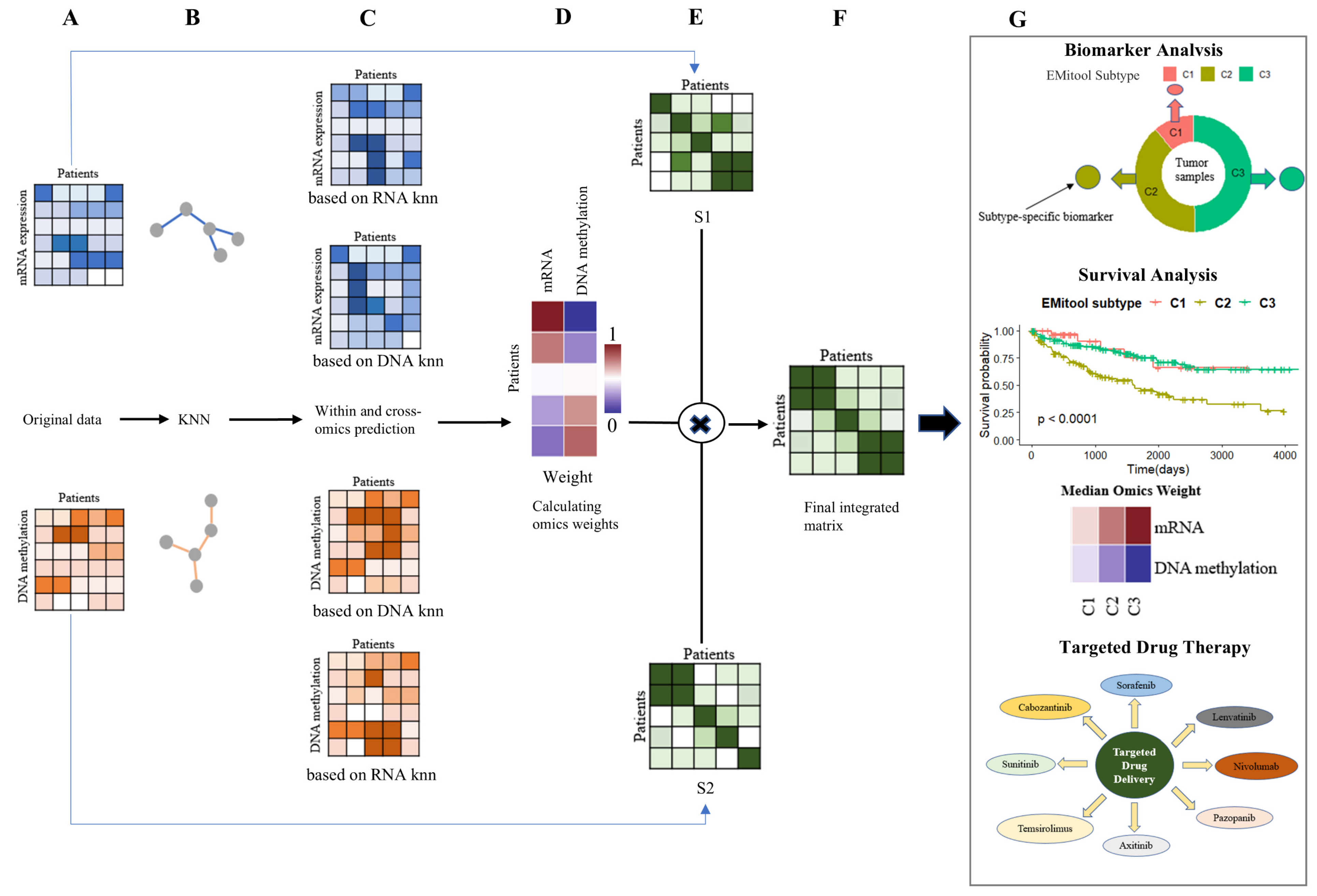
2.1. Overview of EMitool for Disease Subtyping
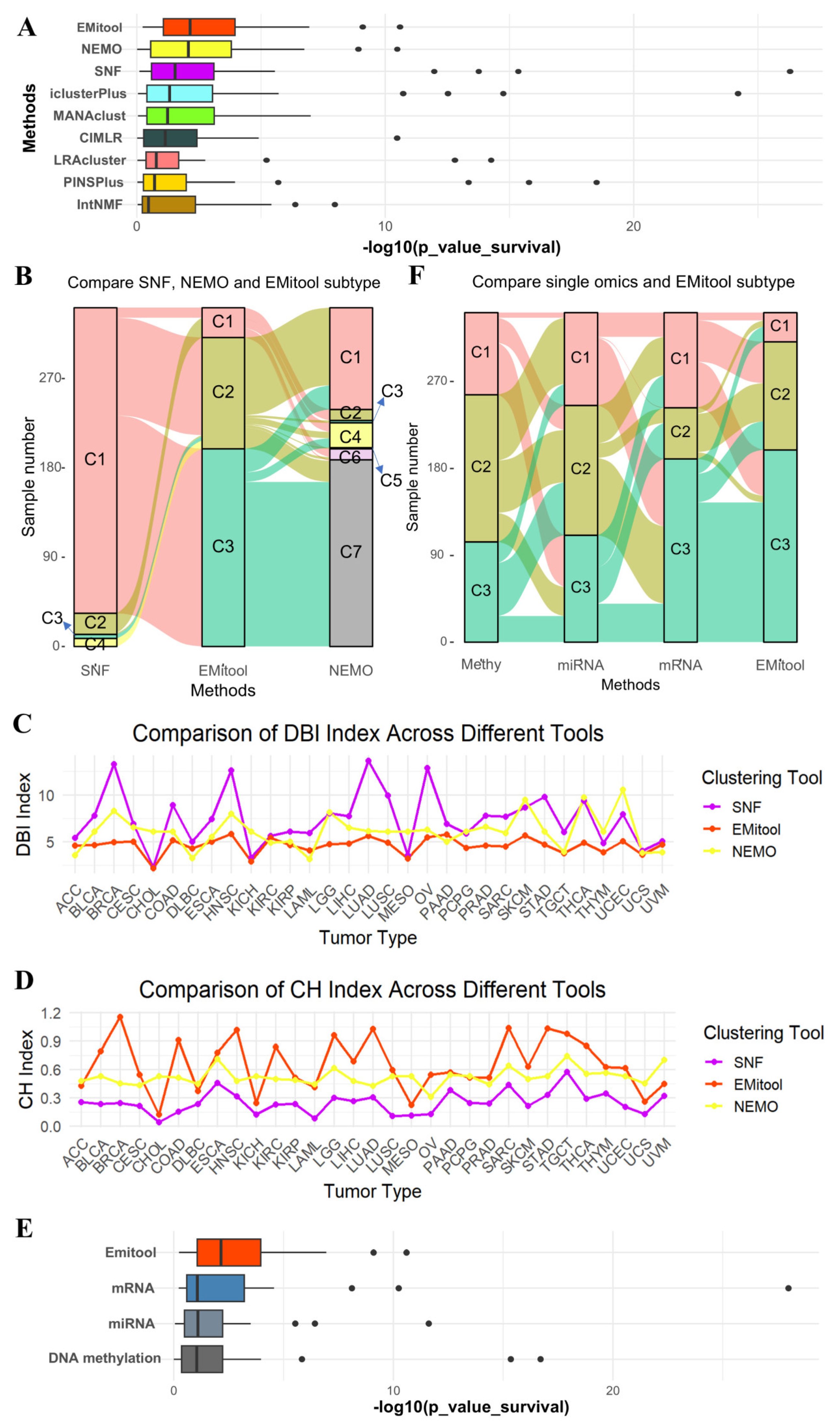
2.2. Comparative Analysis of EMitool and Eight Advanced Methods in Cancer Subtyping
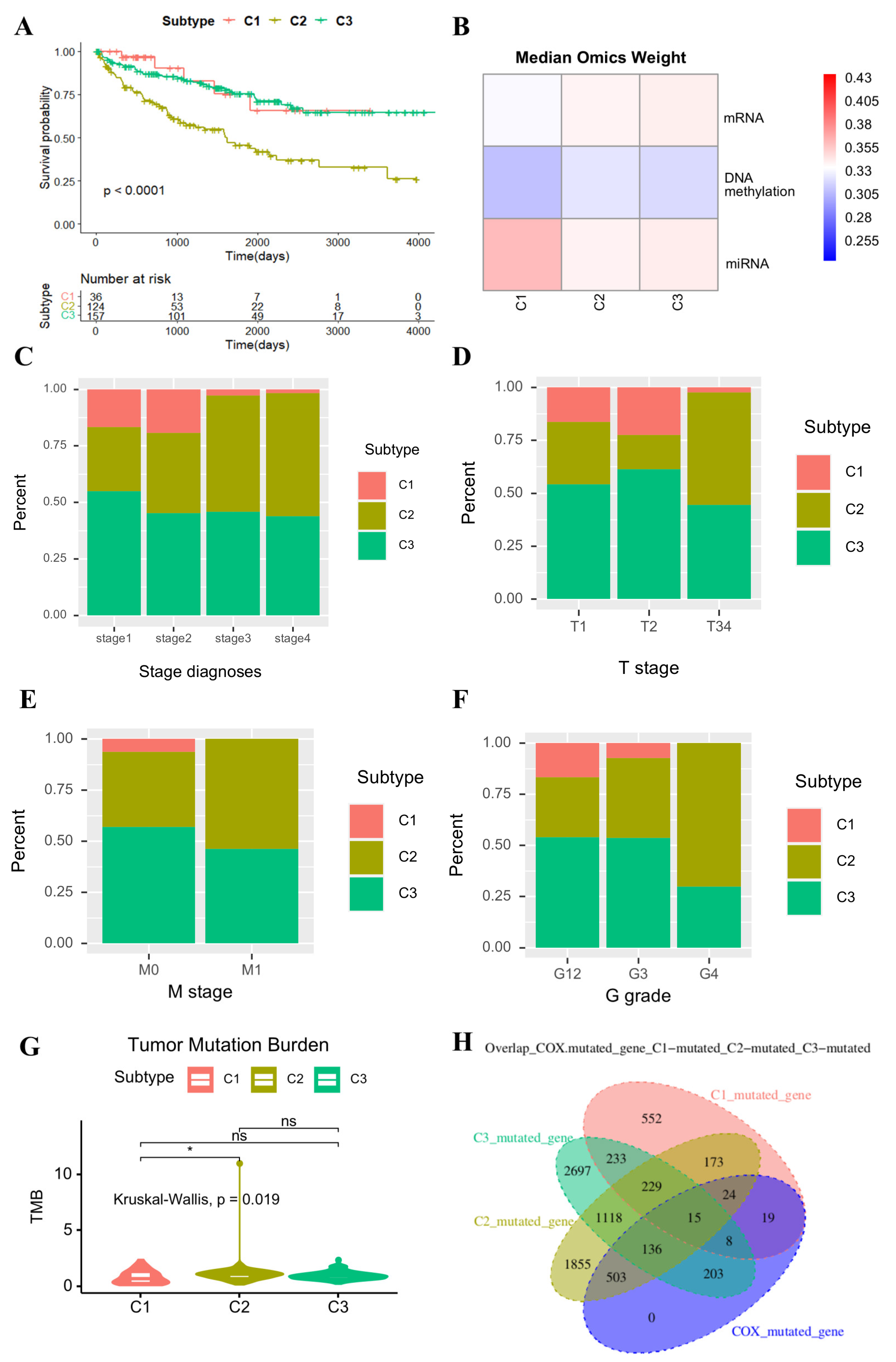
2.3. Clinical Significance of EMitool’s Subtyping Results
2.4. Immune Microenvironment Analysis Across Different Subtypes
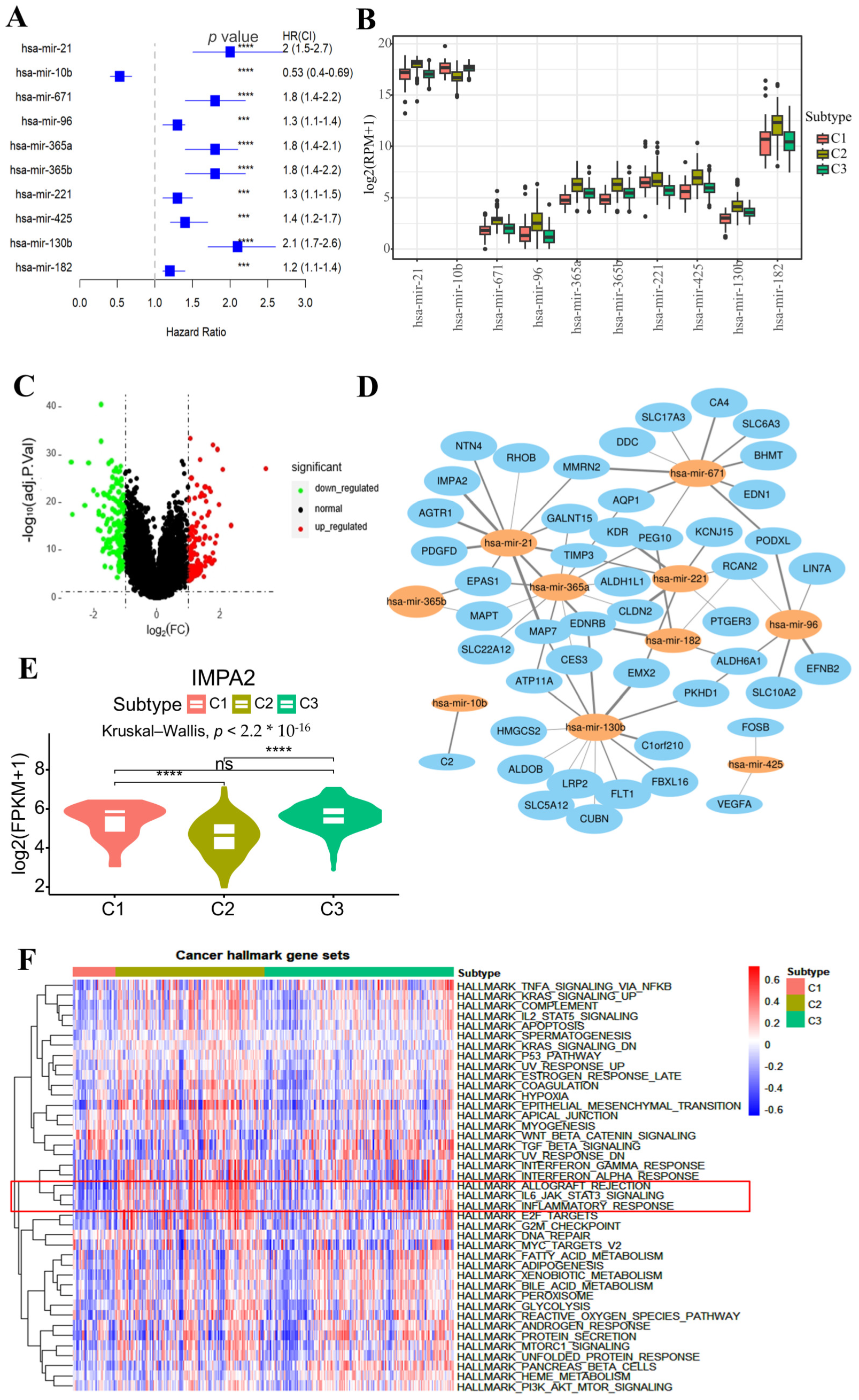
2.5. Subtype-Specific Biomarker Identification
2.6. Drug Response Analysis for the Subtypes
3. Discussion
4. Materials and Methods
4.1. Data Processing and Normalization
4.2. Explainable Multi-Omics Data Integration
4.3. Selection of the Number of Clusters
4.4. Clustering Validation Metrics
4.5. Prognosis Analysis
4.6. Immune Cell Gene Signature Scoring
4.7. Gene Set Variation Analysis
4.8. Drug Recommendation Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johansson, Å.; Andreassen, O.A.; Brunak, S.; Franks, P.W.; Hedman, H.; Loos, R.J.F.; Meder, B.; Melén, E.; Wheelock, C.E.; Jacobsson, B. Precision medicine in complex diseases-Molecular subgrouping for improved prediction and treatment stratification. J. Intern. Med. 2023, 294, 378–396. [Google Scholar] [CrossRef] [PubMed]
- Crimini, E.; Repetto, M.; Aftimos, P.; Botticelli, A.; Marchetti, P.; Curigliano, G. Precision medicine in breast cancer: From clinical trials to clinical practice. Cancer Treat. Rev. 2021, 98, 102223. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.D.; Yao, H.X.; Tijms, B.M.; Wang, P.; Wang, D.W.; Song, C.Y.; Yang, H.W.; Zhang, Z.Q.; Zhao, K.; Qu, Y.D.; et al. Four Distinct Subtypes of Alzheimer’s Disease Based on Resting-State Connectivity Biomarkers. Biol. Psychiat 2023, 93, 759–769. [Google Scholar] [CrossRef] [PubMed]
- Pourzinal, D.; Yang, J.; Lawson, R.A.; McMahon, K.L.; Byrne, G.J.; Dissanayaka, N.N. Systematic review of data-driven cognitive subtypes in Parkinson disease. Eur. J. Neurol. 2022, 29, 3395–3417. [Google Scholar] [CrossRef]
- Vahabi, N.; Michailidis, G. Unsupervised Multi-Omics Data Integration Methods: A Comprehensive Review. Front. Genet. 2022, 13, 854752. [Google Scholar] [CrossRef]
- Xie, G.; Zhu, L.; Liu, S.; Li, C.; Diao, X.; Zhang, Y.; Su, X.; Song, Y.; Cao, G.; Zhong, L.; et al. Multi-omics analysis of attenuated variant reveals potential evaluation marker of host damaging for SARS-CoV-2 variants. Sci. China Life Sci. 2024, 67, 83–95. [Google Scholar] [CrossRef]
- Li, G.; Zhu, D.; Cheng, C.; Chu, H.; Wei, F.; Zhang, Z. Multi-omics analysis reveals the genetic and environmental factors in shaping the gut resistome of a keystone rodent species. Sci. China Life Sci. 2024, 67, 2459–2470. [Google Scholar] [CrossRef]
- Yan, J.W.; Risacher, S.L.; Shen, L.; Saykin, A.J. Network approaches to systems biology analysis of complex disease: Integrative methods for multi-omics data. Brief. Bioinform. 2018, 19, 1370–1381. [Google Scholar] [CrossRef]
- Jiang, S.H.; Li, R.K.; Liu, D.J.; Xue, J.L.; Yu, M.H.; Zhang, S.; Liu, L.M.; Zhang, J.F.; Hua, R.; Sun, Y.W.; et al. The genomic, transcriptomic, and immunological profiles of perineural invasion in pancreatic ductal adenocarcinoma. Sci. China Life Sci. 2023, 66, 183–186. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Yang, N.; Zhu, X.; Lu, Z.; Cai, Y.; Li, B.; Zhu, Y.; Li, X.; Wei, Y.; et al. Prioritization of risk genes in colorectal cancer by integrative analysis of multi-omics data and gene networks. Sci. China Life Sci. 2024, 67, 132–148. [Google Scholar] [CrossRef]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333–337. [Google Scholar] [CrossRef]
- Nguyen, H.; Shrestha, S.; Draghici, S.; Nguyen, T. PINSPlus: A tool for tumor subtype discovery in integrated genomic data. Bioinformatics 2019, 35, 2843–2846. [Google Scholar] [CrossRef] [PubMed]
- Rappoport, N.; Shamir, R. NEMO: Cancer subtyping by integration of partial multi-omic data. Bioinformatics 2019, 35, 3348–3356. [Google Scholar] [CrossRef] [PubMed]
- Mo, Q.; Wang, S.; Seshan, V.E.; Olshen, A.B.; Schultz, N.; Sander, C.; Powers, R.S.; Ladanyi, M.; Shen, R. Pattern discovery and cancer gene identification in integrated cancer genomic data. Proc. Natl. Acad. Sci. USA 2013, 110, 4245–4250. [Google Scholar] [CrossRef] [PubMed]
- Tyler, S.R.; Chun, Y.; Ribeiro, V.M.; Grishina, G.; Grishin, A.; Hoffman, G.E.; Do, A.N.; Bunyavanich, S. Merged Affinity Network Association Clustering: Joint multi-omic/clinical clustering to identify disease endotypes. Cell Rep. 2021, 35, 108975. [Google Scholar] [CrossRef]
- Chalise, P.; Fridley, B.L. Integrative clustering of multi-level ‘omic data based on non-negative matrix factorization algorithm. PLoS ONE 2017, 12, e0176278. [Google Scholar] [CrossRef]
- Wu, D.; Wang, D.; Zhang, M.Q.; Gu, J. Fast dimension reduction and integrative clustering of multi-omics data using low-rank approximation: Application to cancer molecular classification. BMC Genom. 2015, 16, 1022. [Google Scholar] [CrossRef]
- Ramazzotti, D.; Lal, A.; Wang, B.; Batzoglou, S.; Sidow, A. Multi-omic tumor data reveal diversity of molecular mechanisms that correlate with survival. Nat. Commun. 2018, 9, 4453. [Google Scholar] [CrossRef]
- Duan, R.; Gao, L.; Gao, Y.; Hu, Y.; Xu, H.; Huang, M.; Song, K.; Wang, H.; Dong, Y.; Jiang, C.; et al. Evaluation and comparison of multi-omics data integration methods for cancer subtyping. PLoS Comput. Biol. 2021, 17, e1009224. [Google Scholar] [CrossRef]
- Samstein, R.M.; Lee, C.H.; Shoushtari, A.N. Tumor mutational load predicts survival after immunotherapy across multiple cancer types. Nat. Genet. 2019, 51, 202–206. [Google Scholar] [CrossRef]
- Riviere, P.; Goodman, A.M.; Okamura, R. High Tumor Mutational Burden Correlates with Longer Survival in Immunotherapy-Naïve Patients with Diverse Cancers. Mol. Cancer Ther. 2020, 19, 2139–2145. [Google Scholar] [CrossRef] [PubMed]
- Combes, A.J.; Samad, B.; Tsui, J.; Chew, N.W.; Yan, P.; Reeder, G.C.; Kushnoor, D.; Shen, A.; Davidson, B.; Barczak, A.J.; et al. Discovering dominant tumor immune archetypes in a pan-cancer census. Cell 2022, 185, 184–203.e119. [Google Scholar] [CrossRef] [PubMed]
- Micke, P.; Strell, C.; Mattsson, J.; Martín-Bernabé, A.; Brunnström, H.; Huvila, J.; Sund, M.; Wärnberg, F.; Ponten, F.; Glimelius, B.; et al. The prognostic impact of the tumour stroma fraction: A machine learning-based analysis in 16 human solid tumour types. EBioMedicine 2021, 65, 103269. [Google Scholar] [CrossRef]
- Bruni, D.; Angell, H.K. The immune contexture and Immunoscore in cancer prognosis and therapeutic efficacy. Nat. Rev. Cancer 2020, 20, 662–680. [Google Scholar] [CrossRef]
- Kiryu, S.; Ito, Z.; Suka, M.; Bito, T.; Kan, S.; Uchiyama, K.; Saruta, M.; Hata, T.; Takano, Y.; Fujioka, S.; et al. Prognostic value of immune factors in the tumor microenvironment of patients with pancreatic ductal adenocarcinoma. BMC Cancer 2021, 21, 1197. [Google Scholar] [CrossRef]
- Yang, X.; Wu, W.; Pan, Y.; Zhou, Q.; Xu, J.; Han, S. Immune-related genes in tumor-specific CD4(+) and CD8(+) T cells in colon cancer. BMC Cancer 2020, 20, 585. [Google Scholar] [CrossRef]
- Bai, Y.; Liu, Y.; Wu, J.; Miao, R.; Xu, Z.; Hu, C.; Zhou, J.; Guo, J.; Xie, J.; Shi, Z.; et al. CD4 levels and NSCLC metastasis: The benefits of maintaining moderate levels. J. Cancer Res. Clin. Oncol. 2023, 149, 16827–16836. [Google Scholar] [CrossRef]
- Deng, S.; Zhu, Q.; Chen, H.; Xiao, T.; Zhu, Y.; Gao, J.; Li, Q.; Gao, Y. Screening of prognosis-related Immune cells and prognostic predictors in Colorectal Cancer Patients. BMC Cancer 2023, 23, 195. [Google Scholar] [CrossRef]
- Saito, Y.; Komori, S.; Kotani, T.; Murata, Y.; Matozaki, T. The Role of Type-2 Conventional Dendritic Cells in the Regulation of Tumor Immunity. Cancers 2022, 14, 1976. [Google Scholar] [CrossRef]
- Kuei, C.H.; Lin, H.Y.; Lee, H.H. IMPA2 Downregulation Enhances mTORC1 Activity and Restrains Autophagy Initiation in Metastatic Clear Cell Renal Cell Carcinoma. J. Clin. Med. 2020, 9, 956. [Google Scholar] [CrossRef]
- Liberzon, A.; Birger, C.; Thorvaldsdóttir, H.; Ghandi, M.; Mesirov, J.P.; Tamayo, P. The Molecular Signatures Database (MSigDB) hallmark gene set collection. Cell Syst. 2015, 1, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Knox, C.; Wilson, M.; Klinger, C.M.; Franklin, M.; Oler, E.; Wilson, A.; Pon, A.; Cox, J.; Chin, N.E.L.; Strawbridge, S.A.; et al. DrugBank 6.0: The DrugBank Knowledgebase for 2024. Nucleic Acids Res. 2024, 52, D1265–D1275. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, G.; Li, D.; Zhang, J.; Hu, P.; Hu, L. Integrating Fuzzy Clustering and Graph Convolution Network to Accurately Identify Clusters From Attributed Graph. IEEE Trans. Netw. Sci. Eng. 2025, 12, 1112–1125. [Google Scholar] [CrossRef]
- Li, G.; Zhao, B.; Su, X.; Yang, Y.; Hu, P.; Zhou, X.; Hu, L. Discovering Consensus Regions for Interpretable Identification of RNA N6-Methyladenosine Modification Sites via Graph Contrastive Clustering. IEEE J. Biomed. Health Inform. 2024, 28, 2362–2372. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, S.; Andersen-Nissen, E.; Mauck, W.M., 3rd; Zheng, S.; Butler, A.; Lee, M.J.; Wilk, A.J.; Darby, C.; Zager, M.; et al. Integrated analysis of multimodal single-cell data. Cell 2021, 184, 3573–3587.e3529. [Google Scholar] [CrossRef]
- Wilkerson, M.D.; Hayes, D.N. ConsensusClusterPlus: A class discovery tool with confidence assessments and item tracking. Bioinformatics 2010, 26, 1572–1573. [Google Scholar] [CrossRef]
- Xu, S.; Qiao, X.; Zhu, L.; Zhang, Y.; Xue, C.; Li, L. Reviews on Determining the Number of Clusters. Appl. Math. Inf. Sci. 2016, 10, 1493–1512. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Robinson, M.D.; Oshlack, A. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010, 11, R25. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. Author Correction: SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 352. [Google Scholar] [CrossRef] [PubMed]
- Hanzelmann, S.; Castelo, R.; Guinney, J. GSVA: Gene set variation analysis for microarray and RNA-seq data. BMC Bioinform. 2013, 14, 7–14. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wu, J.; Chen, C.; Ouyang, J.; Li, D.; Shi, T. EMitool: Explainable Multi-Omics Integration for Disease Subtyping. Int. J. Mol. Sci. 2025, 26, 4268. https://doi.org/10.3390/ijms26094268
Xu Y, Wu J, Chen C, Ouyang J, Li D, Shi T. EMitool: Explainable Multi-Omics Integration for Disease Subtyping. International Journal of Molecular Sciences. 2025; 26(9):4268. https://doi.org/10.3390/ijms26094268
Chicago/Turabian StyleXu, Yong, Jun Wu, Chen Chen, Jian Ouyang, Dawei Li, and Tieliu Shi. 2025. "EMitool: Explainable Multi-Omics Integration for Disease Subtyping" International Journal of Molecular Sciences 26, no. 9: 4268. https://doi.org/10.3390/ijms26094268
APA StyleXu, Y., Wu, J., Chen, C., Ouyang, J., Li, D., & Shi, T. (2025). EMitool: Explainable Multi-Omics Integration for Disease Subtyping. International Journal of Molecular Sciences, 26(9), 4268. https://doi.org/10.3390/ijms26094268





