The Influence of Energy Levels and Defects on the Thermoluminescence of LiF: SiO5 Phosphors Doped with Ce3+
Abstract
1. Introduction
2. Results and Discussion
2.1. X-Ray Diffraction (XRD) Pattern Studies
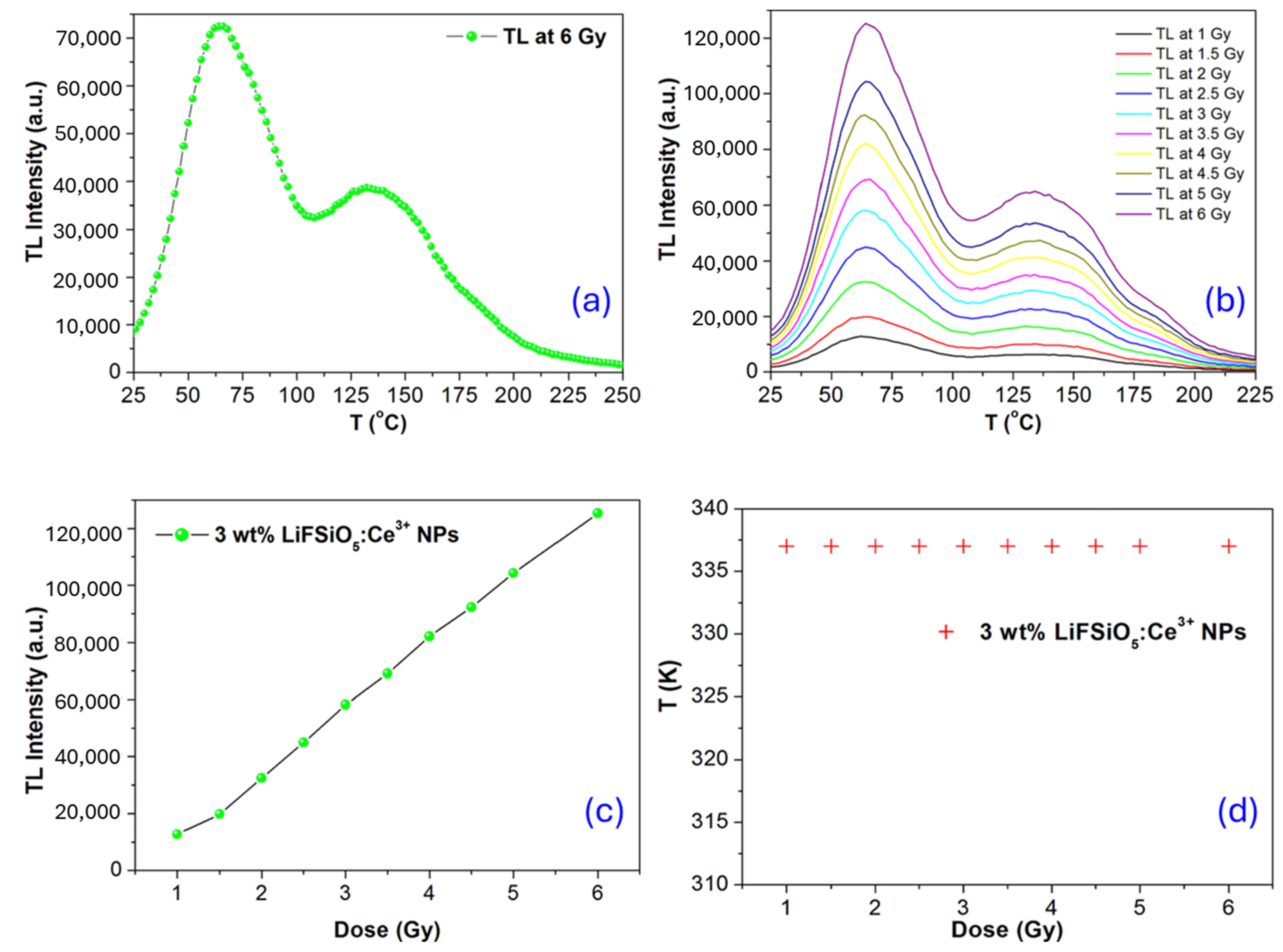
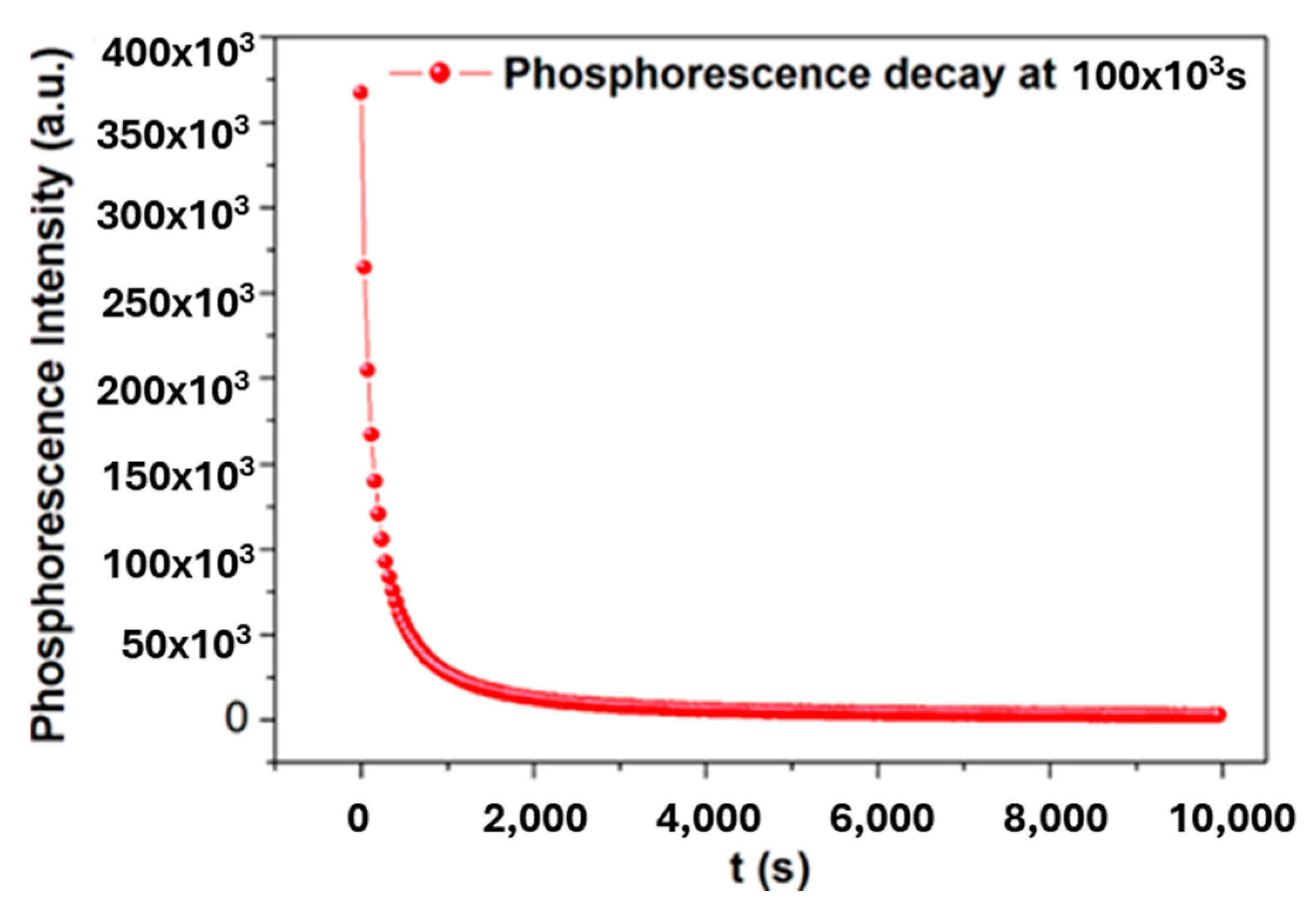
2.2. Trap-Emptying Process Dynamics
2.3. TL Luminescence Characteristics Studies
Simple Model for Thermoluminescence
3. Experimental Section
3.1. Preparation of Materials and Methods
3.2. Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vij, D.R. Luminescence of Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kumar, V.; Kumar, R.; Lochab, S.P.; Singh, N. Thermoluminescence studies of CaS: Bi nanocrystalline phosphors. J. Phys. D Appl. Phys. 2006, 39, 5137–5142. [Google Scholar] [CrossRef]
- Le Masne de Chermont, Q.; Chanéac, C.; Seguin, J.; Pellé, F.; Maîtrejean, S.; Jolivet, J.P.; Gourier, D.; Bessodes, M.; Scherman, D. Nanoprobes with near-infrared persistent luminescence for in vivo imaging. Proc. Natl. Acad. Sci. USA 2007, 104, 9266–9271. [Google Scholar] [CrossRef]
- Zhao, Q.; Huang, C.; Li, F. Phosphorescent heavy-metal complexes for bioimaging. Chem. Soc. Rev. 2011, 40, 2508–2524. [Google Scholar] [CrossRef]
- Lo, K.K.-W.; Li, S.P.-Y. Utilization of the photophysical and photochemical properties of phosphorescent transition metal complexes in the development of photofunctional cellular sensors, imaging reagents, and cytotoxic agents. RSC Adv. 2014, 4, 10560–10585. [Google Scholar] [CrossRef]
- Chen, L.; Han, H. Recent advances in the use of near-infrared quantum dots as optical probes for bioanalytical, imaging and solar cell application. Microchim. Acta 2014, 181, 1485–1495. [Google Scholar] [CrossRef]
- Ru, J.; Mi, X.; Guan, L.; Tang, X.; Ju, Z.; Zhang, G.; Wang, C.; Liu, W. Design and application of a water-soluble phosphorescent Ru(ii) complex as turn-on sensing material for Hg2+. J. Mater. Chem. B 2015, 3, 6205–6212. [Google Scholar] [CrossRef] [PubMed]
- Jüstel, T.; Nikol, H. Optimization of luminescent materials for plasma display panels. Adv. Mater. 2000, 12, 527–530. [Google Scholar] [CrossRef]
- Haile, H.T.; Dejene, F.B. Influence of oxygen deposition pressure on the structural, morphological, photoluminescence and thermoluminescence properties of Y2SiO5: Ce3+ by pulsed laser deposition method. Inorg. Chem. Commun. 2021, 127, 108554. [Google Scholar] [CrossRef]
- Dieke, G.H.; Crosswhite, H.M. The spectra of the doubly and triply ionized rare earths. Appl. Opt. 1963, 2, 675–686. [Google Scholar] [CrossRef]
- Chennappa, T.; Kamath, S.D. Review—Structural and Optical Interpretations on Phosphor-Based Optical Thermometry. ECS J. Solid. State Sci. Technol. 2024, 13, 077002. [Google Scholar] [CrossRef]
- Dramićanin, M. Luminescence Thermometry: Methods, Materials, and Applications; Woodhead Publishing: Cambridge, UK, 2018. [Google Scholar]
- Litster, S.; Hackett, R.Q. Structural and Optical Interpretations on Phosphor-Based Optical Thermometry. ECS J. Solid State Sci. Technol. 2024, 13, 077002. [Google Scholar]
- Qin, X.; Huang, W.; Bettinelli, M.; Liu, X. Lanthanide-Activated Phosphors Based on 4f-5d Optical Transitions: Theoretical and Experimental Aspects. Chem. Rev. 2017, 117, 4488–4527. [Google Scholar] [PubMed]
- Al-Hamdi, A.; Sillanpää, M. Photocatalytic activities of antimony, iodide, and rare for the photodegradation earth metals of on phenol SnO2 under UV, solar, and visible light irradiations. Adv. Water Treat. Adv. Oxid. Process. 2020, 141, 129. [Google Scholar]
- Li, Z.; Xie, J.; Faizan, M.; Wang, S.; Chen, X.; Zhang, L. Luminescence From Localized States in Solids: A First-Principles Perspective. Adv. Funct. Mater. 2025, 2422716. [Google Scholar] [CrossRef]
- ul Hassan, S.M.; Akram, W.; Noureen, A.; Ahmed, F.; Hassan, A.; Ullah, A. Advances in transition metals and rare earth elements doped ZnO as thermoluminescence dosimetry material. Radiat. Phys. Chem. 2024, 223, 111929. [Google Scholar]
- Cheung, Y.; Gayen, S.; Gualtieri, D. LASER-INDUCED PHOTOCHROMIC CENTERS IN Ce3+: La2Be205. In Second Annual Research Center for Optical Physics (RCOP) Forum: Proceedings of a Forum; National Aeronautics and Space Administration Langley Research Center: Hampton, VA, USA, 1995. [Google Scholar]
- Mascher, P.; Lockwood, D.J.; Rosei, F. Nanoscale Luminescent Materials 5; The Electrochemical Society: New Jersey, NJ, USA, 2018. [Google Scholar]
- Haddock, S.H.; Moline, M.A.; Case, J.F. Bioluminescence in the sea. Annu. Rev. Mar. Sci. 2010, 15, 443–493. [Google Scholar]
- Kalinkin, M.; Akulov, D.; Abashev, R.; Surdo, A.; Kuznetsov, M.; Kellerman, D. The role of defects in thermoluminescence of pure and rare-earth-doped magnesium tetraborate phosphor. J. Lumin. 2023, 263, 120119. [Google Scholar]
- Kaur, R.; Rakesh, R.B.; Mhatre, S.G.; Bhatia, V.; Kumar, D.; Singh, H.; Singh, S.P.; Kumar, A. Thermoluminescence, structural and optical properties of Ce3+ doped borosilicate doped glasses. J. Mater. Sci. Mater. Electron. 2021, 32, 18381–18396. [Google Scholar]
- Hassan, Z.; Abd, H.R.; Alsultany, F.H.; Omar, A.; Ahmed, N.M. Investigation of sintering temperature and Ce3+ concentration in YAG:Ce phosphor powder prepared by microwave combustion for white-light-emitting diode luminance applications. Mater. Chem. Phys. 2019, 229, 22–31. [Google Scholar]
- Sinclair, S.; Pech-Canul, M. Development feasibility of TLD phosphors and thermoluminescent composite materials for potential applications in dosimetry: A review. Chem. Eng. J. 2022, 443, 136522. [Google Scholar]
- Malik, W.U.; Tuli, G.D.; Madan, R.D. Selected Topics in Inorganic Chemistry; S. Chand Publishing: New Delhi, India, 1988. [Google Scholar]
- Shinde, K.N.; Dhoble, S.; Swart, H.; Park, K. Phosphate Phosphors for Solid-State Lighting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lakshmanan, A. Luminescence and Display Phosphors: Phenomena and Applications; Nova Publishers: New York, NY, USA, 2008. [Google Scholar]
- Nambi, K.; Bapat, V.; Ganguly, A. Thermoluminescence of CaSO4 doped with rare earths. J. Phys. C Solid. State Phys. 1974, 7, 4403. [Google Scholar] [CrossRef]
- Kirsh, Y.; Kristianpoller, N. UV induced processes in pure and doped SrF2. J. Lumin. 1977, 15, 35–46. [Google Scholar] [CrossRef]
- Kristianpoller, N.; Kirsh, Y.; Shoval, S.; Weiss, D.; Chen, R. Thermoluminescent properties of mica. Int. J. Radiat. Appl. Instrum. Part D Nucl. Tracks Radiat. Meas. 1988, 14, 101–104. [Google Scholar] [CrossRef]
- Sastry, S.; Sapru, S. Mechanism of thermoluminescence in europium doped rubidium bromide. J. Lumin. 1981, 23, 281–291. [Google Scholar] [CrossRef]
- Happek, U.; Basun, S.; Choi, J.; Krebs, J.; Raukas, M. Electron transfer processes in rare earth doped insulators. J. Alloy. Compd. 2000, 303–304, 198–206. [Google Scholar] [CrossRef]
- Dash, P.; Yang, J.-M.; Lin, H.; Lin, A.S. Preparation and characterization of zinc gallate phosphor for electrochemical luminescence. J. Lumin. 2020, 228, 117593. [Google Scholar] [CrossRef]
- Dejene, F.B.; Etefa, H.F. Thermoluminescence (TL) properties of Eu3+ incorporated with CaB4O7 phosphors prepared by solution-combustion process. Appl. Radiat. Isot. 2024, 214, 111522. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Introduction Solid State Physics; John Wiley & Sons: Philadelphia, NJ, USA, 2018. [Google Scholar]
- Kelly, P.; Bräunlich, P.I. Phenomenological theory of thermoluminescence. Phys. Rev. B 1970, 1, 1587. [Google Scholar] [CrossRef]
- Major, F.G.; Gheorghe, V.N.; Werth, G. Charged Particle Traps: Physics and Techniques of Charged Particle. Field Confinement; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Haile, H.T. Material Properties of Cerium Doped Yttrium Silicate (Y2SiO5: Ce3+) by Pulsed Laser Deposition Method for Display Applications. Ph.D. Thesis, University of the Free State, Bloemfontein, South Africa, 2020. [Google Scholar]
- Xu, S.Y.; Zhang, X.S.; Zhou, Y.L.; Xi, Q.; Li, L. Influence of Si4+ substitution on the temperature-dependent characteristics of Y3Al5O12: Ce. Chin. Phys. B 2011, 20, 037804. [Google Scholar] [CrossRef]
- McKeever, S.W. Thermoluminescence of Solids; Cambridge university press: Cambridge, UK, 1985; Volume 3. [Google Scholar]
- Jabłoński, A. Über den Mechanismus der Photolumineszenz von Farbstoffphosphoren. Eur. Phys. J. A 1935, 94, 38–46. [Google Scholar] [CrossRef]
- Wigner, E.P.; Witmer, E.E. Über die Struktur der zweiatomigen Molekelspektren nach der Quantenmechanik. Collect. Work. Eugene Paul. Wigner Part A Sci. Pap. 1993, 1, 167–194. [Google Scholar]
- Ejerso, A.B.; Etefa, H.F.; Dejene, F.B. Excitation function of neutron induced reaction on isotopes of cadmium (106Cd, 108Cd &110Cd) in the energy range of 13–15 MeV. Int. J. Adv. Nucl. React. Des. Technol. 2023, 5, 137–143. [Google Scholar]
- Poulsen, T.D.; Ogilby, P.R.; Mikkelsen, K.V. Quadratic response of molecules in a nonequilibrium and equilibrium solvation model: Generalizations to include both singlet and triplet perturbations. J. Chem. Phys. 1999, 111, 2678–2685. [Google Scholar]
- Messiah, A. Quantum Mechanics; Courier Corporation: Cambridge, UK, 2014. [Google Scholar]
- Preto, P.D.; Vidyavathy, B.; Dhabekar, B.S. Preparation, thermoluminescence, photoluminescence and dosimetric characteristics of LiF: Mg, Cu, P., B phosphor. Indian J. Phys. 2017, 91, 25–31. [Google Scholar] [CrossRef]
- Preto, P.D.; Balraj, V.; Dhabekar, B.S.; Watanabe, S.; Rao, T.G.; Cano, N.F. Synthesis, thermoluminescence, defect center and dosimetric characteristics of LiF: Mg, Cu, P., Si phosphor. Appl. Radiat. Isot. 2017, 130, 21–28. [Google Scholar]

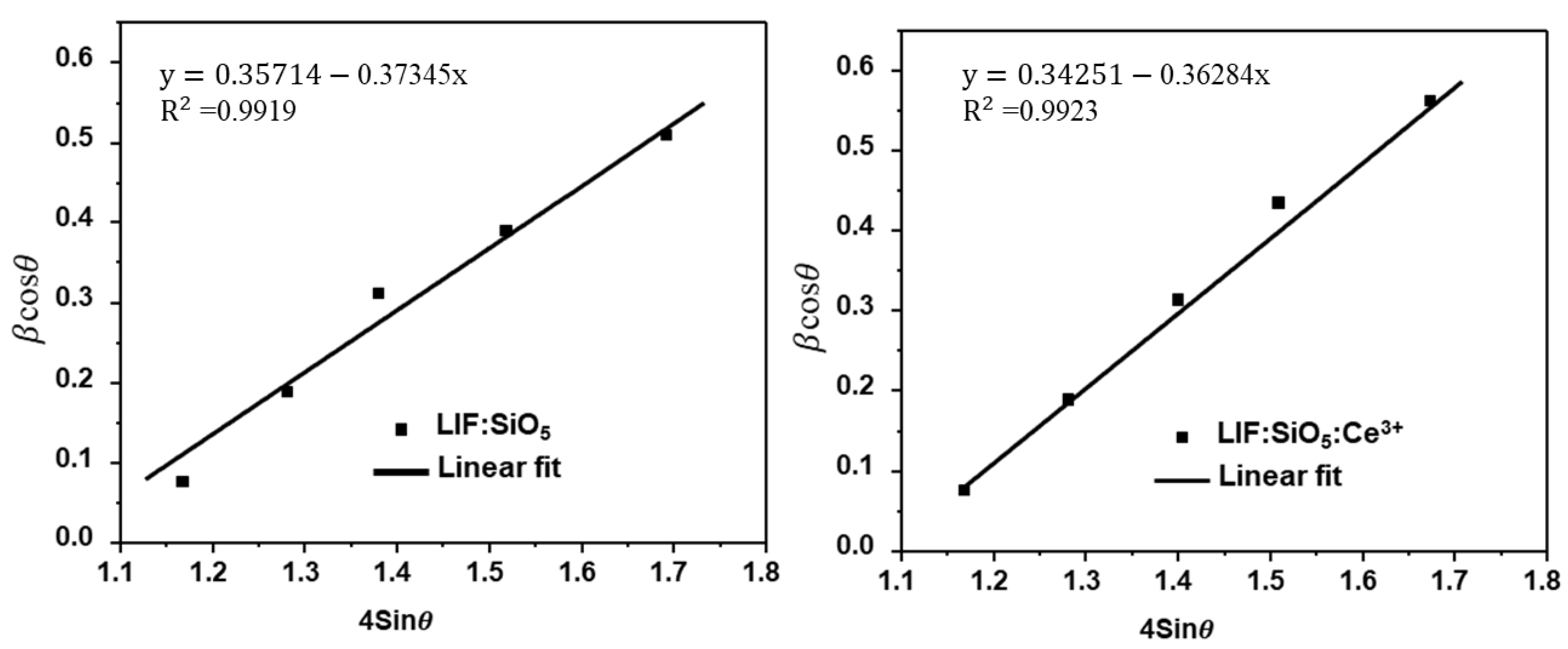
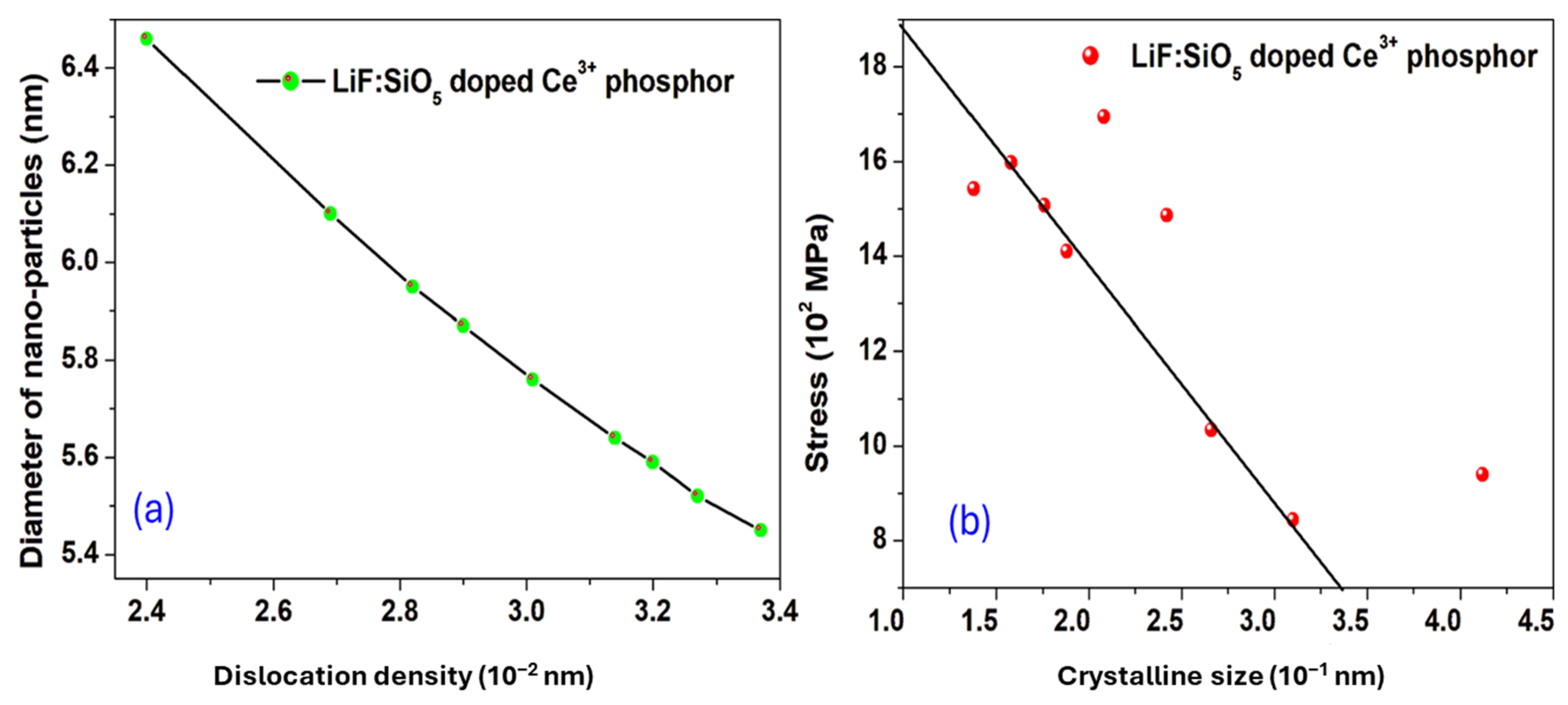

| Peak Pos (2θ°) | FWHM (β) | d-Spacing | D (nm) | δ (10−2 nm−2) | ε (10−2) | σ (102 MPa) |
|---|---|---|---|---|---|---|
| 21.57 | 0.2622 | 4.12 | 5.45 | 3.37 | 6.44 | 9.40 |
| 28.78 | 0.2388 | 3.10 | 5.52 | 3.28 | 5.78 | 8.44 |
| 33.66 | 0.2959 | 2.66 | 5.59 | 3.20 | 7.08 | 10.34 |
| 37.14 | 0.4294 | 2.42 | 5.64 | 3.14 | 10.18 | 14.86 |
| 43.52 | 0.4996 | 2.08 | 5.76 | 3.01 | 11.60 | 16.94 |
| 48.47 | 0.4236 | 1.88 | 5.87 | 2.90 | 9.66 | 14.10 |
| 52.04 | 0.4592 | 1.76 | 5.95 | 2.82 | 10.32 | 15.07 |
| 57.46 | 0.4992 | 1.58 | 6.10 | 2.69 | 10.94 | 15.97 |
| 68.05 | 0.5097 | 1.38 | 6.46 | 2.40 | 10.56 | 15.42 |
| Phosphor Composition | Main TL Peak Temperature (°C) | Linear Dose Response Range | Ref. |
|---|---|---|---|
| LiF:Mg, Cu, P, B | 220 | Up to 10 Gy | [46] |
| LiF:Mg, Cu, P, Si | 220 | Up to 10 Gy | [46,47] |
| LiF:Mg, Cu, P | 205 | Not specified | [47] |
| LiF:Mg, Cu | 205 | Not specified | [46] |
| LiF:Mg, Cu, P | 202 | Low dose range | [47] |
| LiF:SiO5, Ce3+ | 140–150 | Up to 6 Gy | Present |
| Temperature (°C) | τ (K) | δ (K) | ω (K) | μ | s (s−1) | |
|---|---|---|---|---|---|---|
| 64 | 39 | 42 | 81 | 0.519 | 1.096 × 10−15 | 1.096 × 10−15 |
| 164 | 28 | 36 | 64 | 0.563 | 4.100 × 10−13 | 1.096 × 10−13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etefa, H.F.; Mbuyise, X.G.; Geldasa, F.T.; Mola, G.T.; Chithambo, M.L.; Dejene, F.B. The Influence of Energy Levels and Defects on the Thermoluminescence of LiF: SiO5 Phosphors Doped with Ce3+. Int. J. Mol. Sci. 2025, 26, 3183. https://doi.org/10.3390/ijms26073183
Etefa HF, Mbuyise XG, Geldasa FT, Mola GT, Chithambo ML, Dejene FB. The Influence of Energy Levels and Defects on the Thermoluminescence of LiF: SiO5 Phosphors Doped with Ce3+. International Journal of Molecular Sciences. 2025; 26(7):3183. https://doi.org/10.3390/ijms26073183
Chicago/Turabian StyleEtefa, Habtamu F., Xolani G. Mbuyise, Fikadu T. Geldasa, Genene T. Mola, Makaiko L. Chithambo, and Francis B. Dejene. 2025. "The Influence of Energy Levels and Defects on the Thermoluminescence of LiF: SiO5 Phosphors Doped with Ce3+" International Journal of Molecular Sciences 26, no. 7: 3183. https://doi.org/10.3390/ijms26073183
APA StyleEtefa, H. F., Mbuyise, X. G., Geldasa, F. T., Mola, G. T., Chithambo, M. L., & Dejene, F. B. (2025). The Influence of Energy Levels and Defects on the Thermoluminescence of LiF: SiO5 Phosphors Doped with Ce3+. International Journal of Molecular Sciences, 26(7), 3183. https://doi.org/10.3390/ijms26073183






