A Combined Thermodynamic and Computational Study of Alkaline Earth Metal Cations Complexation by a Fluorescent Calix[4]arene Receptor
Abstract
1. Introduction
2. Results and Discussion
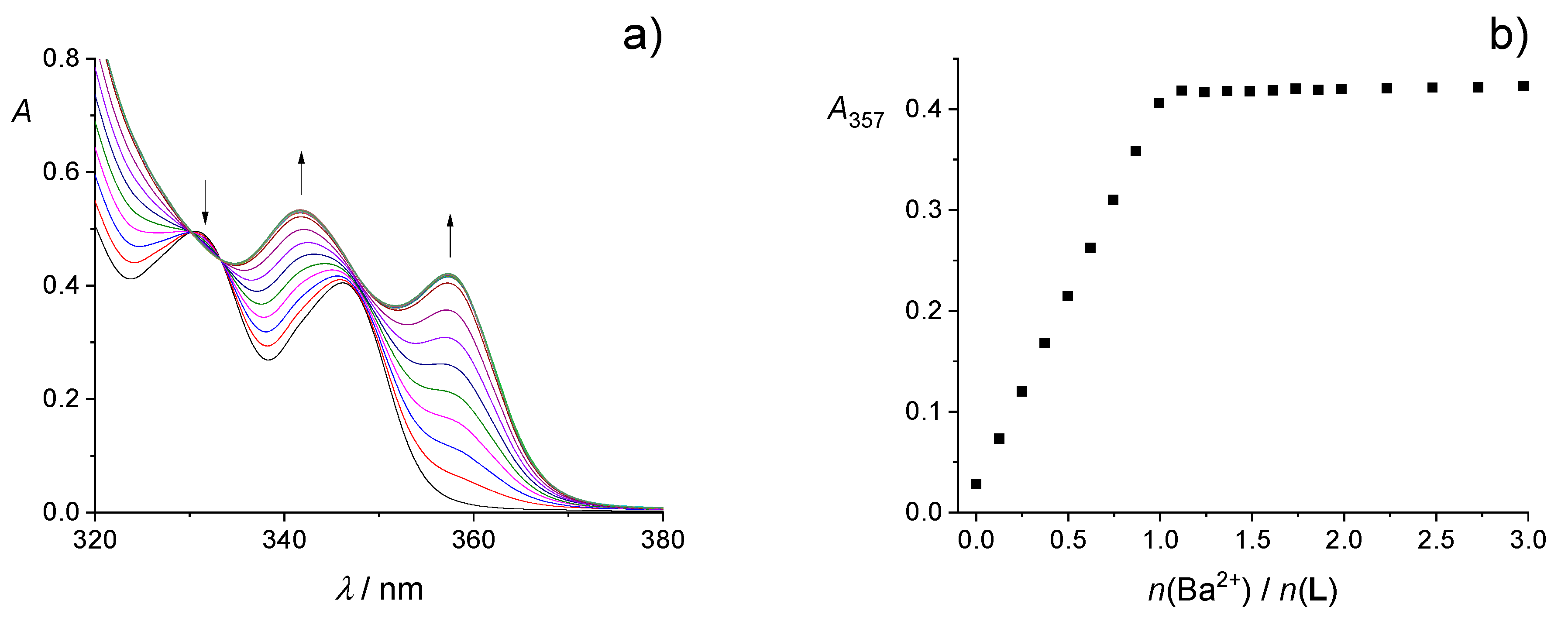
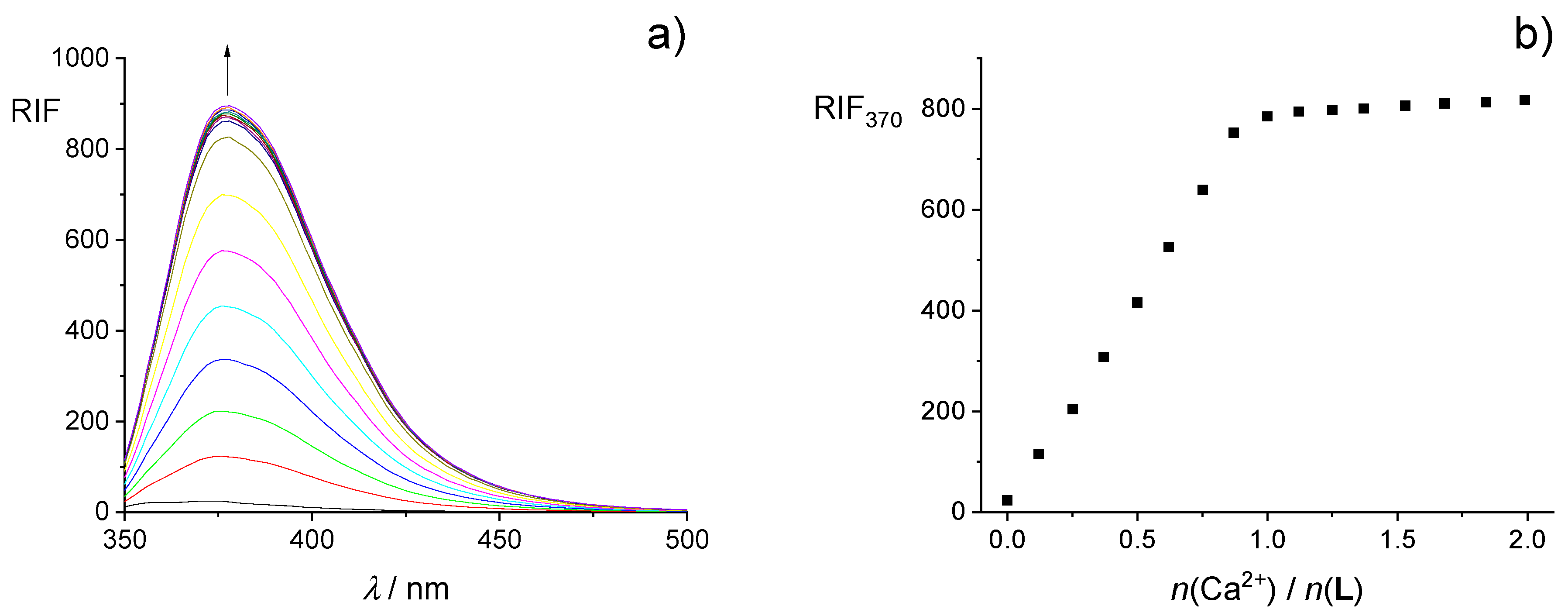
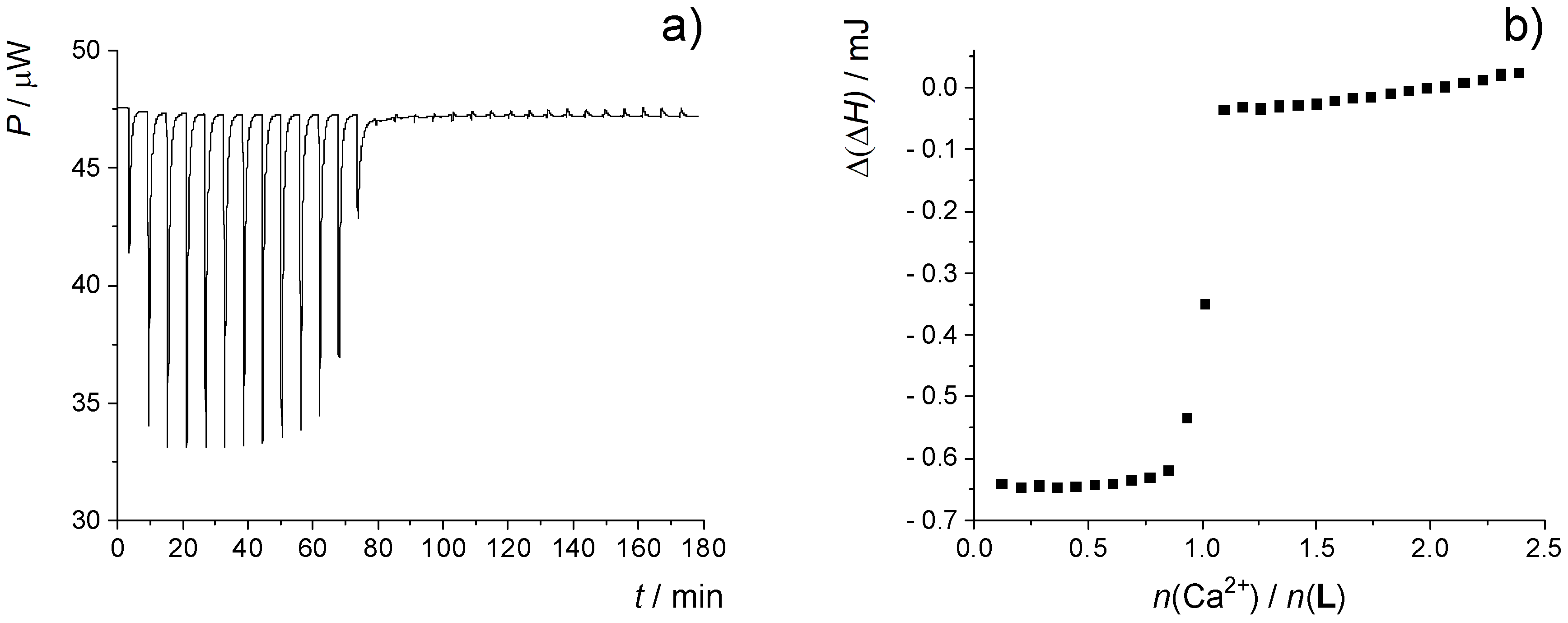
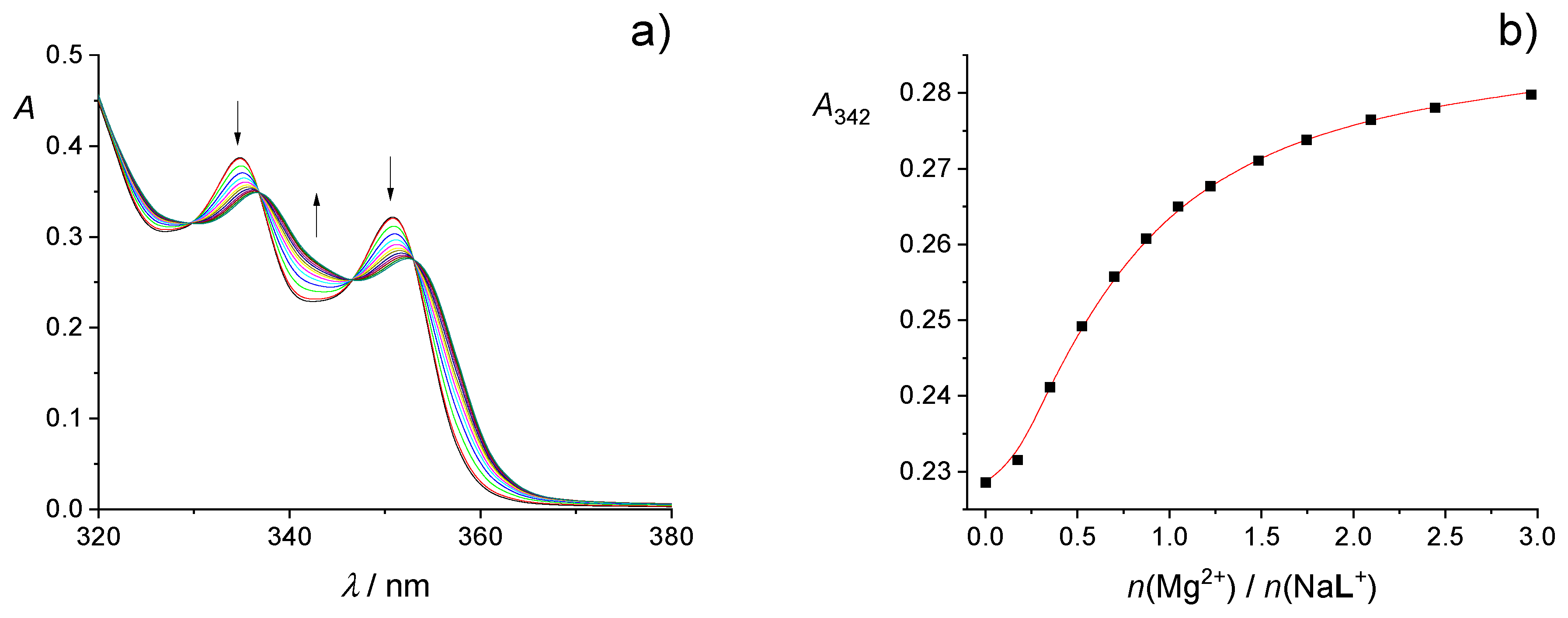
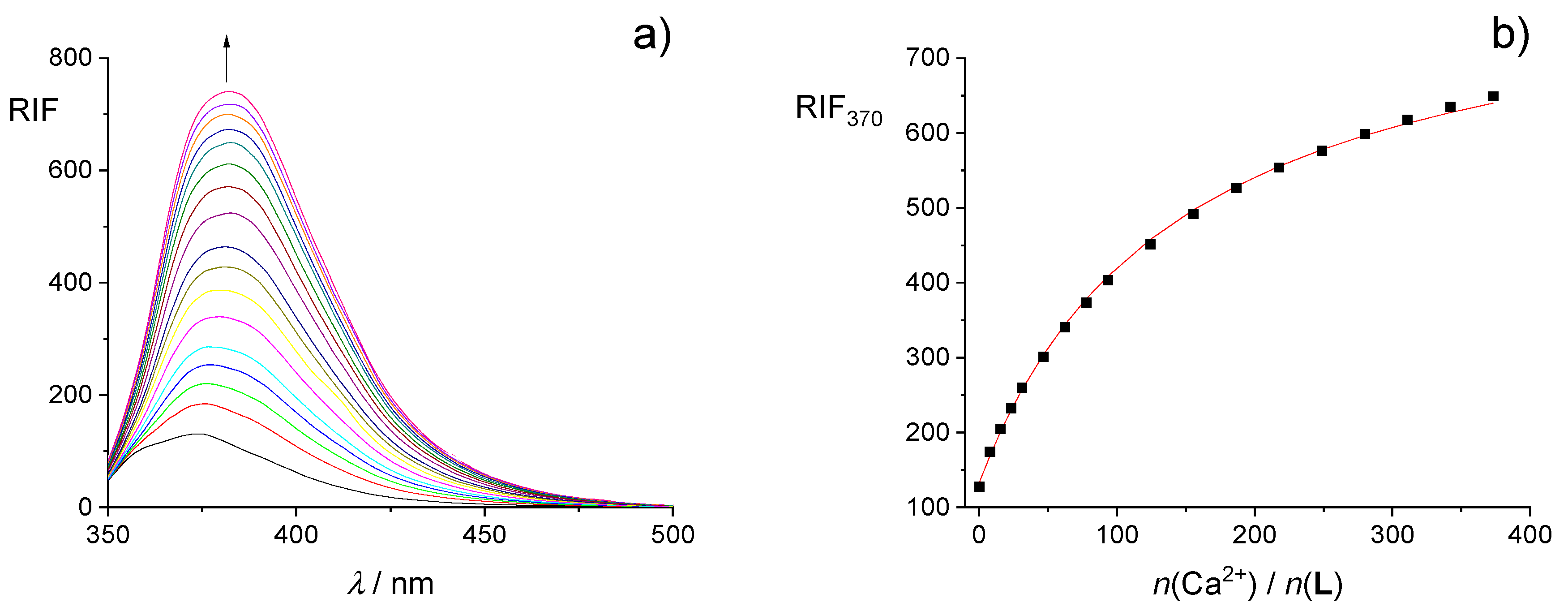
2.1. Complexation in Acetonitrile
2.2. Complexation in Methanol and Ethanol
2.3. NMR Study of Solvent Inclusion in the Hydrophobic Cavity of L and ML2+ Complexes
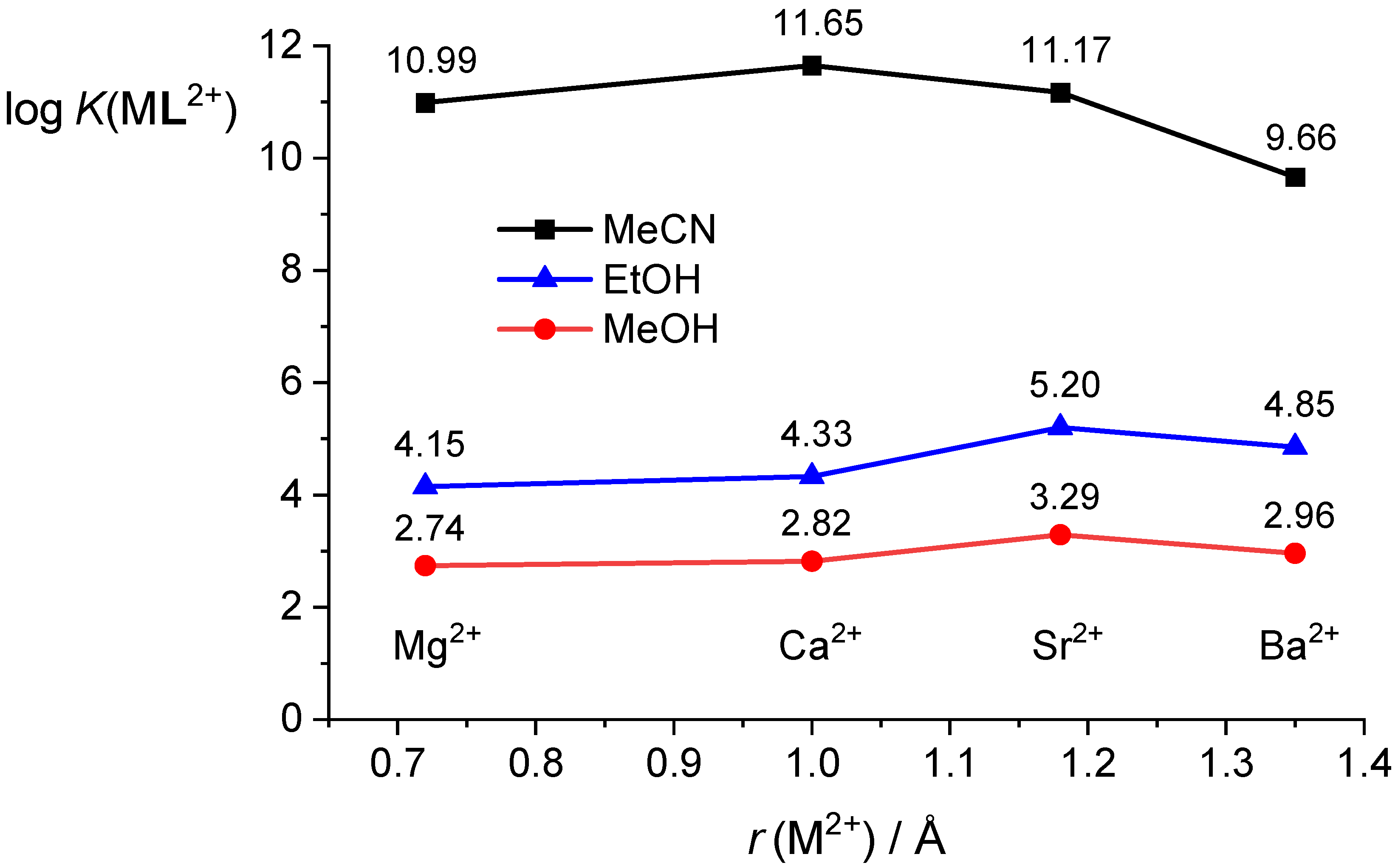
2.4. Comparison of Thermodynamic Complexation Parameters in Acetonitrile and Alcohols
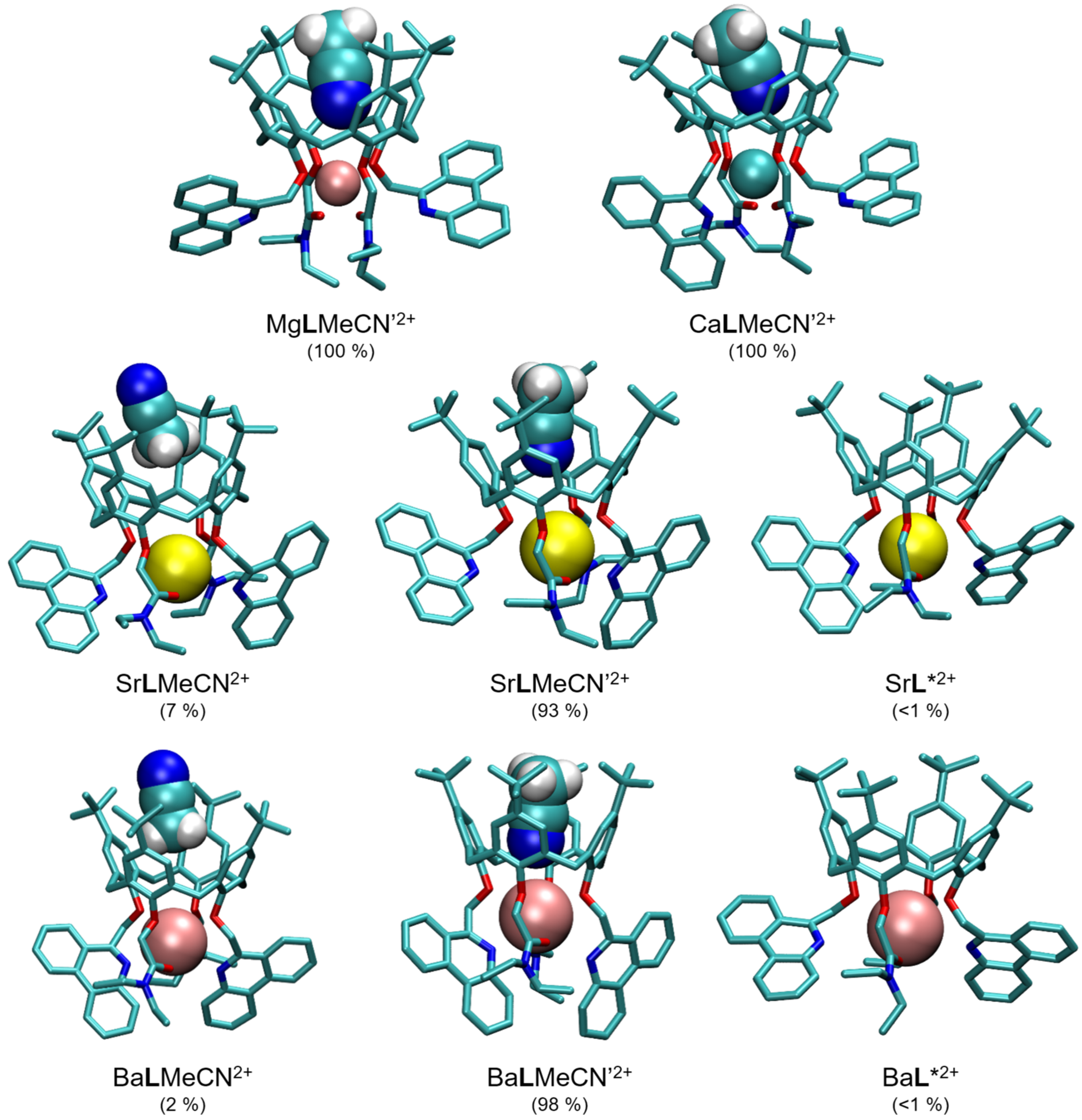
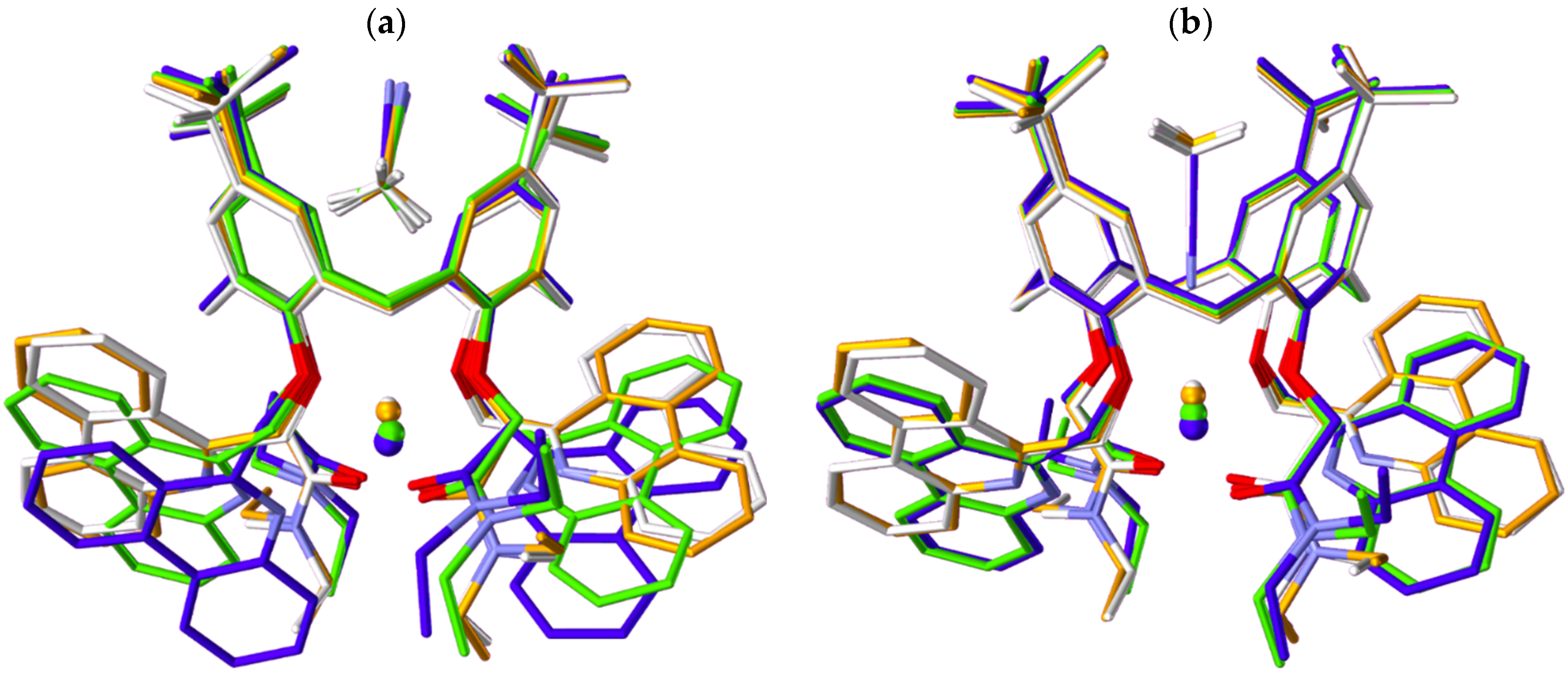
2.5. Quantum Chemical Calculations
3. Materials and Methods
3.1. Physicochemical Measurements
3.2. Computational Investigations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Asfari, Z. Calixarenes 2001; Böhmer, V., Harrowfield, J., Vicens, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; ISBN 978-0-306-47522-1. [Google Scholar]
- Gutsche, C.D. Calixarenes: An Introduction. In Monographs in Supramolecular Chemistry, 2nd ed.; RSC publishing: Cambridge, MA, USA, 2008; ISBN 978-0-85404-258-6. [Google Scholar]
- Neri, P.; Sessler, J.L.; Wang, M.-X. (Eds.) Calixarenes and Beyond; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-31865-3. [Google Scholar]
- Baldini, L.; Sansone, F.; Casnati, A.; Ungaro, R. Calixarenes in Molecular Recognition. In Supramolecular Chemistry; Gale, P.A., Steed, J.W., Eds.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-74640-0. [Google Scholar]
- Kumar, R.; Sharma, A.; Singh, H.; Suating, P.; Kim, H.S.; Sunwoo, K.; Shim, I.; Gibb, B.C.; Kim, J.S. Revisiting Fluorescent Calixarenes: From Molecular Sensors to Smart Materials. Chem. Rev. 2019, 119, 9657–9721. [Google Scholar] [CrossRef] [PubMed]
- Macreadie, L.K.; Gilchrist, A.M.; McNaughton, D.A.; Ryder, W.G.; Fares, M.; Gale, P.A. Progress in Anion Receptor Chemistry. Chem 2022, 8, 46–118. [Google Scholar] [CrossRef]
- Mohammed, F.A.; Xiao, T.; Wang, L.; Elmes, R.B.P. Macrocyclic Receptors for Anion Recognition. Chem. Commun. 2024, 60, 11812–11836. [Google Scholar] [CrossRef]
- Prata, J.V.; Barata, P.D. Fostering Protein–Calixarene Interactions: From Molecular Recognition to Sensing. RSC Adv. 2016, 6, 1659–1669. [Google Scholar] [CrossRef]
- Crowley, P.B. Protein–Calixarene Complexation: From Recognition to Assembly. Acc. Chem. Res. 2022, 55, 2019–2032. [Google Scholar] [CrossRef]
- Chung, T.D.; Kim, H. Electrochemistry of Calixarene and Its Analytical Applications. J. Incl. Phenom. Mol. Recognit. Chem. 1998, 32, 179–193. [Google Scholar] [CrossRef]
- Beer, P.D.; Gale, P.A. Anion Recognition and Sensing: The State of the Art and Future Perspectives. Angew. Chem. Int. Ed. 2001, 40, 486–516. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; Alharthi, S.; El Gamouz, A.; Al Hakawati, N.; Cox, B.G. Calix[4]Based Hg(II) Ion Selective Electrodes: A Thermodynamic Protocol to Address the Selectivity versus the Hosting Capacity Paradigm in the Selection of the Carrier. Electrochim. Acta 2018, 290, 686–694. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; Cleverley, R.M.; Zapata-Ormachea, M.L. Thermodynamics of Calixarene Chemistry. Chem. Rev. 1998, 98, 2495–2526. [Google Scholar] [CrossRef]
- Arnaud-Neu, F.; Barrett, G.; Fanni, S.; Marrs, D.; McGregor, W.; McKervey, M.A.; Schwing-Weill, M.-J.; Vetrogon, V.; Wechsler, S. Extraction and Solution Thermodynamics of Complexation of Alkali and Alkaline-Earth Cations by Calix[4]Arene Amides. J. Chem. Soc. Perkin Trans. 1995, 2, 453. [Google Scholar] [CrossRef]
- Creaven, B.S.; Donlon, D.F.; McGinley, J. Coordination Chemistry of Calix[4]Arene Derivatives with Lower Rim Functionalisation and Their Applications. Coord. Chem. Rev. 2009, 253, 893–962. [Google Scholar] [CrossRef]
- Podyachev, S.N.; Kashapova, N.E.; Syakaev, V.V.; Sudakova, S.N.; Zainullina, R.R.; Gruner, M.; Habicher, W.D.; Barsukova, T.A.; Yang, F.; Konovalov, A.I. Mercury(II) and Silver(I) Receptors Based on Tetrathiacalix[4]Arene Hydrazones. J. Incl. Phenom. Macrocycl. Chem. 2014, 78, 371–380. [Google Scholar] [CrossRef]
- Sviben, I.; Galić, N.; Tomišić, V.; Frkanec, L. Extraction and Complexation of Alkali and Alkaline Earth Metal Cations by Lower-Rim Calix[4]Arene Diethylene Glycol Amide Derivatives. New J. Chem. 2015, 39, 6099–6107. [Google Scholar] [CrossRef]
- Aparicio-Aragon, W.B.; Ramos, T.D.; Namor, A.F.D.D. Effect of the Number of Donor Atoms in Calix[4]Arene Derivatives for Selective Complexation and Extraction of Mercury(II) Cations, Thermodynamics and Extraction Studies. Adv. Chem. Eng. Sci. 2021, 11, 165–179. [Google Scholar] [CrossRef]
- Francisco, V.; Basílio, N.; Garcia-Rio, L.; Leis, J.R.; Maques, E.F.; Vázquez-Vázquez, C. Novel Catanionic Vesicles from Calixarene and Single-Chain Surfactant. Chem. Commun. 2010, 46, 6551–6553. [Google Scholar] [CrossRef]
- Basílio, N.; Garcia-Rio, L.; Martín-Pastor, M. Calixarene-Based Surfactants: Evidence of Structural Reorganization upon Micellization. Langmuir 2012, 28, 2404–2414. [Google Scholar] [CrossRef]
- Basílio, N.; Gómez, B.; Garcia-Rio, L.; Francisco, V. Using Calixarenes to Model Polyelectrolyte Surfactant Nucleation Sites. Chem. Eur. J. 2013, 19, 4570–4576. [Google Scholar] [CrossRef]
- Homden, D.M.; Redshaw, C. The Use of Calixarenes in Metal-Based Catalysis. Chem. Rev. 2008, 108, 5086–5130. [Google Scholar] [CrossRef]
- Sachdeva, G.; Vaya, D.; Srivastava, C.M.; Kumar, A.; Rawat, V.; Singh, M.; Verma, M.; Rawat, P.; Rao, G.K. Calix[n]Arenes and Its Derivatives as Organocatalysts. Coord. Chem. Rev. 2022, 472, 214791. [Google Scholar] [CrossRef]
- Bakirci, H.; Koner, A.L.; Dickman, M.H.; Kortz, U.; Nau, W.M. Dynamically Self-Assembling Metalloenzyme Models Based on Calixarenes. Angew. Chem. Int. Ed. 2006, 45, 7400–7404. [Google Scholar] [CrossRef]
- Schühle, D.T.; Peters, J.A.; Schatz, J. Metal Binding Calixarenes with Potential Biomimetic and Biomedical Applications. Coord. Chem. Rev. 2011, 255, 2727–2745. [Google Scholar] [CrossRef]
- Nimse, S.B.; Kim, T. Biological Applications of Functionalized Calixarenes. Chem. Soc. Rev. 2013, 42, 366–386. [Google Scholar] [CrossRef] [PubMed]
- Rebilly, J.-N.; Colasson, B.; Bistri, O.; Over, D.; Reinaud, O. Biomimetic Cavity-Based Metal Complexes. Chem. Soc. Rev. 2015, 44, 467–489. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Hu, X.; Guo, D. Biomedical Applications of Calixarenes: State of the Art and Perspectives. Angew. Chem. Int. Ed. 2021, 60, 2768–2794. [Google Scholar] [CrossRef] [PubMed]
- Martins, J.N.; Raimundo, B.; Rioboo, A.; Folgar-Cameán, Y.; Montenegro, J.; Basílio, N. Photoswitchable Calixarene Activators for Controlled Peptide Transport across Lipid Membranes. J. Am. Chem. Soc. 2023, 145, 13126–13133. [Google Scholar] [CrossRef]
- Lazar, A.-N.; Perret, F.; Perez-Lloret, M.; Michaud, M.; Coleman, A.W. Promises of Anionic Calix[n]Arenes in Life Science: State of the Art in 2023. Eur. J. Med. Chem 2024, 264, 115994. [Google Scholar] [CrossRef]
- Webber, M.J.; Langer, R. Drug Delivery by Supramolecular Design. Chem. Soc. Rev. 2017, 46, 6600–6620. [Google Scholar] [CrossRef]
- Gaeta, C.; La Manna, P.; De Rosa, M.; Soriente, A.; Talotta, C.; Neri, P. Supramolecular Catalysis with Self-assembled Capsules and Cages: What Happens in Confined Spaces. ChemCatChem 2021, 13, 1638–1658. [Google Scholar] [CrossRef]
- Fan, X.; Guo, X. Development of Calixarene-Based Drug Nanocarriers. J. Mol. Liq. 2021, 325, 115246. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, Y.; Tian, D.; Shin, W.S.; Kim, J.S.; Li, H. Selective Molecular Recognition on Calixarene-Functionalized 3D Surfaces. Chem. Commun. 2016, 52, 12685–12693. [Google Scholar] [CrossRef]
- Kongor, A.R.; Mehta, V.A.; Modi, K.M.; Panchal, M.K.; Dey, S.A.; Panchal, U.S.; Jain, V.K. Calix-Based Nanoparticles: A Review. Top. Curr. Chem. 2016, 374, 28. [Google Scholar] [CrossRef] [PubMed]
- Wei, A. Calixarene-Encapsulated Nanoparticles: Synthesis, Stabilization, and Self-Assembly. In Calixarenes and Beyond; Neri, P., Sessler, J.L., Wang, M.-X., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 921–939. ISBN 978-3-319-31865-3. [Google Scholar]
- Danil de Namor, A.F.; Kowalska, D.; Castellano, E.E.; Piro, O.E.; Sueros Velarde, F.J.; Villanueva Salas, J. Lower Rim Calix(4)Arene Ketone Derivatives and Their Interaction with Alkali Metal Cations. Structural and Thermodynamic (Solution and Complexation) Characterisation of the Tetraphenyl Ketone Derivative and Its Sodium Complex. Phys. Chem. Chem. Phys. 2001, 3, 4010–4021. [Google Scholar] [CrossRef]
- Śliwa, W. Calixarene Complexes with Transition Metal Ions. J. Incl. Phenom. Macrocycl. Chem. 2005, 52, 13–37. [Google Scholar] [CrossRef]
- Śliwa, W.; Girek, T. Calixarene Complexes with Metal Ions. J. Incl. Phenom. Macrocycl. Chem. 2010, 66, 15–41. [Google Scholar] [CrossRef]
- Danil de Namor, A.F. Thermodynamics of Calixarene-Ion Interactions. In Calixarenes 2001; Asfari, Z., Böhmer, V., Harrowfield, J., Vicens, J., Saadioui, M., Eds.; Springer: Dordrecht, The Netherlands, 2001; pp. 346–364. ISBN 978-0-306-47522-1. [Google Scholar]
- Horvat, G.; Frkanec, L.; Cindro, N.; Tomišić, V. A Comprehensive Study of the Complexation of Alkali Metal Cations by Lower Rim Calix[4]Arene Amide Derivatives. Phys. Chem. Chem. Phys. 2017, 19, 24316–24329. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; Matsufuji-Yasuda, T.T.; Zegarra-Fernandez, K.; Webb, O.A.; El Gamouz, A. An Enchiridion of Supramolecular Thermodynamics: Calix[N]Arene (N=4,5,6) Tertiary Amide Derivatives and Their Ionic Recognition. Croat. Chem. Acta 2013, 86, 1–19. [Google Scholar] [CrossRef]
- Horvat, G.; Stilinović, V.; Hrenar, T.; Kaitner, B.; Frkanec, L.; Tomišić, V. An Integrated Approach (Thermodynamic, Structural, and Computational) to the Study of Complexation of Alkali-Metal Cations by a Lower-Rim Calix[4]Arene Amide Derivative in Acetonitrile. Inorg. Chem. 2012, 51, 6264–6278. [Google Scholar] [CrossRef]
- Horvat, G.; Stilinović, V.; Kaitner, B.; Frkanec, L.; Tomišić, V. The Effect of Specific Solvent-Solute Interactions on Complexation of Alkali-Metal Cations by a Lower-Rim Calix[4]Arene Amide Derivative. Inorg. Chem. 2013, 52, 12702–12712. [Google Scholar] [CrossRef]
- Požar, J.; Nikšić-Franjić, I.; Cvetnić, M.; Leko, K.; Cindro, N.; Pičuljan, K.; Borilović, I.; Frkanec, L.; Tomišić, V. Solvation Effect on Complexation of Alkali Metal Cations by a Calix[4]Arene Ketone Derivative. J. Phys. Chem. B 2017, 121, 8539–8550. [Google Scholar] [CrossRef]
- Nomura, E.; Takagaki, M.; Nakaoka, C.; Uchida, M.; Taniguchi, H. Effects on Metal Binding of Circular NH---OC Intramolecular Hydrogen Bonding in Hydrophilic Pseudocavities of p-Tert-Butylcalix[4]Arenes Carrying Amino Acid Moieties. J. Org. Chem. 1999, 64, 3151–3156. [Google Scholar] [CrossRef]
- Frkanec, L.; Višnjevac, A.; Kojić-Prodić, B.; Žinić, M. Calix[4]Arene Amino Acid Derivatives. Intra- and Intermolecular Hydrogen-Bonded Organisation in Solution and the Solid State. Chem. Eur. J. 2000, 6, 442–453. [Google Scholar] [CrossRef]
- Tomišić, V.; Galić, N.; Bertoša, B.; Frkanec, L.; Simeon, V.; Žinić, M. Hydrogen Bonding and Solvent Effects on Complexation of Alkali Metal Cations by Lower Rim Calix[4]Arene Tetra(O-[N-Acetyl-D-Phenylglycine Methyl Ester]) Derivative. J. Incl. Phenom. Macrocycl. Chem. 2005, 53, 263–268. [Google Scholar] [CrossRef]
- Požar, J.; Cvetnić, M.; Usenik, A.; Cindro, N.; Horvat, G.; Leko, K.; Modrušan, M.; Tomišić, V. The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]Arene Derivatives. Molecules 2022, 27, 470. [Google Scholar] [CrossRef] [PubMed]
- Danil de Namor, A.F.; Chahine, S.; Kowalska, D.; Castellano, E.E.; Piro, O.E. Selective Interaction of Lower Rim Calix[4]Arene Derivatives and Bivalent Cations in Solution. Crystallographic Evidence of the Versatile Behavior of Acetonitrile in Lead(II) and Cadmium(II) Complexes. J. Am. Chem. Soc. 2002, 124, 12824–12836. [Google Scholar] [CrossRef]
- Leko, K.; Bregović, N.; Cvetnić, M.; Cindro, N.; Tranfić Bakić, M.; Požar, J.; Tomišić, V. Complexation of Alkali Metal Cations by a Tertiary Amide Calix[4]Arene Derivative in Strongly Cation Solvating Solvents. Croat. Chem. Acta 2017, 90, 307–314. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; Chahine, S.; Castellano, E.E.; Piro, O.E. Solvent Control on the Selective, Nonselective, and Absent Response of a Partially Substituted Lower Rim Calix(4)Arene Derivative for Soft Metal Cations (Mercury(II) and Silver(I)). Structural and Thermodynamic Studies. J. Phys. Chem. A 2005, 109, 6743–6751. [Google Scholar] [CrossRef]
- De Araujo, A.S.; Piro, O.E.; Castellano, E.E.; Danil de Namor, A.F. Combined Crystallographic and Solution Molecular Dynamics Study of Allosteric Effects in Ester and Ketonep-tert-Butylcalix[4]Arene Derivatives and Their Complexes with Acetonitrile, Cd(II), and Pb(II). J. Phys. Chem. A 2008, 112, 11885–11894. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; De Sueros, N.A.; McKervey, M.A.; Barrett, G.; Neu, F.A.; Schwing-Weill, M.J. The Solution Thermodynamics of Ethyl p-tert-Butylcalix[4]Arene Tetraacetate and Its Alkali Metal Complexes in Acetonitrile and Methanol. J. Chem. Soc. Chem. Commun. 1991, 21, 1546. [Google Scholar] [CrossRef]
- Kim, J.S.; Quang, D.T. Calixarene-Derived Fluorescent Probes. Chem. Rev. 2007, 107, 3780–3799. [Google Scholar] [CrossRef]
- Mako, T.L.; Racicot, J.M.; Levine, M. Supramolecular Luminescent Sensors. Chem. Rev. 2019, 119, 322–477. [Google Scholar] [CrossRef]
- Tranfić Bakić, M.; Jadreško, D.; Hrenar, T.; Horvat, G.; Požar, J.; Galić, N.; Sokol, V.; Tomaš, R.; Alihodžić, S.; Žinić, M.; et al. Fluorescent Phenanthridine-Based Calix[4]Arene Derivatives: Synthesis and Thermodynamic and Computational Studies of Their Complexation with Alkali-Metal Cations. RSC Adv. 2015, 5, 23900–23914. [Google Scholar] [CrossRef]
- Galić, N.; Burić, N.; Tomaš, R.; Frkanec, L.; Tomišić, V. Synthesis and Cation Binding Properties of Fluorescent Calix[4]Arene Derivatives Bearing Tryptophan Units at the Lower Rim. Supramol. Chem. 2011, 23, 389–397. [Google Scholar] [CrossRef]
- Bregović, N.; Cindro, N.; Frkanec, L.; Tomišić, V. Complexation of Fluoride Anion and Its Ion Pairs with Alkali Metal Cations by Tetra-Substituted Lower Rim Calix[4]Arene Tryptophan Derivative. Supramol. Chem. 2016, 28, 608–615. [Google Scholar] [CrossRef]
- Tranfić Bakić, M.; Leko, K.; Cindro, N.; Portada, T.; Hrenar, T.; Frkanec, L.; Horvat, G.; Požar, J.; Tomišić, V. Synthesis of Fluorescent Diphenylantracene-Based Calix[4]Arene Derivatives and Their Complexation with Alkali Metal Cations. Croat. Chem. Acta 2017, 90, 711–725. [Google Scholar] [CrossRef]
- Leko, K.; Usenik, A.; Cindro, N.; Modrušan, M.; Požar, J.; Horvat, G.; Stilinović, V.; Hrenar, T.; Tomišić, V. Enhancing the Cation-Binding Ability of Fluorescent Calixarene Derivatives: Structural, Thermodynamic, and Computational Studies. ACS Omega 2023, 8, 43074–43087. [Google Scholar] [CrossRef]
- Modrušan, M.; Cindro, N.; Usenik, A.; Leko, K.; Glazer, L.; Tomaš, R.; Horvat, G.; Požar, J.; Tomišić, V. Complexation of Alkali and Alkaline Earth Metal Cations by Fluorescent Glycoconjugated Calix[4]Arene Derivative: Thermodynamic and Computational Studies. Croat. Chem. Acta 2024, 97, 1–15. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31278-1. [Google Scholar]
- Valeur, B.; Leray, I. Ion-Responsive Supramolecular Fluorescent Systems Based on Multichromophoric Calixarenes: A Review. Inorg. Chim. Acta 2007, 360, 765–774. [Google Scholar] [CrossRef]
- Požar, J.; Preočanin, T.; Frkanec, L.; Tomišić, V. Thermodynamics of Complexation of Alkali Metal Cations by a Lower-Rim Calix[4]Arene Amino Acid Derivative. J. Solut. Chem. 2010, 39, 835–848. [Google Scholar] [CrossRef]
- Marcus, Y. Ion Properties; Dekker: New York, NY, USA; Basel, Switzerland, 1997; ISBN 978-0-8247-0011-9. [Google Scholar]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 95th ed.; CRC Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Gans, P.; Sabatini, A.; Vacca, A. Investigation of Equilibria in Solution. Determination of Equilibrium Constants with the HYPERQUAD Suite of Programs. Talanta 1996, 43, 1739–1753. [Google Scholar] [CrossRef]
- Briggner, L.-E.; Wadsö, I. Test and Calibration Processes for Microcalorimeters, with Special Reference to Heat Conduction Instruments Used with Aqueous Systems. J. Biochem. Biophys. Methods 1991, 22, 101–118. [Google Scholar] [CrossRef]
- Gans, P.; Sabatini, A.; Vacca, A. Simultaneous Calculation of Equilibrium Constants and Standard Formation Enthalpies from Calorimetric Data for Systems with Multiple Equilibria in Solution. J. Solut. Chem. 2008, 37, 467–476. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Van Der Spoel, D.; Van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; Van Der Spoel, D. GROMACS 3.0: A Package for Molecular Simulation and Trajectory Analysis. J. Mol. Model. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Won, Y. Force Field for Monovalent, Divalent, and Trivalent Cations Developed under the Solvent Boundary Potential. J. Phys. Chem. A 2012, 116, 11763–11767. [Google Scholar] [CrossRef]
- Allouche, A.-R. Gabedit—A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM General Force Field to Sulfonyl-containing Compounds and Its Utility in Biomolecular Simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed]
- Goga, N.; Rzepiela, A.J.; De Vries, A.H.; Marrink, S.J.; Berendsen, H.J.C. Efficient Algorithms for Langevin and DPD Dynamics. J. Chem. Theory Comput. 2012, 8, 3637–3649. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics. Phys. Chem. Chem. Phys. 2012, 14, 16187–16191. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Hrenar, T.; Primožič, I.; Fijan, D.; Majerić Elenkov, M. Conformational Analysis of Spiro-Epoxides by Principal Component Analysis of Molecular Dynamics Trajectories. Phys. Chem. Chem. Phys. 2017, 19, 31706–31713. [Google Scholar] [CrossRef] [PubMed]
- Primožič, I.; Hrenar, T.; Baumann, K.; Krišto, L.; Križić, I.; Tomić, S. Mechanochemical and Conformational Study of N-Heterocyclic Carbonyl-Oxime Transformations. Croat. Chem. Acta 2014, 87, 153–160. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Jović, O.; Smolić, T.; Primožič, I.; Hrenar, T. Spectroscopic and Chemometric Analysis of Binary and Ternary Edible Oil Mixtures: Qualitative and Quantitative Study. Anal. Chem. 2016, 88, 4516–4524. [Google Scholar] [CrossRef] [PubMed]
- Ramić, A.; Skočibušić, M.; Odžak, R.; Čipak Gašparović, A.; Milković, L.; Mikelić, A.; Sović, K.; Primožič, I.; Hrenar, T. Antimicrobial Activity of Quasi-Enantiomeric Cinchona Alkaloid Derivatives and Prediction Model Developed by Machine Learning. Antibiotics 2021, 10, 659. [Google Scholar] [CrossRef] [PubMed]
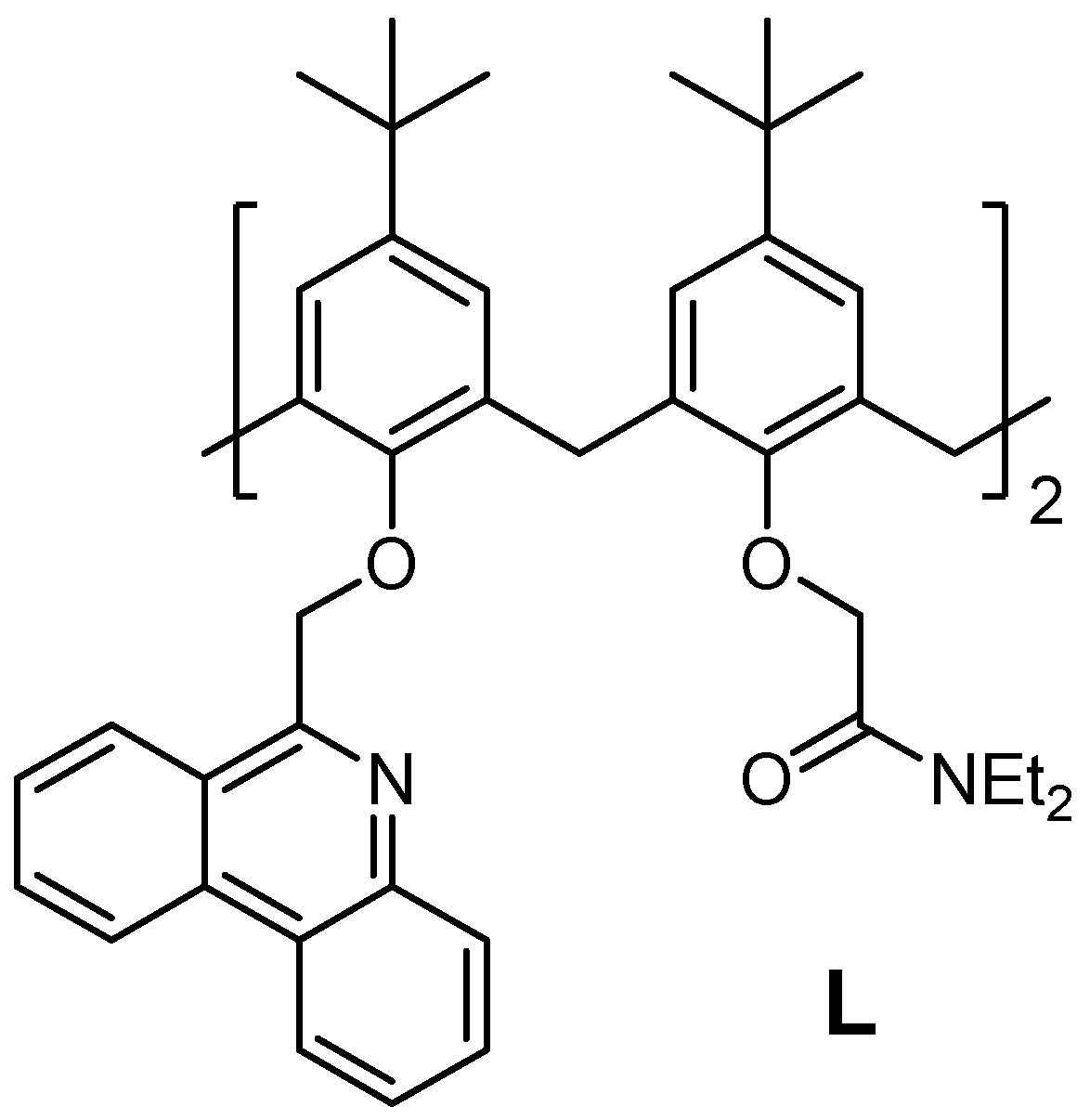




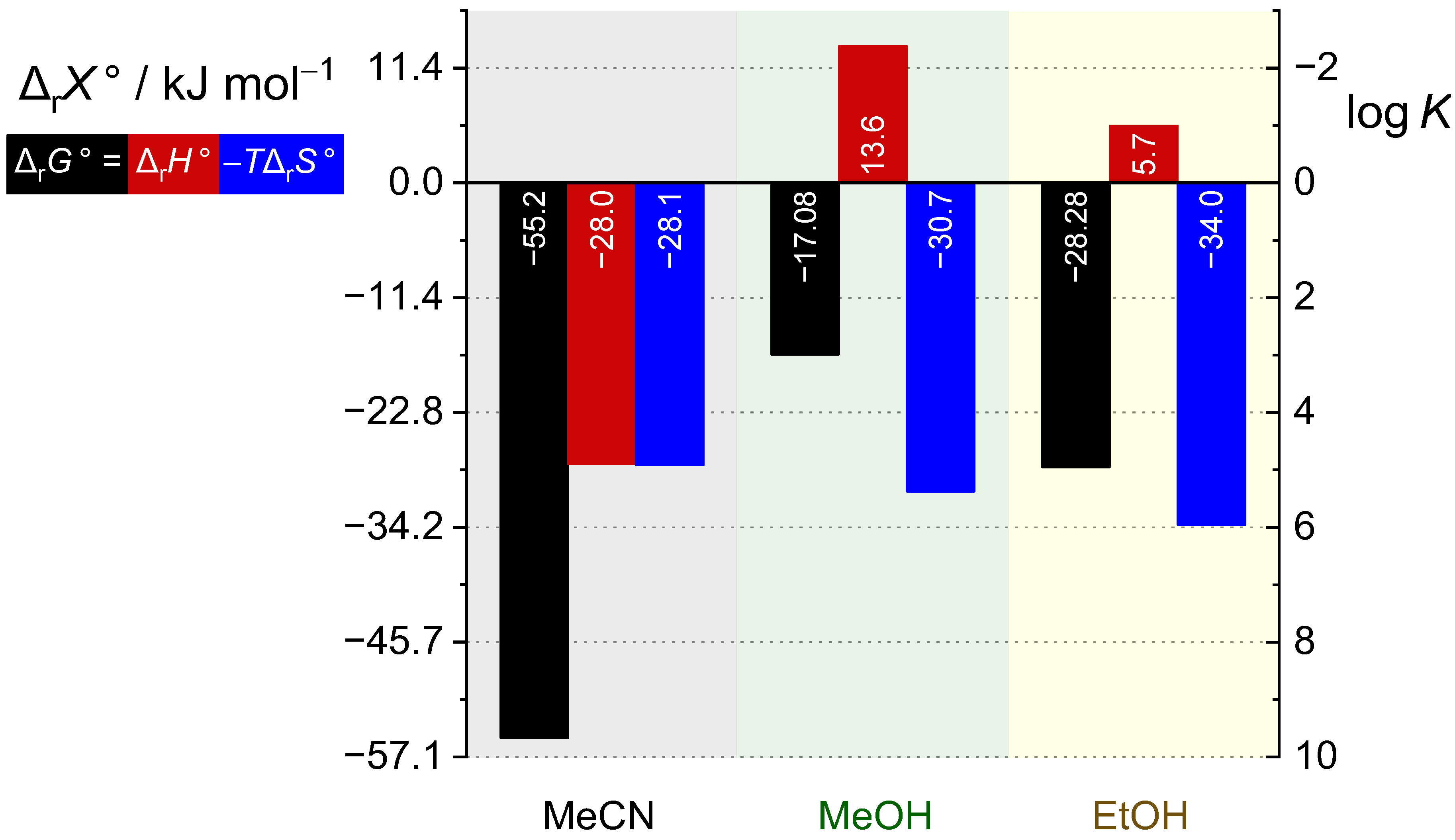
| Cation | a | a | b | a,b |
|---|---|---|---|---|
| Mg2+ | 10.99(3) | −62.7(2) | ||
| Ca2+ | 11.65(5) | −66.5(3) | −49.4(7) −47.28(4) c | 59(3) |
| Sr2+ | 11.17(2) | −63.7(1) | −37.3(5) | 91(2) |
| Ba2+ | 9.66(2) | −55.2(1) | −28.0(4) −28.5(5) c | 94(1) |
| Solvent | Cation | c | c | ||||
|---|---|---|---|---|---|---|---|
| a | b | c | |||||
| MeOH | Mg2+ | 2.74(2) | −15.6(1) a | ≈0 | |||
| Ca2+ | 2.82(2) | 2.15(4) | −16.1(1) a | ||||
| Sr2+ | 3.29(2) | 3.29(2) | 3.49(2) | −19.9(1) c | 12.2(4) | 108(1) | |
| Ba2+ | 2.96(1) | 2.69(1) | 2.99(1) | −17.08(1) c | 13.6(5) | 103(2) | |
| EtOH | Mg2+ | 4.15(2) | −23.7(1) a | ≈0 | |||
| Ca2+ | 4.33(2) | 3.78(1) | 4.30(5) | −24.6(3) c | 7.2(5) | 107(1) | |
| Sr2+ | 5.20(2) | 5.25(1) | 5.09(2) | −29.1(2) c | 3.5(1) | 109(1) | |
| Ba2+ | 4.85(3) | 4.87(2) | 4.95(1) | −28.28(5) c | 5.7(2) | 114(1) | |
| Cation | ML*2+ | MLMeCN2+ | MLMeCN′2+ |
|---|---|---|---|
| r/Å (Plane a to Cation) | |||
| Mg2+ | 0.678 | 0.684 | 0.451 |
| Ca2+ | 0.770 | 0.788 | 0.566 |
| Sr2+ | 1.225 | 1.237 | 0.948 |
| Ba2+ | 1.399 | 1.411 | 1.207 |
| r/Å (Plane a to Solvent b) | |||
| Mg2+ | – | 4.757 | 3.112 |
| Ca2+ | – | 4.821 | 3.280 |
| Sr2+ | – | 4.839 | 3.082 |
| Ba2+ | – | 4.808 | 3.027 |
| r/Å (Cation to Solvent b) | |||
| Mg2+ | – | 5.494 | 3.564 |
| Ca2+ | – | 5.655 | 3.847 |
| Sr2+ | – | 6.129 | 4.030 |
| Ba2+ | – | 6.262 | 4.234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usenik, A.; Modrušan, M.; Leko, K.; Borovec, J.; Marinac, S.; Hok, L.; Cindro, N.; Vianello, R.; Horvat, G.; Požar, J.; et al. A Combined Thermodynamic and Computational Study of Alkaline Earth Metal Cations Complexation by a Fluorescent Calix[4]arene Receptor. Int. J. Mol. Sci. 2025, 26, 1264. https://doi.org/10.3390/ijms26031264
Usenik A, Modrušan M, Leko K, Borovec J, Marinac S, Hok L, Cindro N, Vianello R, Horvat G, Požar J, et al. A Combined Thermodynamic and Computational Study of Alkaline Earth Metal Cations Complexation by a Fluorescent Calix[4]arene Receptor. International Journal of Molecular Sciences. 2025; 26(3):1264. https://doi.org/10.3390/ijms26031264
Chicago/Turabian StyleUsenik, Andrea, Matija Modrušan, Katarina Leko, Jakov Borovec, Sven Marinac, Lucija Hok, Nikola Cindro, Robert Vianello, Gordan Horvat, Josip Požar, and et al. 2025. "A Combined Thermodynamic and Computational Study of Alkaline Earth Metal Cations Complexation by a Fluorescent Calix[4]arene Receptor" International Journal of Molecular Sciences 26, no. 3: 1264. https://doi.org/10.3390/ijms26031264
APA StyleUsenik, A., Modrušan, M., Leko, K., Borovec, J., Marinac, S., Hok, L., Cindro, N., Vianello, R., Horvat, G., Požar, J., Hrenar, T., & Tomišić, V. (2025). A Combined Thermodynamic and Computational Study of Alkaline Earth Metal Cations Complexation by a Fluorescent Calix[4]arene Receptor. International Journal of Molecular Sciences, 26(3), 1264. https://doi.org/10.3390/ijms26031264











