Cost-Effective, Ester-Based Molecular Doping in Silicon
Abstract
1. Introduction
2. Materials and Methods
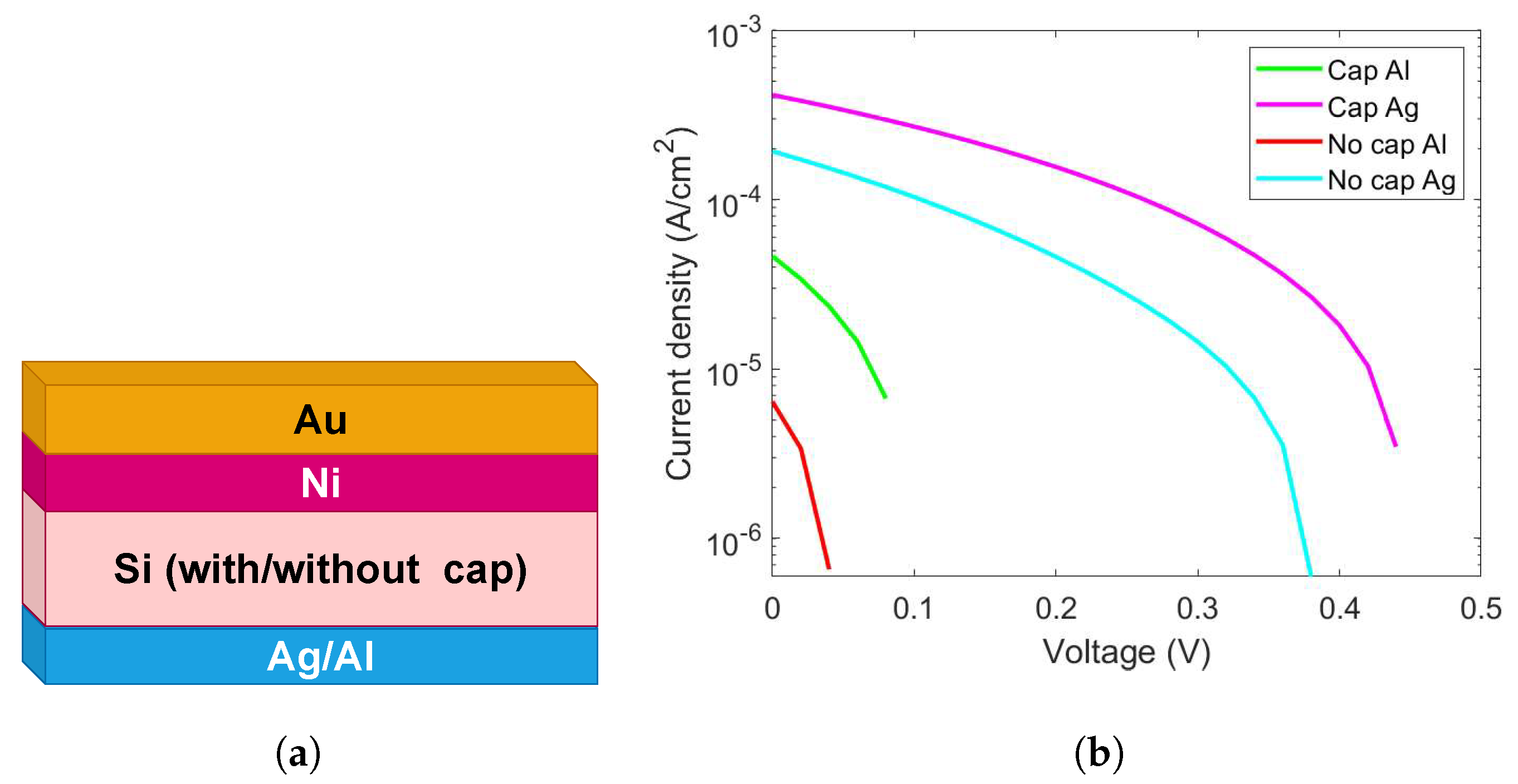
2.1. Device Fabrication
2.2. Shockley Equation Fit
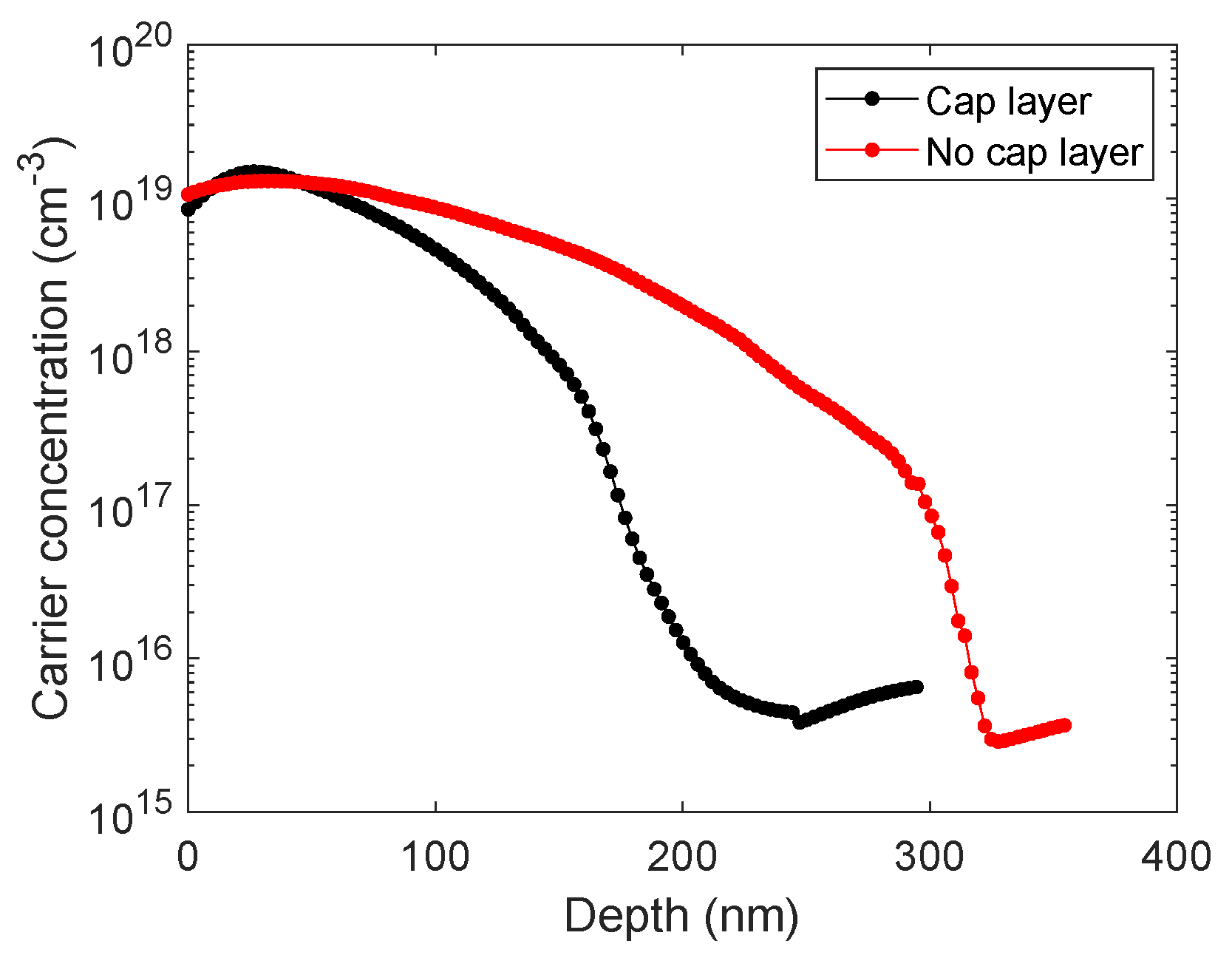
3. Results and Discussion
Fitting Results
4. Solar Cell Simulation (Proof-of-Principle)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ray, A.; Nori, R.; Bhatt, P.; Lodha, S.; Pinto, R.; Rao, V.R.; Jomard, F.; Neumann-Spallart, M. Optimization of a plasma immersion ion implantation process for shallow junctions in silicon. J. Vac. Sci. Technol. A 2014, 32, 061302. [Google Scholar] [CrossRef]
- Ho, J.C.; Yerushalmi, R.; Jacobson, Z.A.; Fan, Z.; Alley, R.L.; Javey, A. Controlled nanoscale doping of semiconductors via molecular monolayers. Nat. Mater. 2008, 7, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.C.; Yerushalmi, R.; Smith, G.; Majhi, P.; Bennett, J.; Halim, J.; Faifer, V.N.; Javey, A. Wafer-Scale, Sub-5 nm Junction Formation by Monolayer Doping and Conventional Spike Annealing. Nano Lett. 2009, 9, 725–730. [Google Scholar] [CrossRef][Green Version]
- Ho, J.C.; Ford, A.C.; Chueh, Y.L.; Leu, P.W.; Ergen, O.; Takei, K.; Smith, G.; Majhi, P.; Bennett, J.; Javey, A. Nanoscale doping of InAs via sulfur monolayers. Appl. Phys. Lett. 2009, 95, 72108. [Google Scholar] [CrossRef]
- Gouzman, I.; Dubey, M.; Carolus, M.D.; Schwartz, J.; Bernasek, S.L. Monolayer vs. multilayer self-assembled alkylphosphonate films: X-ray photoelectron spectroscopy studies. Surf. Sci. 2006, 600, 773–781. [Google Scholar] [CrossRef]
- Voorthuijzen, W.P.; Yilmaz, M.D.; Naber, W.J.M.; Huskens, J.; van der Wiel, W.G. Local Doping of Silicon Using Nanoimprint Lithography and Molecular Monolayers. Adv. Mater. 2011, 23, 1346–1350. [Google Scholar] [CrossRef]
- Garozzo, C.; Giannazzo, F.; Italia, M.; La Magna, A.; Privitera, V.; Puglisi, R.A. Radial junctions formed by conformal chemical doping for innovative hole-based solar cells. Mater. Sci. Eng. B 2013, 178, 686–690. [Google Scholar] [CrossRef]
- Elbersen, R.; Vijselaar, W.; Tiggelaar, R.M.; Gardeniers, H.; Huskens, J. Fabrication and Doping Methods for Silicon Nano- and Micropillar Arrays for Solar-Cell Applications: A Review. Adv. Mater. 2015, 27, 6781–6796. [Google Scholar] [CrossRef]
- Alphazan, T.; Mathey, L.; Schwarzwälder, M.; Lin, T.H.; Rossini, A.J.; Wischert, R.; Enyedi, V.; Fontaine, H.; Veillerot, M.; Lesage, A.; et al. Monolayer Doping of Silicon through Grafting a Tailored Molecular Phosphorus Precursor onto Oxide-Passivated Silicon Surfaces. Chem. Mater. 2016, 28, 3634–3640. [Google Scholar] [CrossRef]
- Fu, J.; Chen, K.; Chang, S.; Zhi, K.; Gao, X.; Wei, H.; Dan, Y. Dopant activation and photoresponses of boron-doped silicon by self-assembled molecular monolayers. AIP Adv. 2019, 9, 125219. [Google Scholar] [CrossRef]
- Pizzone, M.; Grimaldi, M.G.; La Magna, A.; Rahmani, N.; Scalese, S.; Adam, J.; Puglisi, R.A. Study of the Molecule Adsorption Process during the Molecular Doping. Nanomaterials 2021, 11, 1899. [Google Scholar] [CrossRef] [PubMed]
- Longo, R.C.; Mattson, E.C.; Vega, A.; Cabrera, W.; Cho, K.; Chabal, Y.J.; Thissen, P. Mechanism of Arsenic Monolayer Doping of Oxide-Free Si(111). Chem. Mater. 2016, 28, 1975–1979. [Google Scholar] [CrossRef]
- Caccamo, S.; Puglisi, R.A.; Di Franco, S.; D’Urso, L.; Indelicato, V.; Italia, M.; Pannitteri, S.; La Magna, A. Silicon doped by molecular doping technique: Role of the surface layers of doped Si on the electrical characteristics. Mat. Sci. Semic. Proc. 2016, 42, 200–203. [Google Scholar] [CrossRef]
- Pizzone, M.; Grimaldi, M.G.; La Magna, A.; Scalese, S.; Adam, J.; Puglisi, R.A. Molecule Clustering Dynamics in the Molecular Doping Process of Si(111) with Diethyl-propyl-phosphonate. Int. J. Mol. Sci. 2023, 24, 6877. [Google Scholar] [CrossRef]
- Barnett, J.; Hill, R.; Loh, W.Y.; Hobbs, C.; Majhi, P.; Jammy, R. Advanced techniques for achieving ultra-shallow junctions in future CMOS devices. In Proceedings of the 2010 International Workshop on Junction Technology Extended Abstracts, Shanghai, China, 10–11 May 2010; pp. 1–4. [Google Scholar] [CrossRef]
- O’Connell, J.; Verni, G.A.; Gangnaik, A.; Shayesteh, M.; Long, B.; Georgiev, Y.M.; Petkov, N.; McGlacken, G.P.; Morris, M.A.; Duffy, R.; et al. Organo-arsenic Molecular Layers on Silicon for High-Density Doping. ACS Appl. Mater. Interfaces 2015, 7, 15514–15521. [Google Scholar] [CrossRef]
- Kwon, B.; Bae, H.; Lee, H.; Kim, S.; Hwang, J.; Lim, H.; Lee, J.H.; Cho, K.; Ye, J.; Lee, S.; et al. Ultrasensitive N-Channel Graphene Gas Sensors by Nondestructive Molecular Doping. ACS Nano 2022, 16, 2176–2187. [Google Scholar] [CrossRef]
- Puglisi, R.A.; Lombardo, V.; Caccamo, S. Silicon Quasi-One-Dimensional Nanostructures for Photovoltaic Applications. In Nanowires-New Insights; Maaz, K., Ed.; IntechOpen: Rijeka, Croatia, 2017; Chapter 7. [Google Scholar] [CrossRef]
- Palmisano, L.; Diantoro, M.; Suprayogi, T.; Hidayat, A.; Taufiq, A.; Fuad, A.; Suryana, R. Shockley’s Equation Fit Analyses for Solar Cell Parameters from I-V Curves. Int. J. Photoenergy 2018, 2018, 9214820. [Google Scholar] [CrossRef]
- Servaites, J.D.; Yeganeh, S.; Marks, T.J.; Ratner, M.A. Efficiency Enhancement in Organic Photovoltaic Cells: Consequences of Optimizing Series Resistance. Adv. Funct. Mater. 2010, 20, 97–104. [Google Scholar] [CrossRef]
- Bowden, S.; Rohatgi, A. Rapid and Accurate Determination of Series Resistance and Fill Factor Losses in Industrial Silicon Solar Cells. In Proceedings of the 17th European Photovoltaic Solar Energy Conference, Munich, Germany, 22 October 2001. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Navi Mumbai, MA, USA, 2007. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- LMFIT: Non-Linear Least-Squares Minimization and Curve-Fitting for Python. 2021. Available online: https://lmfit.github.io/lmfit-py/ (accessed on 20 July 2021).
- Puglisi, R.A.; Caccamo, S.; Bongiorno, C.; Fisicaro, G.; Genovese, L.; Goedecker, S.; Mannino, G.; La Magna, A. Direct observation of single organic molecules grafted on the surface of a silicon nanowire. Sci. Rep. 2019, 9, 5647. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Guan, B.; Mesli, A.; Chen, K.; Dan, Y. Deep level transient spectroscopic investigation of phosphorus-doped silicon by self-assembled molecular monolayers. Nat. Commun. 2018, 9, 118. [Google Scholar] [CrossRef] [PubMed]
- Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced electrical simulation of thin film solar cells. Thin Solid Film. 2013, 535, 296–301. [Google Scholar] [CrossRef]
- Decock, K.; Zabierowski, P.; Burgelman, M. Modeling metastabilities in chalcopyrite-based thin film solar cells. J. Appl. Phys. 2012, 111, 043703. [Google Scholar] [CrossRef]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics, 95th ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]

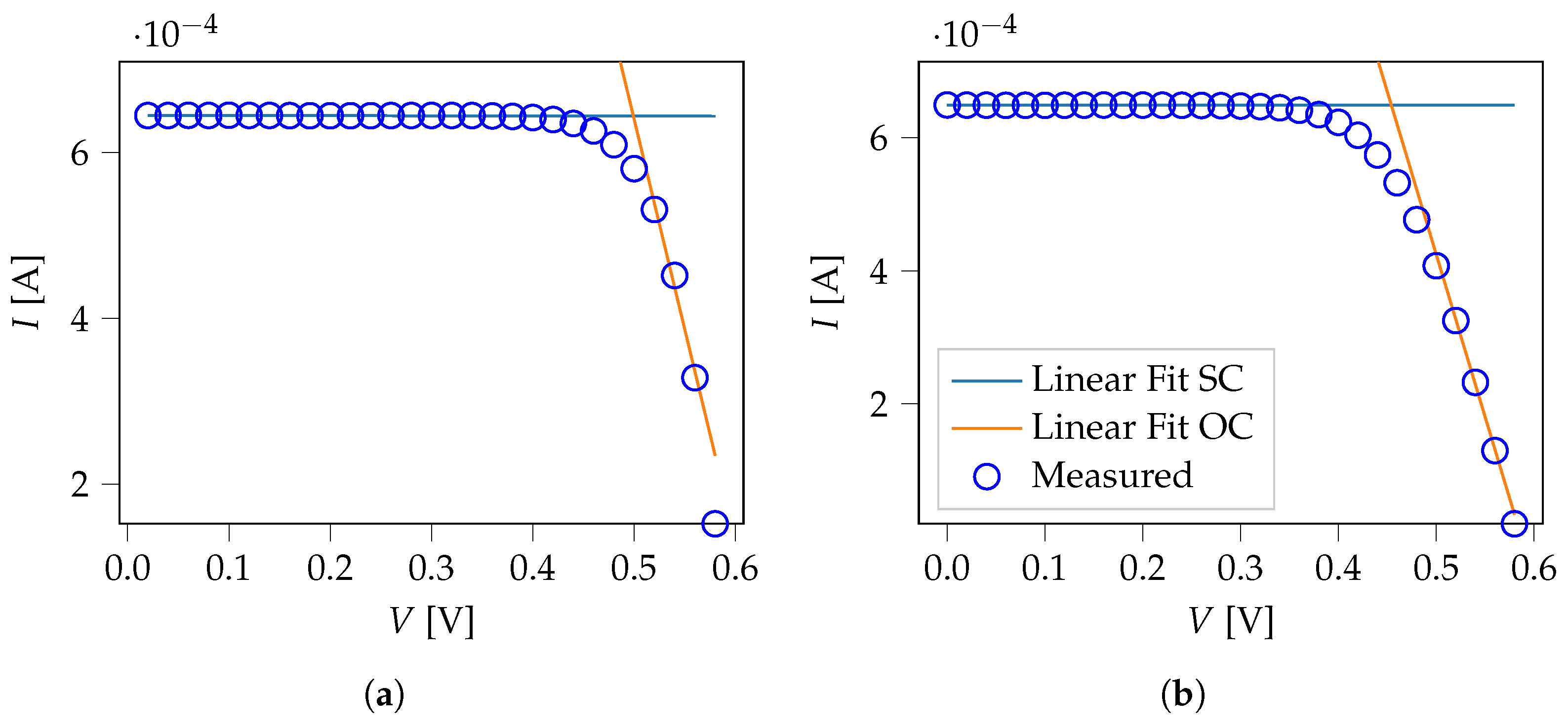

| Cell | (A) | (A) | () | () | n | |
|---|---|---|---|---|---|---|
| 1 | 6.45 × 10−4 | 6.84 × 10−12 | 32.57 | 6.04 × 1012 | 1.26 | 3.94 × 10−12 |
| 2 | 6.49 × 10−4 | 1.78 × 10−11 | 123.55 | 4.12 × 1013 | 1.30 | 7.15 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrivastava, A.; Adam, J.; Puglisi, R.A. Cost-Effective, Ester-Based Molecular Doping in Silicon. Int. J. Mol. Sci. 2025, 26, 1024. https://doi.org/10.3390/ijms26031024
Shrivastava A, Adam J, Puglisi RA. Cost-Effective, Ester-Based Molecular Doping in Silicon. International Journal of Molecular Sciences. 2025; 26(3):1024. https://doi.org/10.3390/ijms26031024
Chicago/Turabian StyleShrivastava, Anup, Jost Adam, and Rosaria A. Puglisi. 2025. "Cost-Effective, Ester-Based Molecular Doping in Silicon" International Journal of Molecular Sciences 26, no. 3: 1024. https://doi.org/10.3390/ijms26031024
APA StyleShrivastava, A., Adam, J., & Puglisi, R. A. (2025). Cost-Effective, Ester-Based Molecular Doping in Silicon. International Journal of Molecular Sciences, 26(3), 1024. https://doi.org/10.3390/ijms26031024







