Self-Guided Molecular Simulation Methods
Abstract
1. Introduction
2. Methods and Algorithms
2.1. The Equation of Self-Guided Motion
2.2. Conformational Distribution of SGMD/SGLD
2.3. A Leap-Frog Algorithm for SGMD/SGLD
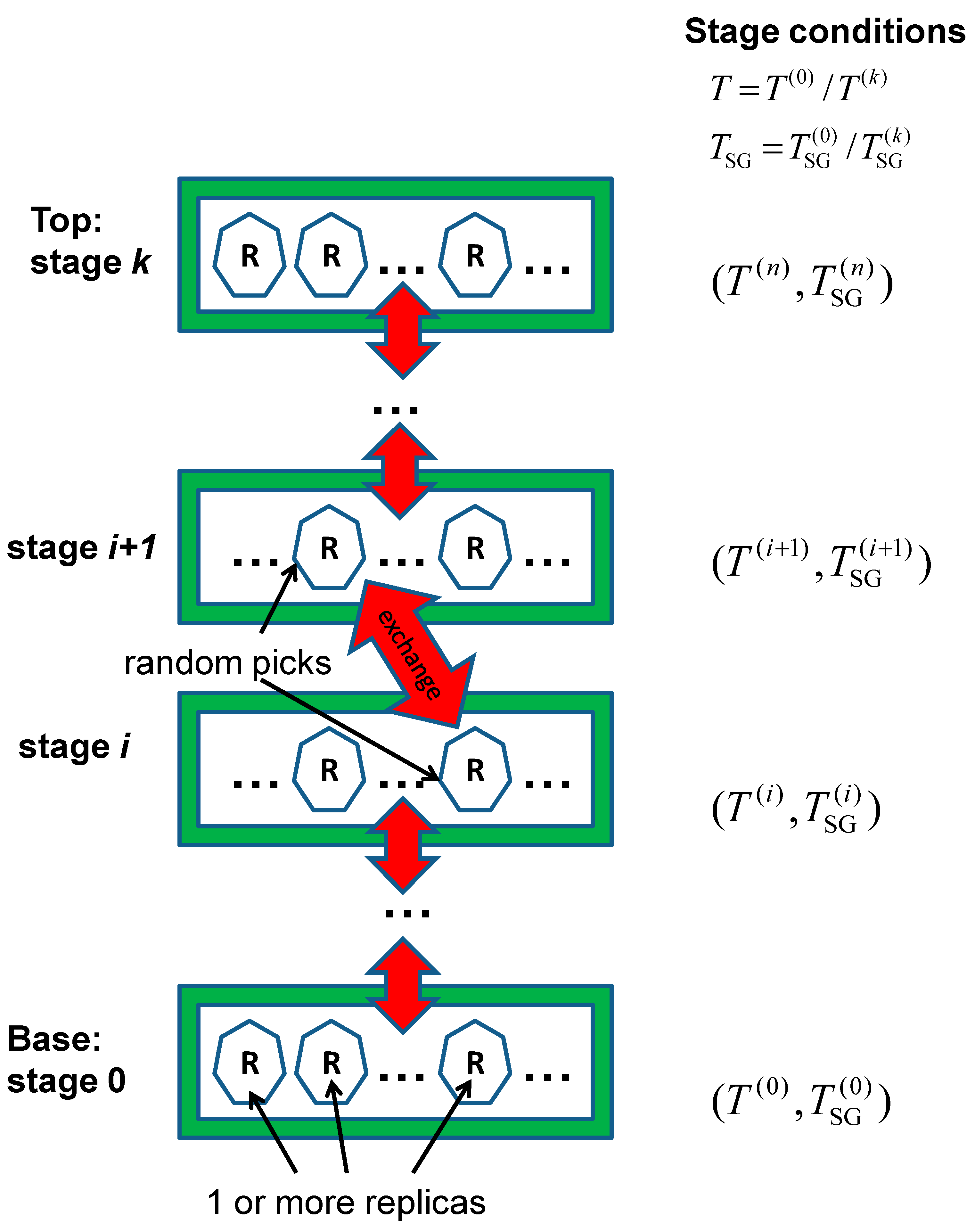
2.4. Replica-Exchanging Self-Guided Langevin Dynamics (RXSGLD)
2.5. Self-Guided Langevin Dynamics via Generalized Langevin Equation
3. Example Simulations
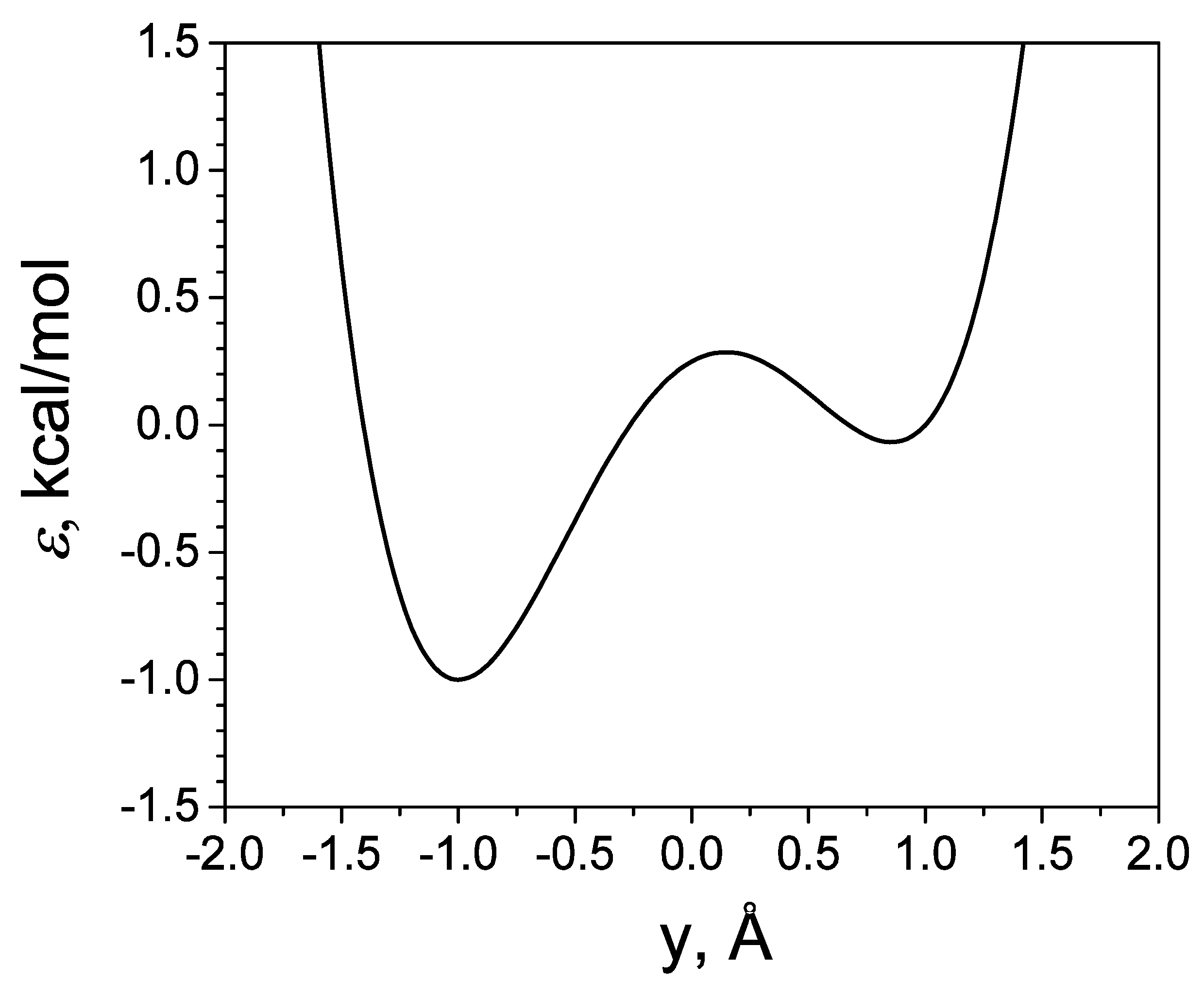
3.1. SGLD Simulation of a Skewed Double Well System
3.2. SGMD Simulation of Liquid Argon
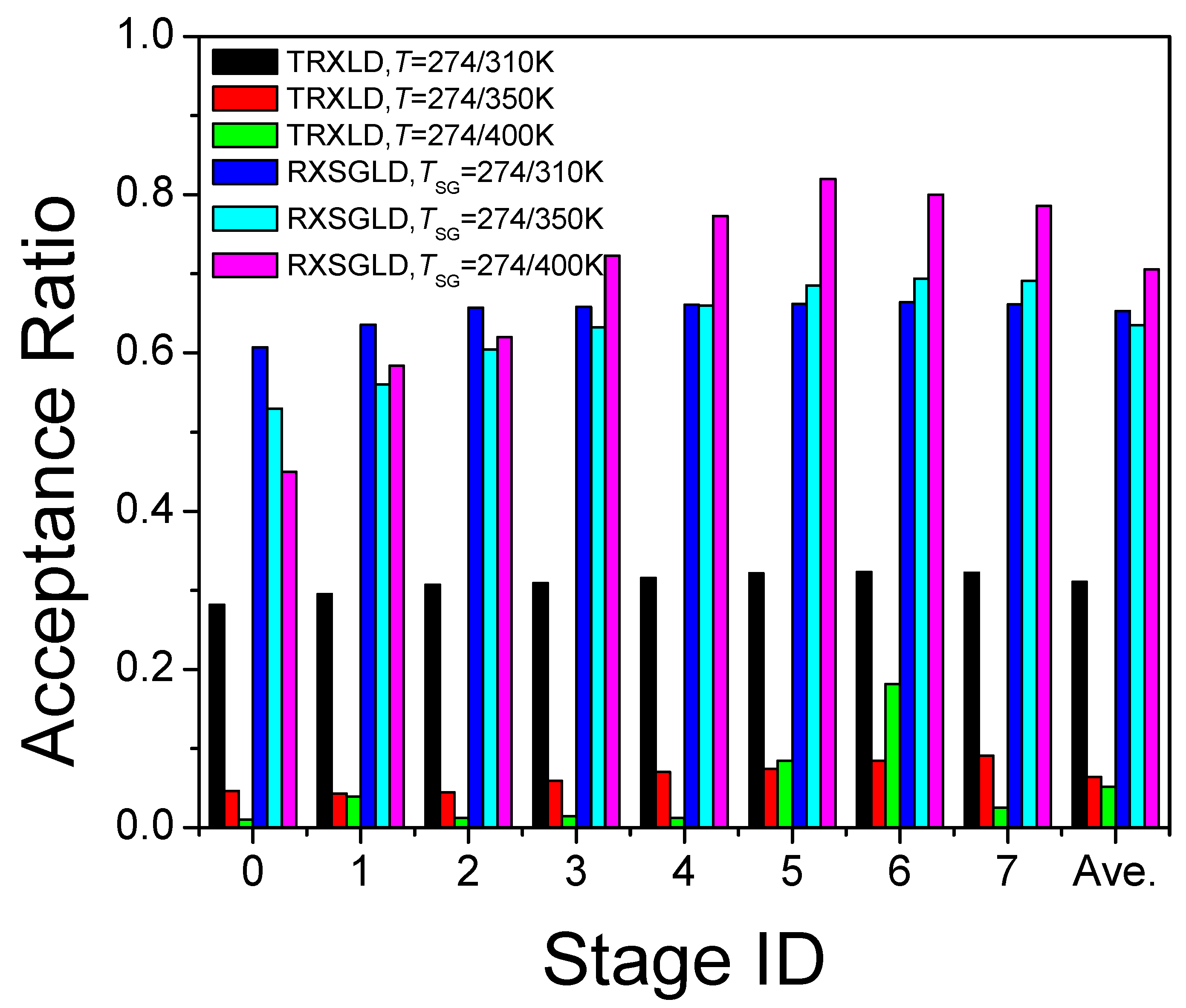
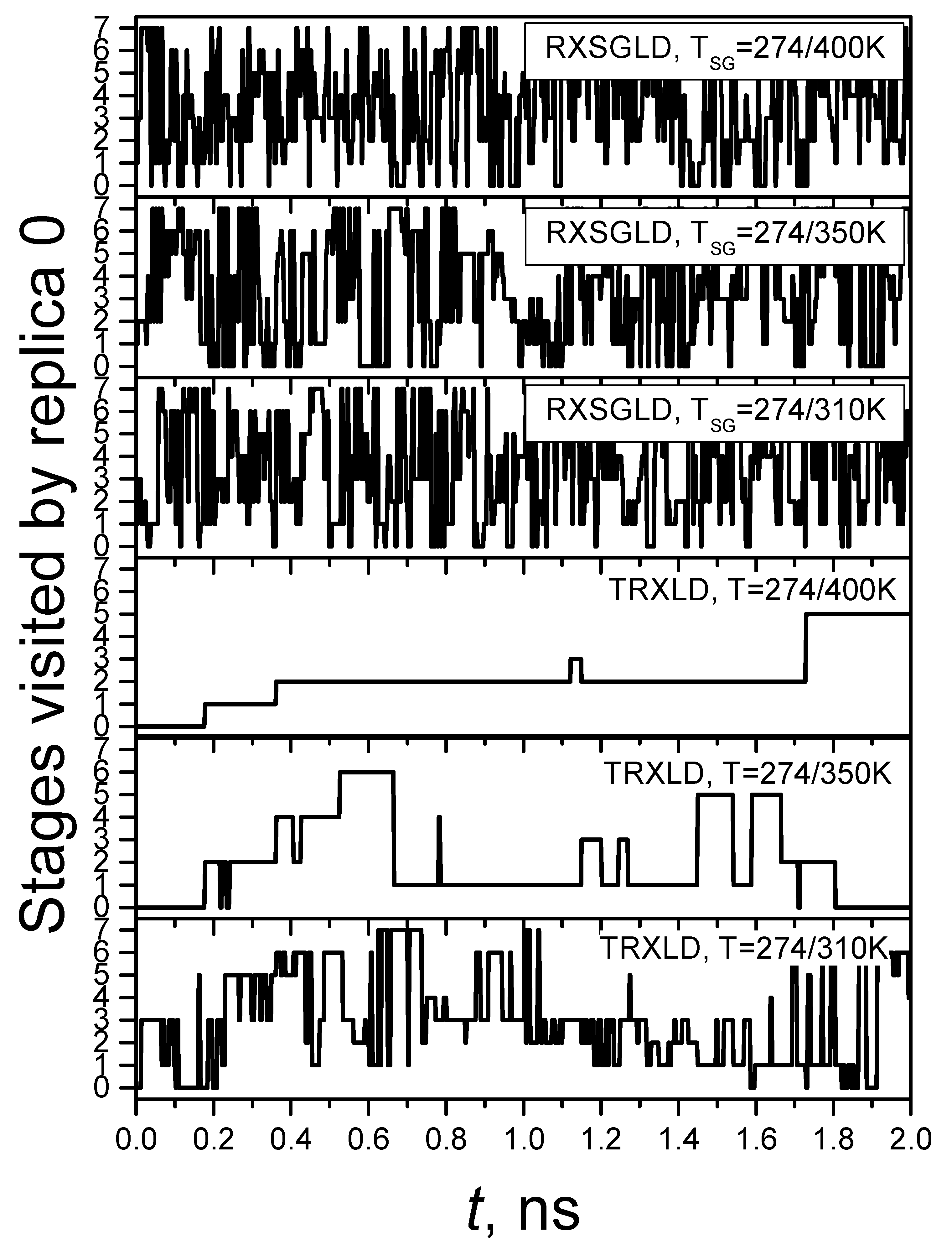
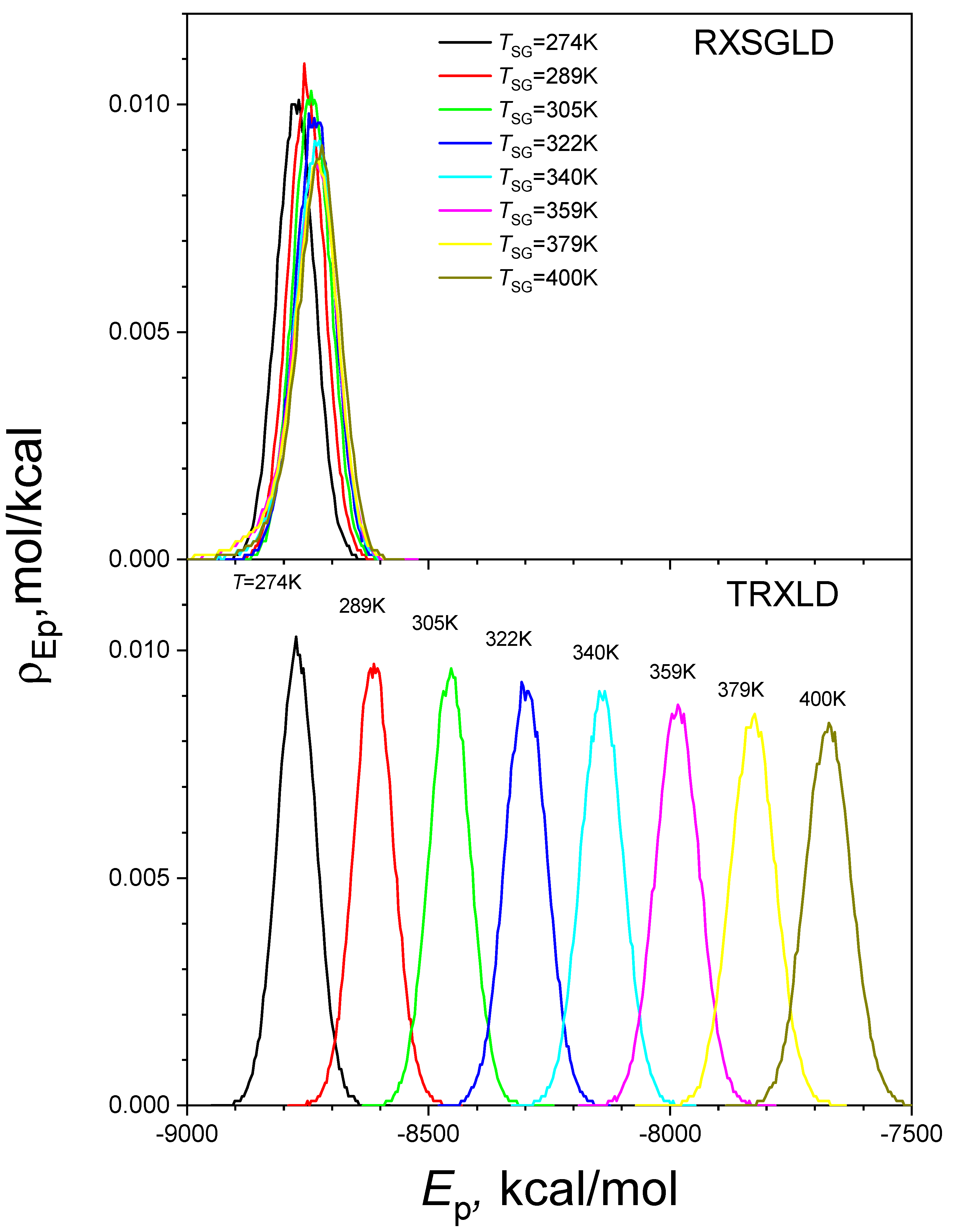
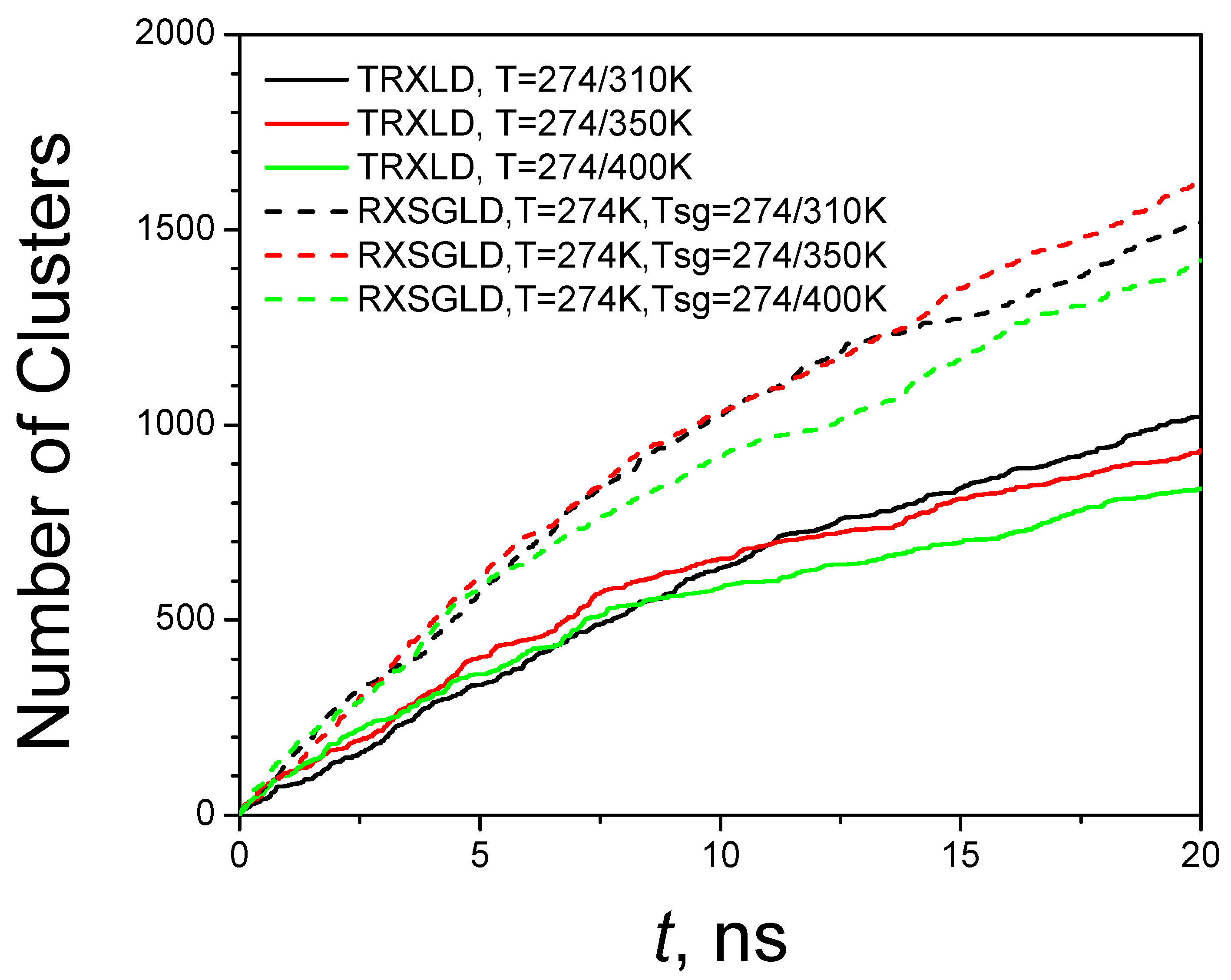
3.3. RXSGLD Simulation of β-Hairpin Folding
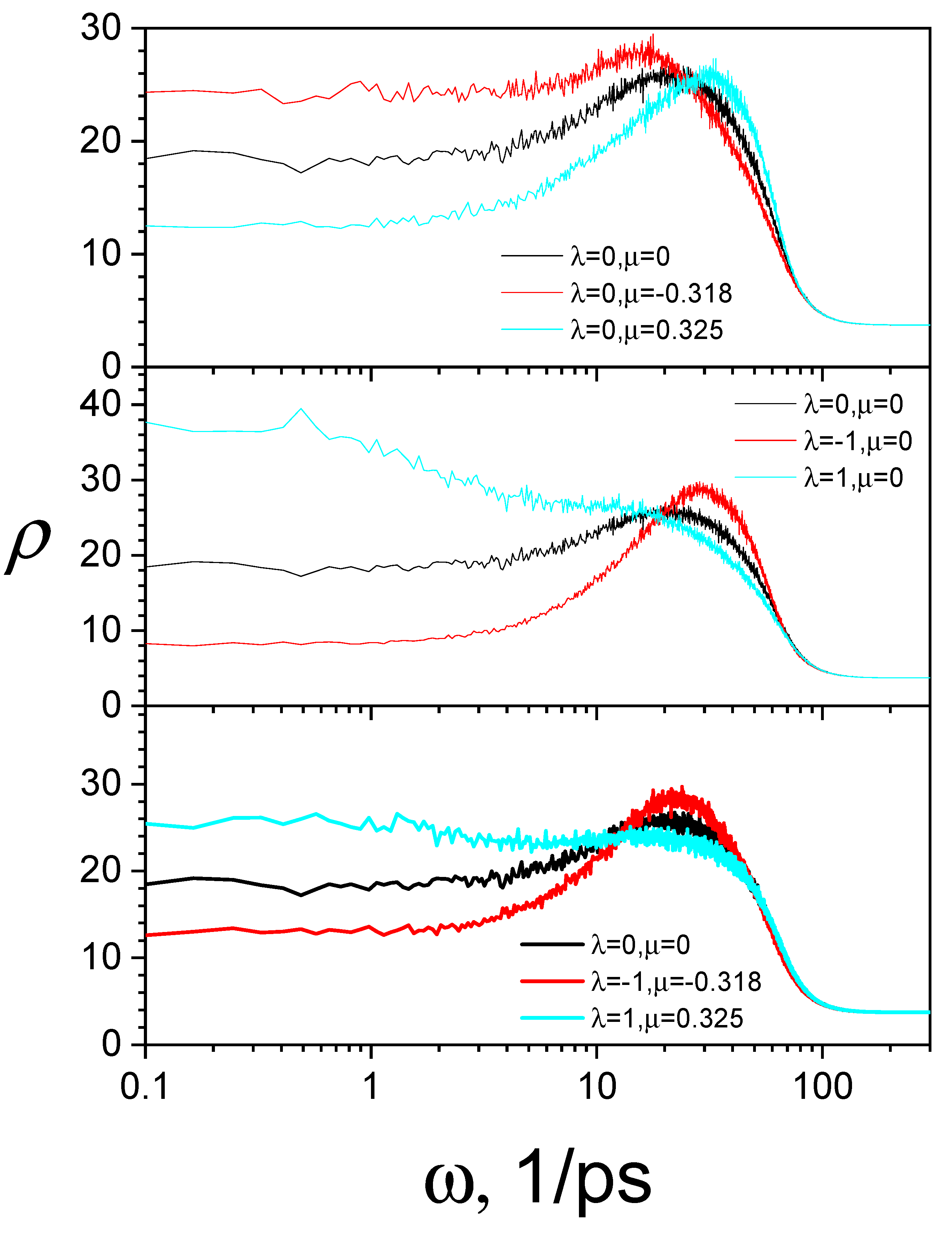
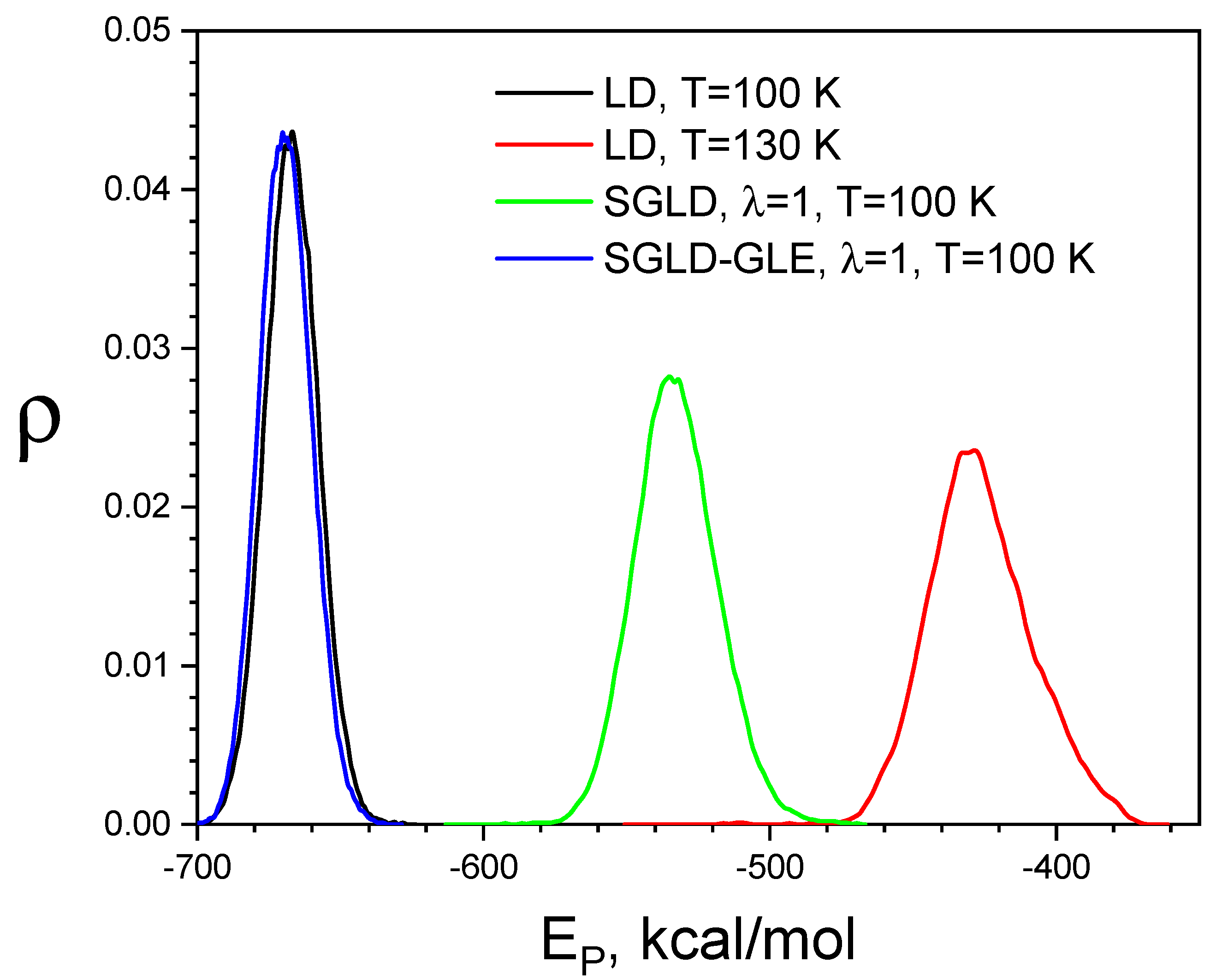
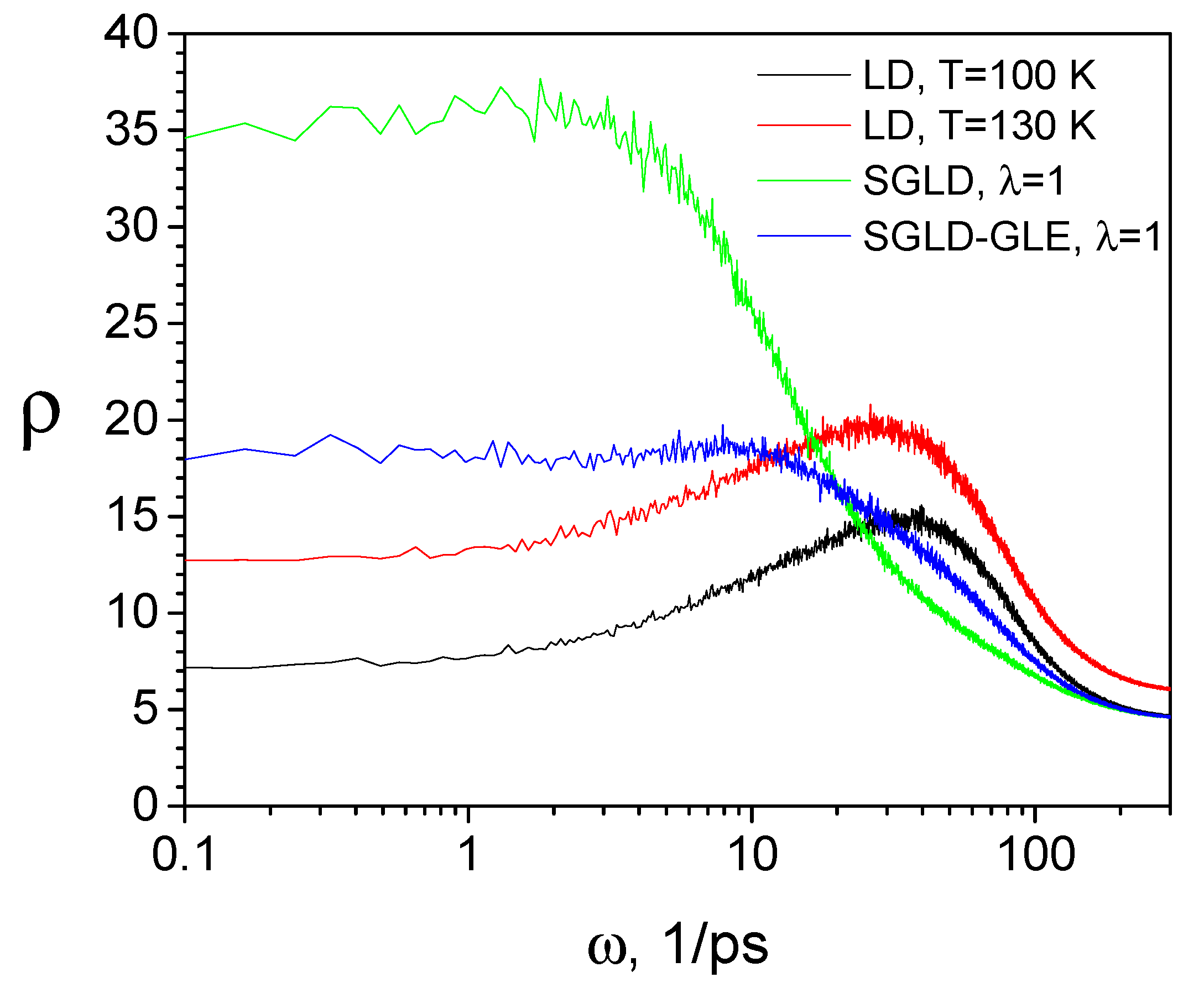
3.4. SGLD-GLE Simulation of Liquid Argon
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christen, M.; Van Gunsteren, W.F. On searching in, sampling of, and dynamically moving through conformational space of biomolecular systems: A review. J. Comput. Chem. 2008, 29, 157–166. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef]
- Gao, N.; Yang, L.; Gao, F.; Kurtz, R.J.; West, D.; Zhang, S. Long-time atomistic dynamics through a new self-adaptive accelerated molecular dynamics method. J. Phys. Condens. Matter 2017, 29, 145201. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S. Enhancing systematic motion in molecular dynamics simulation. J. Chem. Phys. 1999, 110, 9401–9410. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S. Self-guided molecular dynamics simulation for efficient conformational search. J. Phys. Chem. B 1998, 102, 7238–7250. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Self-guided Langevin dynamics simulation method. Chem. Phys. Lett. 2003, 381, 512–518. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Toward canonical ensemble distribution from self-guided Langevin dynamics simulation. J. Chem. Phys. 2011, 134, 134108. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Damjanovic, A.; Brooks, B.R. Efficient and Unbiased Sampling of Biomolecular Systems in the Canonical Ensemble: A Review of Self-Guided Langevin Dynamics. In Advances in Chemical Physics; Rice, S.A., Dinner, A.R., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 255–326. [Google Scholar]
- Wu, X.; Brooks, B.R.; Vanden-Eijnden, E. Self-guided Langevin dynamics via generalized Langevin equation. J. Comput. Chem. 2016, 37, 595–601. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B.R. Reformulation of the self-guided molecular simulation method. J. Chem. Phys. 2020, 153, 094112. [Google Scholar] [CrossRef]
- Agostini, F.P.; Soares-Pinto, D.D.O.; Moret, M.A.; Osthoff, C.; Pascutti, P.G. Generalized simulated annealing applied to protein folding studies. J. Comput. Chem. 2006, 27, 1142–1155. [Google Scholar] [CrossRef]
- Frausto-Solis, J.; Linan-Garcia, E.; Sanchez-Hernandez, J.P.; Gonzalez-Barbosa, J.J.; Gonzalez-Flores, C.; Castilla-Valdez, G. Multiphase Simulated Annealing Based on Boltzmann and Bose-Einstein Distribution Applied to Protein Folding Problem. Adv. Bioinform. 2016, 2016, 7357123. [Google Scholar] [CrossRef]
- Grigoriev, I.V.; Rakhmaninova, A.B.; Mironov, A.A. Simulated annealing for alpha-helical protein folding: Searches in vicinity of the “molten globule” state. J. Biomol. Struct. Dyn. 1998, 16, 115–122. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S.; Brooks, B.R. Direct observation of the folding and unfolding of a beta-hairpin in explicit water through computer simulation. J. Am. Chem. Soc. 2002, 124, 5282–5283. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S. Helix folding of an alanine-based peptide in explicit water. J. Phys. Chem. B 2001, 105, 2227–2235. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S. Folding studies of a linear pentamer peptide adopting a reverse turn conformation in aqueous solution Through molecular dynamics simulation. J. Phys. Chem. B 2000, 104, 8023–8034. [Google Scholar] [CrossRef]
- Wu, X.W.; Sung, S.S. Simulation of peptide folding with explicit water—A mean solvation method. Proteins 1999, 34, 295–302. [Google Scholar] [CrossRef]
- Damjanovic, A.; Wu, X.; García-Moreno E., B.; Brooks, B.R. Backbone relaxation coupled to the ionization of internal groups in proteins: A self-guided Langevin dynamics study. Biophys. J. 2008, 95, 4091–4101. [Google Scholar] [CrossRef] [PubMed]
- Damjanovic, A.; Miller, B.T.; Wenaus, T.J.; Maksimovic, P.; Bertrand Garcia-Moreno, E.; Brooks, B.R. Open science grid study of the coupling between conformation and water content in the interior of a protein. J. Chem. Inf. Model. 2008, 48, 2021–2029. [Google Scholar] [CrossRef] [PubMed]
- Damjanović, A.; García-Moreno E., B.; Brooks, B.R. Self-guided Langevin dynamics study of regulatory interactions in NtrC. Proteins Struct. Funct. Bioinform. 2009, 76, 1007–1019. [Google Scholar] [CrossRef]
- Pendse, P.Y.; Brooks, B.R.; Klauda, J.B. Probing the periplasmic-open state of lactose permease in response to sugar binding and proton translocation. J. Mol. Biol. 2010, 404, 506–521. [Google Scholar] [CrossRef]
- Ramans-Harborough, S.; Kalverda, A.P.; Manfield, I.W.; Thompson, G.S.; Kieffer, M.; Uzunova, V.; Quareshy, M.; Prusinska, J.M.; Roychoudhry, S.; Hayashi, K.-I.; et al. Intrinsic disorder and conformational coexistence in auxin coreceptors. Proc. Natl. Acad. Sci. USA 2023, 120, e2221286120. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B.R. Beta-hairpin folding mechanism of a nine-residue peptide revealed from molecular dynamics simulations in explicit water. Biophys. J. 2004, 86, 1946–1958. [Google Scholar] [CrossRef]
- Varady, J.; Wu, X.; Wang, S. Competitive and reversible binding of a guest molecule to its host in aqueous solution Through molecular dynamics simulation: Benzyl alcohol/Î2-cyclodextrin system. J. Phys. Chem. B 2002, 106, 4863–4872. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Force-momentum-based self-guided Langevin dynamics: A rapid sampling method that approaches the canonical ensemble. J. Chem. Phys. 2011, 135, 204101. [Google Scholar] [CrossRef]
- Wu, X.; Hodoscek, M.; Brooks, B.R. Replica-exchanging self-guided Langevin dynamics for efficient and accurate conformational sampling. J. Chem. Phys. 2012, 137, 044106. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., 3rd; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Case, D.A.; Betz, R.M.; Botello-Smith, W.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; et al. AMBER 2024; University of California: San Francisco, CA, USA, 2024. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical-Integration of Cartesian Equations of Motion of a System with Constraints—Molecular-Dynamics of N-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Isotropic periodic sum: A method for the calculation of long-range interactions. J. Chem. Phys. 2005, 122, 44107. [Google Scholar] [CrossRef]
- Blanco, F.J.; Jimenez, M.A.; Herranz, J.; Rico, M.; Santoro, J.; Nieto, J.L. NMR evidence of a short linear peptide that folds into a .beta.-hairpin in aqueous solution. J. Am. Chem. Soc. 1993, 115, 5887–5888. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular moldeing and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Using the isotropic periodic sum method to calculate long-range interactions of heterogeneous systems. J. Chem. Phys. 2008, 129, 154115. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R. Isotropic periodic sum of electrostatic interactions for polar systems. J. Chem. Phys. 2009, 131, 024107. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Brooks, B.R. Self-Guided Molecular Simulation Methods. Int. J. Mol. Sci. 2025, 26, 10410. https://doi.org/10.3390/ijms262110410
Wu X, Brooks BR. Self-Guided Molecular Simulation Methods. International Journal of Molecular Sciences. 2025; 26(21):10410. https://doi.org/10.3390/ijms262110410
Chicago/Turabian StyleWu, Xiongwu, and Bernard R. Brooks. 2025. "Self-Guided Molecular Simulation Methods" International Journal of Molecular Sciences 26, no. 21: 10410. https://doi.org/10.3390/ijms262110410
APA StyleWu, X., & Brooks, B. R. (2025). Self-Guided Molecular Simulation Methods. International Journal of Molecular Sciences, 26(21), 10410. https://doi.org/10.3390/ijms262110410




