Exploring Cyclodextrin-Based Nanosponges as Drug Delivery Systems: Evaluation of Spectroscopic Methods for Examining Structure and Dynamics of Nanosponges
Abstract
1. Introduction
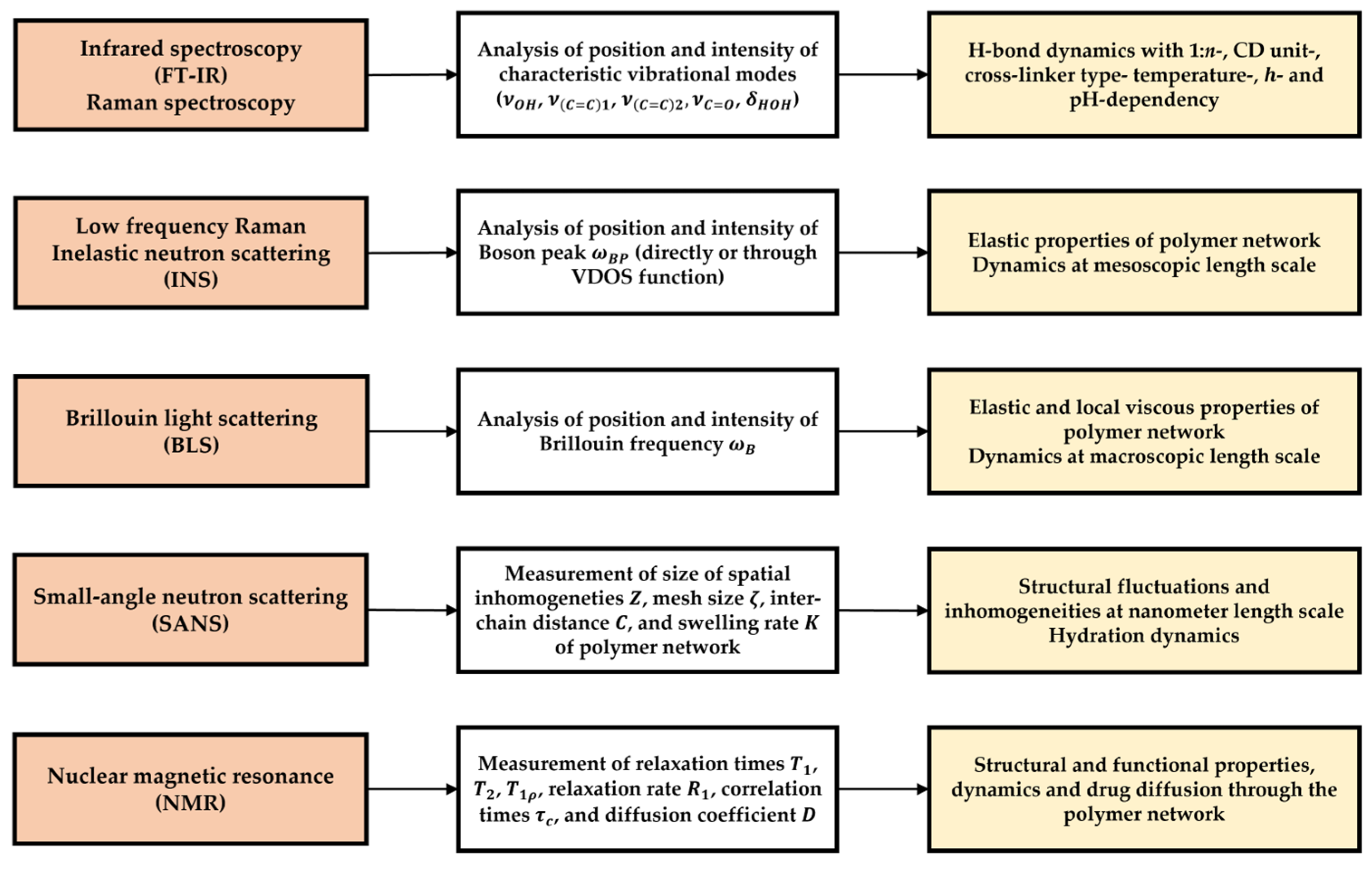
2. IR and Raman Spectroscopies
2.1. —OH Stretching Band
2.1.1. General Analysis

2.1.2. Sub-Band Analysis
2.2. —Carbonyl Stretching Band
2.2.1. General Analysis
2.2.2. Sub-Band Analysis
2.3. —Water Bending Mode
2.4. —Aromatic Stretching of PMDA Ring
2.5. UV Raman in H-Bond Dynamics
2.6. Comparison of FT-IR and Raman in CDNS Studies
3. Other Scattering Methods
3.1. Introduction to Scattering
3.2. Low-Frequency Raman Spectroscopy
3.2.1. Boson Peak Evolution
3.2.2. Vibrational Density of States (VDOS)
3.3. Inelastic Neutron Scattering (INS)
3.4. Brillouin Light Scattering (BLS)
3.5. Small-Angle Neutron Scattering (SANS)
4. Nuclear Magnetic Resonance (NMR)
4.1. Cross-Polarization NMR (CP NMR)
4.2. Diffusion NMR
4.3. Fast Field Cycling (FFC) NMR Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| α-/β-/γ-CD | α-/β-/γ-Cyclodextrin |
| Acq | Acquisition field |
| ATR-FT-IR | Attenuated total reflection |
| BET theory | Brunauer–Emmett–Teller theory |
| BJH theory | Barrett–Joyner–Halenda theory |
| BLS | Brillouin light scattering |
| BP | Boson peak |
| BPP-LED | Bipolar pulse longitudinal eddy current decay |
| Caf | Caffeine |
| CDI | 1,1′-Carbonyldiimiazole |
| CDNS | Cyclodextrin nanosponge |
| CP | Cross-polarization |
| DHO | Damped harmonic oscillator |
| DPC | Diphenyl carbonate |
| DOSY | Diffusion-ordered spectroscopy |
| DWF | Debye–Waller factor |
| EDTA | Ethylenediaminetetraacetic dianhydride |
| EISF | elastic incoherent structure factor |
| FID | Free induction decay |
| FFC | Fast field cycling |
| FWHM | Full width at half maximum |
| H-bond | Hydrogen bond |
| HMDI | Hexamethylene diisocyanate |
| HR | High resolution |
| HV | Depolarized |
| IbuNa | Ibuprofen sodium salt |
| INS | Inelastic neutron scattering |
| MAS | Magic angle spinning |
| MSD | Mean square displacement |
| NMR | Nuclear magnetic resonance |
| NP | Non-polarized |
| PGSE | Pulse gradient spin echo |
| PiroNa | Piroxicam sodium salt |
| Pol | Polarization field |
| PMDA | Pyromellitic dianhydride |
| PP | Pre-polarized |
| RF | Radio frequency |
| Rlx | Relaxation field |
| QE | Quasi-elastic |
| SANS | Small-angle neutron scattering |
| SLD | Scattering length density |
| TDI | Toluene-2,4-diisocyanate |
| UV | Ultraviolet |
| VCT | Variable contact time |
| VDOS | Vibrational density of states |
| VV | Polarized |
Appendix A
Appendix A.1. Resolving Spectral Line Shape
| Lorentzian Function | Gaussian Function | |
|---|---|---|
| Form | ||
| Characteristic parameters | γ | σ |
| Relation to signal shape and intensity |
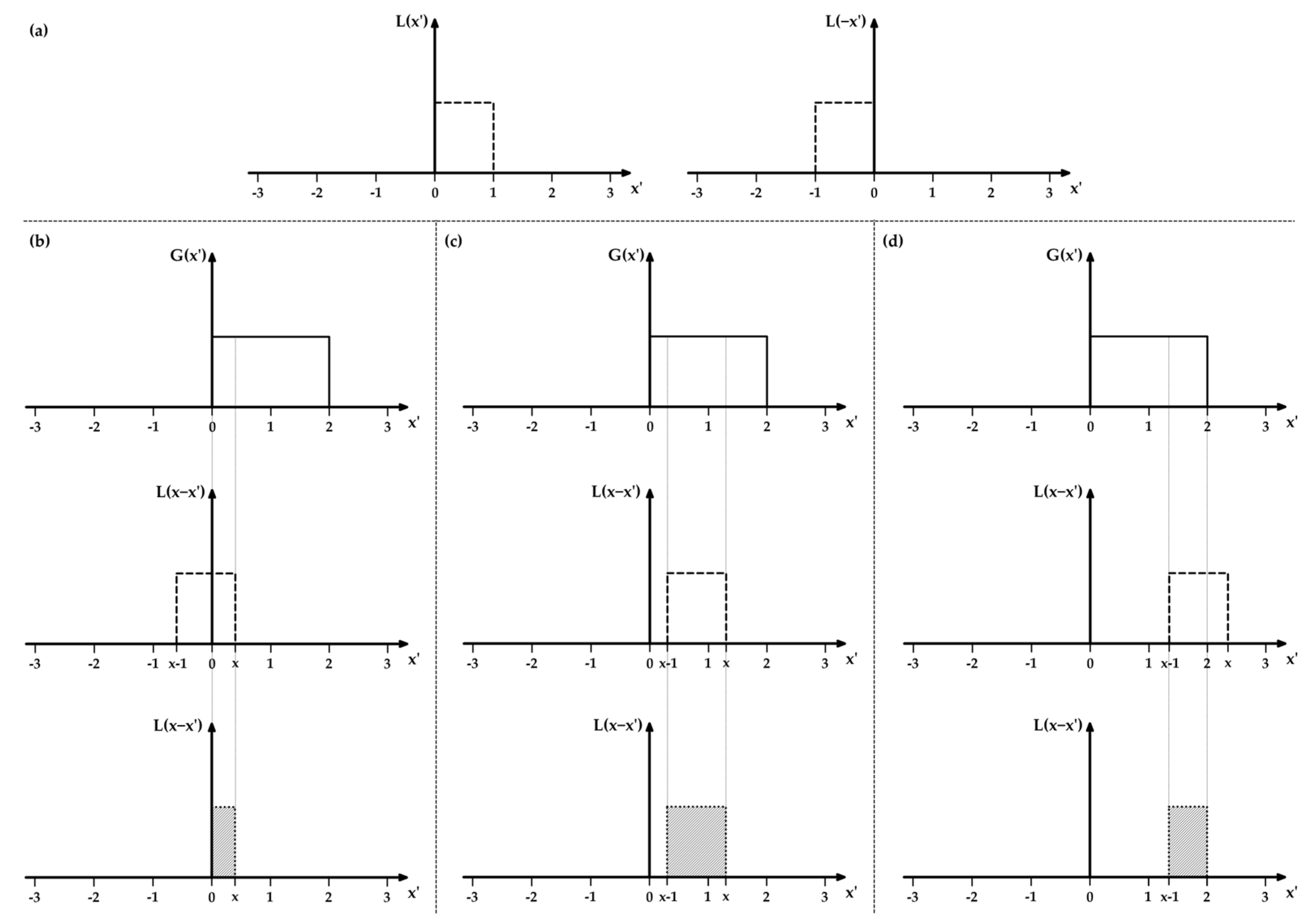
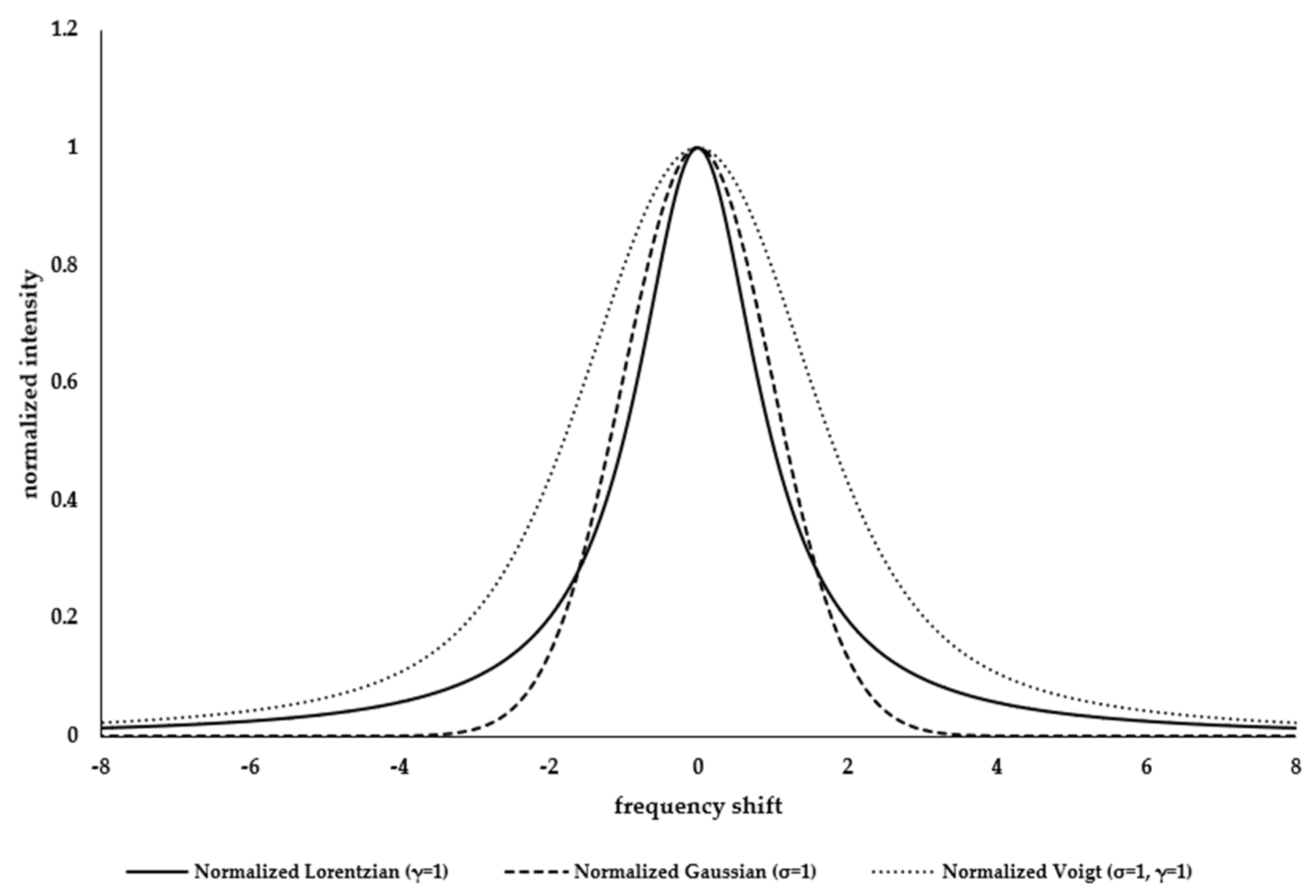
Appendix A.2. UV Raman Spectroscopy
Appendix A.3. Scattering Cross-Sections
Appendix A.4. Importance of Energy Distribution of Molecules in NMR
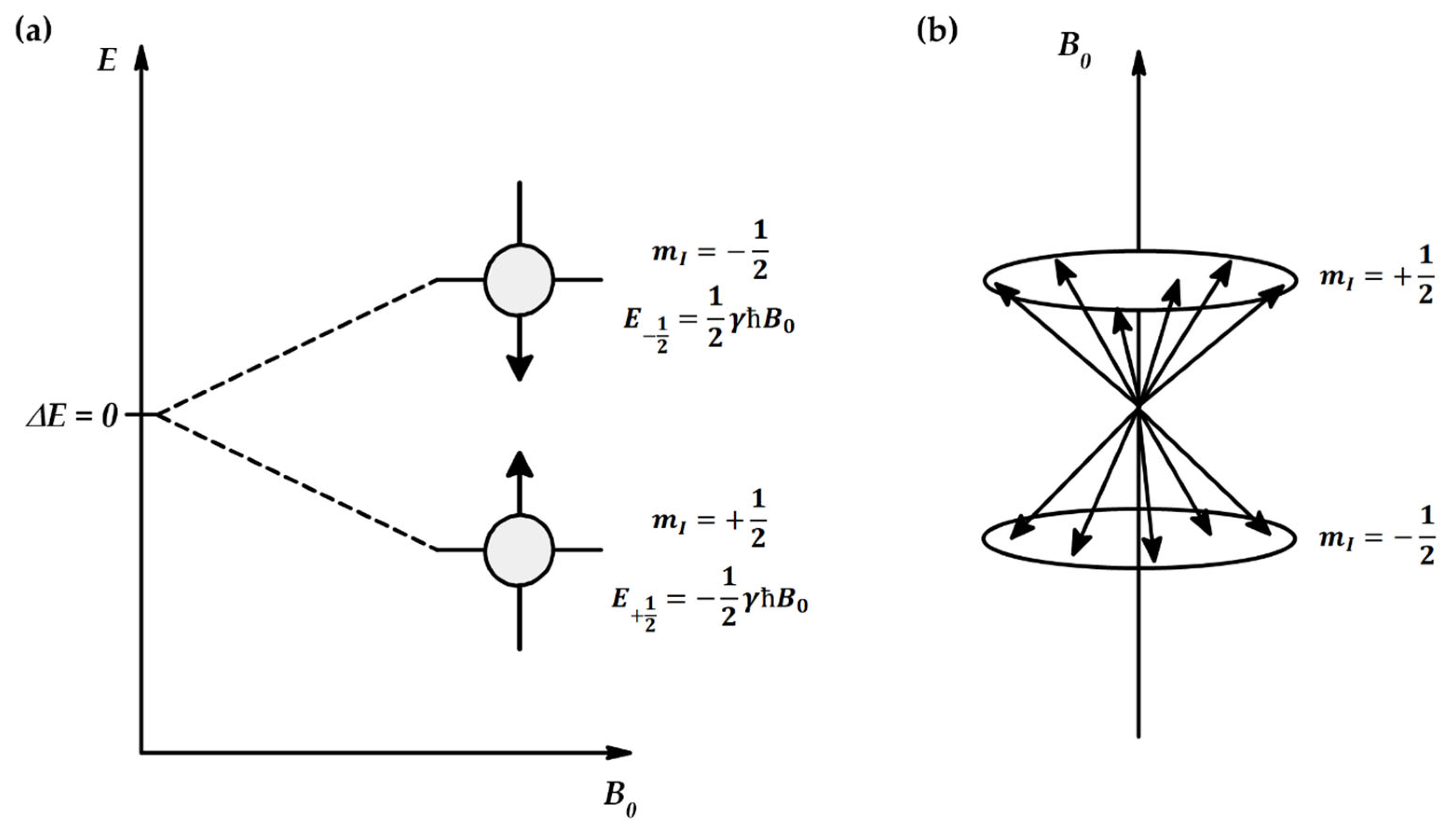
Appendix A.5. Kinetics of Magnetization Transfer [99]
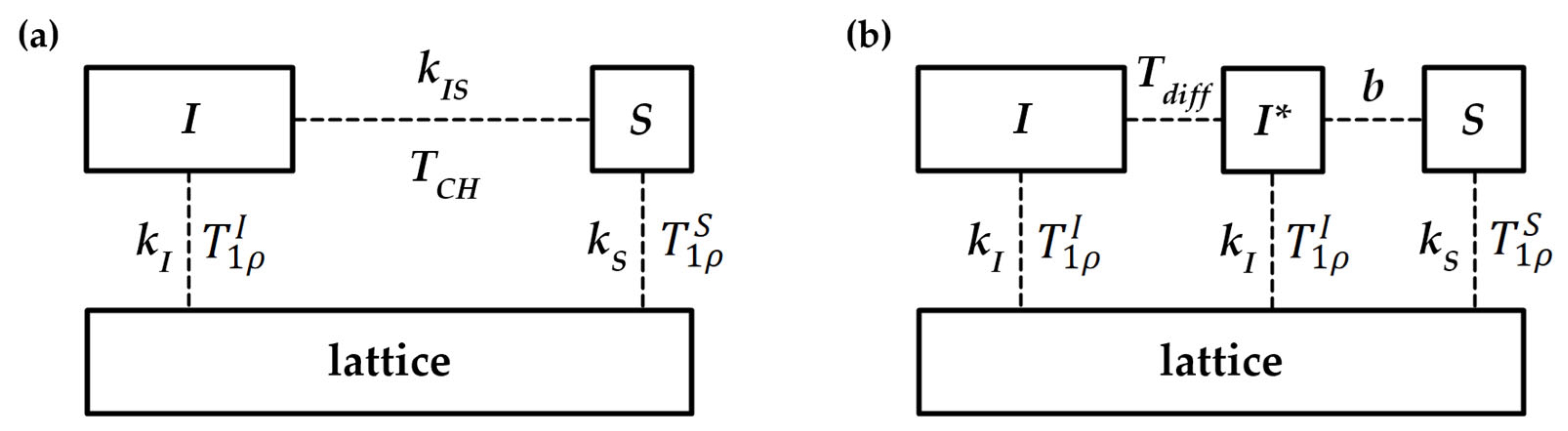
Appendix A.6. Extraction of Diffusion Coefficient from Release Profile Data
- Mass transfer at the cylinder surface with respect to the hydrogel and solution, respectively:
- 2.
- Initial conditions for concentration in the hydrogel and solution, respectively:
- 3.
- Boundary conditions for the center of the cylinder (no flux) and at the cylinder surface (flux continuity, equating the diffusive flux inside the cylinder to the convective mass transfer in the solution):
References
- Allahyari, S.; Trotta, F.; Valizadeh, H.; Jelvehgari, M.; Zakeri-Milani, P. Cyclodextrin-based nanosponges as promising carriers for active agents. Expert Opin. Drug Deliv. 2019, 16, 467–479. [Google Scholar] [CrossRef]
- Vyas, A.; Saraf, S.; Saraf, S. Cyclodextrin based novel drug delivery systems. J. Incl. Phenom. Macrocycl. Chem. 2008, 62, 23–42. [Google Scholar] [CrossRef]
- Loftsson, T.; Brewster, M.E. Pharmaceutical applications of cyclodextrins: Basic science and product development. J. Pharm. Pharmacol. 2010, 62, 1607–1621. [Google Scholar] [CrossRef]
- Szejtli, J. The properties and potential uses of cyclodextrin derivatives. J. Incl. Phenom. Mol. Recognit. Chem. 1992, 14, 25–36. [Google Scholar] [CrossRef]
- Jawaharlal, S.; Subramanian, S.; Palanivel, V.; Devarajan, G.; Veerasamy, V. Cyclodextrin-based nanosponges as promising carriers for active pharmaceutical ingredient. J. Biochem. Mol. Toxicol. 2024, 38, e23597. [Google Scholar] [CrossRef] [PubMed]
- Goyal, N.; Amar, A.; Gulati, S.; Varma, R.S. Cyclodextrin-based nanosponges as an environmentally sustainable solution for water treatment: A review. ACS Appl. Nano Mater. 2023, 6, 13766–13791. [Google Scholar] [CrossRef]
- Liu, B.; Chen, K. Advances in hydrogel-based drug delivery systems. Gels 2024, 10, 262. [Google Scholar] [CrossRef]
- Narayanaswamy, R.; Torchilin, V.P. Hydrogels and their applications in targeted drug delivery. Molecules 2019, 24, 603. [Google Scholar] [CrossRef]
- Gangadharappa, H.V.; Prasad, S.M.C.; Singh, R.P. Formulation, in vitro and in vivo evaluation of celecoxib nanosponge hydrogels for topical application. J. Drug Deliv. Sci. Technol. 2017, 41, 488–501. [Google Scholar] [CrossRef]
- Castiglione, F.; Crupi, V.; Majolino, D.; Mele, A.; Rossi, B.; Trotta, F.; Venuti, V. Inside new materials: An experimental numerical approach for the structural elucidation of nanoporous cross-linked polymers. J. Phys. Chem. B 2012, 116, 13133–13140. [Google Scholar] [CrossRef]
- Pyrak, B.; Rogacka-Pyrak, K.; Gubica, T.; Szeleszczuk, Ł. Exploring cyclodextrin-based nanosponges as drug delivery systems: Understanding the physicochemical factors influencing drug loading and release kinetics. Int. J. Mol. Sci. 2024, 25, 3527. [Google Scholar] [CrossRef] [PubMed]
- Szejtli, J. Introduction and general overview of cyclodextrin chemistry. Chem. Rev. 1998, 98, 1743–1753. [Google Scholar] [CrossRef] [PubMed]
- Szejtli, J. Past, present, and future of cyclodextrin research. Pure Appl. Chem. 2004, 76, 1825–1845. [Google Scholar] [CrossRef]
- Loftsson, T. Cyclodextrins and the Biopharmaceutics classification system of drugs. J. Incl. Phenom. Macrocycl. Chem. 2002, 44, 63–67. [Google Scholar] [CrossRef]
- Loftsson, T.; Hreinsdóttir, D.; Másson, M. Evaluation of cyclodextrin solubilization of drugs. Int. J. Pharm. 2005, 302, 18–28. [Google Scholar] [CrossRef]
- Brewster, M.E.; Loftsson, T. Cyclodextrins as pharmaccutical solubilizers. Adv. Drug Deliv. Rev. 2007, 59, 645–666. [Google Scholar] [CrossRef]
- Napiórkowska, E.; Szeleszczuk, Ł. Review of applications of β-cyclodextrin as a chiral selector for effective enantioseparation. Int. J. Mol. Sci. 2024, 25, 10126. [Google Scholar] [CrossRef]
- Kowalska, A.; Szeleszczuk, Ł. Cyclodextrin inclusion complexes with hydrocortisone-type corticosteroids. Pharmaceutics 2024, 16, 1544. [Google Scholar] [CrossRef]
- Krabicova, I.; Appleton, S.L.; Tannous, M.; Hoti, G.; Caldera, F.; Pedrazzo, A.R.; Cecone, C.; Cavalli, R.; Trotta, F. History of cyclodextrin nanosponges. Polymers 2020, 12, 1122. [Google Scholar] [CrossRef]
- Utzeri, G.; Matias, P.M.C.; Murtinho, D.; Valente, A.J.M. Cyclodextrin-based nanosponges: Overview and opportunities. Front. Chem. 2022, 10, 859406. [Google Scholar] [CrossRef]
- Trotta, F.; Zanetti, M.; Cavalli, R. Cyclodextrin-based nanosponges as drug carriers. Beilstein J. Org. Chem. 2012, 8, 2091–2099. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, K.; Bhattacharya, S. The ascension of nanosponges as a drug delivery carrier: Preparation, characterization, and applications. J. Mater. Sci. Mater. Med. 2022, 33, 28. [Google Scholar] [CrossRef] [PubMed]
- Chilajwar, S.V.; Pednekar, P.P.; Jadhav, K.R.; Gupta, G.J.C.; Kadam, V.J. Cyclodextrin-based nanosponges: A propitious platform for enhancing drug delivery. Expert Opin. Drug Deliv. 2014, 11, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Pyrak, B.; Rogacka-Pyrak, K.; Gubica, T. Cyclodextrin nanosponges as bioenhancers of phytochemicals. Prospect. Pharm. Sci. 2024, 22, 170–177. [Google Scholar] [CrossRef]
- Mele, A.; Castiglione, F.; Malpezzi, L.; Ganazzoli, F.; Raffaini, G.; Trotta, F.; Rossi, B.; Fontana, A.; Giunchi, G. HR MAS NMR, powder XRD and Raman spectroscopy study of inclusion phenomena in βCD nanosponges. J. Incl. Phenom. Macrocycl. Chem. 2011, 69, 403–409. [Google Scholar] [CrossRef]
- Rossi, B.; Caponi, S.; Castiglione, F.; Corezzi, S.; Fontana, A.; Giarola, M.; Mariotto, G.; Mele, A.; Petrillo, C.; Trotta, F.; et al. Networking properties of cyclodextrin-based cross-linked polymers probed by inelastic light-scattering experiments. J. Phys. Chem. B 2012, 116, 5323–5327. [Google Scholar] [CrossRef]
- Castiglione, F.; Crupi, V.; Majolino, D.; Mele, A.; Rossi, B.; Trotta, F.; Venuti, V. Effect of cross-linking properties on the vibrational dynamics of cyclodextrins-based polymers: An experimental-numerical study. J. Phys. Chem. B 2012, 116, 7952–7958. [Google Scholar] [CrossRef]
- Castiglione, F.; Crupi, V.; Majolino, D.; Mele, A.; Rossi, B.; Trotta, F.; Venuti, V. Vibrational spectroscopy investigation of swelling phenomena in cyclodextrin nanosponges. J. Raman Spectrosc. 2013, 44, 1463–1469. [Google Scholar] [CrossRef]
- Crupi, V.; Fontana, A.; Giarola, M.; Majolino, D.; Mariotto, G.; Mele, A.; Melone, L.; Punta, C.; Rossi, B.; Trotta, F.; et al. Connection between the vibrational dynamics and the cross-linking properties in cyclodextrins-based polymers. J. Raman Spectrosc. 2013, 44, 1457–1462. [Google Scholar] [CrossRef]
- Crupi, V.; Majolino, D.; Mele, A.; Rossi, B.; Trotta, F.; Venuti, V. Modelling the interplay between covalent and physical interactions in cyclodextrin-based hydrogel: Effect of water confinement. Soft Matter 2013, 9, 6457–6464. [Google Scholar] [CrossRef]
- Rossi, B.; Fontana, A.; Giarola, M.; Mariotto, G.; Mele, A.; Punta, C.; Melone, L.; Toraldo, F.; Trotta, F. Glass-like dynamics of new cross-linked polymeric systems: Behavior of the Boson peak. J. Non-Cryst. Solids 2014, 401, 73–77. [Google Scholar] [CrossRef]
- Crupi, V.; Majolino, D.; Mele, A.; Melone, L.; Punta, C.; Rossi, B.; Toraldo, F.; Trotta, F.; Venuti, V. Direct evidence of gel-sol transition in cyclodextrin-based hydrogels as revealed by FTIR-ATR spectroscopy. Soft Matter 2014, 10, 2320–2326. [Google Scholar] [CrossRef] [PubMed]
- Crupi, V.; Fontana, A.; Giarola, M.; Longeville, S.; Majolino, D.; Mariotto, G.; Mele, A.; Paciaroni, A.; Rossi, B.; Trotta, F.; et al. Vibrational density of states and elastic properties of cross-linked polymers: Combining inelastic light and neutron scattering. J. Phys. Chem. B 2014, 118, 624–633. [Google Scholar] [CrossRef] [PubMed]
- Crupi, V.; Fontana, A.; Majolino, D.; Mele, A.; Melone, L.; Punta, C.; Rossi, B.; Rossi, F.; Trotta, F.; Venuti, V. Hydrogen-bond dynamics of water confined in cyclodextrin nanosponges hydrogel. J. Incl. Phenom. Macrocycl. Chem. 2014, 80, 69–75. [Google Scholar] [CrossRef]
- Castiglione, F.; Crupi, V.; Majolino, D.; Mele, A.; Melone, L.; Panzeri, W.; Punta, C.; Rossi, B.; Trotta, F.; Venuti, V. Gel-sol evolution of cyclodextrin-based nanosponges: Role of the macrocycle size. J. Incl. Phenom. Macrocycl. Chem. 2014, 80, 77–83. [Google Scholar] [CrossRef]
- Ferro, M.; Castiglione, F.; Punta, C.; Melone, L.; Panzeri, W.; Rossi, B.; Trotta, F.; Mele, A. Anomalous diffusion of ibuprofen in cyclodextrin nanosponge hydrogels: An HRMAS NMR study. Beilstein J. Org. Chem. 2014, 10, 2715–2723. [Google Scholar] [CrossRef]
- Ferro, M.; Castiglione, F.; Punta, C.; Melone, L.; Panzeri, W.; Rossi, B.; Trotta, F.; Mele, A. Transport properties of ibuprofen encapsulated in cyclodextrin nanosponge hydrogels: A proton HR-MAS NMR spectroscopy study. J. Vis. Exp. 2016, 15, 53769. [Google Scholar] [CrossRef]
- Rossi, B.; Venuti, V.; Mele, A.; Punta, C.; Melone, L.; Crupi, V.; Majolino, D.; Trotta, F.; D’Amico, F.; Gessini, A.; et al. Probing the molecular connectivity of water confined in polymer hydrogels. J. Chem. Phys. 2015, 142, 014901. [Google Scholar] [CrossRef]
- Rossi, B.; Venuti, V.; D’Amico, F.; Gessini, A.; Castiglione, F.; Mele, A.; Punta, C.; Melone, L.; Crupi, V.; Majolino, D.; et al. Water and polymer dynamics in a model polysaccharide hydrogel: The role of hydrophobic/hydrophilic balance. Phys. Chem. Chem. Phys. 2015, 17, 963–971. [Google Scholar] [CrossRef]
- Venuti, V.; Rossi, B.; D’Amico, F.; Mele, A.; Castiglione, F.; Punta, C.; Melone, L.; Crupi, V.; Majolino, D.; Trotta, F.; et al. Combining Raman and infrared spectroscopy as a powerful tool for the structural elucidation of cyclodextrin-based polymeric hydrogels. Phys. Chem. Chem. Phys. 2015, 17, 10274–10282. [Google Scholar] [CrossRef]
- Venuti, V.; Crupi, V.; Rossi, B.; Fontana, A.; Mele, A.; Melone, L.; Punta, C.; Trotta, F.; Giarola, M.; Mariotto, G. Relationship between elastic properties and gel-to-sol transition in cyclodextrin-based hydrogel. Pharm. Anal. Acta 2015, 6, 356. [Google Scholar] [CrossRef]
- Rossi, B.; Venuti, V.; D’Amico, F.; Gessini, A.; Mele, A.; Punta, C.; Melone, L.; Crupi, V.; Majolino, D.; Trotta, F.; et al. Toward an understanding of the thermosensitive behaviour of pH-responsive hydrogels based on cyclodextrins. Soft Matter 2015, 11, 5862–5871. [Google Scholar] [CrossRef] [PubMed]
- Rossi, B.; Venuti, V.; Mele, A.; Punta, C.; Melone, L.; D’Amico, F.; Gessini, A.; Crupi, V.; Majolino, D.; Trotta, F.; et al. Vibrational signatures of the water behaviour upon confinement in nanoporous hydrogels. Phys. Chem. Chem. Phys. 2016, 18, 12252–12259. [Google Scholar] [CrossRef] [PubMed]
- Rossi, B.; Venuti, V.; D’Amico, F.; Gessini, A.; Mele, A.; Punta, C.; Melone, L.; Crupi, V.; Majolino, D.; Masciovecchio, C. Guest-matrix interactions affect the solvation of cyclodextrin-based polymeric hydrogels: A UV Raman scattering study. Soft Matter 2016, 12, 8861–8868. [Google Scholar] [CrossRef] [PubMed]
- Ferro, M.; Castiglione, F.; Pastori, N.; Punta, C.; Melone, L.; Panzeri, W.; Rossi, B.; Trotta, F.; Mele, A. Dynamics and interactions of ibuprofen in cyclodextrin nanosponges by solid-state NMR spectroscopy. Beilstein J. Org. Chem. 2017, 13, 182–194. [Google Scholar] [CrossRef]
- Rossi, B.; Paciaroni, A.; Venuti, V.; Fadda, G.C.; Melone, L.; Punta, C.; Crupi, V.; Majolino, D.; Mele, A. SANS investigation of water adsorption in tunable cyclodextrin-based polymeric hydrogels. Phys. Chem. Chem. Phys. 2017, 19, 6022–6029. [Google Scholar] [CrossRef]
- Bottari, C.; Comez, L.; Corezzi, S.; D’Amico, F.; Gessini, A.; Mele, A.; Punta, C.; Melone, L.; Pugliese, A.; Masciovecchio, C.; et al. Correlation between collective and molecular dynamics in pH-responsive cyclodextrin-based hydrogels. Phys. Chem. Chem. Phys. 2017, 19, 22555–22563. [Google Scholar] [CrossRef]
- Rossi, B.; Bottari, C.; Comez, L.; Corezzi, S.; Paolantoni, M.; Gessini, A.; Masciovecchio, C.; Mele, A.; Punta, C.; Melone, L.; et al. Structural and molecular response in cyclodextrin-based pH-sensitive hydrogels by the joint use of Brillouin, UV Raman and small angle neutron scattering techniques. J. Mol. Liq. 2018, 271, 738–746. [Google Scholar] [CrossRef]
- Lo Meo, P.; Mundo, F.; Terranova, S.; Conte, P.; Chillura Martino, D. Water dynamics at the solid-liquid interface to unveil the textural features of synthetic nanosponges. J. Phys. Chem. B 2020, 124, 1847–1857. [Google Scholar] [CrossRef]
- Pivato, R.V.; Rossi, F.; Ferro, M.; Castiglione, F.; Trotta, F.; Mele, A. β-cyclodextrin nanosponge hydrogels as drug delivery nanoarchitectonics for multistep drug release kinetics. ACS Appl. Polym. Mater. 2021, 3, 6562–6571. [Google Scholar] [CrossRef]
- Kiefer, W.; Laane, J. Comparison of FT-IR and Raman spectroscopy. In Analytical Applications of FT-IR to Molecular and Biological Systems, 1st ed.; Durig, J.R., Ed.; Reidel: Dordrecht, The Netherlands, 1980; pp. 537–577. [Google Scholar]
- Sathyanarayana, D.N. Vibrational Spectroscopy: Theory and Applications, 1st ed.; New Age International: New Delhi, India, 2004; pp. 300–309. [Google Scholar]
- Hadjiivanov, K.I.; Panayotov, D.A.; Mihaylov, M.Y.; Ivanova, E.Z.; Chakarova, K.K.; Andonova, S.M.; Drenchev, N.L. Power of infrared and Raman spectroscopies to characterize metal-organic frameworks and investigate their interaction with guest molecules. Chem. Rev. 2021, 121, 1286–1424. [Google Scholar] [CrossRef]
- Jukić, I.; Požar, M.; Lovrinčević, B.; Perera, A. Universal features in the lifetime distribution of clusters in hydrogen-bonding liquids. Phys. Chem. Chem. Phys. 2021, 23, 19537–19546. [Google Scholar] [CrossRef]
- Crupi, V.; Majolino, D.; Migliardo, P.; Venuti, V. Inter- and intramolecular hydrogen bond in liquid polymers: A Fourier transform infrared response. Mol. Phys. 2000, 98, 1589–1594. [Google Scholar] [CrossRef]
- Castellanos, M.M.; McAuley, A.; Curtis, J.E. Investigating structure and dynamics of proteins in amorphous phases using neutron scattering. Comput. Struct. Biotechnol. J. 2017, 15, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Li, D.N.; Zhang, K. Unifying the concepts of scattering and structure factor in ordered and disordered samples. J. Appl. Crystallogr. 2021, 54, 644–660. [Google Scholar] [CrossRef]
- Newton, R.G. Scattering Theory of Waves and Particles, 2nd ed.; Springer: New York, NY, USA, 1982; pp. 3–28, 54–97, 211–227. [Google Scholar]
- Langel, W. Introduction to neutron scattering. ChemTexts 2023, 9, 12. [Google Scholar] [CrossRef]
- Masciovecchio, C.; Gessini, A.; Santucci, S.C. Ultraviolet Brillouin scattering as a new tool to investigate disordered systems. J. Non-Cryst. Solids 2006, 352, 5126–5129. [Google Scholar] [CrossRef]
- Small Angle Neutron Scattering: Report of a Coordinated Research Project, 2000–2003. International Atomic Energy Agency: Vienna, Austria, 2006; pp. 9–22.
- Bensley, K.A.; Chimenti, R.V.; Lofland, S.E. Low-frequency Raman spectroscopy of polymers. Macromol. Chem. Phys. 2025, 226, 70004. [Google Scholar] [CrossRef]
- Crupi, V.; Fontana, A.; Giarola, M.; Guella, G.; Majolino, D.; Mancini, I.; Mariotto, G.; Paciaroni, A.; Rossi, B.; Venuti, V. Cyclodextrin-complexation effects on the low-frequency vibrational dynamics of ibuprofen by combined inelastic light and neutron scattering experiments. J. Phys. Chem. B 2013, 117, 3917–3926. [Google Scholar] [CrossRef]
- Hong, L.; Begen, B.; Kisliuk, A.; Alba-Simionesco, C.; Novikov, V.N.; Sokolov, A.P. Pressure and density dependence of the boson peak in polymers. Phys. Rev. B 2008, 78, 134201. [Google Scholar] [CrossRef]
- Gonçalves, S.; Bonadeo, H. Vibrational densities of states from molecular-dynamics calculations. Phys. Rev. B 1992, 46, 12019–12021. [Google Scholar] [CrossRef] [PubMed]
- Shuker, R.; Gammon, R.W. Raman-scattering selection-rule breaking and the density of states in amorphous materials. Phys. Rev. Lett. 1970, 25, 222–225. [Google Scholar] [CrossRef]
- Fontana, A.; Dell’Anna, R.; Montagna, M.; Rossi, F.; Viliani, G.; Ruocco, G.; Sampoli, M.; Buchenau, U.; Wischnewski, A. The Raman coupling function in amorphous silica and the nature of the long-wavelength excitations in disordered systems. Europhys. Lett. 1999, 47, 56–62. [Google Scholar] [CrossRef]
- Majolino, D.; Mallamace, F.; Migliardo, P.; Aliotta, F.; Micali, N.; Vasi, C. Spectral evidence of connected structures in liquid water—Effective Raman density of vibrational-states. Phys. Rev. E 1993, 47, 2669–2675. [Google Scholar] [CrossRef]
- Carini, G.; Dangelo, G.; Tripodo, G.; Fontana, A.; Leonardi, A.; Saunders, G.A.; Brodin, A. Excess of low-energy excitations in glasses. Phys. Rev. B 1995, 52, 9342–9353. [Google Scholar] [CrossRef]
- Blanks, K.A. The role of the Raman coupling coefficient in an inelastic light scattering process in amorphous solids. J. Non-Cryst. Solids 1996, 208, 81–88. [Google Scholar] [CrossRef]
- Fitter, J.; Lechner, R.E.; Dencher, N.A. Picosecond molecular motions in bacteriorhodopsin from neutron scattering. Biophys. J. 1997, 73, 2126–2137. [Google Scholar] [CrossRef]
- Gabel, F.; Bellissent-Funel, M.-C. C-phycocyanin hydration water dynamics in the presence of trehalose: An incoherent elastic neutron scattering study at different energy resolutions. Biophys. J. 2007, 92, 4054–4063. [Google Scholar] [CrossRef]
- Döge, S.; Liu, C.-Y.; Young, A.; Morkel, C. Incoherent approximation for neutron up-scattering cross sections and its corrections for slow neutrons and low crystal temperatures. Phys. Rev. C 2021, 103, 054606. [Google Scholar] [CrossRef]
- Crupi, V.; Magazu, S.; Majolino, D.; Migliardo, P.; Wanderlingh, U.; Kagunya, W.W. Incoherent quasi-elastic neutron scattering in water-PEG solutions. Phys. B Condens. Matter 1997, 241, 979–981. [Google Scholar] [CrossRef]
- Crupi, V.; Guella, G.; Longeville, S.; Majolino, D.; Mancini, I.; Paciaroni, A.; Rossi, B.; Venuti, V. Influence of chirality on vibrational and relaxational properties of (S)- and (R,S)-ibuprofen/methyl-β-cyclodextrin inclusion complexes: An INS and QENS study. J. Phys. Chem. B 2013, 117, 11466–11472. [Google Scholar] [CrossRef]
- Frick, B.; Richter, D. The microscopic basis of the glass-transition in polymers from neutron-scattering studies. Science 1995, 267, 1939–1945. [Google Scholar] [CrossRef]
- Wijesinghe, P.; Kennedy, B.F.; Sampson, D.D. Optical elastography on the microscale. In Tissue Elasticity Imaging, 1st ed.; Alam, S.K., Garra, B.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 185–229. [Google Scholar]
- Ishijima, A.; Okabe, S.; Sakuma, I.; Nakagawa, K. Dispersive coherent Brillouin scattering spectroscopy. Photoacoustics 2023, 29, 100447. [Google Scholar] [CrossRef]
- Polian, A. Brillouin scattering at high pressure: An overview. J. Raman Spectrosc. 2003, 34, 633–637. [Google Scholar] [CrossRef]
- Bouvet, P.; Bevilacqua, C.; Ambekar, Y.; Antonacci, G.; Au, J.; Caponi, S.; Chagnon-Lessard, S.; Czarske, J.; Dehoux, T.; Fioretto, D.; et al. Consensus statement on Brillouin light scattering microscopy of biological materials. Nat. Photon. 2025, 19, 681–691. [Google Scholar] [CrossRef]
- Palombo, F.; Fioretto, D. Brillouin light scattering: Applications in biomedical sciences. Chem. Rev. 2019, 119, 7833–7847. [Google Scholar] [CrossRef]
- Bottani, C.E.; Fioretto, D. Brillouin scattering of phonons in complex materials. Adv. Phys. X 2018, 3, 1467281. [Google Scholar] [CrossRef]
- Fioretto, D.; Caponi, S.; Palombo, F. Brillouin-Raman mapping of natural fibers with spectral moment analysis. Biomed. Opt. Express 2019, 10, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Fioretto, D.; Comez, L.; Socino, G.; Verdini, L.; Corezzi, S.; Rolla, P.A. Dynamics of density fluctuations of a glass-forming epoxy resin revealed by Brillouin light scattering. Phys. Rev. E 1999, 59, 1899–1907. [Google Scholar] [CrossRef]
- Ko, J.H.; Kojima, S. Brillouin scattering study on glass-forming ethanol. J. Non-Cryst. Solids 2002, 307, 154–160. [Google Scholar] [CrossRef]
- Grillo, I. Small-angle neutron scattering and applications in soft condensed matter. In Soft Matter Characterization; Borsali, R., Pecora, R., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 723–782. [Google Scholar]
- Svergun, D.I.; Koch, M.H. Small-angle scattering studies of biological macromolecules in solution. Rep. Prog. Phys. 2003, 66, 1735. [Google Scholar] [CrossRef]
- Krueger, S. Planning, executing and assessing the validity of SANS contrast variation experiments. Methods Enzymol. 2022, 677, 127–155. [Google Scholar] [CrossRef] [PubMed]
- Krueger, S. Small-angle neutron scattering contrast variation studies of biological complexes: Challenges and triumphs. Curr. Opin. Struct. Biol. 2022, 74, 102375. [Google Scholar] [CrossRef]
- Banc, A.; Charbonneau, C.; Dahesh, M.; Appavou, M.S.; Fu, Z.; Morel, M.H.; Ramos, L. Small angle neutron scattering contrast variation reveals heterogeneities of interactions in protein gels. Soft Matter 2016, 12, 5340–5352. [Google Scholar] [CrossRef]
- Hammouda, B.; Ho, D.; Kline, S. SANS from poly(ethylene oxide)/water systems. Macromolecules 2002, 35, 8578–8585. [Google Scholar] [CrossRef]
- Shibayama, M. Structure-mechanical property relationship of tough hydrogels. Soft Matter 2012, 8, 8030–8038. [Google Scholar] [CrossRef]
- Shibayama, M. Small-angle neutron scattering on polymer gels: Phase behavior, inhomogeneities and deformation mechanisms. Polym. J. 2011, 43, 18–34. [Google Scholar] [CrossRef]
- Wilson, L.D.; Mohamed, M.H.; Berhaut, C.L. Sorption of aromatic compounds with copolymer sorbent materials containing β-cyclodextrin. Materials 2011, 4, 1528–1542. [Google Scholar] [CrossRef]
- Hrabe, J.; Kaur, G.; Guilfoyle, D.N. Principles and limitations of NMR diffusion measurements. J. Med. Phys. 2007, 32, 34–42. [Google Scholar] [CrossRef]
- Kuchel, P.W.; Pagès, G.; Nagashima, K.; Velan, S.; Vijayaragavan, V.; Nagarajan, V.; Chuang, K.H. Stejskal-Tanner equation derived in full. Concepts Magn. Reson. Part A 2012, 40A, 205–214. [Google Scholar] [CrossRef]
- Borisov, A.S.; Hazendonk, P.; Hayes, P.G. Solid-state nuclear magnetic resonance spectroscopy: A review of modern techniques and applications for inorganic polymers. J. Inorg. Organomet. Polym. Mater. 2010, 20, 183–212. [Google Scholar] [CrossRef]
- Zou, T.; Sadler, P.J. Speciation of precious metal anti-cancer complexes by NMR spectroscopy. Drug Discov. Today Technol. 2015, 16, 7–15. [Google Scholar] [CrossRef]
- Kolodziejski, W.; Klinowski, J. Kinetics of cross-polarization in solid-state NMR: a guide for chemists. Chem. Rev. 2002, 102, 613–628. [Google Scholar] [CrossRef]
- Wu, D.H.; Chen, A.D.; Johnson, C.S. An improved diffusion-ordered spectroscopy experiment incorporating bipolar-gradient pulses. J. Magn. Reson. Ser. A 1995, 115, 260–264. [Google Scholar] [CrossRef]
- Assemat, G.; Gouilleux, B.; Bouillaud, D.; Farjon, J.; Gilard, V.; Giraudeau, P.; Malet-Martino, M. Diffusion-ordered spectroscopy on a benchtop spectrometer for drug analysis. J. Pharm. Biomed. Anal. 2018, 160, 268–275. [Google Scholar] [CrossRef]
- Barjat, H.; Morris, G.A.; Smart, S.; Swanson, A.G.; Williams, S.C.R. High-resolution diffusion-ordered 2D spectroscopy (HR-DOSY)—A new tool for the analysis of complex-mixtures. J. Magn. Reson. Ser. B 1995, 108, 170–172. [Google Scholar] [CrossRef]
- Raffaini, G.; Ganazzoli, F.; Mele, A.; Castiglione, F. A molecular dynamics study of cyclodextrin nanosponge models. J. Incl. Phenom. Macrocycl. Chem. 2013, 75, 263–268. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Gurny, R.; Doelker, E.; Buri, P.; Peppas, N.A. Mechanisms of solute release from porous hydrophilic polymers. Int. J. Pharm. 1983, 15, 25–35. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A simple equation for description of solute release II. Fickian and anomalous release from swellable devices. J. Control. Release 1987, 5, 37–42. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances. I. computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- D’Amico, F.; Bencivenga, F.; Gessini, A.; Principi, E.; Cucini, R.; Masciovecchio, C. Investigation of acetic acid hydration shell formation through Raman spectra line-shape analysis. J. Phys. Chem. B 2012, 116, 13219–13227. [Google Scholar] [CrossRef]
- Mariani, L.; Morresi, A.; Cataliotti, R.S.; Giorgini, M.G. Application of the Kubo–Anderson band shape equation to vibrational relaxation studies in the frequency domain and to an improved determination of spectral second moments from experimental data. J. Chem. Phys. 1996, 104, 914–922. [Google Scholar] [CrossRef]
- Chatterji, T. Magnetic Neutron Scattering. In Neutron Scattering from Magnetic Materials, 1st ed.; Chatterji, T., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2006; pp. 1–24. [Google Scholar]
- Rossi, F.; Castiglione, F.; Ferro, M.; Marchini, P.; Mauri, E.; Moioli, M.; Mele, A.; Masi, M. Drug–polymer interactions in hydrogel-based drug delivery systems: An experimental and theoretical study. ChemPhysChem 2015, 16, 2818–2825. [Google Scholar] [CrossRef]
- Santoro, M.; Marchetti, P.; Rossi, F.; Perale, G.; Castiglione, F.; Mele, A.; Masi, M. Smart approach to evaluate drug diffusivity in injectable agar-carbomer hydrogels for drug delivery. J. Phys. Chem. B 2011, 115, 2503–2510. [Google Scholar] [CrossRef]
- Rossi, F.; Ferrari, R.; Papa, S.; Moscatelli, D.; Casalini, T.; Forloni, G.; Perale, G.; Veglianese, P. Tunable hydrogel—Nanoparticles release system for sustained combination therapies in the spinal cord. Colloids Surf. B Biointerfaces 2013, 108, 169–177. [Google Scholar] [CrossRef] [PubMed]

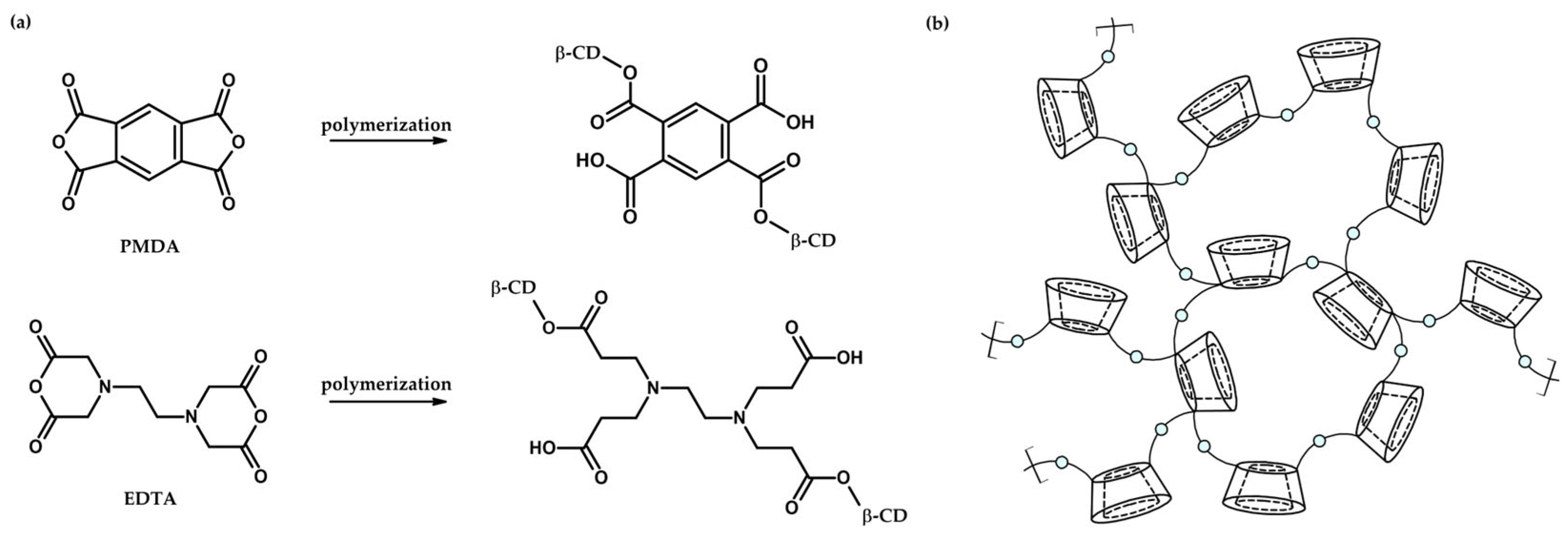
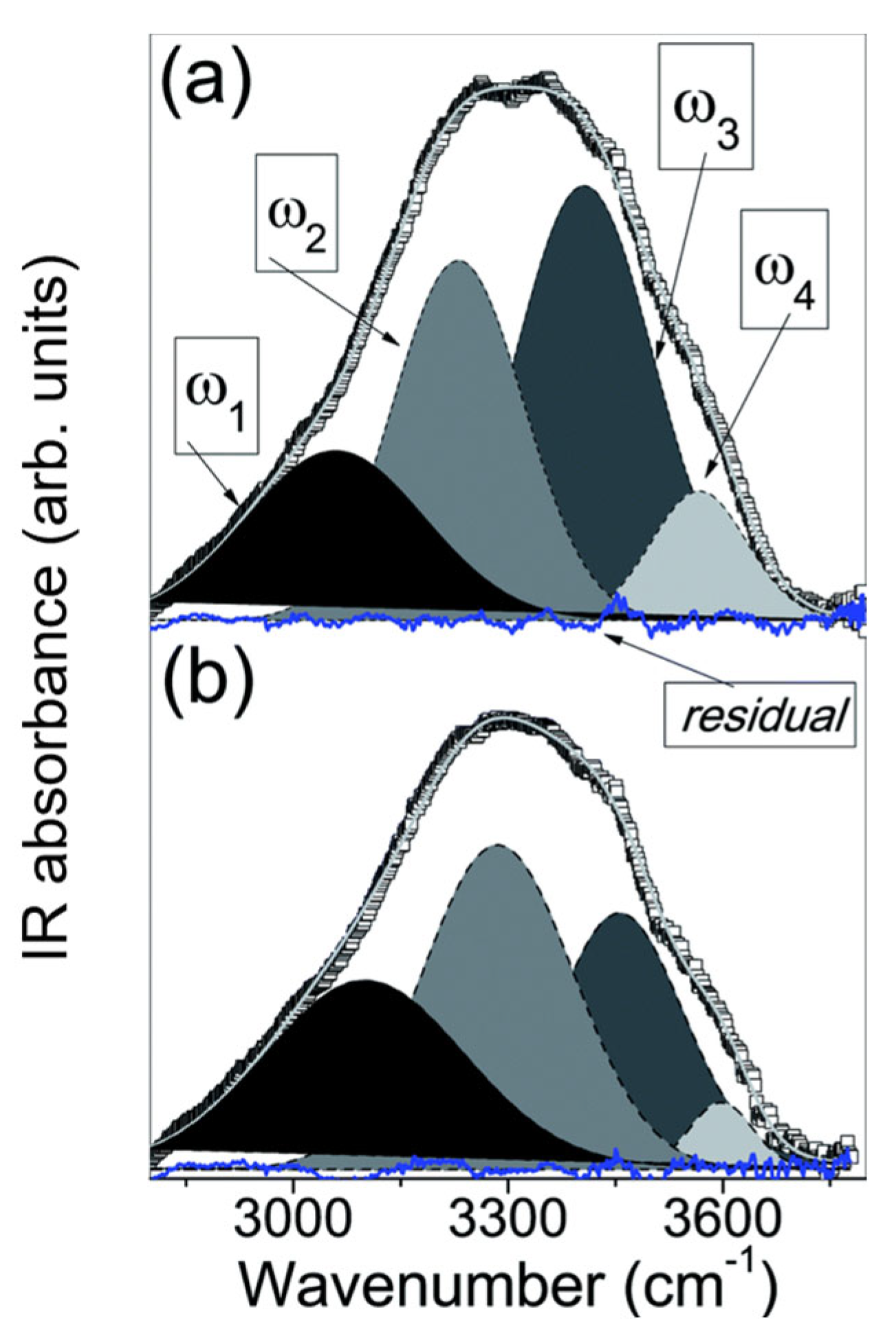
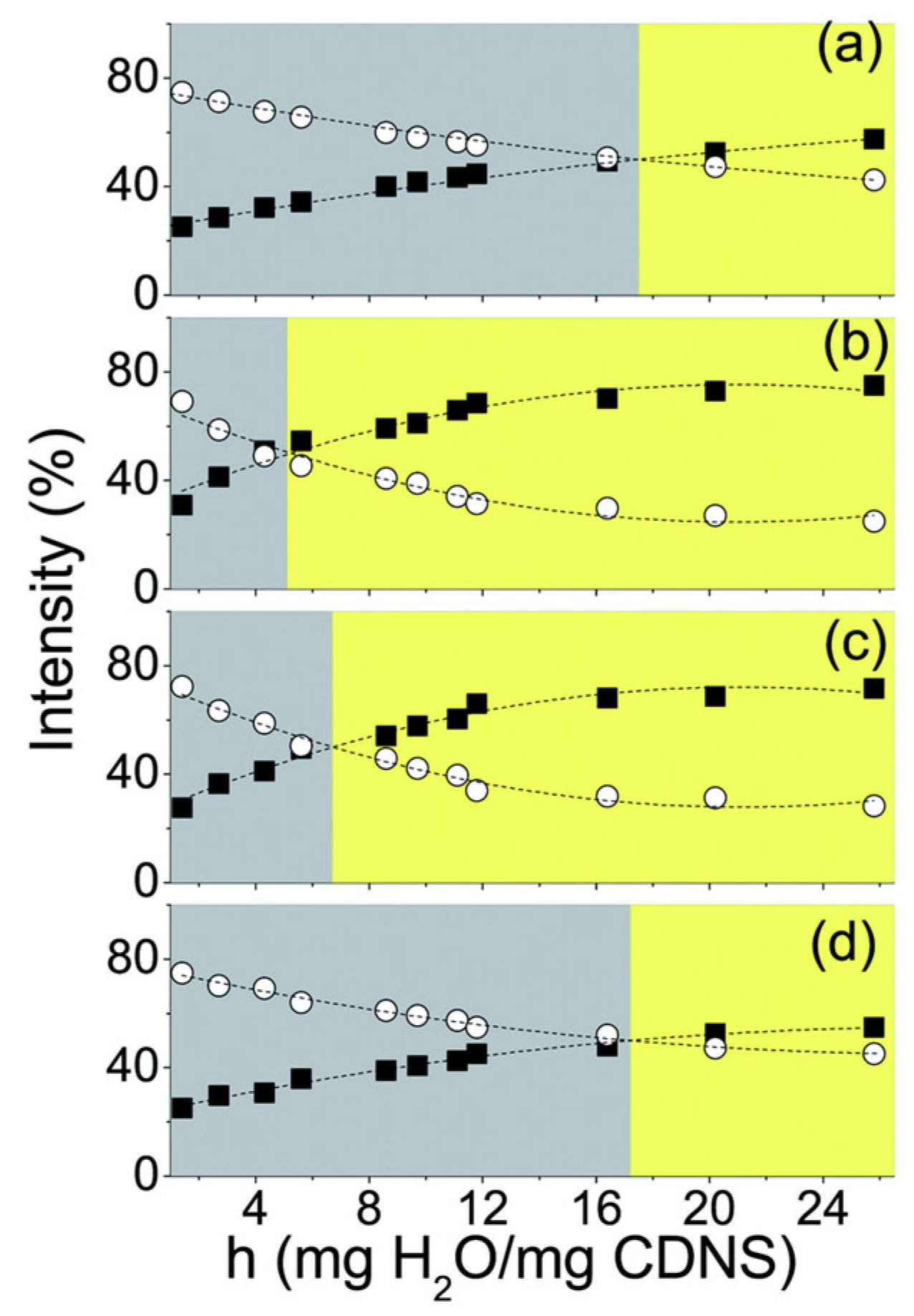
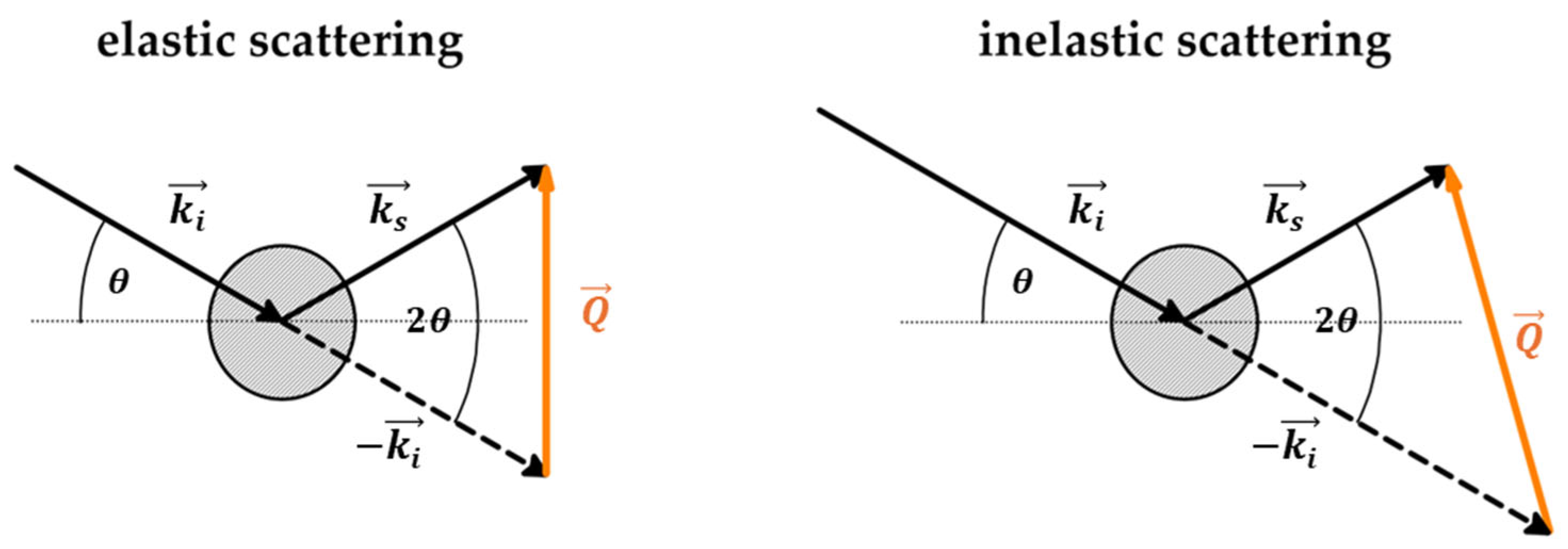

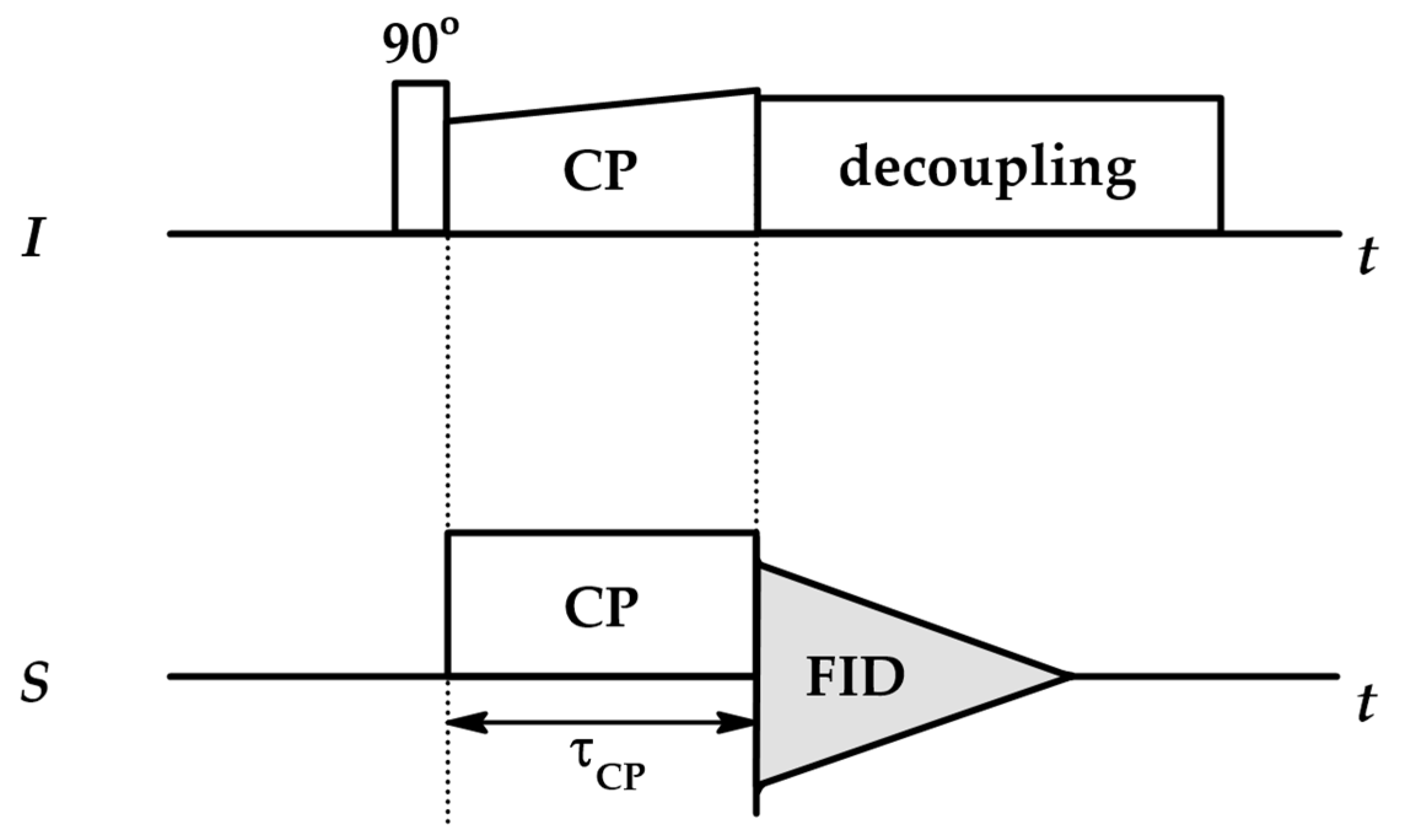
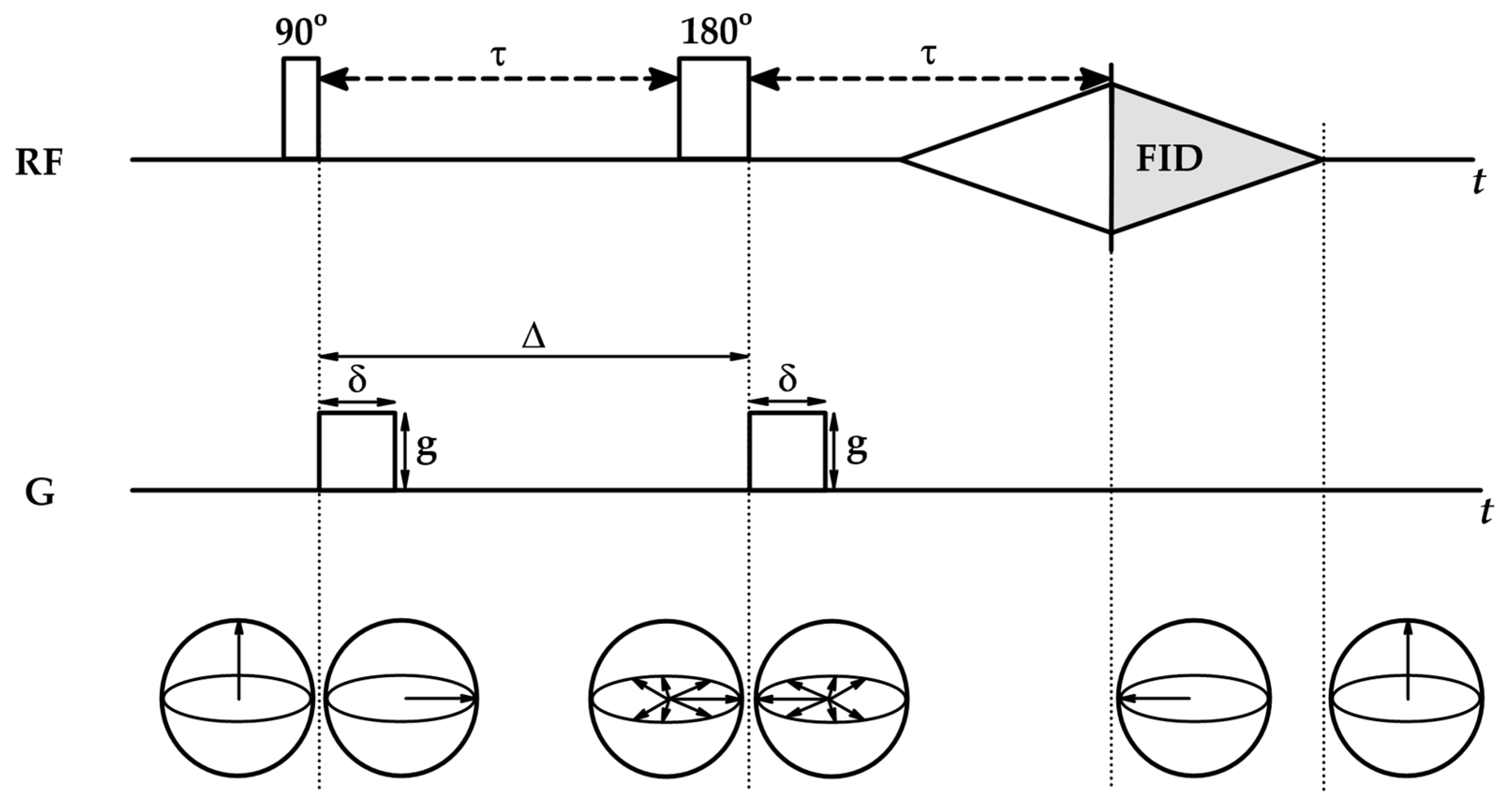
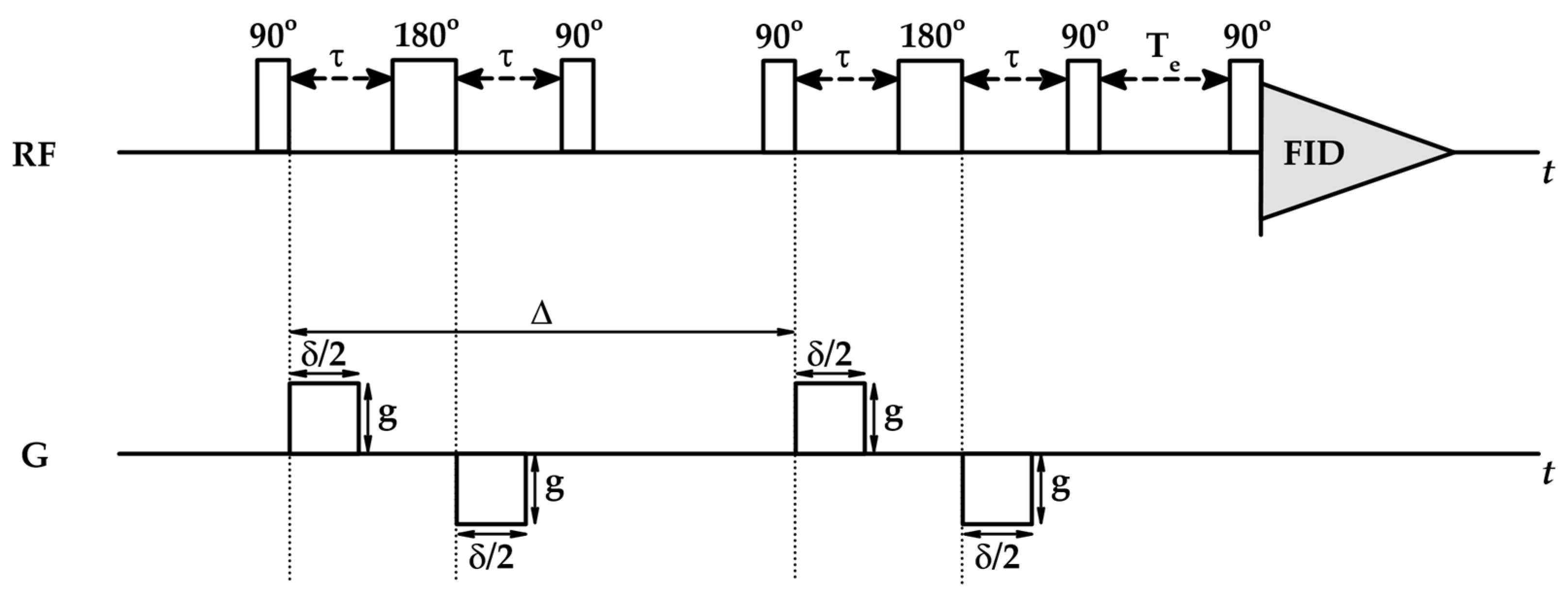

| No | CDNS | Form | 1:n Range | Methods of Examination | Ref. |
|---|---|---|---|---|---|
| 1 | β-CD:PMDA | Dry CDNSs and hydrogels (D2O) | 1:2–1:10 | Low- and high-frequency Raman, diffusion NMR (BPP-LED) | [25] |
| 2 | β-CD:PMDA | Dry CDNSs | 1:2–1:10 | Low-frequency Raman, BLS | [26] |
| 3 | β-CD:PMDA | Dry CDNSs | 1:2–1:10 | ATR-FT-IR, high-frequency Raman | [27] |
| 4 | β-CD:PMDA | Dry CDNSs and hydrogels (H2O, = 3.3 and 5) | 1:4–1:10 | ATR-FT-IR, high-frequency Raman | [28] |
| 5 | β-CD:EDTA | Dry CDNSs | 1:4–1:10 | ATR-FT-IR, low- and high-frequency Raman | [29] |
| 6 | β-CD:PMDA | Hydrogels (D2O, = 3.3 and 5) | 1:4–1:10 | ATR-FT-IR, high-frequency Raman | [30] |
| 7 | α-/γ-CD:EDTA | Dry CDNSs | 1:2–1:10 | Low-frequency Raman | [31] |
| 8 | β-CD:EDTA | Hydrogels (H2O, = 1.4–25.8) | 1:4–1:10 | ATR-FT-IR | [32] |
| 9 | β-CD:PMDA | Dry CDNSs | 1:2–1:8 | Low- and high-frequency Raman, INS | [33] |
| 10 | β-CD:PMDA | Hydrogels (H2O, = 3–25) | 1:4 | High-frequency Raman | [34] |
| 11 | α-CD:EDTA | Hydrogels (H2O, = 2–25.5) | 1:2–1:10 | ATR-FT-IR | [35] |
| 12 | IbuNa@β-CD:EDTA | Hydrogels (D2O) | 1:4, 1:8 | Diffusion NMR (PGSE) | [36] |
| 13 | IbuNa@β-CD:EDTA | Hydrogels (D2O) | 1:4, 1:8 | Diffusion NMR (BPP-LED) | [37] |
| 14 | β-CD:PMDA | Dry CDNSs and hydrogels (H2O and D2O, = 0.4 and 4) | 1:4–1:10 | ATR-FT-IR, high-frequency UV Raman | [38] |
| 15 | β-CD:PMDA | Dry CDNSs and hydrogels (H2O, = 2.7–12) | 1:4–1:10 | ATR-FT-IR, high-frequency UV Raman | [39] |
| 16 | β-CD:EDTA | Hydrogels (H2O and D2O, = 0.4 and 4) | 1:4–1:10 | ATR-FT-IR, high-frequency UV Raman | [40] |
| 17 | α-/γ-CD:EDTA | Dry CDNSs and hydrogels (H2O, = 2–25.5) | 1:2–1:10 | ATR-FT-IR, low-frequency Raman | [41] |
| 18 | β-CD:PMDA | Hydrogels (H2O, D2O and 10–25% Na2CO3 in H2O and D2O, = 4, pH = 8.9–10.1) | 1:4 | ATR-FT-IR, high-frequency UV Raman | [42] |
| 19 | β-CD:PMDA | Hydrogels (H2O, D2O and 10–25% Na2CO3 in H2O and D2O, = 4, pH = 8.5–10.1) | 1:4 | ATR-FT-IR, high-frequency UV Raman | [43] |
| 20 | Caf@β-CD:PMDA | Hydrogels (15% Na2CO3 in H2O, = 4, pH = 9.2) | 1:4, 1:8 | High-frequency UV Raman | [44] |
| 21 | IbuNa@β-CD:EDTA | Hydrogels (H2O) | 1:4, 1:8 | 1H-13C VCT CP MAS NMR | [45] |
| 22 | α-/β-/γ-CD:PMDA/EDTA | Hydrogels (D2O) | 1:2–1:10 | SANS | [46] |
| 23 | β-CD:PMDA | Hydrogels (5–20% Na2CO3 in H2O, = 4, pH = 6.3–9.8) | 1:3 | BLS | [47] |
| 24 | β-CD:PMDA/EDTA | Hydrogels (5–25% Na2CO3 solutions in H2O and D2O, = 1–8, pH = 4.9–9.9) | 1:3–1:8 | High-frequency UV Raman, SANS, BLS | [48] |
| 25 | β-CD:HMDI | Dry CDNSs and hydrogels (H2O and D2O) | 1:1–1:4 | FFC NMR relaxometry | [49] |
| 26 | PiroNa@β-CD:PMDA | Hydrogel (10% Na2CO3) | 1:3 | Diffusion NMR (BPP-LED) | [50] |
| Vibrational Mode | Structural Changes Related to Evolution of Vibrational Mode | Evolution with Increasing | Ref. | |||
|---|---|---|---|---|---|---|
| 1:n | Temperature | pH | ||||
| Upshift—H-bond lifetime reduction (H-bond weakening), destruction of H-bond network involving OH groups of CD units and water molecules Downshift—H-bond lifetime increase (H-bond strengthening), reorganization of water molecules into coordinated H-bond network | Upshift—maximum at 6-fold excess of cross-linker; downshift | Upshift—maximum at 6-fold excess of cross-linker; downshift | Continuous upshift with intensity decrease | - | [28,32,40,43] | |
| Upshift—destruction of H-bond network involving carbonyl groups of cross-linker Downshift—reorganization of water molecules into coordinated H-bond network involving carbonyl groups of cross-linker | Downshift—minimum at 6-fold excess of cross-linker; upshift | Continuous upshift with intensity increase | Continuous upshift with intensity increase | - | [30,38,39] | |
| Upshift—reorganization of water molecules into coordinated H-bond network Downshift—destruction of H-bond network of water molecules | Downshift with intensity increase—minimum at 6-fold excess of cross-linker; upshift with intensity reduction (PMDA-based CDNS) Upshift—maximum at 6-fold excess of cross-linker; downshift (EDTA-based CDNS) | Downshift with intensity increase (PMDA-based CDNS) Upshift with intensity reduction (EDTA-based CDNS) | Continuous downshift | Continuous upshift | [28,32,38,39,40,41,43] | |
| Intensity increase—increased perturbation around aromatic C-H groups of PMDA ring induced by water molecules, indicating formation of non-conventional (C-HO-H) H-bonds Intensity decrease—destruction of non-conventional H-bonds involving aromatic C-H groups of PMDA ring | Maximum intensity at 6-fold excess of PMDA | Intensity increase | Continuous downshift with intensity decrease | Continuous downshift | [38,39,42,43] | |
| Method | FT-IR | Raman |
|---|---|---|
| Probed vibrational modes | , , | , , |
| Characteristic feature | Sensitive to water presence | Sensitive to double-bonded chemical groups and aromatic moieties |
| CDNS type preference | EDTA-based CDNS (stronger water uptake properties) | PMDA-based CDNS (probing non-conventional H-bonds) |
| Sensitivity to drug molecule | Molecules easily forming H-bond with CDNS structure, incorporated within polymer in presence of water molecules | Molecules easily interacting and possibly involved in π-π* |
| Scattering Type | Carried Information | Probed Systems |
|---|---|---|
| elastic coherent | collective atomic positions | macrostructures |
| elastic incoherent | relative atomic positions | amorphous systems |
| inelastic coherent | correlated motions | phonons |
| inelastic incoherent | single-atom motion | diffusion, vibrational density of states (VDOS) |
| Method | Momentum Transfer Value | Category | Probed Systems |
|---|---|---|---|
| Raman | optical phonons (local vibrations) | ||
| BLS | acoustic phonons (elastic moduli) | ||
| SANS | large-scale dynamics | ||
| INS | small-scale dynamics |
| Pulse Sequence | ] | ] | ] | ] | ] | Ref. |
|---|---|---|---|---|---|---|
| PGSE | 53 | 0.5–2.5 | 0.1 | - | 300 | [36] |
| BPP-LED | 53.5 | 1.4–3 | 0.05–0.2 | - | 305 | [25] |
| 53.5 | 1.4–3 | 0.05–0.17 | - | 305 | [37] | |
| 53 | 1.3–3 | - | 0.03–0.11 | 305 | [50] |
| Drug Transport Mechanism | Physical Principle | Dominant Drug Release Model | |
|---|---|---|---|
| Fickian diffusion | Fick’s laws | Diffusion-controlled release | |
| Anomalous transport | Fick’s laws, swelling and relaxation of polymeric network | Swelling-controlled release | |
| Case II transport | Swelling and relaxation of polymeric network, time-independent | ||
| Super-case II transport | Relaxation and erosion of polymeric chains | Relaxation-controlled release |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyrak, B.; Rogacka-Pyrak, K.; Gubica, T. Exploring Cyclodextrin-Based Nanosponges as Drug Delivery Systems: Evaluation of Spectroscopic Methods for Examining Structure and Dynamics of Nanosponges. Int. J. Mol. Sci. 2025, 26, 9342. https://doi.org/10.3390/ijms26199342
Pyrak B, Rogacka-Pyrak K, Gubica T. Exploring Cyclodextrin-Based Nanosponges as Drug Delivery Systems: Evaluation of Spectroscopic Methods for Examining Structure and Dynamics of Nanosponges. International Journal of Molecular Sciences. 2025; 26(19):9342. https://doi.org/10.3390/ijms26199342
Chicago/Turabian StylePyrak, Bartłomiej, Karolina Rogacka-Pyrak, and Tomasz Gubica. 2025. "Exploring Cyclodextrin-Based Nanosponges as Drug Delivery Systems: Evaluation of Spectroscopic Methods for Examining Structure and Dynamics of Nanosponges" International Journal of Molecular Sciences 26, no. 19: 9342. https://doi.org/10.3390/ijms26199342
APA StylePyrak, B., Rogacka-Pyrak, K., & Gubica, T. (2025). Exploring Cyclodextrin-Based Nanosponges as Drug Delivery Systems: Evaluation of Spectroscopic Methods for Examining Structure and Dynamics of Nanosponges. International Journal of Molecular Sciences, 26(19), 9342. https://doi.org/10.3390/ijms26199342








