The Fate of Secondary Electrons in Water upon High-Energy Electron Impact: Changes in the Presence of Nanobubbles
Abstract
1. Introduction
2. Results
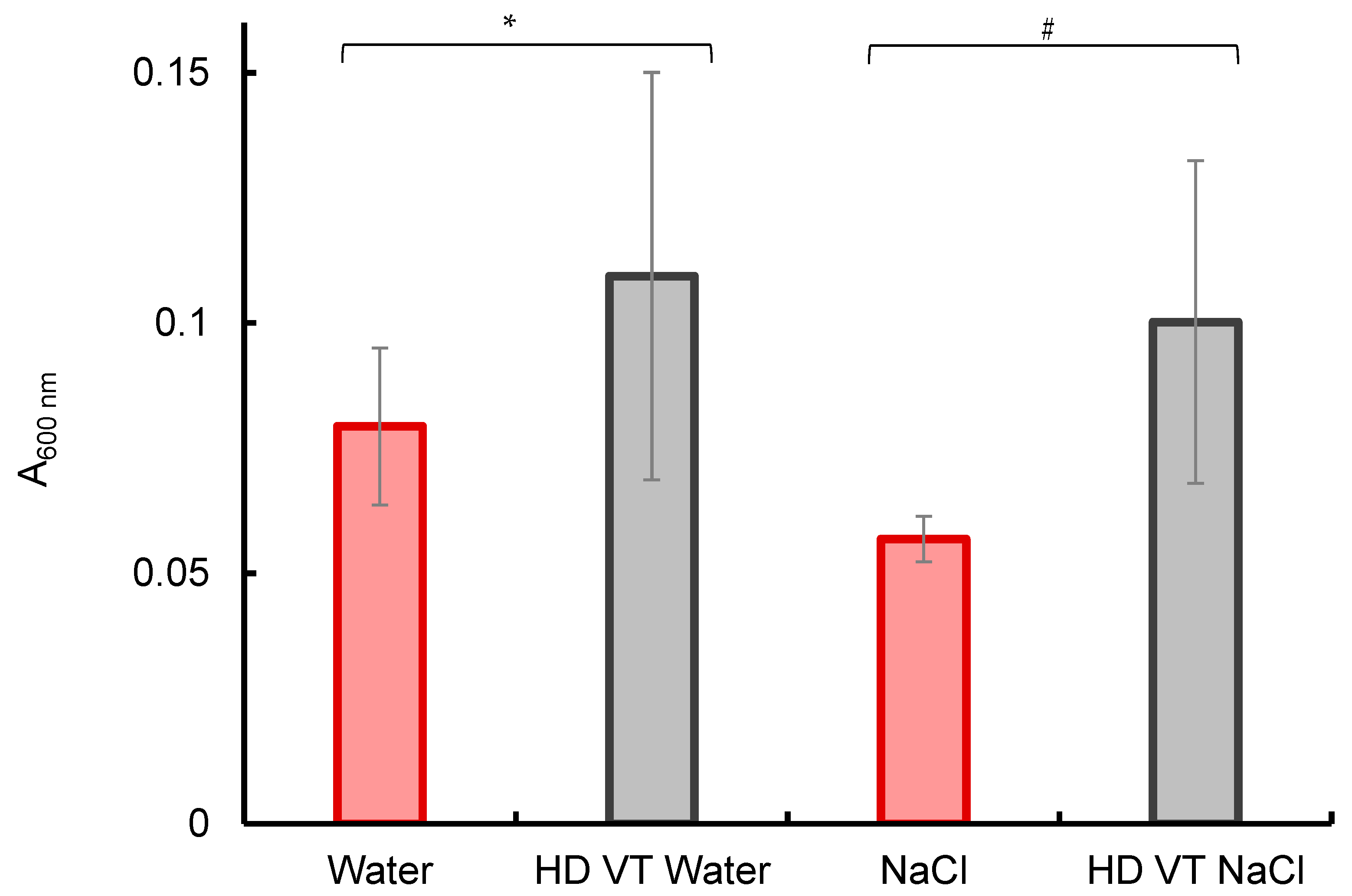
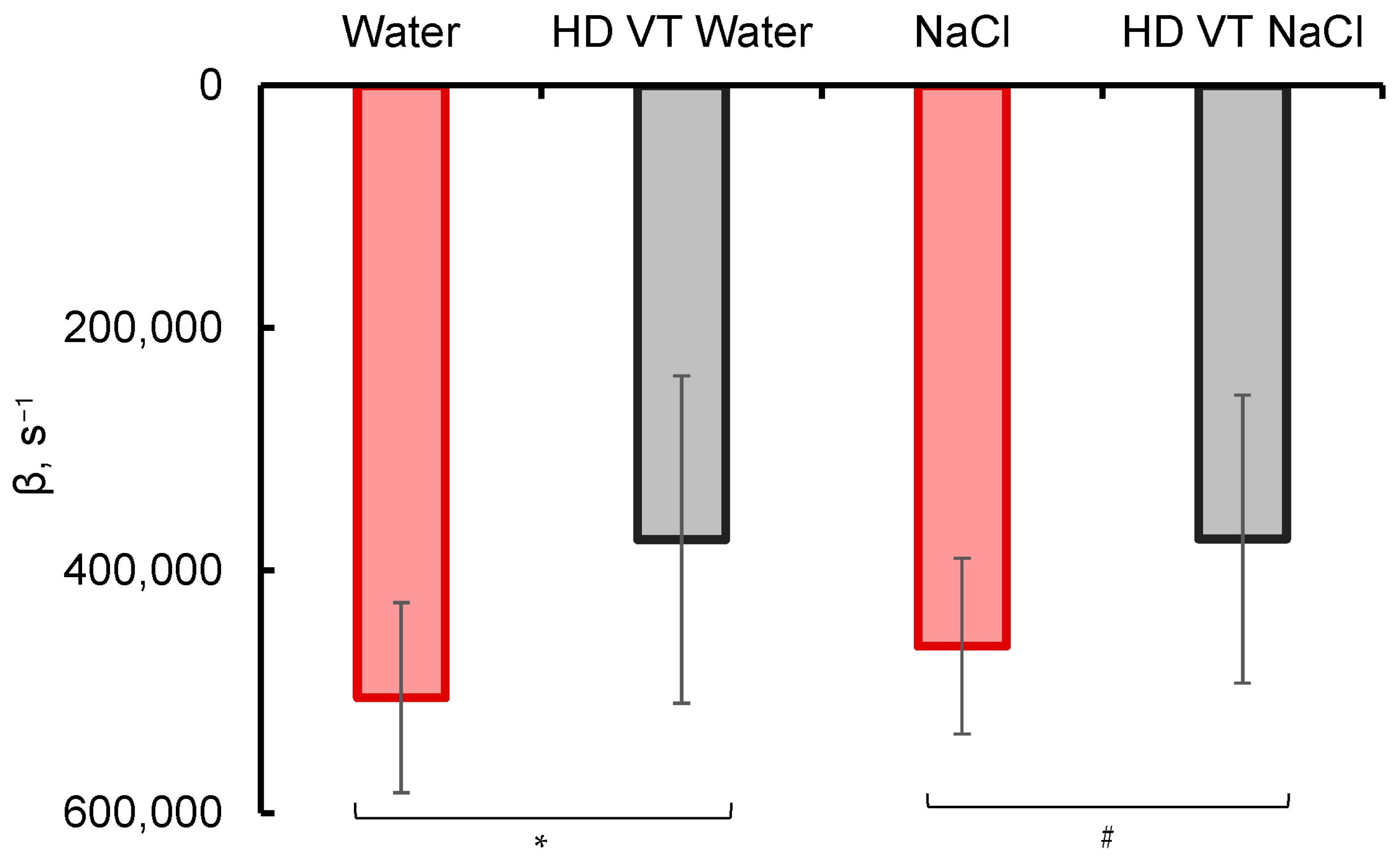
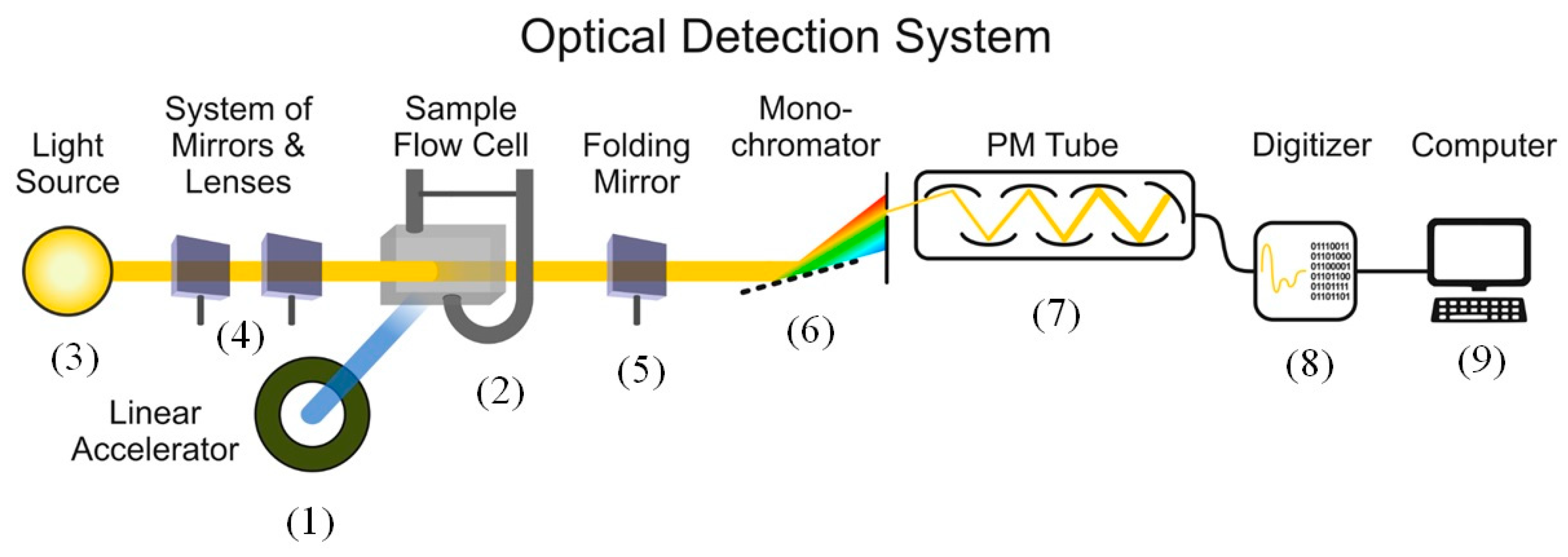
2.1. Spectral Studies
2.2. Nonempirical Simulations: Structural and Energetic Characteristics of Hydrated Electrons and Hydration Complexes of Sodium and Chloride Ions
2.2.1. [Na(H2O)n]+ Aqua Complexes
2.2.2. [Cl(H2O)n]− Aqua Complexes
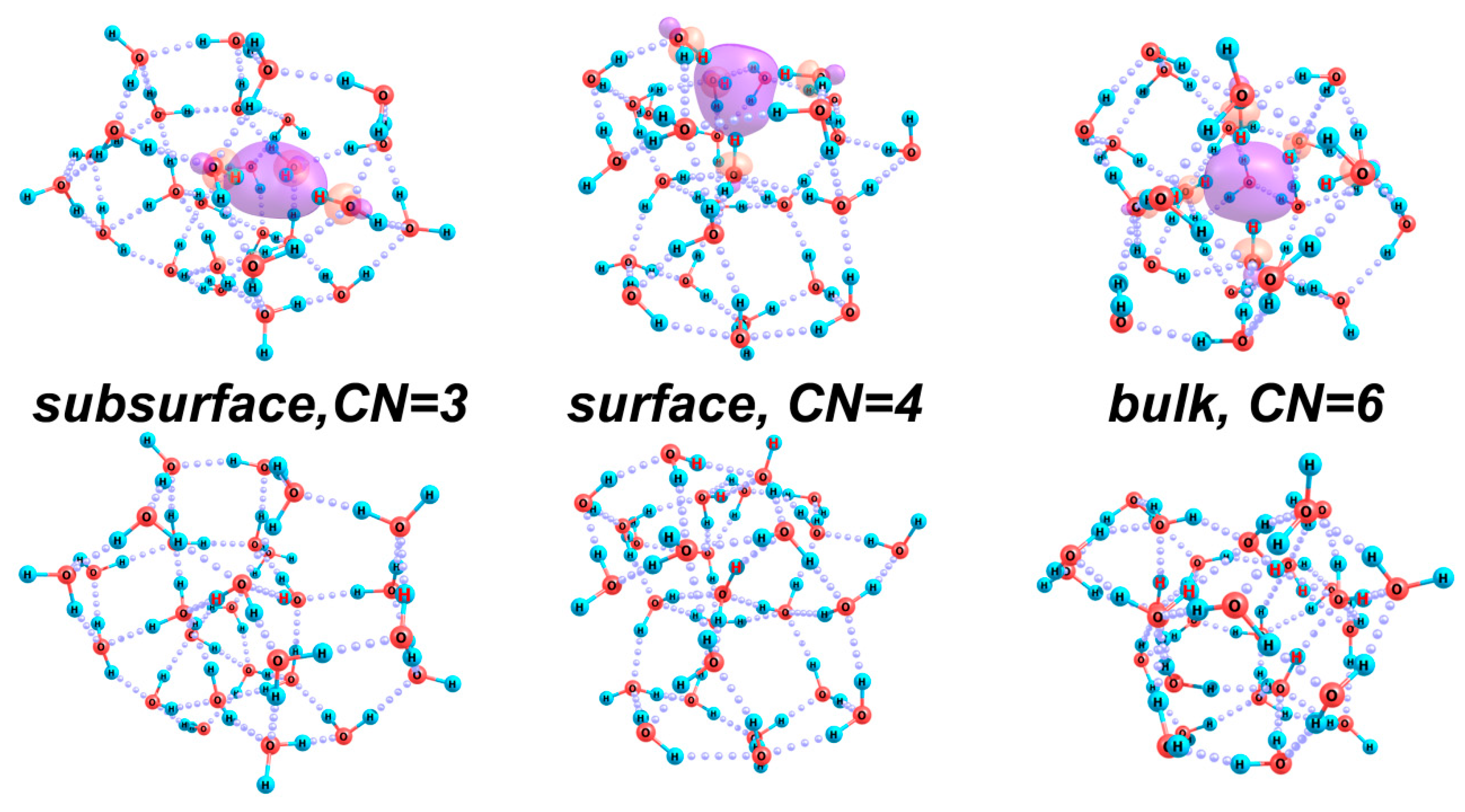
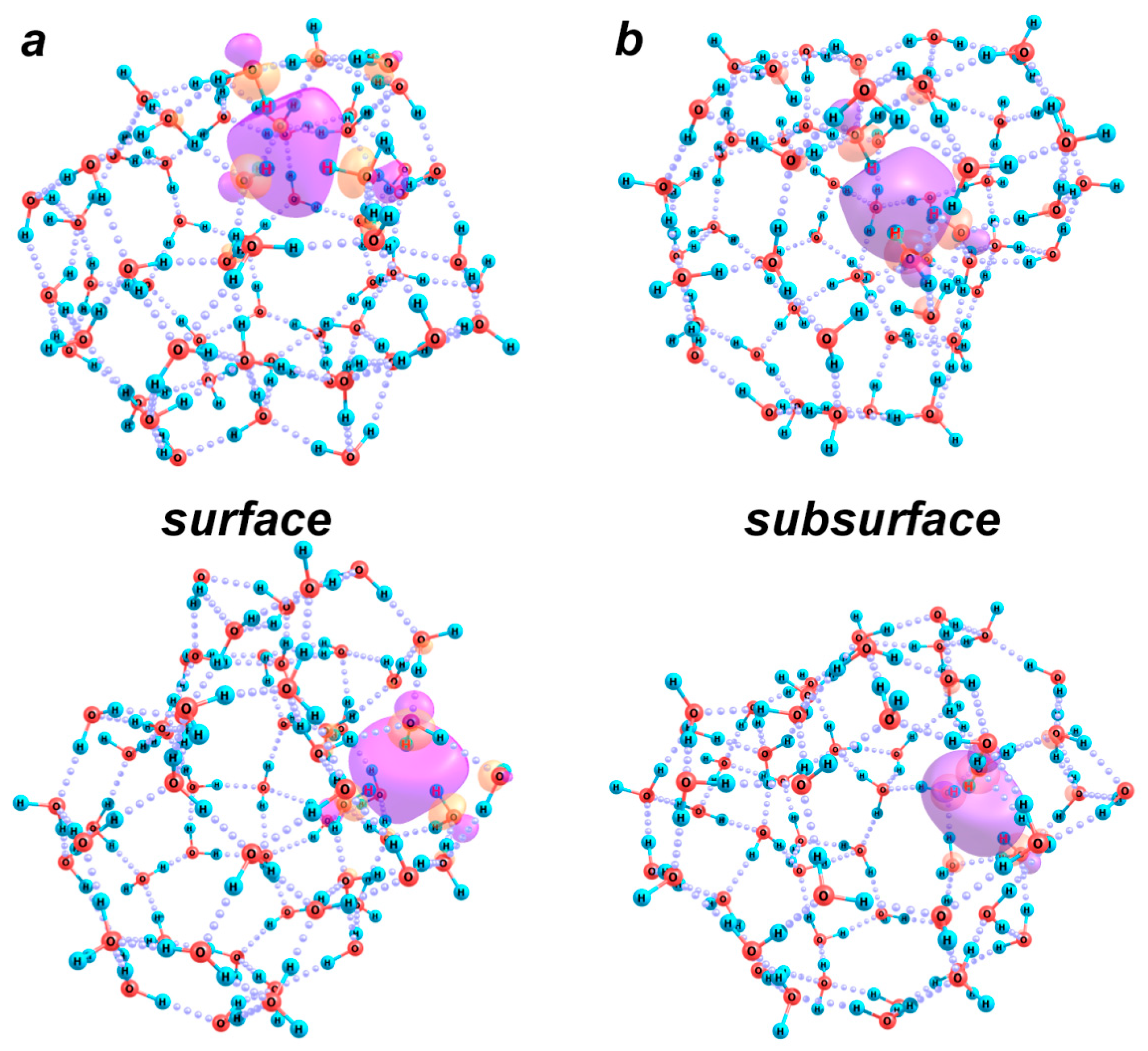
2.2.3. Excess Electron Localization in Water Clusters: [(H2O)n]−
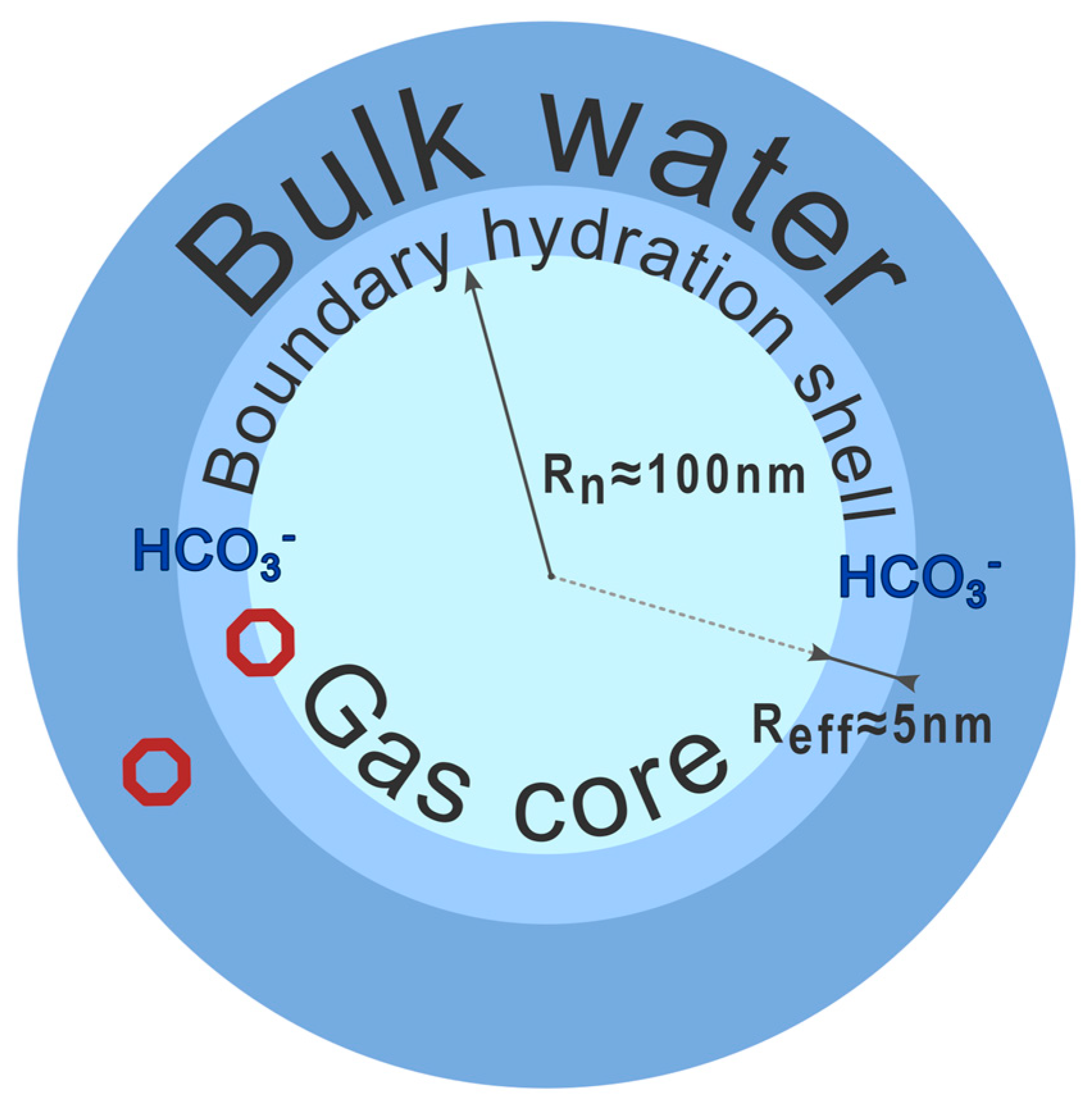
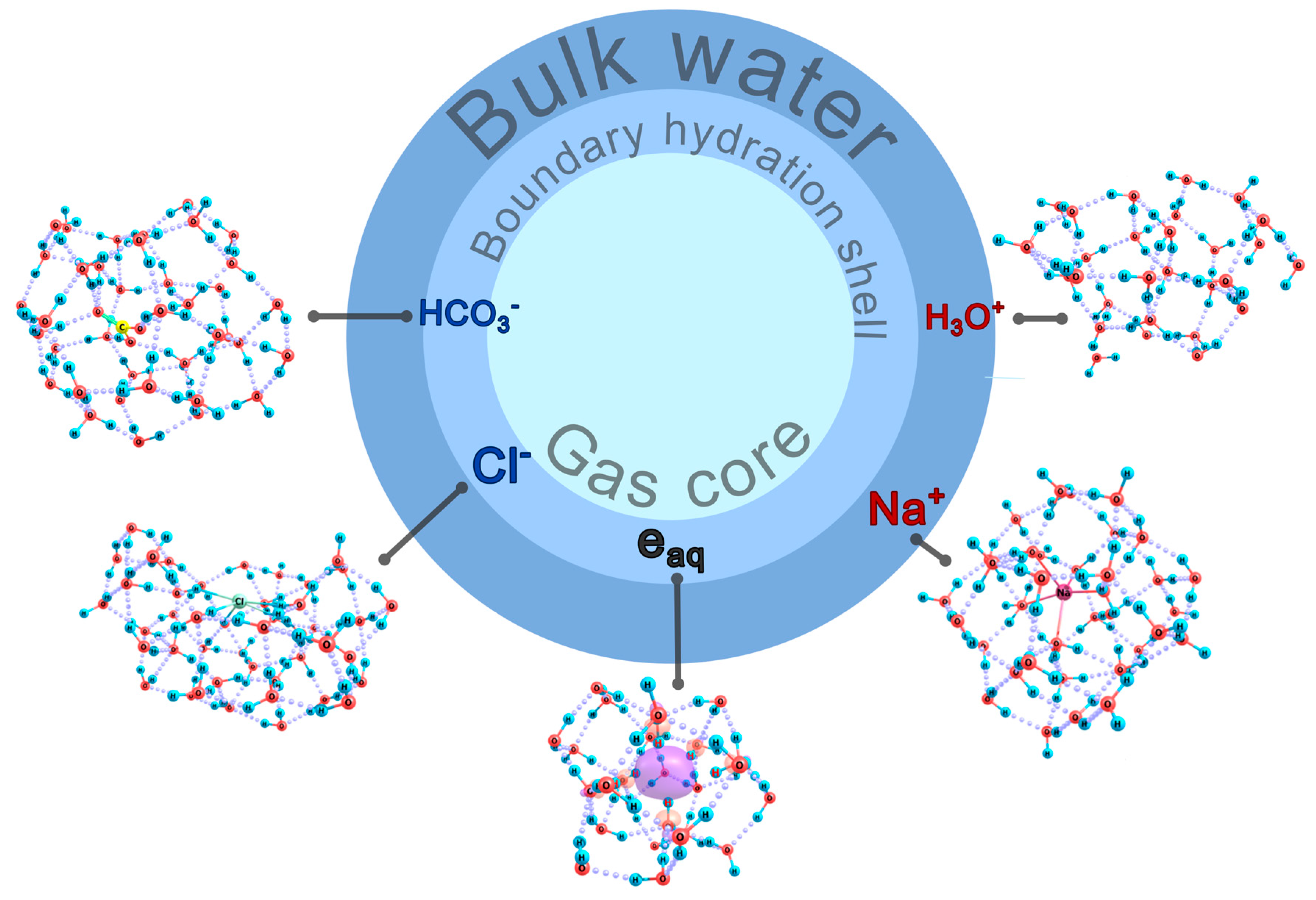
3. Discussion
4. Materials and Methods
4.1. Sample Preparation
- Water—intact liquid not subjected to shaking (reference sample);
- «HD VT NaCl»—vibrationally treated NaCl solution subjected to repeated (high) dilution;
- «HD VT water»—vibrationally treated water subjected to repeated (high) dilution similarly to «HD VT NaCl» samples.
4.2. Photometric Determination of the Content of Radiation-Absorbing Particles
4.3. Experimental Data Analysis
4.4. Quantum Chemical Simulations of the State of Secondary Electrons and Chlorine and Sodium Ions in Water
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VDE | Vertical electron Detachment Energy |
| VEA | Vertical Electron Affinity |
| HD VT | Highly diluted and vibrationally treated |
References
- Bunkin, N.F.; Novakovskaya, Y.V.; Gerasimov, R.Y.; Ninham, B.W.; Tarasov, S.A.; Rodionova, N.N.; Stepanov, G.O. Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range. Int. J. Mol. Sci. 2025, 26, 6811. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Zheng, Y.; Zhu, J. Recent Developments in Hydrodynamic Cavitation Reactors: Cavitation Mechanism, Reactor Design, and Applications. Engineering 2022, 19, 180–198. [Google Scholar] [CrossRef]
- Epstein, P.S.; Plesset, M.S. On the Stability of Gas Bubbles in Liquid-Gas Solutions. J. Chem. Phys. 1950, 18, 1505–1509, Erratum in J. Chem. Phys. 1951, 19, 256. https://doi.org/10.1063/1.1748182. [Google Scholar] [CrossRef]
- Ljunggren, S.; Eriksson, J.C. The Lifetime of a Colloid-Sized Gas Bubble in Water and the Cause of the Hydrophobic Attraction. Colloids Surf. A Physicochem. Eng. Asp. 1997, 129–130, 151–155. [Google Scholar] [CrossRef]
- Yakovlev, E.V.; Kryuchkov, N.P.; Gorbunov, E.A.; Zotov, A.K.; Ovcharov, P.V.; Yurchenko, S.O. The Influence of Salt Concentration on the Dissolution of Microbubbles in Bulk Aqueous Electrolyte Solutions. J. Chem. Phys. 2024, 161, 144704. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Bunkin, F.V. Bubston Structure of Water and Electrolyte Aqueous Solutions. Phys.-Usp. 2016, 59, 846–865. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Shkirin, A.V.; Suyazov, N.V.; Babenko, V.A.; Sychev, A.A.; Penkov, N.V.; Belosludtsev, K.N.; Gudkov, S.V. Formation and Dynamics of Ion-Stabilized Gas Nanobubble Phase in the Bulk of Aqueous NaCl Solutions. J. Phys. Chem. B 2016, 120, 1291–1303. [Google Scholar] [CrossRef]
- Zhou, K.; Chang, A.; Wang, X.; Jiang, Y.; Wang, Y.; Lu, X.; Wang, W. Refractive Index of Single Surface Nanobubbles. Chem. Biomed. Imaging 2023, 1, 387–394. [Google Scholar] [CrossRef]
- Kashkanova, A.D.; Blessing, M.; Gemeinhardt, A.; Soulat, D.; Sandoghdar, V. Precision Size and Refractive Index Analysis of Weakly Scattering Nanoparticles in Polydispersions. Nat. Methods 2022, 19, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Bunkin, N.F.; Shkirin, A.V.; Ninham, B.W.; Chirikov, S.N.; Chaikov, L.L.; Penkov, N.V.; Kozlov, V.A.; Gudkov, S.V. Shaking-Induced Aggregation and Flotation in Immunoglobulin Dispersions: Differences between Water and Water–Ethanol Mixtures. ACS Omega 2020, 5, 14689–14701. [Google Scholar] [CrossRef]
- Hart, E.J.; Boag, J.W. Absorption Spectrum of the Hydrated Electron in Water and in Aqueous Solutions. J. Am. Chem. Soc. 1962, 84, 4090–4095. [Google Scholar] [CrossRef]
- Bartczak, W.M.; Pernal, K. Potential Traps for an Excess Electron in Liquid Water. Geometry, Energy Distributions and Lifetime. Comput. Chem. 2000, 24, 469–482. [Google Scholar] [CrossRef]
- Migus, A.; Gauduel, Y.; Martin, J.L.; Antonetti, A. Excess Electrons in Liquid Water: First Evidence of a Prehydrated State with Femtosecond Lifetime. Phys. Rev. Lett. 1987, 58, 1559–1562. [Google Scholar] [CrossRef]
- Keszei, E.; Nagy, S.; Murphrey, T.H.; Rossky, P.J. Kinetic Analysis of Computer Experiments on Electron Hydration Dynamics. J. Chem. Phys. 1993, 99, 2004–2011. [Google Scholar] [CrossRef]
- Long, F.H.; Lu, H.; Eisenthal, K.B. Femtosecond Studies of the Presolvated Electron: An Excited State of the Solvated Electron? Phys. Rev. Lett. 1990, 64, 1469–1472. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Long, F.H.; Eisenthal, K.B. Femtosecond Studies of Electrons in Liquids. J. Opt. Soc. Am. B 1990, 7, 1511. [Google Scholar] [CrossRef]
- Assel, M.; Laenen, R.; Laubereau, A. Femtosecond Solvation Dynamics of Solvated Electrons in Neat Water. Chem. Phys. Lett. 2000, 317, 13–22. [Google Scholar] [CrossRef]
- Kevan, L. Solvated Electron Structure in Glassy Matrixes. Acc. Chem. Res. 1981, 14, 138–145. [Google Scholar] [CrossRef]
- Assel, M.; Laenen, R.; Laubereau, A. Dynamics of Excited Solvated Electrons in Aqueous Solution Monitored with Femtosecond-Time and Polarization Resolution. J. Phys. Chem. A 1998, 102, 2256–2262. [Google Scholar] [CrossRef]
- Cavanagh, M.C.; Martini, I.B.; Schwartz, B.J. Revisiting the Pump–Probe Polarized Transient Hole-Burning of the Hydrated Electron: Is Its Absorption Spectrum Inhomogeneously Broadened? Chem. Phys. Lett. 2004, 396, 359–366. [Google Scholar] [CrossRef]
- Gottschall, W.C.; Hart, E.J. The Effect of Temperature on the Absorption Spectrum of the Hydrated Electron and on Its Bimolecular Recombination Reaction. J. Phys. Chem. 1967, 71, 2102–2106. [Google Scholar] [CrossRef]
- Hart, E.J.; Michael, B.D.; Schmidt, K.H. Absorption Spectrum of Eaq- in the Temperature Range-4 to 390.Deg. J. Phys. Chem. 1971, 75, 2798–2805. [Google Scholar] [CrossRef]
- Jou, F.-Y.; Freeman, G.R. Temperature and Isotope Effects on the Shape of the Optical Absorption Spectrum of Solvated Electrons in Water. J. Phys. Chem. 1979, 83, 2383–2387. [Google Scholar] [CrossRef]
- Kambhampati, P.; Son, D.H.; Kee, T.W.; Barbara, P.F. Solvation Dynamics of the Hydrated Electron Depends on Its Initial Degree of Electron Delocalization. J. Phys. Chem. A 2002, 106, 2374–2378. [Google Scholar] [CrossRef]
- Madsen, D.; Thomsen, C.L.; Thøgersen, J.; Keiding, S.R. Temperature Dependent Relaxation and Recombination Dynamics of the Hydrated Electron. J. Chem. Phys. 2000, 113, 1126–1134. [Google Scholar] [CrossRef]
- Siefermann, K.R.; Liu, Y.; Lugovoy, E.; Link, O.; Faubel, M.; Buck, U.; Winter, B.; Abel, B. Binding Energies, Lifetimes and Implications of Bulk and Interface Solvated Electrons in Water. Nat. Chem. 2010, 2, 274–279. [Google Scholar] [CrossRef]
- Novakovskaya, Y.V. Flexibility and Regularity of the Hydration Structures of Ions by an Example of Na+: Nonempirical Insight. J. Phys. Chem. A 2022, 126, 8434–8448. [Google Scholar] [CrossRef] [PubMed]
- Novakovskaya, Y.V. Electron Hydration Energy: Nonempirical Estimate. Prot. Met. 2007, 43, 129–140. [Google Scholar] [CrossRef]
- Wang, F.; Schmidhammer, U.; Larbre, J.-P.; Zong, Z.; Marignier, J.-L.; Mostafavi, M. Time-Dependent Yield of the Hydrated Electron and the Hydroxyl Radical in D2 O: A Picosecond Pulse Radiolysis Study. Phys. Chem. Chem. Phys. 2018, 20, 15671–15679. [Google Scholar] [CrossRef]
- Mozumder, A. Fundamentals of Radiation Chemistry; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self—Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular—Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoret. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Granovsky, A.A. Firefly. Version 8.2.0. Available online: http://classic.chem.msu.su/gran/gamess/index.html (accessed on 27 July 2025).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e70019. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Chemcraft. Available online: https://www.chemcraftprog.com (accessed on 22 July 2025).

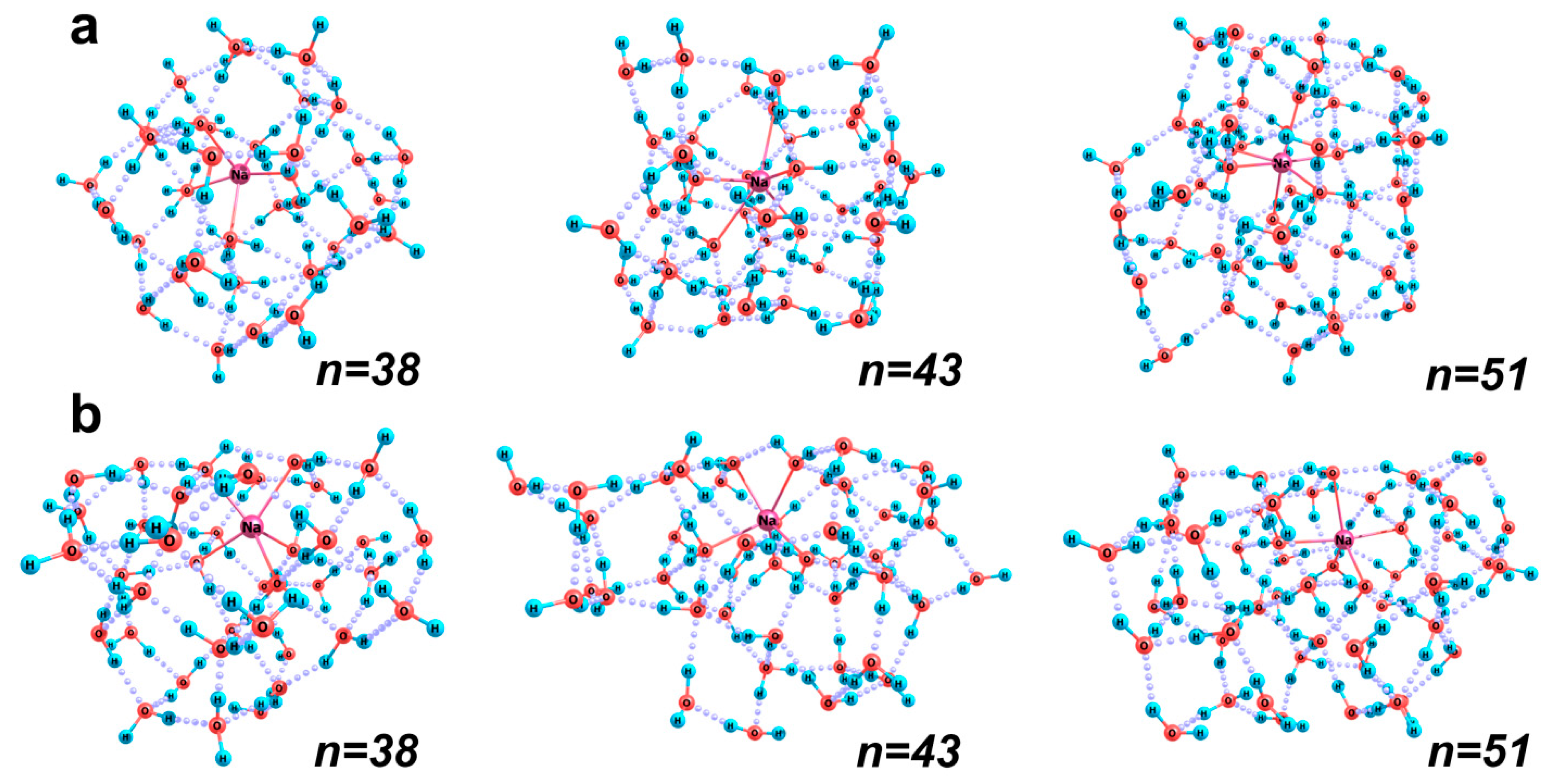
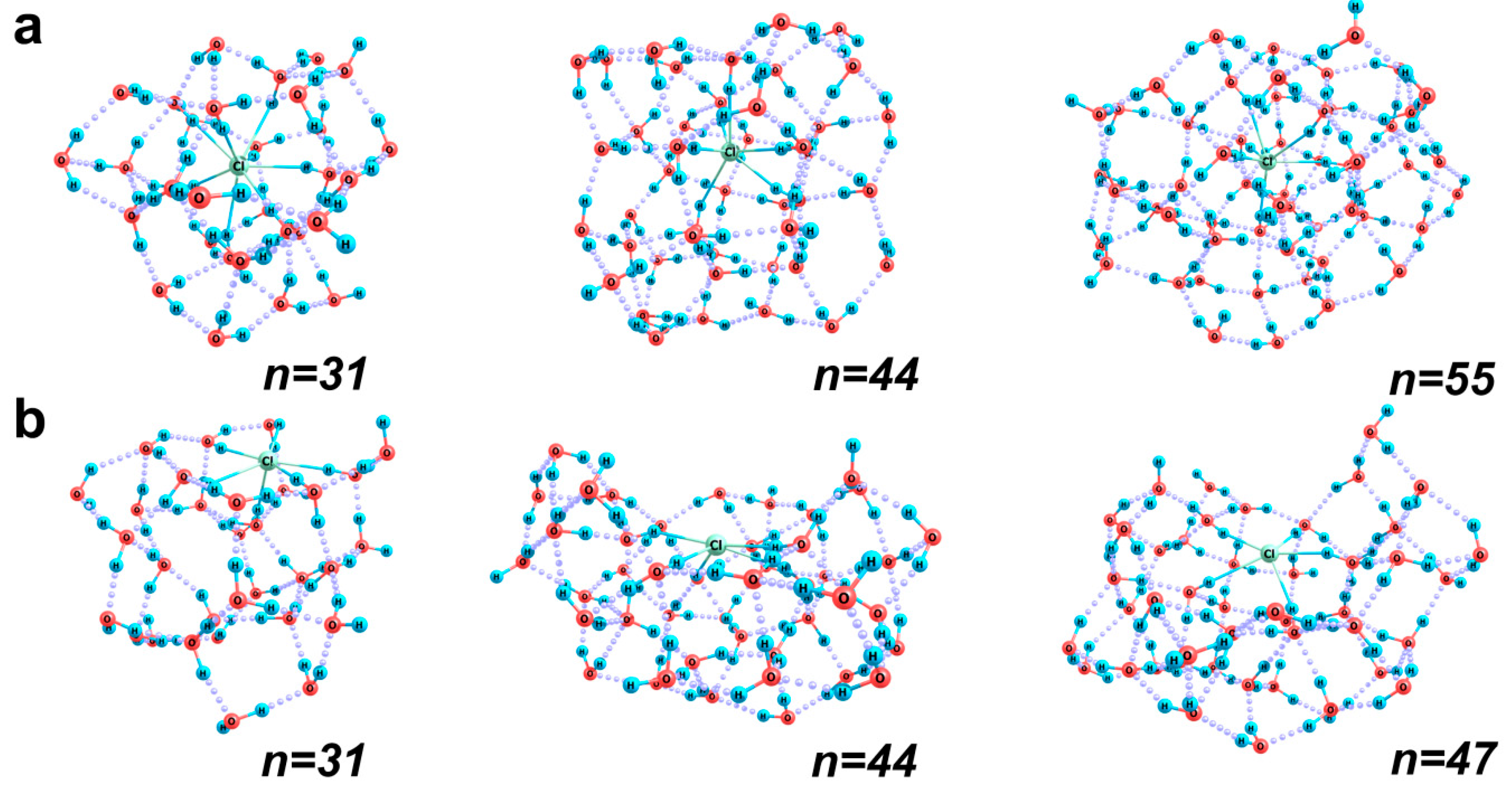

| Structure (n) | 38 | 43 | 51 |
| Bulk structure | 13 | 13 | 14 |
| Surface structure | 11 | 12 | 12 |
| Surface localization | |||||||
| n | 19 | 28 | 33 | 38 | 43 | 46 | 51 |
| VEA, eV | 1.68 | 1.24 | 1.02 | 1.06 | 1.09 | 0.97 | 1.31 |
| Bulk localization | |||||||
| n | 31 | 33 | 38 | 43 | 48 | 51 | 55 |
| VEA, eV | 1.12 | 1.13 | 1.09 | 1.03 | 0.85 | 0.92 | 0.90 |
| n | 20 | 23 | 26 | 31 | 33 | 35 | 37 | 44 | 47 | 55 |
| Surface localization | ||||||||||
| VDE, eV | 6.55 | 6.50 | 6.39 | 6.68 | 6.70 | 6.74 | 6.98 | 6.59 | 6.72 | 6.79 |
| Bulk localization | ||||||||||
| VDE, eV | 6.88 | 6.95 | 6.74 | 6.68 | 6.83 | 6.78 | 6.77 | 6.84 | 6.91 | 6.95 |
| CN | Localization Kind | Erel, kcal/mol | Gvib, kcal/mol | Ereorg, kcal/mol | VDE, eV | ADE, eV |
|---|---|---|---|---|---|---|
| 3 | Subsurface | 3.9 | 4.8 | 39.1 | 22.6 | −16.5 |
| 4 | Surface | 0.0 | 0.0 | 41.1 | 35.3 | −5.9 |
| 6 | Bulk | 5.8 | 4.5 | 58.9 | 62.7 | 3.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novakovskaya, Y.V.; Bunkin, N.F.; Tarasov, S.A.; Rodionova, N.N.; Petrova, A.O.; Stepanov, G.O. The Fate of Secondary Electrons in Water upon High-Energy Electron Impact: Changes in the Presence of Nanobubbles. Int. J. Mol. Sci. 2025, 26, 8909. https://doi.org/10.3390/ijms26188909
Novakovskaya YV, Bunkin NF, Tarasov SA, Rodionova NN, Petrova AO, Stepanov GO. The Fate of Secondary Electrons in Water upon High-Energy Electron Impact: Changes in the Presence of Nanobubbles. International Journal of Molecular Sciences. 2025; 26(18):8909. https://doi.org/10.3390/ijms26188909
Chicago/Turabian StyleNovakovskaya, Yulia V., Nikolai F. Bunkin, Sergey A. Tarasov, Natalia N. Rodionova, Anastasia O. Petrova, and German O. Stepanov. 2025. "The Fate of Secondary Electrons in Water upon High-Energy Electron Impact: Changes in the Presence of Nanobubbles" International Journal of Molecular Sciences 26, no. 18: 8909. https://doi.org/10.3390/ijms26188909
APA StyleNovakovskaya, Y. V., Bunkin, N. F., Tarasov, S. A., Rodionova, N. N., Petrova, A. O., & Stepanov, G. O. (2025). The Fate of Secondary Electrons in Water upon High-Energy Electron Impact: Changes in the Presence of Nanobubbles. International Journal of Molecular Sciences, 26(18), 8909. https://doi.org/10.3390/ijms26188909






