Microbial Growth: Role of Water Activity and Viscoelasticity of the Cell Compartments
Abstract
1. Introduction
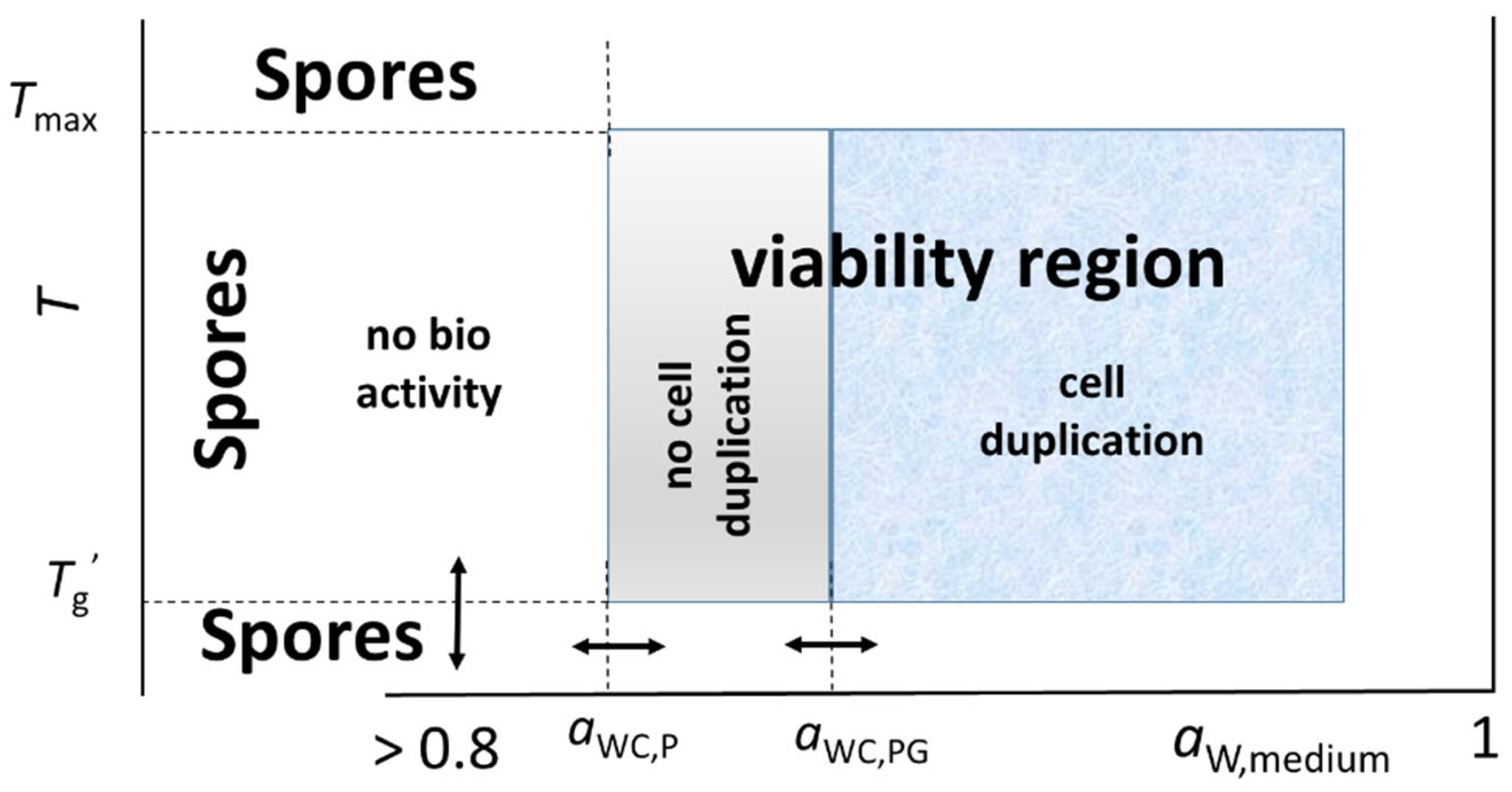
2. Viability of the Cytoplasm for a Closed Batch Microbial Culture
3. No-Growth Water Activity
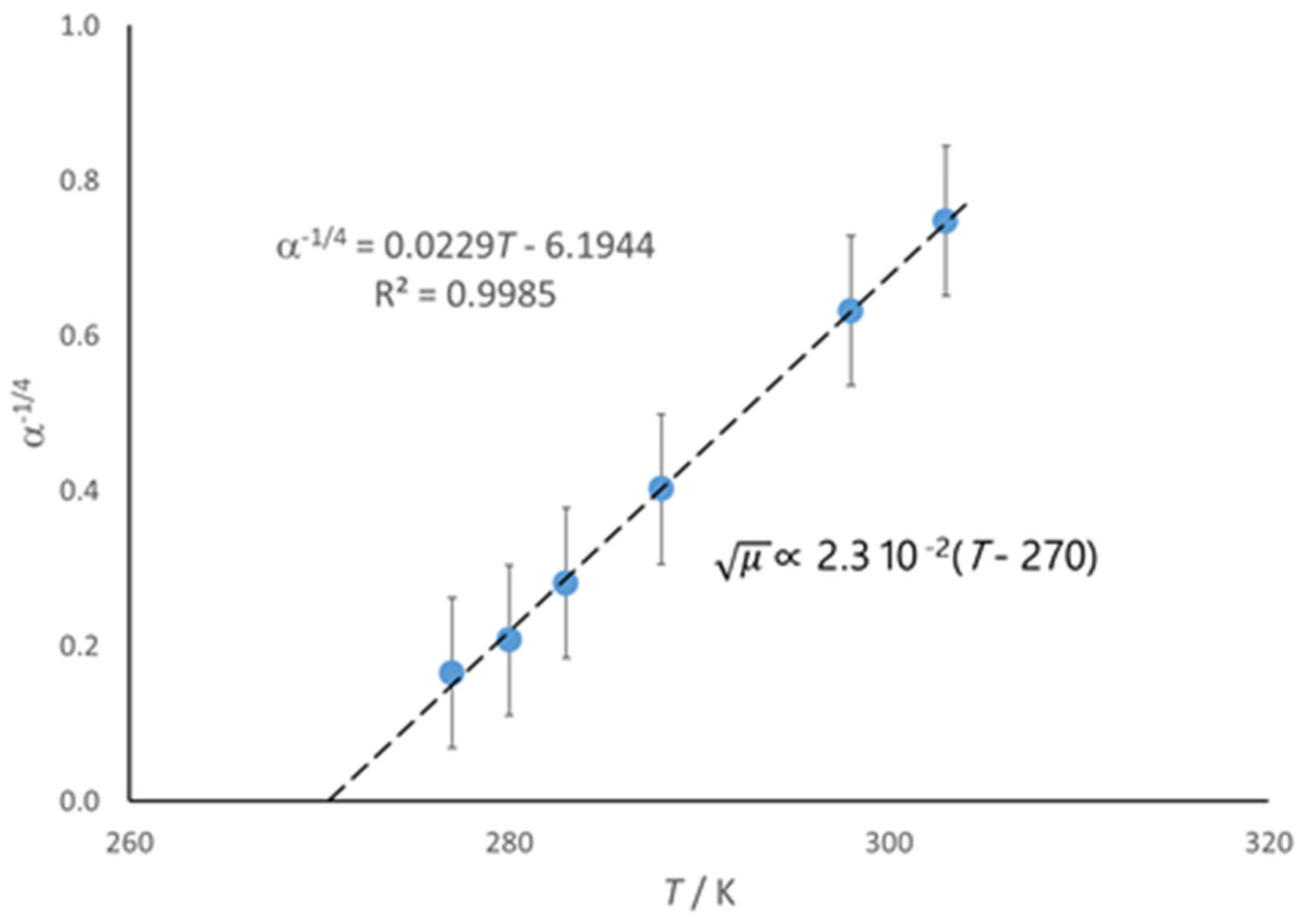
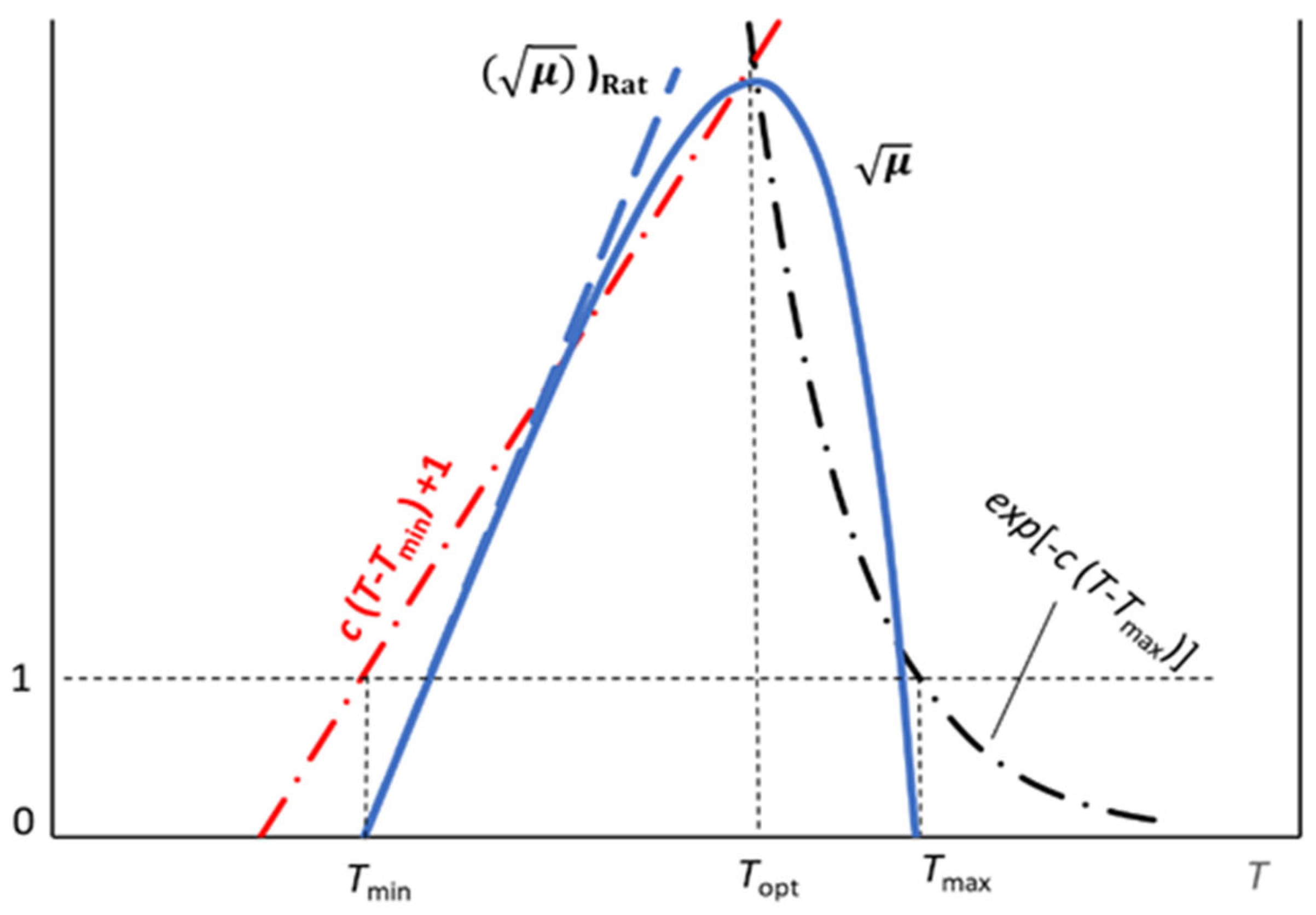
4. The Effect of Temperature
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Reid, D.S.; Fennema, O.R. Fennema’s Food Chemistry, 4th ed.; Damodaran, S., Parkin, K.L., Fennema, O.R., Eds.; CRC Press: Boca Raton, FL, USA, 2008; pp. 17–82. [Google Scholar]
- Labuza, T.P. The effect of water activity on reaction kinetics of food deterioration. Food Technol. 1980, 4, 36–59. [Google Scholar]
- Roos, H.Y. Phase Transitions in Foods; Academic Press Inc.: San Diego, CA, USA, 1995. [Google Scholar]
- Chirife, J.; Buera, M. Water activity, water glass dynamics and the control of microbiological growth in foods. Crit. Rev. Food Sci. Nutr. 1996, 36, 465–513. [Google Scholar] [CrossRef]
- Barbosa-Cànovas, G.V.; Fontana, A.J., Jr.; Schmidt, S.J.; Labuza, T.P. Water Activity in Foods: Fundamentals and Applications; IFT Press Series; Blackwell Publishing: Oxford, UK, 2007. [Google Scholar]
- Polese, P.; Del Torre, M.; Spaziani, M.; Stecchini, M.L. A simplified approach for modelling the bacterial growth/no growth boundary. Food Microbiol. 2011, 28, 384–391. [Google Scholar] [CrossRef]
- Roos, H.Y. Water and Pathogenic Viruses Inactivation—Food Engineering Perspectives. Food Eng. Rev. 2020, 12, 251–267. [Google Scholar] [CrossRef]
- Slade, L.; Levine, H. Beyond water activity: Recent advances based on an alternative approach to the assessment of food quality and safety. CRC Crit. Revs. Food Sci. Nutr. 1991, 30, 115–360. [Google Scholar] [CrossRef]
- Levine, H.; Slade, L. Glass Transitions in Foods. In Physical Chemistry of Foods; Schwartzberg, H.G., Hartel, R.W., Eds.; Marcel Dekker: New York, NY, USA, 1992; pp. 83–221. [Google Scholar]
- Roos, Y.H. Characterization of food Polymers using state diagram. J. Food Eng. 1995, 24, 339–360. [Google Scholar] [CrossRef]
- Rahman, M.S. Food stability determination by macro–micro region concept in the state diagram and by defining a critical temperature. J. Food Eng. 2010, 99, 402–416. [Google Scholar] [CrossRef]
- Ratkowsky, D.A.; Olley, J.; Mcmeekin, T.A.; Ball, A. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 1982, 149, 1–5. [Google Scholar] [CrossRef]
- Parry, B.R.; Surovtsev, I.V.; Cabeen, M.T.; O’Hern, C.S.; Dufresne, E.R.; Jacobs-Wagner, C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell 2014, 156, 183–194. [Google Scholar] [CrossRef]
- Feig, M.; Yu, I.; Wang, P.; Nawrocki, G.; Sugita, Y. Crowding in Cellular Environments at an Atomistic Level from Computer Simulations. J. Phys. Chem. B 2017, 121, 8009–8025. [Google Scholar] [CrossRef]
- Biology Insights Team. Intracellular Water Potential: Key Factors and Biological Impact. 2025. Available online: https://biologyinsights.com/intracellular-water-potential-key-factors-and-biological-impact/ (accessed on 29 April 2025).
- Lu, C.; Prada-Gracia, D.; Rao, F. Structure and dynamics of water in crowded environments slows down peptide conformational changes. J. Chem. Phys. 2014, 141, 045101. [Google Scholar] [CrossRef]
- Testa, A.; Dindo, M.; Rebane, A.A.; Nasouri, B.; Style, R.W.; Golestanian, R.; Dufresne, E.R.; Laurino, P. Sustained enzymatic activity and flow in crowded protein droplets. Nat. Commun. 2021, 12, 6293. [Google Scholar] [CrossRef] [PubMed]
- Nawrocki, G.; Sugita, Y.; Feig, M. Protein Crowding Affects Hydration Structure and Dynamics. J. Am. Chem. Soc. 2012, 134, 4842–4849. [Google Scholar]
- Ellis, R.J. Macromolecular crowding: Obvious but underappreciated. Trends Biochem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- Rivas, G.; Minton, A.P. Biochemical Reactions in Cytomimetic Media. Front. Mol. Biosci. 2020, 6, 145. [Google Scholar] [CrossRef]
- Verkman, A.S. Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem. Sci. 2002, 27, 27–33. [Google Scholar] [CrossRef]
- Cayley, D.S.; Guttman, H.J.; Record, M.T., Jr. Biophysical characterization of changes in amounts and activity of Escherichia coli cell and compartment water and turgor pressure in response to osmotic stress. Biophys. J. 2000, 78, 1748–1764. [Google Scholar] [CrossRef]
- Gurian, E.; Semeraro, S.; Bellich, B.; Rampino, A.; Schneider, C.; Cesàro, A. Cell Biothermodynamics. Can calorimetry dynamically monitor cytoplasmic water activity? J. Therm. Anal. Calorim. 2017, 127, 525–534. [Google Scholar] [CrossRef]
- Schiraldi, A.; Fessas, D.; Signorelli, M. Water Activity in Biological Systems—A Review. Pol. J. Food Nutr. Sci. 2012, 62, 5–13. [Google Scholar] [CrossRef]
- Schiraldi, A. Structural Relaxation and Thermodynamics of Viscous Aqueous Systems: A Simplified Reappraisal. J. Sol. Chem. 2023, 52, 367–384. [Google Scholar] [CrossRef]
- Watson, J.L.; Seinkmane, E.; Styles, C.T.; Mihut, A.; Krüger, L.K.; McNally, K.E.; Planelles-Herrero, V.J.; Dudek, M.; McCall, P.M.; Barbiero, S.; et al. Macromolecular condensation buffers intracellular water potential. Nature 2023, 623, 842–885. [Google Scholar] [CrossRef]
- Tuson, H.H.; Auer, G.K.; Renner, L.D.; Hasebe, M.; Tropini, C.; Salick, M.; Crone, W.C.; Gopinathan, A.; Huang, K.C.; Weibel, D.B. Measuring the stiffness of bacterial cells from growth rates in hydrogels of tunable elasticity. Mol. Microbiol. 2012, 84, 874–891. [Google Scholar] [CrossRef]
- Borisova, M.; Gaupp, R.; Duckworth, A.; Schneider, A.; Dalügge, D.; Mühleck, M.; Deubel, D.; Unsleber, S.; Yu, W.; Muth, G.; et al. Peptidoglycan recycling in Gram-positive bacteria is crucial for survival in stationary phase. mBio 2016, 7, e00923-16. [Google Scholar] [CrossRef]
- Typas, A.; Banzhaf, M.; Gross, C.A.; Vollmer, W. From the regulation of peptidoglycan synthesis to bacterial growth and morphology. Nat. Rev. Microbiol. 2017, 10, 123–136. [Google Scholar] [CrossRef]
- Collins, T.; Margesin, R. Psychrophilic lifestyles: Mechanisms of adaptation and biotechnological tools. Appl. Microbiol. Biotechnol. 2019, 103, 2857–2871. [Google Scholar] [CrossRef]
- Egan, A.J.F.; Errington, J.; Vollmer, W. Regulation of peptidoglycan synthesis and remodeling. Nature 2020, 18, 446–460. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.-L.; Lao, J.; Zhang, S.; Abzalimov, R.; Wang, T.; Chen, X. High Energy and Power Density Peptidoglycan Muscles through Super-Viscous Nanoconfined Water. Adv. Sci. 2022, 9, 2104697. [Google Scholar] [CrossRef]
- Nygaard, R.; Graham, C.L.B.; Dufrisne, M.B.; Colburn, J.D.; Pepe, J.; Hydorn, M.A.; Corradi, S.; Brown, C.M.; Ashraf, K.U.; Vickery, O.N.; et al. Structural basis of peptidoglycan synthesis by E. coli RodA-PBP2 complex. Nat. Commun. 2023, 14, 5151. [Google Scholar] [CrossRef]
- Sperandeo, P.; Martorana, A.M.; Polissi, A. Lipopolysaccharide biosynthesis and transport to the outer membrane of Gram-negative bacteria. In Bacterial Cell Walls and Membranes; Kuhn, A., Ed.; Springer Nature: Cham, Switzerland, 2019; Chapter 2; pp. 9–38. [Google Scholar]
- Corti, H.R.; Angell, C.A.; Auffret, T.; Levine, H.; Buera, M.P.; Reids, D.S.; Roos, Y.H.; Slade, L. Empirical and theoretical models of equilibrium and non-equilibrium transition temperatures of supplemented phase diagrams in aqueous systems (IUPAC Technical Report). Pure Appl. Chem. 2010, 82, 1065–1097. [Google Scholar] [CrossRef]
- Passot, S.; Cenard, S.; Douania, I.; Tréléa, I.C.; Fonseca, F. Critical water activity and amorphous state for optimal preservation of lyophilised lactic acid bacteria. Food Chem. 2012, 132, 1699–1705. [Google Scholar] [CrossRef]
- Roos, Y.H.; Karel, M. Differential Scanning Calorimetry Study of Phase Transitions Affecting the Quality of Dehydrated Materials. Biotechnol. Prog. 1990, 6, 159–163. [Google Scholar] [CrossRef]
- Abiad, M.G.; Campanella, O.H.; Carvajal, M.T. Assessment of Thermal Transitions by Dynamic Mechanical Analysis (DMA) Using a Novel Disposable Powder Holder. Pharmaceutics 2010, 2, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Shoda, M.; Kawai, K.; Koseki, S. Relationship between glass transition temperature, and desiccation and heat tolerance in Salmonella enterica. PLoS ONE 2020, 15, e0233638. [Google Scholar] [CrossRef]
- Persat, A.; Nadell, C.D.; Kim, M.K.; Ingremeau, F.; Siryaporn, A.; Drescher, K.; Wingreen, N.S.; Bassler, B.L.; Gitai, Z.; Stone, H.A. The mechanical world of bacteria. Cell 2015, 161, 988–997. [Google Scholar] [CrossRef]
- Sogabe, T.; Nakagawa, H.; Yamada, T.; Koseki, S.; Kawai, K. Effect of water activity on the mechanical glass transition and dynamical transition of bacteria. Biophys. J. 2022, 121, 3874–3882. [Google Scholar] [CrossRef]
- Hammond, L.R.; White, M.L.; Eswara, P.J. Probing Bacterial Cell Division and Cell Envelope Biogenesis with Live-Cell Fluorescence Microscopy. In The Bacterial Cell Wall. Methods in Molecular Biology; Ton-That, H., Ed.; Humana: New York, NY, USA, 2024; Volume 2727. [Google Scholar] [CrossRef]
- Moreno-Flores, S.; Benitez, R.; dM Vivanco, M.; Toca-Herrera, J.L. Stress relaxation and creep on living cells with the atomic force microscope: A means to calculate elastic moduli and viscosities of cell components. Nanotechnology 2010, 21, 445101. [Google Scholar] [CrossRef]
- Weber, A.; Tyriakowski, D.; Toca-Herrera, J.L. Power laws describe bacterial viscoelasticity. Langmuir 2022, 38, 15552–15558. [Google Scholar] [CrossRef]
- Pazos, M.; Peters, K. Peptidoglycan. In Bacterial Cell Walls and Membranes; Kuhn, A., Ed.; Springer Nature: Cham, Switzerland, 2019; Chapter 5; pp. 127–168. [Google Scholar]
- Voorhaar, L.; Hoogenboom, R. Supramolecular polymer networks: Hydrogels and bulk materials. Chem. Soc. Rev. 2016, 45, 4013–4031. [Google Scholar] [CrossRef]
- Bell, L.N.; Bell, H.M.; Glass, T.E. Water mobility in glassy and rubbery solids as determined by oxygen-17 nuclear magnetic resonance: Impact on chemical stability. Food Sci. Technol. 2002, 35, 108–113. [Google Scholar] [CrossRef]
- Yap, L.-W.; Endres, R.G. A model of cell-wall dynamics during sporulation in Bacillus subtilis. Soft Matter 2017, 13, 8089–8095. [Google Scholar] [CrossRef]
- Stecchini, M.L.; Del Torre, M.; Venir, E.; Morettin, A.; Furlan, P.; Maltini, E. Glassy state in Bacillus subtilis spores analyzed by differential scanning calorimetry. Int. J. Food Microbiol. 2006, 106, 286–290. [Google Scholar] [CrossRef]
- Pérez-Alonso, C.; Beristain, C.I.; Lobato-Calleros, C.; Rodríguez-Huezo, M.E.; Vernon-Carter, E.J. Thermodynamic analysis of the sorption isotherms of pure and blended carbohydrate polymers. J. Food Eng. 2006, 77, 753–760. [Google Scholar] [CrossRef]
- Berendsen, H.J.C. Specific Interactions of Water with Biopolymers. In Water in Disperse Systems; Water; Franks, F., Ed.; Springer: Boston, MA, USA, 1975; Volume 5. [Google Scholar] [CrossRef]
- Heitzer, A.; Kohler, H.-P.E.; Reichert, P.; Hamer, G. Utility of phenomenological models for describing temperature dependence of bacterial growth. Appl. Environ. Microbiol. 1991, 57, 2656–2665. [Google Scholar] [CrossRef] [PubMed]
- Pinto, L.C.; Shimakawa, K. Origin of temperature dependence of bacterial growth rate: Analogy with the viscosity of glass-forming liquids in inorganic materials. Phys. Complex Syst. 2024, 5, 67–73. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth curve of microbial cultures: A model for a visionary reappraisal. Appl. Microbiol. 2023, 3, 288–296. [Google Scholar] [CrossRef]
- Schiraldi, A. The “Growth Curve”: An autocorrelation effect. Appl. Microbiol. 2024, 4, 1257–1267. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth of microbial cultures complies with the laws of thermodynamics. Biophys. Chem. 2024, 307, 107177. [Google Scholar] [CrossRef]
- Schiraldi, A.; Foschino, R. A phenomenological model to infer the microbial growth: A case study for psychrotrophic pathogenic bacteria. J. Appl. Microbiol. 2022, 132, 642–653. [Google Scholar] [CrossRef]
- Ratkowsky, D.A.; Lowry, R.K.; Mcmeekin, T.A.; Stokes, A.N.; Chandler, R.E. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 1983, 154, 1222–1226. [Google Scholar] [CrossRef]
- Rosso, L.; Lobry, R.; Bajard, S.; Flandrois, J.P. Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 1995, 61, 610–616. [Google Scholar] [CrossRef]
- Salter, M.A.; Ross, T.; McMeekin, T.A. Applicability of a model for non-pathogenic Escherichia coli for predicting the growth of pathogenic Escherichia coli. J. Appl. Microbiol. 1998, 85, 357–364. [Google Scholar] [CrossRef]
- Mellefont, L.A.; McMeekin, T.A.; Ross, T. Performance evaluation of a model describing the effects of temperature, water activity, pH and lactic acid concentration on the growth of Escherichia coli. Int. J. Food Microbiol. 2003, 82, 45–58. [Google Scholar] [CrossRef]
- Membré, J.-M.; Leporq, B.; Vialette, M.; Mettler, E.; Perrier, L.; Thuault, D.; Zwietering, M. Temperature effect on bacterial growth rate: Quantitative microbiology approach including cardinal values and variability estimates to perform growth simulations on/in food. Int. J. Food Microbiol. 2005, 100, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Hwang, A.; Phillips, J. Effect of temperature on microbial growth rate–Mathematical analysis: The Arrhenius and Eyring–Polanyi connections. J. Food Sci. 2011, 76, 553–560. [Google Scholar] [CrossRef] [PubMed]
- Matejčeková, Z.; Spodniaková, S.; DujMić, E.; Liptáková, D.; Valík, L. Modelling growth of Lactobacillus plantarum as a function of temperature: Effects of media. J. Food Nutr. Res. 2019, 58, 125–134. [Google Scholar]
- Baranyi, J.; Buss da Silva, N.; Ellouze, M. Rethinking Tertiary Models: Relationships between Growth Parameters of Bacillus cereus Strains. Front. Microbiol. 2017, 8, 1890. [Google Scholar] [CrossRef]
- Gora, G.Y.; Schere, G.W.; Stone, H.A. Bacterial spores respond to humidity similarly to hydrogels. Proc. Natl. Acad. Sci. USA 2024, 121, e2320763121. [Google Scholar] [CrossRef]
- Atrih, A.; Foster, S.J. Analysis of the role of bacterial endospore cortex structure in resistance properties and demonstration of its conservation amongst species. J. Appl. Microbiol. 2001, 91, 364–372. [Google Scholar] [CrossRef]
- Schiraldi, A. Short and long-term evolution of microbial cultures. Int. J. Mol. Sci. 2025, 26, 4187. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiraldi, A. Microbial Growth: Role of Water Activity and Viscoelasticity of the Cell Compartments. Int. J. Mol. Sci. 2025, 26, 8508. https://doi.org/10.3390/ijms26178508
Schiraldi A. Microbial Growth: Role of Water Activity and Viscoelasticity of the Cell Compartments. International Journal of Molecular Sciences. 2025; 26(17):8508. https://doi.org/10.3390/ijms26178508
Chicago/Turabian StyleSchiraldi, Alberto. 2025. "Microbial Growth: Role of Water Activity and Viscoelasticity of the Cell Compartments" International Journal of Molecular Sciences 26, no. 17: 8508. https://doi.org/10.3390/ijms26178508
APA StyleSchiraldi, A. (2025). Microbial Growth: Role of Water Activity and Viscoelasticity of the Cell Compartments. International Journal of Molecular Sciences, 26(17), 8508. https://doi.org/10.3390/ijms26178508




