Structural-Scaling Transitions and Criticality Cascade in DNA with Open States
Abstract
1. Introduction
2. Results
2.1. Genomic Mechanism Determining Cell Fate
2.2. DNA Open States
2.3. Collective Properties of the Open States Ensembles
2.4. Numerical Simulation of the Self-Organized DNA Criticality
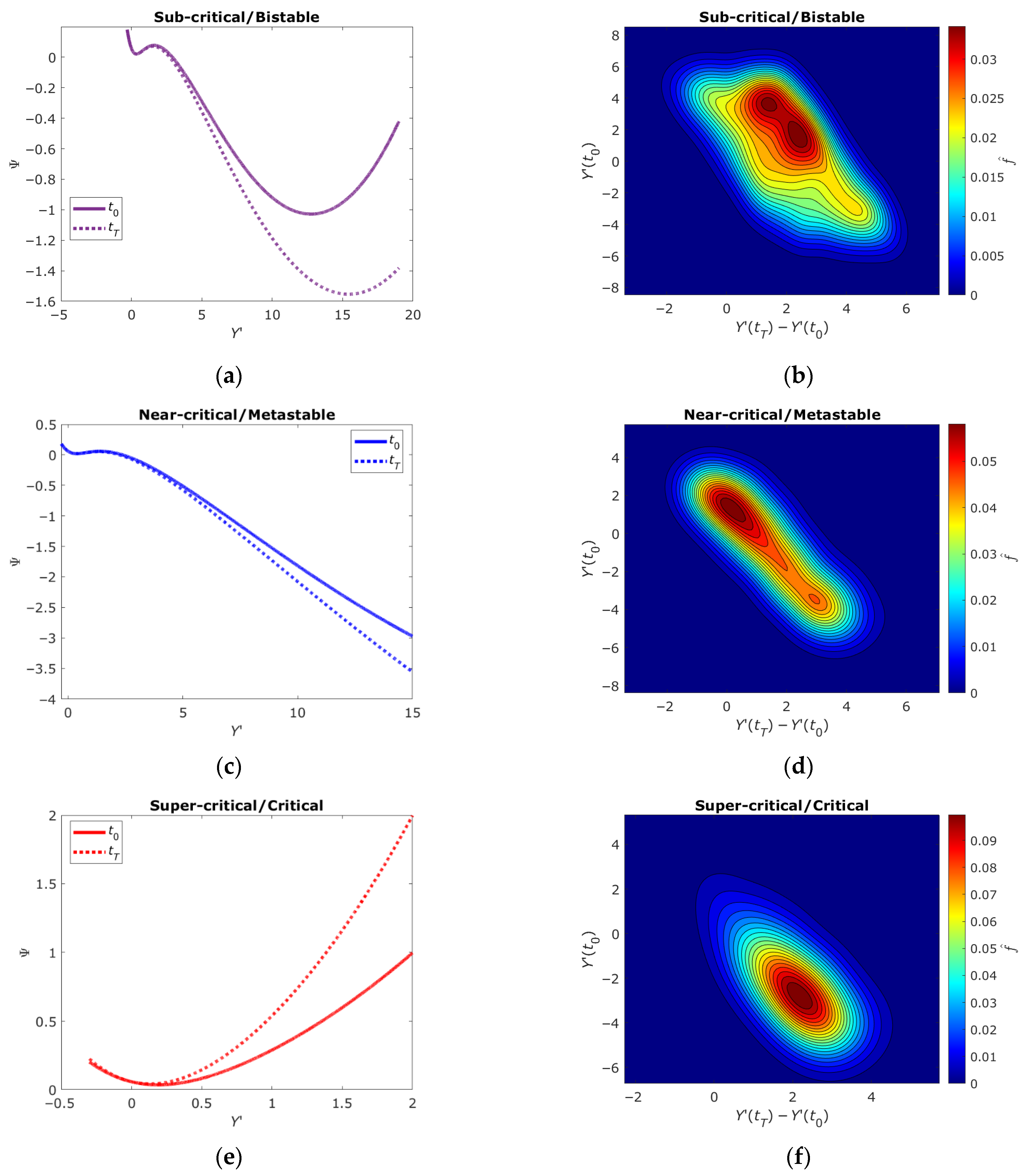
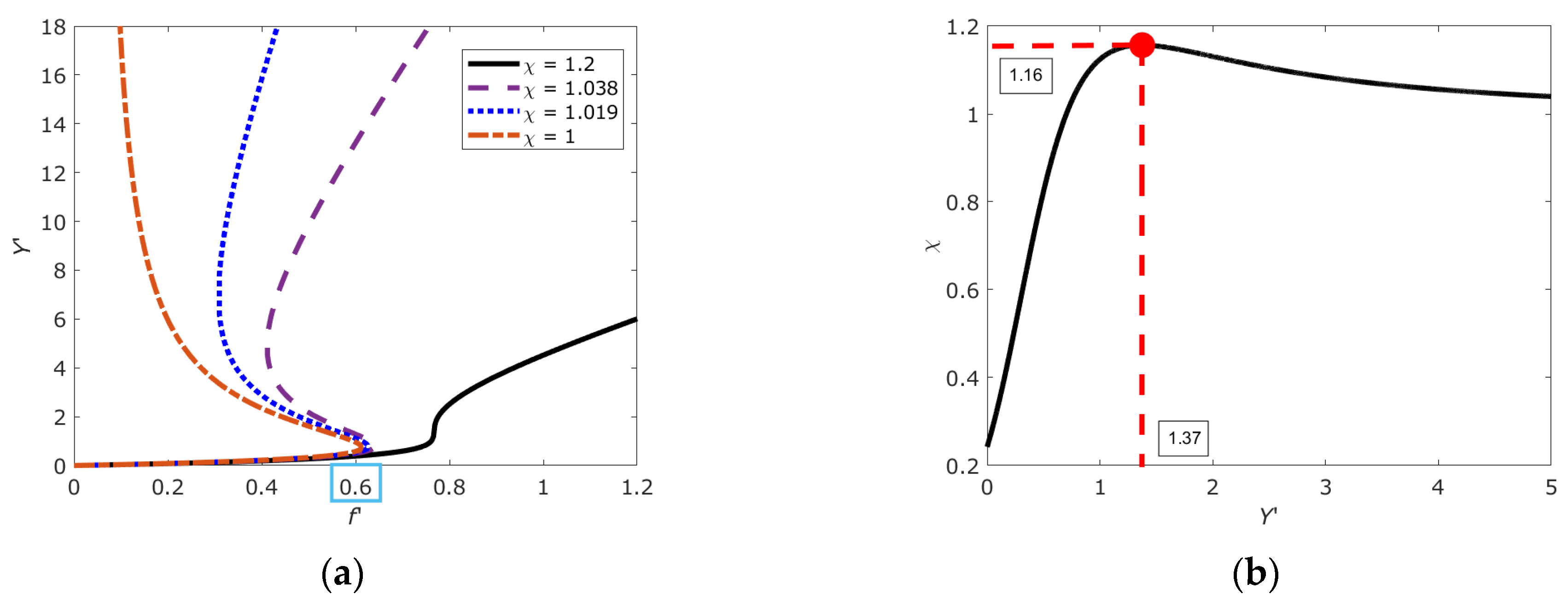
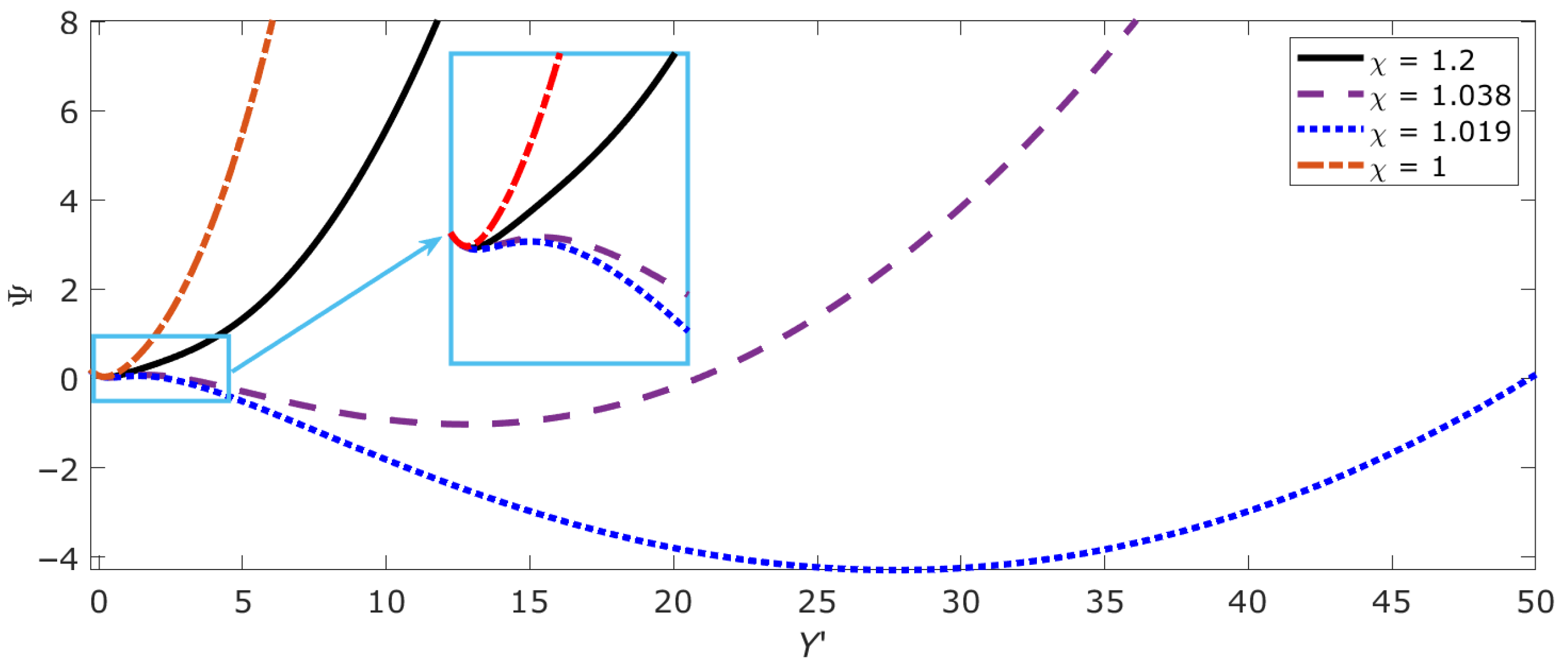
2.5. Bistable, Metastable and Critical States of DNA
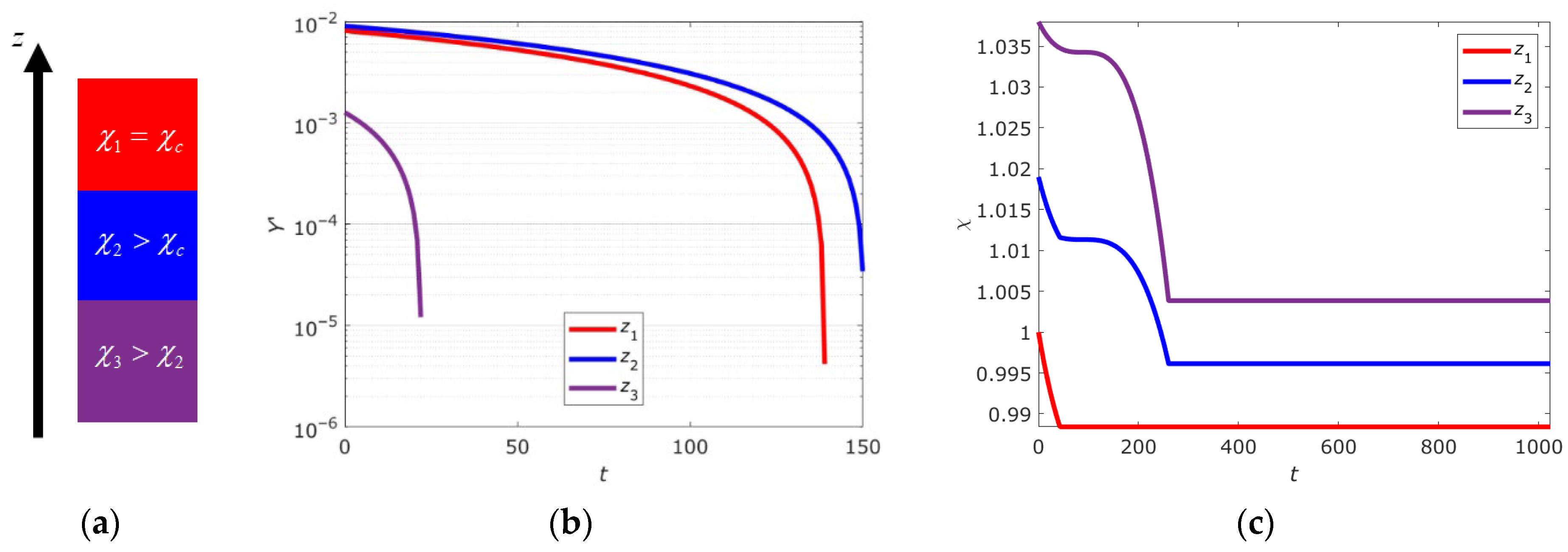
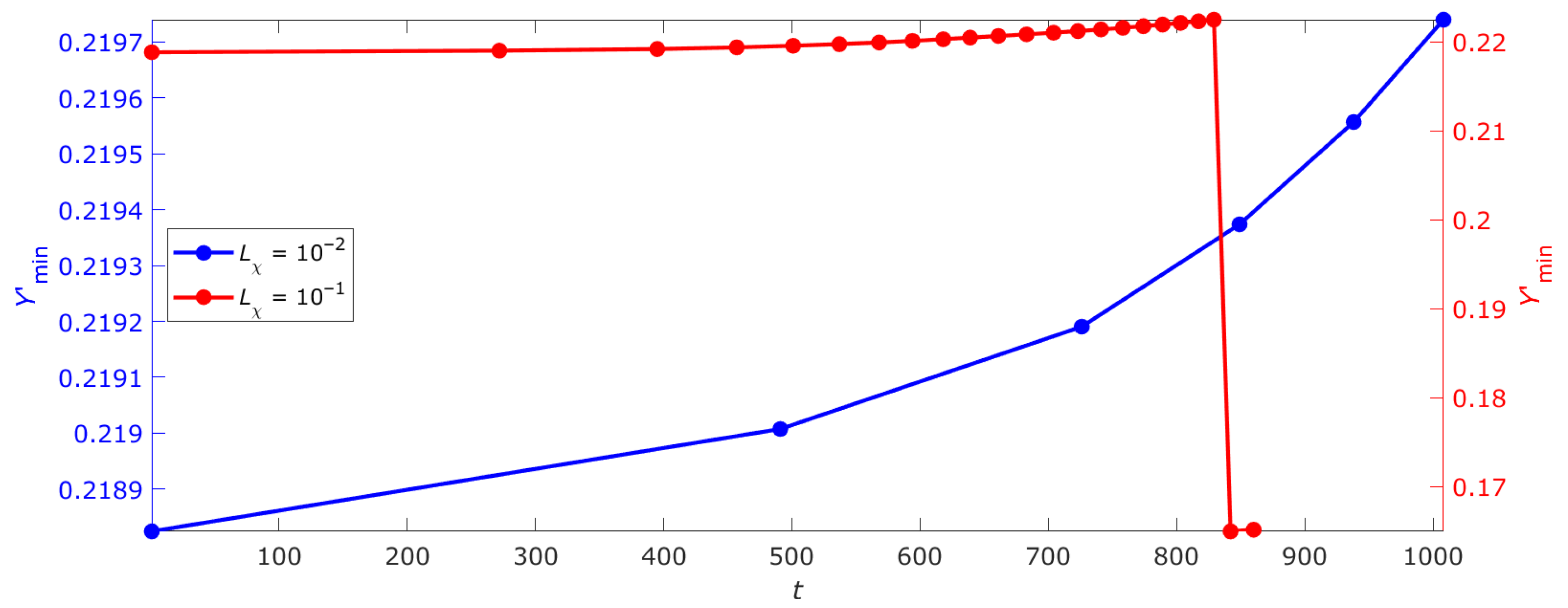
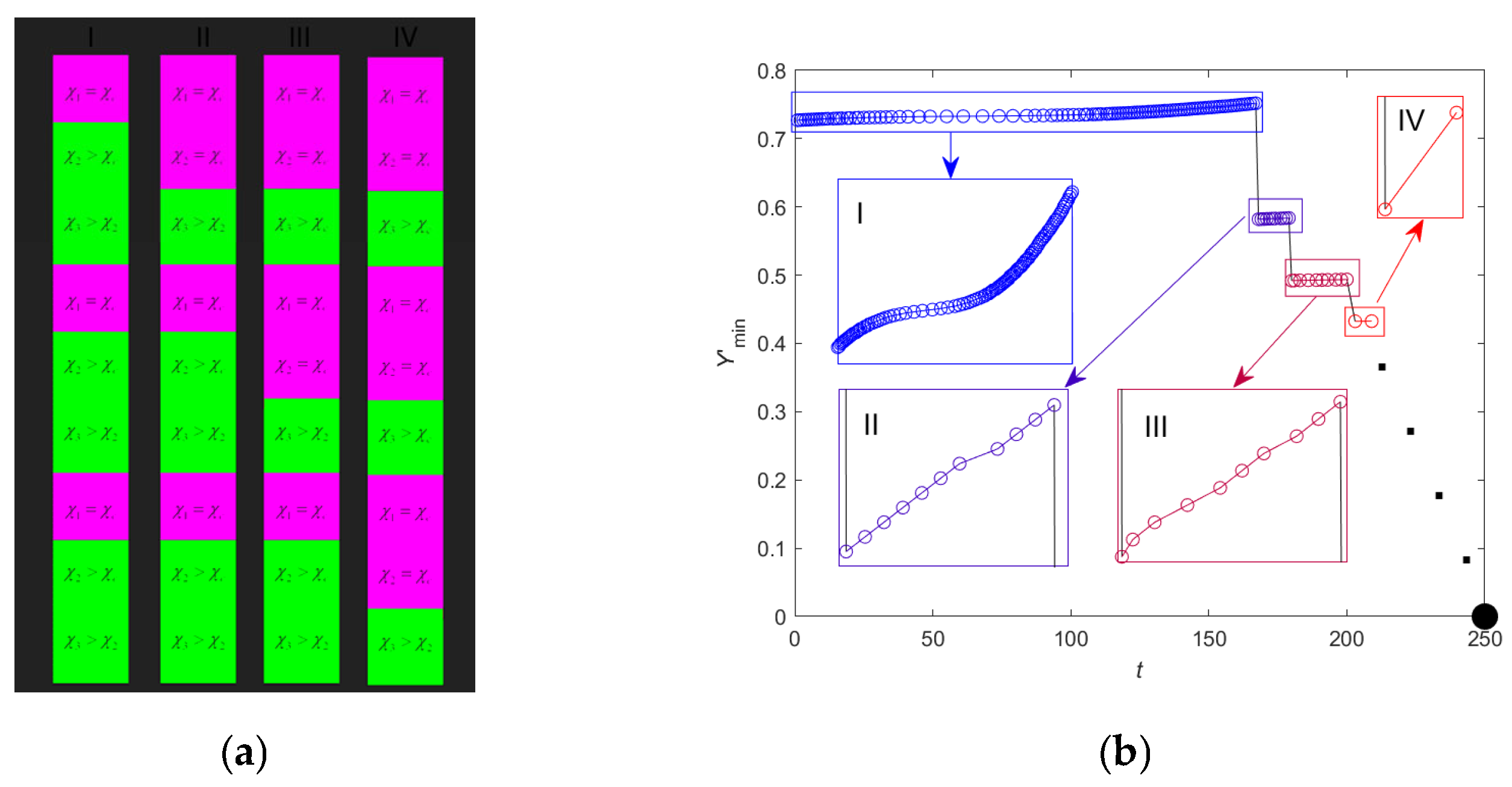
2.6. Criticality Cascade in DNA with Open States
2.7. Experimental Validation of Model Representations
3. Discussion
4. Materials and Methods
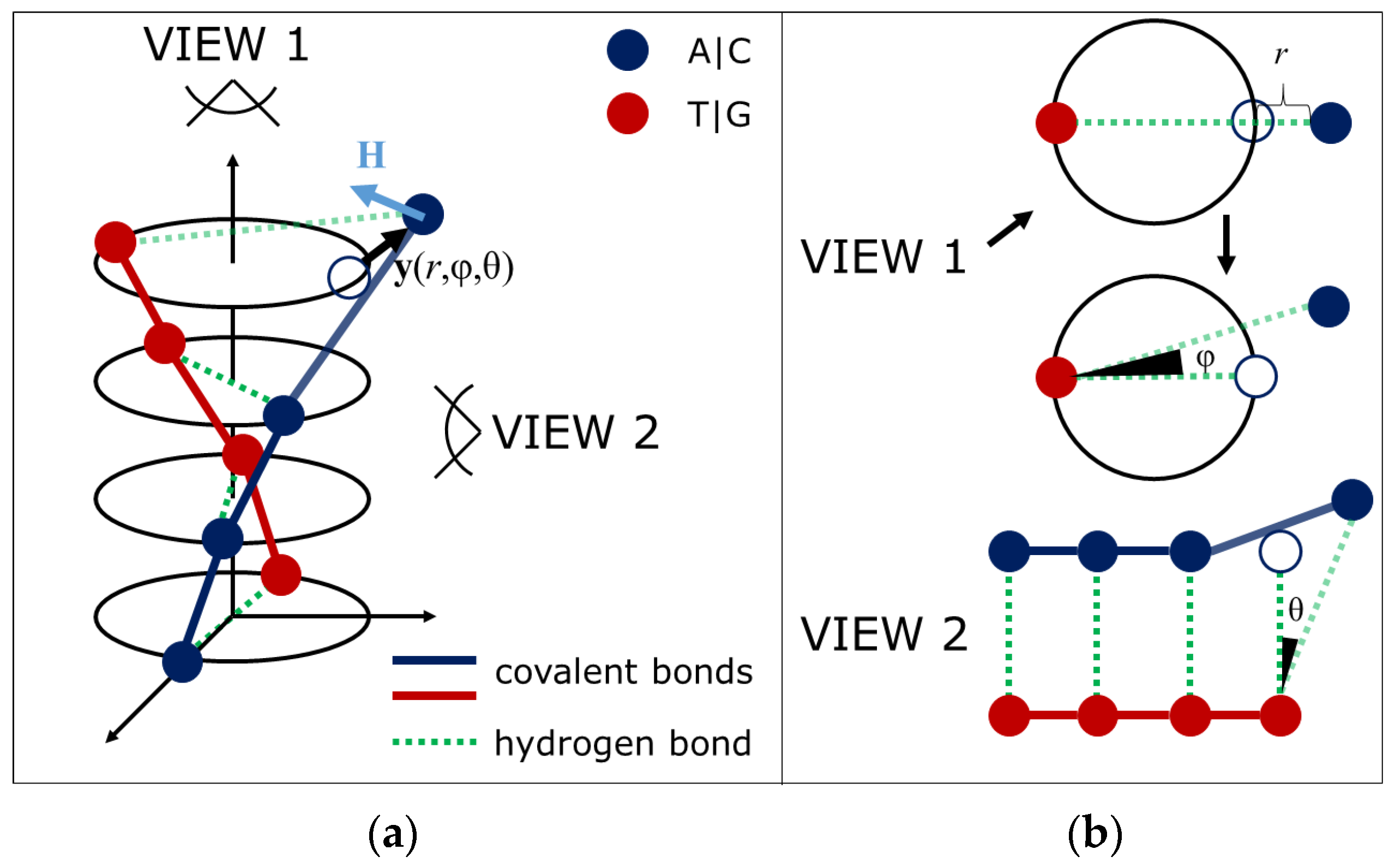
Mechanobiological Model of DNA with Open States
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| I | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| UI | 0.6 | 1.1 | 0.6 | 1 | 0.04 |
| PI | 0.07 | 23.14 | 18.77 | 0.8 | - |
| MI | 8.2 | 25.7 | 18.49 | 19.5 | −0.06 |
References
- Richard, A.; Boullu, L.; Herbach, U.; Bonnafoux, A.; Morin, V.; Vallin, E.; Guillemin, A.; Papili Gao, N.; Gunawan, R.; Cosette, J.; et al. Single-Cell-Based Analysis Highlights a Surge in Cell-to-Cell Molecular Variability Preceding Irreversible Commitment in a Differentiation Process. PLoS Biol. 2016, 14, e1002585. [Google Scholar] [CrossRef] [PubMed]
- Mojtahedi, M.; Skupin, A.; Zhou, J.; Castaño, I.G.; Leong-Quong, R.Y.Y.; Chang, H.; Trachana, K.; Giuliani, A.; Huang, S. Cell Fate Decision as High-Dimensional Critical State Transition. PLoS Biol. 2016, 14, e2000640. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Britten, R.J.; Davidson, E.H. Gene Regulation for Higher Cells: A Theory. Science 1969, 165, 347–357. [Google Scholar] [CrossRef]
- Ferrell, J.E. Bistability, Bifurcations, and Waddington’s Epigenetic Landscape. Curr. Biol. 2012, 22, R458–R466. [Google Scholar] [CrossRef] [PubMed]
- Misteli, T. The Self-Organizing Genome: Principles of Genome Architecture and Function. Cell 2020, 183, 28–45. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Eichler, G.; Bar-Yam, Y.; Ingber, D.E. Cell Fates as High-Dimensional Attractor States of a Complex Gene Regulatory Network. Phys. Rev. Lett. 2005, 94, 128701. [Google Scholar] [CrossRef]
- Ashida, K.; Kitabayashi, A.; Nishiyama, K.; Nakano, S.I. Comprehensive Analysis of Stability and Variability of DNA Minimal I-Motif Structures. Molecules 2025, 30, 1831. [Google Scholar] [CrossRef]
- Postigo, A.; Marcuello, C.; Verstraeten, W.; Sarasa, S.; Walther, T.; Lostao, A.; Göpfrich, K.; del Barrio, J.; Hernández-Ainsa, S. Folding and Functionalizing DNA Origami: A Versatile Approach Using a Reactive Polyamine. J. Am. Chem. Soc. 2025, 147, 3919–3924. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Piras, V.; Giuliani, A.; Tomita, M.; Selvarajoo, K. Collective Dynamics of Specific Gene Ensembles Crucial for Neutrophil Differentiation: The Existence of Genome Vehicles Revealed. PLoS ONE 2010, 5, e12116. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Hashimoto, M.; Takenaka, Y.; Motoike, I.N.; Yoshikawa, K. Global Genetic Response in a Cancer Cell: Self-Organized Coherent Expression Dynamics. PLoS ONE 2014, 9, e97411, Correction in PLoS ONE 2014, 9(8): e105491. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent Self-Organized Criticality in Gene Expression Dynamics: Temporal Development of Global Phase Transition Revealed in a Cancer Cell Line. PLoS ONE 2015, 10, e0128565. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, A.; Tsuchiya, M.; Yoshikawa, K. Self-Organization of Genome Expression from Embryo to Terminal Cell Fate: Single-Cell Statistical Mechanics of Biological Regulation. Entropy 2018, 20, 13. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Giuliani, A.; Yoshikawa, K. Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated. Int. J. Mol. Sci. 2020, 21, 4581. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Brazhnik, P.; Bizzarri, M.; Giuliani, A. Synchronization between Attractors: Genomic Mechanism of Cell-Fate Change. Int. J. Mol. Sci. 2023, 24, 11603. [Google Scholar] [CrossRef]
- Vetsigian, K.; Woese, C.; Goldenfeld, N. Collective Evolution and the Genetic Code. Proc. Natl. Acad. Sci. USA 2006, 103, 10696–10701. [Google Scholar] [CrossRef]
- Goldenfeld, N.; Woese, C. Biology’s next Revolution. Nature 2007, 445, 369. [Google Scholar] [CrossRef]
- Goldenfeld, N.; Woese, C. Life Is Physics: Evolution as a Collective Phenomenon Far From Equilibrium. Annu. Rev. Condens. Matter Phys. 2011, 2, 375–399. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Yoshikawa, K.; Giuliani, A. Genomic-Thermodynamic Phase Synchronization: Maxwell’s Demon-like Regulation of Cell Fate Transition. Int. J. Mol. Sci. 2025, 26, 4911. [Google Scholar] [CrossRef]
- Naimark, O.B. Structural-Scaling Transitions and Localized Distortion Modes in the DNA Double Helix. Phys. Mesomech. 2007, 10, 33–45. [Google Scholar] [CrossRef]
- Naimark, O.B.; Nikitiuk, A.S.; Baudement, M.O.; Forné, T.; Lesne, A. The Physics of Cancer: The Role of Epigenetics and Chromosome Conformation in Cancer Progression. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1760. [Google Scholar] [CrossRef]
- Naimark, O. Mesoscopic Cell Dynamics in Different Environment and Problem of Cancer. AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2167, p. 020237. [Google Scholar] [CrossRef]
- Naimark, O.B.; Bayandin, Y.V.; Grishko, V.V.; Nikitiuk, A.S. Mesoscopic Cell Mechanobiology and the Problem of Cancer. Organisms 2020, 4, 42–56. [Google Scholar] [CrossRef]
- Naimark, O.B.; Bayandin, Y.V.; Beloglazova, Y.A.; Gagarskich, O.N.; Grishko, V.V.; Nikitiuk, A.S.; Voronina, A.O. DNA Transformation, Cell Epigenetic Landscape and Open Complex Dynamics in Cancer Development. Math. Biol. Bioinforma. 2020, 15, 251–267. [Google Scholar] [CrossRef]
- Nikitiuk, A.S.; Bayandin, Y.V.; Naimark, O.B. Statistical Thermodynamics of DNA with Open States. Phys. A Stat. Mech. its Appl. 2022, 607, 128156. [Google Scholar] [CrossRef]
- Liu, R.; Yu, X.; Liu, X.; Xu, D.; Aihara, K.; Chen, L. Identifying Critical Transitions of Complex Diseases Based on a Single Sample. Bioinformatics 2014, 30, 1579–1586. [Google Scholar] [CrossRef]
- Aihara, K.; Liu, R.; Koizumi, K.; Liu, X.; Chen, L. Dynamical Network Biomarkers: Theory and Applications. Gene 2022, 808, 145997. [Google Scholar] [CrossRef]
- Shigaev, A.S.; Ponomarev, O.A.; Lakhno, V.D. Theoretical and Experimental Investigations of DNA Open States. Math. Biol. Bioinforma. 2013, 8, 553–664. [Google Scholar] [CrossRef]
- Poland, D.; Scheraga, H.A. Occurrence of a Phase Transition in Nucleic Acid Models. J. Chem. Phys. 1966, 45, 1464–1469. [Google Scholar] [CrossRef]
- Bustamante, C.; Bryant, Z.; Smith, S.B. Ten Years of Tension: Single-Molecule DNA Mechanics. Nature 2003, 421, 423–427. [Google Scholar] [CrossRef]
- Manning, G.S. The Molecular Theory of Polyelectrolyte Solutions with Applications to the Electrostatic Properties of Polynucleotides. Q. Rev. Biophys. 1978, 11, 179–246. [Google Scholar] [CrossRef]
- Williams, L.D.; Maher, L.J. Electrostatic Mechanisms of DNA Deformation. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 497–521. [Google Scholar] [CrossRef]
- Strick, T.R.; Allemand, J.F.; Bensimon, D.; Bensimon, A.; Croquette, V. The Elasticity of a Single Supercoiled DNA Molecule. Science 1996, 271, 1835–1837. [Google Scholar] [CrossRef] [PubMed]
- Kuetche, V.K. Ab Initio Bubble-Driven Denaturation of Double-Stranded DNA: Self-Mechanical Theory. J. Theor. Biol. 2016, 401, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Cocco, S.; Monasson, R.; Marko, J.F. Force and Kinetic Barriers to Unzipping of the DNA Double Helix. Proc. Natl. Acad. Sci. USA 2001, 98, 8608–8613. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J.C. Theory of Heat; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Experimental Demonstration of Information-to-Energy Conversion and Validation of the Generalized Jarzynski Equality. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Tripathi, T.; Uversky, V.N.; Giuliani, A. ‘Intelligent’ Proteins. Cell. Mol. Life Sci. 2025, 82, 34. [Google Scholar] [CrossRef]
- Naimark, O.B. Defect-Induced Transitions as Mechanisms of Plasticity and Failure in Multifield Continua. In Advances in Multifield Theories for Continua with Substructure; Birkhäuser Boston: Boston, MA, USA, 2004; pp. 75–114. [Google Scholar]
- Gandrillon, O.; Gaillard, M.; Espinasse, T.; Garnier, N.B.; Dussiau, C.; Kosmider, O.; Sujobert, P. Entropy as a Measure of Variability and Stemness in Single-Cell Transcriptomics. Curr. Opin. Syst. Biol. 2021, 27, 100348, Erratum in Systems Biology 2023, 35, 100458. [Google Scholar] [CrossRef]
- Zimatore, G.; Tsuchiya, M.; Hashimoto, M.; Kasperski, A.; Giuliani, A. Self-Organization of Whole-Gene Expression through Coordinated Chromatin Structural Transition. Biophys. Rev. 2021, 2, 031303. [Google Scholar] [CrossRef]
- Hayflick, L.; Moorhead, P.S. The Serial Cultivation of Human Diploid Cell Strains. Exp. Cell Res. 1961, 25, 585–621. [Google Scholar] [CrossRef]
- Galluzzi, L.; Vitale, I.; Aaronson, S.A.; Abrams, J.M.; Adam, D.; Agostinis, P.; Alnemri, E.S.; Altucci, L.; Amelio, I.; Andrews, D.W.; et al. Molecular Mechanisms of Cell Death: Recommendations of the Nomenclature Committee on Cell Death 2018. Cell Death Differ. 2018, 25, 486–541. [Google Scholar] [CrossRef]
- Berezovsky, I.N.; Chen, W.W.; Choi, P.J.; Shakhnovich, E.I. Entropic Stabilization of Proteins and Its Proteomic Consequences. PLoS Comput. Biol. 2005, 1, e47. [Google Scholar] [CrossRef]
- Fernandes de Godoy, M.; Lima Gregório, M. Heart Rate Variability as a Marker of Homeostatic Level. In Autonomic Nervous System-Special Interest Topics; IntechOpen: London, United Kingdom, 2022. [Google Scholar]
- Hosoda, K.; Seno, S.; Kamiura, R.; Murakami, N.; Kondoh, M. Biodiversity and Constrained Information Dynamics in Ecosystems: A Framework for Living Systems. Entropy 2023, 25, 1624. [Google Scholar] [CrossRef]
- Stirzaker, G.G.D.; Grimmett, D.; Grimmett, G.; Stirzaker, D. Probability and Random Processes, 3rd ed.; Oxford university press: Oxford, United Kingdom, 2001. [Google Scholar]
- Eldridge, W.J.; Sheinfeld, A.; Rinehart, M.T.; Wax, A. Imaging Deformation of Adherent Cells Due to Shear Stress Using Quantitative Phase Imaging. Opt. Lett. 2016, 41, 352. [Google Scholar] [CrossRef]
- Steelman, Z.A.; Eldridge, W.J.; Weintraub, J.B.; Wax, A. Is the Nuclear Refractive Index Lower than Cytoplasm? Validation of Phase Measurements and Implications for Light Scattering Technologies. J. Biophotonics 2017, 10, 1714–1722. [Google Scholar] [CrossRef]
- Beloglazova, Y.; Nikitiuk, A.; Voronina, A.; Gagarskikh, O.; Bayandin, Y.; Naimark, O.; Grishko, V. Label-Free Single Cell Viability Assay Using Laser Interference Microscopy. Biology 2021, 10, 590. [Google Scholar] [CrossRef] [PubMed]
- Vasilica Stirbat, T.; Tlili, S.; Houver, T.; Rieu, J.P.; Barentin, C.; Delanoë-Ayari, H. Multicellular Aggregates: A Model System for Tissue Rheology. Eur. Phys. J. E 2013, 36, 84. [Google Scholar] [CrossRef] [PubMed]
- Vikhorev, A.V.; Savelev, I.V.; Polesskaya, O.O.; Rempel, M.M.; Miller, R.A.; Vetcher, A.A.; Myakishev-Rempel, M. The Avoidance of Purine Stretches by Cancer Mutations. Int. J. Mol. Sci. 2024, 25, 11050. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, M.P. Non-Complementary Strand Commutation as a Fundamental Alternative for Information Processing by DNA and Gene Regulation. Nat. Chem. 2023, 15, 70–82. [Google Scholar] [CrossRef]
- Micheelsen, M.A.; Mitarai, N.; Sneppen, K.; Dodd, I.B. Theory for the Stability and Regulation of Epigenetic Landscapes. Phys. Biol. 2010, 7, 026010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikitiuk, A.S.; Bayandin, Y.V.; Naimark, O.B. Structural-Scaling Transitions and Criticality Cascade in DNA with Open States. Int. J. Mol. Sci. 2025, 26, 8428. https://doi.org/10.3390/ijms26178428
Nikitiuk AS, Bayandin YV, Naimark OB. Structural-Scaling Transitions and Criticality Cascade in DNA with Open States. International Journal of Molecular Sciences. 2025; 26(17):8428. https://doi.org/10.3390/ijms26178428
Chicago/Turabian StyleNikitiuk, Aleksandr S., Yuriy V. Bayandin, and Oleg B. Naimark. 2025. "Structural-Scaling Transitions and Criticality Cascade in DNA with Open States" International Journal of Molecular Sciences 26, no. 17: 8428. https://doi.org/10.3390/ijms26178428
APA StyleNikitiuk, A. S., Bayandin, Y. V., & Naimark, O. B. (2025). Structural-Scaling Transitions and Criticality Cascade in DNA with Open States. International Journal of Molecular Sciences, 26(17), 8428. https://doi.org/10.3390/ijms26178428







