Theoretical Investigation of Ca2+ Intercalation in WS2 as a Negative Electrode Material for Calcium-Ion Batteries: Supported by Experimental Evaluation
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Effects of Li+ and Ca2+ Intercalation in WS2 Clusters
2.2. Electronic Structure and Charge Transfer Characteristics of WS2 Clusters
2.3. Electronic Charge Redistribution and Band Structure Evolution in Intercalated WS2
2.4. Orbital Hybridization and Lattice Stabilization in Intercalated WS2
2.5. Surface Adsorption and Ion Diffusion Pathways in Intercalated WS2
2.6. Voltage Profiles and Intercalation Mechanisms in Li+- and Ca2+-Intercalated WS2
2.7. Long-Term Cycling Performance and Structural Stability of Intercalated WS2
3. Materials and Methods
3.1. Computational Methods
3.1.1. Local Electronic Structure and Bonding Analysis via DV-Xα Cluster Modeling
3.1.2. Structural Relaxation and Energetic Profiling via First-Principles DFT
3.1.3. Adsorption Energetics and Open-Circuit Voltage Estimation
3.2. Experimental Method
3.2.1. Fabrication of WS2 Composite Electrodes
3.2.2. Galvanostatic Testing and Electrochemical Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, T.; Song, W.; Son, D.-Y.; Ono, L.K.; Qi, Y. Lithium-ion batteries: Outlook on present, future, and hybridized technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Wakihara, M. Recent developments in lithium ion batteries. Mater. Sci. Eng. R Rep. 2001, 33, 109–134. [Google Scholar] [CrossRef]
- Huang, B.; Pan, Z.; Su, X.; An, L. Recycling of lithium-ion batteries: Recent advances and perspectives. J. Power Sources 2018, 399, 274–286. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; Ji, X.; Li, Y.; Shao, Y.; Chen, Z.; Zhong, C.; Amine, K. Design strategies for nonaqueous multivalent-ion and monovalent-ion battery anodes. Nat. Rev. Mater. 2020, 5, 276–294. [Google Scholar] [CrossRef]
- Liu, Z.; Qin, L.; Cao, X.; Zhou, J.; Pan, A.; Fang, G.; Wang, S.; Liang, S. Ion migration and defect effect of electrode materials in multivalent-ion batteries. Prog. Mater. Sci. 2022, 125, 100911. [Google Scholar] [CrossRef]
- Huie, M.M.; Bock, D.C.; Takeuchi, E.S.; Marschilok, A.C.; Takeuchi, K.J. Cathode materials for magnesium and magnesium-ion based batteries. Coord. Chem. Rev. 2015, 287, 15–27. [Google Scholar] [CrossRef]
- Huang, J.; Xie, X.; Liu, K.; Liang, S.; Fang, G. Perspectives in Electrochemical in situ Structural Reconstruction of Cathode Materials for Multivalent-ion Storage. Energy Environ. Mater. 2023, 6, e12309. [Google Scholar] [CrossRef]
- Taghavi-Kahagh, A.; Roghani-Mamaqani, H.; Salami-Kalajahi, M. Powering the future: A comprehensive review on calcium-ion batteries. J. Energy Chem. 2024, 90, 77–97. [Google Scholar] [CrossRef]
- Gummow, R.J.; Vamvounis, G.; Kannan, M.B.; He, Y. Calcium-ion batteries: Current state-of-the-art and future perspectives. Adv. Mater. 2018, 30, 1801702. [Google Scholar] [CrossRef]
- Ji, B.; He, H.; Yao, W.; Tang, Y. Recent advances and perspectives on calcium-ion storage: Key materials and devices. Adv. Mater. 2021, 33, 2005501. [Google Scholar] [CrossRef]
- Maroni, F.; Dongmo, S.; Gauckler, C.; Marinaro, M.; Wohlfahrt-Mehrens, M. Through the maze of multivalent-ion batteries: A critical review on the status of the research on cathode materials for Mg2+ and Ca2+ ions insertion. Batter. Supercaps. 2021, 4, 1221–1251. [Google Scholar] [CrossRef]
- Deng, X.; Li, L.; Zhang, G.; Zhao, X.; Hao, J.; Han, C.; Li, B. Anode chemistry in calcium ion batteries: A review. Energy Storage Mater. 2022, 53, 467–481. [Google Scholar] [CrossRef]
- Tojo, T.; Tawa, H.; Oshida, N.; Inada, R.; Sakurai, Y. Electrochemical characterization of a layered α-MoO3 as a new cathode material for calcium ion batteries. J. Electroanal. Chem. 2018, 825, 51–56. [Google Scholar] [CrossRef]
- Tinker, H.R.; Howard, C.A.; Zhou, M.; Xu, Y. Exploring anodes for calcium-ion batteries. Mater. Adv. 2023, 4, 2028–2041. [Google Scholar] [CrossRef]
- Yao, Z.; Hegde, V.I.; Aspuru-Guzik, A.; Wolverton, C. Discovery of calcium-metal alloy anodes for reversible Ca-ion batteries. Adv. Energy Mater. 2019, 9, 1802994. [Google Scholar] [CrossRef]
- Gheytani, S.; Liang, Y.; Wu, F.; Jing, Y.; Dong, H.; Rao, K.K.; Chi, X.; Fang, F.; Yao, Y. An aqueous Ca-ion battery. Adv. Sci. 2017, 4, 1700465. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, C.; Zhang, S.; Song, X.; Tang, Y.; Cheng, H.-M. Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage. Nat. Chem. 2018, 10, 667–672. [Google Scholar] [CrossRef]
- Park, J.; Xu, Z.L.; Yoon, G.; Park, S.K.; Wang, J.; Hyun, H.; Park, H.; Lim, J.; Ko, Y.J.; Yun, Y.S. Stable and high-power calcium-ion batteries enabled by calcium intercalation into graphite. Adv. Mater. 2020, 32, 1904411. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, Z.; Hao, X.; Xu, R.; Li, L.; Lv, D.; Huang, X.; Zhao, Q.; Xu, Y.; Wu, Y. Cathode materials for calcium-ion batteries: Current status and prospects. Carbon Neutralization 2023, 2, 551–573. [Google Scholar] [CrossRef]
- Arroyo-de Dompablo, M.E.; Ponrouch, A.; Johansson, P.; Palacín, M.R. Achievements, challenges, and prospects of calcium batteries. Chem. Rev. 2019, 120, 6331–6357. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, W.; Yu, R.; Qiao, F.; Wang, J.; Wang, J.; An, Q. Molecular Engineering to Construct MoS2 with Expanded Interlayer Spacing and Enriched 1T Phase for “Rocking-Chair” Aqueous Calcium-Ion Pouch Cells. ACS Nano 2024, 18, 35286–35295. [Google Scholar] [CrossRef]
- Yan, L.; Yang, W.; Yu, H.; Zhang, L.; Shu, J. Recent progress in rechargeable calcium-ion batteries for high-efficiency energy storage. Energy Storage Mater. 2023, 60, 102822. [Google Scholar] [CrossRef]
- Chen, S.-M. Preparation, characterization, and electrocatalytic oxidation properties of iron, cobalt, nickel, and indium hexacyanoferrate. J. Electroanal. Chem. 2002, 521, 29–52. [Google Scholar] [CrossRef]
- Wang, D.; Gao, X.; Chen, Y.; Jin, L.; Kuss, C.; Bruce, P.G. Plating and stripping calcium in an organic electrolyte. Nat. Mater. 2018, 17, 16–20. [Google Scholar] [CrossRef] [PubMed]
- Adil, M.; Sarkar, A.; Roy, A.; Panda, M.R.; Nagendra, A.; Mitra, S. Practical aqueous calcium-ion battery full-cells for future stationary storage. ACS Appl. Mater. Interfaces 2020, 12, 11489–11503. [Google Scholar] [CrossRef]
- Cong, C.; Shang, J.; Wang, Y.; Yu, T. Optical properties of 2D semiconductor WS2. Adv. Opt. Mater. 2018, 6, 1700767. [Google Scholar] [CrossRef]
- Seifert, G.; Terrones, H.; Terrones, M.; Jungnickel, G.; Frauenheim, T. On the electronic structure of WS2 nanotubes. Solid State Commun. 2000, 114, 245–248. [Google Scholar] [CrossRef]
- Lee, C.; Jeong, Y.-T.; Nogales, P.M.; Song, H.-Y.; Kim, Y.; Yin, R.-Z.; Jeong, S.-K. Electrochemical intercalation of Ca2+ ions into TiS2 in organic electrolytes at room temperature. Electrochem. Commun. 2019, 98, 115–118. [Google Scholar] [CrossRef]
- Kim, H.-C.; Kim, H.; Lee, J.-U.; Lee, H.-B.; Choi, D.-H.; Lee, J.-H.; Lee, W.H.; Jhang, S.H.; Park, B.H.; Cheong, H. Engineering optical and electronic properties of WS2 by varying the number of layers. ACS Nano 2015, 9, 6854–6860. [Google Scholar] [CrossRef]
- Chen, K.; Wan, X.; Wen, J.; Xie, W.; Kang, Z.; Zeng, X.; Chen, H.; Xu, J.-B. Electronic properties of MoS2–WS2 heterostructures synthesized with two-step lateral epitaxial strategy. ACS Nano 2015, 9, 9868–9876. [Google Scholar] [CrossRef]
- Bhandavat, R.; David, L.; Singh, G. Synthesis of surface-functionalized WS2 nanosheets and performance as Li-ion battery anodes. J. Phys. Chem. Lett. 2012, 3, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Huang, L.; Guo, Z.; Liu, H. Synthesis of tungsten disulfide (WS2) nanoflakes for lithium ion battery application. Electrochem. Commun. 2007, 9, 119–122. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, W.; Wu, Y.; Lin, W.; Zhu, H. Theoretical study of the interaction of electron donor and acceptor molecules with monolayer WS2. J. Phys. D Appl. Phys. 2015, 48, 285303. [Google Scholar] [CrossRef]
- Li, J.; Shi, X.; Fang, J.; Li, J.; Zhang, Z. Facile synthesis of WS2 nanosheets–carbon composites anodes for sodium and lithium ion batteries. ChemNanoMat 2016, 2, 997–1002. [Google Scholar] [CrossRef]
- Tang, H.; Hu, D.; Cui, Z.; Ye, H.; Zhang, G. Effects of defect and temperature on the mechanical performance of WS2: A multiscale analysis. J. Phys. Chem. C 2021, 125, 2680–2690. [Google Scholar] [CrossRef]
- Sourisseau, C.; Cruege, F.; Fouassier, M.; Alba, M. Second-order Raman effects, inelastic neutron scattering and lattice dynamics in 2H-WS2. Chem. Phys. 1991, 150, 281–293. [Google Scholar] [CrossRef]
- Toriyama, M.Y.; Ganose, A.M.; Dylla, M.; Anand, S.; Park, J.; Brod, M.K.; Munro, J.M.; Persson, K.A.; Jain, A.; Snyder, G.J. How to analyse a density of states. Mater. Today Electron. 2022, 1, 100002. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Koyama, Y.; Tanaka, I.; Adachi, H. Chemical bondings around intercalated Li atoms in LiTiX2 (X= S, Se, and Te). Jpn. J. Appl. Phys. 1998, 37, 6440. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M.A. Advancements in OCV measurement and analysis for lithium-ion batteries. IEEE Trans. Energy Convers. 2013, 28, 675–681. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Liu, B. First principles study of nanostructured TiS2 electrodes for Na and Mg ion storage. J. Power Sources 2016, 320, 322–331. [Google Scholar] [CrossRef]
- Segall, M.; Shah, R.; Pickard, C.J.; Payne, M. Population analysis of plane-wave electronic structure calculations of bulk materials. Phys. Rev. B 1996, 54, 16317. [Google Scholar] [CrossRef]
- Mayer, I.; Salvador, P. Overlap populations, bond orders and valences for ‘fuzzy’atoms. Chem. Phys. Lett. 2004, 383, 368–375. [Google Scholar] [CrossRef]
- Mizoguchi, T. Overlap population diagram for ELNES and XANES: Peak assignment and interpretation. J. Phys. Condens. Matter 2009, 21, 104215. [Google Scholar] [CrossRef]
- Chaoui, K.; Zaari, H.; Mansouri, Z.; Caballero-Briones, F.; Benyoussef, A.; El Kenz, A.; Sibari, A. MoS2 and WSe2 monolayers as anode materials for future Li, Na, and K ion batteries under electric field effect. J. Energy Storage 2025, 109, 115110. [Google Scholar] [CrossRef]
- Wang, P.-Y.; Yeh, C.-C.; Chiu, M.-J.; Chiu, C.-C. A comparative study on the linear scaling relations for the diffusion of S-vacancies on MoS2 and WS2. Phys. Chem. Chem. Phys. 2024, 26, 5070–5080. [Google Scholar] [CrossRef] [PubMed]
- Yamada, A.; Koizumi, H.; Nishimura, S.; Sonoyama, N.; Kanno, R. Room-temperature miscibility gap in LixFePO4. Nat. Mater. 2006, 5, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Kang, B.; Ceder, G. Battery materials for ultrafast charging and discharging. Nature 2009, 458, 190–193. [Google Scholar] [CrossRef]
- Ellis, B.L.; Lee, K.T.; Nazar, L.F. Positive electrode materials for Li-ion and Li-batteries. Chem. Mater. 2010, 22, 691–714. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, Y.; Zheng, X.; Aoki, T.; Pattengale, B.; Huang, J.; He, X.; Bian, W.; Younan, S.; Williams, N. Atomically engineering activation sites onto metallic 1T-MoS2 catalysts for enhanced electrochemical hydrogen evolution. Nat. Commun. 2019, 10, 982. [Google Scholar] [CrossRef]
- Ariyoshi, K.; Masuda, S. Accelerating the reaction rates of nucleation growth and solid-state diffusion in electrochemical lithium insertion into MgMn2O4 by controlling the particle size. J. Solid State Electrochem. 2024, 28, 3447–3453. [Google Scholar] [CrossRef]
- Bellani, S.; Wang, F.; Longoni, G.; Najafi, L.; Oropesa-Nuñez, R.; Del Rio Castillo, A.E.; Prato, M.; Zhuang, X.; Pellegrini, V.; Feng, X.; et al. WS2–graphite dual-ion batteries. Nano Lett. 2018, 18, 7155–7164. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Kim, T.H.; Tran, T.Q.; Park, H.J.; Kim, D.W.; Hur, J.; Yoon, S.C. Understanding phase evolution and reaction mechanism of WS2 anodes in rechargeable lithium-ion batteries. Nanomaterials 2020, 10, 1336. [Google Scholar] [CrossRef]
- Chen, D.; Ji, G.; Ding, B.; Ma, Y.; Qu, B.; Chen, W.; Lee, J.Y. In situ nitrogenated graphene–few-layer WS2 composites for fast and reversible Li+ storage. Nanoscale 2013, 5, 7890–7896. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wang, K.; Yao, Z.; Kang, J.; Lam, D.; Yang, D.; Ai, W.; Wolverton, C.; Hersam, M.C.; Huang, Y.; et al. In situ atomic-resolution observation of lithiation and sodiation of WS2 nanoflakes: Implications for lithium-ion and sodium-ion batteries. Small 2021, 17, 2100637. [Google Scholar] [CrossRef]
- He, Q.; Yu, B.; Li, Z.; Zhao, Y. Density functional theory for battery materials. Energy Environ. Mater. 2019, 2, 264–279. [Google Scholar] [CrossRef]
- Zhang, T.; Li, D.; Tao, Z.; Chen, J. Understanding electrode materials of rechargeable lithium batteries via DFT calculations. Prog. Nat. Sci. Mater. Int. 2013, 23, 256–272. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Mizuno, M.; Tanaka, I.; Adachi, H. Electronic structure and chemical bonding of TiS2 by cluster calculation. Mater. Trans. JIM 1998, 39, 709–713. [Google Scholar] [CrossRef]
- Tchitchekova, D.S.; Monti, D.; Johansson, P.; Barde, F.; Randon-Vitanova, A.; Palacín, M.R.; Ponrouch, A. On the reliability of half-cell tests for monovalent (Li+, Na+) and divalent (Mg2+, Ca2+) cation based batteries. J. Electrochem. Soc. 2017, 164, A1384–A1392. [Google Scholar] [CrossRef]
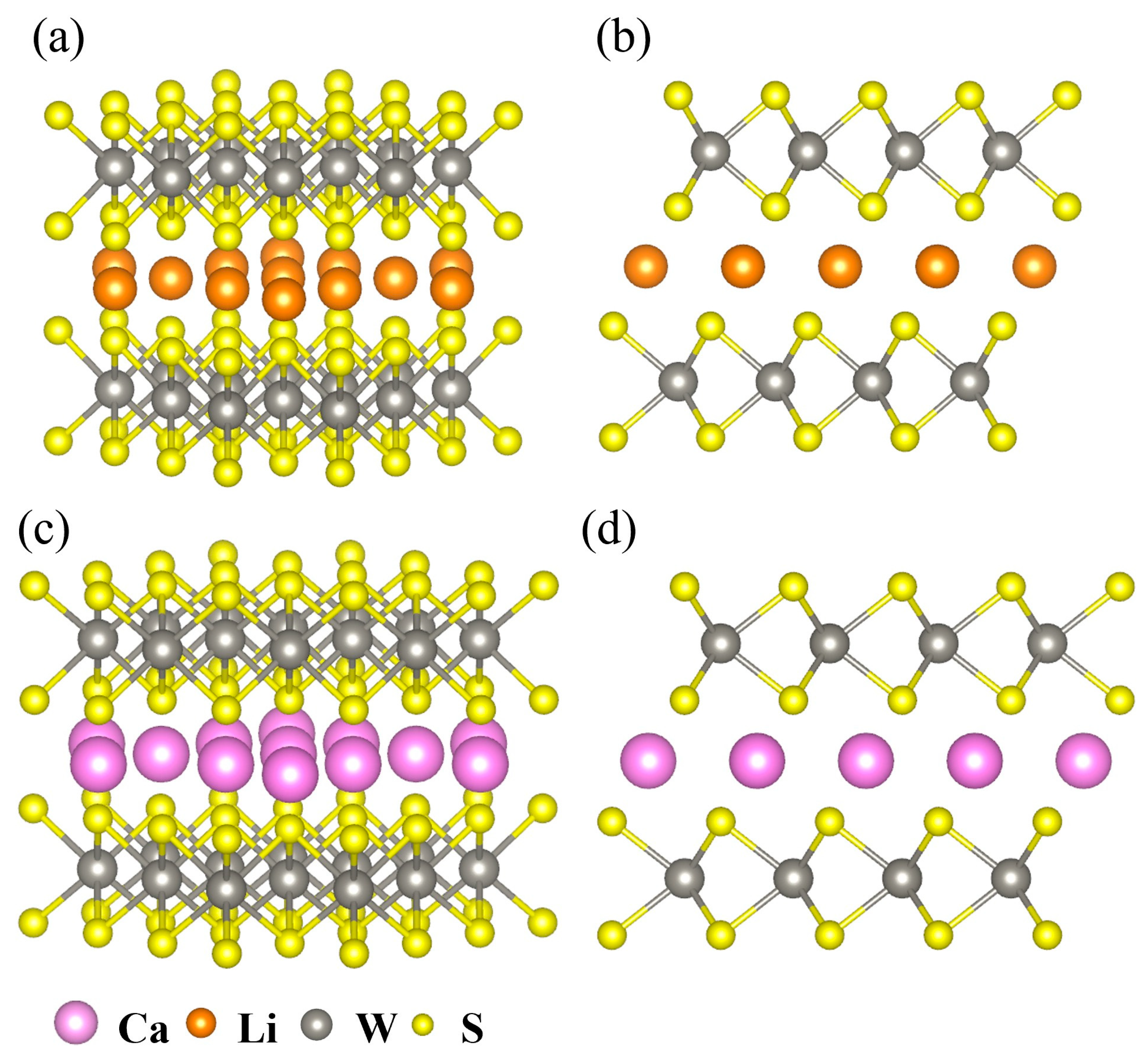
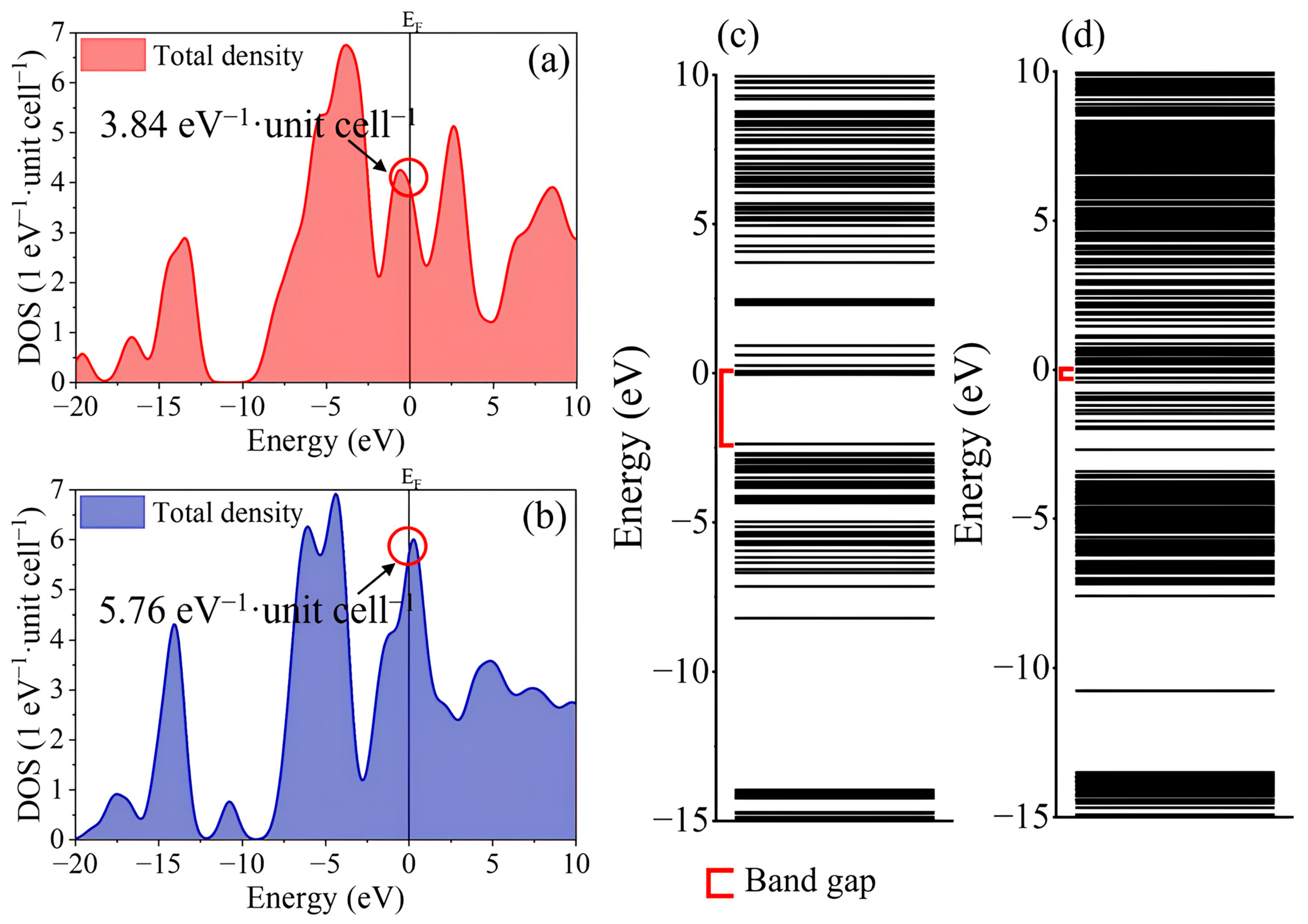


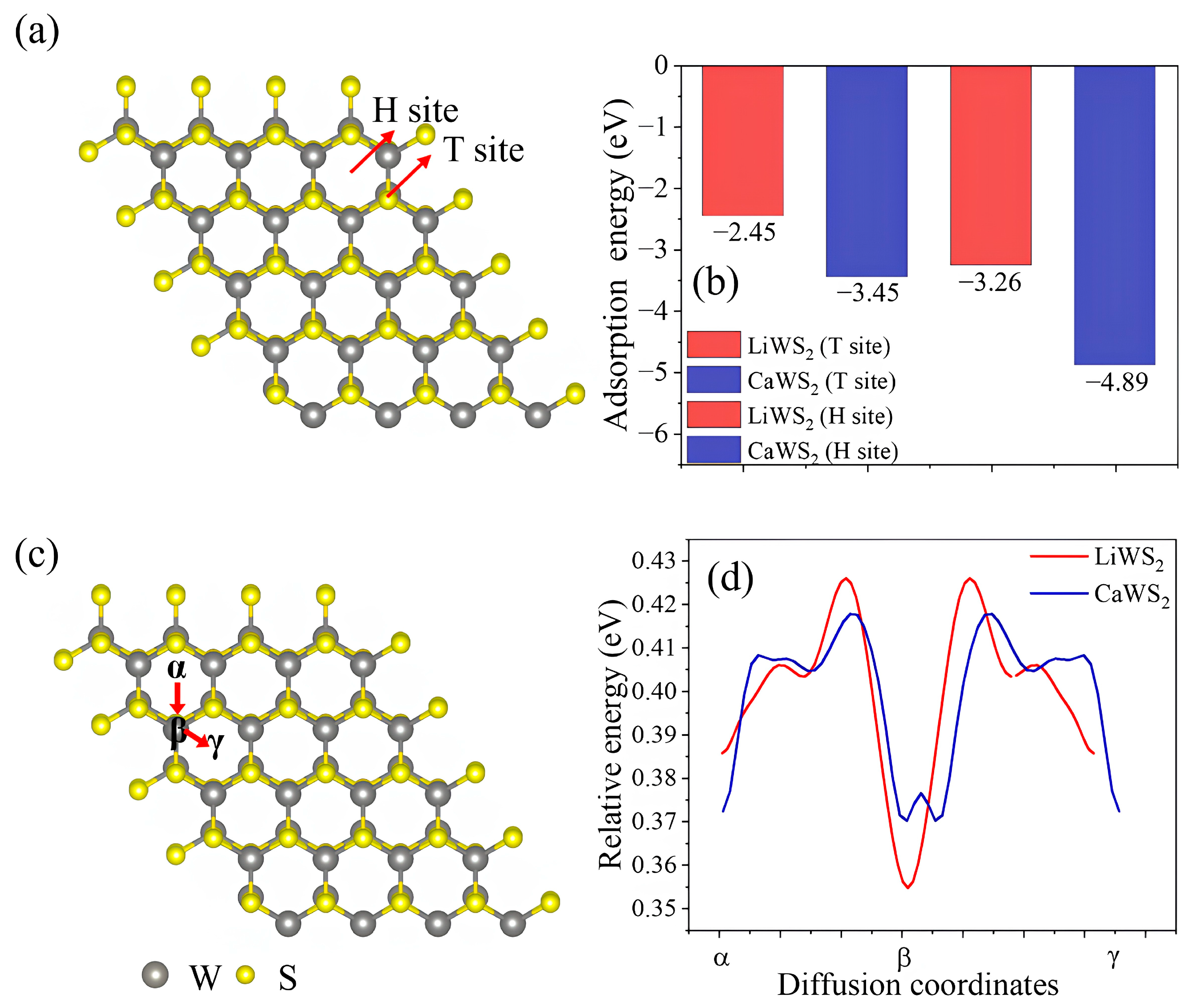

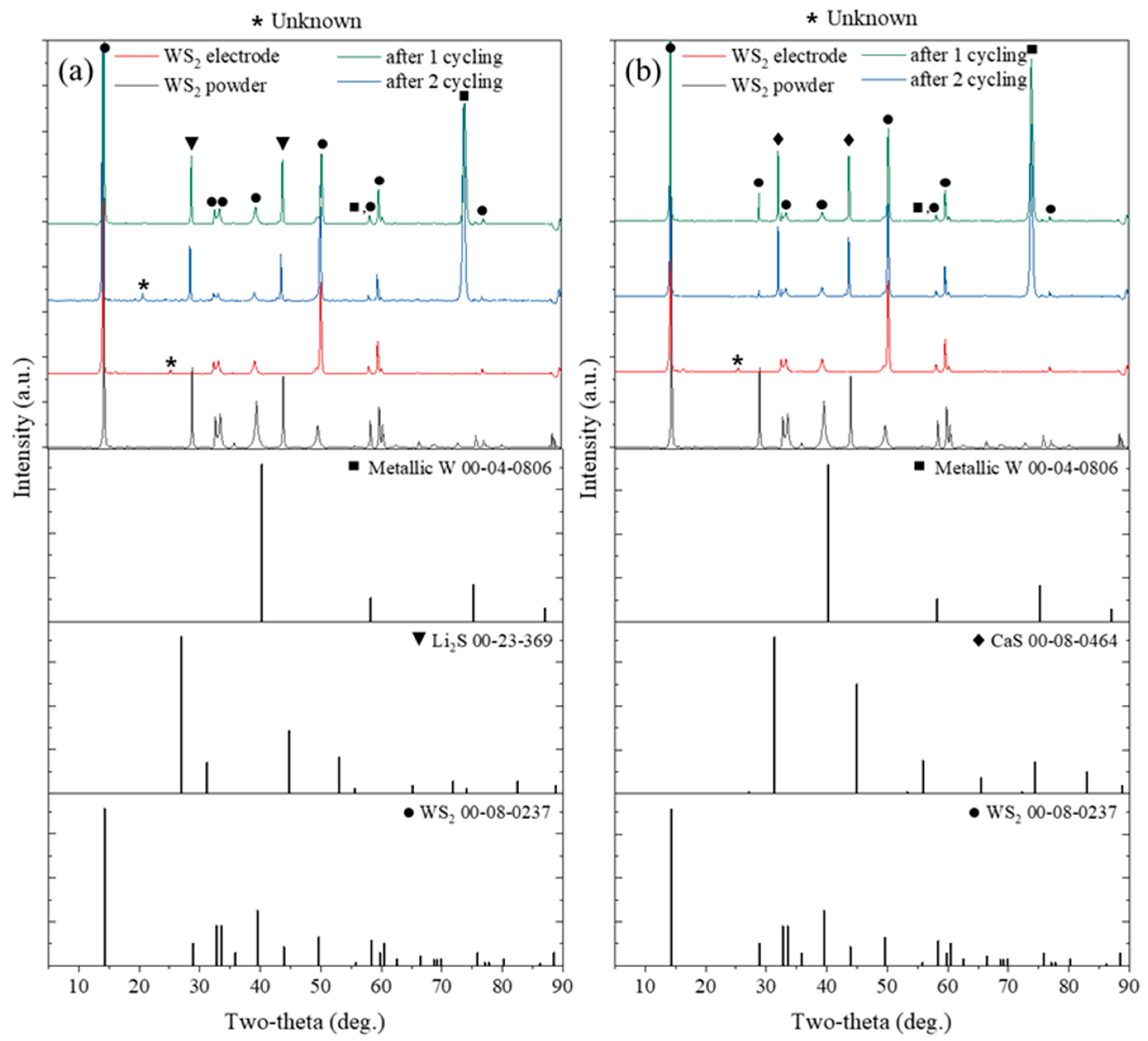

| Structure | Space Group | Lattice Parameter (Å) | |
|---|---|---|---|
| a | c | ||
| W24S48 | P63/mmc (194) | 3.15 | 12.32 |
| (Li13W24S48)7− | 3.17 | 13.04 | |
| (Ca13W24S48)20− | 3.53 | 13.09 | |
| Structure | OCV (V) | Electron Transfer Number (eV−1·unit cell−1) | ||
|---|---|---|---|---|
| Guest Ion (Li+ or Ca2+) | W | S | ||
| (Li13W24S48)7− | 0.21 | 0.26 | 0.61 | −0.31 |
| (Ca13W24S48)20− | 0.37 | 1.04 | 1.06 | −0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Lee, S.; Nogales, P.M.; Kim, Y.; Jeong, S.-K. Theoretical Investigation of Ca2+ Intercalation in WS2 as a Negative Electrode Material for Calcium-Ion Batteries: Supported by Experimental Evaluation. Int. J. Mol. Sci. 2025, 26, 8005. https://doi.org/10.3390/ijms26168005
Yang S, Lee S, Nogales PM, Kim Y, Jeong S-K. Theoretical Investigation of Ca2+ Intercalation in WS2 as a Negative Electrode Material for Calcium-Ion Batteries: Supported by Experimental Evaluation. International Journal of Molecular Sciences. 2025; 26(16):8005. https://doi.org/10.3390/ijms26168005
Chicago/Turabian StyleYang, Seunga, SangYup Lee, Paul Maldonado Nogales, Yangsoo Kim, and Soon-Ki Jeong. 2025. "Theoretical Investigation of Ca2+ Intercalation in WS2 as a Negative Electrode Material for Calcium-Ion Batteries: Supported by Experimental Evaluation" International Journal of Molecular Sciences 26, no. 16: 8005. https://doi.org/10.3390/ijms26168005
APA StyleYang, S., Lee, S., Nogales, P. M., Kim, Y., & Jeong, S.-K. (2025). Theoretical Investigation of Ca2+ Intercalation in WS2 as a Negative Electrode Material for Calcium-Ion Batteries: Supported by Experimental Evaluation. International Journal of Molecular Sciences, 26(16), 8005. https://doi.org/10.3390/ijms26168005








