The Relaxation Behavior of Water Confined in AOT-Based Reverse Micelles Under Temperature-Induced Clustering
Abstract
1. Introduction
2. Results
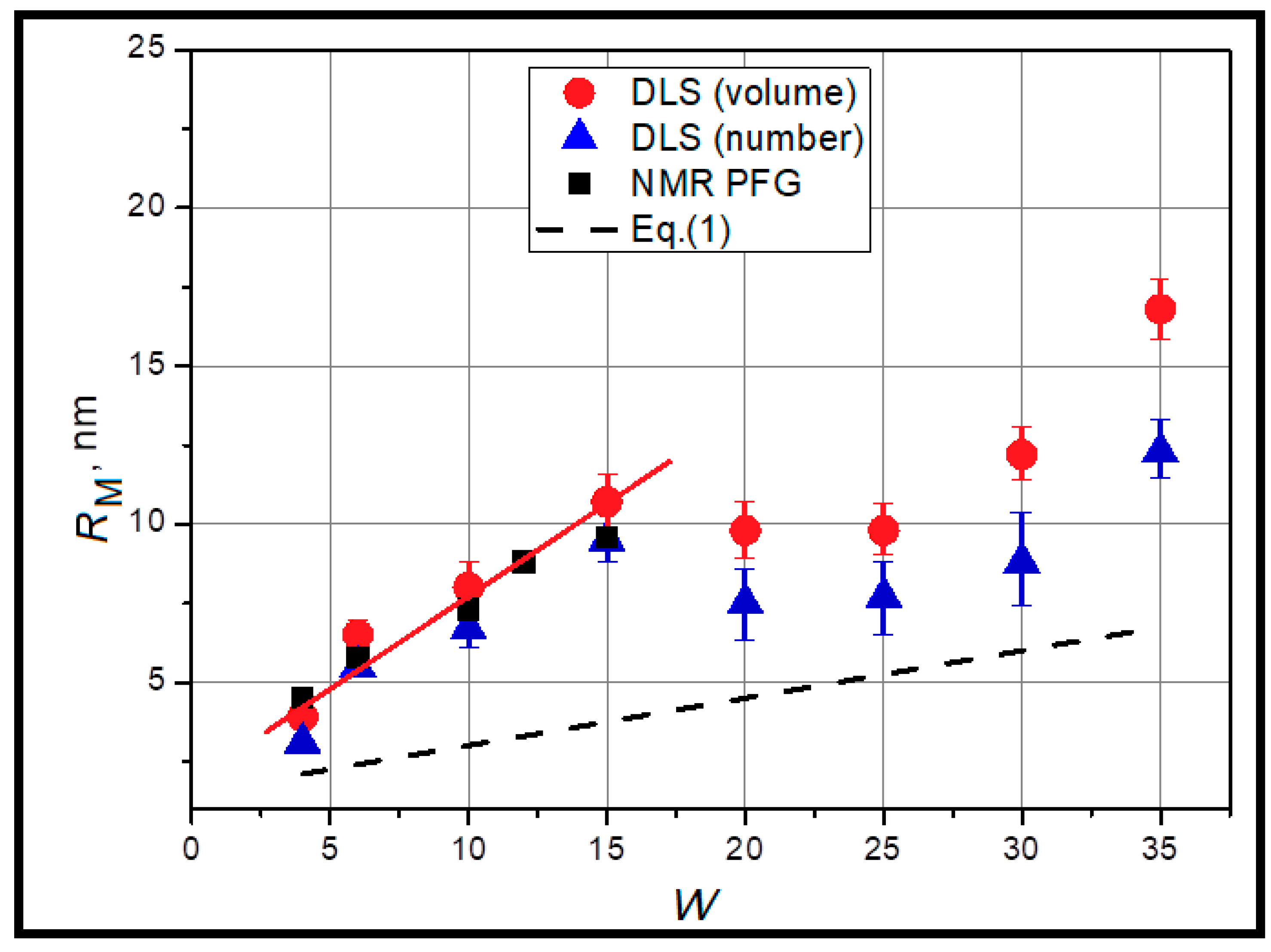
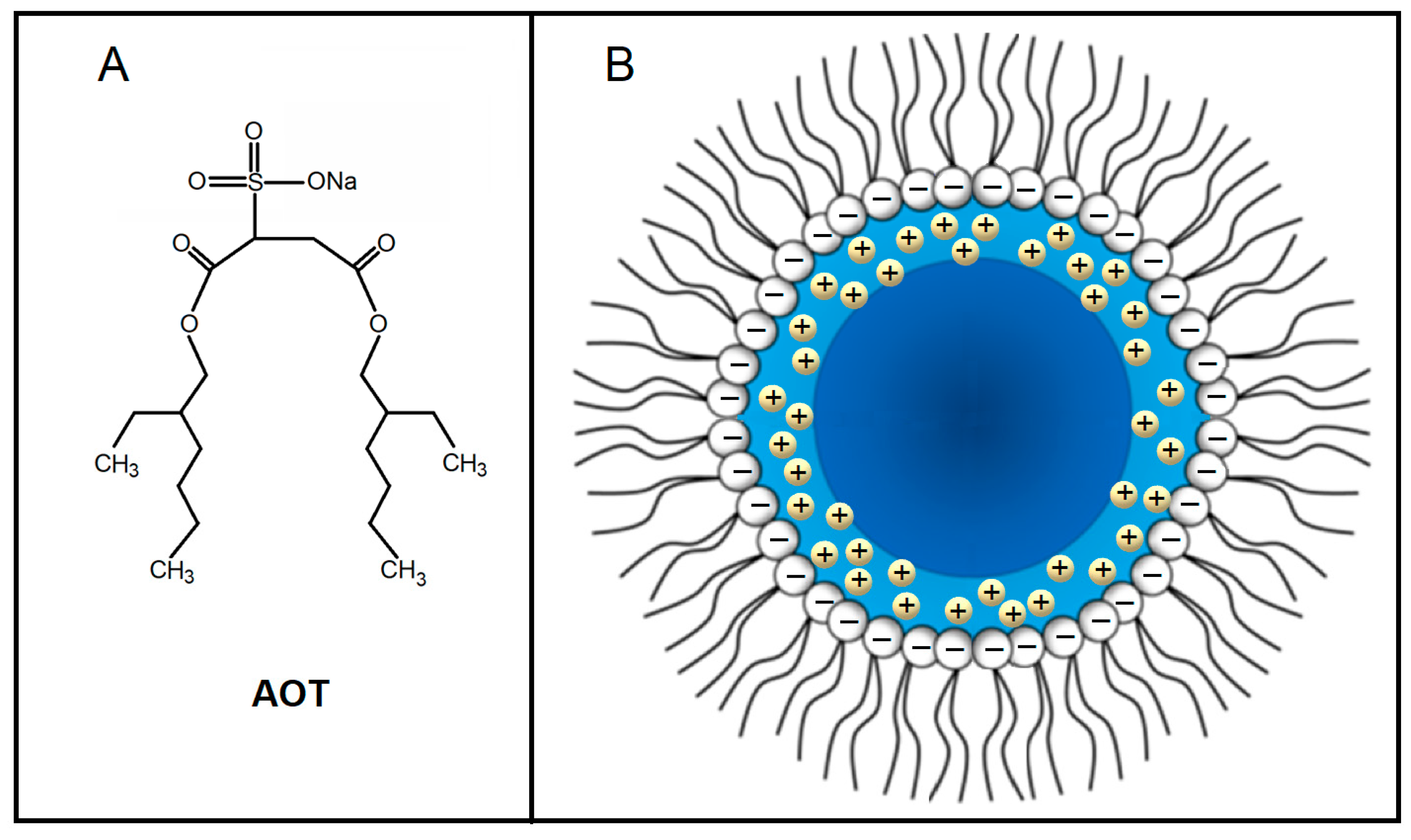
2.1. Structural Features of AOT-Based Water-in-Oil Microemulsions
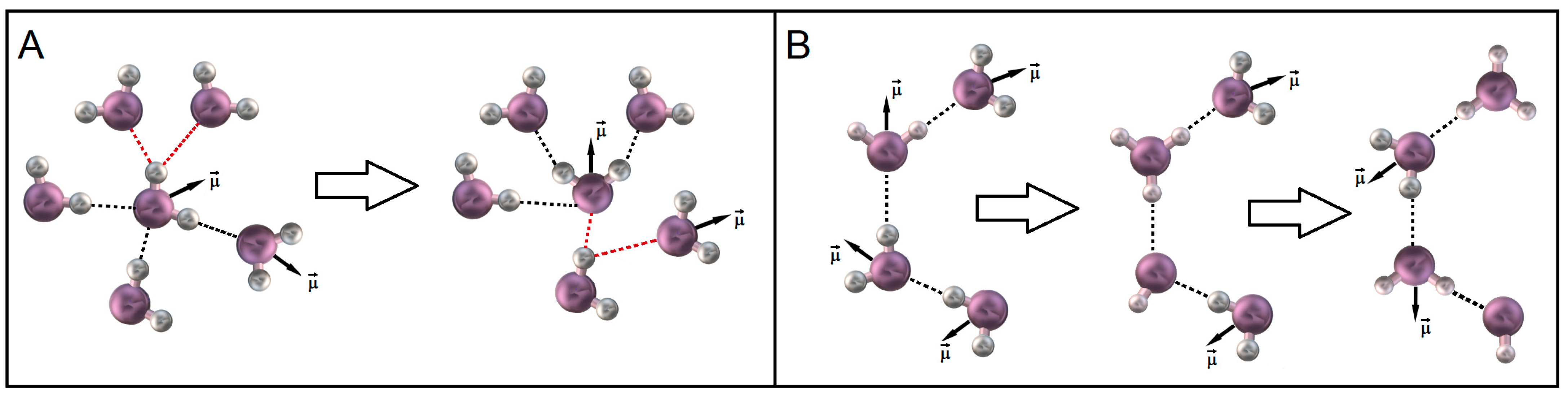
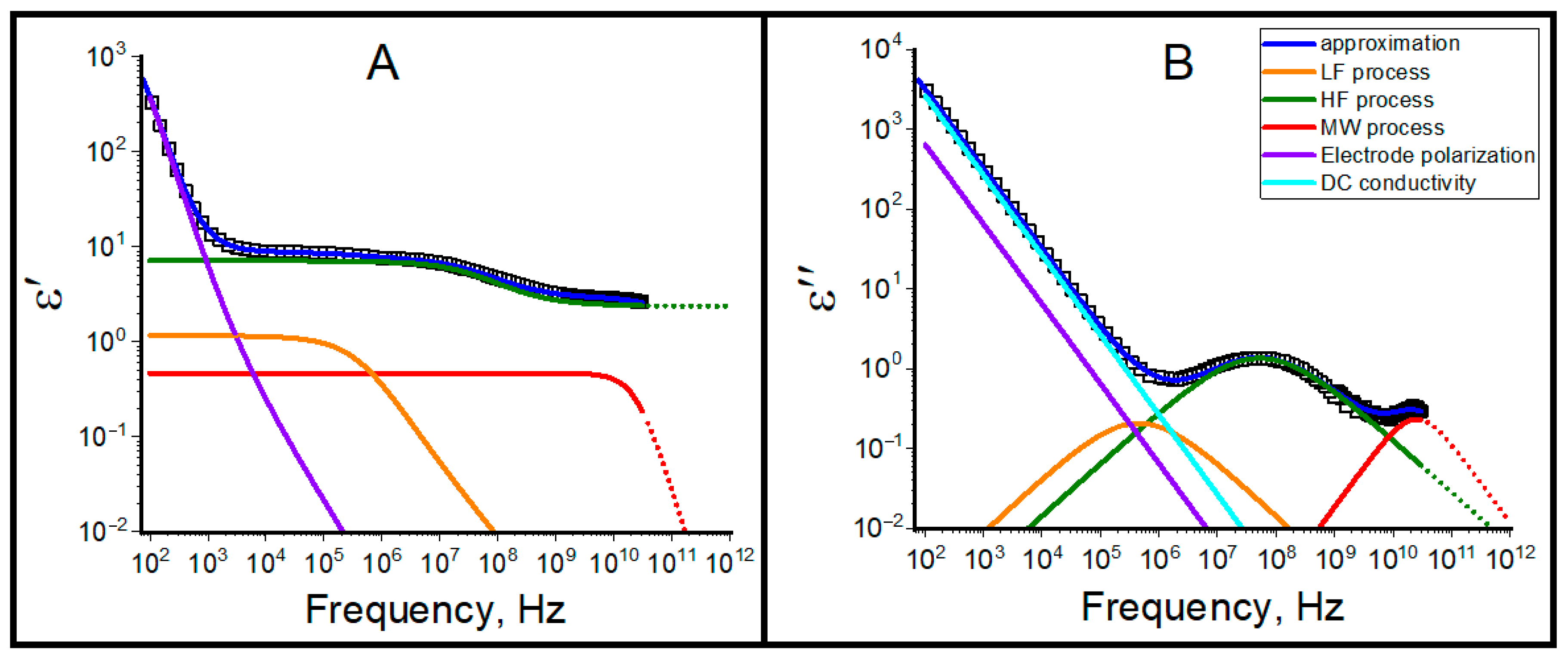
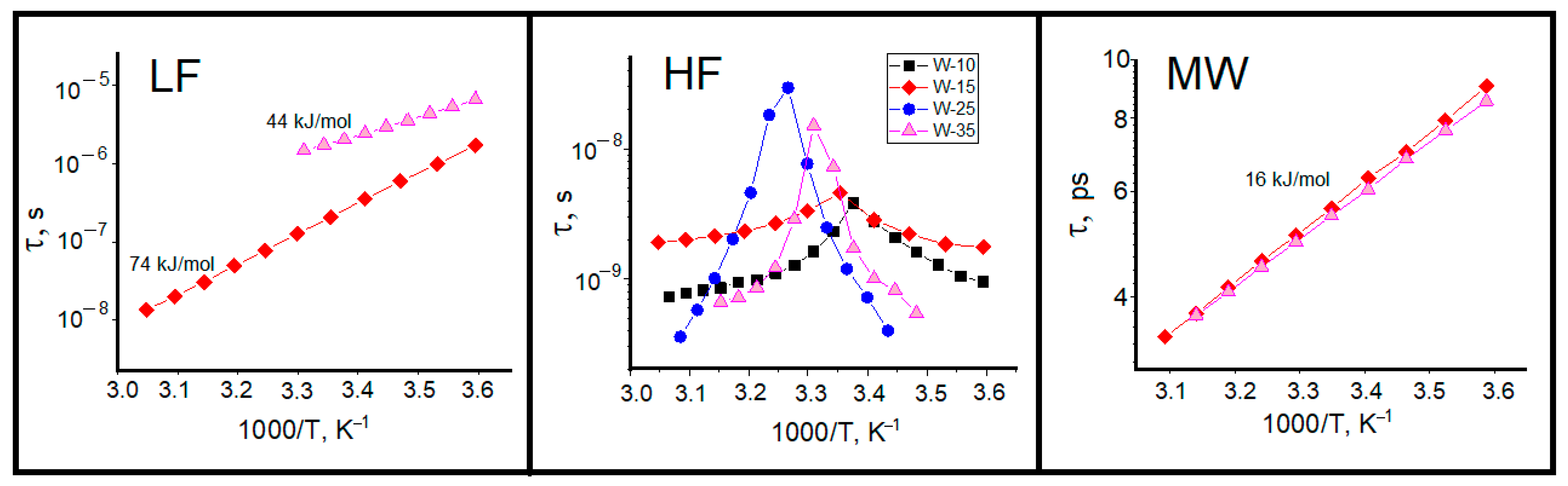
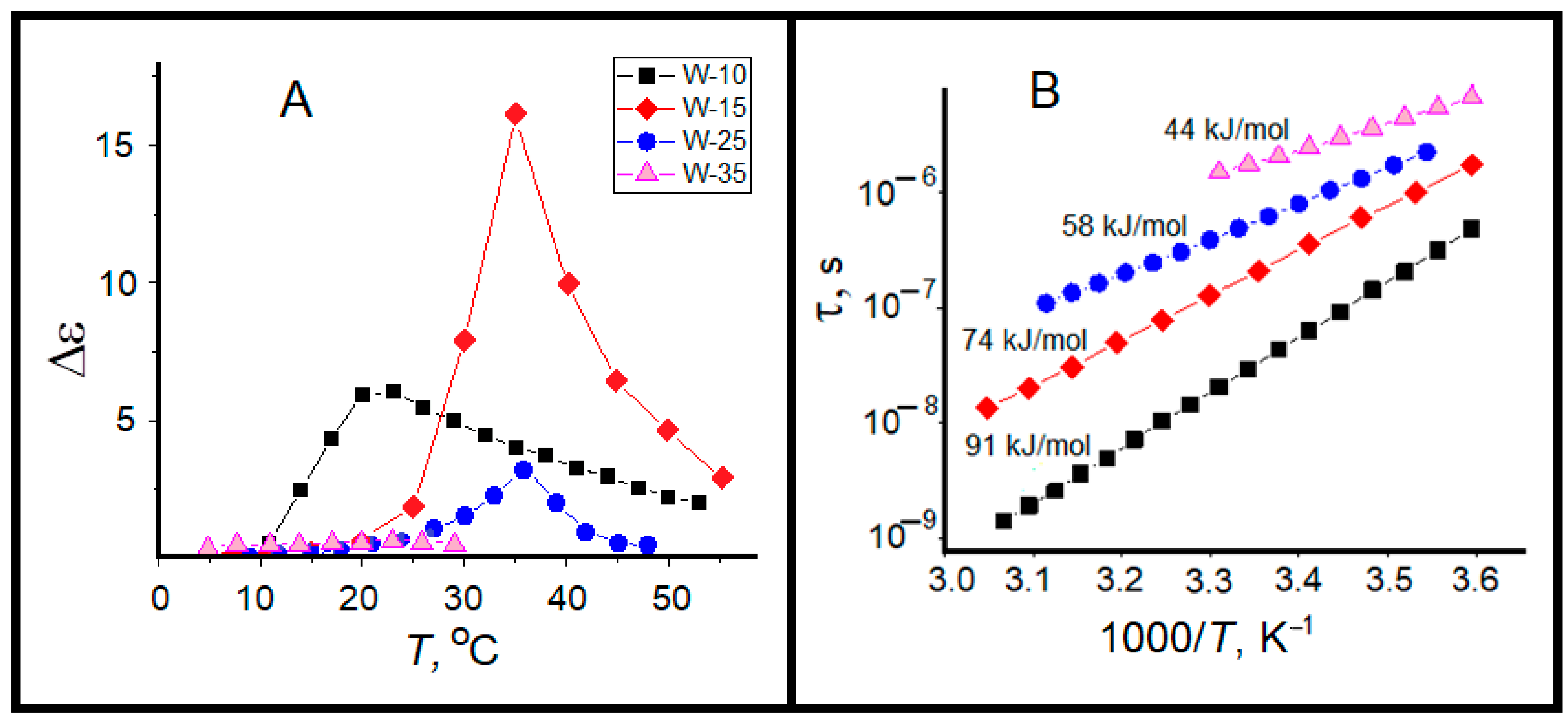
2.2. Dielectric Relaxation
3. Materials and Methods
3.1. Chemicals
3.2. Dielectric Measurements
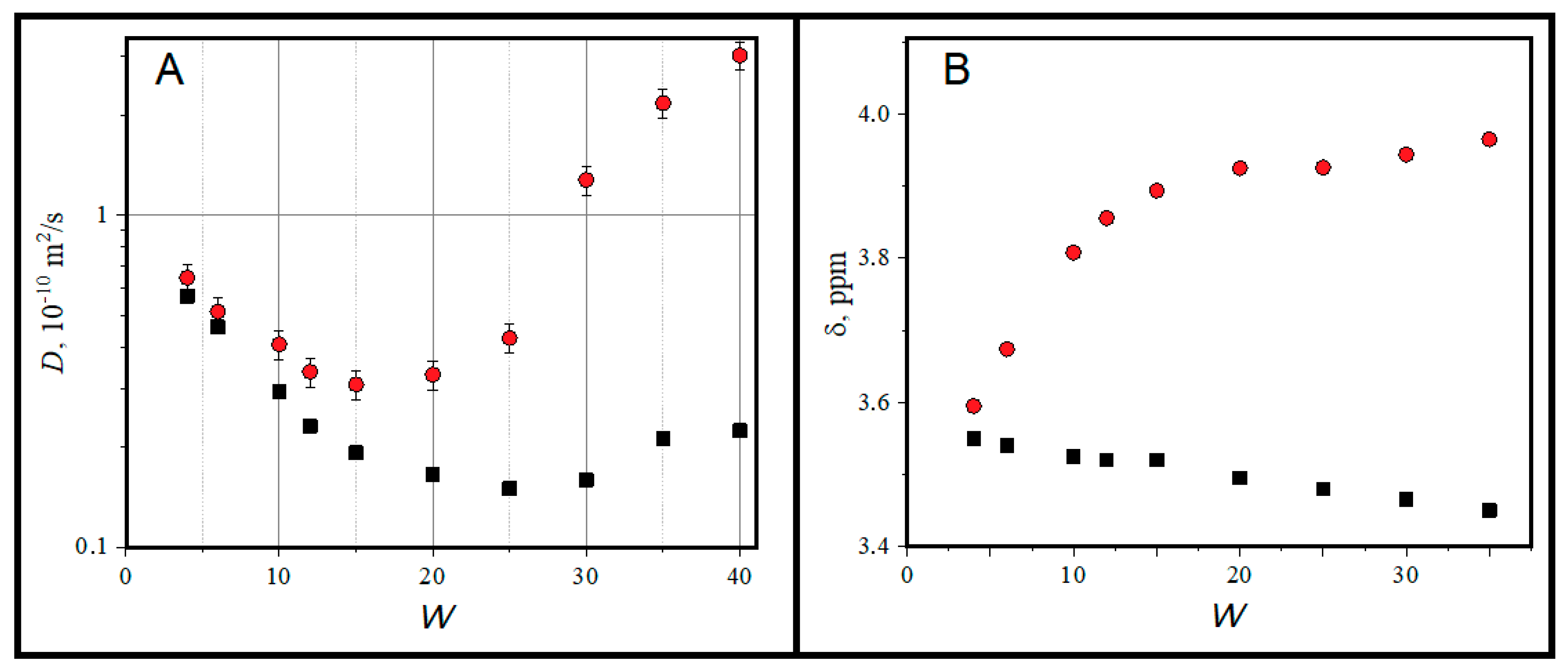
3.3. H NMR Experiments
3.4. Dynamic Light Scattering
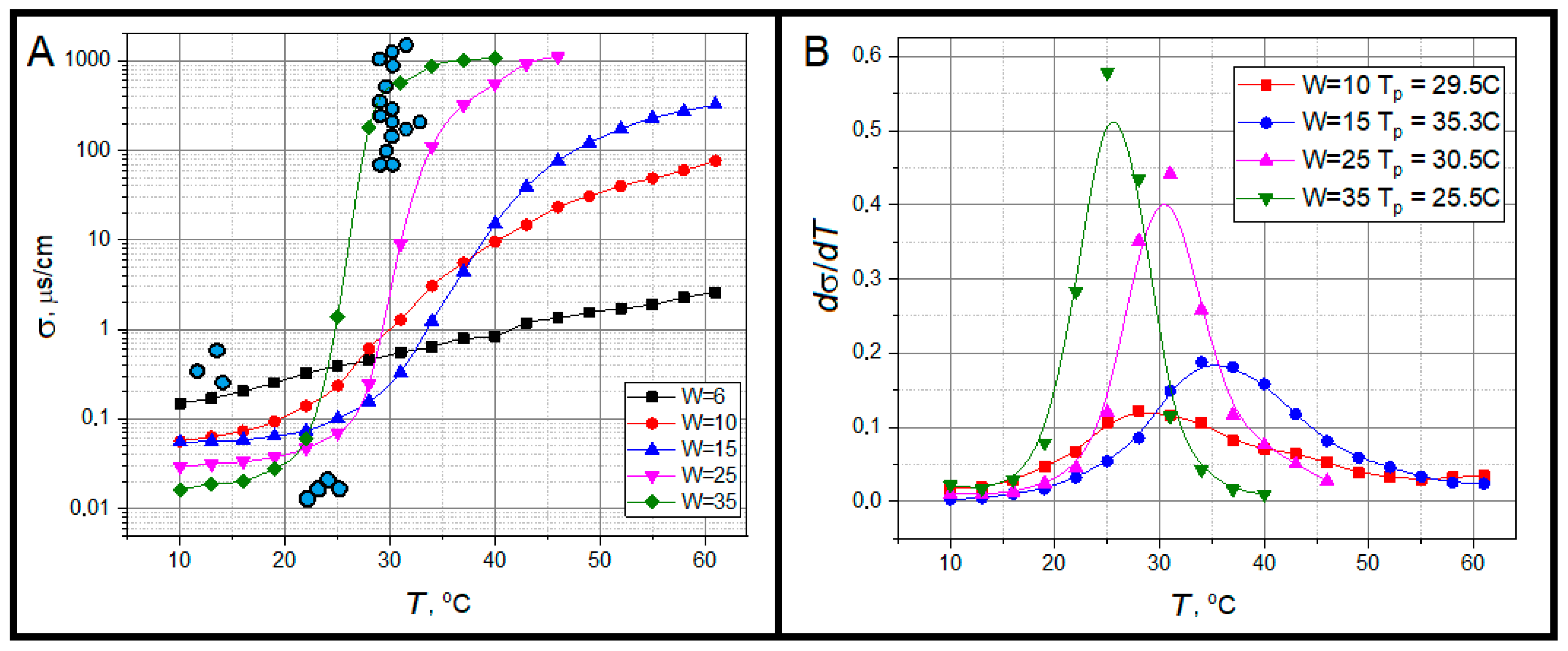
3.5. Electric Conductivity of Microemulsions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sciortino, F.; Geiger, A.; Stanley, H.E. Effect of defects on molecular mobility in liquid water. Nature 1991, 354, 218–221. [Google Scholar] [CrossRef]
- Bernal, J.D.; Fowler, R.H. A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. J. Chem. Phys. 1933, 1, 515–548. [Google Scholar] [CrossRef]
- Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Agmon, N. Liquid Water: From Symmetry Distortions to Diffusive Motion. Acc. Chem. Res. 2012, 45, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.; Ben Ishai, P.; Khamzin, A.; Feldman, Y. The mechanism of the dielectric relaxation in water. Phys. Chem. Chem. Phys. 2016, 18, 13941. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.; Puzenko, A.; Khamzin, A.; Feldman, Y. The dynamic crossover in dielectric relaxation behavior of ice Ih. Phys. Chem. Chem. Phys. 2015, 17, 1489–1497. [Google Scholar] [CrossRef]
- Kaatze, U. Reference liquids for the calibration of dielectric sensors and measurement instruments. Meas. Sci. Technol. 2007, 18, 967–976. [Google Scholar] [CrossRef]
- Sciortino, F.; Geiger, A.; Stanley, H.E. Network defects and molecular mobility in liquid water. J. Chem. Phys. 1992, 96, 3857–3865. [Google Scholar] [CrossRef]
- Sato, T.; Buchner, R. The cooperative dynamics of the H-bond system in 2-propanol/water mixtures: Steric hindrance effects of nonpolar head group. J. Chem. Phys. 2003, 119, 10789–10800. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Chemical Catalog Co.: New York, NY, USA, 1929; 172p. [Google Scholar] [CrossRef]
- Khamzin, A. On Nature of Dielectric Response in Liquid Water (Review). Rensit 2021, 13, 119–128. [Google Scholar] [CrossRef]
- Anderson, J.E. Time-Dependent Reorientation Probabilities and Molecular Relaxation Available to Purchase. J. Chem. Phys. 1967, 47, 4879. [Google Scholar] [CrossRef]
- Bordewijk, P. Defect-diffusion models of dielectric relaxation. Chem. Phys. Lett. 1975, 32, 592–596. [Google Scholar] [CrossRef]
- Zuev, Y.F.; Fedotov, V.D. On the dielectric relaxation mechanisms of water sorbed by the biopolymers. Stud. Biophys. 1986, 111, 165–168. [Google Scholar]
- Moulik, S.P.; Paul, B.K. Structure, dynamics and transport properties of microemulsions. Adv. Colloid Interface Sci. 1998, 78, 99–195. [Google Scholar] [CrossRef]
- Beilinson, Y.; Rassabina, A.; Lunev, I.; Faizullin, D.; Greenbaum, A.; Salnikov, V.; Zuev, Y.; Minibayeva, F.; Feldman, Y. The dielectric response of hydrated water as a structural signature of nanoconfined lichen melanins. Phys. Chem. Chem. Phys. 2022, 24, 22624–22633. [Google Scholar] [CrossRef] [PubMed]
- Beilinson, Y.; Schiller, V.; Regentin, J.; Melillo, J.H.; Greenbaum, A.; Antropova, T.; Cerveny, S.; Vogel, M.; Feldman, Y. The Nature of the Low-Temperature Crossover of Water in Hard Confinement. J. Phys. Chem. B 2023, 127, 5128–5140. [Google Scholar] [CrossRef] [PubMed]
- Zueva, O.S.; Makarova, A.O.; Zvereva, E.R.; Kurbanov, R.K.; Salnikov, V.V.; Turanov, A.N.; Zuev, Y.F. Industrial block copolymer surfactants: Diversity of associative forms and interaction with carbon nanomaterial. J. Mol. Liq. 2022, 359, 119267. [Google Scholar] [CrossRef]
- Zueva, O.S.; Rukhlov, V.S.; Zuev, Y.F. Morphology of Ionic Micelles as Studied by Numerical Solution of the Poisson Equation. ACS Omega 2022, 7, 6174–6183. [Google Scholar] [CrossRef]
- Zueva, O.S.; Kusova, A.M.; Makarova, A.O.; Turanov, A.; Iskhakova, A.; Salnikov, V.V.; Zuev, Y.F. Reciprocal Effects of Multi-Walled Carbon Nanotubes and Oppositely Charged Surfactants in Bulk Water and at Interfaces. Colloids Surf. A Physicochem. Eng. Asp. 2020, 603, 125296. [Google Scholar] [CrossRef]
- Zueva, O.S.; Kazantseva, M.A.; Zuev, Y.F. Nanosized Being of Ionic Surfactant Micelles: An Advanced View on Micellization Process. Colloids Interfaces 2025, 9, 15. [Google Scholar] [CrossRef]
- Paul, B.K.; Moulik, S.P. Uses and Applications of Microemulsions. Curr. Sci. 2001, 80, 990–1001. [Google Scholar]
- Fedotov, V.D.; Zuev, Y.F.; Archipov, V.P.; Idiyatullin, Z.S.; Garti, N. A Fourier transform pulsed-gradient spin echo nuclear magnetic resonance self-diffusion study of microemulsions and the droplet size determination. Colloids Surf. A Physicochem. Eng. Asp. 1997, 128, 39–46. [Google Scholar] [CrossRef]
- Baksi, A.; Ghorai, P.K.; Biswas, R. Dynamic Susceptibility and Structural Heterogeneity of Large Reverse Micellar Water: An Examination of the Core−Shell Model via Probing the Layer-wise Features. J. Phys. Chem. B 2020, 124, 2848–2863. [Google Scholar] [CrossRef]
- Arkhipov, V.P.; Idiyatullin, Z.S.; Arkhipov, R.V.; Zakharchenko, N.L.; Zuev, Y.F.; Fedotov, V.D. Diffusion of water in water—Aerosol OT—Decane microemulsion. Colloid J. 2000, 62, 407–413. [Google Scholar]
- Feldman, Y.; Kozlovich, N.; Nir, I.; Garti, N.; Archipov, V.; Idiatullin, Z.; Zuev, Y.; Fedotov, V. Mechanism of transport of charge carries in the sodium bis (2-ethylhexyl) sulfosuccinate-water-decane microemulsion near the percolation temperature threshold. J. Phys. Chem. 1996, 100, 3745–3748. [Google Scholar] [CrossRef]
- Kumar, P.; Mittal, K.L. (Eds.) Handbook of Microemulsion Science and Technology; Dekker: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Luisi, P.L.; Straub, B.E. (Eds.) Reverse Micelles: Biological and Technological Relevance of Amphiphilic Structures in Apolar Media; Plenum Press: New York, NY, USA; London, UK, 1984. [Google Scholar]
- Romsted, L.S. (Ed.) Surfactants Science and Technology. Retrospects and Prospects; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2014. [Google Scholar]
- Gradzielski, M.; Duvail, M.; Malo de Molina, P.; Simon, M.; Talmon, Y.; Zemb, T. Using Microemulsions: Formulation Based on Knowledge of Their Mesostructure. Chem. Rev. 2021, 121, 5671–5740. [Google Scholar] [CrossRef]
- Qu, J.; Wan, Y.; Tian, M.; Lv, W. Microemulsions Based on Diverse Surfactant Molecular Structure: Comparative Analysis and Mechanistic Study. Processes 2023, 11, 3409. [Google Scholar] [CrossRef]
- Luan, Y.; Xu, G.; Yuan, S.; Xiao, L.; Zhang, Z. Comparative Studies of Structurally Similar Surfactants: Sodium Bis(2-ethylhexyl)phosphate and Sodium Bis(2-ethylhexyl)sulfosuccinate. Langmuir 2002, 18, 8700–8705. [Google Scholar] [CrossRef]
- Mehta, S.K.; Sharma, S.; Bhasin, K.K. On the Temperature Percolation in a w/o Microemulsion in the Presence of Organic Derivatives of Chalcogens. J. Phys. Chem. B 2005, 109, 9751–9759. [Google Scholar] [CrossRef]
- Lang, J.; Jada, A.; Malliaris, A. Structure and dynamics of water-in-oil droplets stabilized by sodium bis(2-ethylhexyl)sulfosuccinate. J. Phys. Chem. 1988, 92, 1946–1953. [Google Scholar] [CrossRef]
- Pileni, M.P. Nanosized particles made in colloidal assemblies. Langmuir 1997, 13, 3266–3276. [Google Scholar] [CrossRef]
- Pileni, M.P.; Zemb, T.; Petit, C. Solubilization by reverse micelles: Solute localization and structure perturbation. Chem. Phys. Lett. 1985, 118, 414–420. [Google Scholar] [CrossRef]
- Zulauf, M.; Eicke, H.F. Inverted Micelles and Microemulsions in the Ternary-System H2O-Aerosol-OT-Isooctane as Studied by Photon Correlation Spectroscopy. J. Phys. Chem. 1979, 83, 480–486. [Google Scholar] [CrossRef]
- Vasquez, V.R.; Williams, B.C.; Graeve, O.A. Stability and Comparative Analysis of AOT/Water/Isooctane Reverse Micelle System Using Dynamic Light Scattering and Molecular Dynamics. J. Phys. Chem. B 2011, 115, 2979–2987. [Google Scholar] [CrossRef]
- Liu, J.C.; Li, G.Z.; Han, B.X. Characteristics of AOT microemulsion structure: A small angle X-ray scattering study. Chin. Chem. Lett. 2001, 12, 1023–1026. [Google Scholar]
- Balakrishnan, S.; Javid, N.; Weingartner, H.; Winter, R. Small-Angle X-Ray Scattering and Near-infrared Vibrational Spectroscopy of Water Confined in Aerosol-OT Reverse Micelles. Chem. Phys. Chem 2008, 9, 2794–2801. [Google Scholar] [CrossRef]
- Pal, N.; Verma, S.D.; Singh, M.K.; Sen, S. Fluorescence Correlation Spectroscopy: An Efficient Tool for Measuring Size, Size-Distribution and Polydispersity of Microemulsion Droplets in Solution. Anal. Chem. 2011, 83, 7736–7744. [Google Scholar] [CrossRef]
- Law, S.J.; Britton, M.M. Sizing of Reverse Micelles in Microemulsions using NMR Measurements of Diffusion. Langmuir 2012, 28, 11699–11706. [Google Scholar] [CrossRef]
- Eicke, H.F.; Borkovec, M.; Das Gupta, B. Conductivity of water-in-oil microemulsions: A quantitative charge fluctuation model. J. Phys. Chem. 1989, 93, 314–317. [Google Scholar] [CrossRef]
- Spehr, T.L.; Frick, B.; Zamponicd, M.; Stühn, B. Dynamics of water confined to reverse AOT micelles. Soft Matter 2011, 7, 5745–5755. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- van Dijk, M.A.; Casteleijn, G.; Joosten, J.G.H.; Levine, Y.K. Percolation in oil-continuous microemulsions. A dielectric study of aerosol OT/water/isooctane. J. Chem. Phys. 1986, 85, 626–631. [Google Scholar] [CrossRef]
- Zuev, Y.F.; Kurbanov, R.K.; Idiyatullin, B.Z.; Us’yarov, O.G. Sodium dodecyl sulfate self-diffusion in premicellar and low-concentrated micellar solutions in the presence of a background electrolyte. Colloid J. 2007, 69, 444–449. [Google Scholar] [CrossRef]
- Zuev, Y.F.; Gnezdilov, O.I.; Zueva, O.S.; Us’yarov, O.G. Effective self-diffusion coefficients of ions in sodium dodecyl sulfate micellar solutions. Colloid J. 2011, 73, 59–64. [Google Scholar] [CrossRef]
- Söderman, O.; Stilbs, P.; Price, W.S. NMR studies of surfactants. Concep. Magn. Reson. A 2004, 23, 121–135. [Google Scholar] [CrossRef]
- Phillies, G.D.J. Reactive contribution to the apparent translational diffusion coefficient of a micelle. J. Phys. Chem. 1981, 85, 3540–3541. [Google Scholar] [CrossRef]
- Gottlieb, H.E.; Kotlyar, V.; Nudelman, A. NMR Chemical Shifts of Common Laboratory Solvents as Trace Impurities. J. Org. Chem. 1997, 62, 7512–7515. [Google Scholar] [CrossRef]
- Tsukahara, T.; Mizutani, W.; Mawatari, K.; Kitamori, T. NMR Studies of Structure and Dynamics of Liquid Molecules Confined in Extended Nanospaces. J. Phys. Chem. B 2009, 113, 10808–10816. [Google Scholar] [CrossRef]
- van Dijk, M.A.; Broekman, E.; Joosten, J.G.H.; Bedeaux, D. Dielectric study of temperature dependent aerosol OT/water/isooctane microemulsion structure. J. Physique 1986, 47, 727–731. [Google Scholar] [CrossRef]
- Feldman, Y.; Kozlovich, N.; Nir, I.; Garti, N. Dielectric spectroscopy of microemulsions. Colloids Surf. A Physicochem. Eng. Asp. 1997, 128, 47–61. [Google Scholar] [CrossRef]
- Bordi, F.; Cametti, C.; Di Biasio, A. High-frequency dielectric polarization mechanism in water-in-oil micro-emulsions below percolation. In Trends in Colloid and Interface Science XIV; Buckin, V., Ed.; Progress in Colloid and Polymer Science; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Cametti, C. Dielectric spectra of ionic water-in-oil microemulsions below percolation: Frequency dependence behavior. Phys. Rev. E 2010, 81, 031403. [Google Scholar] [CrossRef]
- Geethu, P.M.; Yadav, I.; Deshpande, S.K.; Aswal, V.K.; Satapathy, D.K. Soft Confinement Effects on Dynamics of Hydrated Gelatin. Macromolecules 2017, 50, 6518–6528. [Google Scholar] [CrossRef]
- Buchner, R.; Hefter, G.T.; May, P.M. Dielectric Relaxation of Aqueous NaCl Solutions. J. Phys. Chem. A 1999, 103, 1–9. [Google Scholar] [CrossRef]
- Raicu, V.; Feldman, Y. (Eds.) Dielectric Relaxation in Biological Systems: Physical Principles, Methods, and Applications; Oxford University Press: Oxford, MS, USA, 2015. [Google Scholar] [CrossRef]
- Wang, C.L. Jonscher indices for dielectric materials. J. Adv. Dielect. 2019, 9, 1950046. [Google Scholar] [CrossRef]
- Feldman, Y.; Ben Ishai, P. The Microwave Response of Water as the Measure of Interactions in a Complex Liquid. In Broadband Dielectric Spectroscopy: A Modern Analytical Technique; ACS Publications: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Petong, P.; Pottel, R.; Kaatze, U. Water-Ethanol Mixtures at Different Compositions and Temperatures. A Dieletric Relaxation Study. J. Phys. Chem. A 2000, 104, 7420–7428. [Google Scholar] [CrossRef]
- Lu, Z.; Manias, E.; Macdonald, D.D.; Lanagan, M. Dielectric Relaxation in Dimethyl Sulfoxide/Water Mixtures Studied by Microwave Dielectric Relaxation Spectroscopy. J. Phys. Chem. A 2009, 113, 12207–12214. [Google Scholar] [CrossRef]
- Cringus, D.; Bakulin, A.; Lindner, J.; Vo1hringer, P.; Pshenichnikov, M.S.; Wiersma, D.A. Ultrafast Energy Transfer in Water-AOT Reverse Micelles. J. Phys. Chem. B 2007, 111, 14193–14207. [Google Scholar] [CrossRef]
- Foster, K.R.; Schwan, H.P. Dielectric properties of tissues. In CRC Handbook of Biological Effects of Electromagnetic Fields; Polk, C., Possow, E., Eds.; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Kozlovich, N.; Puzenko, A.; Alexandrov, Y.; Feldman, Y. Fluctuation mechanism of the dielectric polarization of water-in-oil microemulsions with ionic surfactant. Phys. Rev. E 1998, 58, 2179–2187. [Google Scholar] [CrossRef]
- Fröhlich, H. Theory of Dielectrics. Dielectric Constant and Dielectric Loss, 2nd ed.; The Calderon Press: Oxford, UK, 1958. [Google Scholar]
- Murgia, S.; Palazzo, G.; Mamusa, M.; Lampisa, S.; Monduzzi, M. Aerosol-OT in water forms fully-branched cylindrical direct micelles in the presence of the ionic liquid 1-butyl-3-methylimidazolium bromide. Phys. Chem. Chem. Phys. 2011, 13, 9238–9245. [Google Scholar] [CrossRef]
- van der Loop, T.H.; Ottosson, N.; Lotze, S.; Kentzinger, E.; Vad, T.; Sager, W.F.C.; Bakker, H.J.; Woutersen, S. Structure and dynamics of water in nanoscopic spheres and tubes. J. Chem. Phys. 2014, 141, 18C535. [Google Scholar] [CrossRef]
- Bjerrum, N. Structure and Properties of Ice. Science 1952, 115, 385–390. [Google Scholar] [CrossRef]
- von Hippel, A. The Dielectric-Relaxation Spectra of Water, Ice, and Aqueous-Solutions, and Their Interpretation. III. Proton Organization and Proton-Transfer in Ice. IEEE T. Electr. Insul. 1988, 23, 825–840. [Google Scholar] [CrossRef]
- Popov, I.; Lunev, I.; Khamzin, A.; Greenbaum, A.; Gusev, Y.; Feldman, Y. The low-temperature dynamic crossover in dielectric relaxation of ice Ih. Phys. Chem. Chem. Phys. 2017, 19, 28610. [Google Scholar] [CrossRef] [PubMed]
- Piletic, I.R.; Moilanen, D.E.; Spry, D.B.; Levinger, N.E.; Fayer, M.D. Testing the Core/Shell Model of Nanoconfined Water in Reverse Micelles Using Linear and Nonlinear IR Spectroscopy. J. Phys. Chem. A 2006, 110, 4985–4999. [Google Scholar] [CrossRef] [PubMed]
- Faeder, J.; Ladanyi, B.M. Molecular Dynamics Simulations of the Interior of Aqueous Reverse Micelles. J. Phys. Chem. B 2000, 104, 1033–1046. [Google Scholar] [CrossRef]
- Maitra, A. Determination of size parameters of water-Aerosol OT-oil reverse micelles from their nuclear magnetic resonance data. J. Phys. Chem. 1984, 88, 5122–5125. [Google Scholar] [CrossRef]
- Cowan, M.L.; Bruner, B.D.; Huse, N.; Dwyer, J.R.; Chugh, B.; Nibbering, E.T.J.; Elsaesser, T.; Miller, R.J.D. Ultrafast memory loss and energy redistribution in the hydrogen bond network of liquid H2O. Nature 2005, 434, 199–202. [Google Scholar] [CrossRef]
- Rey, R.; Møller, K.B.; Hynes, J.T. Hydrogen Bond Dynamics in Water and Ultrafast Infrared Spectroscopy. J. Phys. Chem. A 2002, 106, 11993–11996. [Google Scholar] [CrossRef]
- Lawrence, C.P.; Skinner, J.L. Vibrational spectroscopy of HOD in liquid. II. Infrared line shapes and vibrational Stokes shift. J. Chem. Phys. 2002, 117, 8847–8854. [Google Scholar] [CrossRef]
- Lawrence, C.P.; Skinner, J.L. Ultrafast infrared spectroscopy probes hydrogen-bonding dynamics in liquid water. Chem. Phys. Lett. 2003, 369, 472–477. [Google Scholar] [CrossRef]
- Schwarzer, D.; Lindner, J.; Vöhringer, P. OH-Stretch Vibrational Relaxation of HOD in Liquid to Supercritical D2O. J. Phys. Chem. A 2006, 110, 2858–2867. [Google Scholar] [CrossRef]
- Axelrod, N.; Axelrod, E.; Gutina, A.; Puzenko, A.; Ishai, B.P.; Feldman, Y. Dielectric spectroscopy data treatment: I. Frequency domain. Meas. Sci. Technol. 2004, 15, 755–764. [Google Scholar] [CrossRef]
- Idiyatullin, B.Z.; Zuev, Y.F.; Potarikina, K.S.; Us’yarov, O.G.; Zueva, O.S. Association of sodium dodecyl sulfate in aqueous solutions according to chemical shifts in 1H NMR spectra. Colloid J. 2013, 75, 532–537. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lunev, I.V.; Turanov, A.N.; Klimovitskaya, M.A.; Galiullin, A.A.; Zueva, O.S.; Zuev, Y.F. The Relaxation Behavior of Water Confined in AOT-Based Reverse Micelles Under Temperature-Induced Clustering. Int. J. Mol. Sci. 2025, 26, 7152. https://doi.org/10.3390/ijms26157152
Lunev IV, Turanov AN, Klimovitskaya MA, Galiullin AA, Zueva OS, Zuev YF. The Relaxation Behavior of Water Confined in AOT-Based Reverse Micelles Under Temperature-Induced Clustering. International Journal of Molecular Sciences. 2025; 26(15):7152. https://doi.org/10.3390/ijms26157152
Chicago/Turabian StyleLunev, Ivan V., Alexander N. Turanov, Mariya A. Klimovitskaya, Artur A. Galiullin, Olga S. Zueva, and Yuriy F. Zuev. 2025. "The Relaxation Behavior of Water Confined in AOT-Based Reverse Micelles Under Temperature-Induced Clustering" International Journal of Molecular Sciences 26, no. 15: 7152. https://doi.org/10.3390/ijms26157152
APA StyleLunev, I. V., Turanov, A. N., Klimovitskaya, M. A., Galiullin, A. A., Zueva, O. S., & Zuev, Y. F. (2025). The Relaxation Behavior of Water Confined in AOT-Based Reverse Micelles Under Temperature-Induced Clustering. International Journal of Molecular Sciences, 26(15), 7152. https://doi.org/10.3390/ijms26157152








