Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models
Abstract
1. Introduction
2. Results
2.1. Summary Statistics of Key Phenotypic Traits
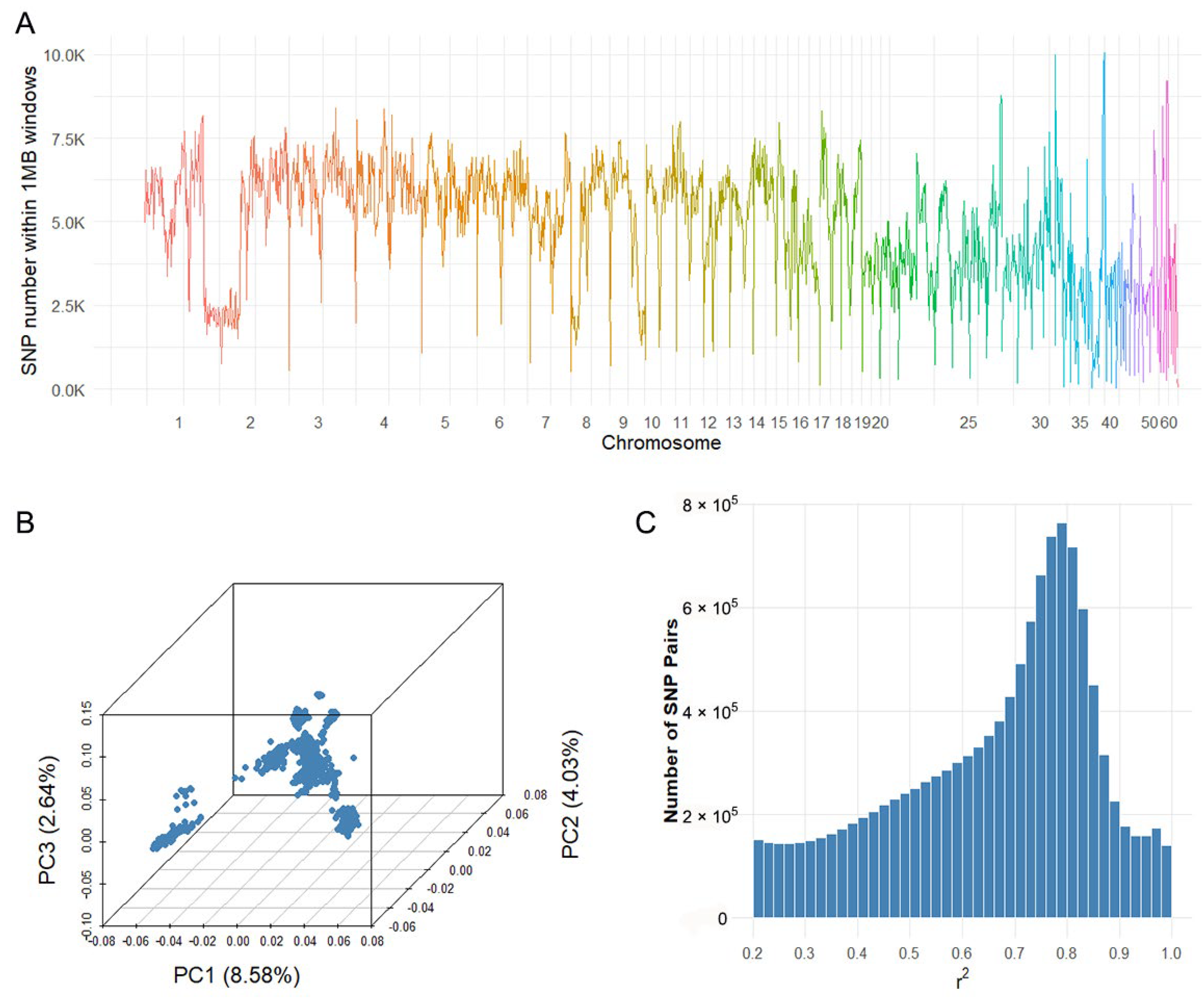
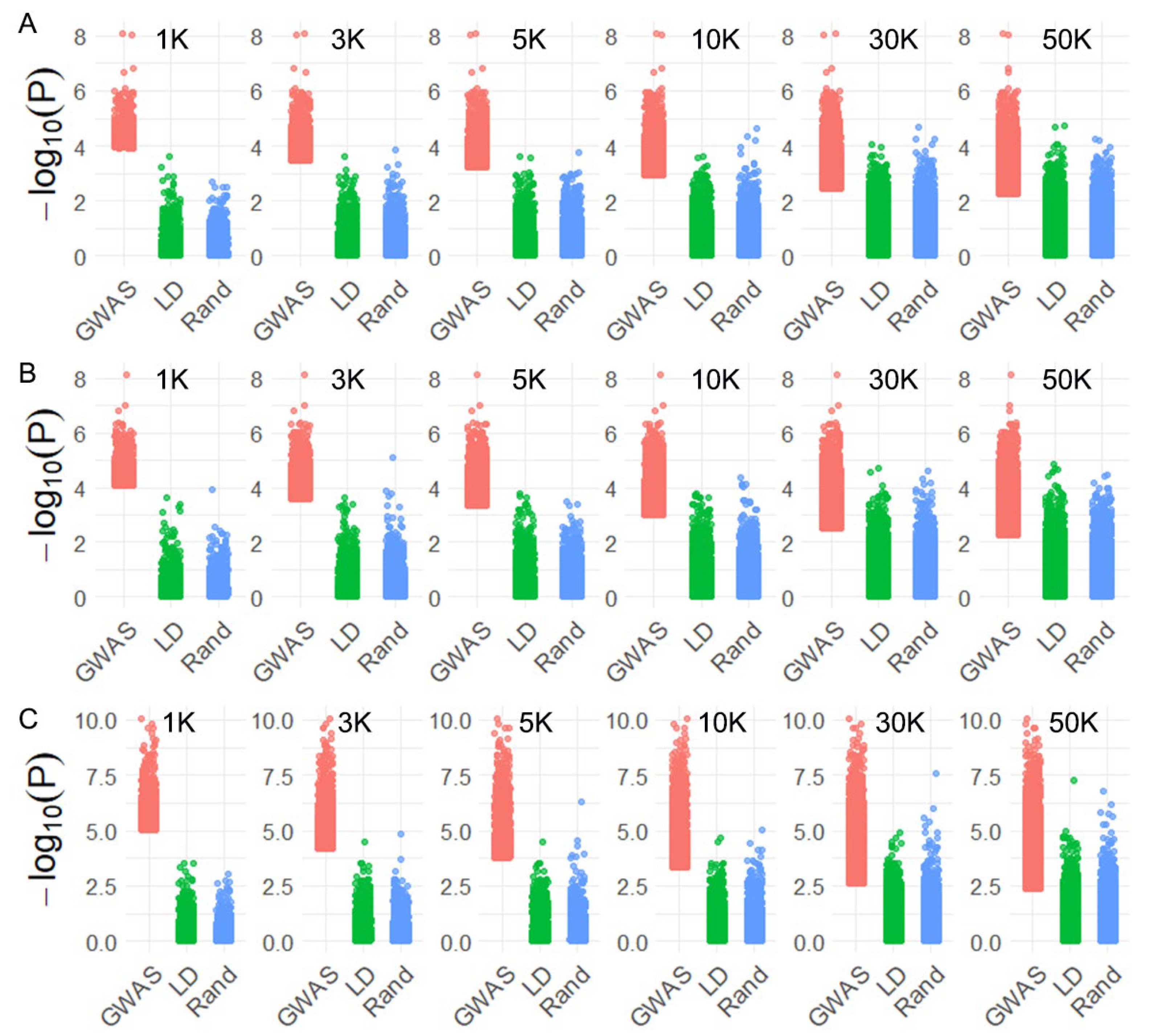
2.2. Whole-Genome Sequencing, Population Structure and Linkage Disequilibrium
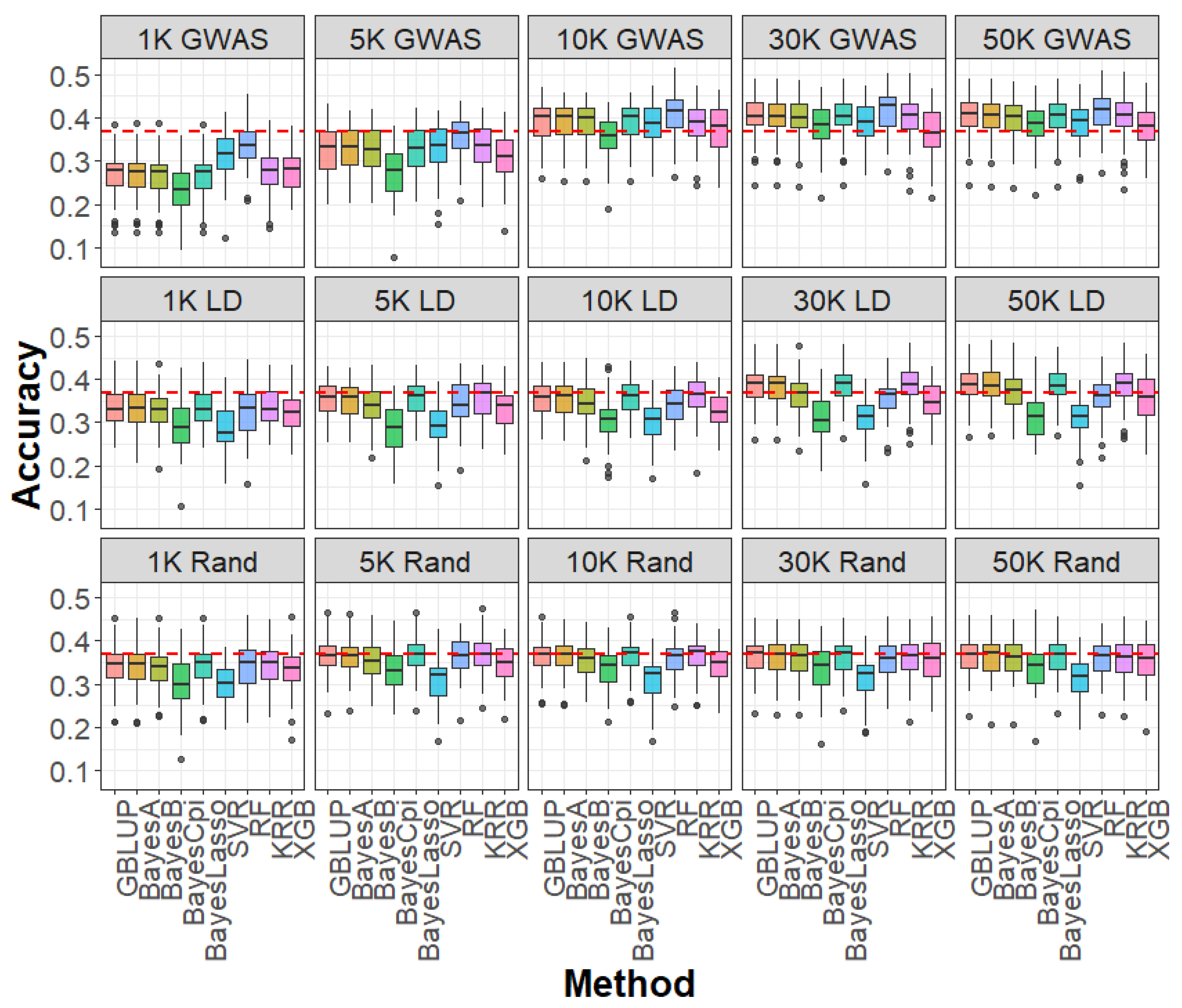
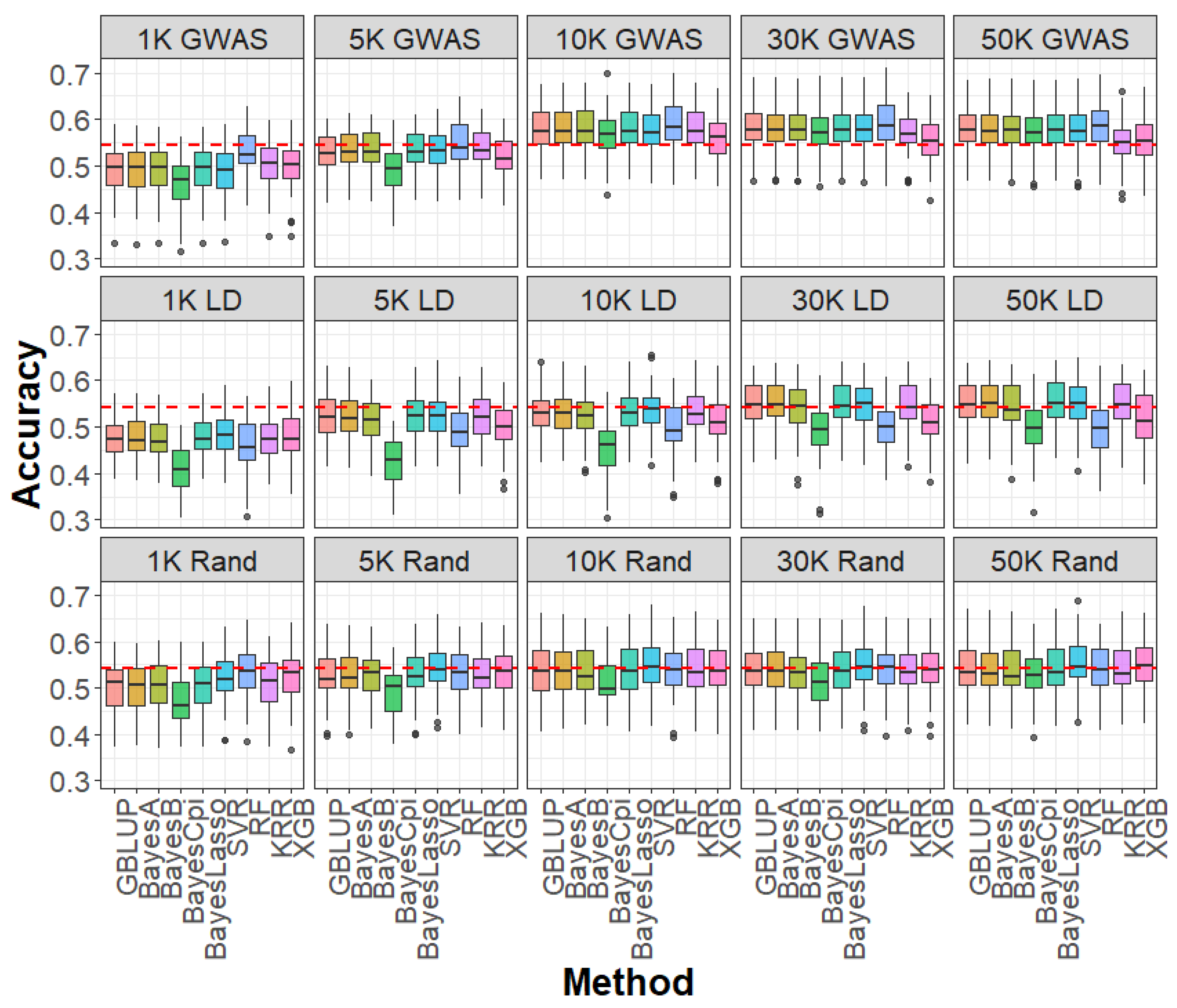
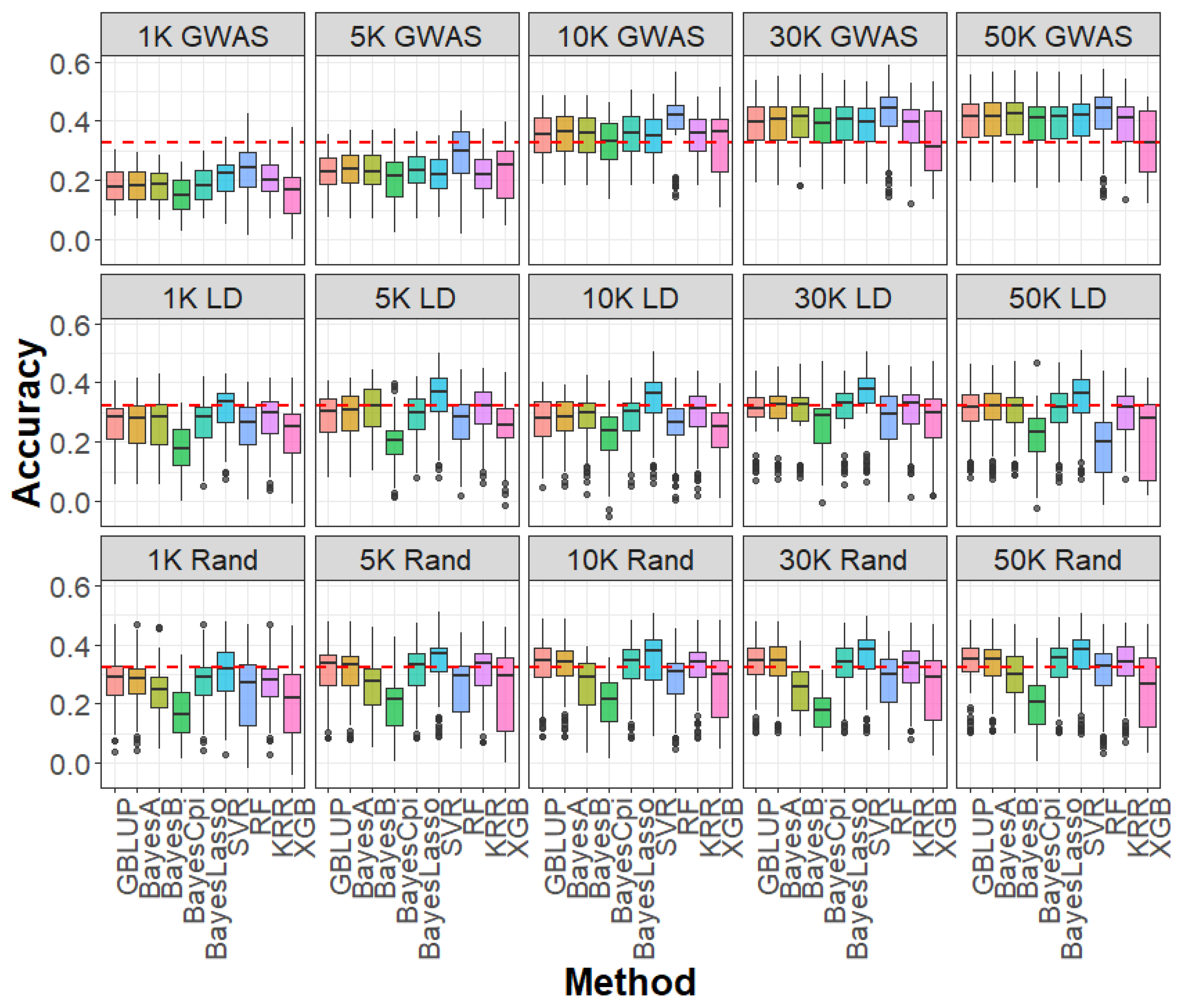
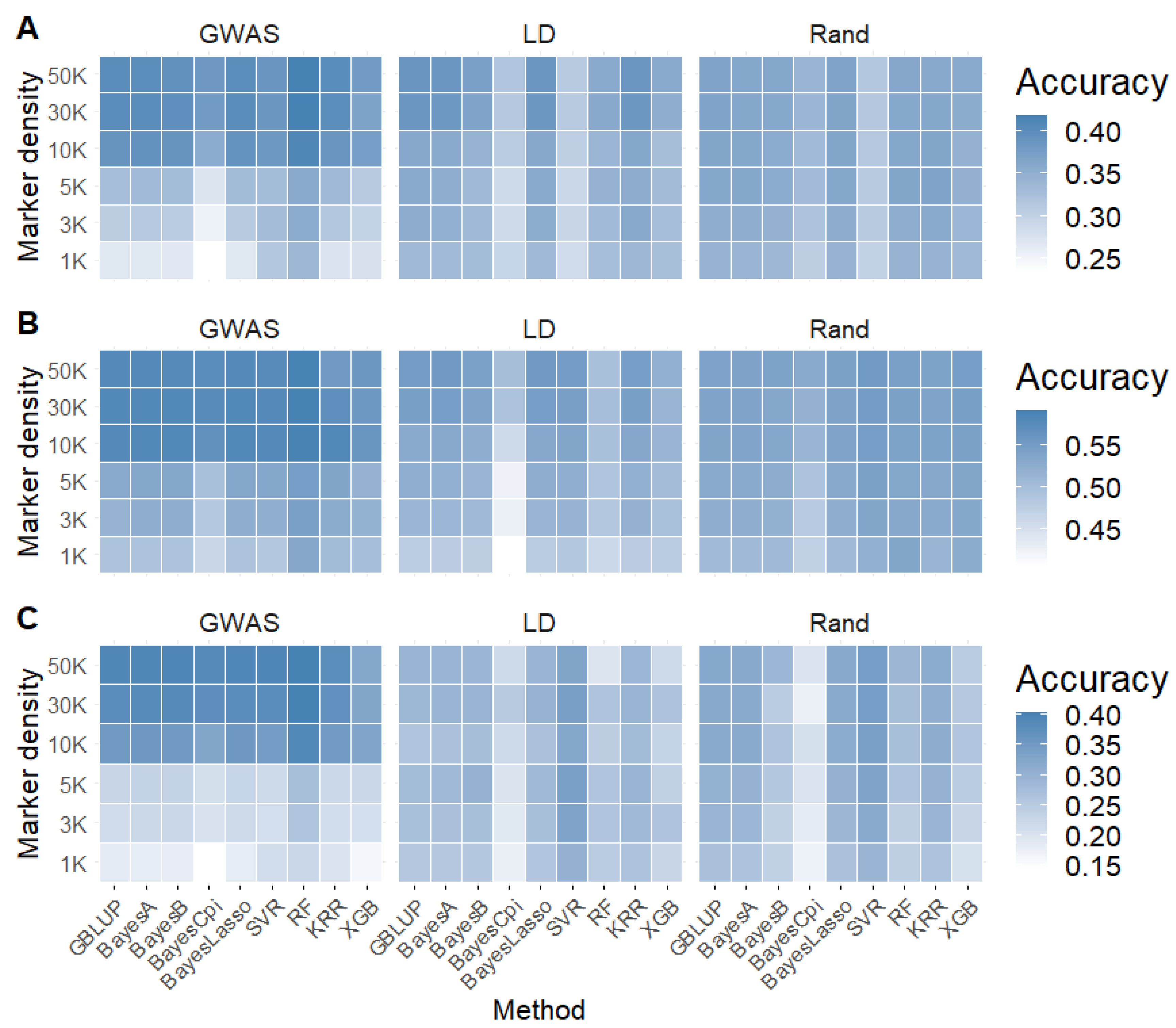
2.3. Impact of SNP Selection Strategies and SNP Density on Genomic Prediction
2.4. Impact of Linear and Machine Learning Models on Genomic Prediction
3. Discussion
4. Materials and Methods
4.1. Sample Collection and Trait Measurement in Russian Sturgeon
4.2. Whole-Genome Sequencing, SNP Detection and Quality Control
4.3. Population Structure and Linkage Disequilibrium Analysis
4.4. Genome-Wide Association Study (GWAS)
4.5. SNP Selection Strategies for Genomic Prediction
4.6. Genomic Prediction Models
4.6.1. Linear Models
GBLUP
Bayesian Models
4.6.2. Machine Learning Models
4.7. Evaluation of Genomic Prediction Accuracy
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| SNPs | Single nucleotide polymorphisms |
| WGS | Whole-genome sequencing |
| GWAS | Genome-wide association study |
| LD | Linkage disequilibrium |
| GS | Genomic selection |
| GEBV | Genomic estimated breeding values |
| QTLs | Quantitative trait loci |
| GBLUP | Genomic best linear unbiased prediction |
| SD | Standard deviation |
| SV | Coefficient of variation |
| PCA | Principal component analysis |
| PVE | Percent of phenotypic variation explained |
| SVR | Support vector regression |
| RF | Random forest |
| KRR | Kernel ridge regression |
| XGB | Extreme gradient boosting |
| MSE | Mean squared error |
| MAE | Mean absolute error |
| MAF | Minor allele frequency |
| QC | Quality control |
| MCMC | Monte Carlo Markov chains |
References
- Shen, Y.; Yang, N.; Liu, Z.; Chen, Q.; Li, Y. Phylogenetic perspective on the relationships and evolutionary history of the Acipenseriformes. Genomics 2020, 112, 3511–3517. [Google Scholar] [CrossRef]
- Stroe Dudu, A.; Georgescu, S.E. Exploring the Multifaceted Potential of Endangered Sturgeon: Caviar, Meat and By-Product Benefits. Animals 2024, 14, 2425. [Google Scholar] [CrossRef]
- Bestin, A.; Brunel, O.; Malledant, A.; Debeuf, B.; Benoit, P.; Mahla, R.; Chapuis, H.; Guemene, D.; Vandeputte, M.; Haffray, P. Genetic parameters of caviar yield, color, size and firmness using parentage assignment in an octoploid fish species, the Siberian sturgeon Acipenser baerii. Aquaculture 2021, 540, 736725. [Google Scholar] [CrossRef]
- FAO. The State of World Fisheries and Aquaculture 2024: Blue Transformation in Action; FAO: Rome, Italy, 2024. [Google Scholar]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Song, H.L.; Dong, T.; Yan, X.Y.; Wang, W.; Tian, Z.H.; Sun, A.; Dong, Y.; Zhu, H.; Hu, H.X. Genomic selection and its research progress in aquaculture breeding. Rev. Aquacult. 2023, 15, 274–291. [Google Scholar] [CrossRef]
- Yáñez, J.M.; Barría, A.; López, M.E.; Moen, T.; Garcia, B.F.; Yoshida, G.M.; Xu, P. Genome-wide association and genomic selection in aquaculture. Rev. Aquacult. 2023, 15, 645–675. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Montesinos-Lopez, O.A.; Montesinos-Lopez, A.; Perez-Rodriguez, P.; Barron-Lopez, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genom. 2021, 22, 19. [Google Scholar] [CrossRef]
- Meuwissen, T.; Goddard, M. Accurate prediction of genetic values for complex traits by whole-genome resequencing. Genetics 2010, 185, 623–631. [Google Scholar] [CrossRef]
- Hayes, B.J.; Macleod, I.M.; Daetwyler, H.D.; Phil, B.J.; Chamberlain, A.J.; Jagt, C.V.; Capitan, A.; Pausch, H.; Stothard, P.; Liao, X. Genomic prediction from whole genome sequence in livestock: The 1000 Bull Genomes Project. In Proceedings of the 10th World Congress on Genetics Applied to Livestock Production (WCGALP), Vancouver, BC, Canada, 17–22 August 2014. [Google Scholar]
- Perez-Enciso, M.; Forneris, N.; de Los Campos, G.; Legarra, A. Evaluating Sequence-Based Genomic Prediction with an Efficient New Simulator. Genetics 2017, 205, 939–953. [Google Scholar] [CrossRef]
- Lu, S.; Liu, Y.; Yu, X.J.; Li, Y.Z.; Yang, Y.M.; Wei, M.; Zhou, Q.; Wang, J.; Zhang, Y.P.; Zheng, W.W.; et al. Prediction of genomic breeding values based on pre-selected SNPs using ssGBLUP, WssGBLUP and BayesB for Edwardsiellosis resistance in Japanese flounder. Genet. Sel. Evol. 2020, 52, 49. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Kemp, R.A.; Stothard, P.; Wang, Z.Q.; Boddicker, N.; Krivushin, K.; Dekkers, J.; Plastow, G. Genomic evaluation of feed efficiency component traits in Duroc pigs using 80K, 650K and whole-genome sequence variants. Genet. Sel. Evol. 2018, 50, 14. [Google Scholar] [CrossRef]
- Song, H.L.; Ye, S.P.; Jiang, Y.F.; Zhang, Z.; Zhang, Q.; Ding, X.D. Using imputation-based whole-genome sequencing data to improve the accuracy of genomic prediction for combined populations in pigs. Genet. Sel. Evol. 2019, 51, 58. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, G.M.; Yáñez, J.M. Increased accuracy of genomic predictions for growth under chronic thermal stress in rainbow trout by prioritizing variants from GWAS using imputed sequence data. Evol. Appl. 2021, 15, 537–552. [Google Scholar] [CrossRef] [PubMed]
- Sukhavachana, S.; Senanan, W.; Tunkijjanukij, S.; Poompuang, S. Improving genomic prediction accuracy for harvest traits in Asian seabass (Lates calcarifer, Bloch 1790) via marker selection. Aquaculture 2022, 550, 737851. [Google Scholar] [CrossRef]
- Song, H.L.; Hu, H.X. Strategies to improve the accuracy and reduce costs of genomic prediction in aquaculture species. Evol. Appl. 2021, 15, 578–590. [Google Scholar] [CrossRef]
- Vu, N.T.; Phuc, T.H.; Oanh, K.T.P.; Sang, N.V.; Trang, T.T.; Nguyen, N.H. Accuracies of genomic predictions for disease resistance of striped catfish to Edwardsiella ictaluri using artificial intelligence algorithms. G3 2022, 12, jkab361. [Google Scholar] [CrossRef]
- Song, H.; Dong, T.; Wang, W.; Jiang, B.; Yan, X.; Geng, C.; Bai, S.; Xu, S.; Hu, H. Cost-effective genomic prediction of critical economic traits in sturgeons through low-coverage sequencing. Genomics 2024, 116, 110874. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
- Yi, N.; Xu, S. Bayesian LASSO for quantitative trait loci mapping. Genetics 2008, 179, 1045–1055. [Google Scholar] [CrossRef]
- Ajasa, A.A.; Boison, S.A.; Gjøen, H.M.; Lillehammer, M. Genome-assisted prediction of amoebic gill disease resistance in different populations of Atlantic salmon during field outbreak. Aquaculture 2024, 578, 740078. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, J.; Ke, Q.Z.; Li, B.J.; Zhou, Z.X.; Wang, J.Y.; Zhou, T.; Zheng, W.Q.; Xu, P. First genomic prediction and genome-wide association for complex growth-related traits in Rock Bream (Oplegnathus fasciatus). Evol. Appl. 2021, 15, 523–536. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Yu, Y.; Bao, Z.N.; Li, F.H. Evaluation of machine learning method in genomic selection for growth traits of Pacific white shrimp. Aquaculture 2024, 581, 740376. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Vu, N.T. Threshold models using Gibbs sampling and machine learning genomic predictions for skin fluke disease recorded under field environment in yellowtail kingfish Seriola lalandi. Aquaculture 2022, 547, 737513. [Google Scholar] [CrossRef]
- Song, H.; Dong, T.; Yan, X.; Wang, W.; Tian, Z.; Hu, H. Using Bayesian threshold model and machine learning method to improve the accuracy of genomic prediction for ordered categorical traits in fish. Agric. Commun. 2023, 1, 100005. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Long, N.; Gianola, D.; Rosa, G.J.M.; Weigel, K.A. Application of support vector regression to genome-assisted prediction of quantitative traits. Theor. Appl. Genet. 2011, 123, 1065–1074. [Google Scholar] [CrossRef]
- Du, K.; Stock, M.; Kneitz, S.; Klopp, C.; Woltering, J.M.; Adolfi, M.C.; Feron, R.; Prokopov, D.; Makunin, A.; Kichigin, I.; et al. The sterlet sturgeon genome sequence and the mechanisms of segmental rediploidization. Nat. Ecol. Evol. 2020, 4, 841–852. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R.; Proc, G.P.D. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef]
- McKenna, A.; Hanna, M.; Banks, E.; Sivachenko, A.; Cibulskis, K.; Kernytsky, A.; Garimella, K.; Altshuler, D.; Gabriel, S.; Daly, M.; et al. The Genome Analysis Toolkit: A MapReduce framework for analyzing next-generation DNA sequencing data. Genome. Res. 2010, 20, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Browning, B.L.; Zhou, Y.; Browning, S.R. A One-Penny Imputed Genome from Next-Generation Reference Panels. Am. J. Hum. Genet. 2018, 103, 338–348. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.A.M.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience 2015, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Klein, R.J.; Zeiss, C.; Chew, E.Y.; Tsai, J.Y.; Sackler, R.S.; Haynes, C.; Henning, A.K.; SanGiovanni, J.P.; Mane, S.M.; Mayne, S.T.; et al. Complement factor H polymorphism in age-related macular degeneration. Science 2005, 308, 385–389. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Shim, H.; Chasman, D.I.; Smith, J.D.; Mora, S.; Ridker, P.M.; Nickerson, D.A.; Krauss, R.M.; Stephens, M. A multivariate genome-wide association analysis of 10 LDL subfractions, and their response to statin treatment, in 1868 Caucasians. PLoS ONE 2015, 10, e0120758. [Google Scholar] [CrossRef]
- Madsen, P.; Milkevych, V.; Gao, H.; Christensen, O.F.; Jensen, J. DMU—A Package for Analyzing Multivariate Mixed Models in Quantitative Genetics and Genomics. In Proceedings of the World Congress on Genetics Applied to Livestock Production (WCGALP), Auckland, New Zealand, 11–16 February 2018; Electronic Poster Session-Methods and Tools-Software. p. 525. [Google Scholar]
- Pérez, P.; de Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Douak, F.; Melgani, F.; Benoudjit, N. Kernel ridge regression with active learning for wind speed prediction. Appl. Energy 2013, 103, 328–340. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| Trait | N | Mean | SD | CV (%) | Max | Min |
|---|---|---|---|---|---|---|
| Caviar yield | 971 | 0.193 | 0.057 | 29.414 | 0.439 | 0.021 |
| Caviar color | 971 | 2.398 | 0.642 | 26.789 | 4.000 | 1.000 |
| Body weight | 971 | 19.806 | 5.096 | 25.732 | 116.800 | 9.700 |
| SNP Density | Caviar Yield | Caviar Color | Body Weight | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GWAS | LD | Random | GWAS | LD | Random | GWAS | LD | Random | |
| 1 K | 0.219 | 0.012 | 0.012 | 0.171 | 0.015 | 0.012 | 0.279 | 0.018 | 0.012 |
| 3 K | 0.722 | 0.028 | 0.039 | 0.449 | 0.038 | 0.037 | 0.697 | 0.045 | 0.037 |
| 5 K | 1.070 | 0.096 | 0.063 | 0.697 | 0.063 | 0.060 | 1.055 | 0.074 | 0.062 |
| 10 K | 1.369 | 0.166 | 0.087 | 1.257 | 0.131 | 0.121 | 1.838 | 0.151 | 0.123 |
| 30 K | 3.092 | 0.548 | 0.382 | 3.145 | 0.383 | 0.366 | 4.318 | 0.419 | 0.362 |
| 50 K | 5.249 | 0.961 | 0.543 | 4.757 | 0.645 | 0.606 | 6.314 | 0.676 | 0.607 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Wang, W.; Dong, T.; Yan, X.; Geng, C.; Bai, S.; Hu, H. Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models. Int. J. Mol. Sci. 2025, 26, 7007. https://doi.org/10.3390/ijms26147007
Song H, Wang W, Dong T, Yan X, Geng C, Bai S, Hu H. Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models. International Journal of Molecular Sciences. 2025; 26(14):7007. https://doi.org/10.3390/ijms26147007
Chicago/Turabian StyleSong, Hailiang, Wei Wang, Tian Dong, Xiaoyu Yan, Chenfan Geng, Song Bai, and Hongxia Hu. 2025. "Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models" International Journal of Molecular Sciences 26, no. 14: 7007. https://doi.org/10.3390/ijms26147007
APA StyleSong, H., Wang, W., Dong, T., Yan, X., Geng, C., Bai, S., & Hu, H. (2025). Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models. International Journal of Molecular Sciences, 26(14), 7007. https://doi.org/10.3390/ijms26147007




