Microscopic Mechanism Study on Gas–Crude-Oil Interactions During the CO2 Flooding Process in Water-Bearing Reservoirs
Abstract
1. Introduction
2. Results and Discussion
2.1. Micro-Mechanism of Gas and Crude-Oil Dissolution
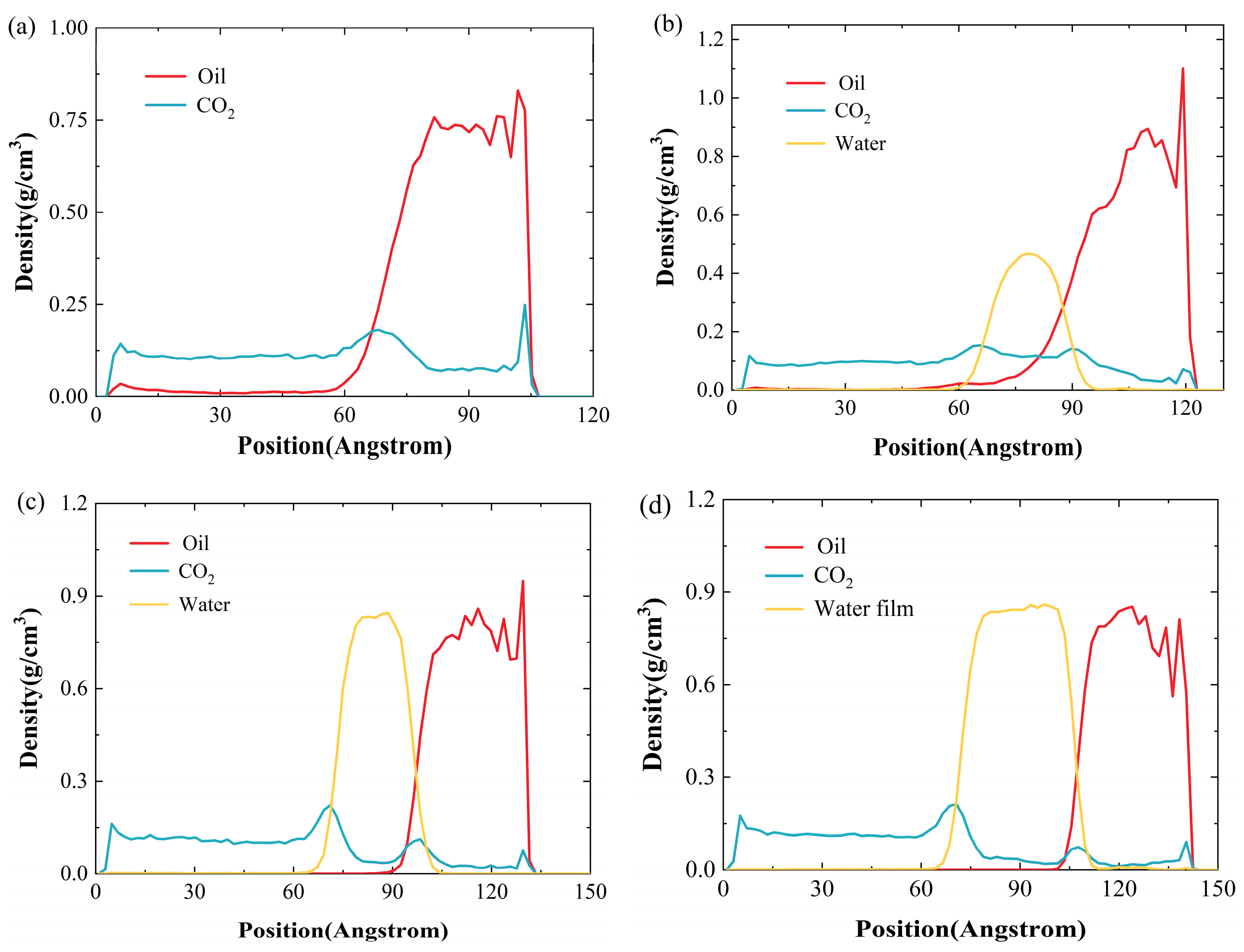
2.1.1. Effect of Water-Film Thickness on Density Distribution
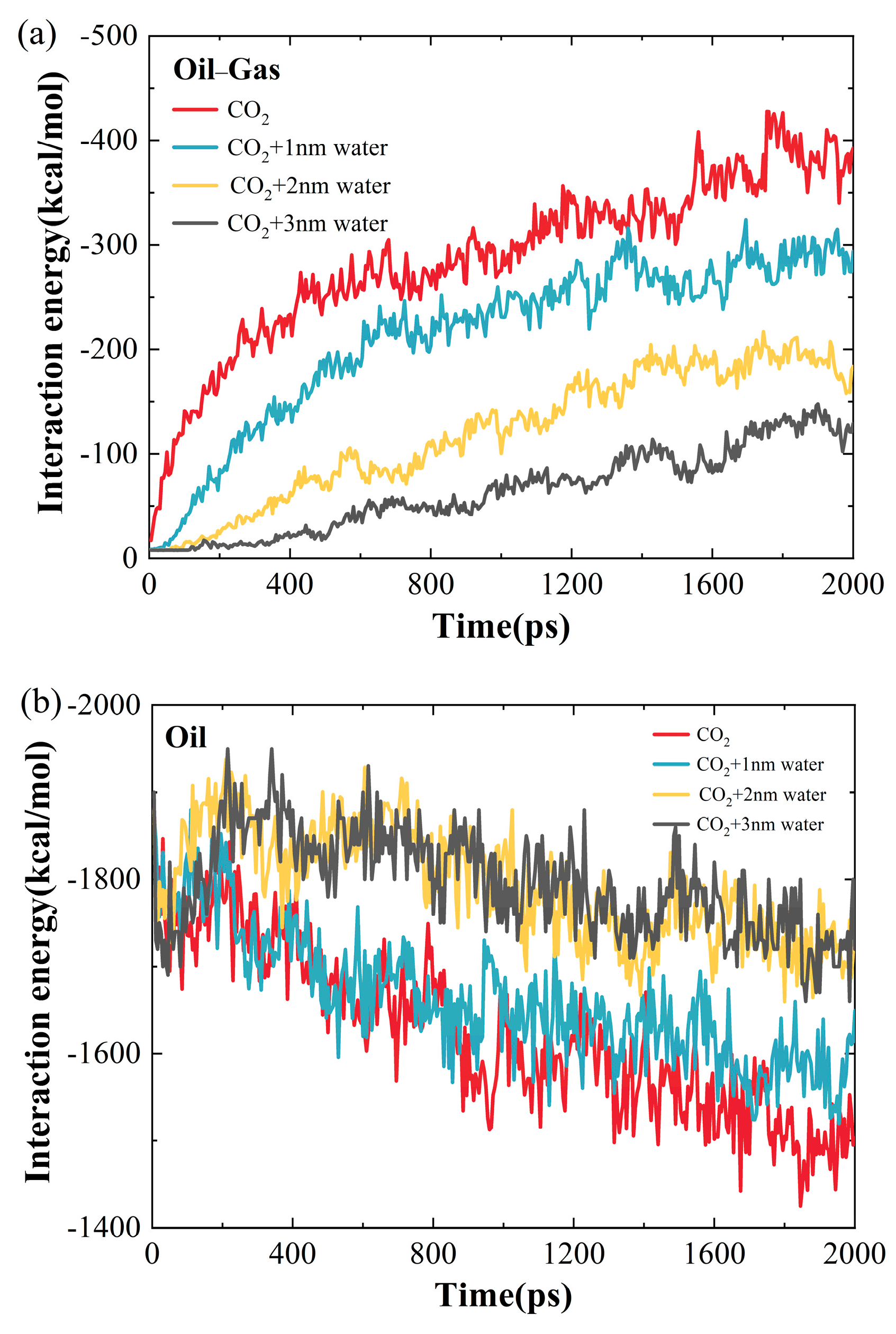
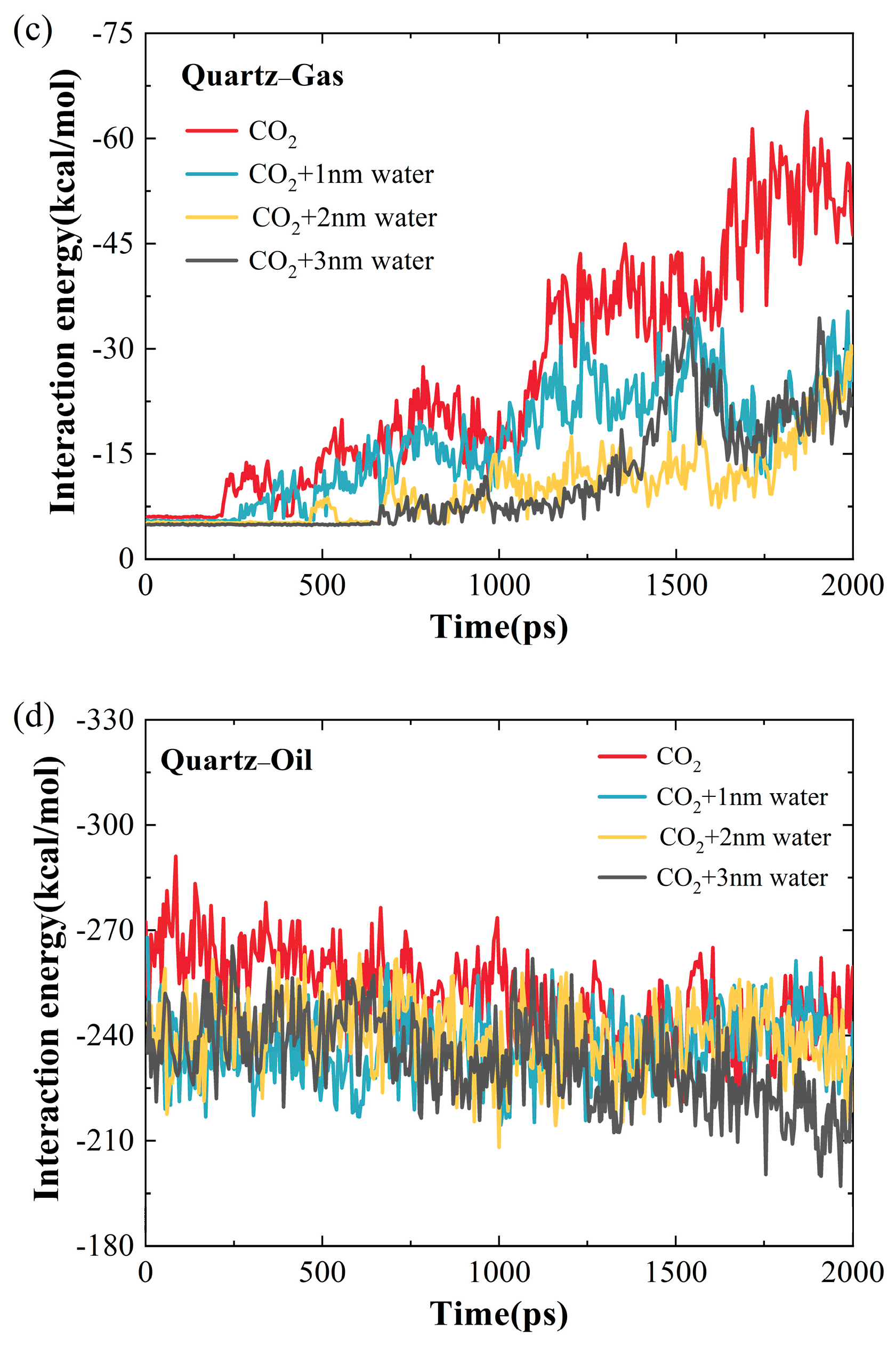
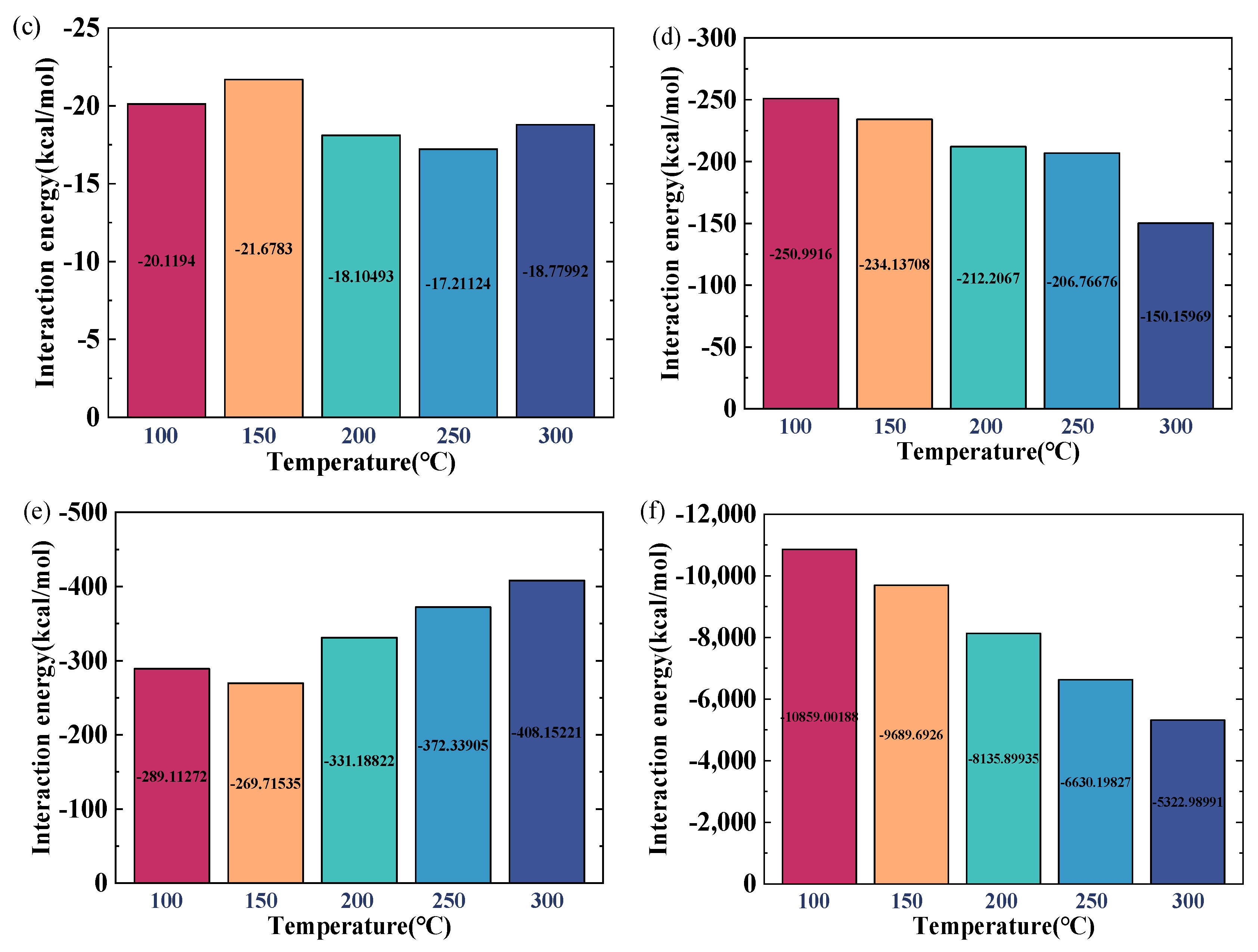
2.1.2. Influence of Water-Film Thickness on the Microscopic Interaction Mechanism of CO2 and Crude Oil
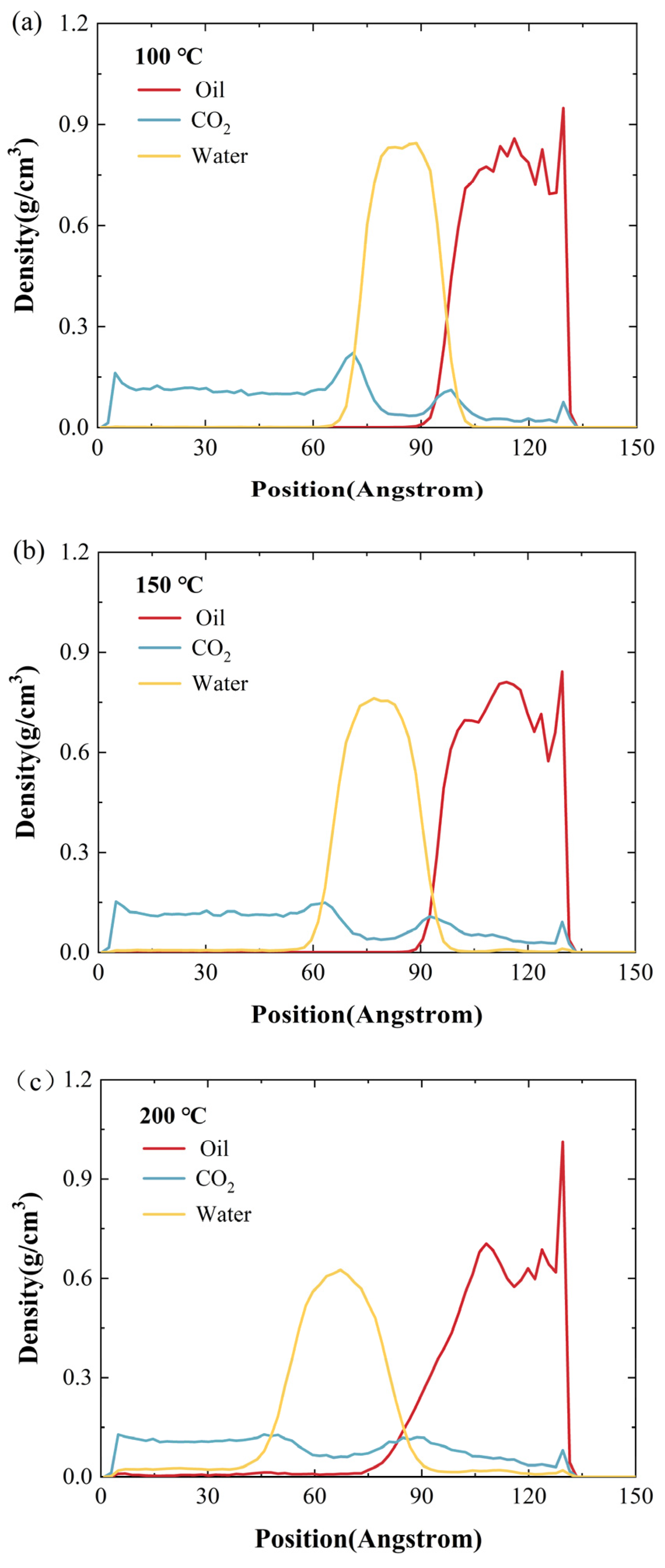
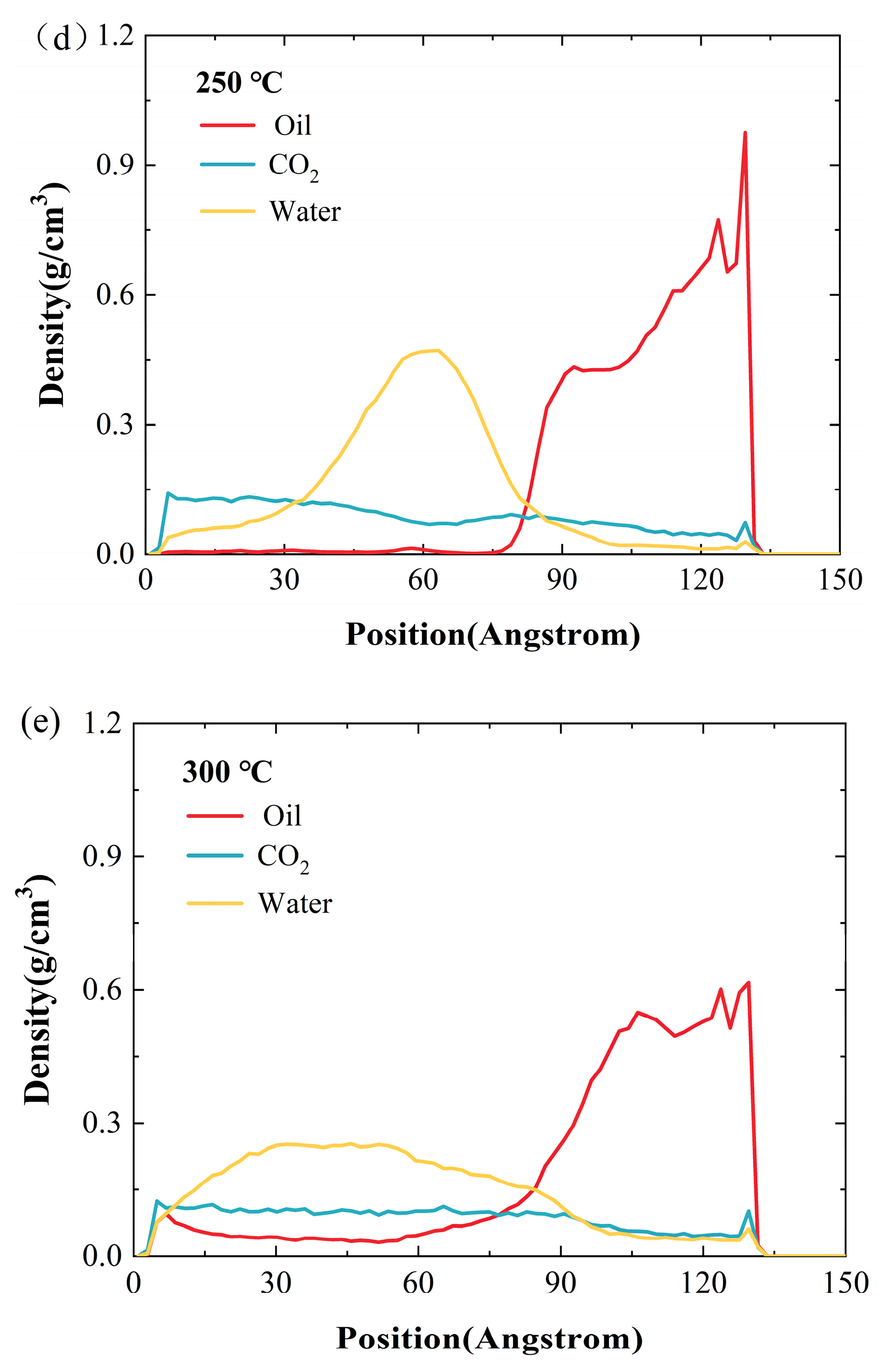
2.2. Effect of Temperature
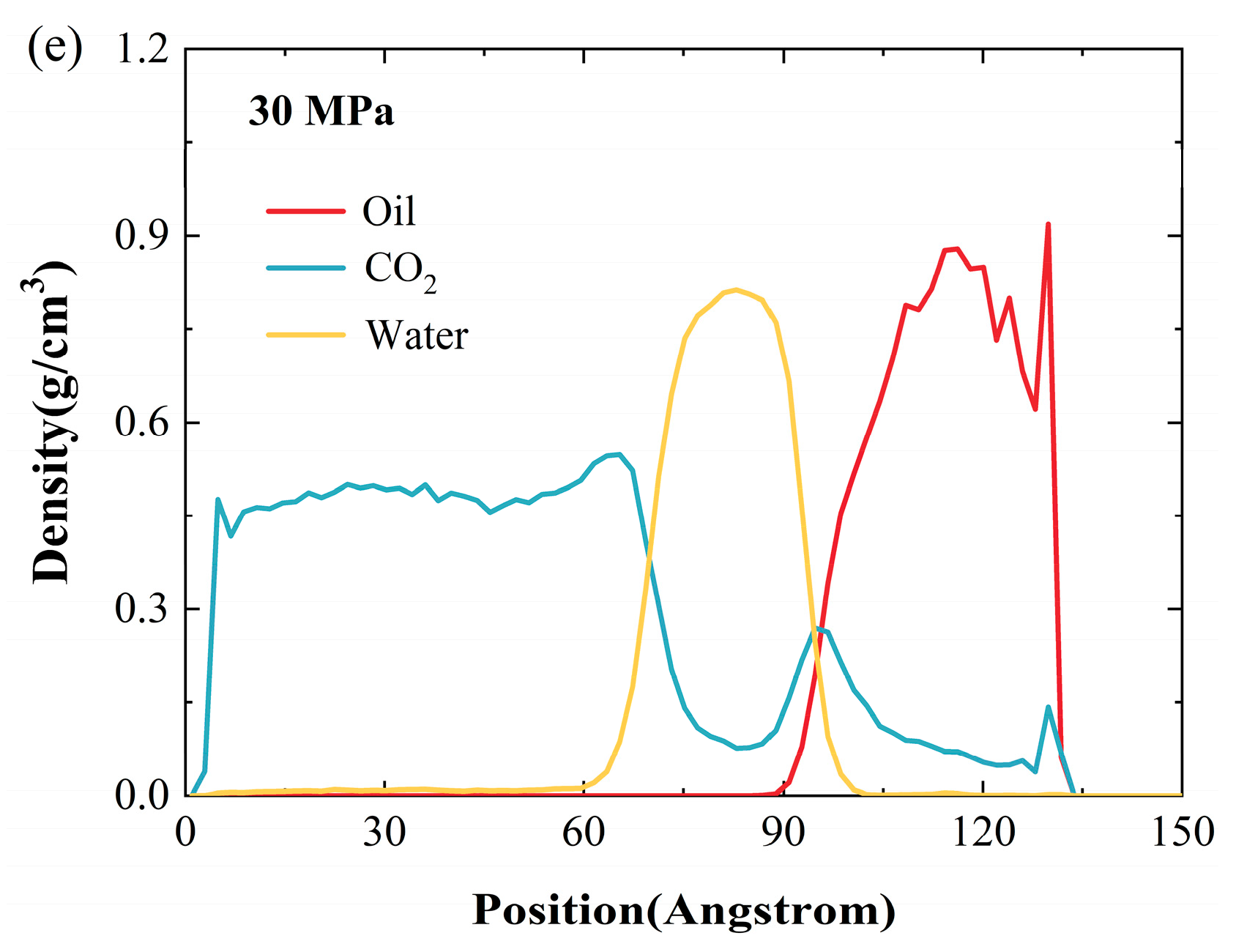
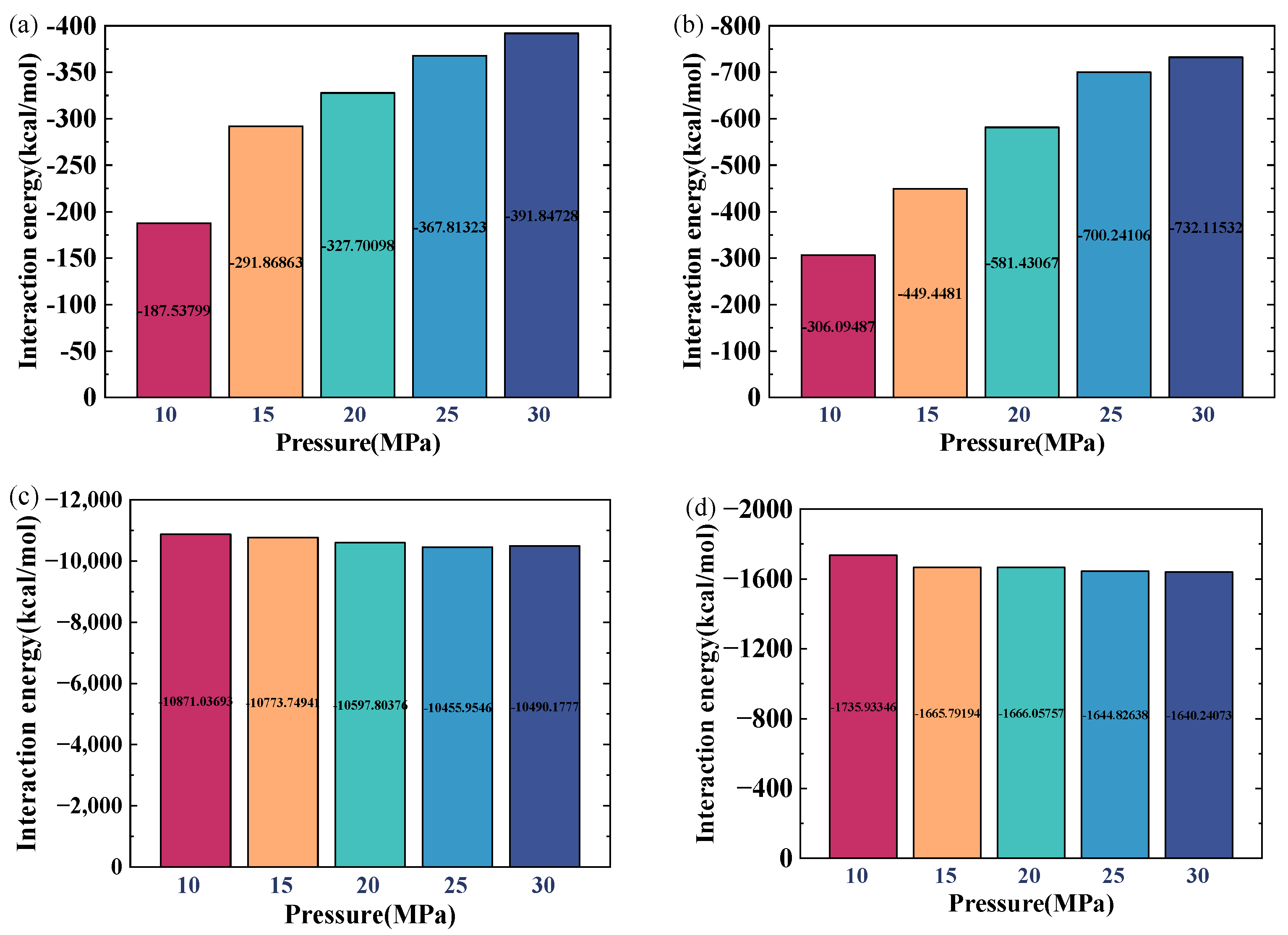
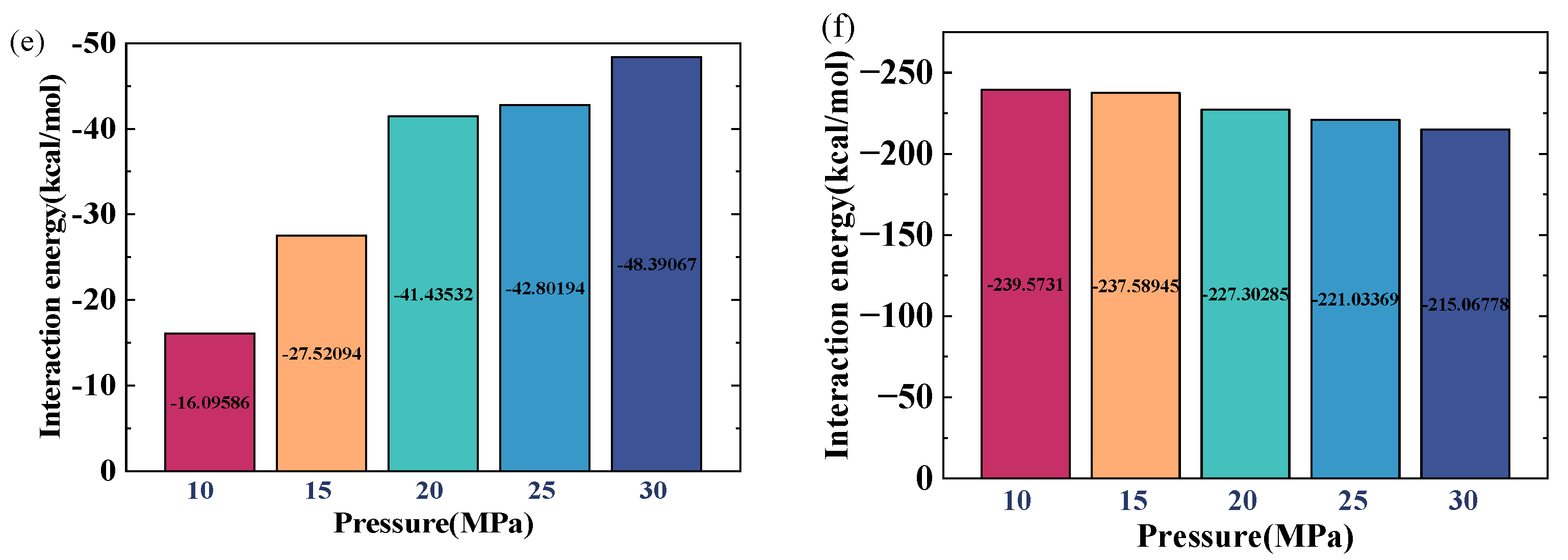
2.3. Effect of Pressure
2.4. Practical Implications for CO2-EOR
3. Methodology and Analysis
3.1. Molecular Model Construction and Validation
3.2. Construction of the Water–Crude-Oil–Rock-Wall Model
3.3. Simulation Details
4. Conclusions
- (1)
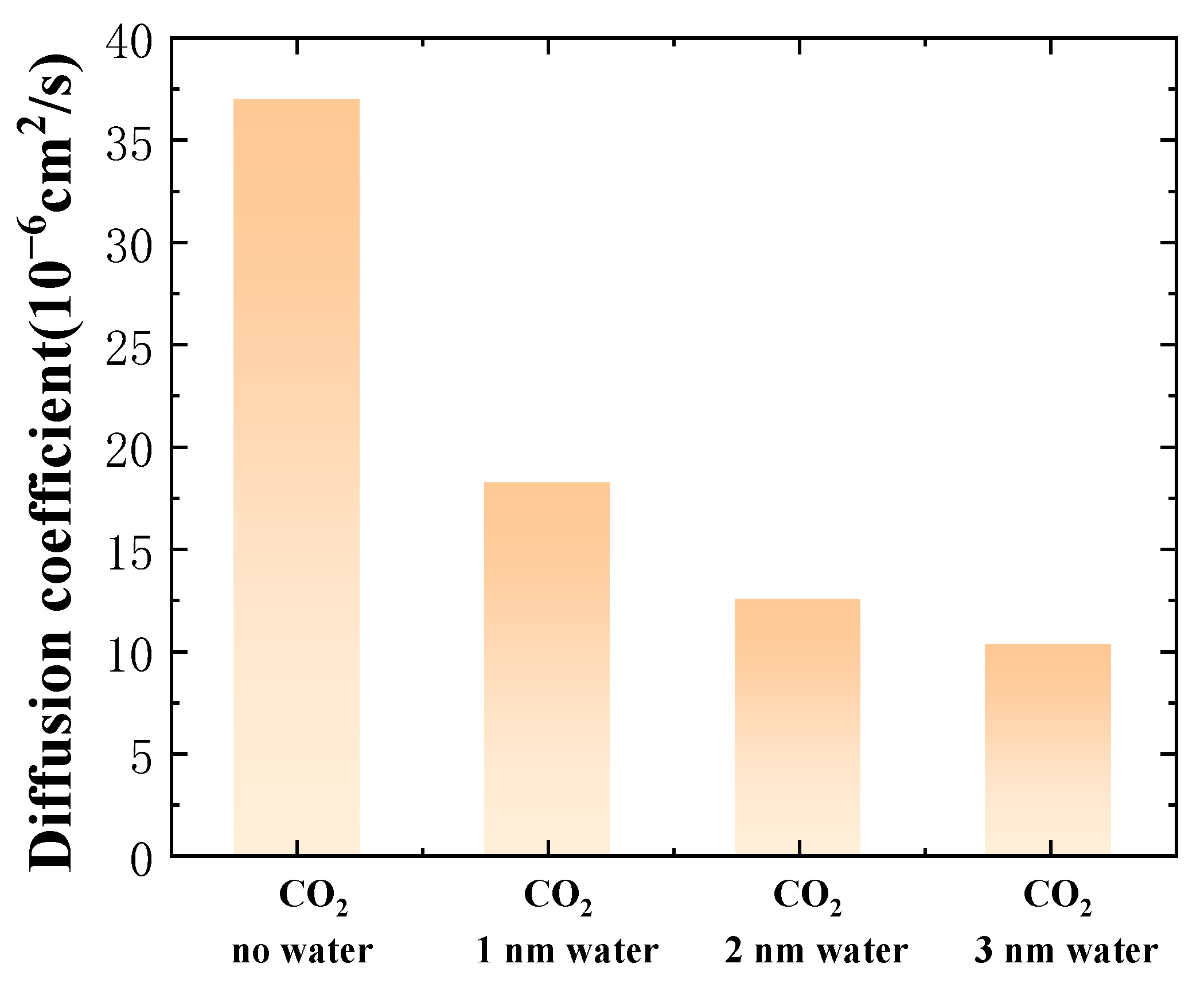
- The water film can impede the migration of CO2 molecules into the oil, resulting in a reduced ability of CO2 to lower the oil density, and this impact becomes more significant as the thickness of the water film increases. As the thickness of the water film increases from 0 nm to 3 nm, the density of oil increases by 86.9%. The water film also hinders the diffusion ability of oil molecules. When the water-film thickness reaches 3 nm, the diffusion coefficient of oil drops by 72.30% relative to a system lacking a water layer.
- (2)
- A rise in temperature significantly improves the ability of CO2 and water to diffuse into oil, thereby reducing the oil’s density. With the pressure of 10 MPa and a 2 nm water film, as the temperature rises from 100 °C to 300 °C, the density of crude oil declines by 32.1%.
- (3)
- Increasing the reservoir pressure results in a decline in the density of crude oil as well as the water film in the water-bearing reservoir. However, the effect of pressure is relatively small compared to the temperature change. At a temperature of 100 °C and a water-film thickness of 2 nm, the oil density decreases by only 4.39% when the pressure increases from 10 MPa to 30 MPa.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brockway, P.E.; Owen, A.; Brand-Correa, L.I.; Hardt, L. Estimation of global final-stage energy-return-on-investment for fossil fuels with comparison to renewable energy sources. Nat. Energy 2019, 4, 612–621. [Google Scholar] [CrossRef]
- Ma, J.; Yao, M.; Yang, Y.; Zhang, X. Comprehensive review on stability and demulsification of unconventional heavy oil-water emulsions. J. Mol. Liq. 2022, 350, 118510. [Google Scholar] [CrossRef]
- Ahmadi, M.; Hou, Q.; Wang, Y.; Chen, Z. Interfacial and molecular interactions between fractions of heavy oil and surfactants in porous media: Comprehensive review. Adv. Colloid Interface Sci. 2020, 283, 102242. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Z.; Luo, H. Simulation research on microscopic remaining oil distribution in high water cut. IOP Conf. Ser. Earth Environ. Sci. 2021, 647, 012074. [Google Scholar] [CrossRef]
- Bai, Y.; Hou, J.; Liu, Y.; Zhao, D.; Bing, S.; Xiao, W.; Zhao, W. Energy-consumption calculation and optimization method of integrated system of injection-reservoir-production in high water-cut reservoir. Energy 2022, 239, 121961. [Google Scholar] [CrossRef]
- Li, C.; Pu, H.; Zhong, X.; Li, Y.; Zhao, J.X. Interfacial interactions between Bakken crude oil and injected gases at reservoir temperature: A molecular dynamics simulation study. Fuel 2020, 276, 118058. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, Q.; Li, Z.; Qi, Y.; Liu, Y. Molecular dynamics study on the diffusion mass transfer behaviour of CO2 and crude oil under simulated reservoir conditions. Molecules 2023, 28, 7948. [Google Scholar] [CrossRef]
- Omrani, S.; Ghasemi, M.; Singh, M.; Mahmoodpour, S.; Zhou, T.; Babaei, M.; Niasar, V. Interfacial Tension–Temperature–Pressure–Salinity Relationship for the Hydrogen–Brine System at Reservoir Conditions; Integration of Molecular Dynamics and Machine Learning. Langmuir 2023, 39, 12680–12691. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.; Shen, Y.; Yao, B.; Wu, Y.S. Simulation study of water cut surge after CO2 injection in tight oil reservoirs. J. Pet. Sci. Eng. 2020, 193, 107349. [Google Scholar] [CrossRef]
- Wei, J.; Li, J.; Shi, X.; Zhou, R. Combination of alkali–surfactant–polymer flooding and horizontal wells to maximize the oil recovery for high water cut oil reservoir. Energy Rep. 2021, 7, 5955–5964. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, Q.; Wang, S.; Xing, X. Oil diffusion in shale nanopores: Insight of molecular dynamics simulation. J. Mol. Liq. 2019, 290, 111183. [Google Scholar] [CrossRef]
- Yang, S.; Dehghanpour, H.; Binazadeh, M.; Dong, P. A molecular dynamics explanation for fast imbibition of oil in organic tight rocks. Fuel 2017, 190, 409–419. [Google Scholar] [CrossRef]
- Lu, P.; Yan, Z.; Lai, J.; Wang, K. Molecular insight into oil displacement by CO2 flooding in water-cut dead-end nanopores. RSC Adv. 2024, 14, 25385–25392. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, L.; Xiao, P.; Liang, Y.; Hua, X.; Tian, W.; Fang, W.; Liu, B. Molecular Insight into CO2 Improving Oil Mobility in Shale Inorganic Nanopores Containing Water Films. Langmuir 2024, 40, 17568–17576. [Google Scholar] [CrossRef]
- Liu, B.; Shi, J.; Wang, M.; Zhang, J.; Sun, B.; Shen, Y.; Sun, X. Reduction in interfacial tension of water–oil interface by supercritical CO2 in enhanced oil recovery processes studied with molecular dynamics simulation. J. Supercrit. Fluids 2016, 111, 171–178. [Google Scholar] [CrossRef]
- Luan, Y.; Liu, B.; Hao, P.; Zhan, K.; Liu, J. Oil displacement by supercritical CO2 in a water cut dead-end pore: Molecular dynamics simulation. J. Pet. Sci. Eng. 2020, 188, 106899. [Google Scholar] [CrossRef]
- Gereben, O.; Petkov, V. Reverse Monte Carlo study of spherical sample under non-periodic boundary conditions: The structure of Ru nanoparticles based on x-ray diffraction data. J. Phys. Condens. Matter 2013, 25, 454211. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Geng, C.; Zhao, Y.; He, X.; Wen, H. Molecular dynamics simulation for surface melting and self-preservation effect of methane hydrate. Sci. China Chem. 2008, 51, 651–660. [Google Scholar] [CrossRef]
- Gong, K.; Fang, T.; Wan, T.; Yan, Y.; Li, W.; Zhang, J. Voltage-gated multilayer graphene nanochannel for K+/Na+ separation: A molecular dynamics study. J. Mol. Liq. 2020, 317, 114025. [Google Scholar] [CrossRef]
- Park, J.W.; Lee, K.B. Molecular dynamics simulations of asphaltene aggregation in heavy oil system for the application to sol-vent deasphalting. Fuel 2022, 323, 124171. [Google Scholar] [CrossRef]
- Rawat, A.; Bhavsar, T.; Khanikar, B.; Samanta, A.; Nguessan, P.; Saha, S.; Bist, N.; Sircar, A. Simulation-driven sensitivity analysis and optimization of critical parameters for maximizing CO2-EOR efficiency. Pet. Res. 2025. [Google Scholar] [CrossRef]
- Davoodi, S.; Thanh, H.V.; Wood, D.A.; Mehrad, M.; Al-Shargabid, M.; Rukavishnikov, V.S. Committee machine learning: A breakthrough in the precise prediction of CO2 storage mass and oil production volumes in unconventional reservoirs. Geoenergy Sci. Eng. 2025, 245, 213533. [Google Scholar] [CrossRef]
- Fang, T.; Wang, M.; Li, J.; Liu, B.; Shen, Y.; Yan, Y.; Zhang, J. Study on the Asphaltene Precipitation in CO2 Flooding: A Perspective from Molecular Dynamics Simulation. Ind. Eng. Chem. Res. 2018, 57, 1071–1077. [Google Scholar] [CrossRef]
- Feng, S.; Liao, Y.; Liu, W.; Dai, J.; Xie, M.; Li, L. Numerical simulation of asphaltene deposition during CO2 and natural gas injection: Impacts on permeability and recovery. Fluid Dyn. Mater. Process. 2024, 20, 275–292. [Google Scholar]
- Li, B.; Liu, G.; Xing, X.; Chen, L.; Lu, X.; Teng, H.; Wang, J. Molecular dynamics simulation of CO2 dissolution in heavy oil res-in-asphaltene. J. CO2 Util. 2019, 33, 303–310. [Google Scholar] [CrossRef]
- Will, G.; Bellotto, M.; Parrish, W.; Hart, M. Crystal Structure of Quartz and Magnesium Germinate by Profile Analysis of Syn-chrotron-Radiation High-Resolution Powder Data. J. Appl. Crystallogr. 1988, 21, 182–191. [Google Scholar] [CrossRef]
- Su, G.; Zhang, H.; Geng, T.; Yuan, S. Effect of SDS on Reducing the Viscosity of Heavy Oil: A Molecular Dynamics Study. Energy Fuels 2019, 33, 4921–4930. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4, Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Gong, L.; Shi, J.-H.; Ding, B.; Huang, Z.-Q.; Sun, S.-Y.; Yao, J. Molecular insight on competitive adsorption and diffusion char-acteristics of shale gas in water-bearing channels. Fuel 2020, 278, 118406. [Google Scholar] [CrossRef]
- Shi, J.; Gong, L.; Sun, S.; Huang, Z.; Ding, B.; Yao, J. Competitive adsorption phenomenon in shale gas displacement processes. RSC Adv. 2019, 9, 25326–25335. [Google Scholar] [CrossRef] [PubMed]




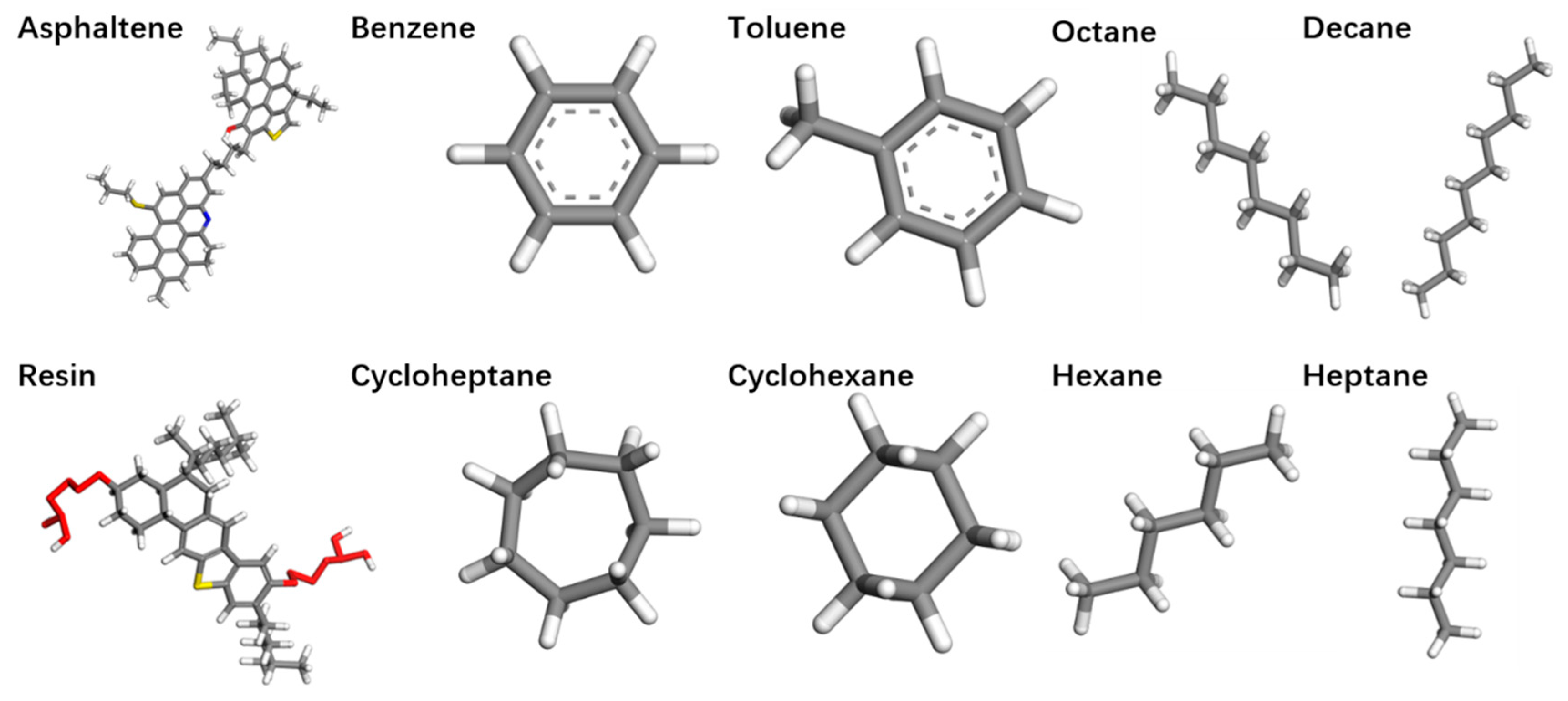



| Substance | Number | Mass Fraction (%) |
|---|---|---|
| Average Asphaltenes | 5 | 13.3 |
| Average Resins | 11 | 24.8 |
| Hexane | 26 | 6.9 |
| Heptane | 24 | 7.4 |
| Octane | 28 | 9.9 |
| Decane | 32 | 14.1 |
| Cyclohexane | 17 | 4.4 |
| Cycloheptane | 28 | 8.5 |
| Benzene | 11 | 2.7 |
| Toluene | 28 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, W.; Wang, Y.-B.; Wu, J.-T.; Zhang, T.; Gong, L.; Zhu, C.-Y. Microscopic Mechanism Study on Gas–Crude-Oil Interactions During the CO2 Flooding Process in Water-Bearing Reservoirs. Int. J. Mol. Sci. 2025, 26, 6402. https://doi.org/10.3390/ijms26136402
Xia W, Wang Y-B, Wu J-T, Zhang T, Gong L, Zhu C-Y. Microscopic Mechanism Study on Gas–Crude-Oil Interactions During the CO2 Flooding Process in Water-Bearing Reservoirs. International Journal of Molecular Sciences. 2025; 26(13):6402. https://doi.org/10.3390/ijms26136402
Chicago/Turabian StyleXia, Wei, Yu-Bo Wang, Jiang-Tao Wu, Tao Zhang, Liang Gong, and Chuan-Yong Zhu. 2025. "Microscopic Mechanism Study on Gas–Crude-Oil Interactions During the CO2 Flooding Process in Water-Bearing Reservoirs" International Journal of Molecular Sciences 26, no. 13: 6402. https://doi.org/10.3390/ijms26136402
APA StyleXia, W., Wang, Y.-B., Wu, J.-T., Zhang, T., Gong, L., & Zhu, C.-Y. (2025). Microscopic Mechanism Study on Gas–Crude-Oil Interactions During the CO2 Flooding Process in Water-Bearing Reservoirs. International Journal of Molecular Sciences, 26(13), 6402. https://doi.org/10.3390/ijms26136402







