A Simple Vortex-Based Method for the Generation of High-Throughput Spherical Micro- and Nanohydrogels
Abstract
1. Introduction
2. Results and Discussion
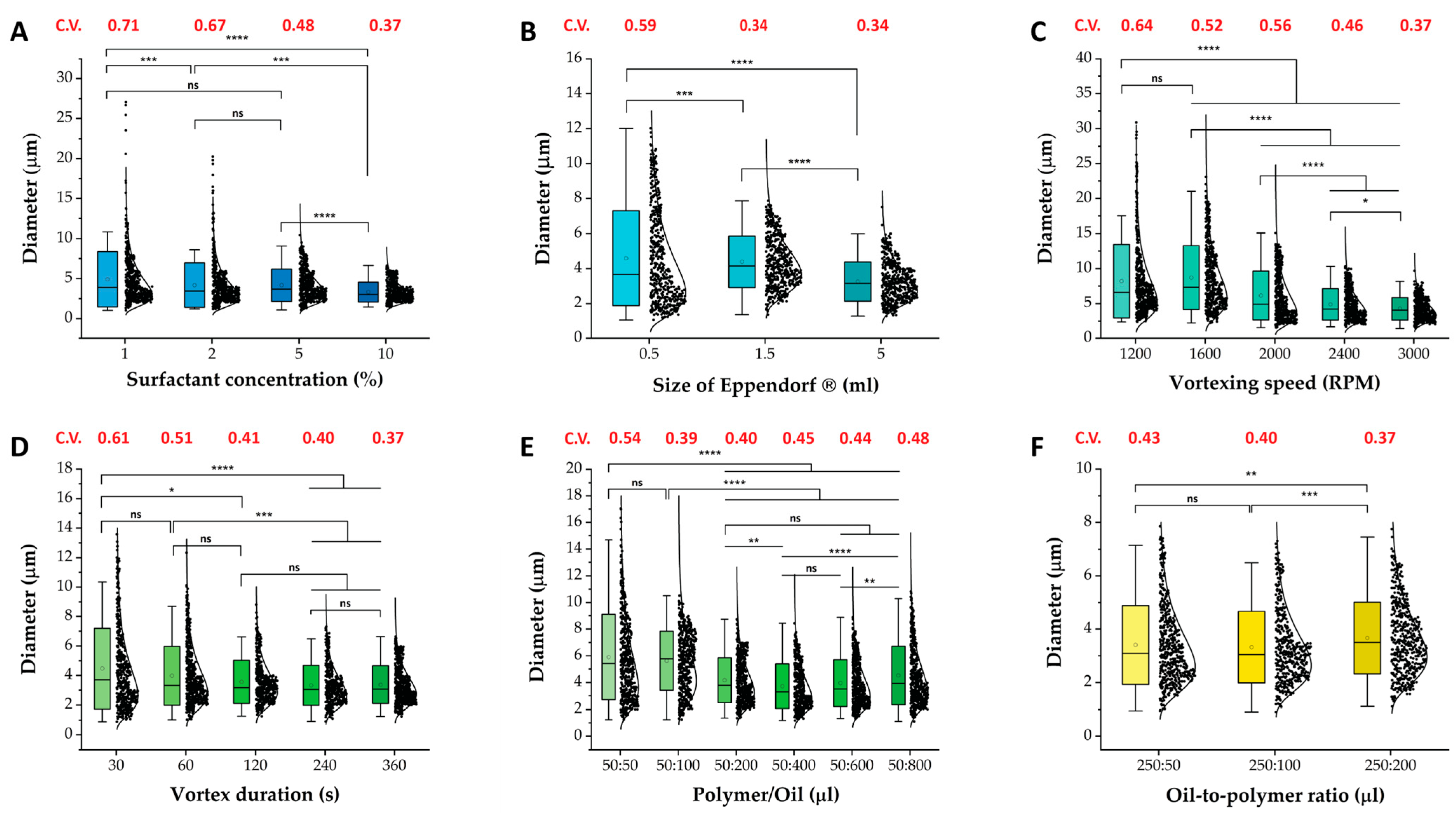
2.1. Variable Effects on Microgels
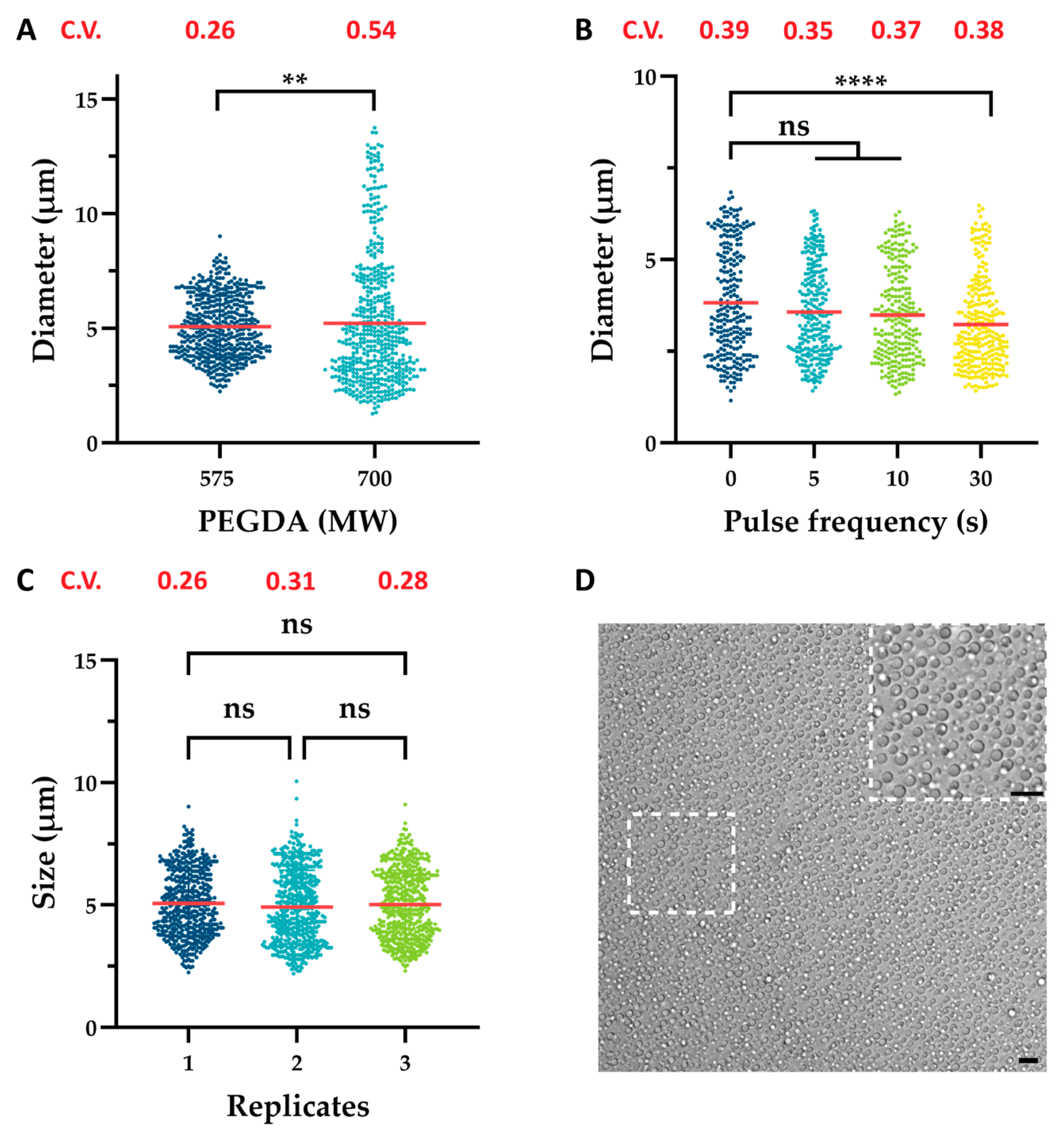
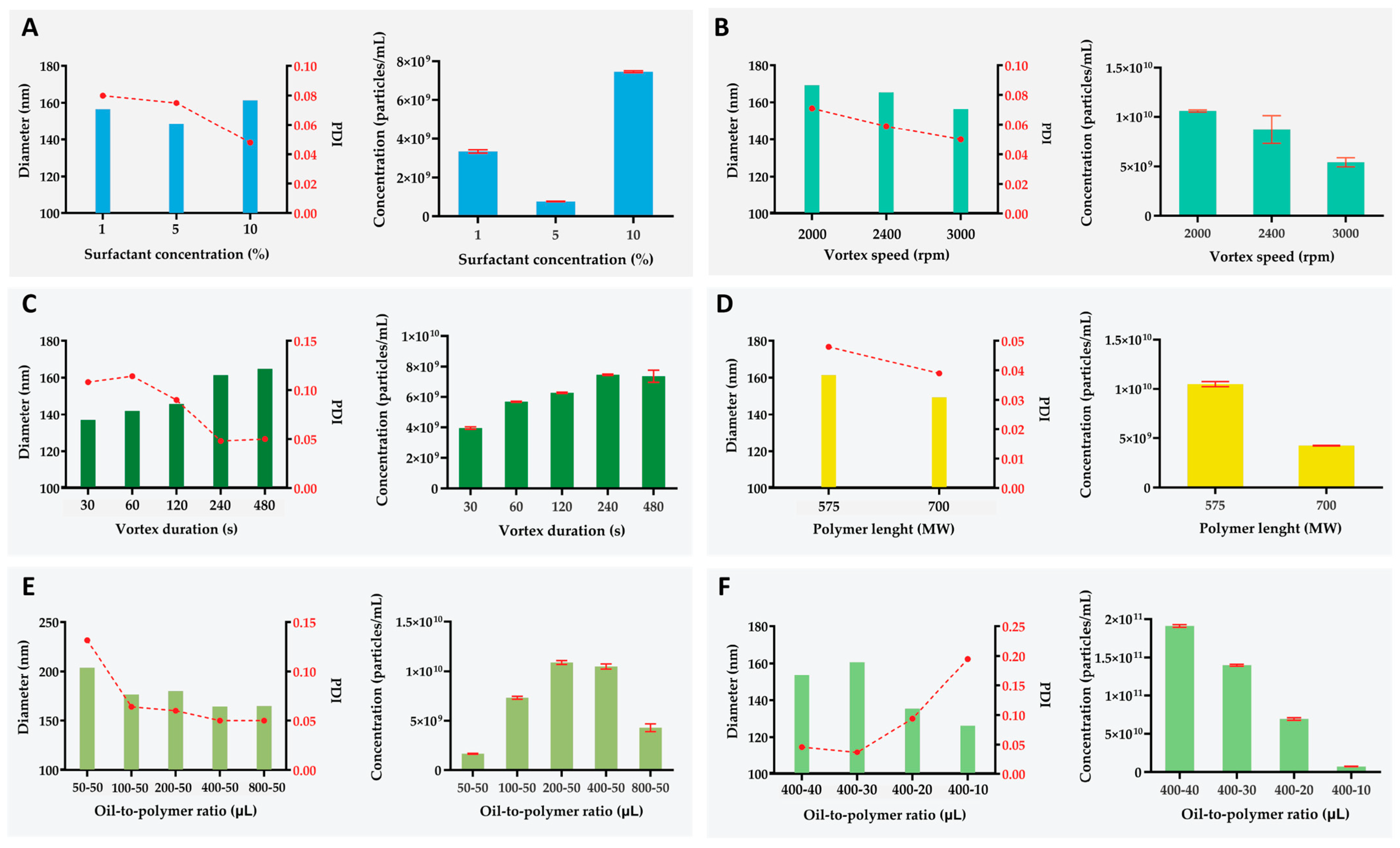
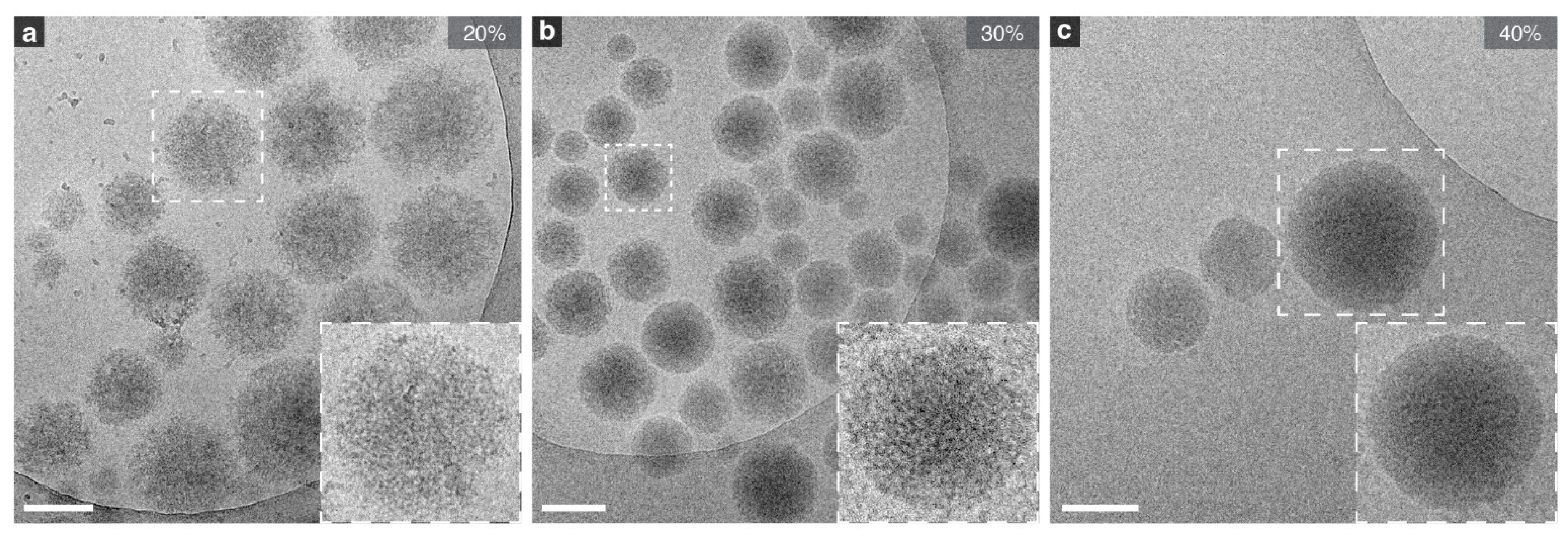
2.2. Variable Effect on Nanogels
2.3. Ratio of Micro- to Nanogels
2.4. Vortex Versus Microfluidics
2.5. Swelling Ratios of Hydrogels
3. Materials and Methods
3.1. Materials
3.2. Instruments
3.3. Methods
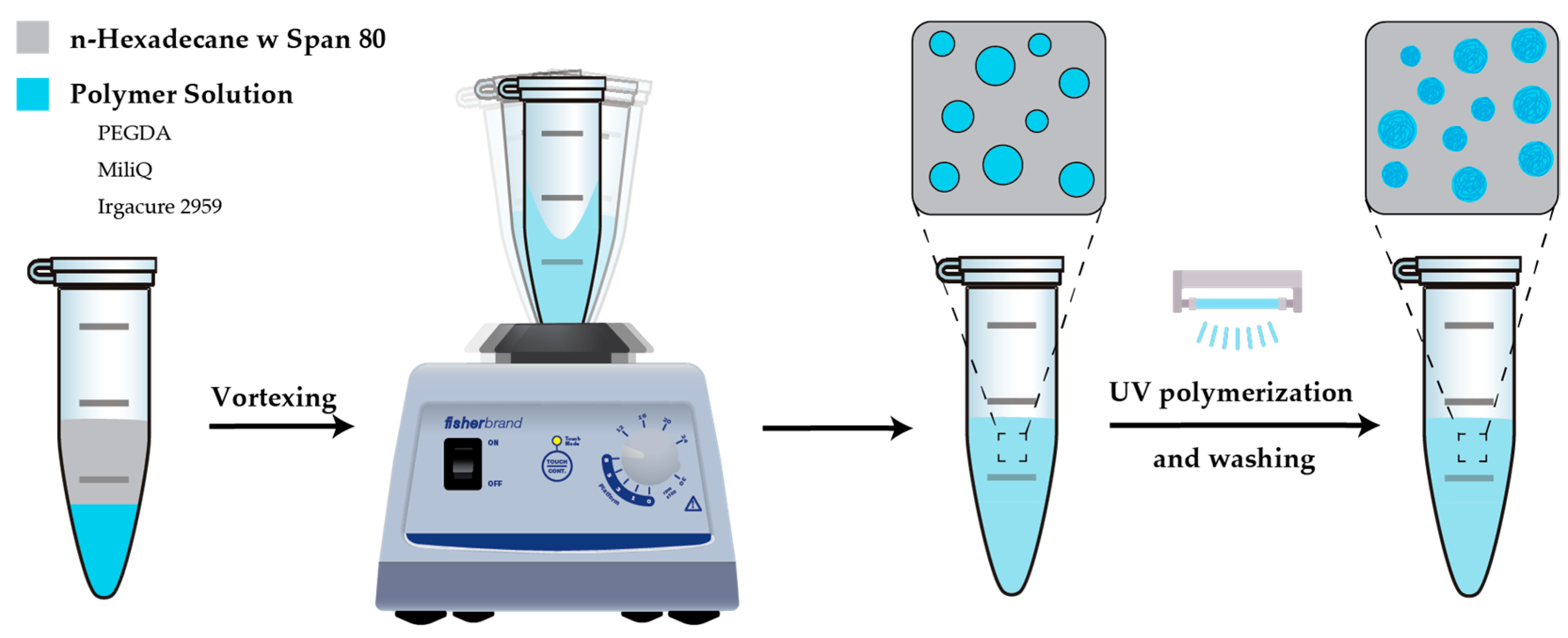
3.3.1. Vortex-Generated Hydrogels
3.3.2. Cryo-TEM Imaging
3.3.3. Particle Concentration Calculations
3.3.4. Statistical Analysis
3.3.5. Viscosity Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| C.V. | Coefficient of Variation |
| PEGDA | Polyethylene Glycol Diacrylate |
| PDI | Polydispersity index |
| MW | Molecular weight |
| N2 | Nitrogen |
| O2 | Oxygen |
| TEM | Transmission Electron Microscope |
| UV | Ultra-Violet |
| W/O | Water in Oil |
References
- Ahmad, Z.; Salman, S.; Khan, S.A.; Amin, A.; Rahman, Z.U.; Al-Ghamdi, Y.O.; Akhtar, K.; Bakhsh, E.M.; Khan, S.B. Versatility of Hydrogels: From Synthetic Strategies, Classification, and Properties to Biomedical Applications. Gels 2022, 8, 167. [Google Scholar] [CrossRef]
- Buwalda, S.J.; Vermonden, T.; Hennink, W.E. Hydrogels for Therapeutic Delivery: Current Developments and Future Directions. Biomacromolecules 2017, 18, 316–330. [Google Scholar] [CrossRef] [PubMed]
- Teora, S.P.; Panavaité, E.; Sun, M.; Kiffen, B.; Wilson, D.A. Anisotropic, Hydrogel Microparticles as pH-Responsive Drug Carriers for Oral Administration of 5-FU. Pharmaceutics 2023, 15, 1380. [Google Scholar] [CrossRef] [PubMed]
- Bordbar, S.; Li, Z.; Lotfibakhshaiesh, N.; Ai, J.; Tavassoli, A.; Beheshtizadeh, N.; Vainieri, L.; Khanmohammadi, M.; Sayahpour, F.A.; Eslaminejad, M.B.; et al. Cartilage tissue engineering using decellularized biomatrix hydrogel containing TGF-β-loaded alginate microspheres in mechanically loaded bioreactor. Sci. Rep. 2024, 14, 11991. [Google Scholar] [CrossRef]
- Liao, S.; Meng, H.; Zhao, J.; Lin, W.; Liu, X.; Tian, Z.; Lan, L.; Yang, H.; Zou, Y.; Xu, Y.; et al. Injectable adipose-derived stem cells-embedded alginate-gelatin microspheres prepared by electrospray for cartilage tissue regeneration. J. Orthop. Transl. 2022, 33, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Butenko, S.; Nagalla, R.R.; Guerrero-Juarez, C.F.; Palomba, F.; David, L.-M.; Nguyen, R.Q.; Gay, D.; Almet, A.A.; Digman, M.A.; Nie, Q.; et al. Hydrogel crosslinking modulates macrophages, fibroblasts, and their communication, during wound healing. Nat. Commun. 2024, 15, 6820. [Google Scholar] [CrossRef]
- Su, C.; Lin, D.; Huang, X.; Feng, J.; Jin, A.; Wang, F.; Lv, Q.; Lei, L.; Pan, W. Developing hydrogels for gene therapy and tissue engineering. J. Nanobiotechnol. 2024, 22, 182. [Google Scholar] [CrossRef]
- Kim, J.; Choi, Y.; Kim, D.-H.; Yoon, H.Y.; Kim, K. Injectable Hydrogel-Based Combination Cancer Immunotherapy for Overcoming Localized Therapeutic Efficacy. Pharmaceutics 2022, 14, 1908. [Google Scholar] [CrossRef]
- Mikhail, A.S.; Morhard, R.; Mauda-Havakuk, M.; Kassin, M.; Arrichiello, A.; Wood, B.J. Hydrogel drug delivery systems for minimally invasive local immunotherapy of cancer. Adv. Drug Deliv. Rev. 2023, 202, 115083. [Google Scholar] [CrossRef]
- Chacko, R.T.; Ventura, J.; Zhuang, J.; Thayumanavan, S. Polymer nanogels: A versatile nanoscopic drug delivery platform. Adv. Drug Deliv. Rev. 2012, 64, 836–851. [Google Scholar] [CrossRef]
- Mimi, H.; Ho, K.M.; Siu, Y.S.; Wu, A.; Li, P. Polyethyleneimine-Based Core-Shell Nanogels: A Promising siRNA Carrier for Argininosuccinate Synthetase mRNA Knockdown in HeLa Cells. J. Control Release 2012, 158, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Ruan, D.; Huang, M.; Tian, M.; Zhu, K.; Gan, Z.; Xiao, Z. Harnessing the potential of hydrogels for advanced therapeutic applications: Current achievements and future directions. Signal Transduct. Target. Ther. 2024, 9, 166. [Google Scholar]
- Sahu, P.; Kashaw, S.K.; Sau, S.; Kushwah, V.; Jain, S.; Agrawal, R.K.; Iyer, A.K. pH triggered and charge attracted nanogel for simultaneous evaluation of penetration and toxicity against skin cancer: In-vitro and ex-vivo study. Int. J. Biol. Macromol. 2019, 128, 740–751. [Google Scholar] [CrossRef]
- Gonciarz, W.; Brzeziński, M.; Orłowska, W.; Wawrzyniak, P.; Lewandowski, A.; Narayanan, V.H.B.; Chmiela, M. Spray-dried pH-sensitive chitosan microparticles loaded with Mycobacterium bovis BCG intended for supporting treatment of Helicobacter pylori infection. Sci. Rep. 2024, 14, 4747. [Google Scholar] [CrossRef] [PubMed]
- Nasu, E.; Kawakami, N.; Takamura, S.; Hotta, A.; Arai, R.; Miyamoto, K. Thermally Reversible Gel–Sol Transition of Hydrogels via Dissociation and Association of an Artificial Protein Nanocage. Biomacromolecules 2024, 25, 2358–2366. [Google Scholar] [CrossRef]
- Valtierra, M.M.; Corral, A.U.; Jiménez-Avalos, J.A.; Avalos, E.B.; Dávila-Rodríguez, J.; Hernández, N.M.; Comas-García, M.; González, G.T.; Oceguera-Villanueva, A.; Cruz-Ramos, J.A.; et al. Patterned PVA Hydrogels with 3D Petri Dish® Micro-Molds of Varying Topography for Spheroid Formation of HeLa Cancer Cells: In Vitro Assessment. Gels 2024, 10, 518. [Google Scholar] [CrossRef]
- Hakami, A.; Narasimhan, K.; Comini, G.; Thiele, J.; Werner, C.; Dowd, E.; Newland, B. Cryogel microcarriers for sustained local delivery of growth factors to the brain. J. Control Release 2024, 369, 404–419. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, K.; Chen, Y.; Xiang, N. Droplet Microfluidics for Current Cancer Research: From Single-Cell Analysis to 3D Cell Culture. ACS Biomater. Sci. Eng. 2024, 10, 1335–1354. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Tian, R.; Lu, H.; Liang, X.; Shafiq, M.; Uchida, S.; Chen, H.; Ma, M. Droplet Microfluidics Powered Hydrogel Microparticles for Stem Cell-Mediated Biomedical Applications. Small 2024, 20, 2401400. [Google Scholar] [CrossRef]
- Luan, J.; Kuijken, P.F.; Chen, W.; Wang, D.; Charleston, L.A.; Wilson, D.A. Microfluidic Design of Streamlined Alginate Hydrogel Micromotors with Run and Tumble Motion Patterns. Adv. Sci. 2023, 10, 2304995. [Google Scholar] [CrossRef]
- Nan, L.; Zhang, H.; Weitz, D.A.; Shum, H.C. Development and future of droplet microfluidics. Lab Chip 2024, 24, 1135–1153. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Wu, H.; Liu, S.; Yan, H.; Jiang, H. Effective colloidal emulsion droplet regulation in flow-focusing glass capillary microfluidic device via collection tube variation. RSC Adv. 2024, 14, 3250–3260. [Google Scholar] [CrossRef] [PubMed]
- Keller, S.; Teora, S.P.; Keskin, A.; Daris, L.J.C.; Samuels, N.A.P.E.; Boujemaa, M.; Wilson, D.A. Spatial Control over Catalyst Positioning for Increased Micromotor Efficiency. Gels 2023, 9, 164. [Google Scholar] [CrossRef] [PubMed]
- Teora, S.P.; van der Knaap, K.H.; Keller, S.; Rijpkema, S.J.; Wilson, D.A. Reversible Speed Control of One-Stimulus-Double-Response, Temperature-Sensitive Asymmetric Hydrogel Micromotors. Chem. Commun. 2022, 58, 10333–10336. [Google Scholar] [CrossRef]
- Hajam, M.I.; Khan, M.M. Microfluidics: A concise review of the history, principles, design, applications, and future outlook. Biomater. Sci. 2024, 12, 218–251. [Google Scholar] [CrossRef]
- Liu, X.; Sun, A.; Brodský, J.; Gablech, I.; Lednický, T.; Vopařilová, P.; Zítka, O.; Zeng, W.; Neužil, P. Microfluidics chips fabrication techniques comparison. Sci. Rep. 2024, 14, 28793. [Google Scholar] [CrossRef]
- Oh, J.K.; Lee, D.I.; Park, J.M. Biopolymer-based microgels/nanogels for drug delivery applications. Prog. Polym. Sci. 2009, 34, 1261–1282. [Google Scholar] [CrossRef]
- Vossoughi, A.; Matthew, H.W.T. Encapsulation of mesenchymal stem cells in glycosaminoglycans-chitosan polyelectrolyte microcapsules using electrospraying technique: Investigating capsule morphology and cell viability. Bioeng. Transl. Med. 2018, 3, 265–274. [Google Scholar] [CrossRef]
- Gansau, J.; Kelly, L.; Buckley, C.T. Influence of key processing parameters and seeding density effects of microencapsulated chondrocytes fabricated using electrohydrodynamic spraying. Biofabrication 2018, 10, 035011. [Google Scholar] [CrossRef]
- Cavett, V.; Chan, A.I.; Cunningham, C.N.; Paegel, B.M. Hydrogel-Encapsulated Beads Enable Proximity-Driven Encoded Library Synthesis and Screening. ACS Central Sci. 2023, 9, 1603–1610. [Google Scholar] [CrossRef]
- Clark, I.C.; Fontanez, K.M.; Meltzer, R.H.; Xue, Y.; Hayford, C.; May-Zhang, A.; D’Amato, C.; Osman, A.; Zhang, J.Q.; Hettige, P.; et al. Microfluidics-free single-cell genomics with templated emulsification. Nat. Biotechnol. 2023, 41, 1557–1566. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, K.T.; Shukla, K.P.; Moctezuma, M.; Braden, A.R.C.; Zhou, J.; Hu, Z.; Tang, L. Studies of the cellular uptake of hydrogel nanospheres and microspheres by phagocytes, vascular endothelial cells, and smooth muscle cells. J. Biomed. Mater. Res. Part A 2009, 88A, 1020–1030. [Google Scholar] [CrossRef]
- Li, D.; Xu, W.; Liu, H. Fabrication of chitosan functionalized dual stimuli-responsive injectable nanogel to control delivery of doxorubicin. Colloid Polym. Sci. 2023, 301, 879–891. [Google Scholar] [CrossRef]
- Vauthier, C.; Bouchemal, K. Methods for the Preparation and Manufacture of Polymeric Nanoparticles. Pharm. Res. 2009, 26, 1025–1058. [Google Scholar] [CrossRef]
- Hu, S.-H.; Chen, S.-Y.; Gao, X. Multifunctional Nanocapsules for Simultaneous Encapsulation of Hydrophilic and Hydrophobic Compounds and On-Demand Release. ACS Nano 2012, 6, 2558–2565. [Google Scholar] [CrossRef] [PubMed]
- Kittel, Y.; Kuehne, A.J.C.; De Laporte, L. Translating Therapeutic Microgels into Clinical Applications. Adv. Health Mater. 2022, 11, 2101989. [Google Scholar] [CrossRef] [PubMed]
- Vadlamudi, S.; Nichols, D.; Papavasiliou, G.; Teymour, F. Phosphate-Loaded Hydrogel Nanoparticles for Sepsis Prevention Prepared via Inverse Miniemulsion Polymerization. Macromol. React. Eng. 2019, 13, 1800066. [Google Scholar] [CrossRef]
- Wang, J.; Hahn, S.; Amstad, E.; Vogel, N. Tailored Double Emulsions Made Simple. Adv. Mater. 2021, 34, 2107338. [Google Scholar] [CrossRef]
- Ge, L.; Jin, H.; Li, X.; Wei, D.; Guo, R. Batch-Scale Preparation of Reverse Janus Emulsions. Langmuir 2019, 35, 3490–3497. [Google Scholar] [CrossRef]
- Liang, S.; Li, J.; Man, J.; Chen, H. Mass-Transfer-Induced Multistep Phase Separation in Emulsion Droplets: Toward Self-Assembly Multilayered Emulsions and Onionlike Microspheres. Langmuir 2016, 32, 7882–7887. [Google Scholar] [CrossRef]
- Lin, S.; Mao, L.; Ying, J.; Berthet, N.; Zhou, J.; Riaud, A. Generation of double emulsions from commercial single-emulsion microfluidic chips: A quality-control study. Microfluid. Nanofluidics 2022, 26, 71. [Google Scholar] [CrossRef]
- Bergfreund, J.; Bertsch, P.; Fischer, P. Effect of the hydrophobic phase on interfacial phenomena of surfactants, proteins, and particles at fluid interfaces. Curr. Opin. Colloid Interface Sci. 2021, 56, 101509. [Google Scholar] [CrossRef]
- Hosseinpour, S.; Götz, V.; Peukert, W. Effect of Surfactants on the Molecular Structure of the Buried Oil/Water Interface. Angew. Chem. Int. Ed. Engl. 2021, 60, 25143–25150. [Google Scholar] [CrossRef]
- L’eStimé, M.; Schindler, M.; Shahidzadeh, N.; Bonn, D. Droplet Size Distribution in Emulsions. Langmuir 2024, 40, 275–281. [Google Scholar] [CrossRef]
- Childs, P.R.N. Rotating Flow; Elsevier Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Katopodes, N.D. Free-Surface Flow; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Zhu, F.; Long, Y.; Shi, W.; Li, B.; Ji, Y.; Bai, X.; Liu, X.; Qi, D.; Sun, B.; Zhang, F.; et al. Vortexing-generated high throughput single-cell droplets for facile analysis of multiplexed microRNA dynamic secretion. Biosens. Bioelectron. 2024, 257, 116303. [Google Scholar] [CrossRef]
- Xue, C.-D.; Chen, X.-D.; Li, Y.-J.; Hu, G.-Q.; Cao, T.; Qin, K.-R. Breakup Dynamics of Semi-dilute Polymer Solutions in a Microfluidic Flow-focusing Device. Micromachines 2020, 11, 406. [Google Scholar] [CrossRef] [PubMed]
- Sathyagal, A.; Ramkrishna, D.; Narsimhan, G. Droplet breakage in stirred dispersions. Breakage functions from experimental drop-size distributions. Chem. Eng. Sci. 1996, 51, 1377–1391. [Google Scholar] [CrossRef]
- Hohl, L.; Röhl, S.; Kraume, M. Drop Size Distributions as a Function of Dispersed Phase Viscosity: Experiments and Modeling. Chem. Eng. Technol. 2023, 46, 1260–1270. [Google Scholar] [CrossRef]
- Vankova, N.; Tcholakova, S.; Denkov, N.D.; Ivanov, I.B.; Vulchev, V.D.; Danner, T. Emulsification in turbulent flow: 1. Mean and maximum drop diameters in inertial and viscous regimes. J. Colloid Interface Sci. 2007, 312, 363–380. [Google Scholar] [CrossRef]
- Thaker, A.H.; Ranade, V.V. Emulsions Using a Vortex-Based Cavitation Device: Influence of Number of Passes, Pressure Drop, and Device Scale on Droplet Size Distributions. Ind. Eng. Chem. Res. 2023, 62, 18837–18851. [Google Scholar] [CrossRef]
- Guillory, J. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals Edited by Maryadele J. O’Neil, Patricia E. Heckelman, Cherie B. Koch, and Kristin J. Roman. Merck, John Wiley & Sons, Inc., Hoboken, NJ. 2006. xiv + 2564 pp. 18 × 26 cm. ISBN 13 978-0-911910-001. $125.00. J. Med. Chem. 2007, 50, 590. [Google Scholar]
- Hrdy, R.C. Viscosity of n-Hexadecane. J. Res. Natl. Bur. Stand. 1958, 61, 433–436. [Google Scholar] [CrossRef]
- Qian, C.; McClements, D.J. Formation of nanoemulsions stabilized by model food-grade emulsifiers using high-pressure homogenization: Factors affecting particle size. Food Hydrocoll. 2011, 25, 1000–1008. [Google Scholar] [CrossRef]
- Tesch, S.; Schubert, H. Influence of increasing viscosity of the aqueous phase on the short-term stability of protein stabilized emulsions. J. Food Eng. 2002, 52, 305–312. [Google Scholar] [CrossRef]
- Behrend, O.; Ax, K.; Schubert, H. Influence of continuous phase viscosity on emulsification by ultrasound. Ultrason. Sonochem. 2000, 7, 77–85. [Google Scholar] [CrossRef]
- Lashkaripour, A.; Rodriguez, C.; Ortiz, L.; Densmore, D. Performance tuning of microfluidic flow-focusing droplet generators. Lab Chip 2019, 19, 1041–1053. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, K.; Luo, G. High-throughput generation of uniform droplets from parallel microchannel droplet generators and the preparation of polystyrene microsphere material. Particuology 2022, 77, 136–145. [Google Scholar] [CrossRef]
- Yelleswarapu, V.R.; Jeong, H.-H.; Yadavali, S.; Issadore, D. Ultra-high throughput detection (1 million droplets per second) of fluorescent droplets using a cell phone camera and time domain encoded optofluidics. Lab Chip 2017, 17, 1083–1094. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.-H.; Yelleswarapu, V.R.; Yadavali, S.; Issadore, D.; Lee, D. Kilo-scale droplet generation in three-dimensional monolithic elastomer device (3D MED). Lab Chip 2015, 15, 4387–4392. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Hwang, Y.; Chen, A.C.; Varghese, S.; Sah, R.L. Cartilage-like mechanical properties of poly (ethylene glycol)-diacrylate hydrogels. Biomaterials 2012, 33, 6682–6690. [Google Scholar] [CrossRef]
- Wieland, J.A.; Houchin-Ray, T.L.; Shea, L.D. Non-viral vector delivery from PEG-hyaluronic acid hydrogels. J. Control Release 2007, 120, 233–241. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boujemaa, M.; Peters, R.; Luan, J.; Mok, Y.H.; Keller, S.; Wilson, D.A. A Simple Vortex-Based Method for the Generation of High-Throughput Spherical Micro- and Nanohydrogels. Int. J. Mol. Sci. 2025, 26, 6300. https://doi.org/10.3390/ijms26136300
Boujemaa M, Peters R, Luan J, Mok YH, Keller S, Wilson DA. A Simple Vortex-Based Method for the Generation of High-Throughput Spherical Micro- and Nanohydrogels. International Journal of Molecular Sciences. 2025; 26(13):6300. https://doi.org/10.3390/ijms26136300
Chicago/Turabian StyleBoujemaa, Moussa, Remi Peters, Jiabin Luan, Yieuw Hin Mok, Shauni Keller, and Daniela A. Wilson. 2025. "A Simple Vortex-Based Method for the Generation of High-Throughput Spherical Micro- and Nanohydrogels" International Journal of Molecular Sciences 26, no. 13: 6300. https://doi.org/10.3390/ijms26136300
APA StyleBoujemaa, M., Peters, R., Luan, J., Mok, Y. H., Keller, S., & Wilson, D. A. (2025). A Simple Vortex-Based Method for the Generation of High-Throughput Spherical Micro- and Nanohydrogels. International Journal of Molecular Sciences, 26(13), 6300. https://doi.org/10.3390/ijms26136300






