FINCHES: A Computational Framework for Predicting Intermolecular Interactions in Intrinsically Disordered Proteins
Abstract
1. Introduction
2. Computational Approaches for IDR Interaction Prediction
Physics-Based Approaches
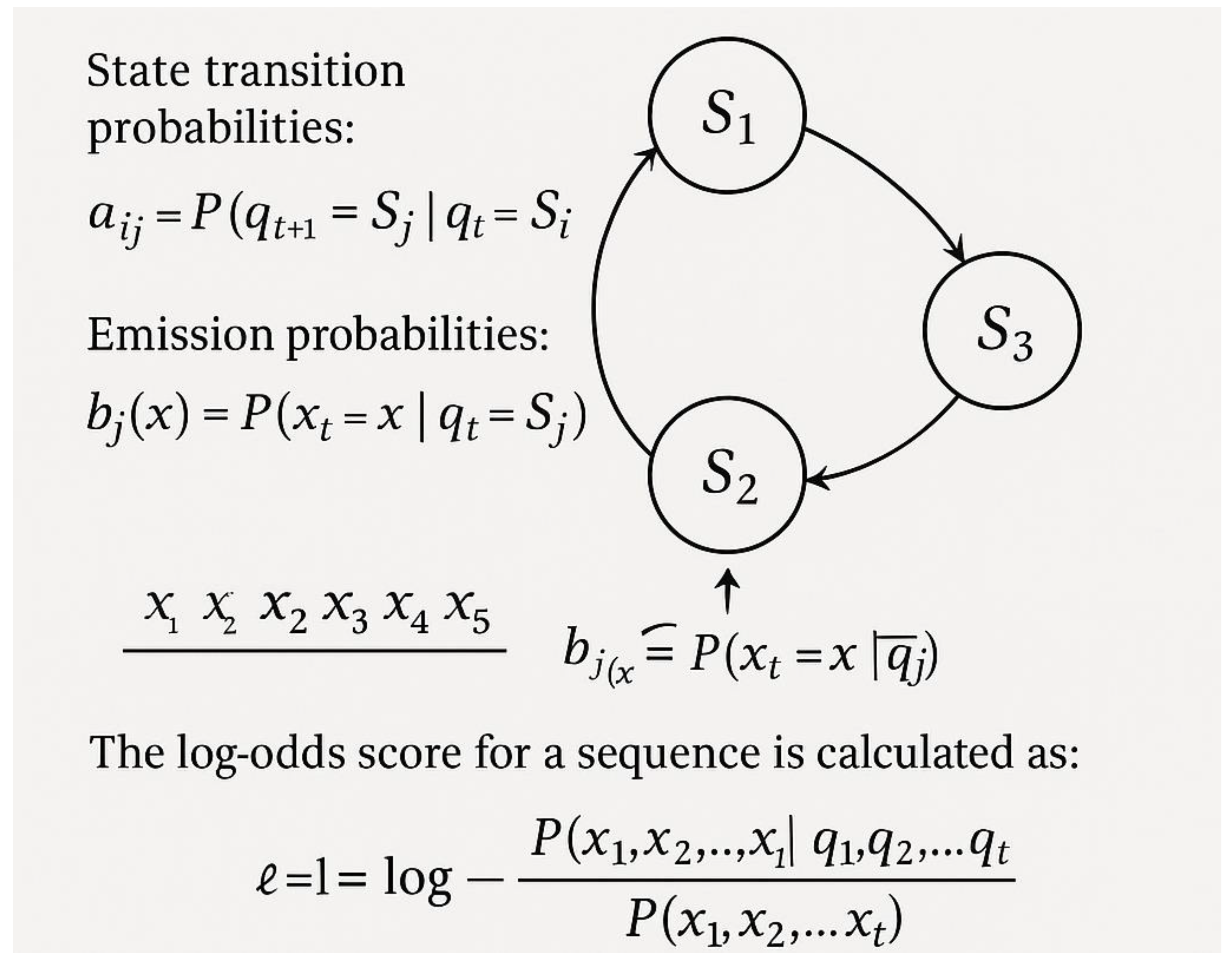
3. Machine Learning Approaches
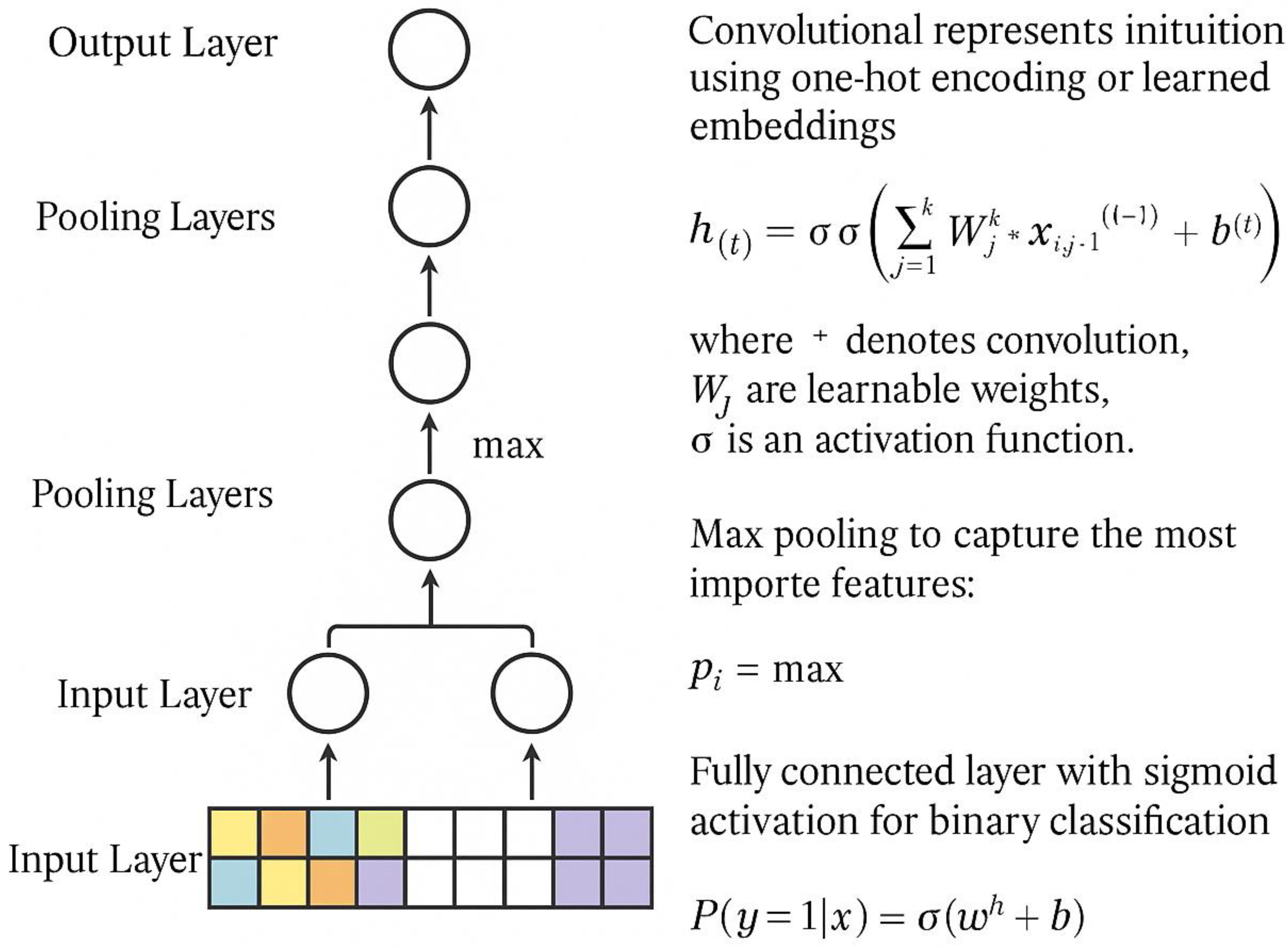
4. Deep Learning Approaches
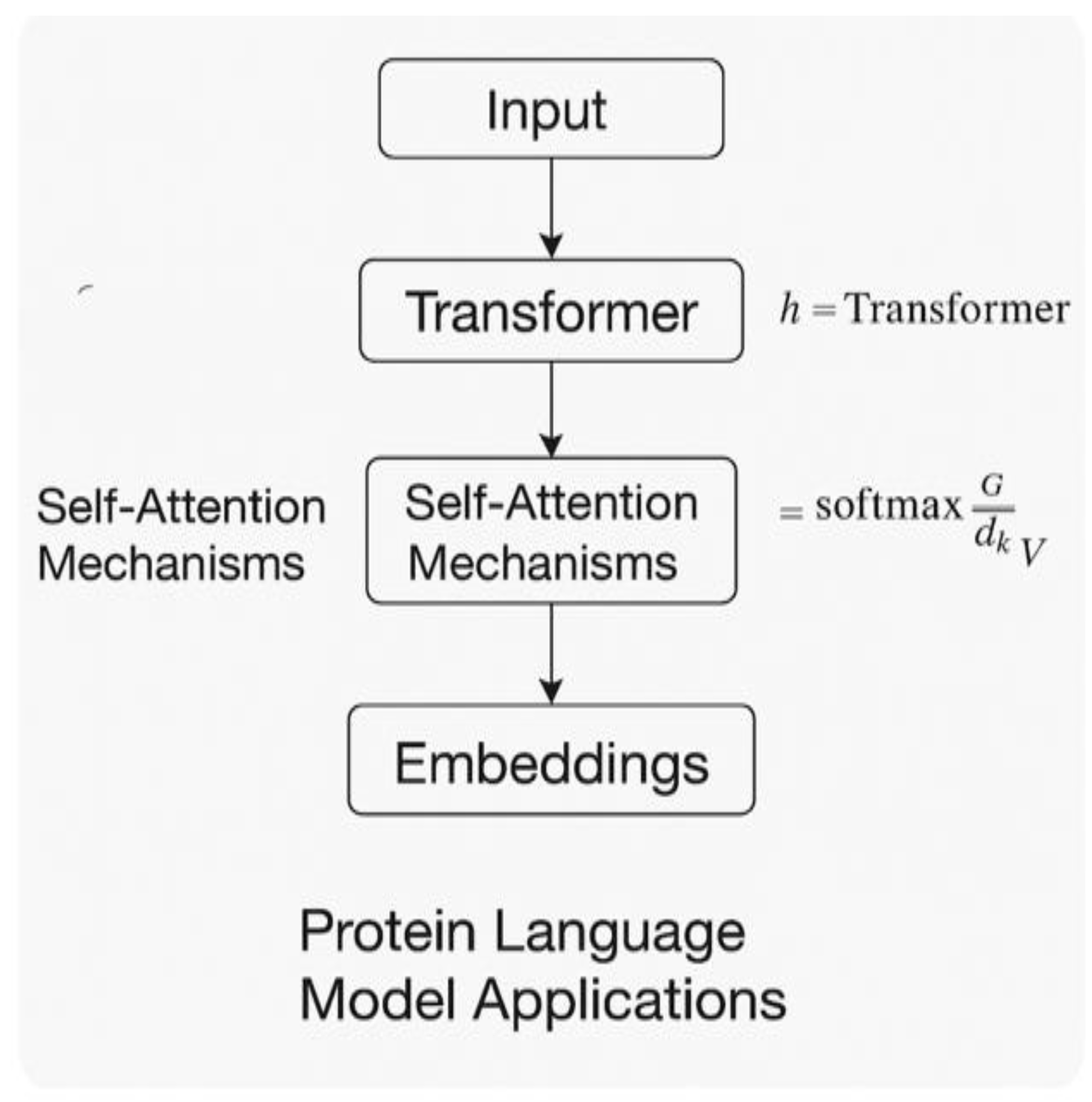
5. Protein Language Model Applications
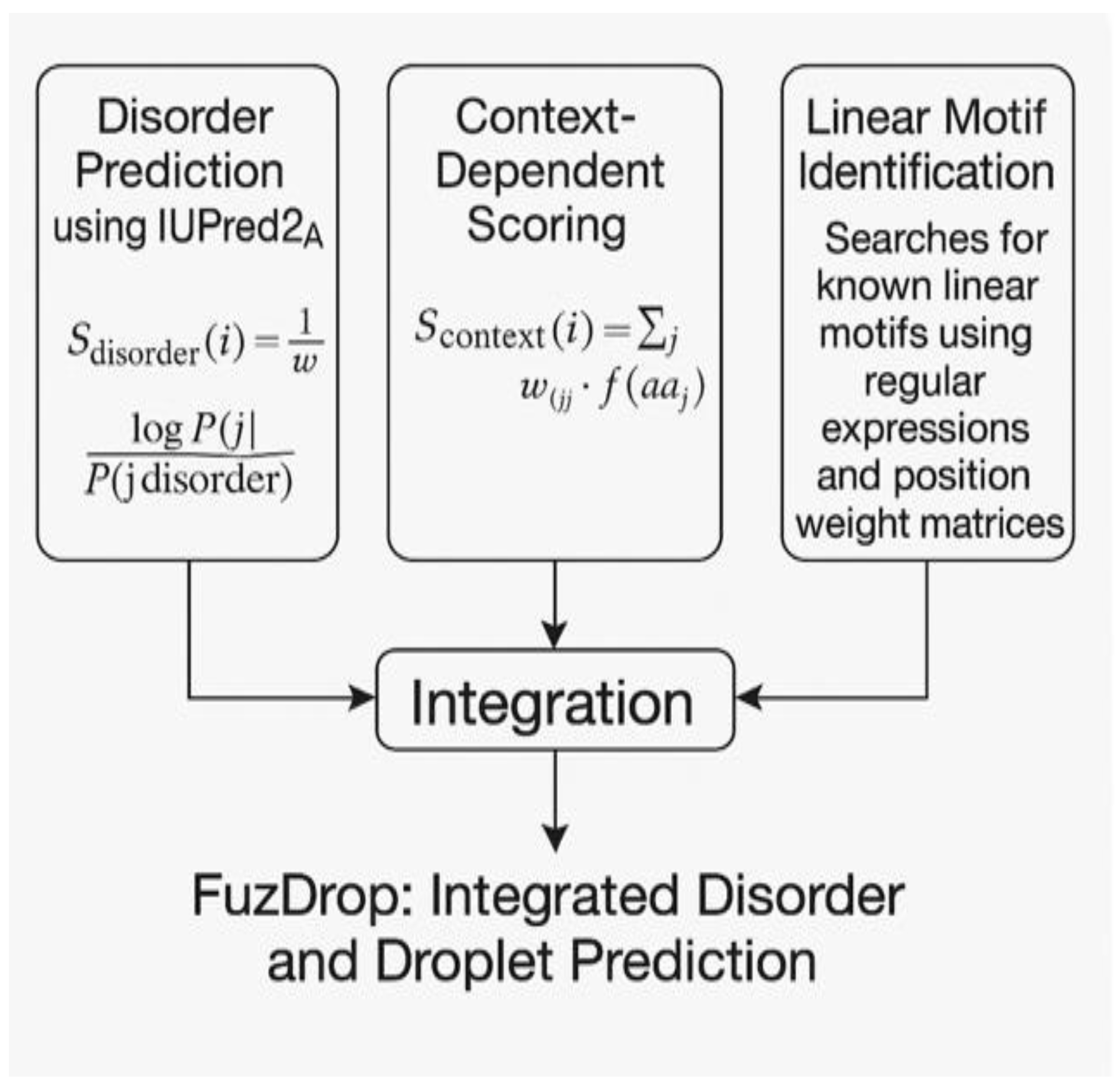
6. FuzDrop: Integrated Disorder and Droplet Prediction
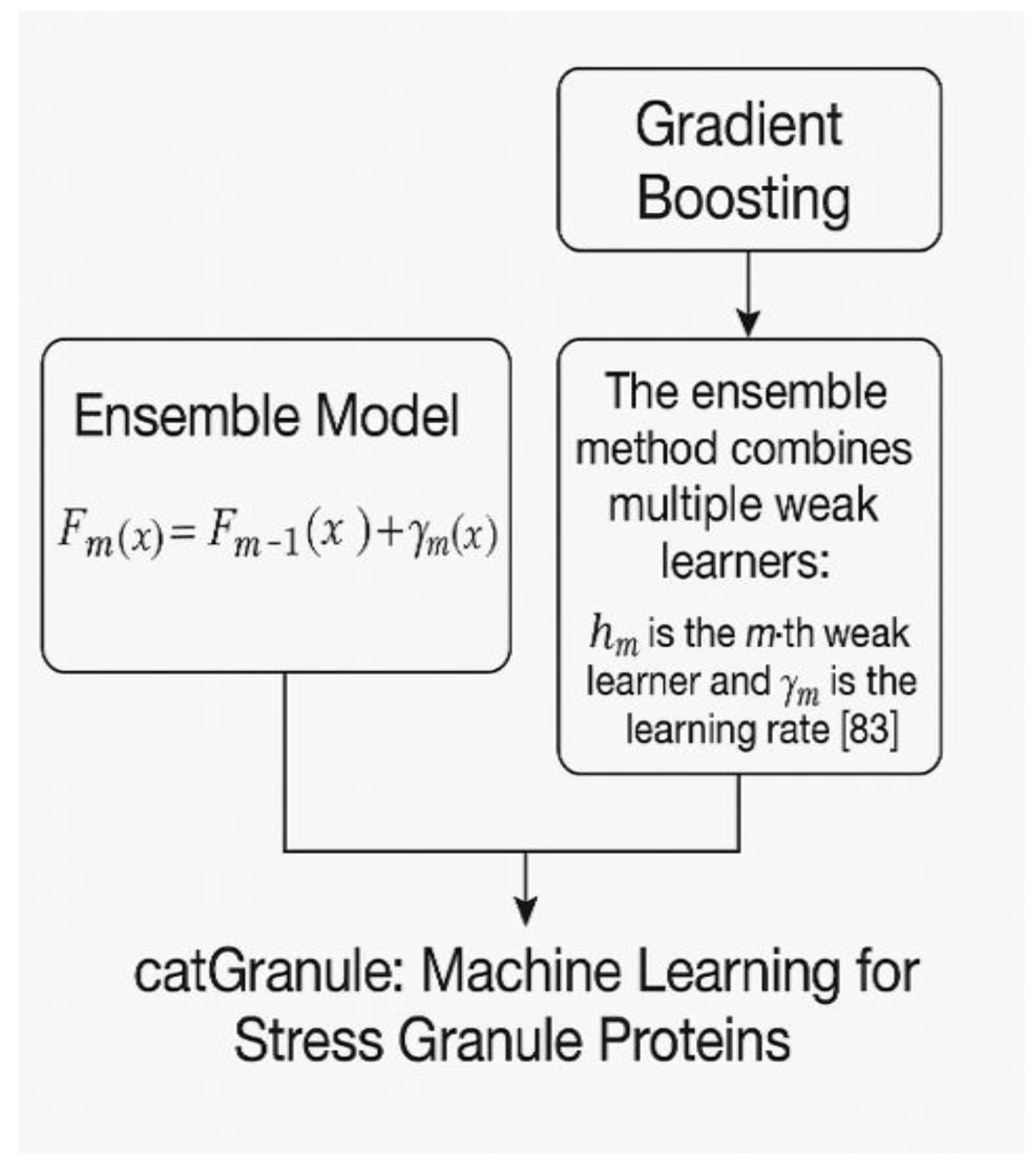
7. catGranule: Machine Learning for Stress Granule Proteins
8. LLPSDB and Database-Driven Approaches
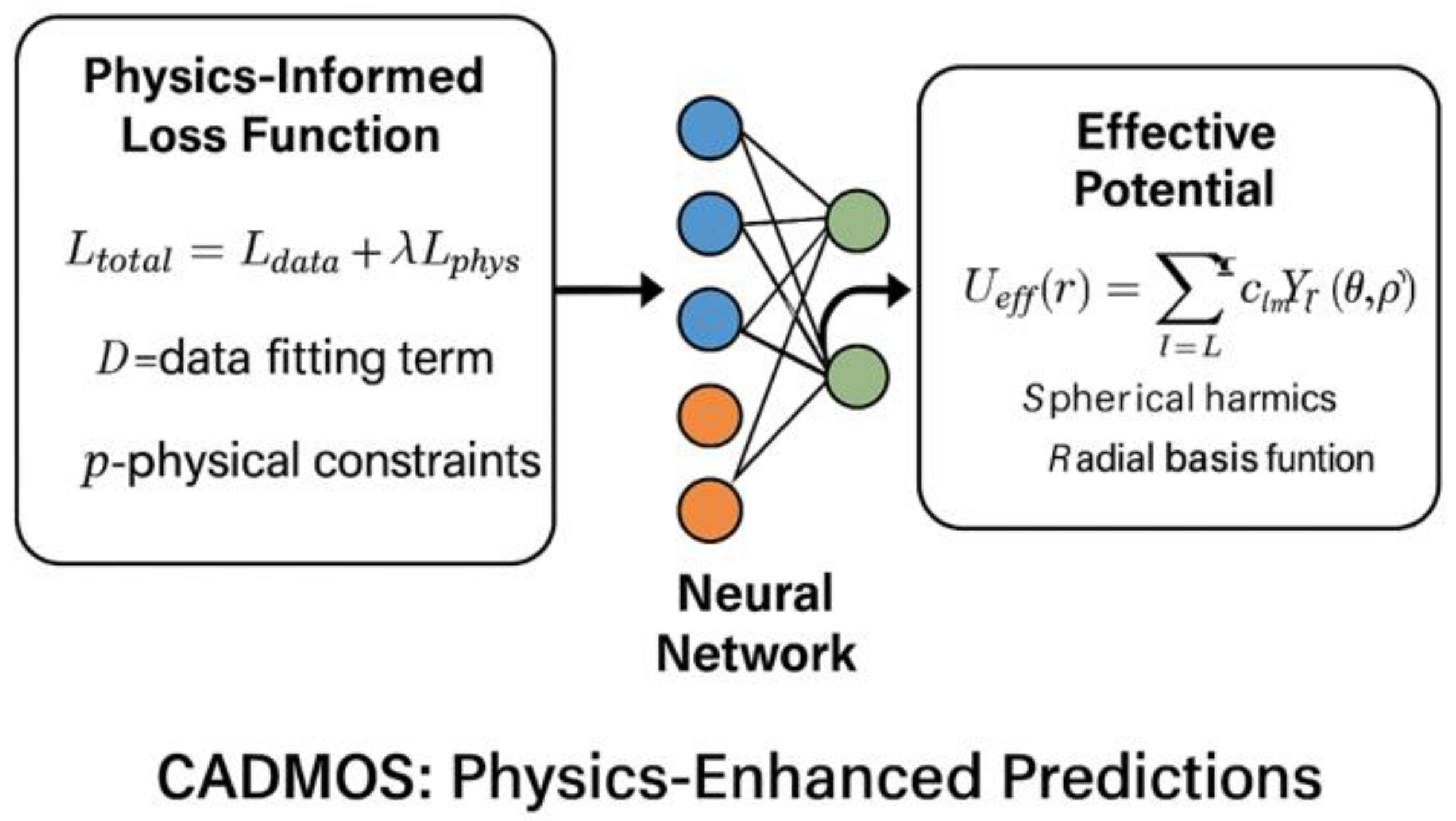
9. Physics-Informed Machine Learning
10. Computational Assessment of Interface Prediction
11. FINCHES Methodology and Theoretical Foundation
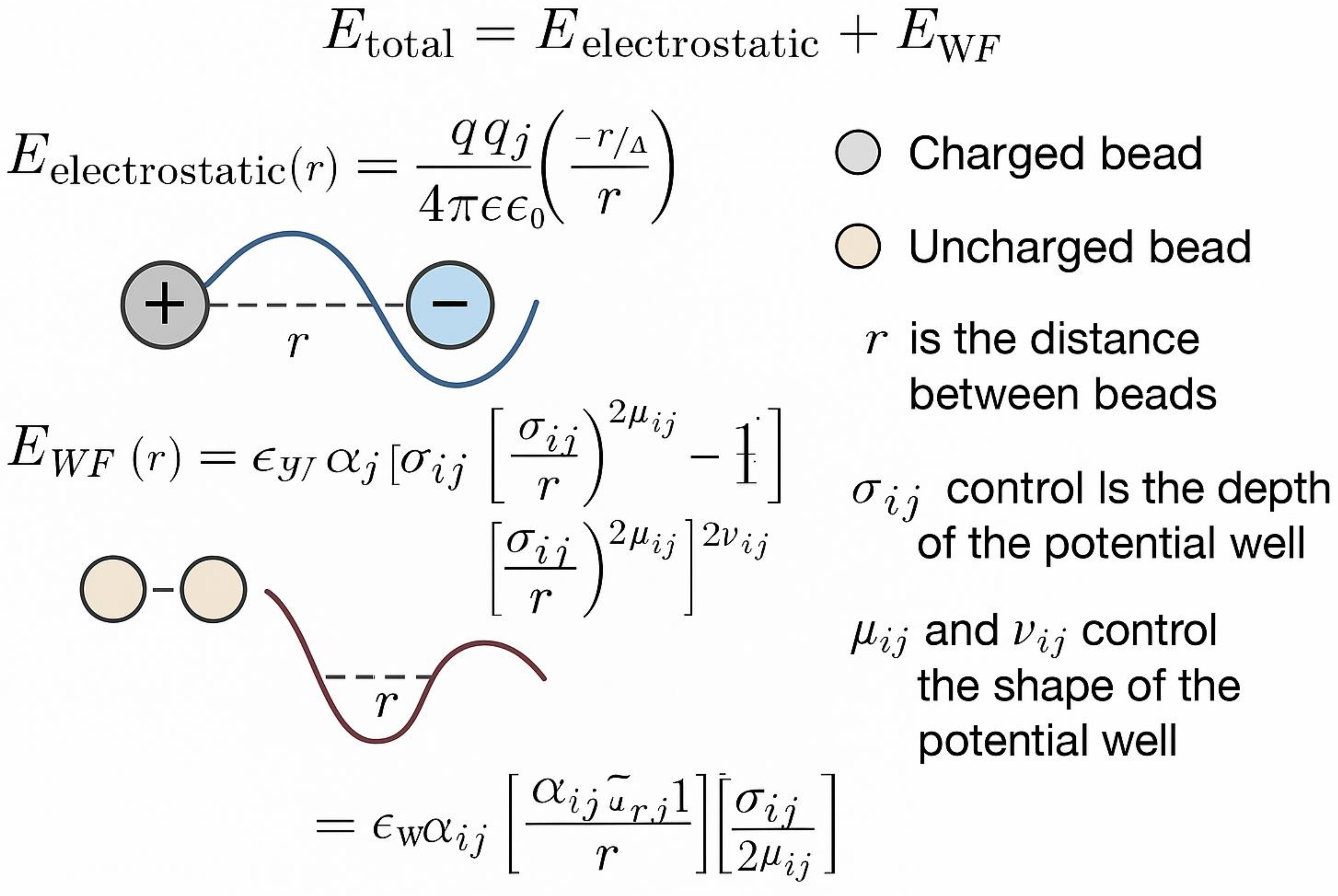
11.1. Force Field Implementation and Selection Rationale
11.2. Sequence Context Corrections
11.3. Mean-Field Calculation
12. Comparative Analysis and Validation
12.1. FUS Low-Complexity Domain
12.2. DDX4 N-Terminal Domain
12.3. p53 Transactivation Domain
12.4. TDP-43 Low-Complexity Domain
12.5. Speed and Scalability Analysis
13. Key Outputs and Interpretations
13.1. Mean-Field Interaction Parameter (ε)
13.2. Intermaps: Spatial Resolution of Interactions
13.3. Phase Diagram Predictions
14. Applications and Experimental Validation
14.1. Proteome-Scale Analysis
14.2. Post-Translational Modification Effects
14.3. Transcription Factor-Coactivator Interactions
14.4. Drug Discovery and Protein Design
15. Limitations and Critical Assessment
15.1. Fundamental Assumptions and Consequences
15.2. Temporal and Dynamic Limitations
15.3. Force Field Limitations
15.4. Experimental Validation Challenges
15.5. Comparative Limitations
16. Future Directions and Improvements
16.1. Integration of Multiple Approaches
16.2. Experimental Integration
17. Conclusions
Funding
Conflicts of Interest
References
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signaling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Holehouse, A.S.; Kragelund, B.B. The molecular basis for cellular function of intrinsically disordered protein regions. Nat. Rev. Mol. Cell Biol. 2024, 25, 187–211. [Google Scholar] [CrossRef] [PubMed]
- van der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Uversky, V.N.; Tompa, P.; Silvestri, E.; Diella, F.; et al. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef] [PubMed]
- Ginell, G.M.; Emenecker, R.J.; Lotthammer, J.M.; Usher, E.T.; Holehouse, A.S. Holehouse Direct prediction of intermolecular interactions driven by disordered regions. bioRxiv 2024. [Google Scholar] [CrossRef]
- .Dignon, G.L.; Zheng, W.; Kim, Y.C.; Best, R.B.; Mittal, J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018, 14, e1005941. [Google Scholar] [CrossRef]
- Das, R.K.; Pappu, R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef]
- Schuler, B.; Soranno, A.; Hofmann, H.; Nettels, D. Single-molecule FRET spectroscopy and the polymer physics of unfolded and intrinsically disordered proteins. Annu. Rev. Biophys. 2016, 45, 207–231. [Google Scholar] [CrossRef]
- Forman-Kay, J.D.; Mittag, T. From sequence and forces to structure, function, and evolution of intrinsically disordered proteins. Structure 2013, 21, 1492–1499. [Google Scholar] [CrossRef]
- Babu, M.M.; van der Lee, R.; de Groot, N.S.; Gsponer, J. Intrinsically disordered proteins: Regulation and disease. Curr. Opin. Struct. Biol. 2011, 21, 432–440. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically disordered proteins and their environment: Effects of strong denaturants, temperature, pH, counter ions, membranes, binding partners, osmolytes, and macromolecular crowding. Protein J. 2013, 32, 203–227. [Google Scholar] [CrossRef]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, C.J.; Dunker, A.K. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Tompa, P. Intrinsically disordered proteins: A 10-year recap. Trends Biochem. Sci. 2012, 37, 509–516. [Google Scholar] [CrossRef]
- Shaw, D.E.; Grossman, J.P.; Bank, J.A.; Batson, B.; Butts, J.A.; Chao, J.C.; Deneroff, M.M.; Dror, R.O.; Even, A.; Fenton, C.H.; et al. Anton 2: Raising the Bar for Performance and Programmability in a Special-Purpose Molecular Dynamics Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 41–53. [Google Scholar] [CrossRef]
- Stone, J.E.; Hardy, D.J.; Ufimtsev, I.S.; Schulten, K. GPU-accelerated molecular modeling applications. J. Mol. Graph. Model. 2010, 29, 116–125. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Tesei, G.; Schulze, T.K.; Crehuet, R.; Lindorff-Larsen, K. Accurate model of liquid–liquid phase behavior of intrinsically disordered proteins from optimization of single-chain properties. Proc. Natl. Acad. Sci. USA USA 2021, 118, e2111696118. [Google Scholar] [CrossRef]
- Lotthammer, J.M.; Ginell, G.M.; Griffith, D.; Emenecker, R.J.; Holehouse, A.S. Direct prediction of intrinsically disordered protein conformational properties from sequence. Nat. Methods 2024, 21, 465–476. [Google Scholar] [CrossRef]
- Uversky, V.N.; Gillespie, J.R.; Fink, A.L. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins Struct. Funct. Bioinform. 2000, 41, 415–427. [Google Scholar] [CrossRef]
- Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence complexity of disordered protein. Proteins: Struct. Funct. Bioinform. 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Ward, J.J.; Sodhi, J.S.; McGuffin, L.J.; Buxton, B.F.; Jones, D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar] [CrossRef] [PubMed]
- Dosztányi, Z.; Csizmok, V.; Tompa, P.; Simon, I. IUPred: Web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics 2005, 21, 3433–3434. [Google Scholar] [CrossRef] [PubMed]
- Linding, R.; Jensen, L.J.; Diella, F.; Bork, P.; Gibson, T.J.; Russell, R.B. Protein disorder prediction: Implications for structural proteomics. Structure 2003, 11, 1453–1459. [Google Scholar] [CrossRef]
- Prilusky, J.; Felder, C.E.; Zeev-Ben-Mordehai, T.; Rydberg, E.H.; Man, O.; Beckmann, J.S.; Silman, I.; Sussman, J.L. FoldIndex©: A simple tool to predict whether a given protein sequence is intrinsically unfolded. Bioinformatics 2005, 21, 3435–3438. [Google Scholar] [CrossRef]
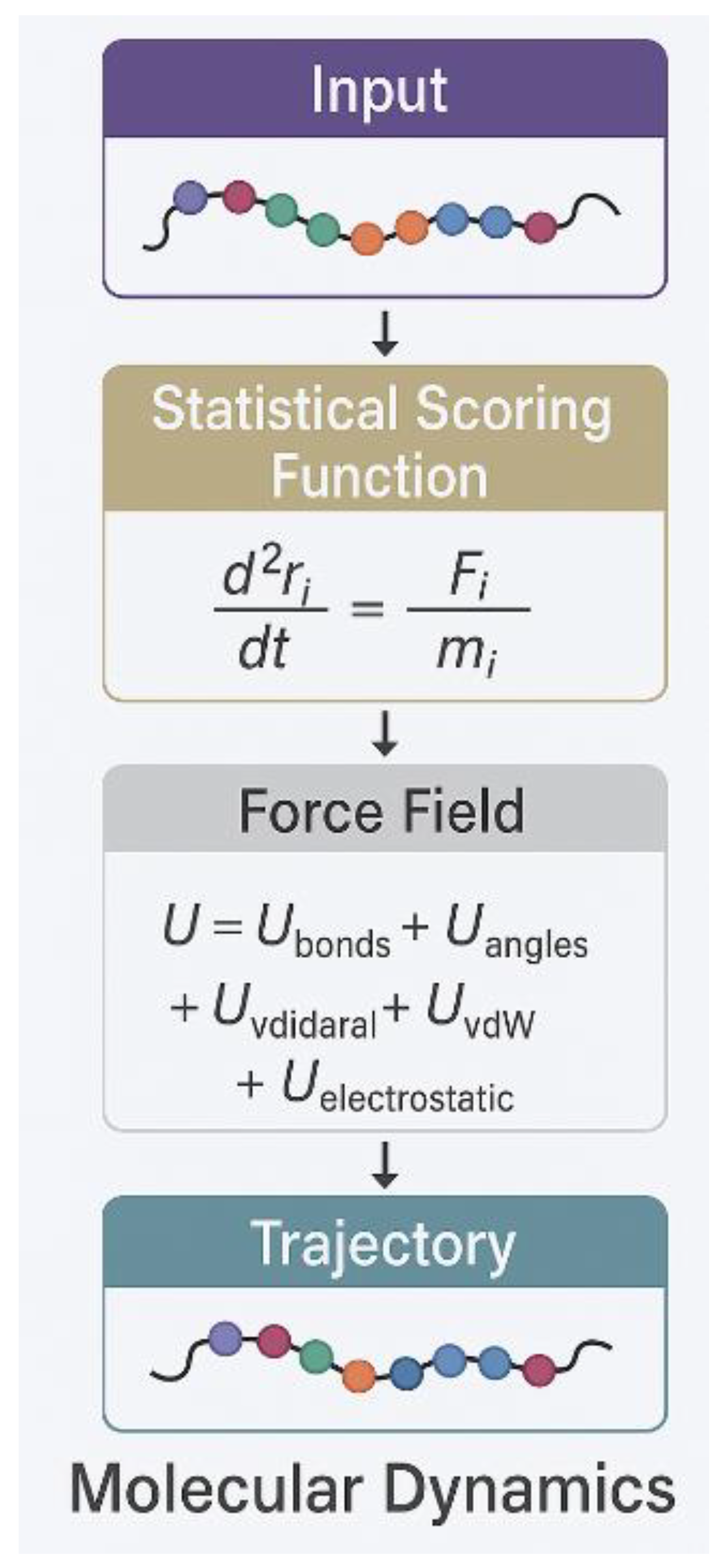
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Best, R.B.; Zheng, W.; Mittal, J. Balanced protein-water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput. 2014, 10, 5113–5124. [Google Scholar] [CrossRef]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef]
- Dror, R.O.; Dirks, R.M.; Grossman, J.P.; Xu, H.; Shaw, D.E. Biomolecular simulation: A computational microscope for molecular biology. Annu. Rev. Biophys. 2012, 41, 429–452. [Google Scholar] [CrossRef]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmüller, H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: A comparison to experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef] [PubMed]
- Palazzesi, F.; Prakash, M.K.; Bonomi, M.; Barducci, A. Accuracy of current all-atom force-fields in modeling protein disordered states. J. Chem. Theory Comput. 2015, 11, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
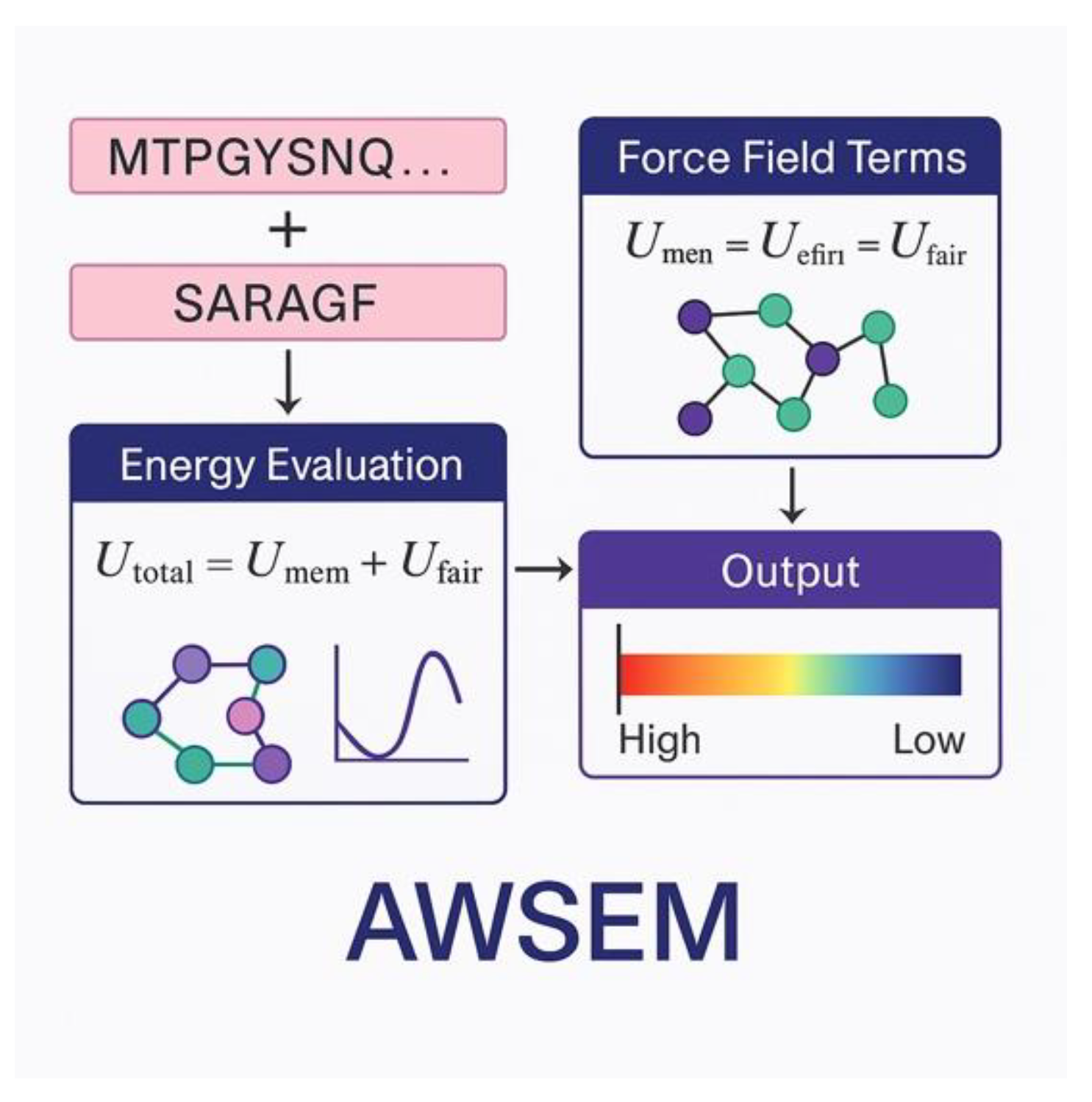
- Davtyan, A.; Schafer, N.P.; Zheng, W.; Clementi, C.; Wolynes, P.G.; Papoian, G.A. AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J. Phys. Chem. B 2012, 116, 8494–8503. [Google Scholar] [CrossRef]
- Chen, M.; Lin, X.; Zheng, W.; Onuchic, J.N.; Wolynes, P.G. Protein folding and structure prediction from the ground up: The atomistic associative memory, water mediated, structure and energy model. J. Phys. Chem. B 2016, 120, 8557–8565. [Google Scholar] [CrossRef]
- Schafer, N.P.; Kim, B.L.; Zheng, W.; Wolynes, P.G. Learning to fold proteins using energy landscape theory. Isr. J. Chem. 2014, 54, 1311–1337. [Google Scholar] [CrossRef]
- Chen, M.; Lin, X.; Lu, W.; Onuchic, J.N.; Wolynes, P.G. Protein Folding and Structure Prediction from the Ground Up II: AAWSEM for α/β Proteins. J. Phys. Chem. B 2017, 121, 3473–3482. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Zheng, W.; Schafer, N.P.; Wolynes, P.G. Frustration in the energy landscapes of multidomain protein misfolding. Proc. Natl. Acad. Sci. USA 2013, 110, 1680–1685. [Google Scholar] [CrossRef]
- Zheng, W.; Dignon, G.L.; Brown, M.; Kim, Y.C.; Mittal, J. Hydropathy patterning complements charge patterning to describe conformational preferences of disordered proteins. J. Phys. Chem. Lett. 2020, 11, 3408–3415. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.A.; Reinhardt, A.; Aguirre, A.; Chew, P.Y.; Russell, K.O.; Espinosa, J.R.; Garaizar, A.; Collepardo-Guevara, R. Physics-driven coarse-grained model for biomolecular phase separation with near-quantitative accuracy. Nat. Comput. Sci. 2021, 1, 732–743. [Google Scholar] [CrossRef] [PubMed]
- Tesei, G.; Lindorff-Larsen, K. Improved predictions of phase behaviour of intrinsically disordered proteins by tuning the interaction range. Open Res. Eur. 2023, 2, 94. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Krainer, G.; Welsh, T.J.; Joseph, J.A.; Espinosa, J.R.; Wittmann, S.; de Csilléry, E.; Sridhar, A.; Toprakcioglu, Z.; Gudiškytė, G.; Ott, M.A.; et al. Reentrant liquid condensation of proteins is enhanced by RNA. Nat. Commun. 2021, 12, 1085. [Google Scholar] [CrossRef]
- Welsh, T.J.; Krainer, G.; Espinosa, J.R.; Joseph, J.A.; Sridhar, A.; Jahnel, M.; Arter, W.E.; Saar, K.L.; Alberti, S.; Collepar-do-Guevara, R.; et al. Surface Electrostatics Govern the Emulsion Stability of Biomolecular Condensates. Nano Lett. 2022, 22, 612–621. [Google Scholar] [CrossRef] [PubMed Central]
- Dignon, G.L.; Zheng, W.; Kim, Y.C.; Mittal, J. Temperature-Controlled Liquid-Liquid Phase Separation of Disordered Proteins. ACS Cent. Sci. 2019, 5, 821–830. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Emenecker, R.J.; Holehouse, A.S.; Strader, L.C. Biological Phase Separation and Biomolecular Condensates in Plants. Annu. Rev. Plant Biol. 2021, 72, 17–46. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Emenecker, R.J.; Griffith, D.; Holehouse, A.S. Metapredict: A fast, accurate, and easy-to-use predictor of consensus disorder and structure. Biophys. J. 2021, 120, 4312–4319. [Google Scholar] [CrossRef]
- Ginell, G.M.; Emenecker, R.J.; Holehouse, A.S. Computational analysis of the sequence-ensemble relationship in intrinsically disordered proteins. In Methods in Molecular Biology; Springer: Berlin/Heidelberg, Germany, 2022; Volume 2141, pp. 209–245. [Google Scholar] [CrossRef]
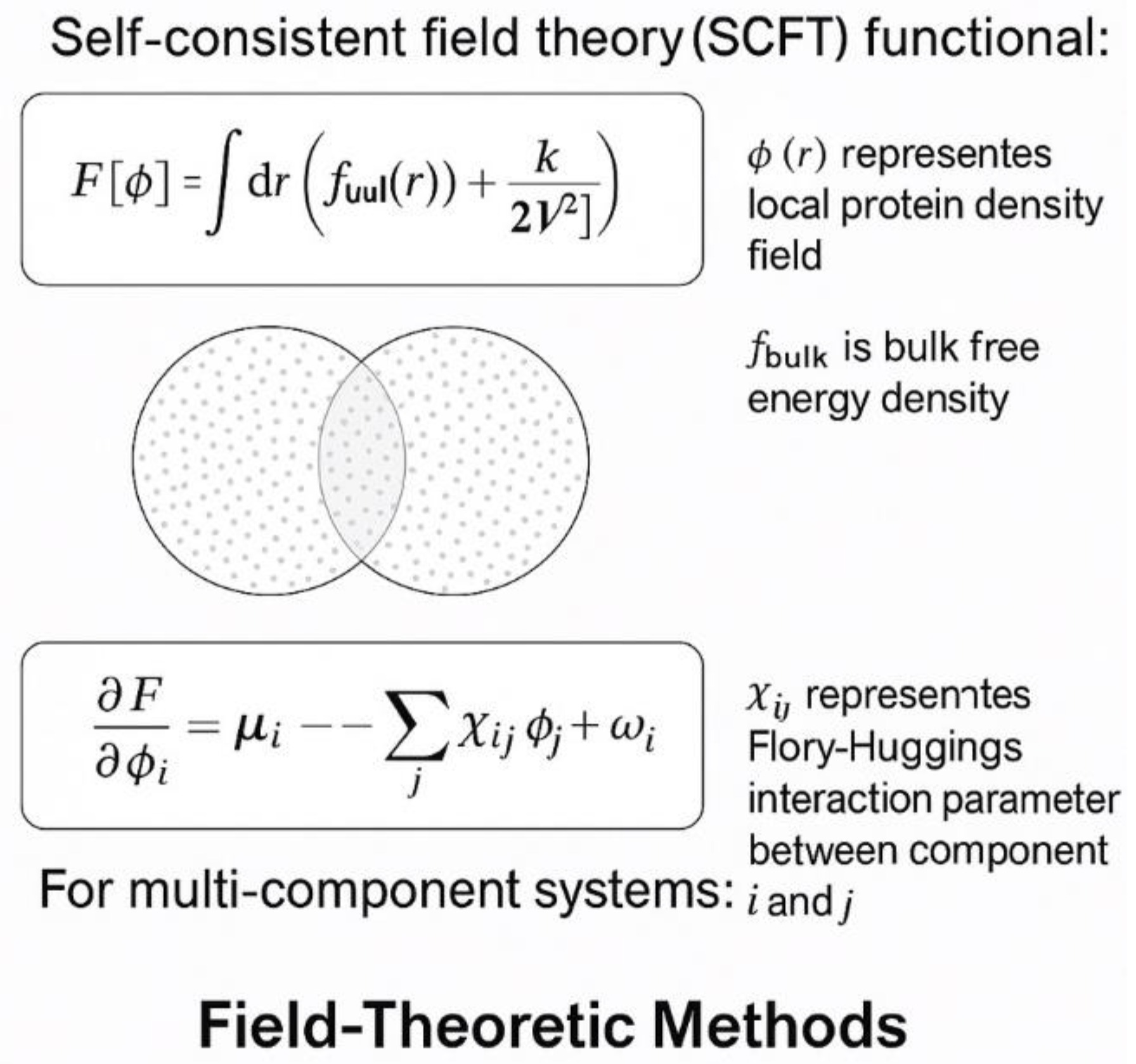
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; Oxford University Press: Oxford, UK, 2006; ISBN 978-0-19-856765-5. [Google Scholar]
- Delaney, K.T.; Fredrickson, G.H. Recent Developments in Fully Fluctuating Field-Theoretic Simulations of Polymer Melts and Solutions. J. Phys. Chem. B 2016, 120, 7615–7634. [Google Scholar] [CrossRef] [PubMed Central]
- Fredrickson, G.H.; Ganesan, V.; Drolet, F. Field-theoretic computer simulation methods for polymers and complex fluids. Macromolecules 2002, 35, 16–39. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- McCarty, J.; Delaney, K.T.; Danielsen, S.P.O.; Fredrickson, G.H.; Shea, J.E. Complete phase diagram for liquid–liquid phase separation of intrinsically disordered proteins. J. Phys. Chem. Lett. 2019, 10, 1644–1652. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Theories for sequence-dependent phase behaviors of biomolecular condensates. Biochemistry 2016, 57, 2499–2508. [Google Scholar] [CrossRef] [PubMed]
- Danielsen, S.P.O.; McCarty, J.; Shea, J.E.; Delaney, K.T.; Fredrickson, G.H. Molecular design of self-coacervation phenomena in block polyampholytes. Proc. Natl. Acad. Sci. USA 2019, 116, 8224–8232. [Google Scholar] [CrossRef]
- Orlando, G.; Silva, A.; Macedo-Ribeiro, S.; Raimondi, D.; Vranken, W.F. Accurate prediction of protein beta-aggregation with generalized statistical potentials. Bioinformatics 2019, 36, 2076–2081. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: London, UK, 2013; ISBN 978-1-4757-3264-1. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001; ISBN 978-0-262-19475-4. [Google Scholar]
- Anderson, P.; Kedersha, N. Stress granules: The Tao of RNA triage. Trends Biochem. Sci. 2008, 33, 141–150. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-03561-3. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Mészáros, B.; Erdős, G.; Szabó, B.; Schád, É.; Tantos, Á.; Abukhairan, R.; Horváth, T.; Murvai, N.; Kovács, O.P.; Kovács, M.; et al. PhaSePro: The database of proteins driving liquid–liquid phase separation. Nucleic Acids Res. 2020, 48, D360–D367. [Google Scholar] [CrossRef]
- Protter, D.S.; Parker, R. Principles and properties of stress granules. Trends Cell Biol. 2016, 26, 668–679. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar] [CrossRef]
- Rives, A.; Meier, J.; Sercu, T.; Goyal, S.; Lin, Z.; Liu, J.; Guo, D.; Ott, M.; Zitnick, C.L.; Ma, J.; et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA 2021, 118, e2016239118. [Google Scholar] [CrossRef]
- Elnaggar, A.; Heinzinger, M.; Dallago, C.; Rehawi, G.; Wang, Y.; Jones, L.; Gibbs, T.; Feher, T.; Angerer, C.; Steinegger, M.; et al. ProtTrans: Toward understanding the language of life through self-supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7112–7127. [Google Scholar] [CrossRef]
- Raimondi, D.; Orlando, G.; Fariselli, P.; Moreau, Y. Insight into the protein solubility driving forces with neural attention. PLoS Comput. Biol. 2022, 18, e1010204. [Google Scholar] [CrossRef]
- Savastano, A.; Ibáñez de Opakua, A.; Rankovic, M.; Zweckstetter, M. Nucleocapsid protein of SARS-CoV-2 phase separates into RNA-rich polymerase-containing condensates. Nat. Commun. 2020, 11, 6041. [Google Scholar] [CrossRef]
- Lancaster, A.K.; Nutter-Upham, A.; Lindquist, S.; King, O.D. PLAAC: A web and command-line application to identify proteins with prion-like amino acid composition. Bioinformatics 2014, 30, 2501–2502. [Google Scholar] [CrossRef]
- Alberti, S.; Halfmann, R.; King, O.; Kapila, A.; Lindquist, S. A systematic survey of the intrinsic tendency of aggregation of the yeast proteome. Mol. Cell 2009, 35, 755–764. [Google Scholar] [CrossRef][Green Version]
- Johnson, B.S.; Snead, D.; Lee, J.J.; McCaffery, J.M.; Shorter, J.; Gitler, A.D. TDP-43 is intrinsically aggregation-prone, and amyotrophic lateral sclerosis-linked mutations accelerate aggregation and increase toxicity. J. Biol. Chem. 2009, 284, 20329–20339. [Google Scholar] [CrossRef]
- Mackenzie, I.R.; Rademakers, R.; Neumann, M. TDP-43 and FUS in amyotrophic lateral sclerosis and frontotemporal dementia. Lancet Neurol. 2010, 9, 995–1007. [Google Scholar] [CrossRef]
- Erdős, G.; Dosztányi, Z. Analyzing protein disorder with IUPred2A. Curr. Protoc. Bioinform. 2020, 70, e99. [Google Scholar] [CrossRef] [PubMed]
- Mészáros, B.; Erdős, G.; Dosztányi, Z. IUPred2A: Context-dependent prediction of protein disorder as a function of redox state and protein binding. Nucleic Acids Res. 2018, 46, W329–W337. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Gouw, M.; Michael, S.; Sámano-Sánchez, H.; Pancsa, R.; Glavina, J.; Diakogianni, A.; Valverde, J.A.; Bukirova, D.; Čalyševa, J.; et al. ELM-the eukaryotic linear motif resource in 2020. Nucleic Acids Res. 2020, 48, D296–D306. [Google Scholar] [CrossRef]
- Johansson, K.E.; Lindorff-Larsen, K.; Winther, J.R. Protein disorder and the evolution of molecular recognition by induced fit. Protein Sci. 2014, 23, 1274–1284. [Google Scholar] [CrossRef]
- Santner, A.A.; Croy, C.H.; Vasanwala, F.H.; Uversky, V.N.; Van, Y.Y.J.; Dunker, A.K. Sweeping away protein aggregation with entropic bristles: Intrinsically disordered protein fusions enhance soluble expression. Biochemistry 2012, 51, 7250–7262. [Google Scholar] [CrossRef]
- Klim, J.R.; Williams, L.A.; Limone, F.; Guerra San Juan, I.; Davis-Dusenbery, B.N.; Mordes, D.A.; Burberry, A.; Steinbaugh, M.J.; Gamage, K.K.; Kirchner, R.; et al. ALS-implicated protein TDP-43 sustains levels of STMN2, a mediator of motor neuron growth and repair. Nat. Neurosci. 2019, 22, 167–179. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Guillén-Boixet, J.; Kopach, A.; Holehouse, A.S.; Wittmann, S.; Jahnel, M.; Schlüßler, R.; Kim, K.; Trussina, I.R.E.A.; Wang, J.; Mateju, D.; et al. RNA-induced conformational switching and clustering of G3BP drive stress granule assembly by condensation. Cell 2020, 181, 346–361. [Google Scholar] [CrossRef]
- Li, Q.; Peng, X.; Li, Y.; Tang, W.; Zhu, J.; Huang, J.; Qi, Y.; Jiang, T. LLPSDB: A database of proteins undergoing liquid–liquid phase separation in vitro. Nucleic Acids Res. 2020, 48, D320–D327. [Google Scholar] [CrossRef]
- Ning, W.; Guo, Y.; Lin, S.; Mei, B.; Wu, Y.; Jiang, P.; Tan, X.; Zhang, W.; Chen, G.; Peng, D.; et al. DrLLPS: A data resource of liquid–liquid phase separation in eukaryotes. Nucleic Acids Res. 2020, 48, D288–D295. [Google Scholar] [CrossRef]
- You, K.; Huang, Q.; Yu, C.; Shen, B.; Sevilla, C.; Shi, M.; Hermjakob, H.; Chen, Y.; Li, T. PhaSepDB: A database of liquid–liquid phase separation related proteins. Nucleic Acids Res. 2020, 48, D354–D359. [Google Scholar] [CrossRef] [PubMed]
- Maristany, M.J.; Gonzalez, A.A.; Espinosa, J.R.; Huertas, J.; Collepardo-Guevara, R.; Joseph, J.A. Decoding phase separation of prion-like domains through data-driven scaling laws. eLife 2025, 13, RP99068. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Joseph, J.A.; Sanchez-Burgos, I.; Garaizar, A.; Frenkel, D.; Collepardo-Guevara, R. Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components. Proc. Natl. Acad. Sci. USA 2020, 117, 13238–13247. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct. Funct. Bioinform. 2006, 65, 712–725. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- MacKerell Jr, A.D.; Bashford, D.; Bellott, M.L.D.R.; Dunbrack Jr, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Debye, P.; Hückel, E. Zur theorie der elektrolyte. I. Gefrierpunktserniedrigung Und Verwandte Erscheinungen. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-12-375182-9. [Google Scholar]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [PubMed]
- Fossat, M.J.; Posey, A.E.; Pappu, R.V. Quantifying charge state heterogeneity for proteins with multiple ionizable residues. Biophys. J. 2021, 120, 5438–5453. [Google Scholar] [CrossRef] [PubMed]
- Kozlowski, L.P. IPC--isoelectric point calculator. Biol. Direct 2016, 11, 55. [Google Scholar] [CrossRef]
- Riback, J.A.; Bowman, M.A.; Zmyslowski, A.M.; Knoverek, C.R.; Jumper, J.M.; Hinshaw, J.R.; Green, E.B.; Regan, L.; Daggett, V.; Sosnick, T.R. Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water. Science 2017, 358, 238–241. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Hatch, H.W. Natively unfolded protein stability as a coil-to-globule transition in charge/hydropathy space. J. Am. Chem. Soc. 2008, 130, 9536–9542. [Google Scholar] [CrossRef]
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112. [Google Scholar] [CrossRef]
- Pappu, R.V.; Wang, X.; Vitalis, A.; Crick, S.L. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch. Biochem. Biophys. 2008, 469, 132–141. [Google Scholar] [CrossRef]
- Lin, Y.; Currie, S.L.; Rosen, M.K. Intrinsically disordered sequences enable modulation of protein phase separation through distributed tyrosine motifs. J. Biol. Chem. 2017, 292, 19110–19120. [Google Scholar] [CrossRef]
- Schwartz, J.C.; Wang, X.; Podell, E.R.; Cech, T.R. RNA seeds higher-order assembly of FUS protein. Cell Rep. 2013, 5, 918–925. [Google Scholar] [CrossRef]
- Wang, J.; Choi, J.M.; Holehouse, A.S.; Lee, H.O.; Zhang, X.; Jahnel, M.; Maharana, S.; Lemaitre, R.; Pozniakovsky, A.; Drechsel, D.; et al. A molecular grammar governing the driving forces for phase separation of prion-like RNA binding proteins. Cell 2018, 174, 688–699. [Google Scholar] [CrossRef]
- Martin, E.W.; Holehouse, A.S.; Peran, I.; Farag, M.; Incicco, J.J.; Bremer, A.; Grace, C.R.; Soranno, A.; Pappu, R.V.; Mittag, T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 2020, 367, 694–699. [Google Scholar] [CrossRef]
- Choi, J.M.; Holehouse, A.S.; Pappu, R.V. Physical principles underlying the complex biology of intracellular phase transitions. Annu. Rev. Biophys. 2020, 49, 107–133. [Google Scholar] [CrossRef] [PubMed]
- Bremer, A.; Farag, M.; Borcherds, W.M.; Peran, I.; Martin, E.W.; Pappu, R.V.; Mittag, T. Deciphering how naturally occurring sequence features impact the phase behaviours of disordered prion-like domains. Nat. Chem. 2022, 14, 196–207. [Google Scholar] [CrossRef] [PubMed]
- Ruff, K.M.; Harmon, T.S.; Pappu, R.V. CAMELOT: A machine learning approach for coarse-grained simulations of aggregation of block-copolymeric protein sequences. J. Chem. Phys. 2015, 143, 243123. [Google Scholar] [CrossRef]
- Chong, S.H.; Ham, S. Impact of chemical heterogeneity on protein self-assembly in water. Proc. Natl. Acad. Sci. USA 2019, 116, 13744–13753. [Google Scholar] [CrossRef]
- Patel, A.; Lee, H.O.; Jawerth, L.; Maharana, S.; Jahnel, M.; Hein, M.Y.; Stoynov, S.; Mahamid, J.; Saha, S.; Franzmann, T.M.; et al. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell 2015, 162, 1066–1077. [Google Scholar] [CrossRef]
- Vernon, R.M.; Chong, P.A.; Tsang, B.; Kim, T.H.; Bah, A.; Farber, P.; Lin, H.; Forman-Kay, J.D. Pi-Pi contacts are an overlooked protein feature relevant to phase separation. eLife 2018, 7, e31486. [Google Scholar] [CrossRef]
- Nott, T.J.; Petsalaki, E.; Farber, P.; Jervis, D.; Fussner, E.; Plochowietz, A.; Craggs, T.D.; Bazett-Jones, D.P.; Pawson, T.; Forman-Kay, J.D.; et al. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell 2015, 57, 936–947. [Google Scholar] [CrossRef]
- Elbaum-Garfinkle, S.; Kim, Y.; Szczepaniak, K.; Chen, C.C.H.; Eckmann, C.R.; Myong, S.; Brangwynne, C.P. The disordered P granule protein LAF-1 drives phase separation into droplets with tunable viscosity and dynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 7189–7194. [Google Scholar] [CrossRef]
- Pak, C.W.; Kosno, M.; Holehouse, A.S.; Padrick, S.B.; Mittal, A.; Ali, R.; Yunus, A.A.; Liu, D.R.; Pappu, R.V.; Rosen, M.K. Sequence determinants of intracellular phase separation by complex coacervation of a disordered protein. Mol. Cell 2016, 63, 72–85. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chan, H.S. Phase separation and single-chain compactness of charged disordered proteins are strongly correlated. Biophys. J. 2017, 112, 2043–2046. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.M.; Dar, F.; Pappu, R.V. LASSI: A lattice model for simulating phase transitions of multivalent proteins. PLoS Comput. Biol. 2019, 15, e1007028. [Google Scholar] [CrossRef] [PubMed]
- Regy, R.M.; Dignon, G.L.; Zheng, W.; Kim, Y.C.; Mittal, J. Sequence dependent phase separation of protein-polynucleotide mixtures elucidated using molecular simulations. Nucleic Acids Res. 2021, 49, 12593–12603. [Google Scholar] [CrossRef] [PubMed]
- Brady, J.P.; Farber, P.J.; Sekhar, A.; Lin, Y.H.; Huang, R.; Bah, A.; Nott, T.J.; Chan, H.S.; Baldwin, A.J.; Forman-Kay, J.D.; et al. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. USA 2017, 114, E8194–E8203. [Google Scholar] [CrossRef]
- Murthy, A.C.; Dignon, G.L.; Kan, Y.; Zerze, G.H.; Parekh, S.H.; Mittal, J.; Fawzi, N.L. Molecular interactions underlying liquid− liquid phase separation of the FUS low-complexity domain. Nat. Struct. Mol. Biol. 2019, 26, 637–648. [Google Scholar] [CrossRef]
- Lee, C.W.; Ferreon, J.C.; Ferreon, A.C.; Arai, M.; Wright, P.E. Graded enhancement of p53 binding to CREB-binding protein (CBP) by multisite phosphorylation. Proc. Natl. Acad. Sci. USA 2010, 107, 19290–19295. [Google Scholar] [CrossRef]
- Raj, N.; Attardi, L.D. The transactivation domains of the p53 protein. Cold Spring Harb. Perspect. Med. 2017, 7, a026047. [Google Scholar] [CrossRef]
- Laptenko, O.; Shiff, I.; Freed-Pastor, W.; Zupnick, A.; Mattia, M.; Freulich, E.; Shamir, I.; Kadouri, N.; Kahan, T.; Manfredi, J.; et al. The p53 C terminus controls site-specific DNA binding and promotes structural changes within the central DNA binding domain. Mol. Cell 2015, 57, 1034–1046. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Krois, A.S.; Ferreon, J.C.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Recognition of the disordered p53 transactivation domain by the transcriptional adapter zinc finger domains of CREB-binding protein. Proc. Natl. Acad. Sci. USA 2016, 113, E1853–E1862. [Google Scholar] [CrossRef]
- Kussie, P.H.; Gorina, S.; Marechal, V.; Elenbaas, B.; Moreau, J.; Levine, A.J.; Pavletich, N.P. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science 1996, 274, 948–953. [Google Scholar] [CrossRef]
- Mészáros, B.; Simon, I.; Dosztányi, Z. Prediction of protein binding regions in disordered proteins. PLoS Comput. Biol. 2009, 5, e1000376. [Google Scholar] [CrossRef] [PubMed]
- Davey, N.E.; Van Roey, K.; Weatheritt, R.J.; Toedt, G.; Uyar, B.; Altenberg, B.; Budd, A.; Diella, F.; Dinkel, H.; Gibson, T.J. Attributes of short linear motifs. Mol. BioSyst. 2012, 8, 268–281. [Google Scholar] [CrossRef] [PubMed]
- Sreedharan, J.; Blair, I.P.; Tripathi, V.B.; Hu, X.; Vance, C.; Rogelj, B.; Ackerley, S.; Durnall, J.C.; Williams, K.L.; Buratti, E.; et al. TDP-43 mutations in familial and sporadic amyotrophic lateral sclerosis. Science 2008, 319, 1668–1672. [Google Scholar] [CrossRef] [PubMed]
- Kabashi, E.; Valdmanis, P.N.; Dion, P.; Spiegelman, D.; McConkey, B.J.; Vande Velde, C.; Bouchard, J.P.; Lacomblez, L.; Pochigaeva, K.; Salachas, F.; et al. TARDBP mutations in individuals with sporadic and familial amyotrophic lateral sclerosis. Nat. Genet. 2008, 40, 572–574. [Google Scholar] [CrossRef]
- Jiang, L.L.; Che, M.X.; Zhao, J.; Zhou, C.J.; Xie, M.Y.; Li, H.Y.; He, J.H.; Hu, H.Y. Structural transformation of the amyloidogenic core region of TDP-43 protein initiates its aggregation and cytoplasmic inclusion. J. Biol. Chem. 2013, 288, 19614–19624. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Conicella, A.E.; Zerze, G.H.; Mittal, J.; Fawzi, N.L. ALS mutations disrupt phase separation mediated by α-helical structure in the TDP-43 low-complexity C-terminal domain. Structure 2016, 24, 1537–1549. [Google Scholar] [CrossRef]
- Wang, A.; Conicella, A.E.; Schmidt, H.B.; Martin, E.W.; Rhoads, S.N.; Reeb, A.N.; Nourse, A.; Ramirez, D.A.; Ragunathan, K.; Howcroft, J.; et al. A single N-terminal phosphomimic disrupts TDP-43 polymerization, phase separation, and RNA splicing. EMBO J. 2018, 37, e97452. [Google Scholar] [CrossRef]
- Gruijs da Silva, L.A.; Simonetti, F.; Hutten, S.; Riemenschneider, H.; Sternburg, E.L.; Pietrek, L.M.; Gebel, J.; Dotsch, V.; Edbauer, D.; Baumeister, W.; et al. Disease-linked TDP-43 hyperphosphorylation suppresses TDP-43 condensation and aggregation. EMBO J. 2022, 41, e108443. [Google Scholar] [CrossRef]
- McGurk, L.; Gomes, E.; Guo, L.; Mojsilovic-Petrovic, J.; Tran, V.; Kalb, R.G.; Shorter, J.; Bonini, N.M. Poly (ADP-ribose) prevents pathological phase separation of TDP-43 by promoting liquid demixing and stress granule localization. Mol. Cell 2018, 71, 703–717. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically disordered proteins and their “mysterious” (meta) physics. Front. Phys. 2019, 7, 10. [Google Scholar] [CrossRef]
- Hornbeck, P.V.; Zhang, B.; Murray, B.; Kornhauser, J.M.; Latham, V.; Skrzypek, E. PhosphoSitePlus, 2014: Mutations, PTMs and recalibrations. Nucleic Acids Res. 2015, 43, D512–D520. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.; Thornton, J.M. Principles of protein-protein interactions. Proc. Natl. Acad. Sci. USA 1996, 93, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Moal, I.H.; Fernández-Recio, J. SKEMPI: A Structural Kinetic and Energetic database of Mutant Protein Interactions and its use in empirical models. Bioinformatics 2012, 28, 2600–2607. [Google Scholar] [CrossRef] [PubMed]
- Mittal, J.; Best, R.B. Thermodynamics and kinetics of protein folding under confinement. Proc. Natl. Acad. Sci. USA 2008, 105, 20233–20238. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The protein-folding problem, 50 years on. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef]
- Tanford, C. Protein denaturation. Adv. Protein Chem. 1968, 23, 121–282. [Google Scholar] [CrossRef]
- Borcherds, W.; Bremer, A.; Borgia, M.B.; Mittag, T. How do intrinsically disordered protein regions encode a driving force for liquid-liquid phase separation? Curr. Opin. Struct. Biol. 2021, 67, 41–50. [Google Scholar] [CrossRef]
- Monahan, Z.; Ryan, V.H.; Janke, A.M.; Burke, K.A.; Rhoads, S.N.; Zerze, G.H.; O’Meally, R.; Dignon, G.L.; Conicella, A.E.; Zheng, W.; et al. Phosphorylation of the FUS low-complexity domain disrupts phase separation, aggregation, and toxicity. EMBO J. 2017, 36, 2951–2967. [Google Scholar] [CrossRef]
- Ryan, V.H.; Dignon, G.L.; Zerze, G.H.; Chabata, C.V.; Silva, R.; Conicella, A.E.; Amaya, J.; Burke, K.A.; Mittal, J.; Fawzi, N.L. Mechanistic view of hnRNPA2 low-complexity domain structure, interactions, and phase separation altered by mutation and arginine methylation. Mol. Cell 2018, 69, 465–479. [Google Scholar] [CrossRef]
- Staller, M.V.; Holehouse, A.S.; Swain-Lenz, D.; Das, R.K.; Pappu, R.V.; Cohen, B.A. A high-throughput mutational scan of an intrinsically disordered acidic transcriptional activation domain. Cell Syst. 2018, 6, 444–455. [Google Scholar] [CrossRef]
- Boija, A.; Klein, I.A.; Sabari, B.R.; Dall’Agnese, A.; Coffey, E.L.; Zamudio, A.V.; Li, C.H.; Shrinivas, K.; Manteiga, J.C.; Hannett, N.M.; et al. Transcription factors activate genes through the phase-separation capacity of their activation domains. Cell 2018, 175, 1842–1855. [Google Scholar] [CrossRef] [PubMed]
- Sabari, B.R.; Dall’Agnese, A.; Boija, A.; Klein, I.A.; Coffey, E.L.; Shrinivas, K.; Abraham, B.J.; Hannett, N.M.; Zamudio, A.V.; Manteiga, J.C.; et al. Coactivator condensation at super-enhancers links phase separation and gene control. Science 2018, 361, eaar3958. [Google Scholar] [CrossRef] [PubMed]
- Cho, W.K.; Spille, J.H.; Hecht, M.; Lee, C.; Li, C.; Grube, V.; Cisse, I.I. Mediator and RNA polymerase II clusters associate in transcription-dependent condensates. Science 2018, 361, 412–415. [Google Scholar] [CrossRef]
- Guo, Y.E.; Manteiga, J.C.; Henninger, J.E.; Sabari, B.R.; Dall’Agnese, A.; Hannett, N.M.; Spille, J.H.; Afeyan, L.K.; Zamudio, A.V.; Shrinivas, K.; et al. Pol II phosphorylation regulates a switch between transcriptional and splicing condensates. Nature 2019, 572, 543–548. [Google Scholar] [CrossRef]
- Qian, D.; Michaels, T.C.; Knowles, T.P. Analytical solution to the Flory-Huggins model. J. Phys. Chem. Lett. 2022, 13, 7853–7860. [Google Scholar] [CrossRef]
- Huggins, M.L. Theory of solutions of high polymers. J. Am. Chem. Soc. 1942, 64, 1712–1719. [Google Scholar] [CrossRef]
- Dignon, G.L.; Zheng, W.; Best, R.B.; Kim, Y.C.; Mittal, J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2018, 115, 9929–9934. [Google Scholar] [CrossRef]
- Tesei, G.; Trolle, A.I.; Jonsson, N.; Betz, J.; Knudsen, F.E.; Pesce, F.; Johansson, K.E.; Lindorff-Larsen, K. Conformational ensembles of the human intrinsically disordered proteome. Nature 2024, 626, 897–904. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.J.; McGuffin, L.J.; Bryson, K.; Buxton, B.F.; Jones, D.T. The DISOPRED server for the prediction of protein disorder. Bioinformatics 2004, 20, 2138–2139. [Google Scholar] [CrossRef]
- Hein, M.Y.; Hubner, N.C.; Poser, I.; Cox, J.; Nagaraj, N.; Toyoda, Y.; Gak, I.A.; Weisswange, I.; Bauer, G.; Zarnack, K.; et al. A human interactome in three quantitative dimensions organized by stoichiometries and abundances. Cell 2015, 163, 712–723. [Google Scholar] [CrossRef]
- Hnisz, D.; Shrinivas, K.; Young, R.A.; Chakraborty, A.K.; Sharp, P.A. A phase separation model for transcriptional control. Cell 2017, 169, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Brangwynne, C.P. Liquid phase condensation in cell physiology and disease. Science 2017, 357, eaaf4382. [Google Scholar] [CrossRef] [PubMed]
- Matlock, M.K.; Holehouse, A.S.; Naegle, K.M. ProteomeScout: A repository and analysis resource for post-translational modifications and proteins. Nucleic Acids Res. 2015, 43, D521–D530. [Google Scholar] [CrossRef] [PubMed]
- Reimand, J.; Wagih, O.; Bader, G.D. The mutational landscape of phosphorylation signaling in cancer. Sci. Rep. 2013, 3, 2651. [Google Scholar] [CrossRef]
- Gomes, E.; Shorter, J. The molecular language of membraneless organelles. J. Biol. Chem. 2019, 294, 7115–7127. [Google Scholar] [CrossRef]
- Protter, D.S.; Rao, B.S.; Van Treeck, B.; Lin, Y.; Mizoue, L.; Rosen, M.K.; Parker, R. Intrinsically disordered regions can contribute promiscuous interactions to RNP granule assembly. Cell Rep. 2018, 22, 1401–1412. [Google Scholar] [CrossRef]
- Bah, A.; Forman-Kay, J.D. Modulation of intrinsically disordered protein function by post-translational modifications. J. Biol. Chem. 2016, 291, 6696–6705. [Google Scholar] [CrossRef]
- Staller, M.V.; Ramirez, E.; Kotha, S.R.; Holehouse, A.S.; Pappu, R.V.; Cohen, B.A. Directed mutational scanning reveals a balance between acidic and hydrophobic residues in strong human activation domains. Cell Syst. 2022, 13, 334–345. [Google Scholar] [CrossRef]
- Brzovic, P.S.; Heikaus, C.C.; Kisselev, L.; Vernon, R.; Herbig, E.; Pacheco, D.; Warfield, L.; Littlefield, P.; Baker, D.; Klevit, R.E.; et al. The acidic transcription activator Gcn4 binds the mediator subunit Gal11/Med15 using a simple protein interface forming a fuzzy complex. Mol. Cell 2011, 44, 942–953. [Google Scholar] [CrossRef]
- Warfield, L.; Tuttle, L.M.; Pacheco, D.; Klevit, R.E.; Hahn, S. A sequence-specific transcription activator motif and powerful synthetic variants that bind Mediator using a fuzzy protein interface. Proc. Natl. Acad. Sci. USA 2014, 111, E3506–E3513. [Google Scholar] [CrossRef]
- Tuttle, L.M.; Pacheco, D.; Warfield, L.; Luo, J.; Ranish, J.; Hahn, S.; Klevit, R.E. Gcn4-mediator specificity is mediated by a large and dynamic fuzzy protein-protein complex. Cell Rep. 2018, 22, 3251–3264. [Google Scholar] [CrossRef] [PubMed]
- Piskacek, M.; Havelka, M.; Rezacova, M.; Knight, A. The 9aaTAD transactivation domains: From Gal4 to p53. PLoS ONE 2016, 11, e0162842. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, G.R.; Schreiber, S.L. Three-part inventions: Intracellular signaling and induced proximity. Trends Biochem. Sci. 2011, 36, 130–137. [Google Scholar] [CrossRef]
- Schreiber, S.L. The rise of molecular glues. Cell 2021, 184, 3–9. [Google Scholar] [CrossRef]
- Klein, I.A.; Boija, A.; Afeyan, L.K.; Hawken, S.W.; Fan, M.; Dall’Agnese, A.; Oksuz, O.; Henninger, J.E.; Shrinivas, K.; Sabari, B.R.; et al. Partitioning of cancer therapeutics in nuclear condensates. Science 2020, 368, 1386–1392. [Google Scholar] [CrossRef]
- Schmidt, H.B.; Barreau, A. Phase separation-deficient TDP43 remains functional in splicing. Nat. Commun. 2019, 10, 4890. [Google Scholar] [CrossRef]
- Kim, T.H.; Payliss, B.J.; Nosella, M.L.; Lee, I.T.; Toyama, Y.; Forman-Kay, J.D.; Kay, L.E. Interaction hot spots for phase separation revealed by NMR studies of a CAPRIN1 condensed phase. Proc. Natl. Acad. Sci. USA 2021, 118, e2104897118. [Google Scholar] [CrossRef]
- Bugge, K.; Brakti, I.; Fernandes, C.B.; Dreier, J.E.; Lundsgaard, J.E.; Olsen, J.G.; Skriver, K.; Kragelund, B.B. Interactions by disorder--a matter of context. Front. Mol. Biosci. 2020, 7, 110. [Google Scholar] [CrossRef]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef]
- Kiefhaber, T.; Bachmann, A.; Jensen, K.S. Dynamics and mechanisms of coupled protein folding and binding reactions. Curr. Opin. Struct. Biol. 2012, 22, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M.; Tompa, P. Fuzzy complexes: A more stochastic view of protein function. Adv. Exp. Med. Biol. 2012, 725, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mollica, L.; Bessa, L.M.; Hanoulle, X.; Jensen, M.R.; Blackledge, M.; Schneider, R. Binding mechanisms of intrinsically disordered proteins: Theory, simulation, and experiment. Front. Mol. Biosci. 2016, 3, 52. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef]
- Schreiber, G.; Haran, G.; Zhou, H.X. Fundamental aspects of protein− protein association kinetics. Chem. Rev. 2009, 109, 839–860. [Google Scholar] [CrossRef]
- Zhou, H.X.; Bates, P.A. Modeling protein association mechanisms and kinetics. Curr. Opin. Struct. Biol. 2013, 23, 887–893. [Google Scholar] [CrossRef]
- Okur, H.I.; Hladílková, J.; Rembert, K.B.; Cho, Y.; Heyda, J.; Dzubiella, J.; Cremer, P.S.; Jungwirth, P. Beyond the Hofmeister series: Ion-specific effects on proteins and their biological functions. J. Phys. Chem. B 2017, 121, 1997–2014. [Google Scholar] [CrossRef]
- Rivas, G.; Minton, A.P. Macromolecular crowding in vitro, in vivo, and in between. Trends Biochem. Sci. 2016, 41, 970–981. [Google Scholar] [CrossRef]
- Zhou, H.X.; Rivas, G.; Minton, A.P. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008, 37, 375–397. [Google Scholar] [CrossRef]
- Nerenberg, P.S.; Head-Gordon, T. New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol. 2018, 49, 129–138. [Google Scholar] [CrossRef]
- Piana, S.; Robustelli, P.; Tan, D.; Chen, S.; Shaw, D.E. Development of a force field for the simulation of single-chain proteins and protein--protein complexes. J. Chem. Theory Comput. 2020, 16, 2494–2507. [Google Scholar] [CrossRef] [PubMed]
- Hunter, C.A.; Sanders, J.K. The nature of π-π interactions. J. Am. Chem. Soc. 1990, 112, 5525–5534. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Vitalis, A.; Pappu, R.V. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef]
- Moses, D.; Yu, F.; Ginell, G.M.; Shamoon, N.M.; Koenig, P.S.; Holehouse, A.S.; Sukenik, S. Revealing the hidden sensitivity of intrinsically disordered proteins to their chemical environment. J. Phys. Chem. Lett. 2020, 11, 10131–10136. [Google Scholar] [CrossRef]
- Wei, M.T.; Elbaum-Garfinkle, S.; Holehouse, A.S.; Chen, C.C.H.; Feric, M.; Arnold, C.B.; Priestley, R.D.; Pappu, R.V.; Brangwynne, C.P. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem. 2017, 9, 1118–1125. [Google Scholar] [CrossRef]
- Alberti, S.; Gladfelter, A.; Mittag, T. Considerations and challenges in studying liquid-liquid phase separation and biomolecular condensates. Cell 2019, 176, 419–434. [Google Scholar] [CrossRef]
- McSwiggen, D.T.; Mir, M.; Darzacq, X.; Tjian, R. Evaluating phase separation in live cells: Diagnosis, caveats, and functional consequences. Genes Dev. 2019, 33, 1619–1634. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Mittag, T.; Pappu, R.V. A conceptual framework for understanding phase separation and addressing open questions and challenges. Mol. Cell 2022, 82, 2201–2214. [Google Scholar] [CrossRef]
- Darling, A.L.; Uversky, V.N. Intrinsic disorder and posttranslational modifications: The darker side of the biological dark matter. Front. Genet. 2018, 9, 158. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zheng, W.; Freddolino, P.L.; Zhang, Y. MetaGO: Predicting gene ontology of non-homologous proteins through low-resolution protein structure prediction and protein--protein network mapping. J. Mol. Biol. 2018, 430, 2256–2265. [Google Scholar] [CrossRef] [PubMed]
- Radivojac, P.; Clark, W.T.; Oron, T.R.; Schnoes, A.M.; Wittkop, T.; Sokolov, A.; Graim, K.; Funk, C.; Verspoor, K.; Ben-Hur, A.; et al. A large-scale evaluation of computational protein function prediction. Nat. Methods 2013, 10, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Oron, T.R.; Clark, W.T.; Bankapur, A.R.; D’Andrea, D.; Lepore, R.; Funk, C.S.; Kahanda, I.; Verspoor, K.M.; Ben-Hur, A.; et al. An expanded evaluation of protein function prediction methods shows an improvement in accuracy. Genome Biol. 2016, 17, 184. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-grained protein models and their applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Ingólfsson, H.I.; Lopez, C.A.; Uusitalo, J.J.; de Jong, D.H.; Gopal, S.M.; Periole, X.; Marrink, S.J. The power of coarse graining in biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 225–248. [Google Scholar] [CrossRef]
- Bernardi, R.C.; Melo, M.C.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2015, 1850, 872–877. [Google Scholar] [CrossRef]
- González, M.A. Force fields and molecular dynamics simulations. École Thématique De La Société Française De La Neutron. 2011, 12, 169–200. [Google Scholar] [CrossRef]
- Monticelli, L.; Tieleman, D.P. Force fields for classical molecular dynamics. In Biomolecular Simulations; Humana Press: Totowa, NJ, USA, 2013; pp. 197–213. [Google Scholar] [CrossRef]
- Freddolino, P.L.; Harrison, C.B.; Liu, Y.; Schulten, K. Challenges in protein-folding simulations. Nat. Phys. 2010, 6, 751–758. [Google Scholar] [CrossRef]
- Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The protein folding problem. Annu. Rev. Biophys. 2008, 37, 289–316. [Google Scholar] [CrossRef]
- Zhang, Y. Progress and challenges in protein structure prediction. Curr. Opin. Struct. Biol. 2008, 18, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)--Round XII. Proteins: Struct. Funct. Bioinform. 2018, 86, 7–15. [Google Scholar] [CrossRef] [PubMed]
- McGuffee, S.R.; Elcock, A.H. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 2010, 6, e1000694. [Google Scholar] [CrossRef]
- Feig, M.; Harada, R.; Mori, T.; Yu, I.; Takahashi, K.; Sugita, Y. Complete atomistic model of a bacterial cytoplasm for integrating physics, biochemistry, and systems biology. J. Mol. Graph. Model. 2015, 58, 1–9. [Google Scholar] [CrossRef]
- Yu, I.; Mori, T.; Ando, T.; Harada, R.; Jung, J.; Sugita, Y.; Feig, M. Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. eLife 2016, 5, e19274. [Google Scholar] [CrossRef]
- Levy, Y.; Wolynes, P.G.; Onuchic, J.N. Protein topology determines binding mechanism. Proc. Natl. Acad. Sci. USA 2004, 101, 511–516. [Google Scholar] [CrossRef]
- Hammes, G.G.; Chang, Y.C.; Oas, T.G. Conformational selection or induced fit: A flux description of reaction mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 13737–13741. [Google Scholar] [CrossRef]
- Voelz, V.A.; Bowman, G.R.; Beauchamp, K.; Pande, V.S. Molecular simulation of ab initio protein folding for a millisecond folder NTL9 (1–39). J. Am. Chem. Soc. 2010, 132, 1526–1528. [Google Scholar] [CrossRef]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Roux, B.; Weare, J. On the statistical equivalence of restrained-ensemble simulations with the maximum entropy method. J. Chem. Phys. 2013, 138, 084107. [Google Scholar] [CrossRef]
- Pancsa, R.; Tompa, P. Structural disorder in eukaryotes. PLoS ONE 2012, 7, e34687. [Google Scholar] [CrossRef] [PubMed]
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Levy, R.M.; Haris, S.A.; Karplus, M. Molecular dynamics simulations of an α-helix in water: Solvation and dynamical aspects. Biochim. Biophys. Acta (BBA)-Protein Struct. 1979, 577, 177–189. [Google Scholar]




| Method | System Studied | Prediction Type | Experimental Validation | Accuracy/Agreement | Computational Time | Reference |
|---|---|---|---|---|---|---|
| FINCHES | FUS LCD variants | Phase diagrams | Y→S mutations prevent LLPS | r = 0.91 for Tc prediction | 1 s per variant | [4] |
| CALVADOS | hnRNPA1 LCD | Phase behavior | Aromatic mutant effects | r = 0.89 for phase boundaries | 2 h per system | [17] |
| All-atom MD | p53 TAD | Binding mechanism | NMR chemical shifts | RMSD = 2.1 Å from experiment | 5 days per trajectory | [32] |
| PSPredictor | Stress granule proteins | Binary classification | Localization experiments | 85% accuracy (239 proteins) | 0.1 s per protein | [56] |
| PLAAC | TDP-43 variants | Prion-like propensity | Aggregation assays | 79% for ALS mutations | 0.05 s per protein | [70] |
| FuzDrop | RNA-binding proteins | Droplet regions | Fluorescence microscopy | 92% sensitivity | 1 s per protein | [74] |
| AWSEM | α-synuclein | Aggregation pathway | Fiber morphology | Correct fibril structure | 12 h per trajectory | [38] |
| Field Theory | Elastin-like polypeptides | Critical temperature | Turbidity measurements | ±5 K accuracy | 10 min per system | [53] |
| Method | System Size | Time per Prediction | Scalability | Hardware Requirements |
|---|---|---|---|---|
| FINCHES | Any sequence | 0.001 s | Linear with the sequence length | Standard CPU |
| CALVADOS | 1–10 proteins | 1–10 h | Quadratic with system size | GPU recommended |
| All-atom MD | 1–5 proteins | 1–100 days | Exponential with system size | Specialized clusters |
| PSPredictor | Single protein | 0.1 s | Constant | Standard CPU |
| PLAAC | Single protein | 0.05 s | Linear | Standard CPU |
| FuzDrop | Single protein | 1 s | Linear | Standard CPU |
| Field Theory | Parameter space | 10–60 min | Linear with parameters | Standard CPU |
| Prediction Type | FINCHES | CALVADOS | PSPredictor | Field Theory | All-Atom MD |
|---|---|---|---|---|---|
| Phase Separation Binary | 87% correct | 94% correct | 85% correct | 91% correct | N/A |
| Critical Temperature | r = 0.85 | r = 0.91 | N/A | r = 0.78 | N/A |
| Interface Prediction | 73% agreement | N/A | N/A | N/A | 89% agreement |
| Mutation Effects | 82% correct | 88% correct | 45% (poor) | N/A | N/A |
| System | Experimental Observation | FINCHES Prediction | Agreement | Reference |
|---|---|---|---|---|
| FUS LCD variants | Y→S mutations prevent phase separation | Highly repulsive ε values for Y→S | Excellent | [135] |
| DDX4-NTD | R2K variant shows reduced condensation | Reduced attractive interactions | Good | [130] |
| TDP-43 LCD | Phosphorylation suppresses aggregation | Weakened attractive interactions | Excellent | [135] |
| hnRNPA1 LCD | Aromatic mutations alter phase behavior | Predicted phase diagram changes | Good | [137] |
| Transcription factors | AD strength correlates with coactivator binding | ε values with Gal11 correlate with activity | Good | [157] |
| CAPRIN-1 | Salt enhances phase separation | Reduced repulsion at higher salt | Good | [165] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niazi, S.K. FINCHES: A Computational Framework for Predicting Intermolecular Interactions in Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2025, 26, 6246. https://doi.org/10.3390/ijms26136246
Niazi SK. FINCHES: A Computational Framework for Predicting Intermolecular Interactions in Intrinsically Disordered Proteins. International Journal of Molecular Sciences. 2025; 26(13):6246. https://doi.org/10.3390/ijms26136246
Chicago/Turabian StyleNiazi, Sarfaraz K. 2025. "FINCHES: A Computational Framework for Predicting Intermolecular Interactions in Intrinsically Disordered Proteins" International Journal of Molecular Sciences 26, no. 13: 6246. https://doi.org/10.3390/ijms26136246
APA StyleNiazi, S. K. (2025). FINCHES: A Computational Framework for Predicting Intermolecular Interactions in Intrinsically Disordered Proteins. International Journal of Molecular Sciences, 26(13), 6246. https://doi.org/10.3390/ijms26136246






